1. Introduction
Farmers face a complicated task managing resources and performing sustainable agricultural production [
1]. Decisions regarding planning, purchasing and the application of mechanical units comprise a major part of farm management. The choice of machinery unit often does not correspond to the farm’s needs, thus leading to various adverse impacts [
2]. Farm machinery parameters are mainly overestimated with the purpose of arriving at greater efficiencies and increased productivity. Dimensional and functional excess of different parameters can significantly impact the farm economic output and expected results. Overestimated consideration of the main parameters, such as mass and power, can promote an increase in soil compaction and CO
2 emissions [
3,
4,
5,
6]. Additionally, a considerable rise in parameters requires more massive investments and more significant farm costs [
7,
8,
9]. Rational distribution of resources and optimization of costs is needed to ensure farm productivity, yield, farm income and environmental protection (CAP 2020) [
10,
11]. To support management and planning of balanced decisions, regulatory mechanisms and measures for appropriate and proportionate agricultural machinery selection are needed [
10,
12,
13,
14]. Prediction models, farm management software and optimization tools replace the traditional drivers of the selection procedure, leading to a better fleet organization and planning methodology [
13,
14,
15,
16]. Forecasting models for optimization of machinery unit’s selection provide an economically viable and environmentally sustainable solution and lead to the simplification of the decision-making process [
17,
18,
19]. Following the latter concept, a large study was carried out (5000 models of machinery included) on the development and implementation of reference models for main agricultural machinery groups [
20,
21,
22]. Reference models predicting main functional parameters and price were developed for sowing, spraying and harvesting operations. The current study focuses on soil cultivation implements, completing the main groups of agricultural operations for crop cultivation, allowing prediction analyses to be performed and fleet planning and farm management to be undertaken.
Operating parameters and performance of tillage implements have a primary impact on the economic output of the soil cultivation. Cost of tillage operations largely depends on the tillage method (conventional, reduced, minimum tillage), cropping program (continuous cropping and crop fallow) and is influenced by farm size and operation time. According to Bauer and McEvoy (1990), differences between tillage methods has greater economic impact than agronomic, and there is a need of a consideration of the fact of cost differences between tillage systems during the planning stage [
23]. Indeed, literature provides comparison studies related to the tillage method’s economic benefits [
1,
23,
24]. However, despite the degree of applied mechanical intervention, investment costs for the soil cultivation machinery are still considerable.
The effectiveness of the operation largely depends on the association between tractor and implement and operational adjustment (traction-assist system, hitching, uniform and adequate penetration of the tools and depth of operation). Power source requirements for the operation change depending on the depth of operation, degree of pulverization, forward speed, shape of the working element, soil structure, etc. The type of the power supply varies as well based on the tillage equipment (power take-off, drawbar). A balanced adjustment of parameters and their correct application play a critical role in the use of available power (working width, speed) [
25].
The selection of machinery and implement requires consideration and understanding of soil conditions as well. Soil conditions guarantee the plant growth and profitable yield. Heavy machines and wheels’ load can create soil stress and lead to soil compaction. Moreover, during conventional tillage operation, the wheel load is increased by approximately 25% due to the mass redistribution and draft force of the implement [
3]. The impact of historical increase of the weight of the machinery on the soil qualities has been studied by Keller et al. (2019). The study showed that vehicle weights’ historical expansion increased subsoil compaction levels and led to higher costs [
3,
26]: in the last 50 years, the load of tractors has increased by 3 tonnes [
3]. The increase of the agricultural machinery load (during the last century) led to the rise of pressure at the soil surface by approximately 10 times (at 0.5 m depth) [
5]. The issue was addressed by Lassen et al. (2013) with the development of the soil stress distribution, compaction evaluation and simulation model Terranimo [
26]. The model allows soil stress to be calculated for a specific machine and implement, and therefore the possible overload during operation to be avoided. Therefore, consideration of dimensions and prevention of the possible consequences of chosen parameters are needed during tractor/implement selection and operation [
27,
28]. Thanks to the machinery unit’s proper operation, justification of the higher investment on larger equipment can be compensated by an increase of efficiency and reduction of fixed costs [
29]. However, poor mechanical skills and insufficient resources make it difficult to achieve or practice effective soil cultivation, leading to the notable economic side effects and impacting return of investment.
Solutions such as controlled traffic farming allow having a better understanding of the field work, the performance of the machinery and better plan the cultivation. However, there are still visible limitations to the proper selection of units and, afterwards, the management of existing mechanical and financial resources and definition of reference price boundaries. Decisions regarding fleet renewal and selection of machinery unit are linked to the preliminary estimation of the parameters based on the actual farm needs and, therefore, the corresponding definition of the related investments. Farmers lack the basic information related to the parameter’s relation, their selection and association importance, investment planning tools and supportive methods. The relation of the functional parameters to the price of the machinery is almost not even discussed. It is clear that a farmer cannot impact the machinery unit’s cost, but to avoid this overestimation of the investment can be performed. The relevant studies regarding the functional and operational parameters have narrow spectrum of application: mainly they refer to a specific crop cultivation, consider a unique implement or even the working element of the implement, what makes it complicated to widen the results of the experiments and methods for general application [
30,
31,
32,
33,
34,
35,
36,
37]. The other biggest limitation is the complexity of the proposed solutions, they are too sophisticated for the farmer to use. In particular, regarding farm machinery selection and cost prediction, most of the models are considering only economic aspects of the operation and corresponding involvement of a machine or have very complex algorithms that require special knowledge/software/skills for their application. Available agricultural machinery management standards, models and cost calculators (e.g., ASAE, AMACA, etc.) mainly refer to the machinery cost determination and calculation/prediction of variable and fixed costs [
38,
39,
40], and operation expenses in general, thus bypassing the machinery price definition, which indeed has fundamental importance for farmers, for the investment planning and farm management. Moreover, for such calculations the price of the machinery unit is considered as input data [
40].
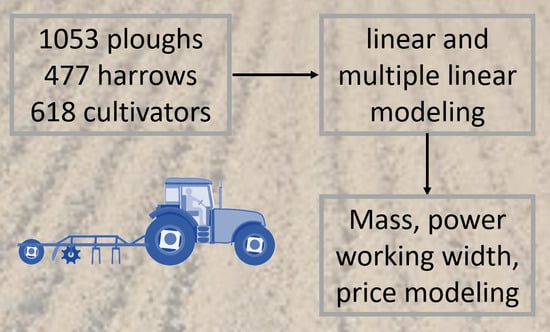
In the current study, the main technical parameters of tillage implements were analyzed with the purpose to investigate their possible intercorrelations and impact on the price, to develop reference models for the prediction of machine price, power, mass, and working width, thus facilitating the simplification of the machinery selection process and optimizing the decision-making process.
2. Materials and Methods
The study relies on a statistical analysis of functional parameters and price of implements for soil cultivation, seedbed preparation and weed control. For that reason, a large database was created based on the collection and processing of machinery specifications and performance-related technical characteristics of tillage implements available in the European market. Data were based on the models provided from 27 leading agricultural machinery constructors (Amazone, KUHN, Kverneland, Pottinger, Nardi, Sfoggia, etc.) representing 8 countries including Austria, United Kingdom, Italy, Norway, Denmark, etc. Data were collected from available agricultural machinery producers, agricultural machinery associations, open-source databases and continuously updated in collaboration with Informatore Agrario srl. (Verona, Italy).
The database populated by 2148 models includes large variability in commercial-scale cultivation equipment for a complete performance of tillage practices mainly following the conventional treatment. The database has been subsequently split into sub-datasets adapted to cultivation approach. Three groups of tillage implements were created based on the adopted mechanical interventions of soil: primary tillage (plough, 1053 models), secondary tillage and seedbed preparation (harrow, 477 models), after mechanical cultivation treatment and weed control (cultivators, 618 models). The relevant technical, dimensional and performance parameters and general implement information have been merged, properly filtered and sorted (
Table 1).
The collected complete information related to each model underwent relevance assessment and parameters impacting price formation. Thus, power, mass, working width and list price of tillage implements are the main parameters included in the analysis. The studied samples represent the basic design and structure provided by the manufacturing companies.
Broad inclusion of the models in the dataset, presented by various constructors from different countries, provides a complete overview of the available market of the implements and can be considered reliable for prediction analysis and modelling parameters and price. The range of maximum and minimum values of relevant parameters is summarized in
Table 2.
Implements for primary tillage include 1053 models of mounted, semi-mounted and trailed ploughs with the depth of the cultivation from 0.25 to 0.7 m and up to 4 m of working width. The dataset involves a variation of the different types and design of working elements (up to 9 elements) requiring up to 270 kW power availability. The second dataset involves 477 models of harrows for secondary tillage and seedbed preparation. Data collected cover harrows with disc, tooth, knife, vertical rotor, anchor type functional elements providing up to 9 m working width. The last group of implements include a combination of cultivators, row crop cultivators, rotary tillers and strip-tillers mainly for weed control, cut of surface residuals, soil pulverization, etc.
As previously mentioned, the analyses of tillage implements presented in this work are a part of a larger investigation that involve multiple agricultural machinery groups [
20,
21,
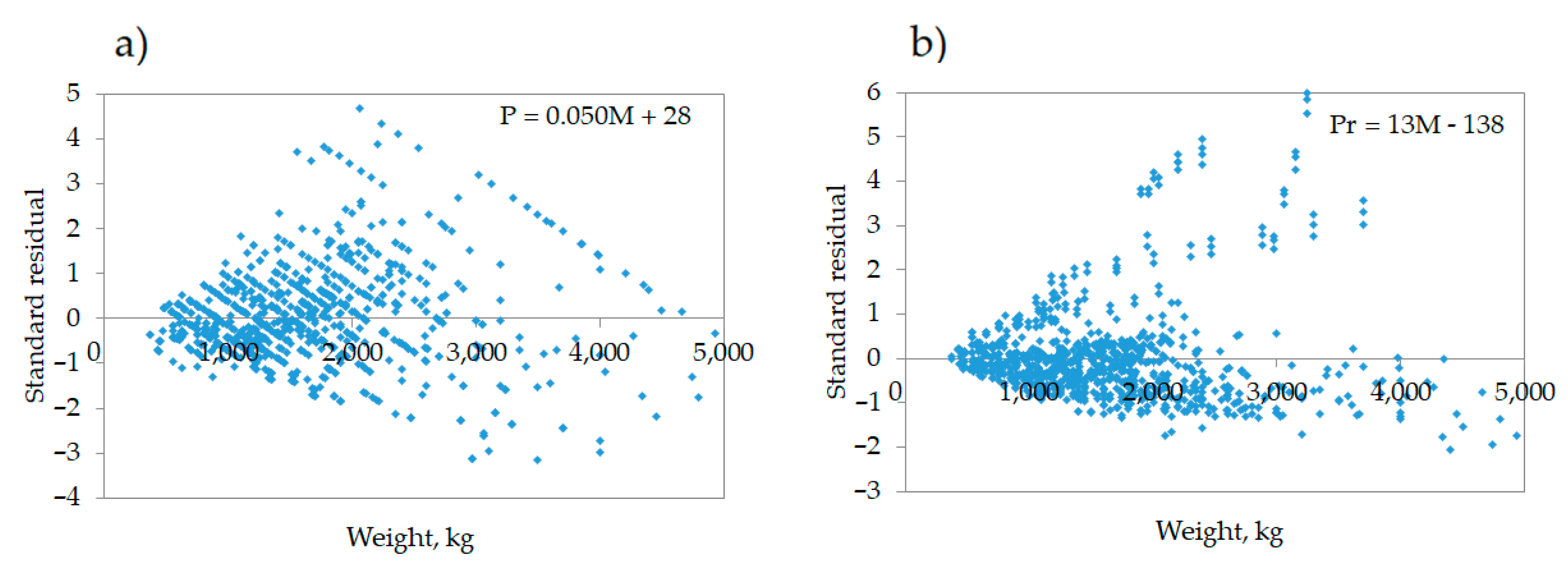
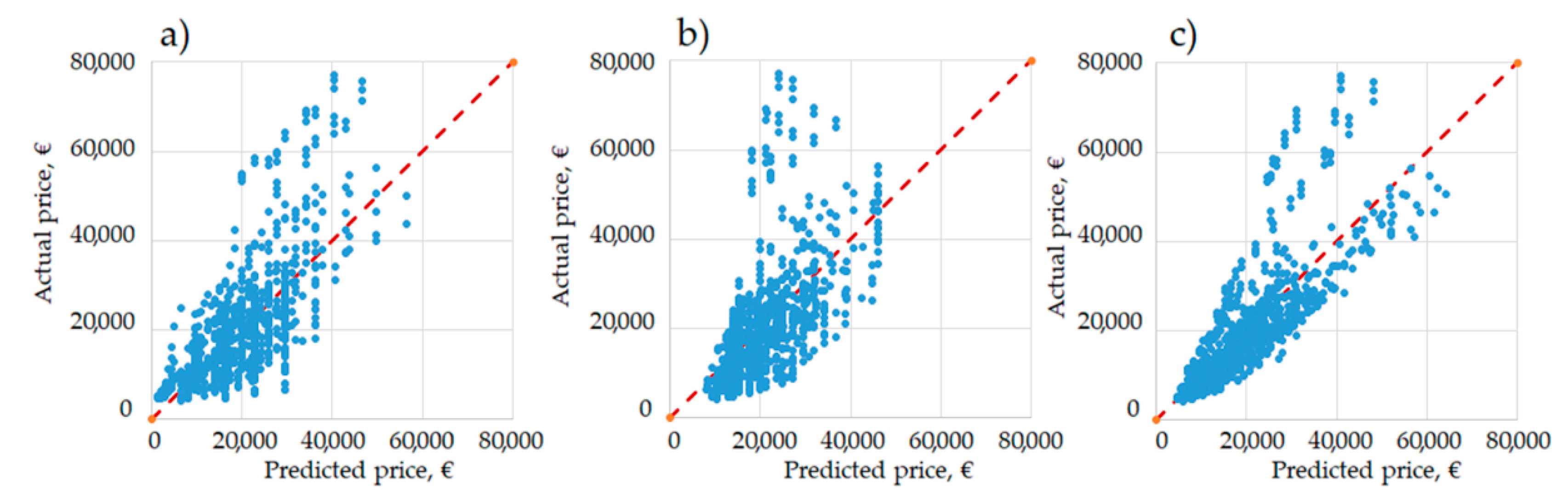
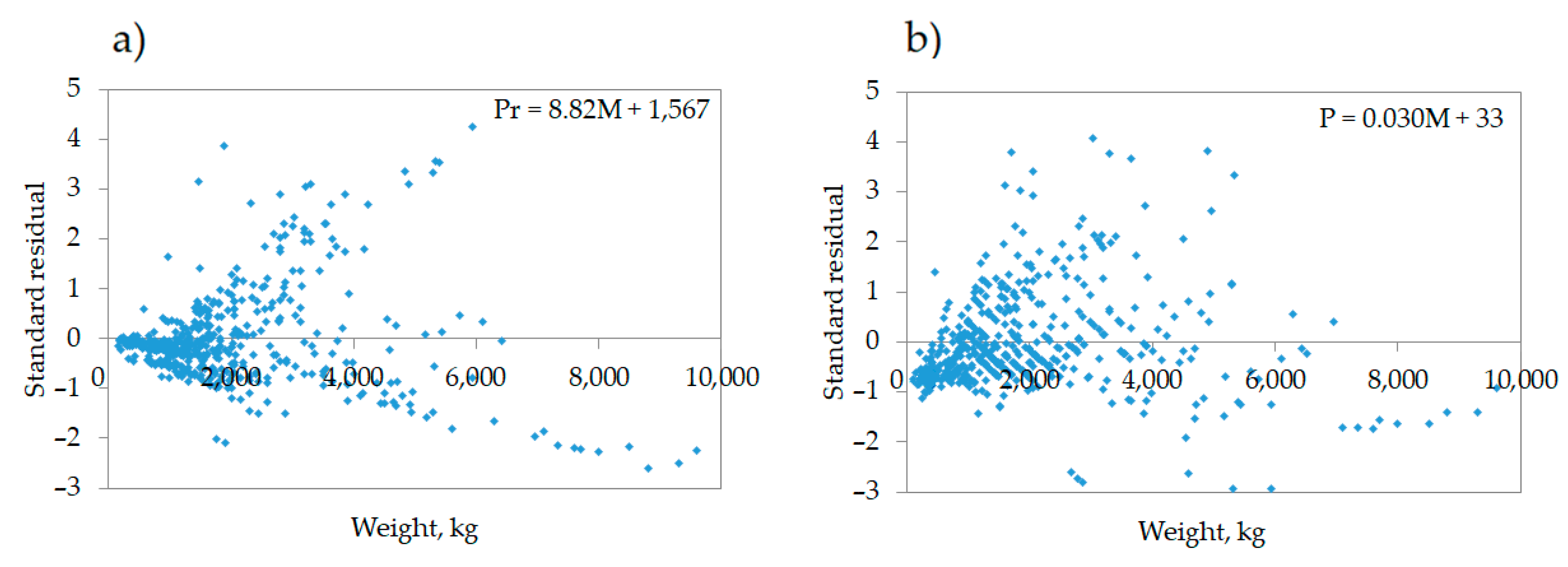
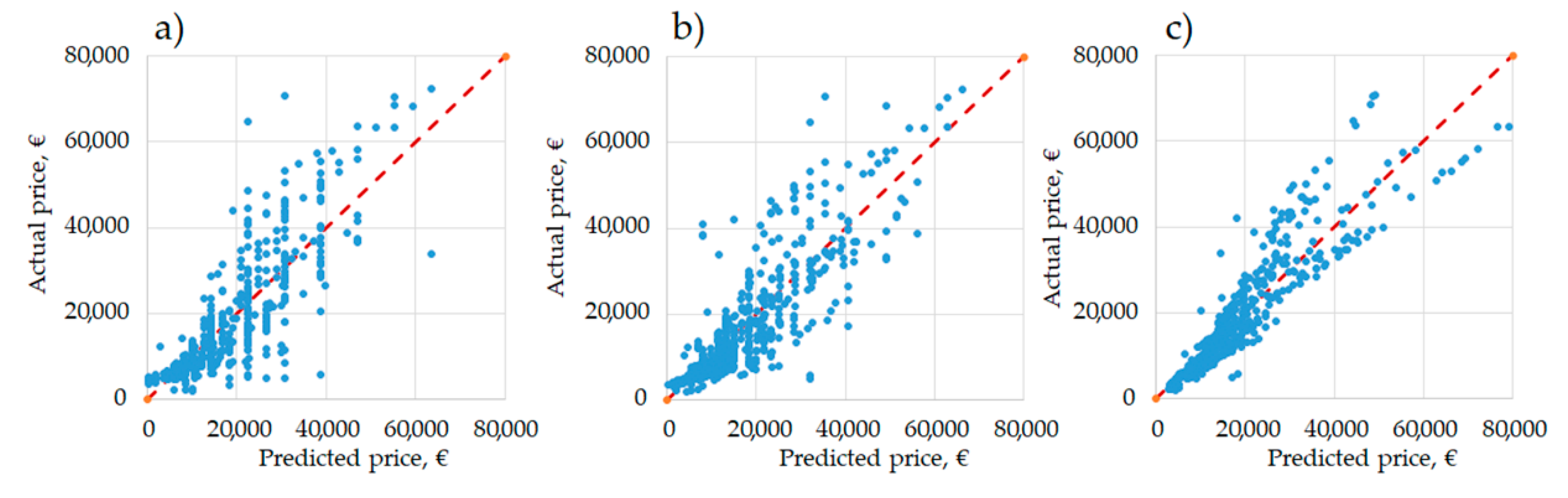
22]. The approach that has been used in analyzing the datasets of these studies involves the use of linear, multiple linear and second degree regression analyses to model the relation between variables and to evaluate the relevance of the model parameters. The choice of using linear, multi-linear and second degree modeling is explained by the need to obtain simplified models between the predictors and the price. Despite linear models having lower predicting capabilities compared to, e.g., stepwise regression analyses, their ease of use is a key factor for practical decision-making applications, especially if the aim is to simply obtain rough preliminary estimates. Instead, to obtain more accurate models and prediction of the parameters and price, stepwise regression analyses are used. Applied backward elimination method allows to evaluate the statistical significance of each independent variable included in the model analysis (power, mass, working width) and their relation to the response variable (e.g., price) providing more accurate and robust values. Therefore, multiple linear models have more complex structure and take into consideration more than one parameter, which guarantees higher predictive qualities. Also second degree regressions are reported, which however show only marginal increment of the prediction ability.
The statistical analyses were done with Microsoft Excel (Microsoft Corporation, Redmond, WA, USA).
4. Conclusions
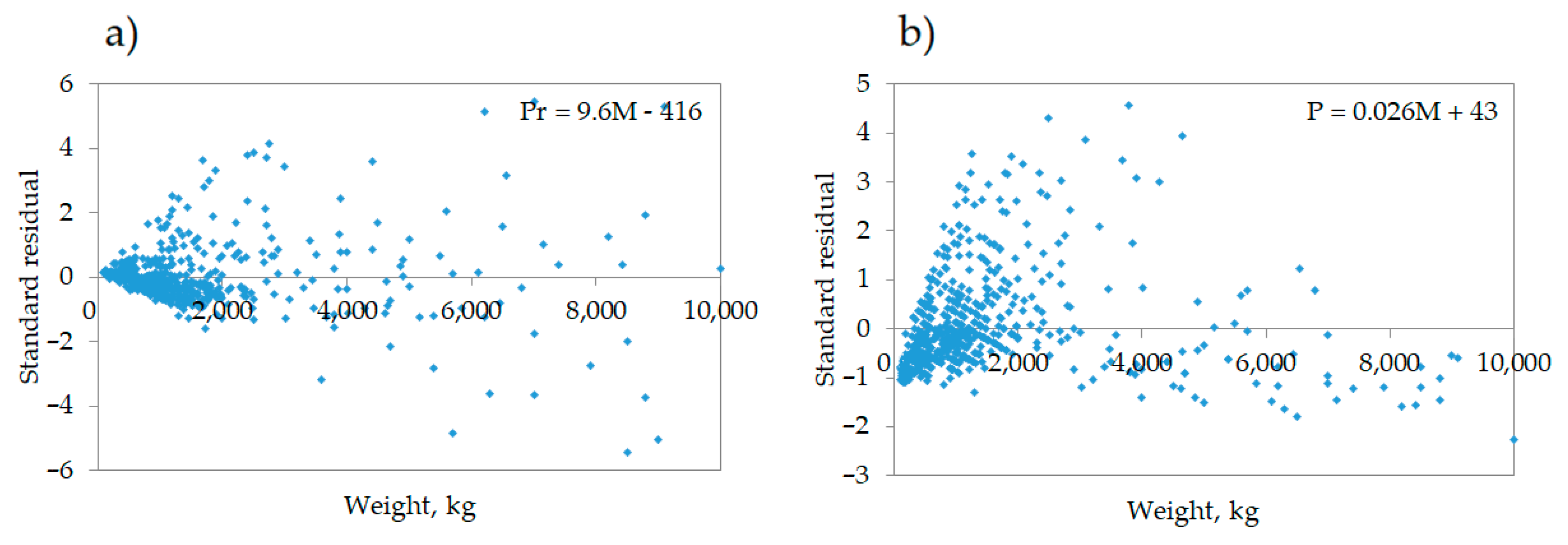
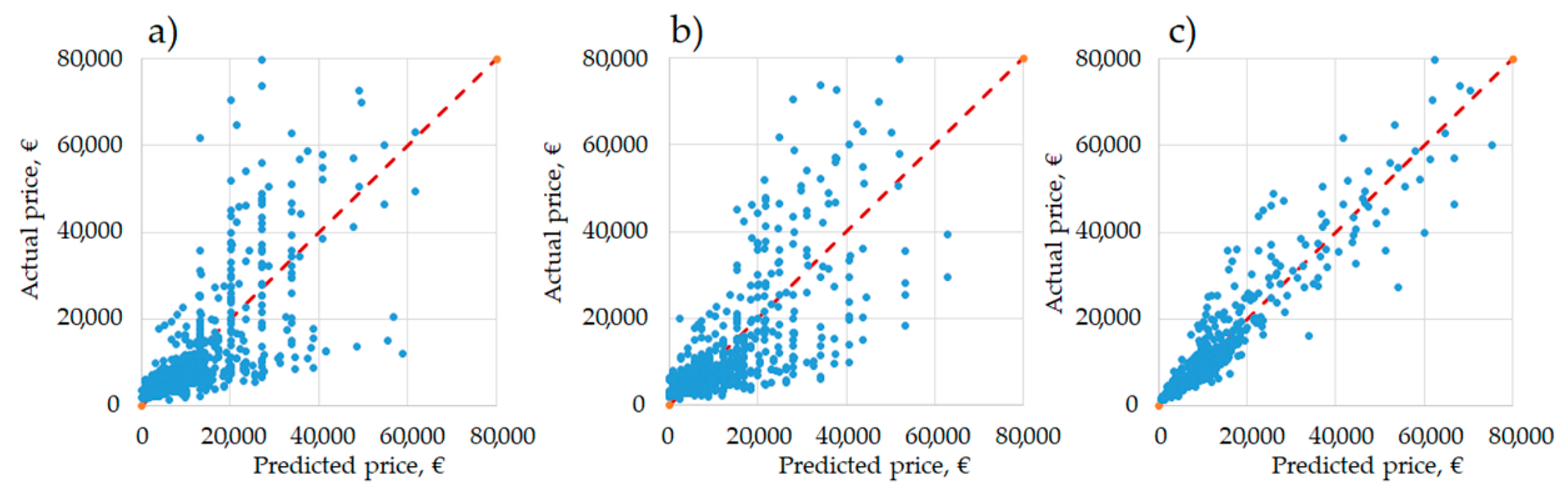
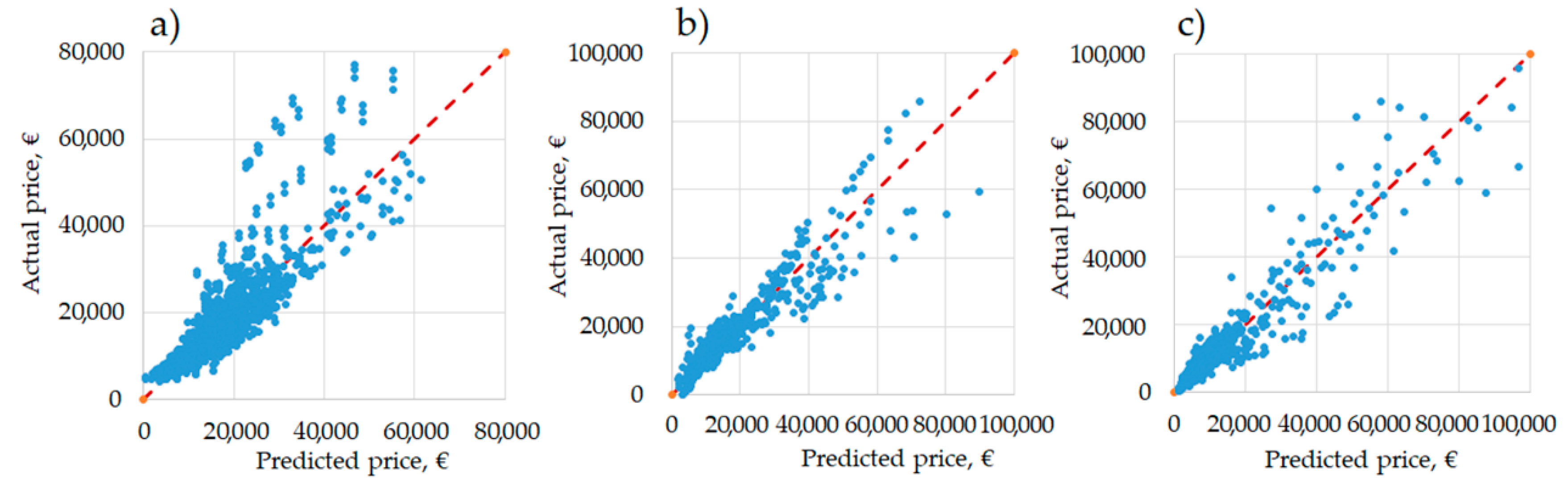
Tillage operation management requires precise planning and adjustment of the power unit, implement, and operation performance. Consideration of soil structure and corresponding tractor-implement association are required for effective operation management, productivity and return of investment. To this end, a systematic approach and consideration of the operation should be considered as an interrelated chain of the parameters and factors that impact quality and costs. In the present paper, a modelling approach was implemented for definition of parameter-price relation, simplification of the machinery unit selection process and decision making. Performed analyses allowed us to investigate the main relevant technical parameters of tillage implements, quantifying their impact, and elaborating prediction models for price, power, mass and working width. Linear and multiple linear models were provided for each group of studied implements. The dependencies between studied parameters expressed high values for harrows and cultivators and provided better predictive qualities, especially for price-mass relation (R2 > 0.8). For ploughs, power and mass relation has a primary output (R2 = 0.7). Therefore, approximately 1000 euro of investment has to be counted for each 0.1t of the tillage implement. On average, for all groups of implements power of 40 kW is needed for operation of an implement with one meter of working width. Both linear and multiple linear models showed a comparatively high error of prediction for all groups of implements regarding larger equipment models.
Besides the simplicity of the application, proposed prediction models allow a valid assessment of price on the base of technical parameters. Proposed models are subject to obsolescence: however, based on the response of provided model, it is in the intention of the authors to provide regular updates of the models for all of the published implements, with a five-year frequency. Such a frequency seems to be acceptable, based on market and model evolution in the last 20 years. Such models or updated models might be applied to manage existing fleets, to program and optimize appropriate combinations and adjustment of a tractor and implement, or in the replacement phase to calculate the required investments. Models can be applied for economic and environmental assessment of agricultural production, for planning and quantification of the costs (operation, farm, production), design of the farm fleet and evaluation and reduction of machinery-associated emissions. Practical application of the models can be useful for comparison analysis of crop cultivation methods (conventional, conservation, precision), technologies, strategies and their economic feasibility from machinery unit acquisition and management point of view. The latter will allow investments to be correctly managed based on real farm needs and the selection of the right machinery management approach. Knowing and managing available resources will allow better management of the farm and production to be performed, simplifying the decisions regarding selection, cultivation and application.