Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions
Abstract
1. Introduction
2. Experimental Section
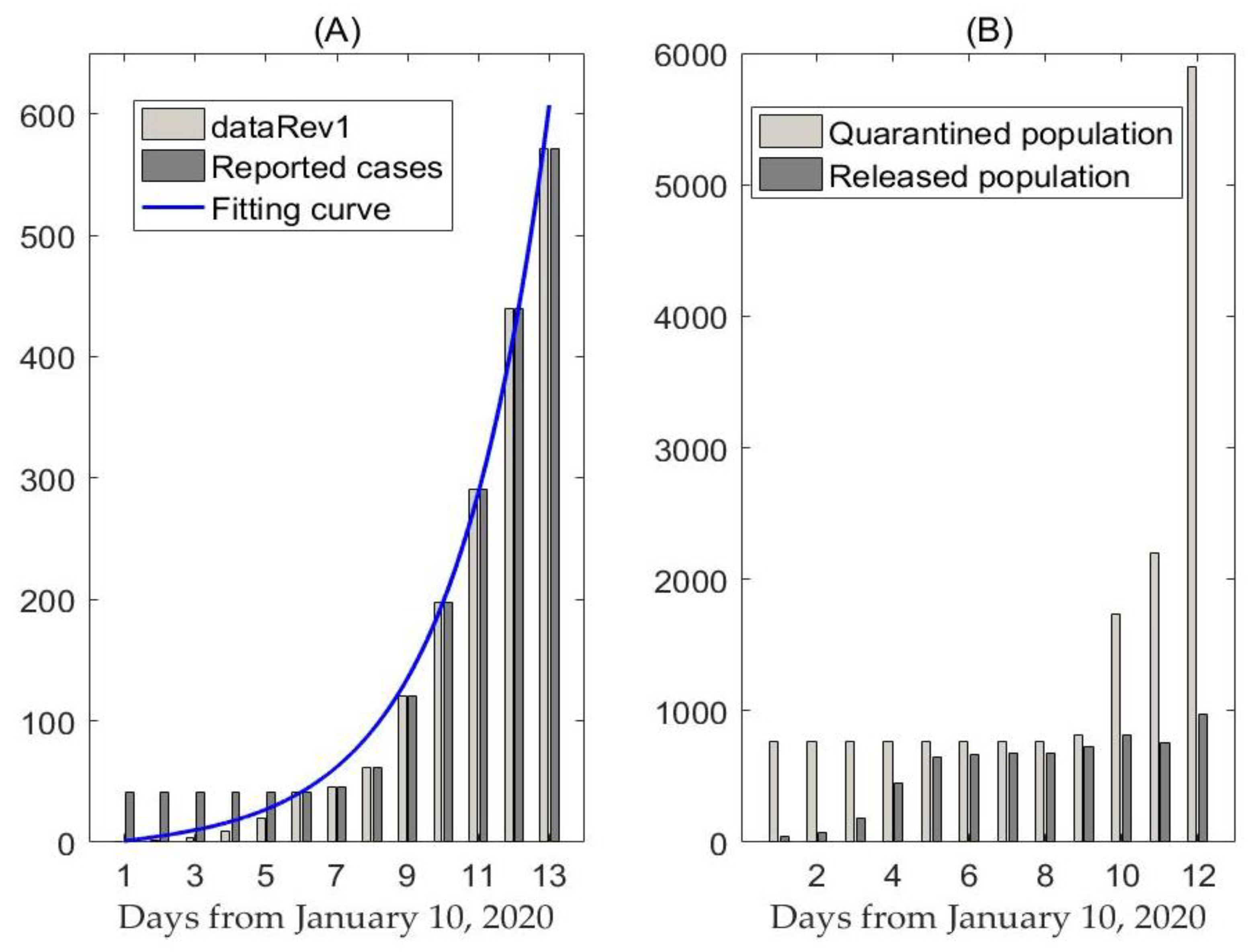
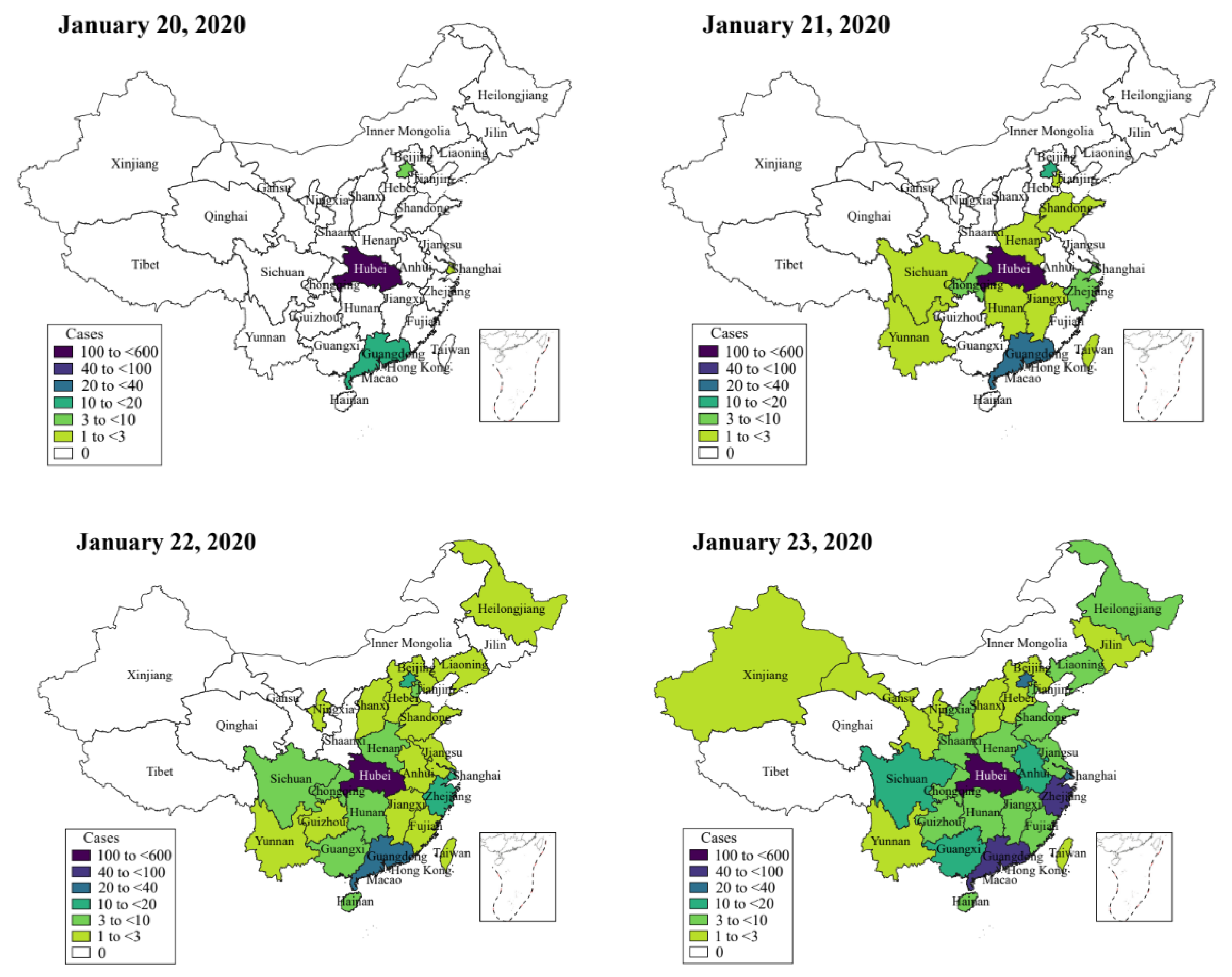
2.1. Data
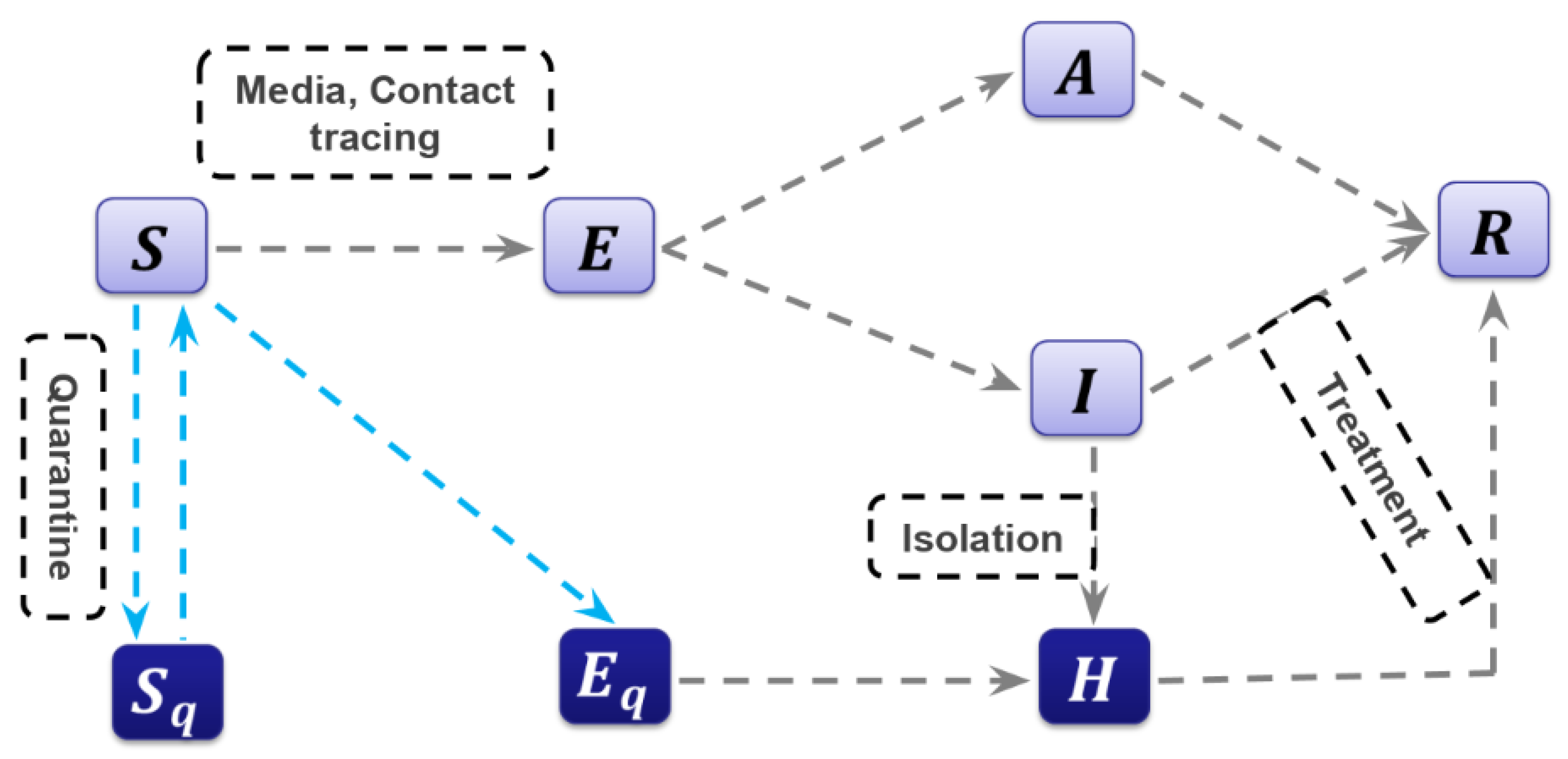
2.2. The Model
2.3. Model-Based Method for Estimation
2.4. Likelihood-Based Method for Estimation
2.5. Simulation
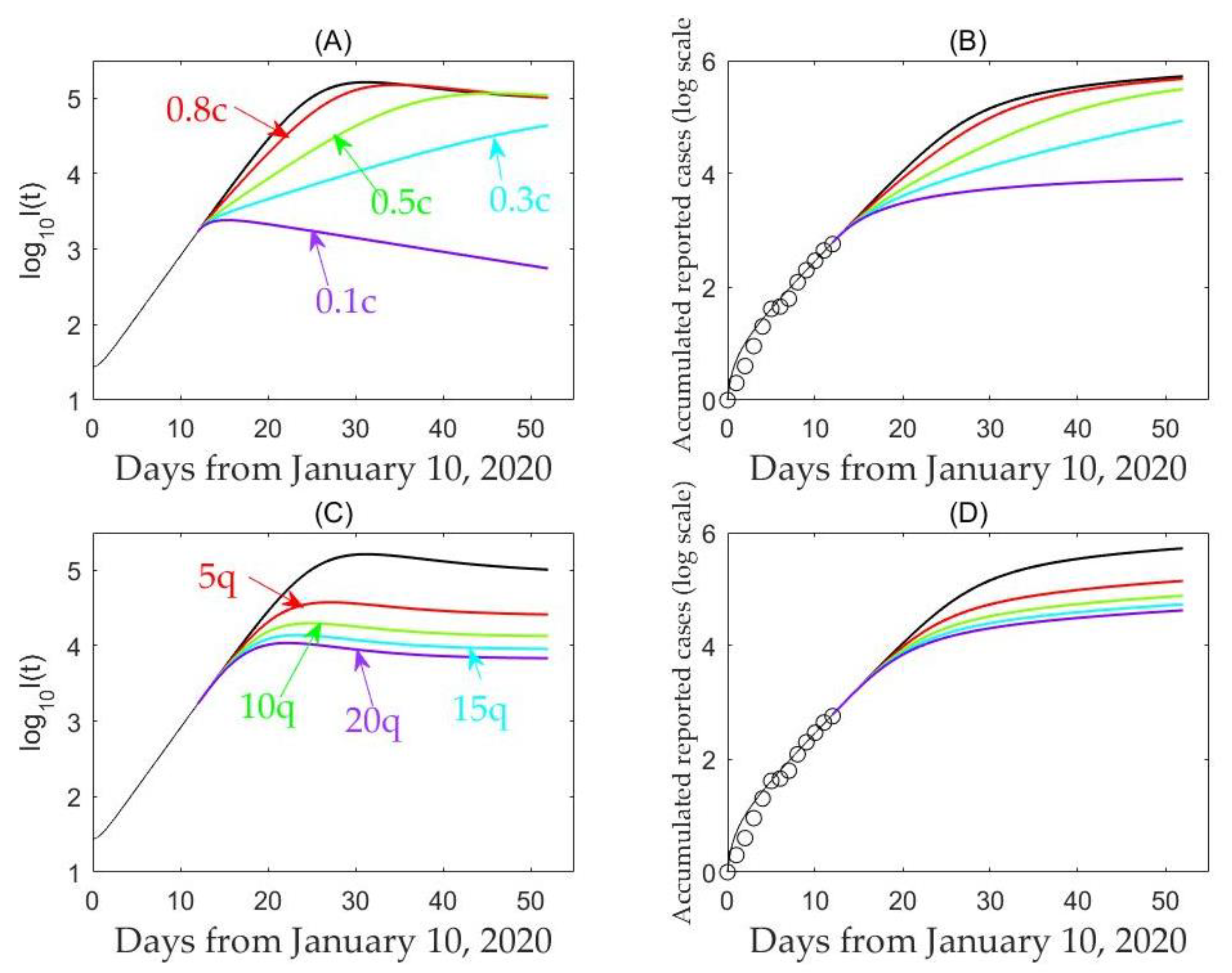
3. Results
3.1. Likelihood-Based Estimates
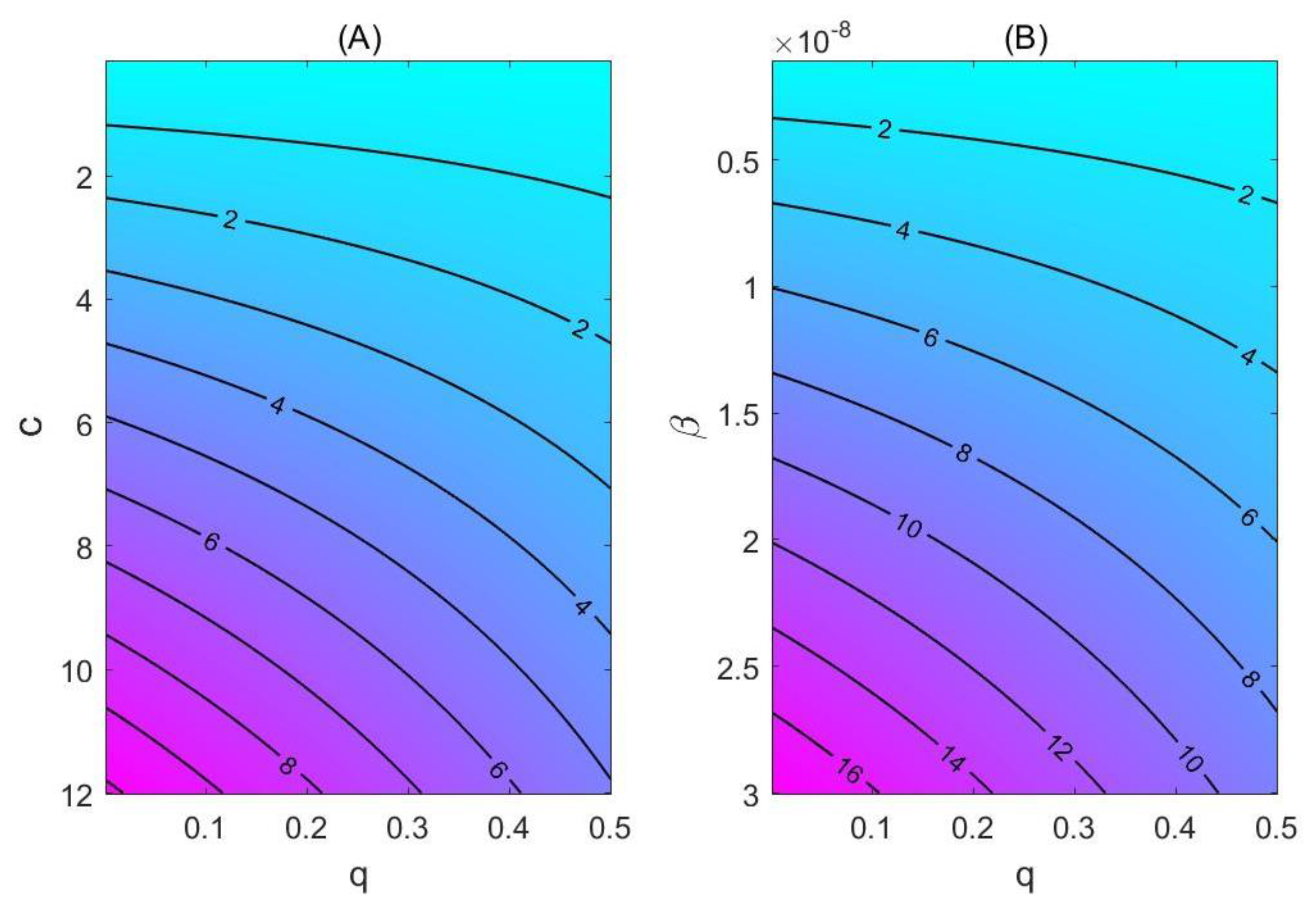
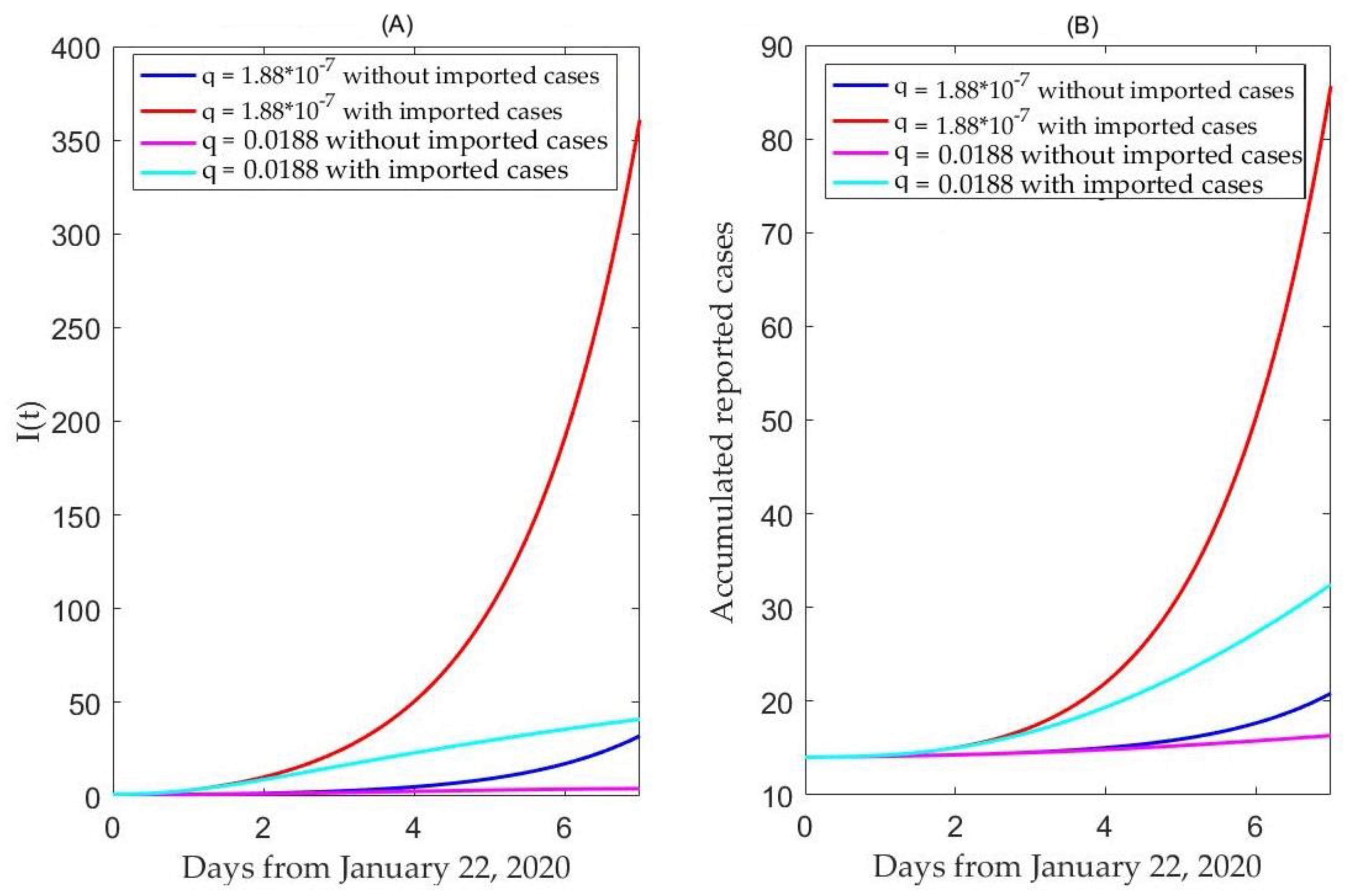
3.2. Model-Based Estimates
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Y.; Liu, Q.; Guo, D. Coronaviruses: Genome structure, replication, and pathogenesis. J. Med. Virol. 2020. [Google Scholar] [CrossRef] [PubMed]
- Kahn, J.S.; McIntosh, K. History and recent advances in coronavirus discovery. Pediatr. Infect. Dis. J. 2005, 24, S223–S227. [Google Scholar] [CrossRef] [PubMed]
- Hui, D.S.C.; Zumla, A. Severe acute respiratory syndrome: Historical, epidemiologic, and clinical features. Infect. Dis. Clin. North Am. 2019, 33, 869–889. [Google Scholar] [CrossRef] [PubMed]
- de Wit, E.; van Doremalen, N.; Falzarano, D.; Munster, V.J. SARS and MERS: Recent insights into emerging coronaviruses. Nat. Rev. Microbiol. 2016, 14, 523–534. [Google Scholar] [CrossRef]
- Killerby, M.E.; Biggs, H.M.; Midgley, C.M.; Gerber, S.I.; Watson, J.T. Middle East respiratory syndrome coronavirus transmission. Emerg. Infect. Dis. 2020, 26, 191–198. [Google Scholar] [CrossRef]
- Kim, K.H.; Tandi, T.E.; Choi, J.W.; Moon, J.M.; Kim, M.S. Middle East respiratory syndrome coronavirus (MERS-CoV) outbreak in South Korea, 2015: Epidemiology, characteristics and public health implications. J. Hosp. Infect. 2017, 95, 207–213. [Google Scholar] [CrossRef]
- Willman, M.; Kobasa, D.; Kindrachuk, J. A Comparative analysis of factors influencing two outbreaks of middle eastern respiratory syndrome (MERS) in Saudi Arabia and South Korea. Viruses 2019, 11, 1119. [Google Scholar] [CrossRef]
- Kwok, K.O.; Tang, A.; Wei, V.W.I.; Park, W.H.; Yeoh, E.K.; Riley, S. Epidemic models of contact tracing: Systematic review of transmission studies of severe acute respiratory syndrome and Middle East respiratory syndrome. Comput. Struct. Biotechnol. J. 2019, 17, 186–194. [Google Scholar] [CrossRef]
- Cohen, J.; Normile, D. New SARS-like virus in China triggers alarm. Science 2020, 367, 234–235. [Google Scholar] [CrossRef]
- Lu, H.; Stratton, C.W.; Tang, Y.W. Outbreak of pneumonia of unknown etiology in Wuhan China: The mystery and the miracle. J. Med. Virol. 2020. [Google Scholar] [CrossRef]
- Parry, J. China coronavirus: Cases surge as official admits human to human transmission. BMJ 2020, 368, m236. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization (WHO). Coronavirus. Available online: https://www.who.int/health-topics/coronavirus (accessed on 23 January 2020).
- Egger, M.; Johnson, L.; Althaus, C.; Schöni, A.; Salanti, G.; Low, N.; Norris, S.L. Developing WHO guidelines: Time to formally include evidence from mathematical modelling studies. F1000Research 2017, 6, 1584. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Rui, J.; Wang, Q.; Zhao, Z.; Cui, J.-A.; Yin, L. A mathematical model for simulating the transmission of Wuhan novel coronavirus. bioRxiv 2020. [Google Scholar] [CrossRef]
- Imai, N.; Dorigatti, I.; Cori, A.; Donnelly, C.; Riley, S.; Ferguson, N.M. Report 2: Estimating the Potential Total Number of Novel Coronavirus Cases in Wuhan City, China. Available online: https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/2019-nCoV-outbreak-report-22-01-2020.pdf (accessed on 23 January 2020).
- World Health Organization (WHO). Novel Coronavirus—China, Disease Outbreak News: Update. Available online: https://www.who.int/csr/don/12-january-2020-novel-coronavirus-china/en/ (accessed on 23 January 2020).
- World Health Organization (WHO). Situation Report. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200123-sitrep-3-2019-ncov.pdf (accessed on 23 January 2020).
- Health Commission of Hubei Province. Available online: http://wjw.hubei.gov.cn/bmdt/ztzl/fkxxgzbdgrfyyq/ (accessed on 23 January 2020).
- National Health Commission of the People’s Republic of China. Available online: http://www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml (accessed on 23 January 2020).
- Castillo-Chavez, C.; Castillo-Garsow, C.W.; Yakubu, A. Mathematical models of isolation and quarantine. JAMA 2003, 290, 2876–2877. [Google Scholar] [CrossRef]
- Tang, S.; Xiao, Y.; Yang, Y.; Zhou, Y.; Wu, J.; Ma, Z. Community-based measures for mitigating the 2009 H1N1 pandemic in China. PLoS ONE 2010, 5, e10911. [Google Scholar] [CrossRef]
- Xiao, Y.; Tang, S.; Wu, J. Media impact switching surface during an infectious disease outbreak. Sci. Rep. 2015, 5, 7838. [Google Scholar] [CrossRef]
- White, L.F.; Pagano, M. A likelihood-based method for real-time estimation of the serial interval and reproductive number of an epidemic. Stat. Med. 2008, 27, 2999–3016. [Google Scholar] [CrossRef]
- World Health Organization (WHO). Available online: https://www.who.int/news-room/detail/23-01-2020-statement-on-the-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-outbreak-of-novel-coronavirus-(2019-ncov) (accessed on 23 January 2020).
- Bogoch, I.I.; Watts, A.; Thomas-Bachli, A.; Huber, C.; Kraemer, M.U.G.; Khan, K. Pneumonia of unknown etiology in Wuhan, China: Potential for international spread via commercial air travel. J. Travel Med. 2020. [Google Scholar] [CrossRef]
- Gumel, A.B.; Ruan, S.G.; Day, T.; Watmough, J.; Brauer, F.; van den Driessche, P.; Gabrielson, D.; Bowman, C.; Alexander, M.E.; Ardal, S.; et al. Modelling strategies for controlling SARS outbreaks. Proc. R. Soc. Lond. B. 2004, 271, 2223–2232. [Google Scholar] [CrossRef]
- Majumder, M.S.; Rivers, C.; Lofgren, E.; Fisman, D. Estimation of MERS-Coronavirus reproductive number and case fatality rate for the Spring 2014 Saudi Arabia outbreak: Insights from publicly available data. PLoS Curr. 2014, 18, 6. [Google Scholar]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.Y.; et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 2020. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Lin, Q.; Ran, J.; Musa, S.S.; Yang, G.; Wang, W.; Lou, Y.; Gao, D.; Yang, L.; He, D.; et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. Int. J. Infect. Dis. 2020. [Google Scholar] [CrossRef] [PubMed]
- Guerra, F.M.; Bolotin, S.; Lim, G.; Heffernan, J.; Deeks, S.L.; Li, Y.; Crowcroft, N.S. The basic reproduction number (R0) of measles: A systematic review. Lancet Infect. Dis. 2017, 17, e420–e428. [Google Scholar] [CrossRef]
- Rothe, C.; Schunk, M.; Sothmann, P.; Bretzel, G.; Froeschl, G.; Wallrauch, C.; Zimmer, T.; Thiel, V.; Janke, C.; Guggemos, W.; et al. Transmission of 2019-nCoV infection from an asymptomatic contact in Germany. N. Engl. J. Med. 2020. [Google Scholar] [CrossRef] [PubMed]
- Hui, D.S.; Azhar, E.E.I.; Madani, T.A.; Ntoumi, F.; Kock, R.; Dar, O.; Ippolito, G.; Mchugh, T.D.; Memish, Z.A.; Drosten, C.; et al. The continuing 2019-nCoV epidemic threat of novel coronaviruses to global health-The latest 2019 novel coronavirus outbreak in Wuhan, China. Int. J. Infect. Dis. 2020, 91, 264–266. [Google Scholar] [CrossRef]
- Cheng, V.C.C.; Wong, S.C.; To, K.K.W.; Ho, P.L.; Yuen, K.Y. Preparedness and proactive infection control measures against the emerging Wuhan coronavirus pneumonia in China. J. Hosp. Infect. 2020. [Google Scholar] [CrossRef]
| Parameter | Definitions | Estimated Mean Value | Standard Deviation | Data Source |
| Contact rate | MCMC | |||
| Probability of transmission per contact | MCMC | |||
| Quarantined rate of exposed individuals | MCMC | |||
| Transition rate of exposed individuals to the infected class | – | WHO | ||
| Rate at which the quarantined uninfected contacts were released into the wider community | – | [18,19] | ||
| Probability of having symptoms among infected individuals | MCMC | |||
| Transition rate of symptomatic infected individuals to the quarantined infected class | MCMC | |||
| Transition rate of quarantined exposed individuals to the quarantined infected class | MCMC | |||
| Recovery rate of symptomatic infected individuals | MCMC | |||
| Recovery rate of asymptomatic infected individuals | MCMC | |||
| Recovery rate of quarantined infected individuals | MCMC | |||
| Disease-induced death rate | MCMC | |||
| Initial Values | Definitions | Estimated Mean Value | Standard Deviation | Data Source |
| Initial susceptible population | – | [18] | ||
| Initial exposed population | MCMC | |||
| Initial symptomatic infected population | MCMC | |||
| Initial asymptomatic infected population | MCMC | |||
| Initial quarantined susceptible population | – | [18] | ||
| Initial quarantined exposed population | MCMC | |||
| Initial quarantined infected population | – | [18] | ||
| Initial recovered population | – | [18] |
| R0 | V = 2 (dataRev1) | V = 3 (dataRev1) | V = 2 (dataRev2) | V = 3 (dataRev2) |
|---|---|---|---|---|
| E = 2 | 1.4546 | 1.6560 | 1.4545 | 1.6554 |
| E = 3 | 1.7459 | 1.7155 | 1.7456 | 1.7145 |
| E = 4 | 2.5828 | 2.4462 | 2.5815 | 2.4427 |
| E = 5 | 3.9893 | 3.7134 | 3.9802 | 3.6956 |
| E = 6 | 6.3901 | 5.8303 | 6.3164 | 5.7304 |
| E = 7 | 10 | 9.2564 | 9.6409 | 8.7299 |
| E = 8 | 10 | 10 | 10 | 10 |
| Peak Time | days | days | days | days | days |
| Value of at peak time | |||||
| Parameter | |||||
| Peak time | days | days | days | days | days |
| Value of at peak time |
| Date | 01/23 | 01/24 | 01/25 | 01/26 | 01/27 | 01/28 | 01/29 |
|---|---|---|---|---|---|---|---|
| Predicted confirmed cases | 876 | 1266 | 1828 | 2634 | 3784 | 5419 | 7723 |
| Predicted confirmed cases (reduced contact by 50%) | 868 | 1207 | 1624 | 2128 | 2736 | 3464 | 4335 |
| Predicted confirmed cases (reduced contacts by 90%) | 862 | 1163 | 1480 | 1802 | 2120 | 2430 | 2731 |
| Real data of confirmed cases | 830 | 1287 | 1975 | 2744 | 4515 | 5974 | 7711 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions. J. Clin. Med. 2020, 9, 462. https://doi.org/10.3390/jcm9020462
Tang B, Wang X, Li Q, Bragazzi NL, Tang S, Xiao Y, Wu J. Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions. Journal of Clinical Medicine. 2020; 9(2):462. https://doi.org/10.3390/jcm9020462
Chicago/Turabian StyleTang, Biao, Xia Wang, Qian Li, Nicola Luigi Bragazzi, Sanyi Tang, Yanni Xiao, and Jianhong Wu. 2020. "Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions" Journal of Clinical Medicine 9, no. 2: 462. https://doi.org/10.3390/jcm9020462
APA StyleTang, B., Wang, X., Li, Q., Bragazzi, N. L., Tang, S., Xiao, Y., & Wu, J. (2020). Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions. Journal of Clinical Medicine, 9(2), 462. https://doi.org/10.3390/jcm9020462






