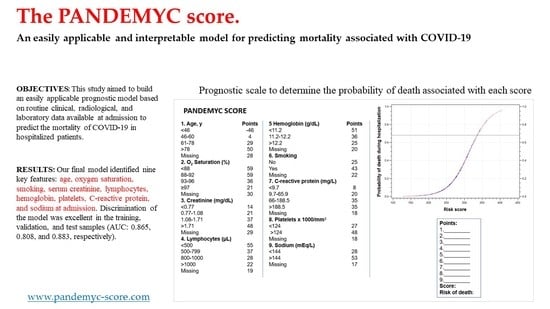
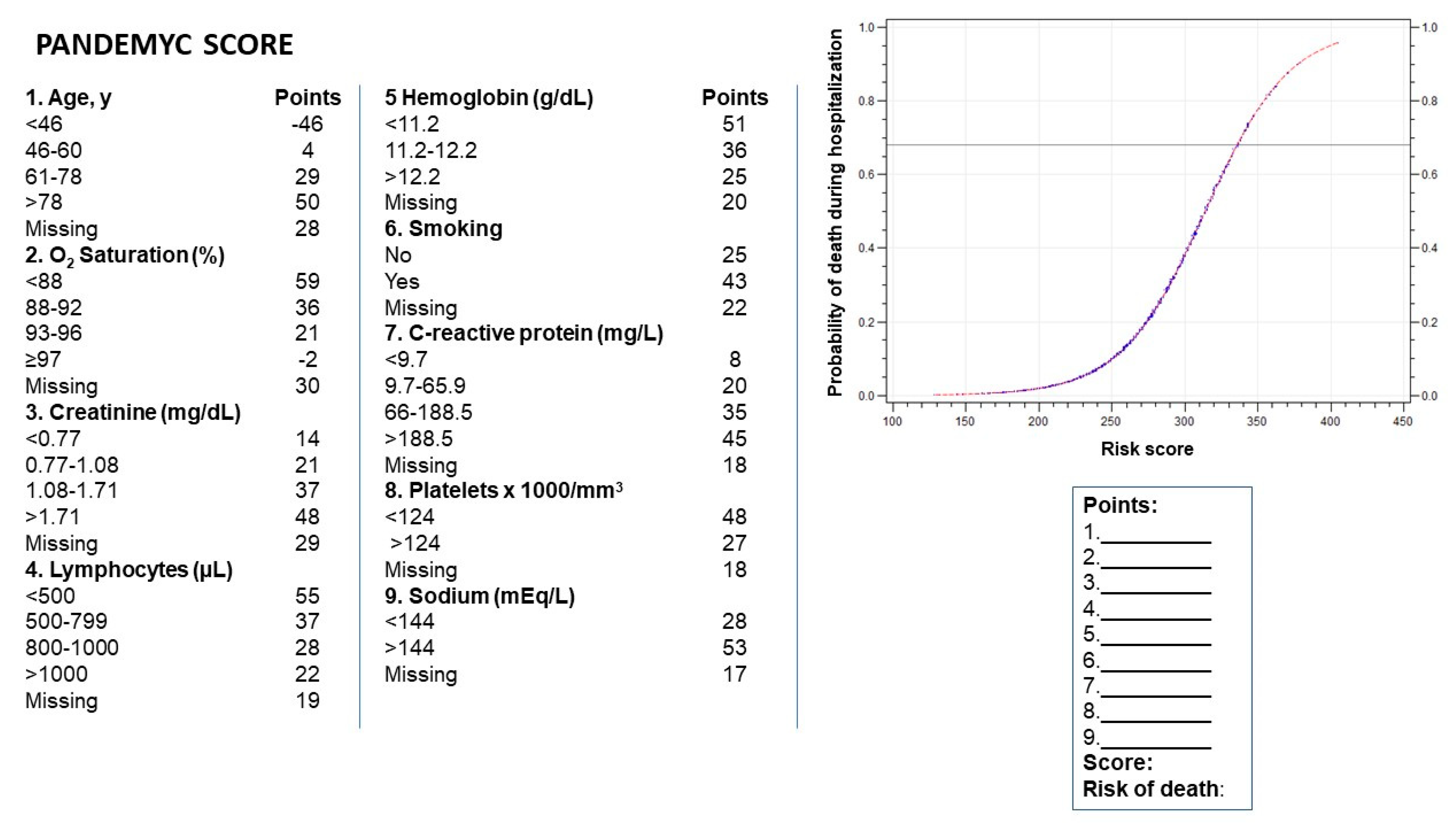
The PANDEMYC Score. An Easily Applicable and Interpretable Model for Predicting Mortality Associated With COVID-19
Abstract
1. Introduction
2. Experimental Section
2.1. Study Design and Data Source
2.2. Ethical Aspects
2.3. COVID-19 Cohort Identification
2.4. Model Development and Statistical Analysis
2.5. Calibration
3. Results
3.1. Patient Cohorts
3.2. Model Development
3.3. Validation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Health Organization (WHO). Coronavirus Disease (COVID-19) Situation Report-182. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200720-covid-19-sitrep-182.pdf?sfvrsn=60aabc5c_2 (accessed on 20 July 2020).
- Ministerio de Sanidad. Centro de Coordinación de Alertas y Emergencias Sanitarias. Actualización no 119. Enfermedad por el coronavirus (COVID-19). 28 May 2020. Available online: https://www.mscbs.gob.es/en/profesionales/saludPublica/ccayes/alertasActual/nCov-China/documentos/Actualizacion_119_COVID-19.pdf (accessed on 6 June 2020).
- Comunidad de Madrid. Transparencia. Covid-19-TIA por municipios y distritos de Madrid. Available online: https://datos.comunidad.madrid/catalogo/dataset/covid19_tia_muni_y_distritos (accessed on 1 June 2020).
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Wynants, L.; Van Calster, B.; Collins, G.S.; Riley, R.D.; Heinze, G.; Schuit, E.; Bonten, M.M.J.; Damen, J.A.A.; Debray, T.P.A.; De Vos, M.; et al. Prediction models for diagnosis and prognosis of covid-19 infection: Systematic review and critical appraisal. Br. Med. J. 2020, 369, 1328. [Google Scholar] [CrossRef]
- Harris, P.A.; Taylor, R.; Thielke, R.; Payne, J.; Gonzalez, N.; Conde, J.G. Research electronic data capture (REDCap)-A metadata-driven methodology and workflow process for providing translational research informatics support. J. Biomed. Inform. 2009, 42, 377–381. [Google Scholar] [CrossRef] [PubMed]
- Brown, L. Developing Credit Risk Models Using SAS Enterprise Miner. and SAS/STAT: Theory and Applications; SAS Institute Inc.: Cary, NC, USA, 2014; ISBN 978-1612906911. [Google Scholar]
- Hand, D.; Henley, W. Statistical Classification Methods in Consumer Credit Scoring: A Review. J. R. Stat. Soc. 1997, 160, 523–541. [Google Scholar] [CrossRef]
- Yap, B.; Ong, S.; Husain, N. Using data mining to improve assessment of credit worthiness via credit scoring models. Expert Syst. Appl. 2011, 38, 13274–13283. [Google Scholar] [CrossRef]
- DeLong, E.; DeLong, D.; Clarke-Pearson, D. Comparing the Areas under Two or More Correlated Receiver Operating Characteristic Curves: A Nonparametric Approach. Biometrics 1988, 44, 837–845. [Google Scholar] [CrossRef] [PubMed]
- Soto-Mota, A.; Garza, B.A.M.; Rodriguez, E.M.; Rodriguez, J.O.B.; Romo, A.E.L.; Minutti, P.A.; Loya, J.V.A.; Talavera, F.E.P.; Avila-Cervera, F.J.; Burciaga, A.N.V. The Low-Harm Score for Predicting Mortality in Patients Diagnosed with Covid-19: A Multicentric Validation Study. medRxiv 2020. [Google Scholar] [CrossRef]
- Xie, J.; Hungerford, D.; Chen, H.; Abrams, S.T.; Li, S.; Wang, G.; Wang, Y.; Kang, H.; Bonnett, L.; Zheng, R.; et al. Development and External Validation of a Prognostic Multivariable Model on Admission for Hospitalized Patients with COVID-19. SSRN Electron. J. 2020. [Google Scholar] [CrossRef]
- Yadaw, A.S.; Li, Y.-C.; Bose, S.; Iyengar, R.; Bunyavanich, S.; Pandey, G. Clinical predictors of COVID-19 mortality. medRxiv 2020. [Google Scholar] [CrossRef]
- Parohan, M.; Yaghoubi, S.; Seraji, A.; Javanbakht, M.H.; Sarraf, P.; Djalali, M. Risk factors for mortality in patients with Coronavirus disease 2019 (COVID-19) infection: A systematic review and meta-analysis of observational studies. Aging Male 2020, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Gong, J.; Ou, J.; Qiu, X.; Jie, Y.; Chen, Y.; Yuan, L.; Cao, J.; Tan, M.; Xu, W.; Zheng, F.; et al. A Tool to Early Predict Severe 2019-Novel Coronavirus Pneumonia (COVID-19): A Multicenter Study using the Risk Nomogram in Wuhan and Guangdong, China. medRxiv 2020. [Google Scholar] [CrossRef]
- Horby, P.; Lim, W.S.; Emberson, J.; Mafham, M.; Bell, J.; Linsell, L.; Staplin, N.; Brightling, C.; Ustianowski, A.; Elmahi, E.; et al. Recovery Collaborative Group. Effect of Dexamethasone in Hospitalized Patients with COVID-19: Preliminary Report. medRxiv 2020. [Google Scholar] [CrossRef]
- Connors, J.M.; Levy, J.H. COVID-19 and its implications for thrombosis and anticoagulation. Blood 2020, 135, 2033–2040. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Meng, M.; Kumar, R.; Wu, Y.; Huang, J.; Lian, N.; Deng, Y.; Lin, S. The impact of COPD and smoking history on the severity of COVID–19: A systemic review and meta-analysis. J. Med. Virol. 2020. [Google Scholar] [CrossRef] [PubMed]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
| Characteristics | Alive n = 1643 | Dead n = 325 | p-Value |
|---|---|---|---|
| Male sex, No. (%) | 882 (54) | 222 (68.7) | <0.001 |
| Age, Median (IQR) | 63 (26) | 82 (16) | <0.001 |
| Born in Spain, No. (%) | 1132 (72.8) | 281 (89.2) | <0.001 |
| Dead, No. (%) | 0 (0) | 325 (100) | <0.001 |
| Comorbid Conditions, No. (%) | |||
| Chronic Heart Disease | 283 (17.8) | 132 (41.2) | <0.001 |
| Hypertension | 765 (48) | 226 (70.6) | <0.001 |
| Chronic Pulmonary Disease | 169 (10.7) | 69 (21.8) | <0.001 |
| Asthma | 138 (8.7) | 18 (5.6) | 0.103 |
| Stage 4 Chronic Kidney Disease | 68 (4.3) | 42 (13.2) | <0.001 |
| Liver Cirrhosis | 22 (1.4) | 9 (2.8) | 0.099 |
| Solid Neoplasm (Active) | 42 (2.6) | 39 (12.3) | <0.001 |
| Hematologic Neoplasm (Active) | 21 (1.3) | 13 (4) | 0.001 |
| HIV Infection | 11 (0.7) | 0 (0) | 0.284 |
| Obesity | 239 (17.8) | 45 (17.3) | 0.809 |
| Diabetes | 337 (21.2) | 99 (31) | <0.001 |
| Dyslipidemia | 347 (33.8) | 97 (53.6) | 0.001 |
| Inflammatory Disease | 74 (4.7) | 25 (7.8) | 0.024 |
| Dementia | 71 (4.5) | 37 (11.7) | <0.001 |
| Malnutrition | 26 (1.8) | 14 (5.2) | 0.003 |
| Smoker | 335 (24.7) | 125 (44.2) | <0.001 |
| Current medications, No. (%) | |||
| Non-Steroidal Anti-Inflammatory Drugs | 46 (3.4) | 6 (2.3) | 0.429 |
| Angiotensin-Converting Enzyme Inhibitors | 339 (22.1) | 93 (29.8) | 0.002 |
| Angiotensin II Receptor Blockers | 223 (14.6) | 70 (22.5) | <0.001 |
| Inhaled Corticosteroids | 134 (8.7) | 39 (12.6) | 0.033 |
| Systemic Corticosteroids | 39 (2.5) | 16 (5.2) | 0.018 |
| Vital signs at admission, median (IQR) | |||
| Temperature °C | 37 (1.2) | 37.2 (1.27) | 0.030 |
| Heart Rate, Beats Per Minute | 89 (21) | 89 (24.2) | 0.849 |
| Oxygen Saturation in Room Air, % | 95 (5) | 89 (11) | <0.001 |
| Admission signs and symptoms, No. (%) | |||
| Fever | 1197 (75.7) | 225 (71.9) | 0.206 |
| Malaise | 652 (41.7) | 140 (45.6) | 0.281 |
| Upper Respiratory Tract Symptoms | 353 (22.5) | 68 (22.1) | 0.879 |
| Dyspnea | 850 (54) | 221 (70.4) | <0.001 |
| Chest Pain | 163 (10.4) | 20 (6.4) | 0.042 |
| Cough | 1070 (68) | 188 (60.1) | 0.015 |
| Sputum Production | 187 (11.9) | 45 (14.5) | 0.244 |
| Hemoptysis | 29 (1.8) | 4 (1.3) | 0.653 |
| Myalgia/Arthralgia | 349 (22.3) | 25 (8.1) | <0.001 |
| Headache | 168 (10.7) | 12 (3.9) | <0.001 |
| Altered Consciousness | 66 (4.2) | 29 (9.3) | <0.001 |
| Seizures | 8 (0.5) | 0 (0) | 0.433 |
| Abdominal Pain | 55 (3.5) | 10 (3.2) | 0.937 |
| Vomiting/Nausea | 201 (12.8) | 18 (5.8) | 0.001 |
| Diarrhea | 290 (18.5) | 37 (11.8) | 0.007 |
| Skin Rash | 9 (0.6) | 1 (0.3) | 0.897 |
| Laboratory findings, median (interquartile range) | |||
| Hemoglobin, G/L | 13.9 (1.9) | 13 (3.1) | <0.001 |
| White Blood Cell Count, X109/L | 6480 (3480) | 7760 (5240) | <0.001 |
| Lymphocyte Count - Cells/ μL | 1000 (700) | 800 (600) | <0.001 |
| Neutrophil Count, Cells/ μL | 4800 (3200) | 6200 (4450) | <0.001 |
| Hematocrit, % | 41.5 (6) | 39.2 (8.8) | <0.001 |
| Platelets, X109/L | 211 (108) | 195 (118) | <0.001 |
| Activated Partial Thromboplastin Time | 25.9 (3.8) | 27.2 (5.1) | <0.001 |
| International Normalized Ratio | 1.08 (0.13) | 1.13 (0.23) | <0.001 |
| Aspartate Aminotransferase, U/L | 36 (32) | 30 (24.2) | <0.001 |
| Alanine Aminotransferase, U/L | 38 (27) | 47 (36.8) | <0.001 |
| Glucose, mg/dL | 110 (34) | 130 (56) | <0.001 |
| Creatinine, mg/dL | 0.96 (0.39) | 1.25 (0.805) | <0.001 |
| Sodium, mEq/L | 139 (5) | 139 (6) | 0.8761 |
| Potassium, mEq/L | 4.3 (0.6) | 4.4 (0.8) | 0.029 |
| C-Reactive Protein, mg/L | 61.1 (98.5) | 112 (144) | <0.001 |
| Radiology | |||
| Pathological chest X-ray on admission, No. (%) | 1424 (91.2) | 287 (91.4) | 0.478 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres-Macho, J.; Ryan, P.; Valencia, J.; Pérez-Butragueño, M.; Jiménez, E.; Fontán-Vela, M.; Izquierdo-García, E.; Fernandez-Jimenez, I.; Álvaro-Alonso, E.; Lazaro, A.; et al. The PANDEMYC Score. An Easily Applicable and Interpretable Model for Predicting Mortality Associated With COVID-19. J. Clin. Med. 2020, 9, 3066. https://doi.org/10.3390/jcm9103066
Torres-Macho J, Ryan P, Valencia J, Pérez-Butragueño M, Jiménez E, Fontán-Vela M, Izquierdo-García E, Fernandez-Jimenez I, Álvaro-Alonso E, Lazaro A, et al. The PANDEMYC Score. An Easily Applicable and Interpretable Model for Predicting Mortality Associated With COVID-19. Journal of Clinical Medicine. 2020; 9(10):3066. https://doi.org/10.3390/jcm9103066
Chicago/Turabian StyleTorres-Macho, Juan, Pablo Ryan, Jorge Valencia, Mario Pérez-Butragueño, Eva Jiménez, Mario Fontán-Vela, Elsa Izquierdo-García, Inés Fernandez-Jimenez, Elena Álvaro-Alonso, Andrea Lazaro, and et al. 2020. "The PANDEMYC Score. An Easily Applicable and Interpretable Model for Predicting Mortality Associated With COVID-19" Journal of Clinical Medicine 9, no. 10: 3066. https://doi.org/10.3390/jcm9103066
APA StyleTorres-Macho, J., Ryan, P., Valencia, J., Pérez-Butragueño, M., Jiménez, E., Fontán-Vela, M., Izquierdo-García, E., Fernandez-Jimenez, I., Álvaro-Alonso, E., Lazaro, A., Alvarado, M., Notario, H., Resino, S., Velez-Serrano, D., & Meca, A. (2020). The PANDEMYC Score. An Easily Applicable and Interpretable Model for Predicting Mortality Associated With COVID-19. Journal of Clinical Medicine, 9(10), 3066. https://doi.org/10.3390/jcm9103066