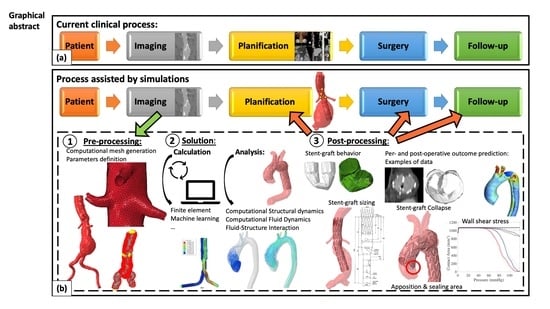
Patient-Specific Numerical Simulations of Endovascular Procedures in Complex Aortic Pathologies: Review and Clinical Perspectives
Abstract
1. Introduction
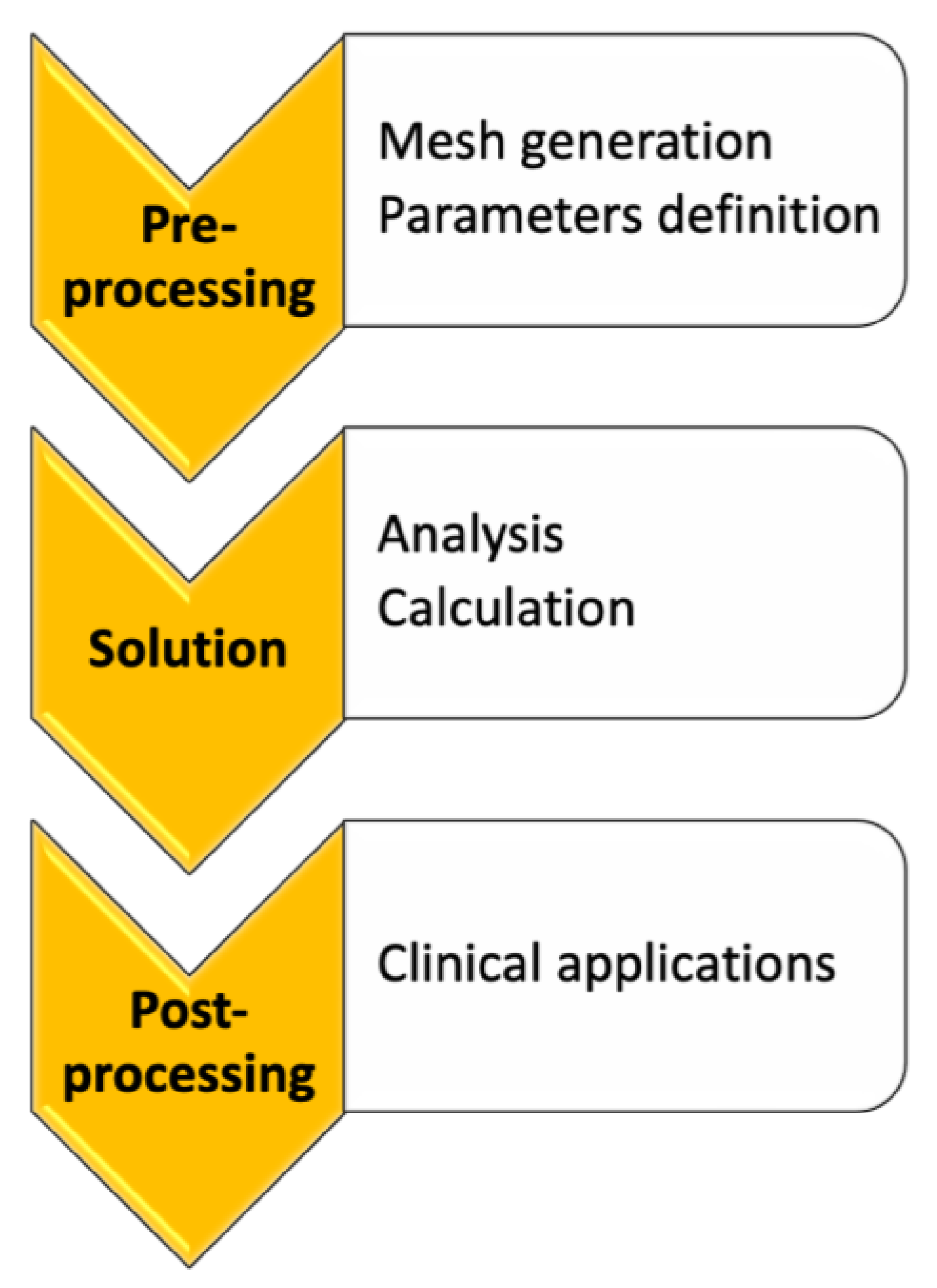
2. Methodology of Numerical Simulations
2.1. Preprocessing: From Medical Images to Patient-Specific Model
2.2. Solution
2.2.1. Types of Analysis
- Computational Structural Dynamics
- Computational Fluid Dynamics (CFD)
- Fluid-Structure Interaction (FSI)
2.2.2. Calculation Methods
- Finite Element (FE) Analysis
- Machine Learning (ML)
2.3. Post Processing: From Numerical Outputs to Clinical Practice in Endovascular Aortic Repair
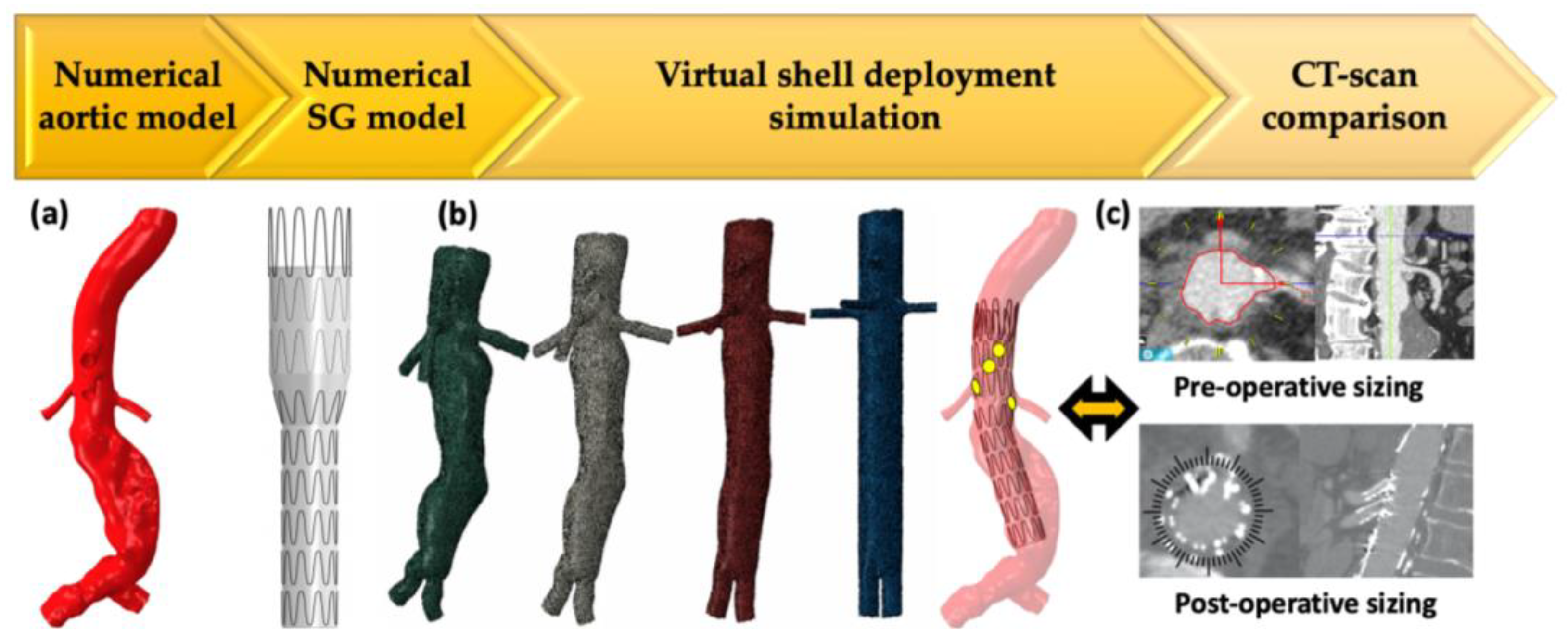
2.3.1. Applications in Abdominal Aortic Aneurysms
- Proximal sealing zone prediction.
- Arterial deformation by device introduction and its impact on sizing
2.3.2. Applications in Thoracic Aortic Aneurysms
- Endovascular treatment for the ascending aorta
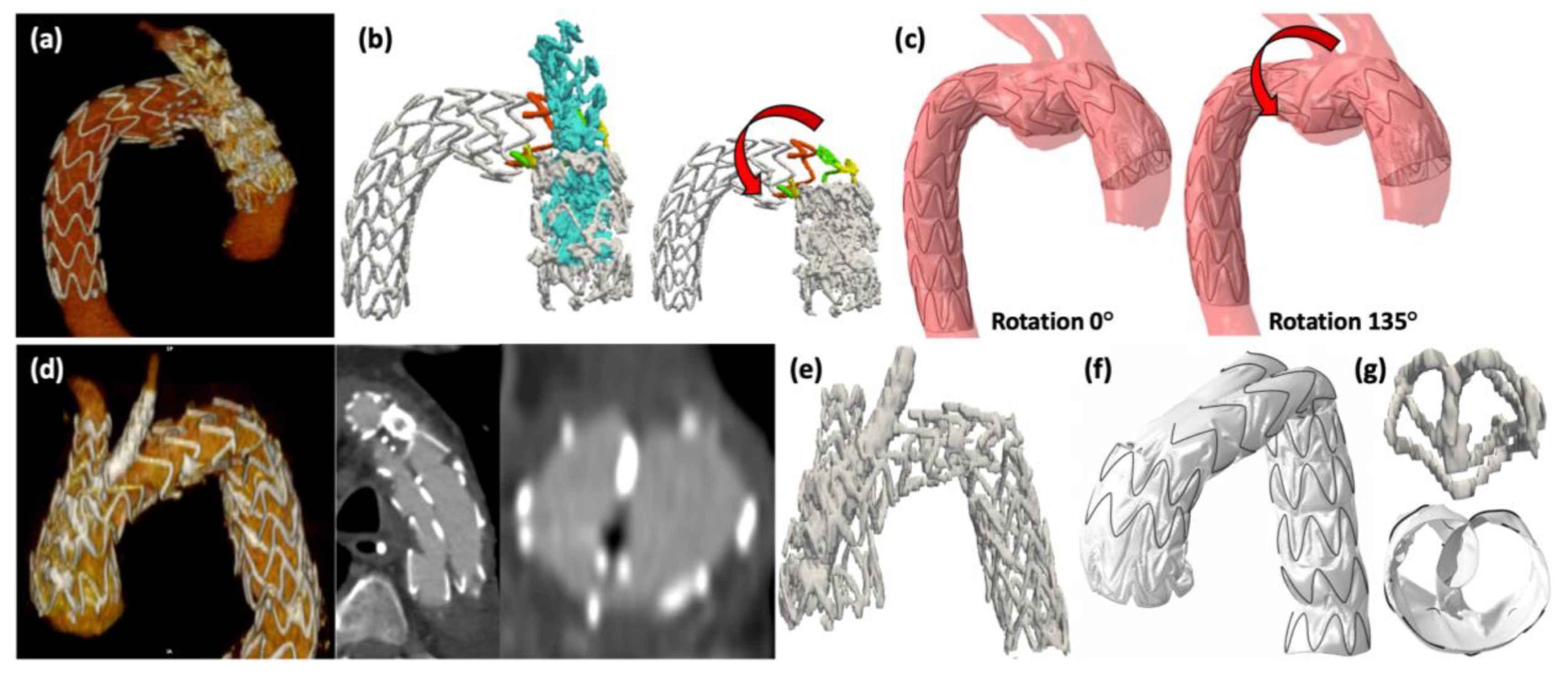
- Aortic arch endovascular treatment planification
- Descending aorta endovascular treatment planification
2.3.3. Applications in Thoraco-Abdominal and Juxta-Renal Aortic Aneurysms
- Arterial deformation by device introduction and its impact on sizing
- Procedural planification
2.3.4. Applications in Aortic Dissections
- Retrograde type A dissection
- Aortic wall remodeling
- Endovascular treatment of type A dissection
3. Focus on Two Specific Clinical Applications
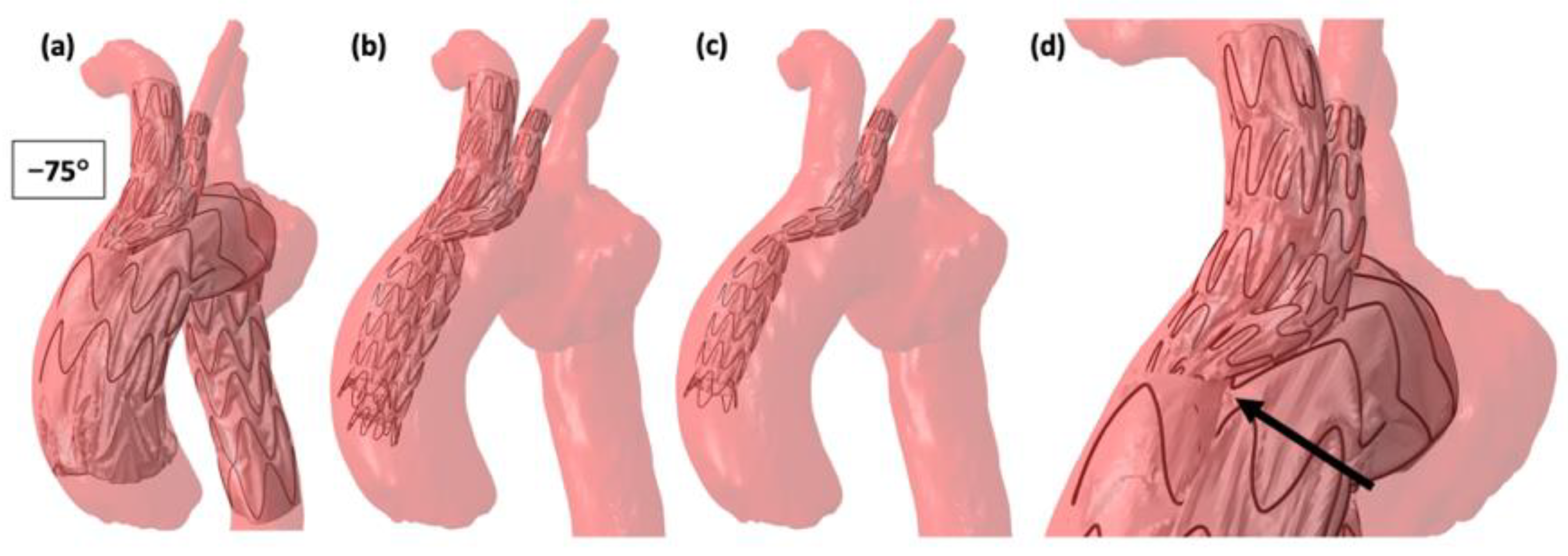
3.1. Planification of FEVAR
3.2. Outcome Prediction in the Aortic Arch
4. Current Challenges of FE Analysis in Endovascular Surgery
5. Future Directions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barbato, E.; Barton, P.J.; Bartunek, J.; Huber, S.; Ibanez, B.; Judge, D.P.; Lara-Pezzi, E.; Stolen, C.M.; Taylor, A.; Hall, J.L. Review and Updates in Regenerative and Personalized Medicine, Preclinical Animal Models, and Clinical Care in Cardiovascular Medicine. J. Cardiovasc. Transl. Res. 2015, 8, 466–474. [Google Scholar] [CrossRef] [PubMed]
- Blaus, A.; Madabushi, R.; Pacanowski, M.; Rose, M.; Schuck, R.N.; Stockbridge, N.; Temple, R.; Unger, E.F. Personalized Cardiovascular Medicine Today: A Food and Drug Administration/Center for Drug Evaluation and Research Perspective. Circulation 2015, 132, 1425–1432. [Google Scholar] [CrossRef] [PubMed]
- Spear, R.; Haulon, S.; Ohki, T.; Tsilimparis, N.; Kanaoka, Y.; Milne, C.P.E.; Debus, S.; Takizawa, R.; Kölbel, T. Editor’s Choice-Subsequent Results for Arch Aneurysm Repair with Inner Branched Endografts. Eur. J. Vasc. Endovasc. Surg. 2016, 51, 380–385. [Google Scholar] [CrossRef] [PubMed]
- Maurel, B.; Mastracci, T.M.; Spear, R.; Hertault, A.; Azzaoui, R.; Sobocinski, J.; Haulon, S. Branched and Fenestrated Options to Treat Aortic Arch Aneurysms. J. Cardiovasc. Surg. 2016, 57, 686–697. [Google Scholar]
- Demanget, N.; Avril, S.; Badel, P.; Orgéas, L.; Geindreau, C.; Albertini, J.-N.; Favre, J.-P. Computational Comparison of the Bending Behavior of Aortic Stent-Grafts. J. Mech. Behav. Biomed. Mater. 2012, 5, 272–282. [Google Scholar] [CrossRef] [PubMed]
- Demanget, N.; Duprey, A.; Badel, P.; Orgéas, L.; Avril, S.; Geindreau, C.; Albertini, J.-N.; Favre, J.-P. Finite Element Analysis of the Mechanical Performances of 8 Marketed Aortic Stent-Grafts. J. Endovasc. Ther. 2013, 20, 523–535. [Google Scholar] [CrossRef]
- De Bock, S.; Iannaccone, F.; De Beule, M.; Van Loo, D.; Vermassen, F.; Verhegghe, B.; Segers, P. Filling the Void: A Coalescent Numerical and Experimental Technique to Determine Aortic Stent Graft Mechanics. J. Biomech. 2013, 46, 2477–2482. [Google Scholar] [CrossRef]
- Gasser, T.C.; Görgülü, G.; Folkesson, M.; Swedenborg, J. Failure Properties of Intraluminal Thrombus in Abdominal Aortic Aneurysm under Static and Pulsating Mechanical Loads. J. Vasc. Surg. 2008, 48, 179–188. [Google Scholar] [CrossRef]
- Roccabianca, S.; Figueroa, C.A.; Tellides, G.; Humphrey, J.D. Quantification of Regional Differences in Aortic Stiffness in the Aging Human. J. Mech. Behav. Biomed. Mater. 2014, 29, 618–634. [Google Scholar] [CrossRef]
- Haskett, D.; Johnson, G.; Zhou, A.; Utzinger, U.; Vande Geest, J. Microstructural and Biomechanical Alterations of the Human Aorta as a Function of Age and Location. Biomech. Model Mechanobiol. 2010, 9, 725–736. [Google Scholar] [CrossRef]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic Modelling of Arterial Layers with Distributed Collagen Fibre Orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Niestrawska, J.A.; Ogden, R.W.; Reinisch, A.J.; Schriefl, A.J. Modelling Non-Symmetric Collagen Fibre Dispersion in Arterial Walls. J. R. Soc. Interface 2015, 12, 20150188. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Li, Z.; Basciano, C.; Seelecke, S.; Farber, M. Computational Mechanics of Nitinol Stent Grafts. J. Biomech. 2008, 41, 2370–2378. [Google Scholar] [CrossRef]
- Auricchio, F.; Conti, M.; Marconi, S.; Reali, A.; Tolenaar, J.L.; Trimarchi, S. Patient-Specific Aortic Endografting Simulation: From Diagnosis to Prediction. Comput. Biol. Med. 2013, 43, 386–394. [Google Scholar] [CrossRef]
- Hemmler, A.; Lutz, B.; Reeps, C.; Kalender, G.; Gee, M.W. A Methodology for in Silico Endovascular Repair of Abdominal Aortic Aneurysms. Biomech. Model. Mechanobiol. 2018, 17, 1139–1164. [Google Scholar] [CrossRef]
- Roy, D.; Kauffmann, C.; Delorme, S.; Lerouge, S.; Cloutier, G.; Soulez, G. A Literature Review of the Numerical Analysis of Abdominal Aortic Aneurysms Treated with Endovascular Stent Grafts. Comput. Math Methods Med. 2012, 2012, 820389. [Google Scholar] [CrossRef]
- Wolf, I.; Vetter, M.; Wegner, I.; Böttger, T.; Nolden, M.; Schöbinger, M.; Hastenteufel, M.; Kunert, T.; Meinzer, H.-P. The Medical Imaging Interaction Toolkit. Med. Image Anal. 2005, 9, 594–604. [Google Scholar] [CrossRef]
- Yoo, T.S.; Ackerman, M.J.; Lorensen, W.E.; Schroeder, W.; Chalana, V.; Aylward, S.; Metaxas, D.; Whitaker, R. Engineering and Algorithm Design for an Image Processing Api: A Technical Report on ITK--the Insight Toolkit. Stud. Health Technol. Inf. 2002, 85, 586–592. [Google Scholar]
- Arthurs, C.J.; Khlebnikov, R.; Melville, A.; Marčan, M.; Gomez, A.; Dillon-Murphy, D.; Cuomo, F.; Silva Vieira, M.; Schollenberger, J.; Lynch, S.R.; et al. CRIMSON: An Open-Source Software Framework for Cardiovascular Integrated Modelling and Simulation. PLoS Comput. Biol. 2021, 17, e1008881. [Google Scholar] [CrossRef]
- Antiga, L.; Piccinelli, M.; Botti, L.; Ene-Iordache, B.; Remuzzi, A.; Steinman, D.A. An Image-Based Modeling Framework for Patient-Specific Computational Hemodynamics. Med. Biol. Eng. Comput. 2008, 46, 1097–1112. [Google Scholar] [CrossRef]
- Toussaint, J.F.; LaMuraglia, G.M.; Southern, J.F.; Fuster, V.; Kantor, H.L. Magnetic Resonance Images Lipid, Fibrous, Calcified, Hemorrhagic, and Thrombotic Components of Human Atherosclerosis in Vivo. Circulation 1996, 94, 932–938. [Google Scholar] [CrossRef] [PubMed]
- Hatsukami, T.S.; Ross, R.; Polissar, N.L.; Yuan, C. Visualization of Fibrous Cap Thickness and Rupture in Human Atherosclerotic Carotid Plaque in Vivo with High-Resolution Magnetic Resonance Imaging. Circulation 2000, 102, 959–964. [Google Scholar] [CrossRef] [PubMed]
- de Jaegere, P.; De Santis, G.; Rodriguez-Olivares, R.; Bosmans, J.; Bruining, N.; Dezutter, T.; Rahhab, Z.; El Faquir, N.; Collas, V.; Bosmans, B.; et al. Patient-Specific Computer Modeling to Predict Aortic Regurgitation after Transcatheter Aortic Valve Replacement. JACC Cardiovasc. Interv. 2016, 9, 508–512. [Google Scholar] [CrossRef] [PubMed]
- Rocatello, G.; El Faquir, N.; De Santis, G.; Iannaccone, F.; Bosmans, J.; De Backer, O.; Sondergaard, L.; Segers, P.; De Beule, M.; de Jaegere, P.; et al. Patient-Specific Computer Simulation to Elucidate the Role of Contact Pressure in the Development of New Conduction Abnormalities after Catheter-Based Implantation of a Self-Expanding Aortic Valve. Circ. Cardiovasc. Interv. 2018, 11, e005344. [Google Scholar] [CrossRef] [PubMed]
- Perrin, D.; Badel, P.; Orgéas, L.; Geindreau, C.; Dumenil, A.; Albertini, J.-N.; Avril, S. Patient-Specific Numerical Simulation of Stent-Graft Deployment: Validation on Three Clinical Cases. J. Biomech. 2015, 48, 1868–1875. [Google Scholar] [CrossRef]
- De Bock, S.; Iannaccone, F.; De Beule, M.; Vermassen, F.; Segers, P.; Verhegghe, B. What If You Stretch the IFU? A Mechanical Insight into Stent Graft Instructions For Use in Angulated Proximal Aneurysm Necks. Med. Eng. Phys. 2014, 36, 1567–1576. [Google Scholar] [CrossRef]
- Derycke, L.; Sénémaud, J.; Perrin, D.; Avril, S.; Desgranges, P.; Albertini, J.-N.; Cochennec, F.; Haulon, S. Patient Specific Computer Modelling for Automated Sizing of Fenestrated Stent Grafts. Eur. J. Vasc. Endovasc. Surg. 2020, 59, 237–246. [Google Scholar] [CrossRef]
- Hemmler, A.; Lin, A.; Thierfelder, N.; Franz, T.; Gee, M.W.; Bezuidenhout, D. Customized Stent-Grafts for Endovascular Aneurysm Repair with Challenging Necks: A Numerical Proof of Concept. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3316. [Google Scholar] [CrossRef]
- He, Y.; Northrup, H.; Le, H.; Cheung, A.K.; Berceli, S.A.; Shiu, Y.T. Medical Image-Based Computational Fluid Dynamics and Fluid-Structure Interaction Analysis in Vascular Diseases. Front. Bioeng. Biotechnol. 2022, 10, 855791. [Google Scholar] [CrossRef]
- Xu, H.; Baroli, D.; Veneziani, A. Global Sensitivity Analysis for Patient-Specific Aortic Simulations: The Role of Geometry, Boundary Condition and Large Eddy Simulation Modeling Parameters. J. Biomech. Eng. 2021, 143, 021012. [Google Scholar] [CrossRef]
- Gallo, D.; De Santis, G.; Negri, F.; Tresoldi, D.; Ponzini, R.; Massai, D.; Deriu, M.A.; Segers, P.; Verhegghe, B.; Rizzo, G.; et al. On the Use of in Vivo Measured Flow Rates as Boundary Conditions for Image-Based Hemodynamic Models of the Human Aorta: Implications for Indicators of Abnormal Flow. Ann. Biomed. Eng. 2012, 40, 729–741. [Google Scholar] [CrossRef]
- Perrin, D.; Badel, P.; Orgeas, L.; Geindreau, C.; du Roscoat, S.R.; Albertini, J.-N.; Avril, S. Patient-Specific Simulation of Endovascular Repair Surgery with Tortuous Aneurysms Requiring Flexible Stent-Grafts. J. Mech. Behav. Biomed. Mater. 2016, 63, 86–99. [Google Scholar] [CrossRef]
- De Bock, S.; Iannaccone, F.; De Santis, G.; De Beule, M.; Van Loo, D.; Devos, D.; Vermassen, F.; Segers, P.; Verhegghe, B. Virtual Evaluation of Stent Graft Deployment: A Validated Modeling and Simulation Study. J. Mech. Behav. Biomed. Mater. 2012, 13, 129–139. [Google Scholar] [CrossRef]
- Raffort, J.; Adam, C.; Carrier, M.; Ballaith, A.; Coscas, R.; Jean-Baptiste, E.; Hassen-Khodja, R.; Chakfé, N.; Lareyre, F. Artificial Intelligence in Abdominal Aortic Aneurysm. J. Vasc. Surg. 2020, 72, 321–333.e1. [Google Scholar] [CrossRef]
- Adam, C.; Fabre, D.; Mougin, J.; Zins, M.; Azarine, A.; Ardon, R.; d’Assignies, G.; Haulon, S. Pre-Surgical and Post-Surgical Aortic Aneurysm Maximum Diameter Measurement: Full Automation by Artificial Intelligence. Eur. J. Vasc. Endovasc. Surg. 2021, 62, 869–877. [Google Scholar] [CrossRef]
- Chakshu, N.K.; Sazonov, I.; Nithiarasu, P. Towards Enabling a Cardiovascular Digital Twin for Human Systemic Circulation Using Inverse Analysis. Biomech. Model Mechanobiol. 2021, 20, 449–465. [Google Scholar] [CrossRef]
- Vad, S.; Eskinazi, A.; Corbett, T.; McGloughlin, T.; Vande Geest, J.P. Determination of Coefficient of Friction for Self-Expanding Stent-Grafts. J. Biomech. Eng. 2010, 132, 121007. [Google Scholar] [CrossRef]
- Hemmler, A.; Lutz, B.; Kalender, G.; Reeps, C.; Gee, M.W. Patient-Specific in Silico Endovascular Repair of Abdominal Aortic Aneurysms: Application and Validation. Biomech. Model. Mechanobiol. 2019, 18, 983–1004. [Google Scholar] [CrossRef]
- Gindre, J.; Bel-Brunon, A.; Rochette, M.; Lucas, A.; Kaladji, A.; Haigron, P.; Combescure, A. Patient-Specific Finite-Element Simulation of the Insertion of Guidewire during an EVAR Procedure: Guidewire Position Prediction Validation on 28 Cases. IEEE Trans. Biomed. Eng. 2016, 64, 1057–1066. [Google Scholar] [CrossRef]
- Hemmler, A.; Lutz, B.; Reeps, C.; Gee, M.W. In Silico Study of Vessel and Stent-Graft Parameters on the Potential Success of Endovascular Aneurysm Repair. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3237. [Google Scholar] [CrossRef]
- Abbott, E.; Dhara, S.; Khabaz, K.; Sankary, S.; Cao, K.; Nguyen, N.; Babrowski, T.; Pocivavsek, L.; Milner, R. Computational Analysis of Endovascular Aortic Repair Proximal Seal Zone Preservation with Endoanchors: A Case Study in Cylindrical Neck Anatomy. JVS-Vasc. Sci. 2021, 2, 170–178. [Google Scholar] [CrossRef] [PubMed]
- Gindre, J.; Bel-Brunon, A.; Kaladji, A.; Duménil, A.; Rochette, M.; Lucas, A.; Haigron, P.; Combescure, A. Finite Element Simulation of the Insertion of Guidewires during an EVAR Procedure: Example of a Complex Patient Case, a First Step toward Patient-Specific Parameterized Models. Int. J. Numer. Methods Biomed. Eng. 2015, 31, e02716. [Google Scholar] [CrossRef] [PubMed]
- Daoudal, A.; Gindre, J.; Lalys, F.; Kafi, M.; Dupont, C.; Lucas, A.; Haigron, P.; Kaladji, A. Use of Numerical Simulation to Predict Iliac Complications During Placement of An Aortic Stent Graft. Ann. Vasc. Surg. 2019, 61, 291–298. [Google Scholar] [CrossRef] [PubMed]
- Isselbacher, E.M.; Preventza, O.; Black, J.H.; Augoustides, J.G.; Beck, A.W.; Bolen, M.A.; Braverman, A.C.; Bray, B.E.; Brown-Zimmerman, M.M.; Chen, E.P.; et al. 2022 ACC/AHA Guideline for the Diagnosis and Management of Aortic Disease: A Report of the American Heart Association/American College of Cardiology Joint Committee on Clinical Practice Guidelines. Circulation 2022, 146, e334–e482. [Google Scholar] [CrossRef] [PubMed]
- Romarowski, R.M.; Conti, M.; Morganti, S.; Grassi, V.; Marrocco-Trischitta, M.M.; Trimarchi, S.; Auricchio, F. Computational Simulation of TEVAR in the Ascending Aorta for Optimal Endograft Selection: A Patient-Specific Case Study. Comput. Biol. Med. 2018, 103, 140–147. [Google Scholar] [CrossRef]
- Arokiaraj, M.C.; De Beule, M.; De Santis, G. A Novel Sax-Stent Method in Treatment of Ascending Aorta and Aortic Arch Aneurysms Evaluated by Finite Element Simulations. JMV-J. De Médecine Vasc. 2017, 42, 39–45. [Google Scholar] [CrossRef]
- Derycke, L.; Perrin, D.; Cochennec, F.; Albertini, J.-N.; Avril, S. Predictive Numerical Simulations of Double Branch Stent-Graft Deployment in an Aortic Arch Aneurysm. Ann. Biomed. Eng. 2019, 47, 1051–1062. [Google Scholar] [CrossRef]
- Altnji, H.-E.; Bou-Said, B.; Walter-Le Berre, H. Numerical Simulation of the Migration Phenomena and Type 1a Endoleak of Thoracic Aneurysm Endograft. Comput. Methods Biomech. Biomed. Engin. 2013, 16 (Suppl. 1), 36–38. [Google Scholar] [CrossRef]
- Altnji, H.-E.; Bou-Saïd, B.; Walter-Le Berre, H. Morphological and Stent Design Risk Factors to Prevent Migration Phenomena for a Thoracic Aneurysm: A Numerical Analysis. Med. Eng. Phys. 2015, 37, 23–33. [Google Scholar] [CrossRef]
- Caimi, A.; Pasquali, M.; Sturla, F.; Pluchinotta, F.R.; Giugno, L.; Carminati, M.; Redaelli, A.; Votta, E. Prediction of Post-Stenting Biomechanics in Coarcted Aortas: A Pilot Finite Element Study. J. Biomech. 2020, 105, 109796. [Google Scholar] [CrossRef]
- Ramella, A.; Migliavacca, F.; Rodriguez Matas, J.F.; Heim, F.; Dedola, F.; Marconi, S.; Conti, M.; Allievi, S.; Mandigers, T.J.; Bissacco, D.; et al. Validation and Verification of High-Fidelity Simulations of Thoracic Stent-Graft Implantation. Ann. Biomed. Eng. 2022, 50, 1941–1953. [Google Scholar] [CrossRef]
- Shahbazian, N.; Doyle, M.G.; Forbes, T.L.; Amon, C.H. A Modeling Framework for Computational Simulations of Thoracic Endovascular Aortic Repair. Int. J. Numer. Methods Biomed. Eng. 2022, e3578. [Google Scholar] [CrossRef]
- Shahbazian, N.; Romero, D.A.; Forbes, T.L.; Amon, C.H. Identification of Geometric and Mechanical Factors Predictive of Bird-Beak Configuration in Thoracic Endovascular Aortic Repair Using Computational Models of Stent Graft Deployment. JVS Vasc. Sci. 2022, 3, 259–273. [Google Scholar] [CrossRef]
- Sanford, R.M.; Crawford, S.A.; Genis, H.; Doyle, M.G.; Forbes, T.L.; Amon, C.H. Predicting Rotation in Fenestrated Endovascular Aneurysm Repair Using Finite Element Analysis. J. Biomech. Eng. 2018, 140. [Google Scholar] [CrossRef]
- Dupont, C.; Kaladji, A.; Rochette, M.; Saudreau, B.; Lucas, A.; Haigron, P. Numerical Simulation of Fenestrated Graft Deployment: Anticipation of Stent Graft and Vascular Structure Adequacy. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e03409. [Google Scholar] [CrossRef]
- Kliewer, M.E.; Bordet, M.; Chavent, B.; Reijnen, M.M.P.J.; Frisch, N.; Midy, D.; Feugier, P.; Millon, A.; Lardenoije, J.-W.; Assadian, A.; et al. Assessment of Fenestrated Anaconda Stent Graft Design by Numerical Simulation: Results of a European Prospective Multicenter Study. J. Vasc. Surg. 2022, 75, 99–108.e2. [Google Scholar] [CrossRef]
- Meng, Z.; Ma, T.; Cai, Y.; Liu, X.; Wang, S.; Dong, Z.; Fu, W. Numerical Modeling and Simulations of Type B Aortic Dissection Treated by Stent-Grafts with Different Oversizing Ratios. Artif. Organs 2020, 44, 1202–1210. [Google Scholar] [CrossRef]
- Ma, T.; Dong, Z.H.; Wang, S.; Meng, Z.Y.; Chen, Y.Y.; Fu, W.G. Computational Investigation of Interaction between Stent Graft and Aorta in Retrograde Type A Dissection after Thoracic Endovascular Aortic Repair for Type B Aortic Dissection. J. Vasc. Surg. 2018, 68, 14S–21S.e2. [Google Scholar] [CrossRef]
- Kan, X.; Ma, T.; Dong, Z.; Xu, X.Y. Patient-Specific Virtual Stent-Graft Deployment for Type B Aortic Dissection: A Pilot Study of the Impact of Stent-Graft Length. Front. Physiol. 2021, 12, 718140. [Google Scholar] [CrossRef]
- Yuan, X.; Kan, X.; Xu, X.Y.; Nienaber, C.A. Finite Element Modeling to Predict Procedural Success of Thoracic Endovascular Aortic Repair in Type A Aortic Dissection. JTCVS Tech. 2020, 4, 40–47. [Google Scholar] [CrossRef]
- Perrin, D.; Demanget, N.; Badel, P.; Avril, S.; Orgéas, L.; Geindreau, C.; Albertini, J.-N. Deployment of Stent Grafts in Curved Aneurysmal Arteries: Toward a Predictive Numerical Tool. Int. J. Numer. Methods Biomed. Eng. 2015, 31, e02698. [Google Scholar] [CrossRef] [PubMed]
- Derycke, L.; Avril, S.; Perrin, D.; Albertini, J.-N.; Cochennec, F. Computer Simulation Model May Prevent Thoracic Stent-Graft Collapse Complication. Circ. Cardiovasc. Imaging 2022, 15, e013764. [Google Scholar] [CrossRef] [PubMed]
- Niestrawska, J.A.; Ch Haspinger, D.; Holzapfel, G.A. The Influence of Fiber Dispersion on the Mechanical Response of Aortic Tissues in Health and Disease: A Computational Study. Comput. Methods Biomech. Biomed. Engin. 2018, 21, 99–112. [Google Scholar] [CrossRef]
- Maier, A.; Gee, M.W.; Reeps, C.; Eckstein, H.-H.; Wall, W.A. Impact of Calcifications on Patient-Specific Wall Stress Analysis of Abdominal Aortic Aneurysms. Biomech. Model Mechanobiol. 2010, 9, 511–521. [Google Scholar] [CrossRef] [PubMed]
- Reeps, C.; Maier, A.; Pelisek, J.; Härtl, F.; Grabher-Meier, V.; Wall, W.A.; Essler, M.; Eckstein, H.-H.; Gee, M.W. Measuring and Modeling Patient-Specific Distributions of Material Properties in Abdominal Aortic Aneurysm Wall. Biomech. Model Mechanobiol. 2013, 12, 717–733. [Google Scholar] [CrossRef]
- Humphrey, J.D.; Holzapfel, G.A. Mechanics, Mechanobiology, and Modeling of Human Abdominal Aorta and Aneurysms. J. Biomech. 2012, 45, 805–814. [Google Scholar] [CrossRef]
- Figueroa, C.A.; Taylor, C.A.; Yeh, V.; Chiou, A.J.; Zarins, C.K. Effect of Curvature on Displacement Forces Acting on Aortic Endografts: A 3-Dimensional Computational Analysis. J. Endovasc. Ther. 2009, 16, 284–294. [Google Scholar] [CrossRef]
- Dal Santo, N.; Manzoni, A.; Pagani, S.; Quarteroni, A. Reduced-Order Modeling for Applications to the Cardiovascular System. In Applications; De Gruyter: Berlin, Germany, 2020; pp. 251–278. [Google Scholar]
- Acosta Santamaría, V.; Daniel, G.; Perrin, D.; Albertini, J.; Rosset, E.; Avril, S. Model Reduction Methodology for Computational Simulations of Endovascular Repair. Comput. Methods Biomech. Biomed. Eng. 2018, 21, 139–148. [Google Scholar] [CrossRef]
- Pionteck, A.; Pierrat, B.; Gorges, S.; Albertini, J.; Avril, S. Simulation of the Deployment of an Endoprosthesis in Real Time. Google Patents FR1908569, 29 July 2019. [Google Scholar]
- Auricchio, F.; Constantinescu, A.; Conti, M.; Scalet, G. Fatigue of Metallic Stents: From Clinical Evidence to Computational Analysis. Ann. Biomed. Eng. 2016, 44, 287–301. [Google Scholar] [CrossRef]
- Munshi, B.; Parker, L.P.; Norman, P.E.; Doyle, B.J. The Application of Computational Modeling for Risk Prediction in Type B Aortic Dissection. J. Vasc. Surg. 2020, 71, 1789–1801.e3. [Google Scholar] [CrossRef]
- Krittanawong, C.; Virk, H.U.H.; Bangalore, S.; Wang, Z.; Johnson, K.W.; Pinotti, R.; Zhang, H.; Kaplin, S.; Narasimhan, B.; Kitai, T.; et al. Machine Learning Prediction in Cardiovascular Diseases: A Meta-Analysis. Sci. Rep. 2020, 10, 16057. [Google Scholar] [CrossRef]
- Nana, P.; Dakis, K.; Brodis, A.; Spanos, K.; Kouvelos, G. Circulating Biomarkers for the Prediction of Abdominal Aortic Aneurysm Growth. J. Clin. Med. 2021, 10, 1718. [Google Scholar] [CrossRef]
- Lareyre, F.; Adam, C.; Carrier, M.; Dommerc, C.; Mialhe, C.; Raffort, J. A Fully Automated Pipeline for Mining Abdominal Aortic Aneurysm Using Image Segmentation. Sci. Rep. 2019, 9, 13750. [Google Scholar] [CrossRef]
- Viceconti, M.; Pappalardo, F.; Rodriguez, B.; Horner, M.; Bischoff, J.; Tshinanu, F.M. In Silico Trials: Verification, Validation and Uncertainty Quantification of Predictive Models Used in the Regulatory Evaluation of Biomedical Products. Methods 2021, 185, 120–127. [Google Scholar] [CrossRef]
- Avril, S.; Gee, M.W.; Hemmler, A.; Rugonyi, S. Patient-Specific Computational Modeling of Endovascular Aneurysm Repair: State of the Art and Future Directions. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e3529. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derycke, L.; Avril, S.; Millon, A. Patient-Specific Numerical Simulations of Endovascular Procedures in Complex Aortic Pathologies: Review and Clinical Perspectives. J. Clin. Med. 2023, 12, 766. https://doi.org/10.3390/jcm12030766
Derycke L, Avril S, Millon A. Patient-Specific Numerical Simulations of Endovascular Procedures in Complex Aortic Pathologies: Review and Clinical Perspectives. Journal of Clinical Medicine. 2023; 12(3):766. https://doi.org/10.3390/jcm12030766
Chicago/Turabian StyleDerycke, Lucie, Stephane Avril, and Antoine Millon. 2023. "Patient-Specific Numerical Simulations of Endovascular Procedures in Complex Aortic Pathologies: Review and Clinical Perspectives" Journal of Clinical Medicine 12, no. 3: 766. https://doi.org/10.3390/jcm12030766
APA StyleDerycke, L., Avril, S., & Millon, A. (2023). Patient-Specific Numerical Simulations of Endovascular Procedures in Complex Aortic Pathologies: Review and Clinical Perspectives. Journal of Clinical Medicine, 12(3), 766. https://doi.org/10.3390/jcm12030766