A Novel Time Lag Method for the Analysis of Mixed Gas Diffusion in Polymeric Membranes by On-Line Mass Spectrometry: Pressure Dependence of Transport Parameters
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Membrane Preparation
2.2.1. Dense SBS Film Preparation
2.2.2. SBS Thin Film Composite Membrane Preparation
2.2.3. Dense PIM-SBF-1 Film Preparation
2.3. Pure Gas Permeation Measurements
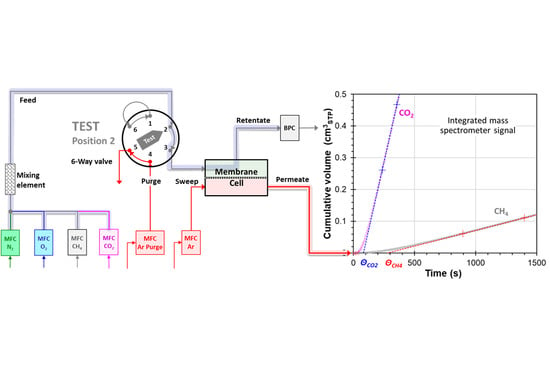
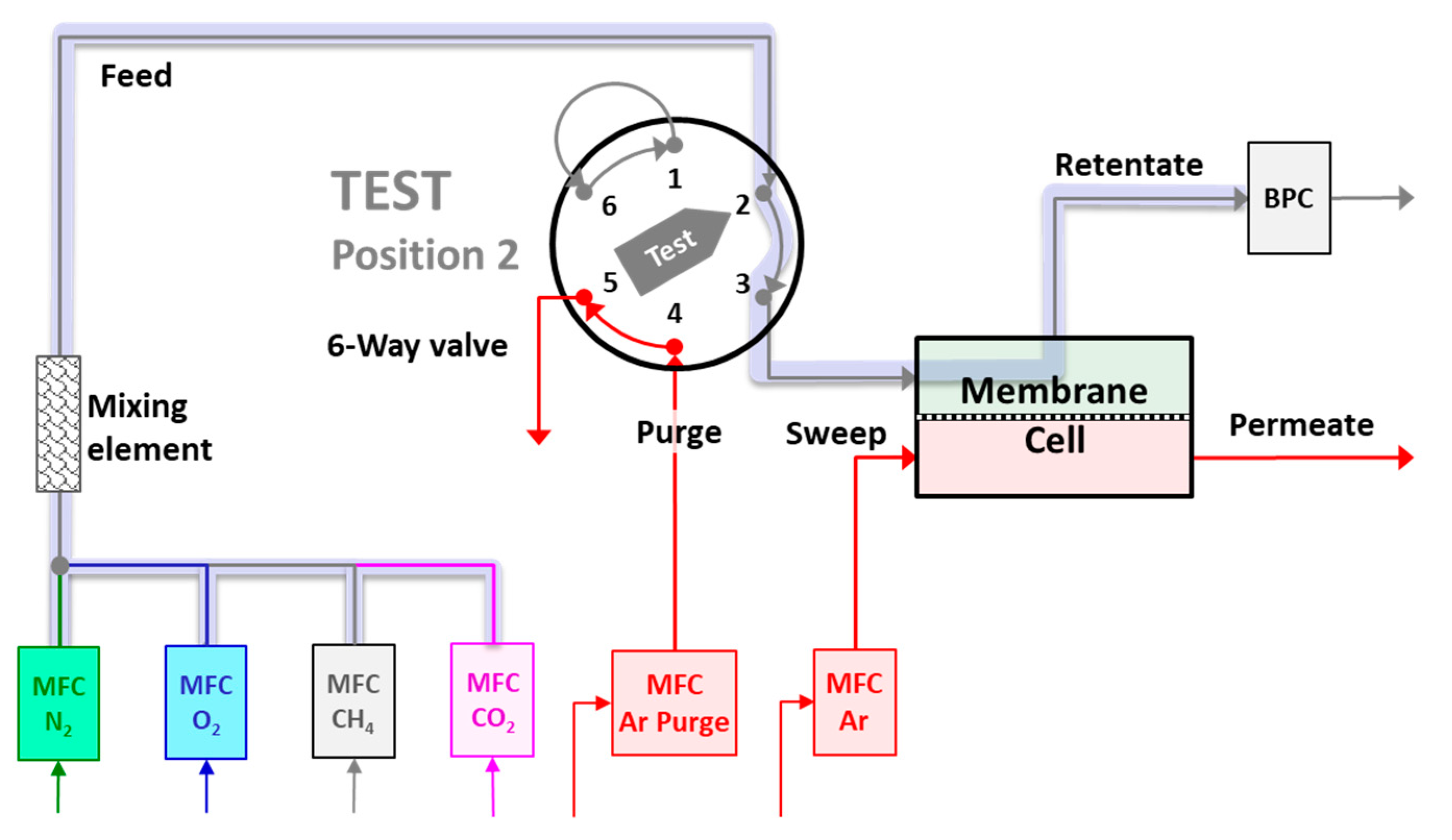
2.4. Mixed Gas Permeation Measurements
3. Results and Discussion
3.1. System Response and Setup
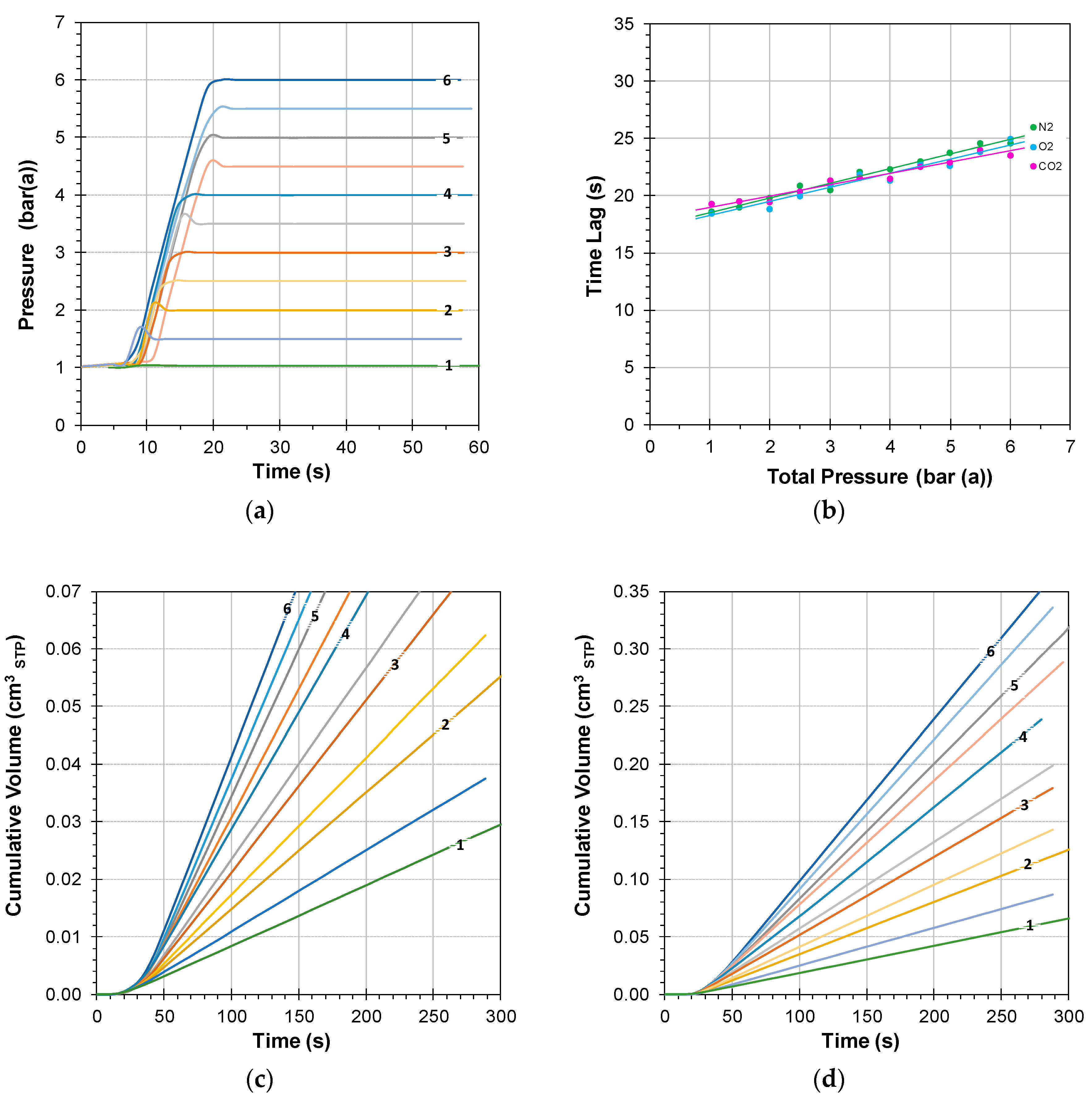
3.1.1. Instrumental Time Lag at Atmospheric Feed Pressure
3.1.2. Instrumental Time Lag at Variable Feed Pressure
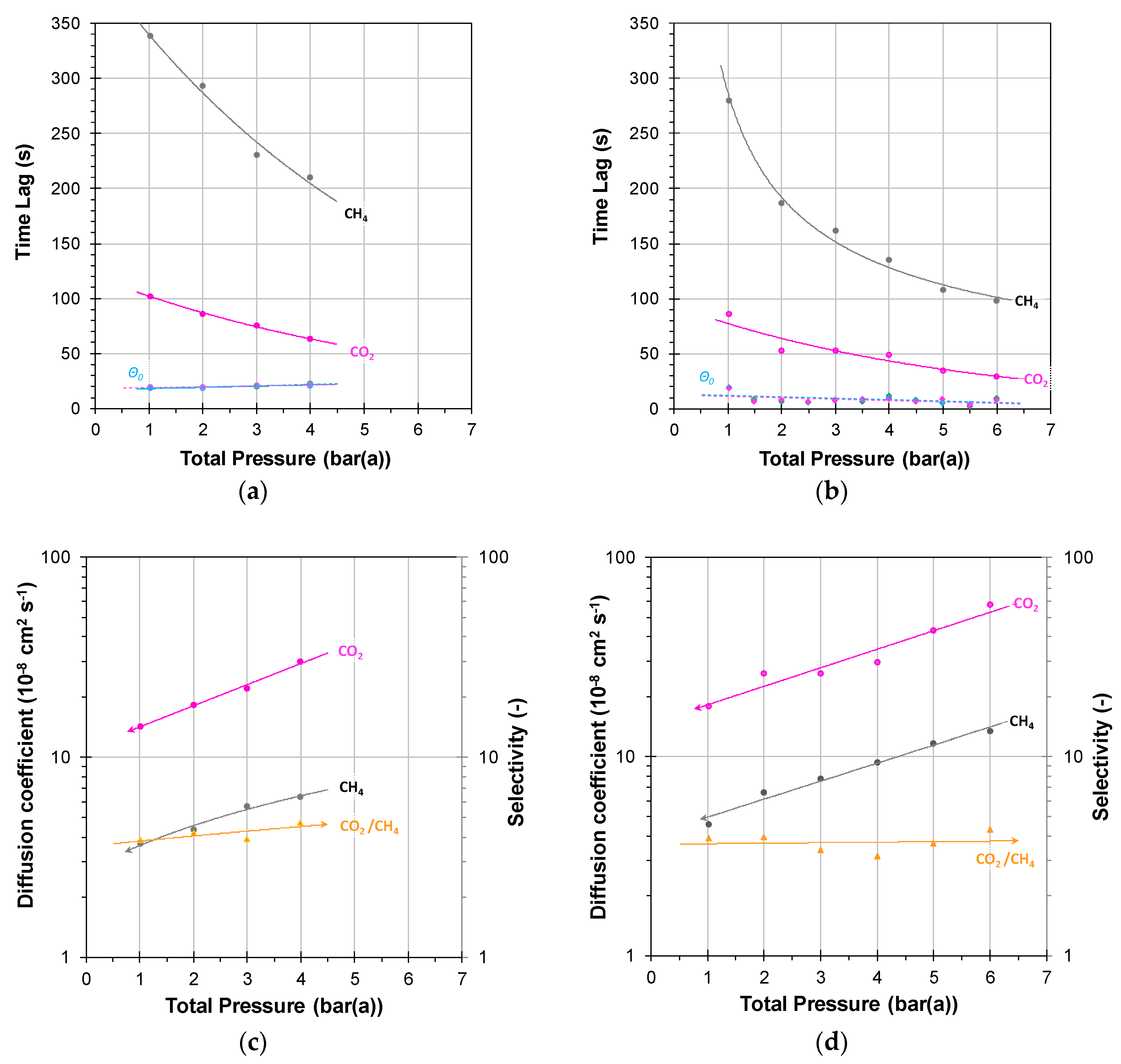
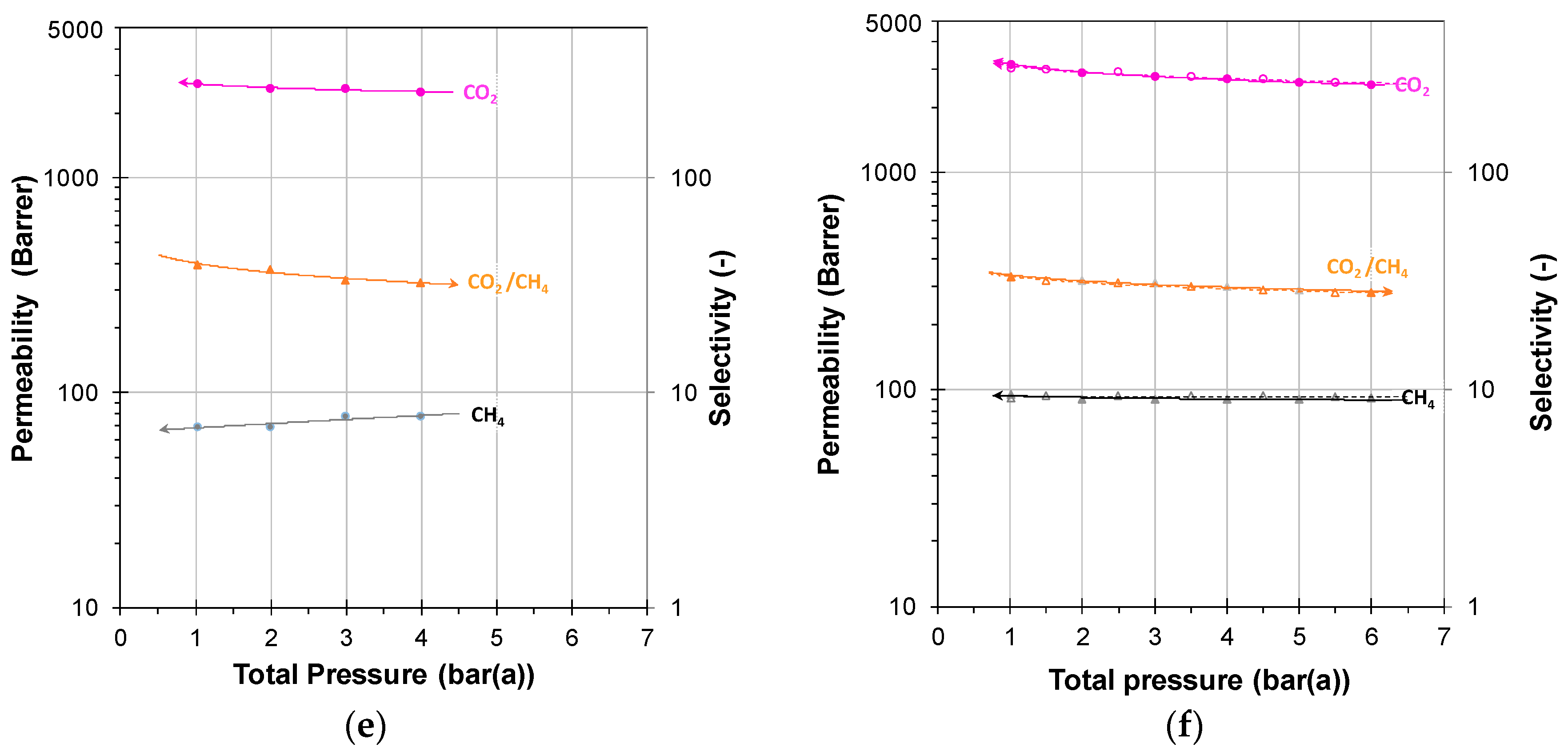
3.2. Mixed Gas Diffusion in the Polymer of Intrinsic Microporosity PIM-SBF-1
3.2.1. Individual Pressure Steps
3.2.2. Incremental Pressure Steps
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Galizia, M.; Chi, W.S.; Smith, Z.P.; Merkel, T.C.; Baker, R.W.; Freeman, B.D. 50th Anniversary perspective: Polymers and mixed matrix membranes for gas and vapor separation: A review and prospective opportunities. Macromolecules 2017, 50, 7809–7843. [Google Scholar] [CrossRef]
- Thomas, S.; Pinnau, I.; Du, N.; Guiver, M.D. Pure- and mixed-gas permeation properties of a microporous spirobisindane-based ladder polymer (PIM-1). J. Memb. Sci. 2009, 333, 125–131. [Google Scholar] [CrossRef]
- Koros, W.J.; Chern, R.T.; Stannett, V.; Hopfenberg, H.B. Model for permeation of mixed gases and vapors in glassy polymers. J. Polym. Sci. Part A-2 Polym. Phys. 1981, 19, 1513–1530. [Google Scholar] [CrossRef]
- Alaslai, N.; Ghanem, B.; Alghunaimi, F.; Litwiller, E.; Pinnau, I. Pure- and mixed-gas permeation properties of highly selective and plasticization resistant hydroxyl-diamine-based 6FDA polyimides for CO2/CH4 separation. J. Membr. Sci. 2016, 505, 100–107. [Google Scholar] [CrossRef]
- Raharjo, R.D.; Freeman, B.D.; Sanders, E.S. Pure and mixed gas CH4 and n-C4H10 sorption and dilation in poly(dimethylsiloxane). J. Membr. Sci. 2007, 292, 45–61. [Google Scholar] [CrossRef]
- Vopička, O.; De Angelis, M.G.; Sarti, G.C. Mixed gas sorption in glassy polymeric membranes: I. CO2/CH4 and n-C4/CH4 mixtures sorption in poly(1-trimethylsilyl-1-propyne) (PTMSP). J. Membr. Sci. 2014, 449, 97–108. [Google Scholar] [CrossRef]
- Vopička, O.; De Angelis, M.G.; Du, N.; Li, N.; Guiver, M.D.; Sarti, G.C. Mixed gas sorption in glassy polymeric membranes: II. CO2/CH4 mixtures in a polymer of intrinsic microporosity (PIM-1). J. Membr. Sci. 2014, 459, 264–276. [Google Scholar] [CrossRef]
- Rizzuto, C.; Caravella, A.; Brunetti, A.; Park, C.H.; Lee, Y.M.; Drioli, E.; Barbieri, G.; Tocci, E. Sorption and Diffusion of CO2/N2 in gas mixture in thermally-rearranged polymeric membranes: A molecular investigation. J. Membr. Sci. 2017, 528, 135–146. [Google Scholar] [CrossRef]
- Minelli, M.; De Angelis, M.G.; Baschetti, M.G.; Doghieri, F.; Sarti, G.C.; Ribeiro, C.P.; Freeman, B.D. Equation of state modeling of the solubility of CO2/C2H6 mixtures in cross-linked poly(ethylene oxide). Ind. Eng. Chem. Res. 2015, 54, 1142–1152. [Google Scholar] [CrossRef]
- Tanis, I.; Brown, D.; Neyertz, S.; Heck, R.; Mercier, R.; Vaidya, M.; Ballaguet, J.P. A comparison of pure and mixed-gas permeation of nitrogen and methane in 6FDA-based polyimides as studied by molecular dynamics simulations. Comput. Mater. Sci. 2018, 141, 243–253. [Google Scholar] [CrossRef]
- Guzmán, J.; Garrido, L. Determination of carbon dioxide transport coefficients in liquids and polymers by NMR spectroscopy. J. Phys. Chem. B 2012, 116, 6050–6058. [Google Scholar] [CrossRef] [PubMed]
- Garrido, L.; García, C.; López-González, M.; Comesaña-Gándara, B.; Lozano, Á.E.; Guzmán, J. Determination of gas transport coefficients of mixed gases in 6FDA-TMPDA polyimide by NMR spectroscopy. Macromolecules 2017, 50, 3590–3597. [Google Scholar] [CrossRef]
- Chen, J.; Loo, L.; Wang, K. A novel time lag method to measure the permeation of vapor-gas mixtures. J. Membr. Sep. Technol. 2012, 1, 94–99. [Google Scholar]
- Schäfer, T.; Vital, J.; Crespo, J.G. Coupled pervaporation/mass spectrometry for investigating membrane mass transport phenomena. J. Membr. Sci. 2004, 241, 197–205. [Google Scholar] [CrossRef]
- Brazinha, C.; Fonseca, A.P.; Teodoro, O.M.N.D.; Crespo, J.G. On-line and real-time monitoring of organophilic pervaporation by mass spectrometry. J. Membr. Sci. 2010, 347, 83–92. [Google Scholar] [CrossRef]
- Fraga, S.C.; Trabucho, L.; Brazinha, C.; Crespo, J.G. Characterisation and modelling of transient transport through dense membranes using on-line mass spectrometry. J. Membr. Sci. 2015, 479, 213–222. [Google Scholar] [CrossRef]
- Tanaka, K.; Kita, H.; Okamoto, K.I.; Noble, R.D.; Falconer, J.L. Isotopic-transient permeation measurements in steady-state pervaporation through polymeric membranes. J. Membr. Sci. 2002, 197, 173–183. [Google Scholar] [CrossRef]
- Tremblay, P.; Savard, M.M.; Vermette, J.; Paquin, R. Gas permeability, diffusivity and solubility of nitrogen, helium, methane, carbon dioxide and formaldehyde in dense polymeric membranes using a new on-line permeation apparatus. J. Membr. Sci. 2006, 282, 245–256. [Google Scholar] [CrossRef]
- Fraga, S.C.; Azevedo, M.A.; Coelhoso, I.M.; Brazinha, C.; Crespo, J.G. Steady-state and transient transport studies of gas permeation through dense membranes using on-line mass spectrometry. Sep. Purif. Technol. 2018, 197, 18–26. [Google Scholar] [CrossRef]
- Zhang, Z.; Chattot, R.; Bonorand, L.; Jetsrisuparb, K.; Buchmüller, Y.; Wokaun, A.; Gubler, L. Mass spectrometry to quantify and compare the gas barrier properties of radiation grafted membranes and Nafion®. J. Membr. Sci. 2014, 472, 55–66. [Google Scholar] [CrossRef]
- Pilnacek, K.; Jansen, J.C.; Bernardo, P.; Clarizia, G.; Bazzarelli, F.; Tasselli, F. Determination of Mixed Gas Permeability of High Free Volume Polymers Using Direct Mass Spectrometric Analysis of the Gas Compositions. Procedia Eng. 2012, 44, 1027–1029. [Google Scholar] [CrossRef]
- Carta, M.; Malpass-Evans, R.; Croad, M.; Rogan, Y.; Jansen, J.C.; Bernardo, P.; Bazzarelli, F.; McKeown, N.B. An Efficient Polymer Molecular Sieve for Membrane Gas Separations. Science 2013, 339, 303–307. [Google Scholar] [CrossRef] [PubMed]
- Khdhayyer, M.R.; Esposito, E.; Fuoco, A.; Monteleone, M.; Giorno, L.; Jansen, J.C.; Attfield, M.P.; Budd, P.M. Mixed matrix membranes based on UiO-66 MOFs in the polymer of intrinsic microporosity PIM-1. Sep. Purif. Technol. 2017, 173, 304–313. [Google Scholar] [CrossRef]
- Tocci, E.; De Lorenzo, L.; Bernardo, P.; Clarizia, G.; Bazzarelli, F.; McKeown, N.B.; Carta, M.; Malpass-Evans, R.; Friess, K.; Pilnáček, K.; et al. Molecular modeling and gas permeation properties of a polymer of intrinsic microporosity composed of ethanoanthracene and Tröger’s base units. Macromolecules 2014, 47, 7900–7916. [Google Scholar] [CrossRef]
- Daynes, H.A. The Process of Diffusion through a Rubber Membrane. Proc. R. Soc. A Math. Phys. Eng. Sci. 1920, 97, 286–307. [Google Scholar] [CrossRef]
- Crank, J.; Park, G.S. Diffusion in Polymers; Academic Press: Cambridge, MA, USA, 1968. [Google Scholar]
- Taveira, P.; Mendes, A.; Costa, C. On the determination of diffusivity and sorption coefficients using different time-lag models. J. Membr. Sci. 2003, 221, 123–133. [Google Scholar] [CrossRef]
- Al-Qasas, N.; Thibault, J.; Kruczek, B. The effect of the downstream pressure accumulation on the time-lag accuracy for membranes with non-linear isotherms. J. Membr. Sci. 2016, 511, 119–129. [Google Scholar] [CrossRef]
- Al-Qasas, N.; Thibault, J.; Kruczek, B. A new characterization method of membranes with nonlinear sorption isotherm systems based on continuous upstream and downstream time-lag measurements. J. Membr. Sci. 2017, 542, 91–101. [Google Scholar] [CrossRef]
- Grzywna, Z.J.; Borys, P.; Kruczek, B. On the well-posed problems for diffusion with time dependent boundary condition. Sep. Sci. Technol. 2011, 46, 2427–2435. [Google Scholar] [CrossRef]
- Rutherford, S.W.; Do, D.D. Review of time lag permeation technique as a method for characterisation of porous media and membranes. Adsorption 1997, 3, 283–312. [Google Scholar] [CrossRef]
- Minelli, M.; Sarti, G.C. Gas transport in glassy polymers: Prediction of diffusional time lag. Membranes 2018, 8, 8. [Google Scholar] [CrossRef] [PubMed]
- Jansen, J.C.; Friess, K.; Drioli, E. Organic vapour transport in glassy perfluoropolymer membranes: A simple semi-quantitative approach to analyze clustering phenomena by time lag measurements. J. Membr. Sci. 2011, 367, 141–151. [Google Scholar] [CrossRef]
- Ziegel, K.D.; Frensdorft, H.K.; Blair, D.E. Measurement of hydrogen isotope transport in poly(vinyl fluoride) films by the permeation-rate method. J. Polym. Sci. Part A-2 Polym. Phys. 1969, 7, 809–819. [Google Scholar] [CrossRef]
- Fraga, S.C.; Monteleone, M.; Lanč, M.; Esposito, E.; Fuoco, A.; Giorno, L.; Pilnáček, K.; Friess, K.; Carta, M.; McKeown, N.B.; et al. A novel time lag method for the analysis of mixed gas diffusion in polymeric membranes by on-line mass spectrometry: Method development and validation. J. Membr. Sci. 2018, 561, 39–58. [Google Scholar] [CrossRef]
- Bezzu, C.G.; Carta, M.; Tonkins, A.; Jansen, J.C.; Bernardo, P.; Bazzarelli, F.; McKeown, N.B. A Spirobifluorene-Based Polymer of Intrinsic Microporosity with Improved Performance for Gas Separation. Adv. Mater. 2012, 24, 5930–5933. [Google Scholar] [CrossRef] [PubMed]
- Bezzu, C.G.; Carta, M.; Ferrari, M.C.; Jansen, J.C.; Monteleone, M.; Esposito, E.; Fuoco, A.; Hart, K.; Liyana-Arachchi, T.P.; Colina, C.M.; et al. The synthesis, chain-packing simulation and long-term gas permeability of highly selective spirobifluorene-based polymers of intrinsic microporosity. J. Mater. Chem. A 2018, 6, 10507–10514. [Google Scholar] [CrossRef]
- Bazzarelli, F.; Bernardo, P.; Tasselli, F.; Clarizia, G.; Dzyubenko, V.G.G.; Vdovin, P.; Jansen, J.C.C. Multilayer composite SBS membranes for pervaporation and gas separation. Sep. Purif. Technol. 2011, 80, 635–642. [Google Scholar] [CrossRef]
- Santoro, S.; Galiano, F.; Jansen, J.C.; Figoli, A. Strategy for scale-up of SBS pervaporation membranes for ethanol recovery from diluted aqueous solutions. Sep. Purif. Technol. 2017, 176, 252–261. [Google Scholar] [CrossRef]
- Vopička, O.; Hynek, V.; Zgažar, M.; Friess, K.; Šípek, M. A new sorption model with a dynamic correction for the determination of diffusion coefficients. J. Membr. Sci. 2009, 330, 51–56. [Google Scholar] [CrossRef]
- Vopička, O.; Friess, K.; Hynek, V.; Sysel, P.; Zgažar, M.; Šípek, M.; Pilnáček, K.; Lanč, M.; Jansen, J.C.; Mason, C.R.; et al. Equilibrium and transient sorption of vapours and gases in the polymer of intrinsic microporosity PIM-1. J. Membr. Sci. 2013, 434, 148–160. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford University Press: New York, NY, USA, 1975. [Google Scholar]
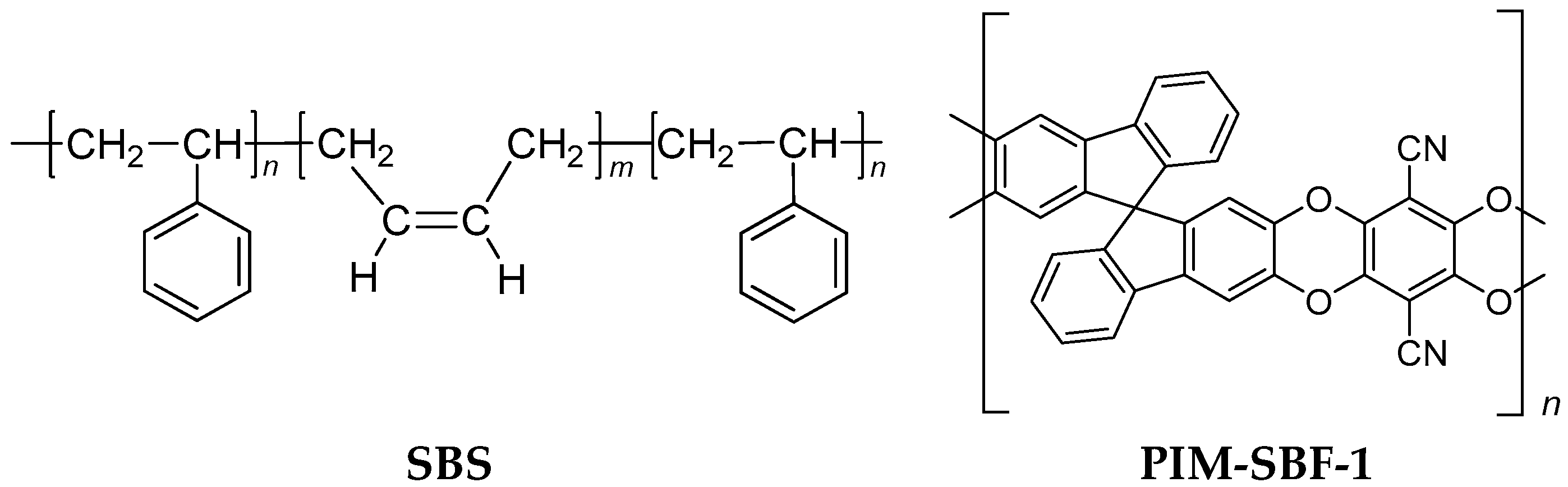

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monteleone, M.; Esposito, E.; Fuoco, A.; Lanč, M.; Pilnáček, K.; Friess, K.; Bezzu, C.G.; Carta, M.; McKeown, N.B.; Jansen, J.C. A Novel Time Lag Method for the Analysis of Mixed Gas Diffusion in Polymeric Membranes by On-Line Mass Spectrometry: Pressure Dependence of Transport Parameters. Membranes 2018, 8, 73. https://doi.org/10.3390/membranes8030073
Monteleone M, Esposito E, Fuoco A, Lanč M, Pilnáček K, Friess K, Bezzu CG, Carta M, McKeown NB, Jansen JC. A Novel Time Lag Method for the Analysis of Mixed Gas Diffusion in Polymeric Membranes by On-Line Mass Spectrometry: Pressure Dependence of Transport Parameters. Membranes. 2018; 8(3):73. https://doi.org/10.3390/membranes8030073
Chicago/Turabian StyleMonteleone, Marcello, Elisa Esposito, Alessio Fuoco, Marek Lanč, Kryštof Pilnáček, Karel Friess, Caterina Grazia Bezzu, Mariolino Carta, Neil Bruce McKeown, and Johannes Carolus Jansen. 2018. "A Novel Time Lag Method for the Analysis of Mixed Gas Diffusion in Polymeric Membranes by On-Line Mass Spectrometry: Pressure Dependence of Transport Parameters" Membranes 8, no. 3: 73. https://doi.org/10.3390/membranes8030073
APA StyleMonteleone, M., Esposito, E., Fuoco, A., Lanč, M., Pilnáček, K., Friess, K., Bezzu, C. G., Carta, M., McKeown, N. B., & Jansen, J. C. (2018). A Novel Time Lag Method for the Analysis of Mixed Gas Diffusion in Polymeric Membranes by On-Line Mass Spectrometry: Pressure Dependence of Transport Parameters. Membranes, 8(3), 73. https://doi.org/10.3390/membranes8030073