Evaluation of the Genericity of an Adaptive Optimal Control Approach to Optimize Membrane Filtration Systems
Abstract
1. Introduction
- (i)
- It generalizes the control approach to multiple membrane systems;
- (ii)
- It tests it under severe disturbance and uncertainty conditions;
- (iii)
- It quantitatively assesses its performance in terms of fouling control, energy savings, and membrane lifespan extension.
2. Materials and Methods
2.1. Control Model
2.1.1. Fouling Dynamics
2.1.2. Productivity and Energy Consumption
2.2. Control Strategies: An Optimal Control Approach
2.2.1. An Optimal Control Strategy and Its Limits
2.2.2. An Adaptive Optimal Control Approach
2.2.3. Control Evaluation
- TM for Temporized Mode. This control refers to the application of filtration and cleaning sequences on a regular basis fixed once and for all without considering any optimization problem;
- OLOC for Open Loop Optimal Control. In such a control strategy, the optimal length of the filtration and cleaning phases are computed again once and for all but are the result of an optimization procedure;
- AOC for adaptive optimal control. In such a strategy, the lengths of the filtration and cleaning phases are optimal and are recomputed on a regular basis in order to adapt the control to the actual state of the system.
2.3. Two Virtual Processes: The Membrane Filtration Simulation Models
3. Results and Discussion
3.1. Identification of Simulation Models
3.1.1. Literature Data Used to Validate the Process Simulation Model
3.1.2. Identification of Simulation Model Parameters
3.2. Comparison of Different Control Laws Applied to Systems A and B
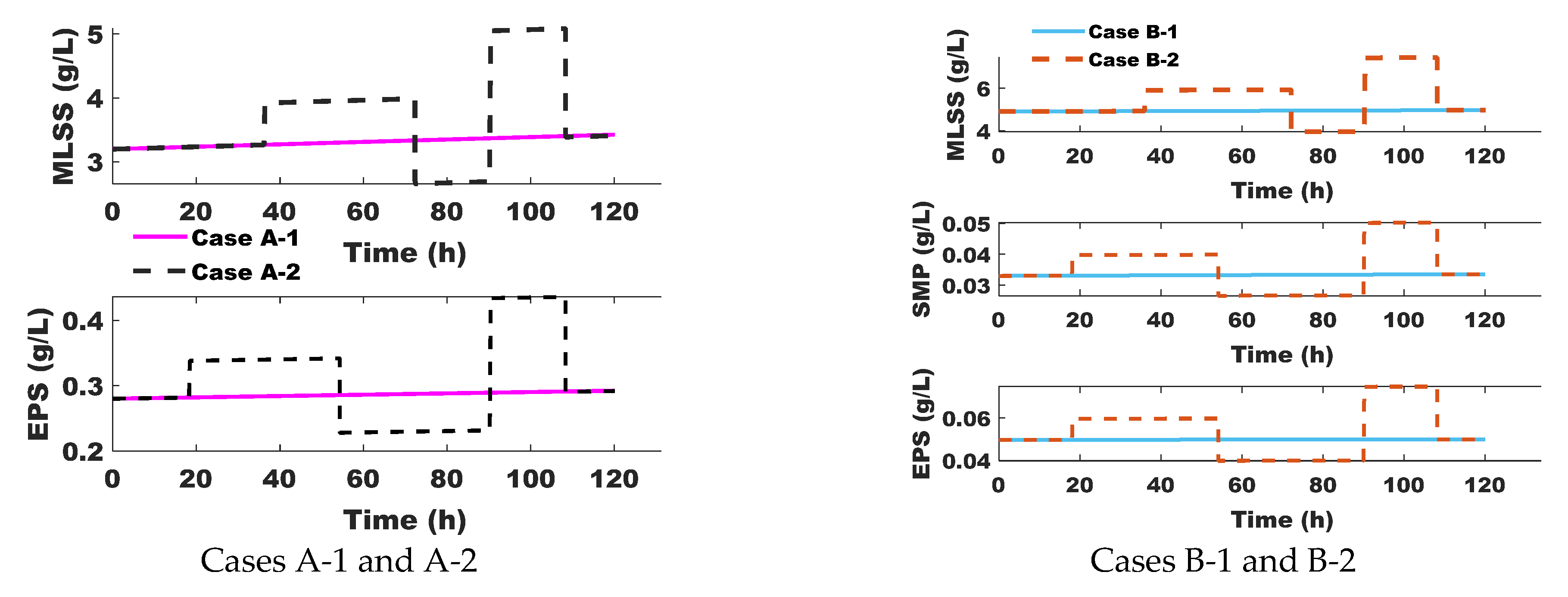
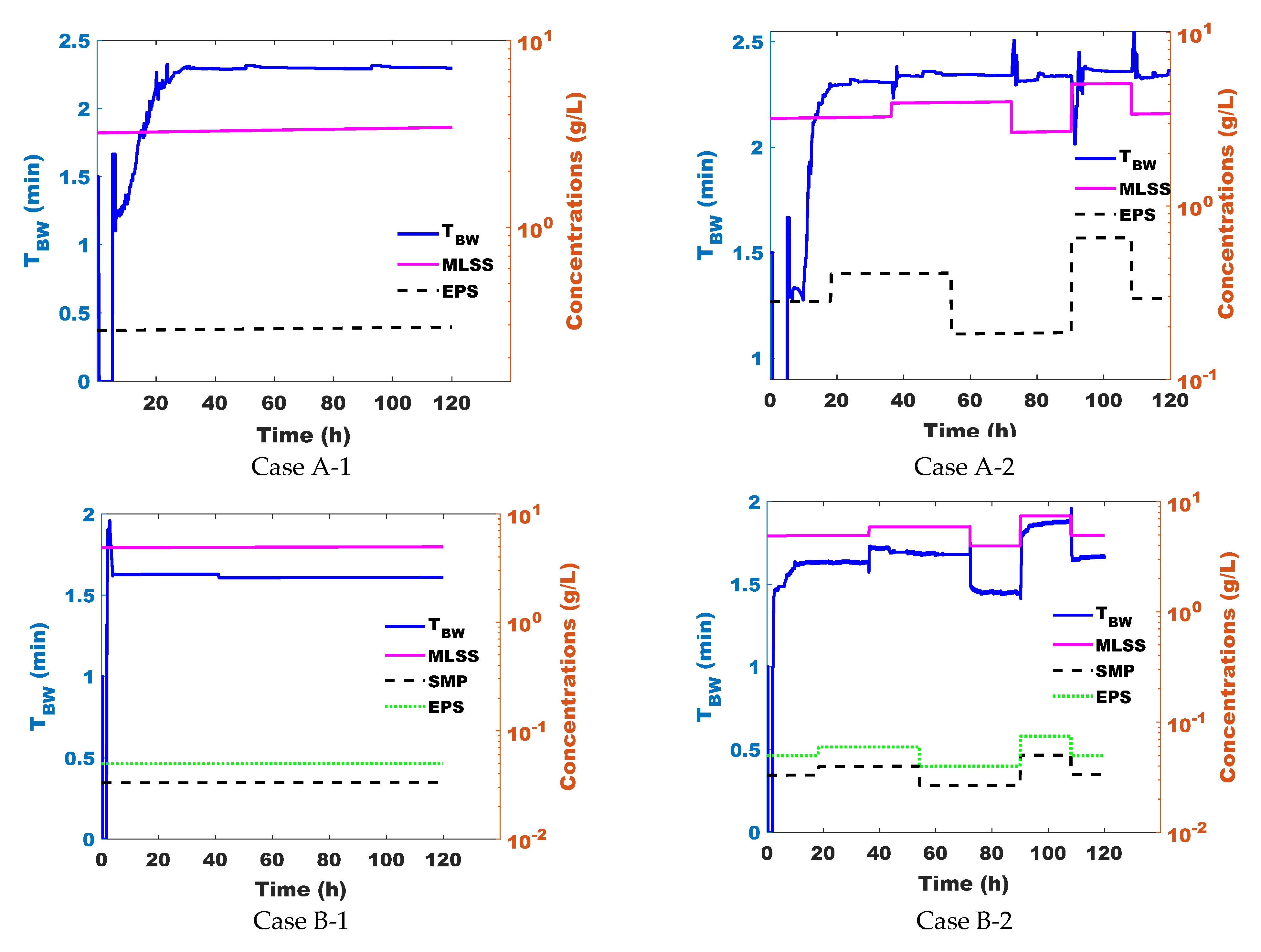
3.2.1. Perturbation Description
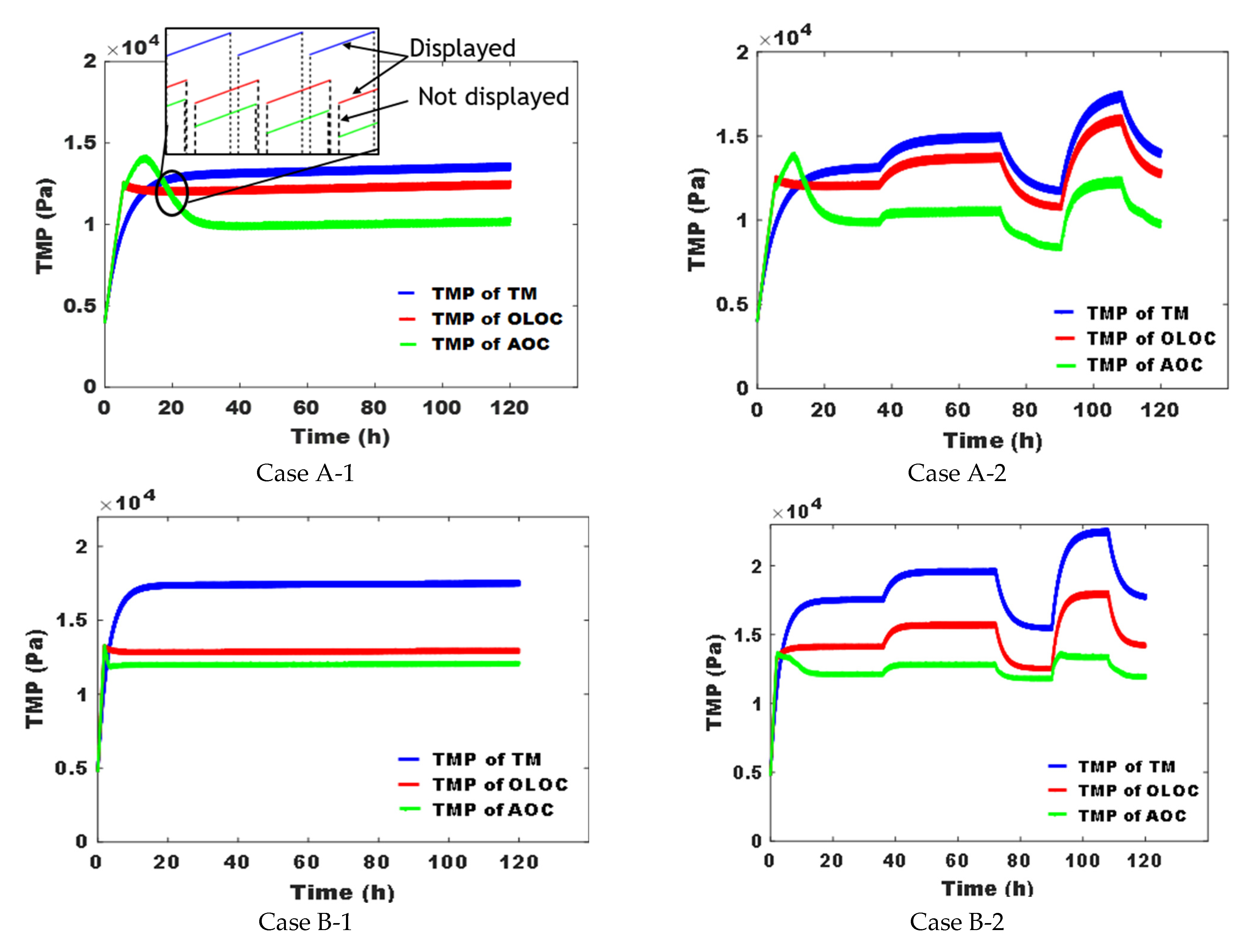
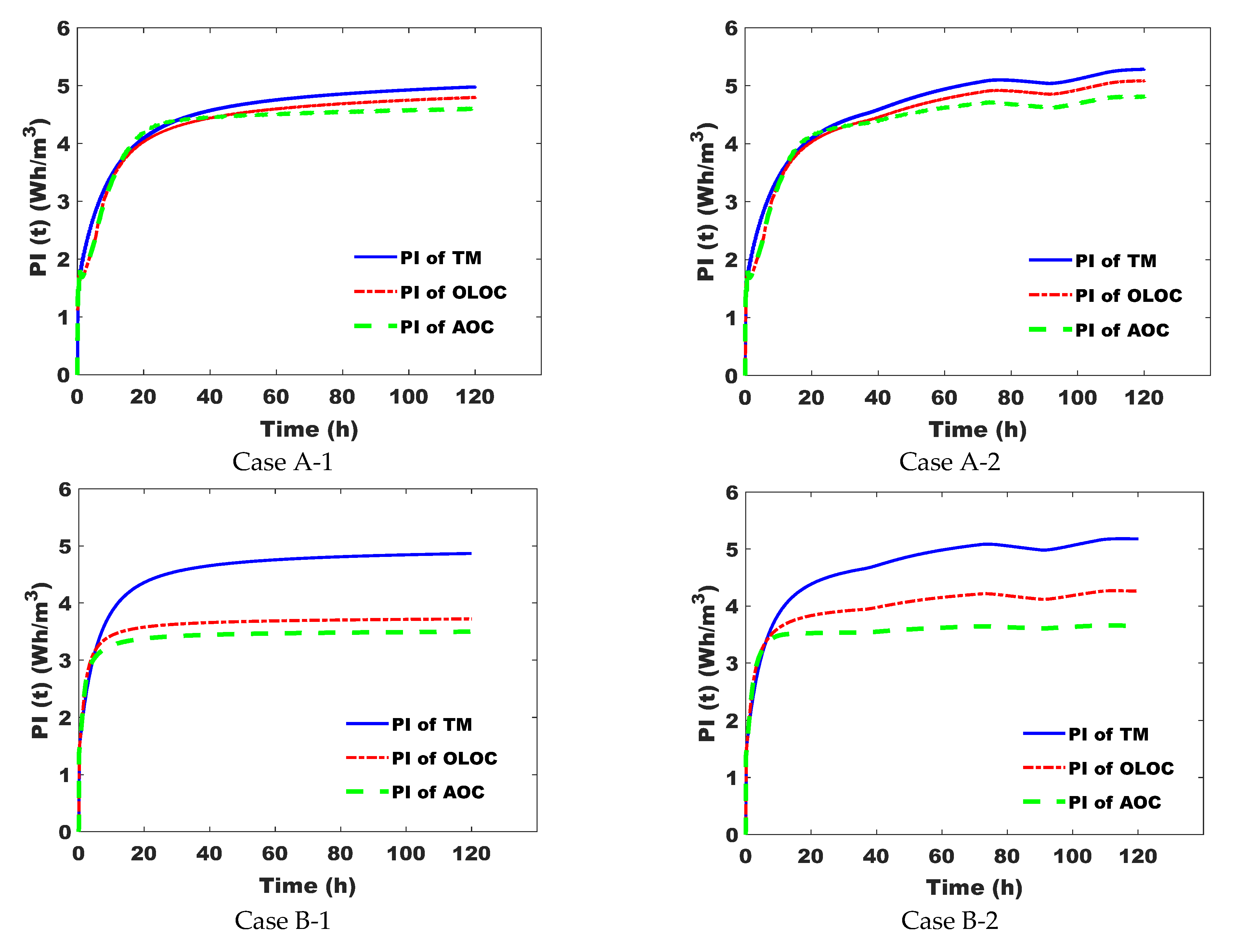
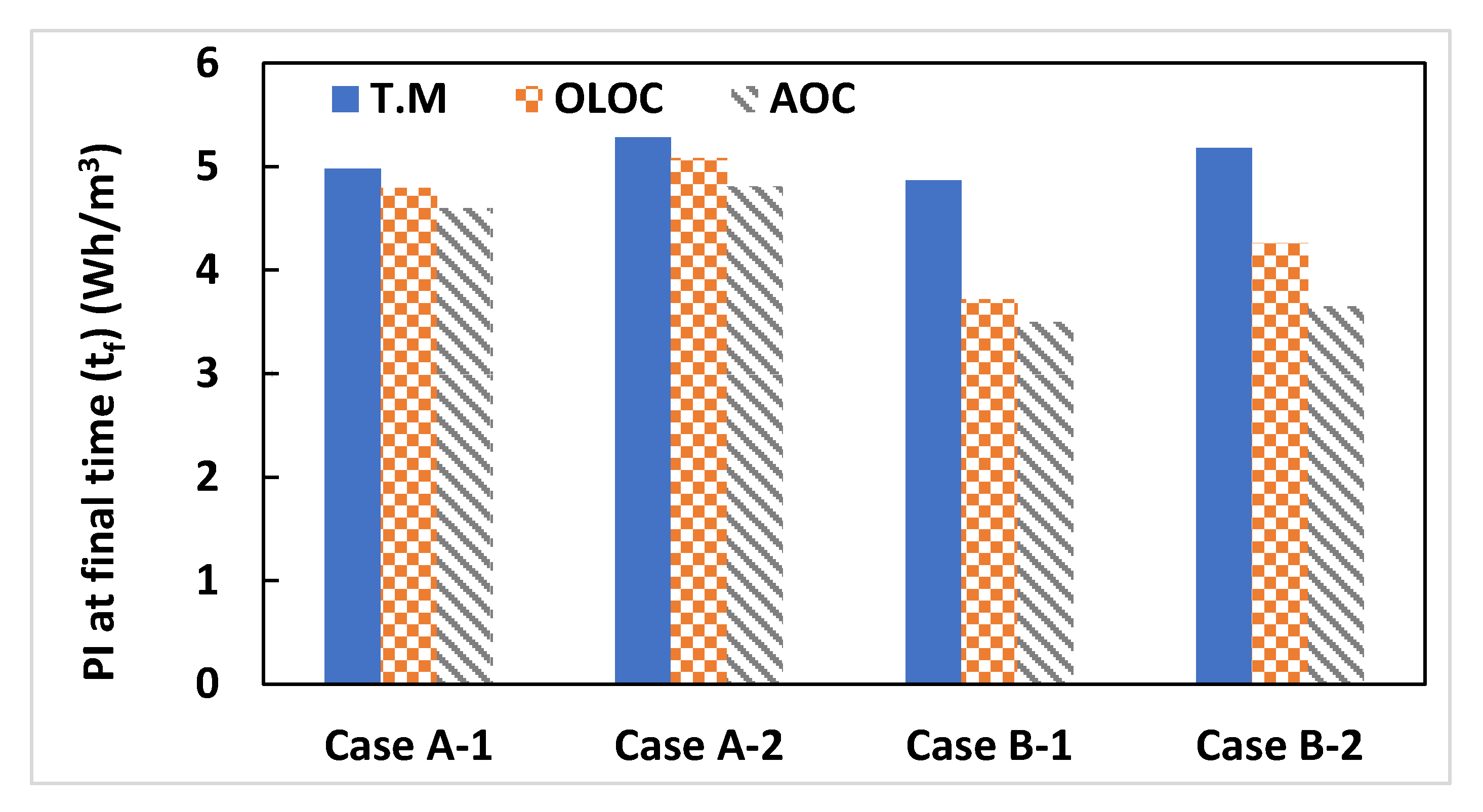
3.2.2. Control Evaluation Scenarios and Simulation Results
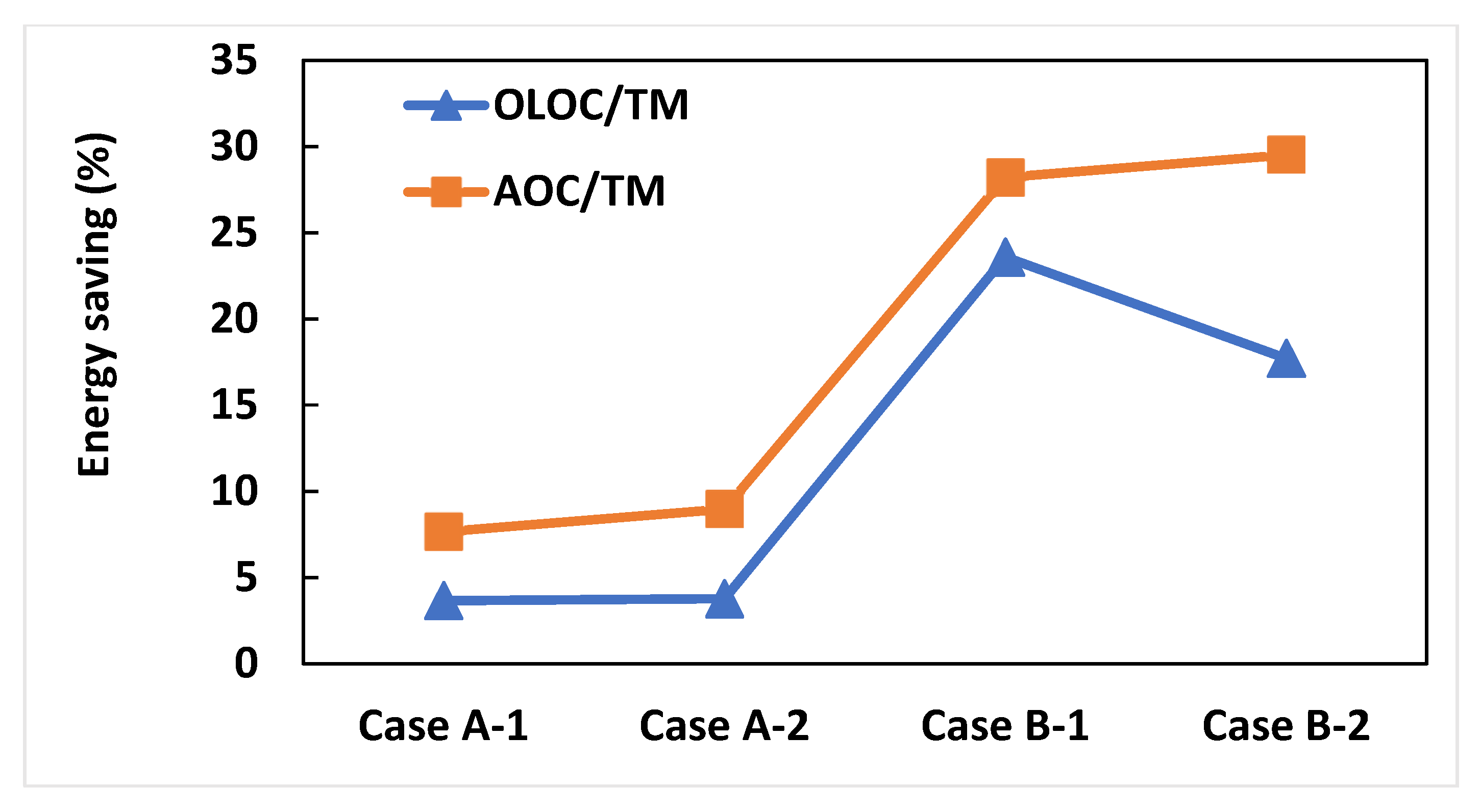
3.2.3. Discussions and Control Performance Assessment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Nomenclature
| Parameter | Signification |
| A0 | Entire membrane surface (m2) |
| AOC | Adaptive optimal control |
| Model parameter related to the mass during filtration (s−1) | |
| Model parameter related to physical cleaning efficiency (s−1) | |
| Model parameter related to filtration (kg·m−2·s−1) | |
| Model parameter related to the filtration energy (m5·Pa·s−1·kg−1) | |
| Model parameter related to the physical cleaning energy (m5·Pa·s−1·kg−1) | |
| Attachment coefficients of soluble products (Si) (s−1) | |
| Attachment coefficients of particulate matter (Xi) (s−1) | |
| Model parameter related to the filtration energy (m3·Pa·s−1) | |
| Model parameter related to the physical cleaning energy (m3·Pa·s−1) | |
| EPS | Extracellular Polymeric Substances (g·L−1) |
| ET | Total required energy pumping (Wh) |
| FUM | Membrane Usage Factor (g·m−3) |
| HRT | Hydraulic Retention Time (d) |
| Permeate flux (LMH) | |
| Physical cleaning flux (LMH) | |
| m (or x) | Deposited mass (g) |
| (or ) | Rate of matter deposition onto the membrane (g·h−1) |
| MLSS | Mixed Liquor Suspended Solids (g·L−1) |
| Optimal mass of cake layer (g) | |
| OLOC | Open-Loop Optimal Control |
| PI | Performance Index (Wh·m−3) |
| Inlet flow rate (L·d−1) | |
| Outlet flow rate (L·d−1) | |
| Rt | Total resistance (m−1) |
| R0 | Virgin membrane resistance (m−1) |
| Rg | Cake layer (m−1) |
| SAD | Specific Aeration Demand (Nm³·h−1) |
| Si | Soluble Products (g·L−1) |
| SMP | Soluble Microbial Products (g·L−1) |
| SRT | Solids Retention Time (d) |
| TBW | Duration of physical cleaning phase (min) |
| TM | Temporized Mode |
| TMP | TransMembrane Pressure (Pa) |
| Control variable | |
| Optimal/singular control variable | |
| Reactor volume (L) | |
| VT | Volume of net produced water (m3) |
| Efficiency of physical cleaning (h−1) | |
| Xi | Particulate matter (g·L−1) |
| α | Specific cake resistance coefficient (m·g−1) |
| Fouling rate (s) | |
| σ | Parameter to normalize units (g) |
| Viscosity (Pa·s) |
Appendix A
Appendix A.1. Optimization Strategy
Appendix B
Appendix B.1. Simulation Results—mc(t), Rc(t), Rt(t), and A(t) for the Simulated Case Studies
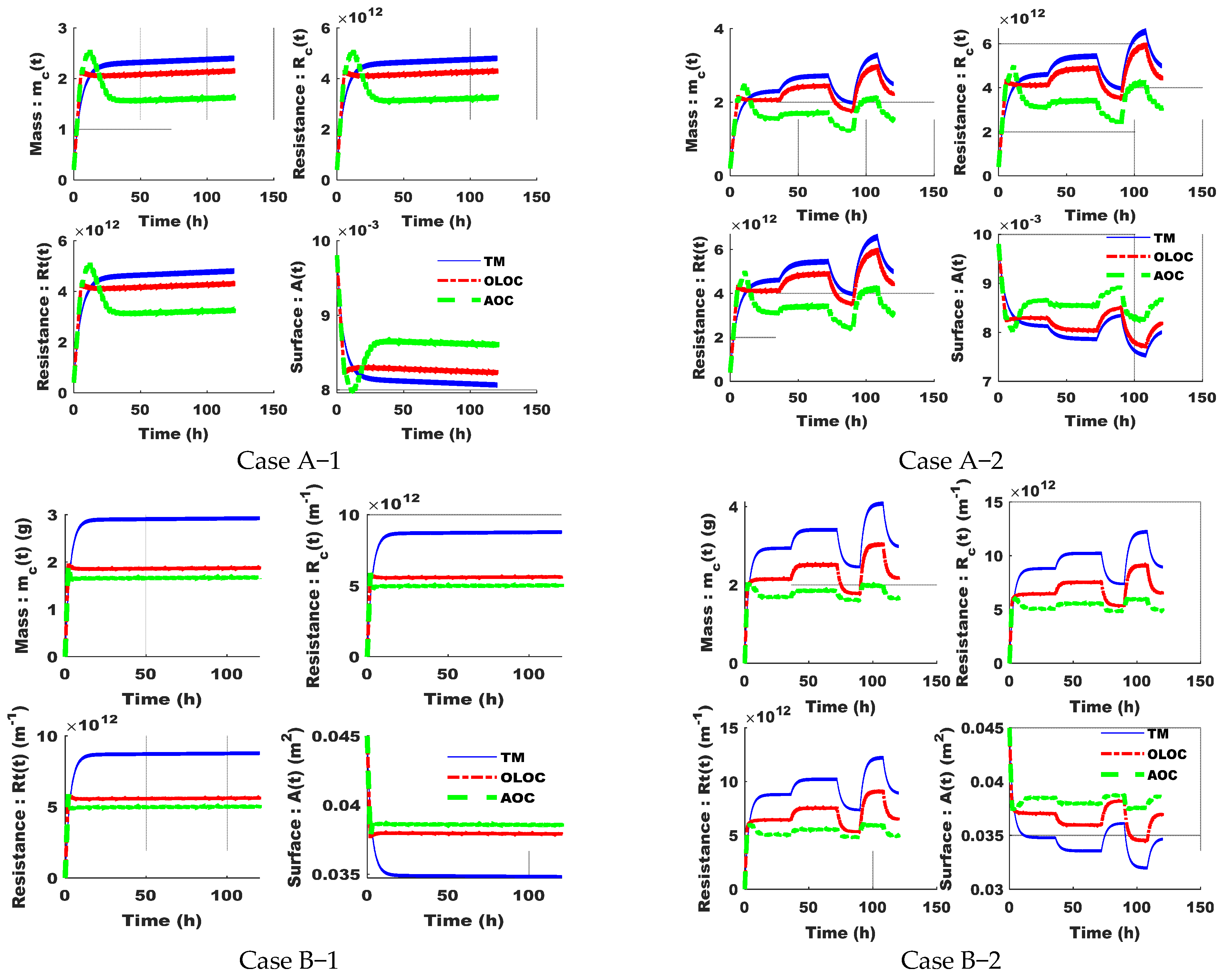
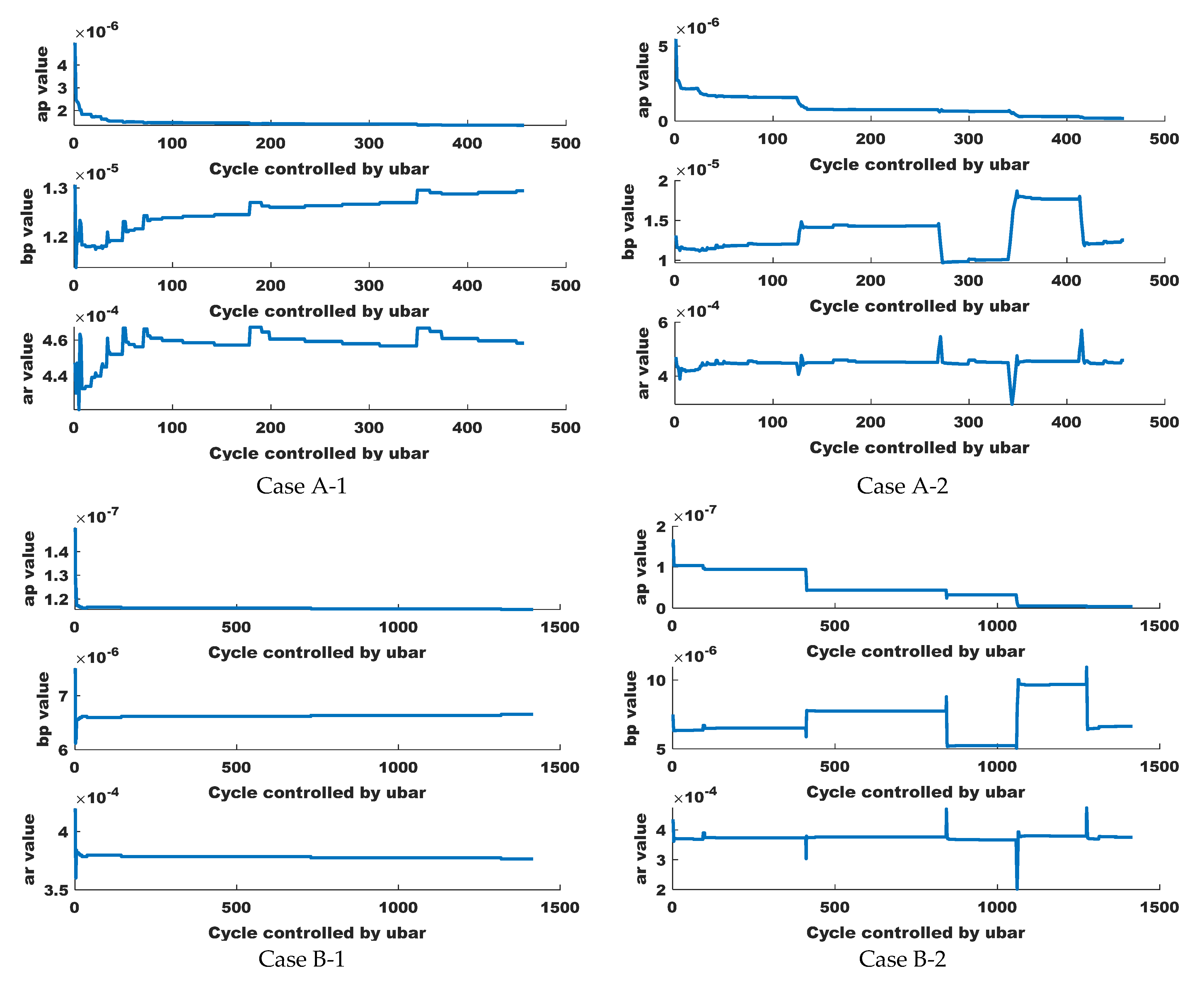
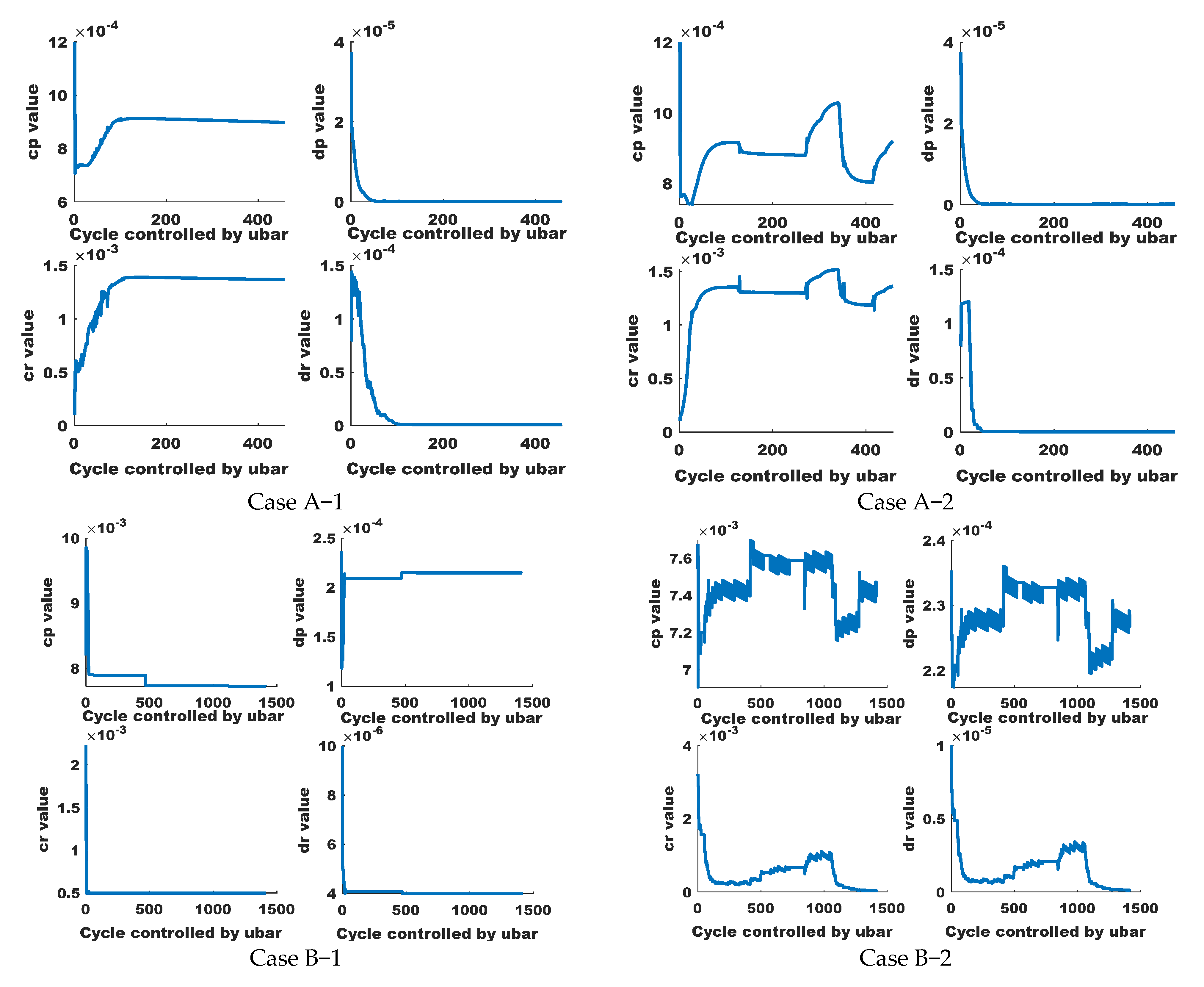
Appendix B.2. Simulation Results—Temporal Variations in the Parameters of the Control Model Identified During the Application of the AOC for the Four Case Studies
References
- Judd, S. The Status of Membrane Bioreactor Technology. Trends Biotechnol. 2008, 26, 109–116. [Google Scholar] [CrossRef]
- Meng, F.; Chae, S.-R.; Drews, A.; Kraume, M.; Shin, H.-S.; Yang, F. Recent Advances in Membrane Bioreactors (MBRs): Membrane Fouling and Membrane Material. Water Res. 2009, 43, 1489–1512. [Google Scholar] [CrossRef]
- Drews, A. Membrane Fouling in Membrane Bioreactors—Characterisation, Contradictions, Cause and Cures. J. Membr. Sci. 2010, 363, 1–28. [Google Scholar] [CrossRef]
- Judd, S. The MBR Book: Principles and Applications of Membrane Bioreactors for Water and Wastewater Treatment; Elsevier: Amsterdam, The Netherlands, 2010; ISBN 978-0-08-096767-7. [Google Scholar]
- Martin, I.; Pidou, M.; Soares, A.; Judd, S.; Jefferson, B. Modelling the Energy Demands of Aerobic and Anaerobic Membrane Bioreactors for Wastewater Treatment. Environ. Technol. 2011, 32, 921–932. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.; Huang, X.; Qian, Y. Domestic Wastewater Treatment Using an Anaerobic Bioreactor Coupled with Membrane Filtration. Process Biochem. 1999, 35, 335–340. [Google Scholar] [CrossRef]
- van Voorthuizen, E.; Zwijnenburg, A.; van der Meer, W.; Temmink, H. Biological Black Water Treatment Combined with Membrane Separation. Water Res. 2008, 42, 4334–4340. [Google Scholar] [CrossRef]
- Chen, J.P.; Kim, S.L.; Ting, Y.P. Optimization of Membrane Physical and Chemical Cleaning by a Statistically Designed Approach. J. Membr. Sci. 2003, 219, 27–45. [Google Scholar] [CrossRef]
- Le-Clech, P.; Chen, V.; Fane, T.A.G. Fouling in Membrane Bioreactors Used in Wastewater Treatment. J. Membr. Sci. 2006, 284, 17–53. [Google Scholar] [CrossRef]
- Robles, A.; Ruano, M.V.; Ribes, J.; Seco, A.; Ferrer, J. Model-Based Automatic Tuning of a Filtration Control System for Submerged Anaerobic Membrane Bioreactors (AnMBR). J. Membr. Sci. 2014, 465, 14–26. [Google Scholar] [CrossRef]
- Cairone, S.; Hasan, S.W.; Choo, K.-H.; Li, C.-W.; Zarra, T.; Belgiorno, V.; Naddeo, V. Integrating Artificial Intelligence Modeling and Membrane Technologies for Advanced Wastewater Treatment: Research Progress and Future Perspectives. Sci. Total Environ. 2024, 944, 173999. [Google Scholar] [CrossRef]
- Chaaben, A.; Ellouze, F.; Amar, N.B.; Rapaport, A.; Héran, M.; Harmand, J. Adaptive Optimal Control of Membrane Processes to Minimize Fouling. In Proceedings of the 2024 European Control Conference (ECC), Stockholm, Sweden, 25–28 June 2024; pp. 1340–1345. [Google Scholar]
- Cogan, N.G.; Chellam, S. A Method for Determining the Optimal Back-Washing Frequency and Duration for Dead-End Microfiltration. J. Membr. Sci. 2014, 469, 410–417. [Google Scholar] [CrossRef]
- Jelemenský, M.; Sharma, A.; Paulen, R.; Fikar, M. Time-Optimal Control of Diafiltration Processes in the Presence of Membrane Fouling. Comput. Chem. Eng. 2016, 91, 343–351. [Google Scholar] [CrossRef]
- Cogan, N.G.; Li, J.; Badireddy, A.R.; Chellam, S. Optimal Backwashing in Dead-End Bacterial Microfiltration with Irreversible Attachment Mediated by Extracellular Polymeric Substances Production. J. Membr. Sci. 2016, 520, 337–344. [Google Scholar] [CrossRef]
- Aichouche, F.; Kalboussi, N.; Rapaport, A.; Harmand, J. Modeling and Optimal Control for Production-Regeneration Systems—Preliminary Results. In Proceedings of the 2020 European Control Conference (ECC), Saint Petersburg, Russia, 12–15 May 2020; pp. 564–569. [Google Scholar]
- Ellouze, F.; Kammoun, Y.; Kalboussi, N.; Rapaport, A.; Harmand, J.; Nasr, S.; Amar, N.B. Optimal Control of Backwash Scheduling for Pumping Energy Saving: Application to the Treatment of Urban Wastewater. J. Water Process Eng. 2023, 56, 104378. [Google Scholar] [CrossRef]
- Benyahia, B.; Charfi, A.; Lesage, G.; Heran, M.; Cherki, B.; Harmand, J. Coupling a Simple and Generic Membrane Fouling Model with Biological Dynamics: Application to the Modeling of an Anaerobic Membrane BioReactor (AnMBR). Membranes 2024, 14, 69. [Google Scholar] [CrossRef]
- Ping Chu, H.; Li, X. Membrane Fouling in a Membrane Bioreactor (MBR): Sludge Cake Formation and Fouling Characteristics. Biotechnol. Bioeng. 2005, 90, 323–331. [Google Scholar] [CrossRef]
- Hermia, J. Blocking Filtration. Application to Non-Newtonian Fluids. In Mathematical Models and Design Methods in Solid-Liquid Separation; Rushton, A., Ed.; Springer: Dordrecht, The Netherlands, 1985; pp. 83–89, ISBN 978-94-009-5091-7. [Google Scholar]
- Gautam, R.K.; Kamilya, T.; Verma, S.; Muthukumaran, S.; Jegatheesan, V.; Navaratna, D. Evaluation of Membrane Cake Fouling Mechanism to Estimate Design Parameters of a Submerged AnMBR Treating High Strength Industrial Wastewater. J. Environ. Manag. 2022, 301, 113867. [Google Scholar] [CrossRef]
- Jeong, Y.; Kim, Y.; Jin, Y.; Hong, S.; Park, C. Comparison of Filtration and Treatment Performance between Polymeric and Ceramic Membranes in Anaerobic Membrane Bioreactor Treatment of Domestic Wastewater. Sep. Purif. Technol. 2018, 199, 182–188. [Google Scholar] [CrossRef]
- Baek, S.H.; Pagilla, K.R.; Kim, H.-J. Lab-Scale Study of an Anaerobic Membrane Bioreactor (AnMBR) for Dilute Municipal Wastewater Treatment. Biotechnol. Bioproc. E 2010, 15, 704–708. [Google Scholar] [CrossRef]
- Domínguez Chabaliná, L.; Baeza Ruiz, J.; Rodríguez Pastor, M.; Prats Rico, D. Influence of EPS and MLSS Concentrations on Mixed Liquor Physical Parameters of Two Membrane Bioreactors. Desalination Water Treat. 2012, 46, 46–59. [Google Scholar] [CrossRef]
- Zsirai, T.; Wang, Z.-Z.; Gabarrón, S.; Connery, K.; Fabiyi, M.; Larrea, A.; Judd, S.J. Biological Treatment and Thickening with a Hollow Fibre Membrane Bioreactor. Water Res. 2014, 58, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Chang, I.-S.; Kim, S.-N. Wastewater Treatment Using Membrane Filtration—Effect of Biosolids Concentration on Cake Resistance. Process Biochem. 2005, 40, 1307–1314. [Google Scholar] [CrossRef]
- Çiçek, N.; Franco, J.P.; Suidan, M.T.; Urbain, V.; Manem, J. Characterization and Comparison of a Membrane Bioreactor and a Conventional Activated-Sludge System in the Treatment of Wastewater Containing High-Molecular-Weight Compounds. Water Environ. Res. 1999, 71, 64–70. [Google Scholar] [CrossRef]
- Levitsky, I.; Duek, A.; Arkhangelsky, E.; Pinchev, D.; Kadoshian, T.; Shetrit, H.; Naim, R.; Gitis, V. Understanding the Oxidative Cleaning of UF Membranes. J. Membr. Sci. 2011, 377, 206–213. [Google Scholar] [CrossRef]
- Abdullah, S.Z.; Bérubé, P.R. Assessing the Effects of Sodium Hypochlorite Exposure on the Characteristics of PVDF Based Membranes. Water Res. 2013, 47, 5392–5399. [Google Scholar] [CrossRef]
- Pellegrin, B.; Prulho, R.; Rivaton, A.; Thérias, S.; Gardette, J.-L.; Gaudichet-Maurin, E.; Causserand, C. Multi-Scale Analysis of Hypochlorite Induced PES/PVP Ultrafiltration Membranes Degradation. J. Membr. Sci. 2013, 447, 287–296. [Google Scholar] [CrossRef]
- Gander, M.; Jefferson, B.; Judd, S. Aerobic MBRs for Domestic Wastewater Treatment: A Review with Cost Considerations. Sep. Purif. Technol. 2000, 18, 119–130. [Google Scholar] [CrossRef]



| Type of Filtration System | Optimization Target | Actuators | Main Results | Reference |
|---|---|---|---|---|
| Dead-end filtration for raw Lake Houston water treatment | Maximize the productivity | Hydraulic backwashing period | By increasing frequency backwashing the total volume is multiplied 4 times during 10 h of operation | [12] |
| Batch diafiltration | Functioning costs | Inflow of the diluant and the permeate flow-rate | More than 80% reduction in the processing time is shown over the traditional operation | [13] |
| Unstirred, dead-end MF cell) | Maximize the productivity | Timing of hydraulic backwashes | Compared to the baseline scenarios, the net volume of water treated increased by between 17% and 61% | [14] |
| MF/UF–Resistance in series model | Functioning costs | Filtration/Backwash time period | Determination of an optimal feedback synthesis with minimization of energy consumption | [15] |
| Submerged membrane bioreactor pilot in WWTP of Charguia (Tunis, Tunisia) | Functioning costs | Filtration/Backwash time period | 7% reduction in consumed hydraulic pump energy | [16] |
| Membrane Characteristics | System A | System B |
|---|---|---|
| Manufacturer | SINAP | Zenon Env |
| Membrane type/Material | Hollow fibre/PVDF | Flat sheet/PVDF |
| Pore size | 0.16 μm | 0.08 μm |
| Membrane surface | 0.01 m2 | 0.045 m2 |
| Initial membrane resistance (m−1) | 1.45 × 10+12 | 3.33 × 10+12 |
| Membrane Characteristics | System A | System B |
|---|---|---|
| Qin (L·d−1) | 2.52 | 4.27 |
| HRT (d) | 1.97 | 0.94 |
| SRT (d) | 4.63 | - |
| Flux Jp (LMH) | 6 | 4 |
| VR (L) | 5 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaaben, A.; Ellouze, F.; Ben Amar, N.; Rapaport, A.; Heran, M.; Harmand, J. Evaluation of the Genericity of an Adaptive Optimal Control Approach to Optimize Membrane Filtration Systems. Membranes 2025, 15, 157. https://doi.org/10.3390/membranes15060157
Chaaben A, Ellouze F, Ben Amar N, Rapaport A, Heran M, Harmand J. Evaluation of the Genericity of an Adaptive Optimal Control Approach to Optimize Membrane Filtration Systems. Membranes. 2025; 15(6):157. https://doi.org/10.3390/membranes15060157
Chicago/Turabian StyleChaaben, Aymen, Fatma Ellouze, Nihel Ben Amar, Alain Rapaport, Marc Heran, and Jérôme Harmand. 2025. "Evaluation of the Genericity of an Adaptive Optimal Control Approach to Optimize Membrane Filtration Systems" Membranes 15, no. 6: 157. https://doi.org/10.3390/membranes15060157
APA StyleChaaben, A., Ellouze, F., Ben Amar, N., Rapaport, A., Heran, M., & Harmand, J. (2025). Evaluation of the Genericity of an Adaptive Optimal Control Approach to Optimize Membrane Filtration Systems. Membranes, 15(6), 157. https://doi.org/10.3390/membranes15060157











