A Review on Membrane Fouling Prediction Using Artificial Neural Networks (ANNs)
Abstract
1. Introduction
2. Fouling Types and Mitigation Strategies
- Water pretreatment is an essential step to remove suspended solids, organic matter, and other foulants that can clog or damage the membrane surface. Pretreatment methods include sedimentation, coagulation/flocculation, microfiltration/ultrafiltration, and dissolved air flotation [36].
- The operating conditions of the membrane-based separation process can have a significant impact on fouling. Factors such as the feed flow rate, cross-flow velocity, pressure, pH, and temperature can be optimized to reduce the extent of fouling [35].
- Antiscalants and dispersants can be added to the feed stream to inhibit the precipitation and accumulation of foulants on the membrane surface. These chemicals work by modifying the surface chemistry of the membrane or by sequestering the foulants in the bulk solution [35].
- The surface chemistry of the membrane can be modified to reduce fouling by introducing hydrophilic or charged functional groups that repel foulants or by creating surface structures that promote shear-induced turbulence [35].
3. Membrane Fouling Prediction Models
3.1. Conventional Models
| Model Type | Advantages | Limitations | Examples | Ref. |
|---|---|---|---|---|
| Empirical models |
|
| Darcy’s law model and the fouling index model | [41,48] |
| Mechanistic models | More accurate and applicable to a wider range of processes |
| Cake filtration model and pore-blocking model | [39,41,48] |
| Artificial intelligence models |
|
| Support vector machines (SVMs) | [41,49,50] |
3.2. AI-Based Models
- Regression is a type of supervised learning problem in which the goal is to predict a continuous output variable. The model learns the relationship between input variables and output variables using labeled training data and then makes predictions on new, unseen data. Linear, polynomial, and support vector regression are common types of regression algorithms.
- Classification is another type of supervised learning problem that aims to predict a categorical output variable. The model learns the relationship between input and output variables using labeled training data and then assigns new data points to specific categories based on the learned rules. Common classification algorithms include logistic regression, decision trees, random forests, and support vector machines.
- Clustering is an unsupervised learning problem that aims to group similar data points into clusters. The model does not use labeled data, but instead finds patterns and structures in the data to group similar data points together. K-means clustering and hierarchical clustering are common clustering algorithms.
- Dimension reduction is a technique used to reduce the number of input variables in a dataset while still retaining important information. The goal is to simplify the data and remove noise or redundant features that may hinder learning. Principal component analysis (PCA) and autoencoders are common dimension reduction algorithms. While most dimension reduction problems are unsupervised, they can be supervised depending on the specific problem and approach.
4. Basic Concepts of ANNs
5. Applications of ANNs for Membrane Fouling Prediction
5.1. Membrane Fouling Prediction in RO and NF Processes
5.2. Membrane Fouling Prediction in MF and UF Processes
5.3. Interfacial Energy Prediction in MBRs
6. Future Directions and Conclusions
- -
- Exploring the inclusion of additional input variables that capture other relevant aspects of the system, such as pretreatment methods, membrane characteristics, and fouling mitigation strategies. This expansion of input variables can lead to more comprehensive and reliable prediction models.
- -
- Incorporating the real-time monitoring of relevant process variables, such as membrane permeability, fouling resistance, and hydraulic parameters, can provide valuable insights into fouling behavior. Integrating these dynamic data into ANN models can enable the continuous prediction and monitoring of fouling progression. This integration may facilitate proactive fouling management strategies, allowing for timely maintenance actions or the optimization of operational conditions to mitigate fouling.
- -
- Integrating analytical techniques to interpret and visualize the learned representations and decision-making processes within ANNs. While ANNs are known for their exceptional predictive capabilities, their black-box nature often limits their interpretability. The ability to explain model predictions and identify key factors influencing fouling can greatly enhance the practical utility of ANN models. This would enable researchers and practitioners to gain valuable insights into fouling mechanisms and optimize operational strategies, accordingly.
- -
- Shifting the focus toward their practical deployment and implementation as the ANN models mature and demonstrate their effectiveness in membrane fouling prediction. Researchers can collaborate with membrane manufacturers, operators, and stakeholders to develop user-friendly software tools or decision support systems that incorporate ANN models. These tools can aid in real-time fouling prediction and the early detection of anomalies and support informed decision-making for fouling control strategies.
- -
- Incorporating hybrid models to leverage the strengths of multiple modeling techniques allows for a more comprehensive understanding of the complex dynamics involved in membrane fouling. Researchers can harness the complementary advantages of each approach by integrating ANNs with other models, such as empirical, mechanistic, or statistical models. By combining the strengths of different models, hybrid methods can enhance prediction accuracy, generalization capabilities, and the incorporation of domain knowledge. As research in this area continues to evolve, the development and refinement of hybrid models hold significant potential for advancing our understanding of fouling mechanisms and optimizing fouling control strategies in membrane-based processes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beuscher, U.; Kappert, E.J.; Wijmans, J.G. Membrane Research beyond Materials Science. J. Membr. Sci. 2022, 643, 119902. [Google Scholar] [CrossRef]
- Cui, Z.F.; Jiang, Y.; Field, R.W. Fundamentals of Pressure-Driven Membrane Separation Processes. In Membrane Technology; Cui, Z., Muralidhara, H., Eds.; Butterworth-Heinemann: Oxford, UK, 2010; pp. 1–18. [Google Scholar] [CrossRef]
- Anis, S.F.; Hashaikeh, R.; Hilal, N. Microfiltration Membrane Processes: A Review of Research Trends over the Past Decade. J. Water Process Eng. 2019, 32, 100941. [Google Scholar] [CrossRef]
- Humudat, Y.R.; Al-Naseri, S.K.; Al-Fatlawy, Y.F. Reducing Endotoxin from Dialysis Water by Using Different Disinfection Processes. Desalination Water Treat. 2020, 185, 71–76. [Google Scholar] [CrossRef]
- Hietala, V.; Horsma-Heikkinen, J.; Carron, A.; Skurnik, M.; Kiljunen, S. The Removal of Endo- and Enterotoxins From Bacteriophage Preparations. Front. Microbiol. 2019, 10, 1674. [Google Scholar] [CrossRef] [PubMed]
- Busby, T.F.; Ingham, K.C. Separation of Macromolecules by Ultrafiltration: Removal of Poly(Ethylene Glycol) from Human Albumin. J. Biochem. Biophys. Methods 1980, 2, 191–206. [Google Scholar] [CrossRef]
- Michael, S.G.; Drigo, B.; Michael-Kordatou, I.; Michael, C.; Jäger, T.; Aleer, S.C.; Schwartz, T.; Donner, E.; Fatta-Kassinos, D. The Effect of Ultrafiltration Process on the Fate of Antibiotic-Related Microcontaminants, Pathogenic Microbes, and Toxicity in Urban Wastewater. J. Hazard. Mater. 2022, 435, 128943. [Google Scholar] [CrossRef]
- Al Aani, S.; Mustafa, T.N.; Hilal, N. Ultrafiltration Membranes for Wastewater and Water Process Engineering: A Comprehensive Statistical Review over the Past Decade. J. Water Process Eng. 2020, 35, 101241. [Google Scholar] [CrossRef]
- Qasim, M.; Badrelzaman, M.; Darwish, N.N.; Darwish, N.A.; Hilal, N. Reverse Osmosis Desalination: A State-of-the-Art Review. Desalination 2019, 459, 59–104. [Google Scholar] [CrossRef]
- García-Triñanes, P.; Chairopoulou, M.A.; Campos, L.C. Investigating Reverse Osmosis Membrane Fouling and Scaling by Membrane Autopsy of a Bench Scale Device. Environ. Technol. 2022, 43, 3198–3211. [Google Scholar] [CrossRef]
- Guo, W.; Ngo, H.H.; Li, J. A Mini-Review on Membrane Fouling. Bioresour. Technol. 2012, 122, 27–34. [Google Scholar] [CrossRef]
- Horseman, T.; Yin, Y.; Christie, K.S.; Wang, Z.; Tong, T.; Lin, S. Wetting, Scaling, and Fouling in Membrane Distillation: State-of-the-Art Insights on Fundamental Mechanisms and Mitigation Strategies. ACS ES&T Eng. 2020, 1, 117–140. [Google Scholar] [CrossRef]
- Arribas, P.; Khayet, M.; García-Payo, M.C.; Gil, L. Advances in Membrane Technologies for Water Treatment (Chapter 8) Novel and Emerging Membranes. In Advances in Membrane Technologies for Water Treatment; Basile, A., Cassano, A., Rastogi, N.K., Eds.; Woodhead Publishing: Cambridge, UK, 2015; pp. 239–285. [Google Scholar]
- Zuthi, M.F.R.; Guo, W.; Ngo, H.H.; Nghiem, D.L.; Hai, F.I.; Xia, S.; Li, J.; Li, J.; Liu, Y. New and Practical Mathematical Model of Membrane Fouling in an Aerobic Submerged Membrane Bioreactor. Bioresour. Technol. 2017, 238, 86–94. [Google Scholar] [CrossRef] [PubMed]
- Hazrati, H.; Moghaddam, A.H.; Rostamizadeh, M. The Influence of Hydraulic Retention Time on Cake Layer Specifications in the Membrane Bioreactor: Experimental and Artificial Neural Network Modeling. J. Environ. Chem. Eng. 2017, 5, 3005–3013. [Google Scholar] [CrossRef]
- Zhang, W.; Ruan, X.; Ma, Y.; Jiang, X.; Zheng, W.; Liu, Y.; He, G. Modeling and Simulation of Mitigating Membrane Fouling under a Baffle-Filled Turbulent Flow with Permeate Boundary. Sep. Purif. Technol. 2017, 179, 13–24. [Google Scholar] [CrossRef]
- Niu, C.; Li, X.; Dai, R.; Wang, Z. Artificial Intelligence-Incorporated Membrane Fouling Prediction for Membrane-Based Processes in the Past 20 Years: A Critical Review. Water Res. 2022, 216, 118299. [Google Scholar] [CrossRef]
- Alsawaftah, N.; Abuwatfa, W.; Darwish, N.; Husseini, G. A Comprehensive Review on Membrane Fouling: Mathematical Modelling, Prediction, Diagnosis, and Mitigation. Water 2021, 13, 1327. [Google Scholar] [CrossRef]
- AlSawaftah, N.; Abuwatfa, W.; Darwish, N.; Husseini, G.A. A Review on Membrane Biofouling: Prediction, Characterization, and Mitigation. Membranes 2022, 12, 1217. [Google Scholar] [CrossRef]
- Yang, H.; Yu, X.; Liu, J.; Tang, Z.; Huang, T.; Wang, Z.; Zhong, Y.; Long, Z.; Wang, L. A Concise Review of Theoretical Models and Numerical Simulations of Membrane Fouling. Water 2022, 14, 3537. [Google Scholar] [CrossRef]
- Nunes, S.P. Can Fouling in Membranes Be Ever Defeated? Curr. Opin. Chem. Eng. 2020, 28, 90–95. [Google Scholar] [CrossRef]
- Warsinger, D.M.; Swaminathan, J.; Guillen-Burrieza, E.; Arafat, H.A.; Lienhard, J.H. Scaling and Fouling in Membrane Distillation for Desalination Applications: A Review. Desalination 2015, 356, 294–313. [Google Scholar] [CrossRef]
- Zhang, M.; Lin, H.; Shen, L.; Liao, B.Q.; Wu, X.; Li, R. Effect of Calcium Ions on Fouling Properties of Alginate Solution and Its Mechanisms. J. Membr. Sci. 2017, 525, 320–329. [Google Scholar] [CrossRef]
- Long, Y.; Yu, G.; Dong, L.; Xu, Y.; Lin, H.; Deng, Y.; You, X.; Yang, L.; Liao, B.Q. Synergistic Fouling Behaviors and Mechanisms of Calcium Ions and Polyaluminum Chloride Associated with Alginate Solution in Coagulation-Ultrafiltration (UF) Process. Water Res. 2021, 189, 116665. [Google Scholar] [CrossRef]
- Shirazi, S.; Lin, C.J.; Chen, D. Inorganic Fouling of Pressure-Driven Membrane Processes—A Critical Review. Desalination 2010, 250, 236–248. [Google Scholar] [CrossRef]
- Sanaei, P.; Cummings, L.J. Membrane Filtration with Multiple Fouling Mechanisms. Phys. Rev. Fluids 2019, 4, 124301. [Google Scholar] [CrossRef]
- Henry, C.; Minier, J.P.; Lefèvre, G. Towards a Description of Particulate Fouling: From Single Particle Deposition to Clogging. Adv. Colloid Interface Sci. 2012, 185–186, 34–76. [Google Scholar] [CrossRef]
- Ly, Q.V.; Hu, Y.; Li, J.; Cho, J.; Hur, J. Characteristics and Influencing Factors of Organic Fouling in Forward Osmosis Operation for Wastewater Applications: A Comprehensive Review. Environ. Int. 2019, 129, 164–184. [Google Scholar] [CrossRef] [PubMed]
- Campo, R.; Capodici, M.; Di Bella, G.; Torregrossa, M. The Role of EPS in the Foaming and Fouling for a MBR Operated in Intermittent Aeration Conditions. Biochem. Eng. J. 2017, 118, 41–52. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, M.; Wang, F.; Meng, F.; Liao, B.Q.; Hong, H.; Chen, J.; Gao, W. A Critical Review of Extracellular Polymeric Substances (EPSs) in Membrane Bioreactors: Characteristics, Roles in Membrane Fouling and Control Strategies. J. Memb. Sci. 2014, 460, 110–125. [Google Scholar] [CrossRef]
- Teng, J.; Zhang, M.; Leung, K.T.; Chen, J.; Hong, H.; Lin, H.; Liao, B.Q. A Unified Thermodynamic Mechanism Underlying Fouling Behaviors of Soluble Microbial Products (SMPs) in a Membrane Bioreactor. Water Res. 2019, 149, 477–487. [Google Scholar] [CrossRef]
- Kunacheva, C.; Soh, Y.N.A.; Stuckey, D.C. Identification of Soluble Microbial Products (SMPs) from the Fermentation and Methanogenic Phases of Anaerobic Digestion. Sci. Total Environ. 2020, 698, 134177. [Google Scholar] [CrossRef]
- Baten, R.; Stummeyer, K. How Sustainable Can Desalination Be? Desalination Water Treat. 2013, 51, 44–52. [Google Scholar] [CrossRef]
- Goh, P.S.; Lau, W.J.; Othman, M.H.D.; Ismail, A.F. Membrane Fouling in Desalination and Its Mitigation Strategies. Desalination 2018, 425, 130–155. [Google Scholar] [CrossRef]
- Alkhatib, A.; Ayari, M.A.; Hawari, A.H. Fouling Mitigation Strategies for Different Foulants in Membrane Distillation. Chem. Eng. Process.-Process Intensif. 2021, 167, 108517. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, J.; Cheng, X.; Chen, H.; Liu, Q.; Yao, P.; Ngo, H.H.; Nghiem, L.D. Mitigation of Reverse Osmosis Membrane Fouling by Electrochemical-Microfiltration- Activated Carbon Pretreatment. J. Membr. Sci. 2022, 656, 120615. [Google Scholar] [CrossRef]
- Li, X.; Cai, T.; Amy, G.L.; Chung, T.S. Cleaning Strategies and Membrane Flux Recovery on Anti-Fouling Membranes for Pressure Retarded Osmosis. J. Membr. Sci. 2017, 522, 116–123. [Google Scholar] [CrossRef]
- Ahmad, A.L.; Che Lah, N.F.; Ismail, S.; Ooi, B.S. Membrane Antifouling Methods and Alternatives: Ultrasound Approach. Sep. Purif. Rev. 2012, 41, 318–346. [Google Scholar] [CrossRef]
- Abdelrasoul, A.; Doan, H.; Lohi, A. A Mechanistic Model for Ultrafiltration Membrane Fouling by Latex. J. Membr. Sci. 2013, 433, 88–99. [Google Scholar] [CrossRef]
- Di Bella, G.; Di Trapani, D. A Brief Review on the Resistance-in-Series Model in Membrane Bioreactors (MBRs). Membranes 2019, 9, 24. [Google Scholar] [CrossRef] [PubMed]
- Cifuentes-Cabezas, M.; Bohórquez-Zurita, J.L.; Gil-Herrero, S.; Vincent-Vela, M.C.; Mendoza-Roca, J.A.; Álvarez-Blanco, S. Deep Study on Fouling Modelling of Ultrafiltration Membranes Used for OMW Treatment: Comparison Between Semi-Empirical Models, Response Surface, and Artificial Neural Networks. Food Bioprocess Technol. 2023, 1, 1–21. [Google Scholar] [CrossRef]
- Mashhadi Meighani, H.; Dehghani, A.; Rekabdar, F.; Hemmati, M.; Goodarznia, I. Artificial Intelligence vs. Classical Approaches: A New Look at the Prediction of Flux Decline in Wastewater Treatment. Desalination Water Treat. 2013, 51, 7476–7489. [Google Scholar] [CrossRef]
- Dalmau, M.; Atanasova, N.; Gabarrón, S.; Rodriguez-Roda, I.; Comas, J. Comparison of a Deterministic and a Data Driven Model to Describe MBR Fouling. Chem. Eng. J. 2015, 260, 300–308. [Google Scholar] [CrossRef]
- Jawad, J.; Hawari, A.H.; Zaidi, S.J. Modeling and Sensitivity Analysis of the Forward Osmosis Process to Predict Membrane Flux Using a Novel Combination of Neural Network and Response Surface Methodology Techniques. Membranes 2021, 11, 70. [Google Scholar] [CrossRef] [PubMed]
- Dimensions. Available online: https://app.dimensions.ai/discover/publication?search_mode=content&search_text=%22ANNs%22%20AND%20%22membrane%20fouling%22%20prediction&search_type=kws&search_field=full_search&or_facet_publication_type=article (accessed on 29 May 2023).
- Liu, Q.F.; Kim, S.H. Evaluation of Membrane Fouling Models Based on Bench-Scale Experiments: A Comparison between Constant Flowrate Blocking Laws and Artificial Neural Network (ANNs) Model. J. Membr. Sci. 2008, 310, 393–401. [Google Scholar] [CrossRef]
- Khayet, M.; Cojocaru, C.; Essalhi, M. Artificial Neural Network Modeling and Response Surface Methodology of Desalination by Reverse Osmosis. J. Membr. Sci. 2011, 368, 202–214. [Google Scholar] [CrossRef]
- Ghandehari, S.; Montazer-Rahmati, M.M.; Asghari, M. A Comparison between Semi-Theoretical and Empirical Modeling of Cross-Flow Microfiltration Using ANN. Desalination 2011, 277, 348–355. [Google Scholar] [CrossRef]
- Hu, J.; Kim, C.; Halasz, P.; Kim, J.F.; Kim, J.; Szekely, G. Artificial Intelligence for Performance Prediction of Organic Solvent Nanofiltration Membranes. J. Membr. Sci. 2021, 619, 118513. [Google Scholar] [CrossRef]
- Corbatón-Báguena, M.J.; Vincent-Vela, M.C.; Gozálvez-Zafrilla, J.M.; Álvarez-Blanco, S.; Lora-García, J.; Catalán-Martínez, D. Comparison between Artificial Neural Networks and Hermia’s Models to Assess Ultrafiltration Performance. Sep. Purif. Technol. 2016, 170, 434–444. [Google Scholar] [CrossRef]
- Bagheri, M.; Akbari, A.; Mirbagheri, S.A. Advanced Control of Membrane Fouling in Filtration Systems Using Artificial Intelligence and Machine Learning Techniques: A Critical Review. Process Saf. Environ. Prot. 2019, 123, 229–252. [Google Scholar] [CrossRef]
- Jiang, T.; Gradus, J.L.; Rosellini, A.J. Supervised Machine Learning: A Brief Primer. Behav. Ther. 2020, 51, 675. [Google Scholar] [CrossRef]
- Kovacs, D.J.; Li, Z.; Baetz, B.W.; Hong, Y.; Donnaz, S.; Zhao, X.; Zhou, P.; Ding, H.; Dong, Q. Membrane Fouling Prediction and Uncertainty Analysis Using Machine Learning: A Wastewater Treatment Plant Case Study. J. Membr. Sci. 2022, 660, 120817. [Google Scholar] [CrossRef]
- Gao, K.; Xi, X.; Wang, Z.; Ma, Y.; Chen, S.; Ye, X.; Li, Y. Use of Support Vector Machine Model to Predict Membrane Permeate Flux. Desalination Water Treat. 2015, 57, 16810–16821. [Google Scholar] [CrossRef]
- Li, W.; Li, C.; Wang, T. Application of machine learning algorithms in MBR simulation under big data platform. Water Pract. Technol. 2020, 15, 1238–1247. [Google Scholar] [CrossRef]
- Li, L.; Rong, S.; Wang, R.; Yu, S. Recent Advances in Artificial Intelligence and Machine Learning for Nonlinear Relationship Analysis and Process Control in Drinking Water Treatment: A Review. Chem. Eng. J. 2021, 405, 126673. [Google Scholar] [CrossRef]
- Safeer, S.; Pandey, R.P.; Rehman, B.; Safdar, T.; Ahmad, I.; Hasan, S.W.; Ullah, A. A Review of Artificial Intelligence in Water Purification and Wastewater Treatment: Recent Advancements. J. Water Process Eng. 2022, 49, 102974. [Google Scholar] [CrossRef]
- Alam, G.; Ihsanullah, I.; Naushad, M.; Sillanpää, M. Applications of Artificial Intelligence in Water Treatment for Optimization and Automation of Adsorption Processes: Recent Advances and Prospects. Chem. Eng. J. 2022, 427, 130011. [Google Scholar] [CrossRef]
- Niemi, H.; Bulsari, A.; Palosaari, S. Simulation of Membrane Separation by Neural Networks. J. Membr. Sci. 1995, 102, 185–191. [Google Scholar] [CrossRef]
- Liu, Q.F.; Kim, S.H.; Lee, S. Prediction of Microfiltration Membrane Fouling Using Artificial Neural Network Models. Sep. Purif. Technol. 2009, 70, 96–102. [Google Scholar] [CrossRef]
- Delgrange-Vincent, N.; Cabassud, C.; Cabassud, M.; Durand-Bourlier, L.; Laîné, J.M. Neural Networks for Long Term Prediction of Fouling and Backwash Efficiency in Ultrafiltration for Drinking Water Production. Desalination 2000, 131, 353–362. [Google Scholar] [CrossRef]
- Choi, Y.J.; Oh, H.; Lee, S.; Nam, S.H.; Hwang, T.M. Investigation of the Filtration Characteristics of Pilot-Scale Hollow Fiber Submerged MF System Using Cake Formation Model and Artificial Neural Networks Model. Desalination 2012, 297, 20–29. [Google Scholar] [CrossRef]
- Viet, N.D.; Jang, D.; Yoon, Y.; Jang, A. Enhancement of Membrane System Performance Using Artificial Intelligence Technologies for Sustainable Water and Wastewater Treatment: A Critical Review. Crit. Rev. Environ. Sci. Technol. 2022, 52, 3689–3719. [Google Scholar] [CrossRef]
- Biyanto, T.R. Fouling Resistance Prediction Using Artificial Neural Network Nonlinear Auto-Regressive with Exogenous Input Model Based on Operating Conditions and Fluid Properties Correlations. AIP Conf. Proc. 2016, 1737, 050001. [Google Scholar] [CrossRef]
- Cabrera, P.; Carta, J.A.; González, J.; Melián, G. Artificial Neural Networks Applied to Manage the Variable Operation of a Simple Seawater Reverse Osmosis Plant. Desalination 2017, 416, 140–156. [Google Scholar] [CrossRef]
- Akthar, S.; Ahamed, K.I. A Study on Neural Network Architectures. Comput. Eng. Intell. Syst. 2016, 7, 17. [Google Scholar]
- Barello, M.; Manca, D.; Patel, R.; Mujtaba, I.M. Neural Network Based Correlation for Estimating Water Permeability Constant in RO Desalination Process under Fouling. Desalination 2014, 345, 101–111. [Google Scholar] [CrossRef]
- Karayiannis, N.B.; Venetsanopoulos, A.N. Artificial Neural Networks: Learning Algorithms, Performance Evaluation, and Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hwang, T.M.; Choi, Y.; Nam, S.H.; Lee, S.; Oh, H.; Hyun, K.; Choung, Y.K. Prediction of Membrane Fouling Rate by Neural Network Modeling. Desalination Water Treat. 2010, 15, 134–140. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, P.; Gao, X.; Wang, M.; Yang, Y.; Wang, P.; Gao, X. A Novel Radial Basis Function Neural Network with High Generalization Performance for Nonlinear Process Modelling. Processes 2022, 10, 140. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, G.; Long, Y.; Teng, J.; You, X.; Liao, B.Q.; Lin, H. Application of Radial Basis Function Artificial Neural Network to Quantify Interfacial Energies Related to Membrane Fouling in a Membrane Bioreactor. Bioresour. Technol. 2019, 293, 122103. [Google Scholar] [CrossRef]
- Aish, A.M.; Zaqoot, H.A.; Abdeljawad, S.M. Artificial Neural Network Approach for Predicting Reverse Osmosis Desalination Plants Performance in the Gaza Strip. Desalination 2015, 367, 240–247. [Google Scholar] [CrossRef]
- Mahmod, N.; Wahab, N.A. Fouling Prediction Using Neural Network Model for Membrane Bioreactor System. Indones. J. Electr. Eng. Comput. Sci. 2017, 6, 200–206. [Google Scholar] [CrossRef][Green Version]
- Shi, Y.; Wang, Z. Prediction of Membrane Fouling Based on GA-RBF Neural Network and PCA. J. Phys. Conf. Ser. 2021, 2033, 012092. [Google Scholar] [CrossRef]
- Hamachi, M.; Cabassud, M.; Davin, A.; Mietton Peuchot, M. Dynamic Modelling of Crossflow Microfiltration of Bentonite Suspension Using Recurrent Neural Networks. Chem. Eng. Process. Process Intensif. 1999, 38, 203–210. [Google Scholar] [CrossRef]
- Piron, E.; Latrille, E.; René, F. Application of Artificial Neural Networks for Crossflow Microfiltration Modelling: “Black-Box” and Semi-Physical Approaches. Comput. Chem. Eng. 1997, 21, 1021–1030. [Google Scholar] [CrossRef]
- Xie, T.; Yu, H.; Wilamowski, B. Comparison between Traditional Neural Networks and Radial Basis Function Networks. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1194–1199. [Google Scholar] [CrossRef]
- Coulibaly, P.; Anctil, F.; Bobée, B. Daily Reservoir Inflow Forecasting Using Artificial Neural Networks with Stopped Training Approach. J. Hydrol. 2000, 230, 244–257. [Google Scholar] [CrossRef]
- Soleimani, R.; Shoushtari, N.A.; Mirza, B.; Salahi, A. Experimental Investigation, Modeling and Optimization of Membrane Separation Using Artificial Neural Network and Multi-Objective Optimization Using Genetic Algorithm. Chem. Eng. Res. Des. 2013, 91, 883–903. [Google Scholar] [CrossRef]
- Rahmanian, B.; Pakizeh, M.; Mansoori, S.A.A.; Esfandyari, M.; Jafari, D.; Maddah, H.; Maskooki, A. Prediction of MEUF Process Performance Using Artificial Neural Networks and ANFIS Approaches. J. Taiwan Inst. Chem. Eng. 2012, 43, 558–565. [Google Scholar] [CrossRef]
- Rudolph, G.; Virtanen, T.; Ferrando, M.; Güell, C.; Lipnizki, F.; Kallioinen, M. A Review of in Situ Real-Time Monitoring Techniques for Membrane Fouling in the Biotechnology, Biorefinery and Food Sectors. J. Membr. Sci. 2019, 588, 117221. [Google Scholar] [CrossRef]
- Rudolph-Schöpping, G.; Schagerlöf, H.; Jönsson, A.S.; Lipnizki, F. Comparison of Membrane Fouling during Ultrafiltration with Adsorption Studied by Quartz Crystal Microbalance with Dissipation Monitoring (QCM-D). J. Membr. Sci. 2023, 672, 121313. [Google Scholar] [CrossRef]
- Meng, X.; Wang, F.; Meng, S.; Wang, R.; Mao, Z.; Li, Y.; Yu, M.; Wang, X.; Zhao, Q.; Yang, L. Novel Surrogates for Membrane Fouling and the Application of Support Vector Machine in Analyzing Fouling Mechanism. Membranes 2021, 11, 990. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, Z.; Du, X.; Gong, B.; Lu, Y.; Li, L. Membrane Fouling Diagnosis of Membrane Components Based on Multi-Feature Information Fusion. J. Membr. Sci. 2022, 657, 120670. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, Y.; Shin, K.; Park, Y.; Lee, S. Analysis of Long-Term Performance of Full-Scale Reverse Osmosis Desalination Plant Using Artificial Neural Network and Tree Model. Environ. Eng. Res. 2020, 25, 763–770. [Google Scholar] [CrossRef]
- Barzilai, J. On Neural-Network Training Algorithms. In Human-Machine Shared Contexts; Lawless, W., Mittu, R., Sofge, D., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 307–313. [Google Scholar] [CrossRef]
- Hong, H.; Lin, H.; Mei, R.; Zhou, X.; Liao, B.Q.; Zhao, L. Membrane Fouling in a Membrane Bioreactor: A Novel Method for Membrane Surface Morphology Construction and Its Application in Interaction Energy Assessment. J. Membr. Sci. 2016, 516, 135–143. [Google Scholar] [CrossRef]
- Jeon, S.; Rajabzadeh, S.; Okamura, R.; Ishigami, T.; Hasegawa, S.; Kato, N.; Matsuyama, H. The Effect of Membrane Material and Surface Pore Size on the Fouling Properties of Submerged Membranes. Water 2016, 8, 602. [Google Scholar] [CrossRef]
- Han, H.; Zhang, S.; Qiao, J.; Wang, X. An Intelligent Detecting System for Permeability Prediction of MBR. Water Sci. Technol. 2018, 77, 467–478. [Google Scholar] [CrossRef] [PubMed]
- Lim, S.J.; Kim, Y.M.; Park, H.; Ki, S.; Jeong, K.; Seo, J.; Chae, S.H.; Kim, J.H. Enhancing Accuracy of Membrane Fouling Prediction Using Hybrid Machine Learning Models. Desalination Water Treat. 2019, 146, 22–28. [Google Scholar] [CrossRef]
- Aminian, J.; Shahhosseini, S. Evaluation of ANN Modeling for Prediction of Crude Oil Fouling Behavior. Appl. Therm. Eng. 2008, 28, 668–674. [Google Scholar] [CrossRef]
- Roehl, E.A.; Ladner, D.A.; Daamen, R.C.; Cook, J.B.; Safarik, J.; Phipps, D.W.; Xie, P. Modeling Fouling in a Large RO System with Artificial Neural Networks. J. Membr. Sci. 2018, 552, 95–106. [Google Scholar] [CrossRef]
- Shim, J.; Park, S.; Cho, K.H. Deep Learning Model for Simulating Influence of Natural Organic Matter in Nanofiltration. Natl. Libr. Med. 2021, 197, 117070. [Google Scholar] [CrossRef] [PubMed]
- Shetty, G.R.; Chellam, S. Predicting Membrane Fouling during Municipal Drinking Water Nanofiltration Using Artificial Neural Networks. J. Membr. Sci. 2003, 217, 69–86. [Google Scholar] [CrossRef]
- Park, S.; Baek, S.S.; Pyo, J.C.; Pachepsky, Y.; Park, J.; Cho, K.H. Deep Neural Networks for Modeling Fouling Growth and Flux Decline during NF/RO Membrane Filtration. J. Membr. Sci. 2019, 587, 117164. [Google Scholar] [CrossRef]
- Garg, M.C.; Joshi, H. A New Approach for Optimization of Small-Scale RO Membrane Using Artificial Groundwater. Environ. Technol. 2014, 35, 2988–2999. [Google Scholar] [CrossRef]
- Jafar, M.M.; Zilouchian, A. Prediction of Critical Desalination Parameters Using Radial Basis Functions Networks. J. Intell. Robot. Syst. 2002, 34, 219–230. [Google Scholar] [CrossRef]
- Salgado-Reyna, A.; Soto-Regalado, E.; Gómez-González, R.; Cerino-Córdova, F.J.; García-Reyes, R.B.; Garza-González, M.T.; Alcalá-Rodríguez, M.M. Artificial Neural Networks for Modeling the Reverse Osmosis Unit in a Wastewater Pilot Treatment Plant. Desalination Water Treat. 2013, 53, 1177–1187. [Google Scholar] [CrossRef]
- Madaeni, S.S.; Shiri, M.; Kurdian, A.R. Modelling, Optimization, and Control of Reverse Osmosis Water Treatment in Kazeroon Power Plant Using Neural Network. Chem. Eng. Commun. 2014, 202, 6–14. [Google Scholar] [CrossRef]
- Moradi, A.; Mojarradi, V.; Sarcheshmehpour, M. Prediction of RO Membrane Performances by Use of Artificial Neural Network and Using the Parameters of a Complex Mathematical Model. Res. Chem. Intermed. 2013, 39, 3235–3249. [Google Scholar] [CrossRef]
- Libotean, D.; Giralt, J.; Giralt, F.; Rallo, R.; Wolfe, T.; Cohen, Y. Neural Network Approach for Modeling the Performance of Reverse Osmosis Membrane Desalting. J. Membr. Sci. 2009, 326, 408–419. [Google Scholar] [CrossRef]
- Lee, Y.G.; Lee, Y.S.; Jeon, J.J.; Lee, S.; Yang, D.R.; Kim, I.S.; Kim, J.H. Artificial Neural Network Model for Optimizing Operation of a Seawater Reverse Osmosis Desalination Plant. Desalination 2009, 247, 180–189. [Google Scholar] [CrossRef]
- Abbas, A.; Al-Bastaki, N. Modeling of an RO Water Desalination Unit Using Neural Networks. Chem. Eng. J. 2005, 114, 139–143. [Google Scholar] [CrossRef]
- Chen, J.C.; Seidel, A. Cost Optimization of Nanofiltration with Fouling by Natural Organic Matter. J. Environ. Eng. 2002, 128, 967–973. [Google Scholar] [CrossRef]
- Khaouane, L.; Ammi, Y.; Hanini, S. Modeling the Retention of Organic Compounds by Nanofiltration and Reverse Osmosis Membranes Using Bootstrap Aggregated Neural Networks. Arab. J. Sci. Eng. 2016, 42, 1443–1453. [Google Scholar] [CrossRef]
- Zhao, Y.; Taylor, J.S.; Chellam, S. Predicting RO/NF Water Quality by Modified Solution Diffusion Model and Artificial Neural Networks. J. Membr. Sci. 2005, 263, 38–46. [Google Scholar] [CrossRef]
- Al-Zoubi, H.; Hilal, N.; Darwish, N.A.; Mohammad, A.W. Rejection and Modelling of Sulphate and Potassium Salts by Nanofiltration Membranes: Neural Network and Spiegler–Kedem Model. Desalination 2007, 206, 42–60. [Google Scholar] [CrossRef]
- Ammi, Y.; Khaouane, L.; Hanini, S. Prediction of the Rejection of Organic Compounds (Neutral and Ionic) by Nanofiltration and Reverse Osmosis Membranes Using Neural Networks. Korean J. Chem. Eng. 2015, 32, 2300–2310. [Google Scholar] [CrossRef]
- Salehi, F.; Razavi, S.M.A. Dynamic Modeling of Flux and Total Hydraulic Resistance in Nanofiltration Treatment of Regeneration Waste Brine Using Artificial Neural Networks. Desalination Water Treat. 2012, 41, 95–104. [Google Scholar] [CrossRef]
- Chellam, S. Artificial Neural Network Model for Transient Crossflow Microfiltration of Polydispersed Suspensions. J. Membr. Sci. 2005, 258, 35–42. [Google Scholar] [CrossRef]
- Ahmed, N.; Mir, F.Q. Chromium(VI) Removal Using Micellar Enhanced Microfiltration (MEMF) from an Aqueous Solution: Fouling Analysis and Use of ANN for Predicting Permeate Flux. J. Water Process Eng. 2021, 44, 102438. [Google Scholar] [CrossRef]
- Delgrange, N.; Cabassud, C.; Cabassud, M.; Durand-Bourlier, L.; Lainé, J. Modelling of Ultrafiltration Fouling by Neural Network. Desalination 1998, 118, 213–227. [Google Scholar] [CrossRef]
- Dornier, M.; Decloux, M.; Trystram, G.; Lebert, A. Interest of Neural Networks for the Optimization of the Crossflow Filtration Process. LWT—Food Sci. Technol. 1995, 28, 300–309. [Google Scholar] [CrossRef]
- Chew, C.M.; Aroua, M.K.; Hussain, M.A. A Practical Hybrid Modelling Approach for the Prediction of Potential Fouling Parameters in Ultrafiltration Membrane Water Treatment Plant. J. Ind. Eng. Chem. 2017, 45, 145–155. [Google Scholar] [CrossRef]
- Ghandehari, S.; Montazer-Rahmati, M.M.; Asghari, M. Modeling the Flux Decline during Protein Microfiltration: A Comparison between Feed-Forward Back Propagation and Radial Basis Function Neural Networks. Sep. Sci. Technol. 2013, 48, 1324–1330. [Google Scholar] [CrossRef]
- Nourbakhsh, H.; Emam-Djomeh, Z.; Omid, M.; Mirsaeedghazi, H.; Moini, S. Prediction of Red Plum Juice Permeate Flux during Membrane Processing with ANN Optimized Using RSM. Comput. Electron. Agric. 2014, 102, 1–9. [Google Scholar] [CrossRef]
- Liu, Y.; He, G.; Tan, M.; Nie, F.; Li, B. Artificial Neural Network Model for Turbulence Promoter-Assisted Crossflow Microfiltration of Particulate Suspensions. Desalination 2014, 338, 57–64. [Google Scholar] [CrossRef]
- Aydiner, C.; Demir, I.; Keskinler, B.; Ince, O. Joint Analysis of Transient Flux Behaviors via Membrane Fouling in Hybrid PAC/MF Processes Using Neural Network. Desalination 2010, 250, 188–196. [Google Scholar] [CrossRef]
- Shokrkar, H.; Salahi, A.; Kasiri, N.; Mohammadi, T. Mullite Ceramic Membranes for Industrial Oily Wastewater Treatment: Experimental and Neural Network Modeling. Water Sci. Technol. 2011, 64, 670–676. [Google Scholar] [CrossRef][Green Version]
- Lin, W.; Jing, L.; Zhu, Z.; Cai, Q.; Zhang, B. Removal of Heavy Metals from Mining Wastewater by Micellar-Enhanced Ultrafiltration (MEUF): Experimental Investigation and Monte Carlo-Based Artificial Neural Network Modeling. Water Air Soil Pollut. 2017, 228, 206. [Google Scholar] [CrossRef]
- Peleato, N.M.; Legge, R.L.; Andrews, R.C. Continuous Organic Characterization for Biological and Membrane Filter Performance Monitoring. Am. Water Work. Assoc. 2017, 109, E86–E98. [Google Scholar] [CrossRef]
- Badrnezhad, R.; Mirza, B. Modeling and Optimization of Cross-Flow Ultrafiltration Using Hybrid Neural Network-Genetic Algorithm Approach. J. Ind. Eng. Chem. 2014, 20, 528–543. [Google Scholar] [CrossRef]
- Rahmanian, B.; Pakizeh, M.; Mansoori, S.A.A.; Abedini, R. Application of Experimental Design Approach and Artificial Neural Network (ANN) for the Determination of Potential Micellar-Enhanced Ultrafiltration Process. J. Hazard. Mater. 2011, 187, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Judd, C. Chapter 2: Fundamentals. In The MBR Book; Judd, S., Judd, C., Eds.; Butterworth-Heinemann: Oxford, UK, 2011; pp. 55–207. [Google Scholar] [CrossRef]
- Hoek, E.M.V.; Agarwal, G.K. Extended DLVO Interactions between Spherical Particles and Rough Surfaces. J. Colloid Interface Sci. 2006, 298, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Lou, Y.; Xu, Y.; Ma, G.; Liao, B.Q.; Shen, L.; Lin, H. Effects of Surface Morphology on Alginate Adhesion: Molecular Insights into Membrane Fouling Based on XDLVO and DFT Analysis. Chemosphere 2019, 233, 373–380. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, R.; Sun, C.; Liu, Z.; Zhang, J.; Liang, S.; Wang, X. Quantitative Assessment of Interfacial Interactions Governing Ultrafiltration Membrane Fouling by the Mixture of Silica Nanoparticles (SiO2 NPs) and Natural Organic Matter (NOM): Effects of Solution Chemistry. Membranes 2023, 13, 449. [Google Scholar] [CrossRef]
- Zhao, L.; Shen, L.; He, Y.; Hong, H.; Lin, H. Influence of Membrane Surface Roughness on Interfacial Interactions with Sludge Flocs in a Submerged Membrane Bioreactor. J. Colloid Interface Sci. 2015, 446, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.H.; Park, S.K.; Ng, H.Y. Membrane Fouling in a Submerged Membrane Bioreactor Using Track-Etched and Phase-Inversed Porous Membranes. Sep. Purif. Technol. 2009, 65, 184–192. [Google Scholar] [CrossRef]
- Li, B.; Yue, R.; Shen, L.; Chen, C.; Li, R.; Xu, Y.; Zhang, M.; Hong, H.; Lin, H. A Novel Method Integrating Response Surface Method with Artificial Neural Network to Optimize Membrane Fabrication for Wastewater Treatment. J. Clean. Prod. 2022, 376, 134236. [Google Scholar] [CrossRef]
- Teng, J.; Shen, L.; He, Y.; Liao, B.Q.; Wu, G.; Lin, H. Novel Insights into Membrane Fouling in a Membrane Bioreactor: Elucidating Interfacial Interactions with Real Membrane Surface. Chemosphere 2018, 210, 769–778. [Google Scholar] [CrossRef]
- Yu, G.; Cai, X.; Shen, L.; Chen, J.; Hong, H.; Lin, H.; Li, R. A Novel Integrated Method for Quantification of Interfacial Interactions between Two Rough Bioparticles. J. Colloid Interface Sci. 2018, 516, 295–303. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Lin, H.; Shen, L.; He, Y.; Zhang, M.; Liao, B.Q. Realization of Quantifying Interfacial Interactions between a Randomly Rough Membrane Surface and a Foulant Particle. Bioresour. Technol. 2017, 226, 220–228. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Lou, Y.; Chen, Y.; Lin, H.; Li, R.; Yu, G. Prediction of Interfacial Interactions Related with Membrane Fouling in a Membrane Bioreactor Based on Radial Basis Function Artificial Neural Network (ANN). Bioresour. Technol. 2019, 282, 262–268. [Google Scholar] [CrossRef]
- Chen, Y.; Shen, L.; Li, R.; Xu, X.; Hong, H.; Lin, H.; Chen, J. Quantification of Interfacial Energies Associated with Membrane Fouling in a Membrane Bioreactor by Using BP and GRNN Artificial Neural Networks. J. Colloid Interface Sci. 2020, 565, 1–10. [Google Scholar] [CrossRef]
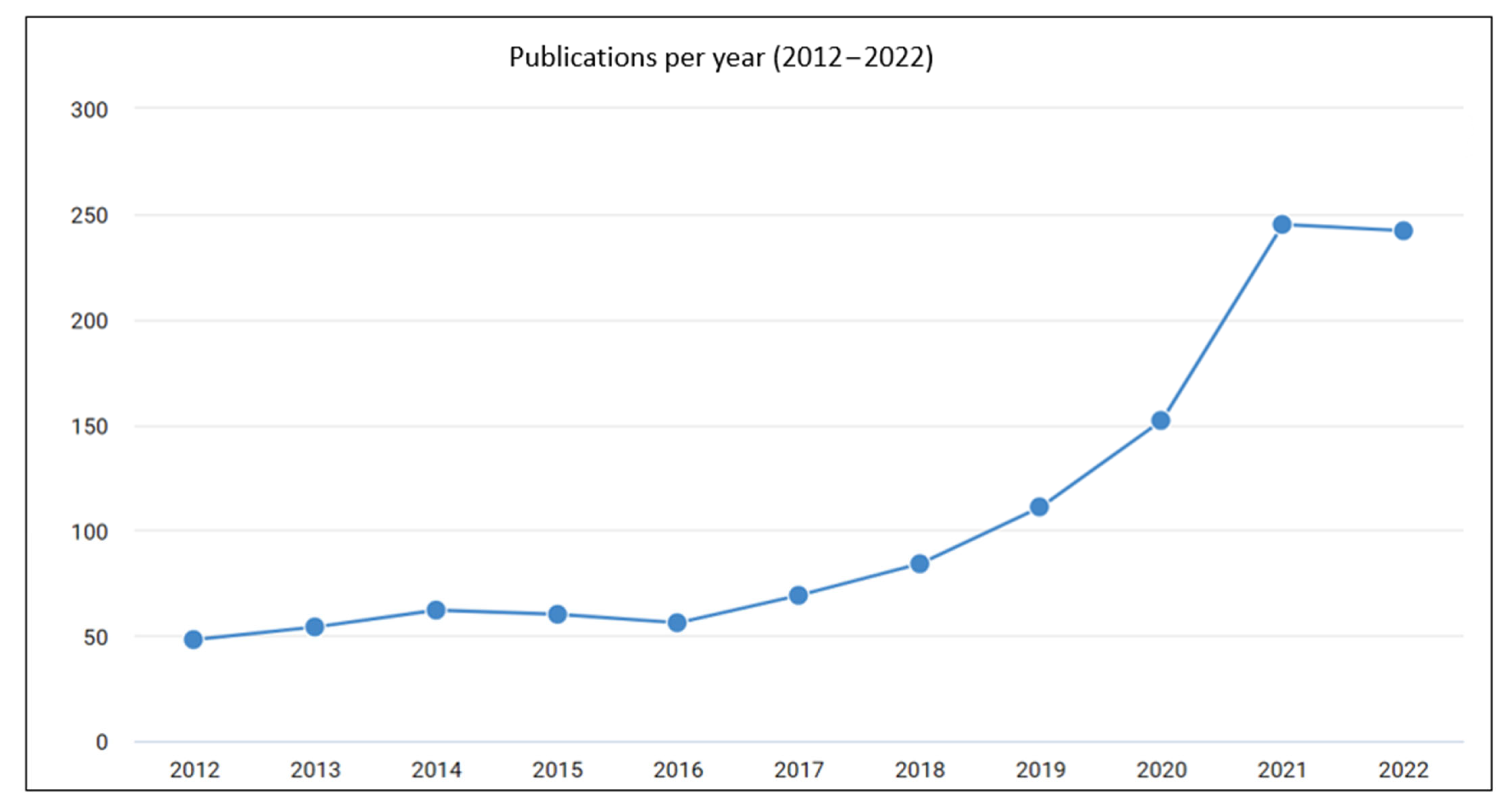
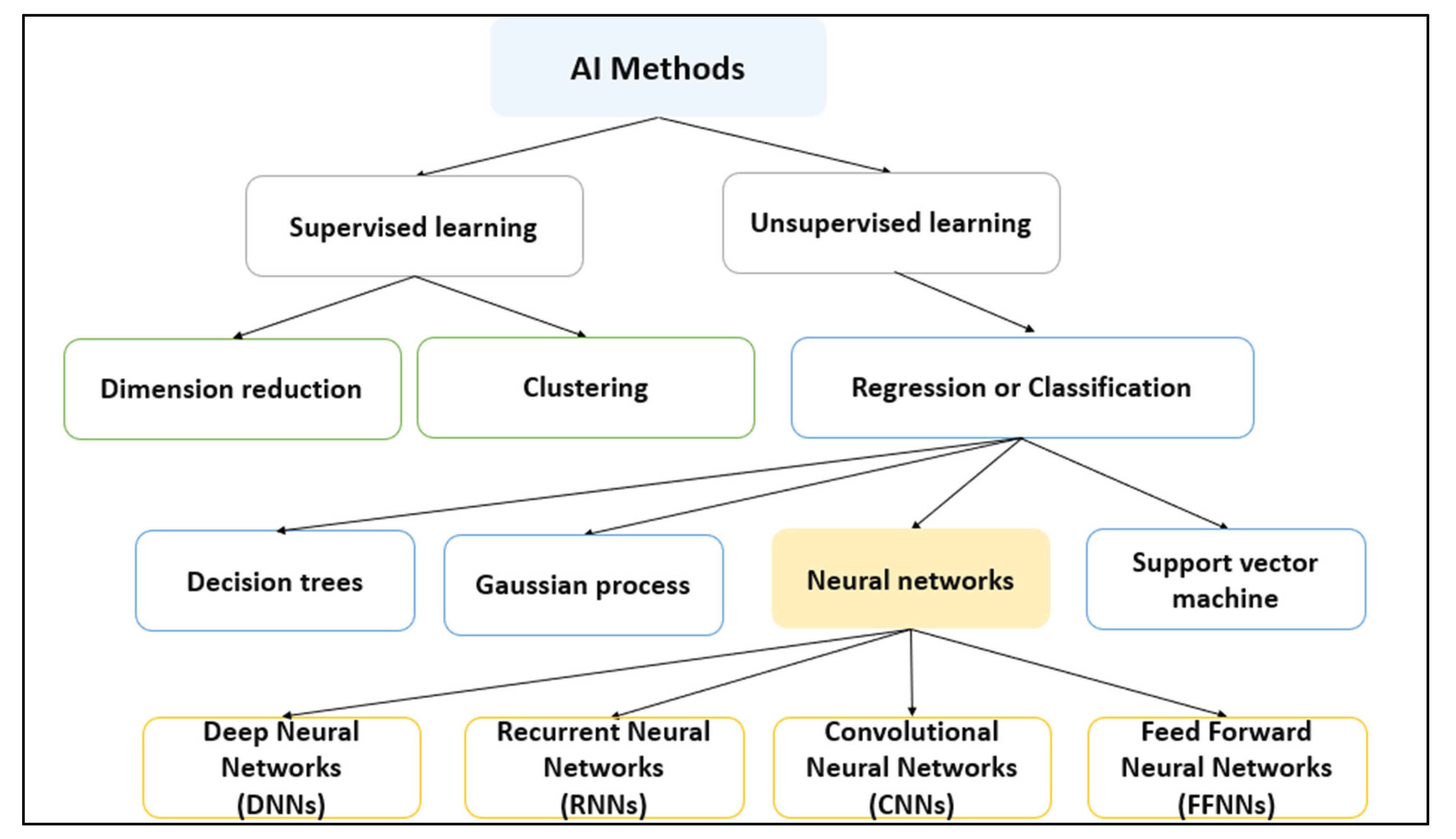
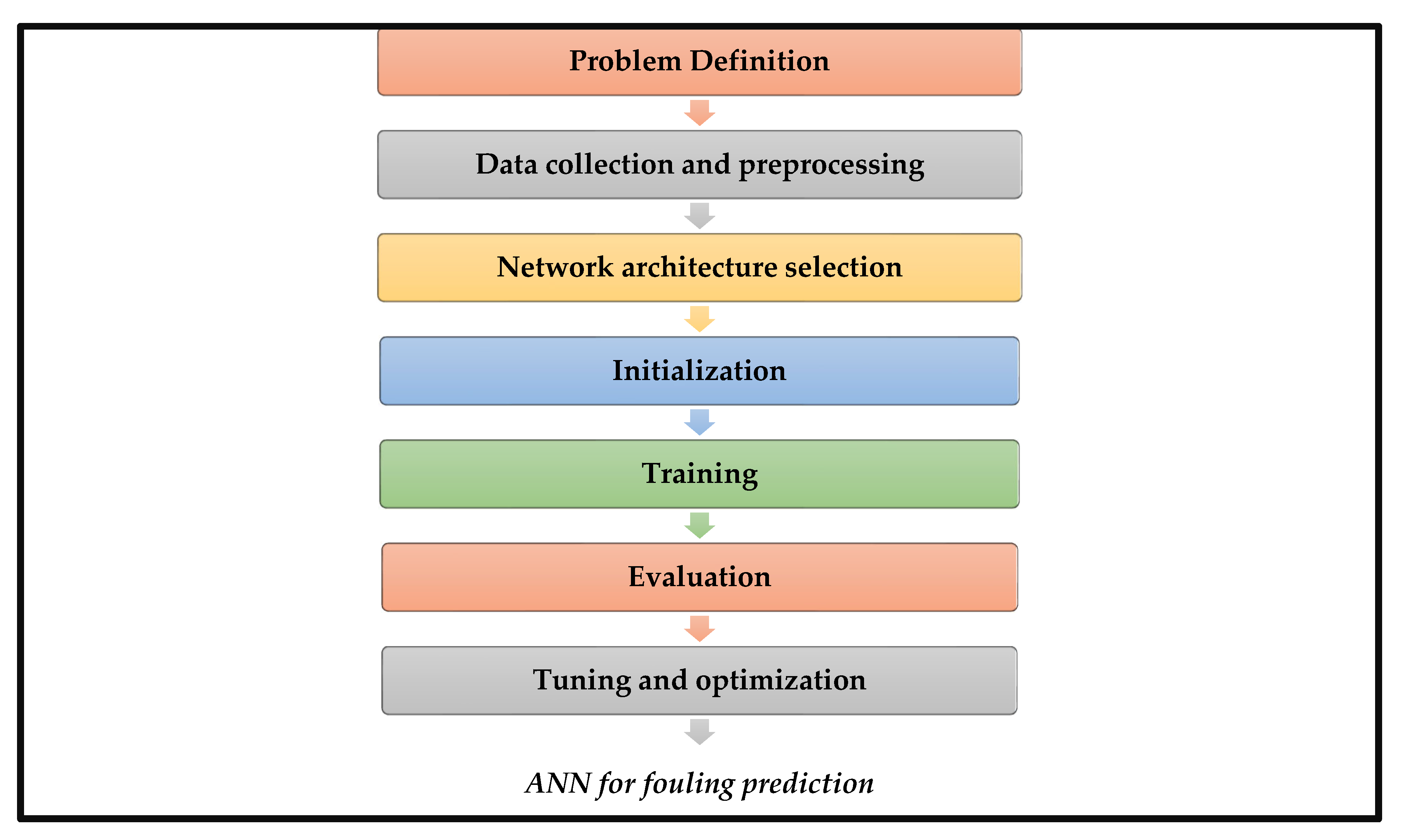
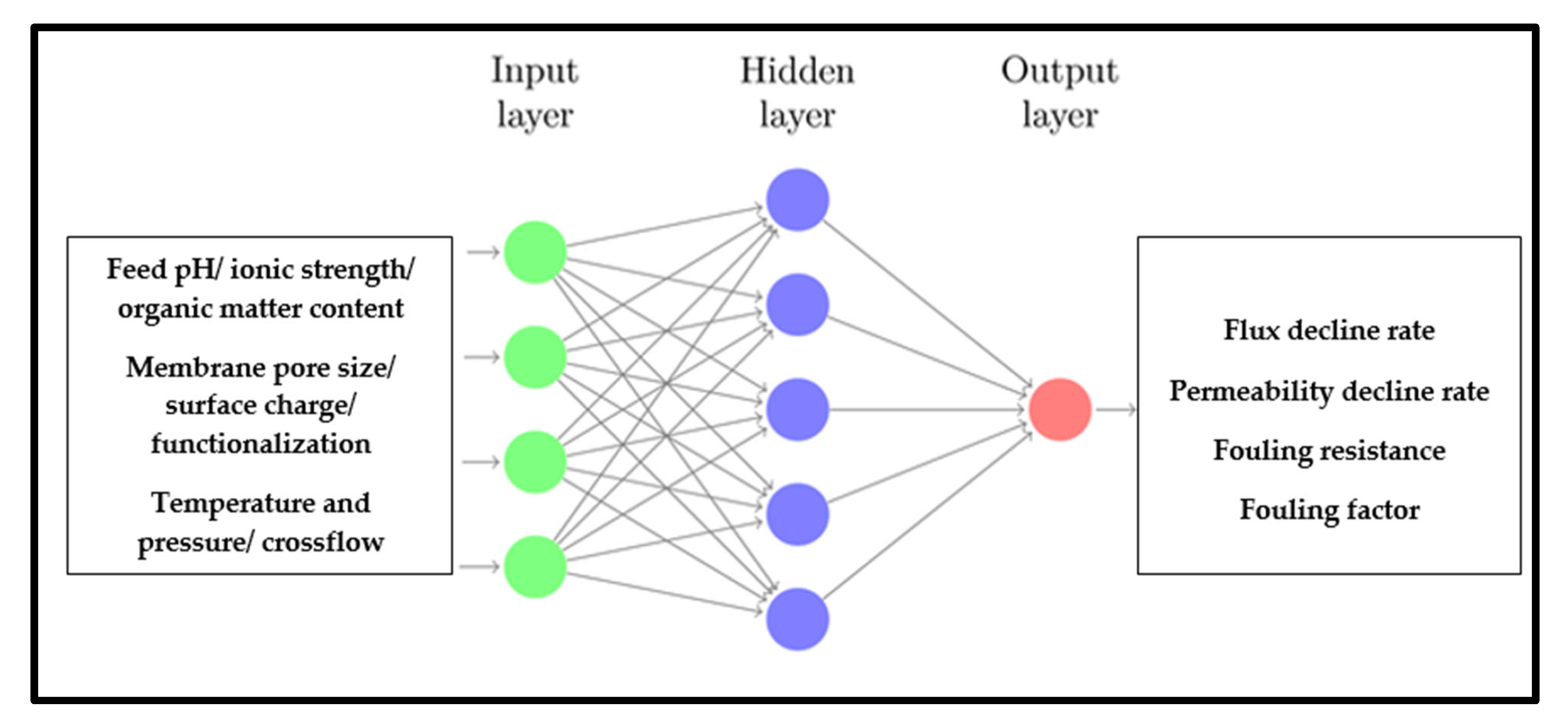
| Toolbox | Advantages | Limitations |
|---|---|---|
| Neural Network Toolbox |
|
|
| Curve Fitting Toolbox |
|
|
| Optimization Toolbox |
|
|
| Deep Learning Toolbox |
|
|
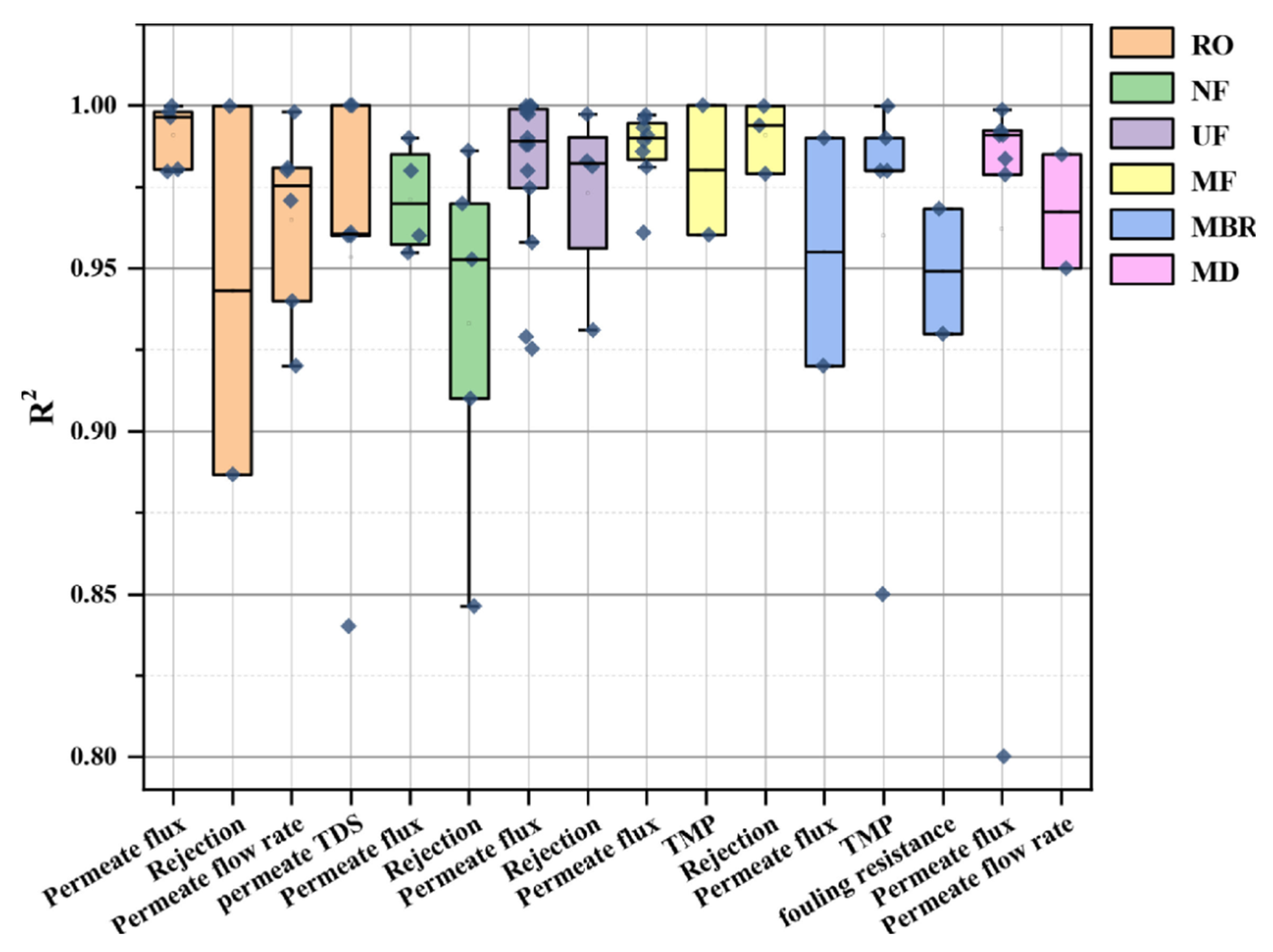
| Process Type | ANN Model | Training Algorithm | Feed Type | Model Inputs | Model Outputs | Ref. |
|---|---|---|---|---|---|---|
| RO | Basic ANN | Levenberg–Marquardt | Groundwater | Feed salinity, operating pressure, run time, membrane type | Water permeability constant (R2 = 0.996) | [67] |
| Basic ANN | Bayesian regularization backpropagation | Formulated artificial groundwater | Feed concentration, pressure, temperature | Water recovery (R2 = 0.9611) Total dissolved solids rejection (R2 = 0.9246) Specific energy consumption (R2 = 0.9044) | [96] | |
| RBF | Orthogonal least squares | Brackish water | Temperature, pH, conductance, pressure | Permeate flow rate (R2 = 0.9853) Total dissolved solids content (R2 = 1) | [72] | |
| RBF | Backpropagation | Groundwater | Clustered input space consisting of an 8-variable vector | Permeate flow rate (R2 = 0.92) Permeate total dissolved solids content (R2 = 0.84) | [97] | |
| MLP | Backpropagation | Wastewater | Run time, total dissolved solids content, feed | Permeate flow rate (R2 = 0.97–0.99) | [98] | |
| MLP | Backpropagation | Brackish water | Time, conductivity, flow rate, transmembrane pressure | Permeate flow (R2 = 0.94) Permeate conductivity (R2 = 0.99) | [99] | |
| MLP | Backpropagation | Dilute saline water | Membrane pore radius, friction constants between solvent, solute, and membrane, feed solute concentration, pressure, temperature | Total flux (R2 = 0.9982) Solvent flux (R2 = 0.9980) Separation factor (R2 = 0.9997) | [100] | |
| MLP | Backpropagation | Brackish water | Feed flow rate, pH, temperature, pressure, feed conductivity | Standardized permeate flux (R2 = 0.68) Percent salt passage (R2 = 0.86) | [101] | |
| MLP | Backpropagation | Seawater | Run time, transmembrane pressure, feed flow rate, feed total dissolved solids content, temperature | Permeate flow rate (R2 = 0.75) Permeate total dissolved solids content (R2 = 0.96) | [102] | |
| MLP | Levenberg–Marquardt | Brackish water | Feed salt concentration, temperature, pressure | Permeate flow rate (R2 = 0.998) | [103] | |
| MLP | Levenberg–Marquardt | Brackish water | Temperature, pH, conductance, pressure | Permeate flow rate (R2 = 0.9904) Permeate total dissolved solids content (R2 = 1) | [72] | |
| NF | Basic ANN | Backpropagation | Humic acid-based feedwater | Cross-flow velocity, initial flux, feed calcium concentration | Permeate flux (absolute relative error <0.1%) | [104] |
| Bootstrap aggregated neural networks (BANNs) | Ensemble creation and aggregation | Organic-contaminated feed | Feed characteristics (dipole moment, molecular weight, zeta potential, pH), recovery %, temperature, pressure | Salt rejection percent (R2 = 0.9862) | [105] | |
| DNN | / | Humic acid-based feedwater | Initial fouling thickness, membrane type, time, initial permeate flux | Permeate flux (R2 = 0.99) Fouling layer thickness (R2 = 0.99) | [95] | |
| RNN | Backpropagation | Artificial saline water | Real-time 2-dimensional OCT images, operation time, initial permeate flux, pressure, fluorescence regional integration, feed dissolved organic carbon content | Permeate flux (R2 = 0.9982) Fouling layer thickness (R2 = 0.9987) | [93] | |
| Normalized RBF | Backpropagation | Groundwater | Feed total dissolved solids, feed flux, recovery %, net driving force | Total dissolved solids concentration (R2 = 0.99) | [106] | |
| MLP | Backpropagation | Organic solvent feed | Membrane characteristics (support material, molecular weight cutoff), solvent properties (molecular weight, viscosity, density, kinetic diameter, etc.), operating conditions (temperature, pressure, solute concentration, solute type) | Permeance (R2 = 0.98) Rejection (R2 = 0.91) | [49] | |
| MLP | Backpropagation | Highly concentrated salt solutions | Feed pressure, salt concentration | Permeate flux, salt rejection | [107] | |
| MLP | Backpropagation | Groundwater | Feed total dissolved solids, feed flux, recovery %, net driving force | Total dissolved solids concentration (R2 = 0.99) | [106] | |
| MLP | Backpropagation | Organic contaminated feed | Feed characteristics (dipole moment, molecular weight, zeta potential, pH), contact angle, recovery %, temperature, pressure | Salt rejection percent (R2 = 9527) | [108] | |
| MLP | Levenberg–Marquardt | Groundwater and surface water | Permeate water flux, feed absorbance, time, pH, total dissolved solids content, temperature, influent flow rate | Membrane fouling resistance (absolute relative error < 5%) | [94] | |
| MLP | Levenberg–Marquardt | Waste brine | Transmembrane pressure, temperature, run time | Permeate flux (R2 = 0.96) Fouling resistance (R2 = 0.98) | [109] |
| Process Type | ANN Model | Training Algorithm | Feed Type | Model Inputs | Model Outputs (R2 Values) | Ref. |
|---|---|---|---|---|---|---|
| MF | Basic ANN | Levenberg–Marquardt | Bovine serum albumin solution | Transmembrane pressure, feed pH, cross-flow velocity | Permeate flux (R2 = 0.9810) Rejection (R2 = 0.99997) | [115] |
| RBF | / | Bovine serum albumin solution | Transmembrane pressure, feed pH, cross-flow velocity | Permeate flux (R2 = 0.9932) Rejection (R2 = 0.97903) | [115] | |
| MLP | Gradient descent with momentum | Red plum juice | Transmembrane pressure, temperature, membrane pore size, feed flow rate, run time | Permeate flux (R2 = 0.961) | [116] | |
| MLP | Backpropagation | Particulate suspensions | Influent velocity, feed concentration, transmembrane pressure | Flux improvement efficiency by turbulence promoter (R2 = 0.9891) | [117] | |
| MLP | Backpropagation | Wastewater | Temperature, pH, transmembrane pressure, cross-flow velocity, filtration time | Permeate flux (R2 = 0.9999) Fouling resistance (R2 = 0.9999) | [79] | |
| MLP | Backpropagation | Nickel-ion-containing aqueous solution | Membrane material, pore size, adsorbent type, surfactant type, surfactant concentration | Transient flux (R2 = 0.986) | [118] | |
| MLP | Levenberg–Marquardt | Industrial oily water | Temperature, transmembrane pressure, cross-flow velocity, feed oil concentration, run time | Permeate flux (R2 = 0.997) | [119] | |
| UF | MLP | Backpropagation | Wastewater | Surfactant-to-metal ratio, pH, cumulative sampling volume | Permeate flux, rejection rate (R2 = 0.9974) | [120] |
| MLP | / | Organic-contaminated feed | Parallel factor analysis (PARAFAC) component maximum fluorescence, pH, turbidity, and historical average slope of the resistance | Fouling resistance (mean absolute relative error < 5%) | [121] | |
| MLP | Backpropagation | Oily wastewater (polyacrylonitrile (PAN)-containing feed) | Temperature, pH, transmembrane pressure, cross-flow velocity, filtration time | Permeate flux decline (R2 = 0.99997) | [122] | |
| MLP | Levenberg–Marquardt | Bovine serum albumin solution | Membrane pore size, protein solution concentration, pH, transmembrane pressure, cross-flow velocity | Permeate flux (R2 = 0.996) Rejection (R2 = 0.994) | [48] | |
| MLP | Levenberg–Marquardt | Synthetic wastewater containing zinc ions | Surfactant-to-metal ratio, pH, feed anionic surfactant concentration, transmembrane pressure, ligand–to-zinc ratio, electrolyte concentration | Permeate flux (R2 = 0.929) Rejection (R2 = 0.981) | [123] | |
| MLP | Levenberg–Marquardt backpropagation | Polyethylene glycol-containing feed | Transmembrane pressure, cross-flow velocity, operation time | Permeate flux (R2 = 0.9977) | [50] | |
| MLP | Bayesian regulation backpropagation algorithm and Levenberg–Marquardt | Wastewater | Temperature, pH, transmembrane pressure, cross-flow velocity, filtration time | Permeate flux (R2 = 0.9999) | [42] | |
| MLP | Backpropagation, scaled conjugate gradient, Levenberg–Marquardt, gradient descent with momentum, adaptive learning rate backpropagation | Synthetic wastewater containing lead ions | Surfactant-to-metal ratio, pH, feed anionic surfactant concentration | Permeate flux (R2 = 0.9254) Rejection (R2 = 0.9813) | [80] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abuwatfa, W.H.; AlSawaftah, N.; Darwish, N.; Pitt, W.G.; Husseini, G.A. A Review on Membrane Fouling Prediction Using Artificial Neural Networks (ANNs). Membranes 2023, 13, 685. https://doi.org/10.3390/membranes13070685
Abuwatfa WH, AlSawaftah N, Darwish N, Pitt WG, Husseini GA. A Review on Membrane Fouling Prediction Using Artificial Neural Networks (ANNs). Membranes. 2023; 13(7):685. https://doi.org/10.3390/membranes13070685
Chicago/Turabian StyleAbuwatfa, Waad H., Nour AlSawaftah, Naif Darwish, William G. Pitt, and Ghaleb A. Husseini. 2023. "A Review on Membrane Fouling Prediction Using Artificial Neural Networks (ANNs)" Membranes 13, no. 7: 685. https://doi.org/10.3390/membranes13070685
APA StyleAbuwatfa, W. H., AlSawaftah, N., Darwish, N., Pitt, W. G., & Husseini, G. A. (2023). A Review on Membrane Fouling Prediction Using Artificial Neural Networks (ANNs). Membranes, 13(7), 685. https://doi.org/10.3390/membranes13070685








