Resistance of Ion Exchange Membranes in Aqueous Mixtures of Monovalent and Divalent Ions and the Effect on Reverse Electrodialysis
Abstract
1. Introduction
2. Materials and Methods
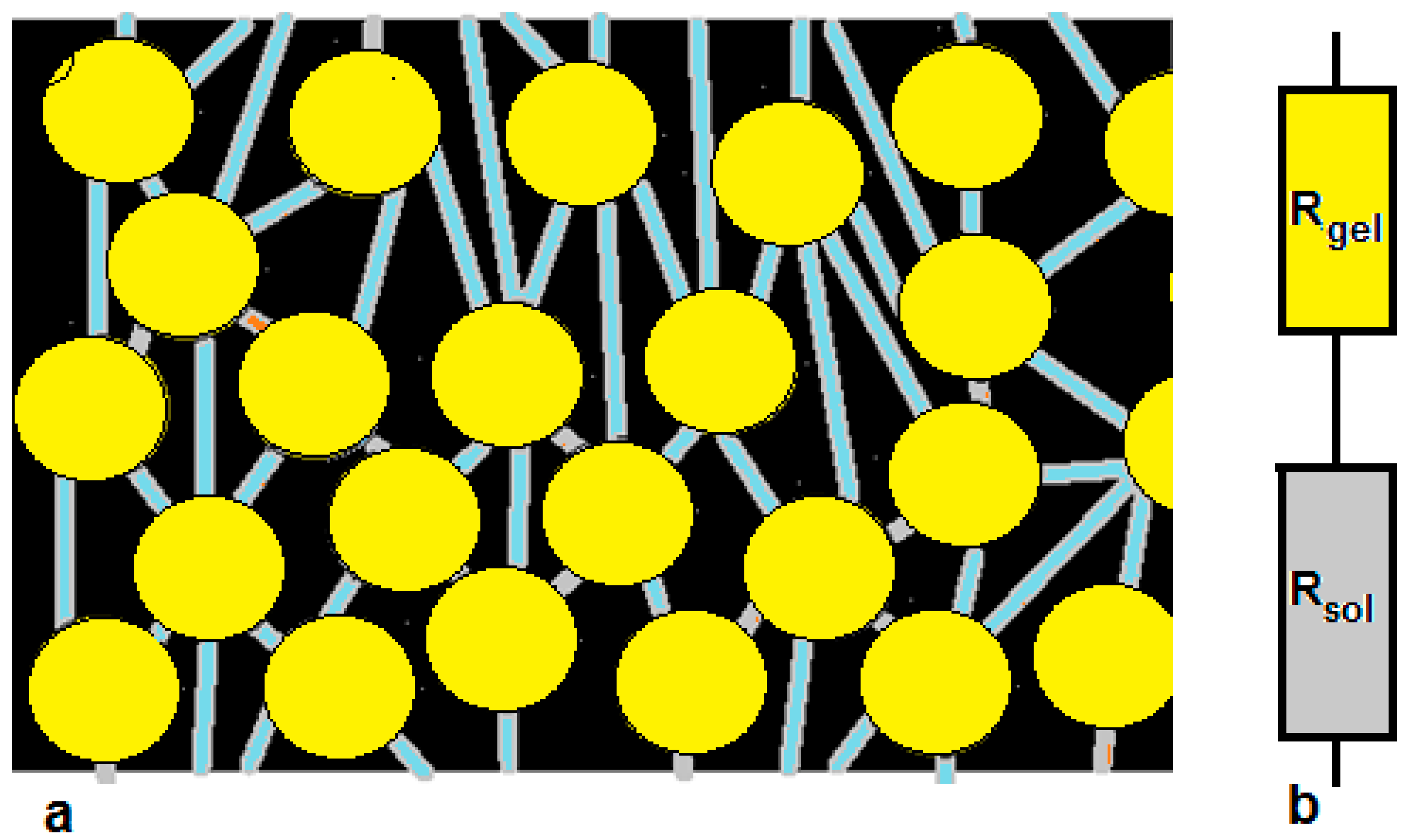
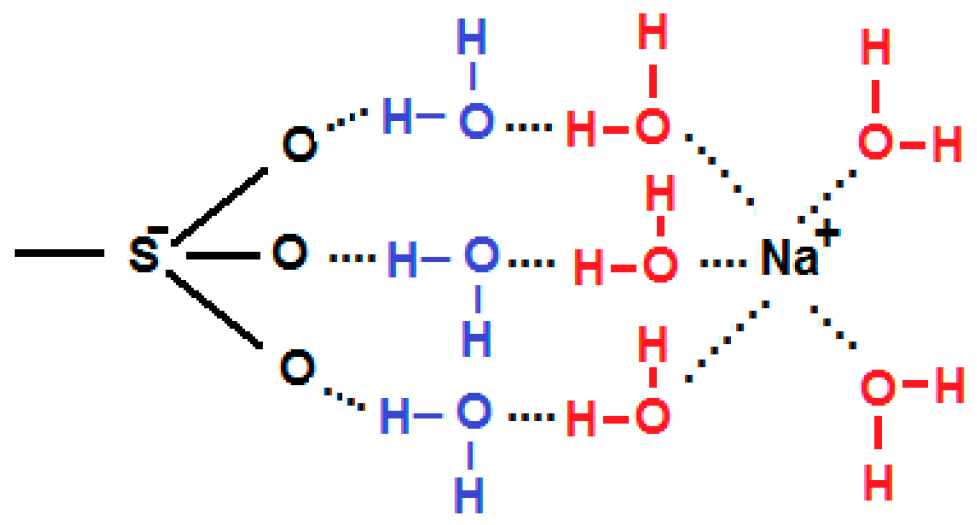
3. Model of Ion Transport in Ion Exchange Membranes
- i.
- Calculation of the concentrations of the ions in the gel from the known bulk concentrations using the Donnan theory.
- ii.
- Assignment of known mobilities to the ions in the solution phase and provisional values to the ions in the gel phase.
- iii.
- Assignment of provisional factors (‘phase factors’) to the conductivity of the gel part and the solution part.
- iv.
- Estimation of the membrane resistance using the one-thread model [8].
- v.
- Fitting the calculated resistances to the experimental values by adjusting the gel phase mobilities and the phase factors.
4. Results
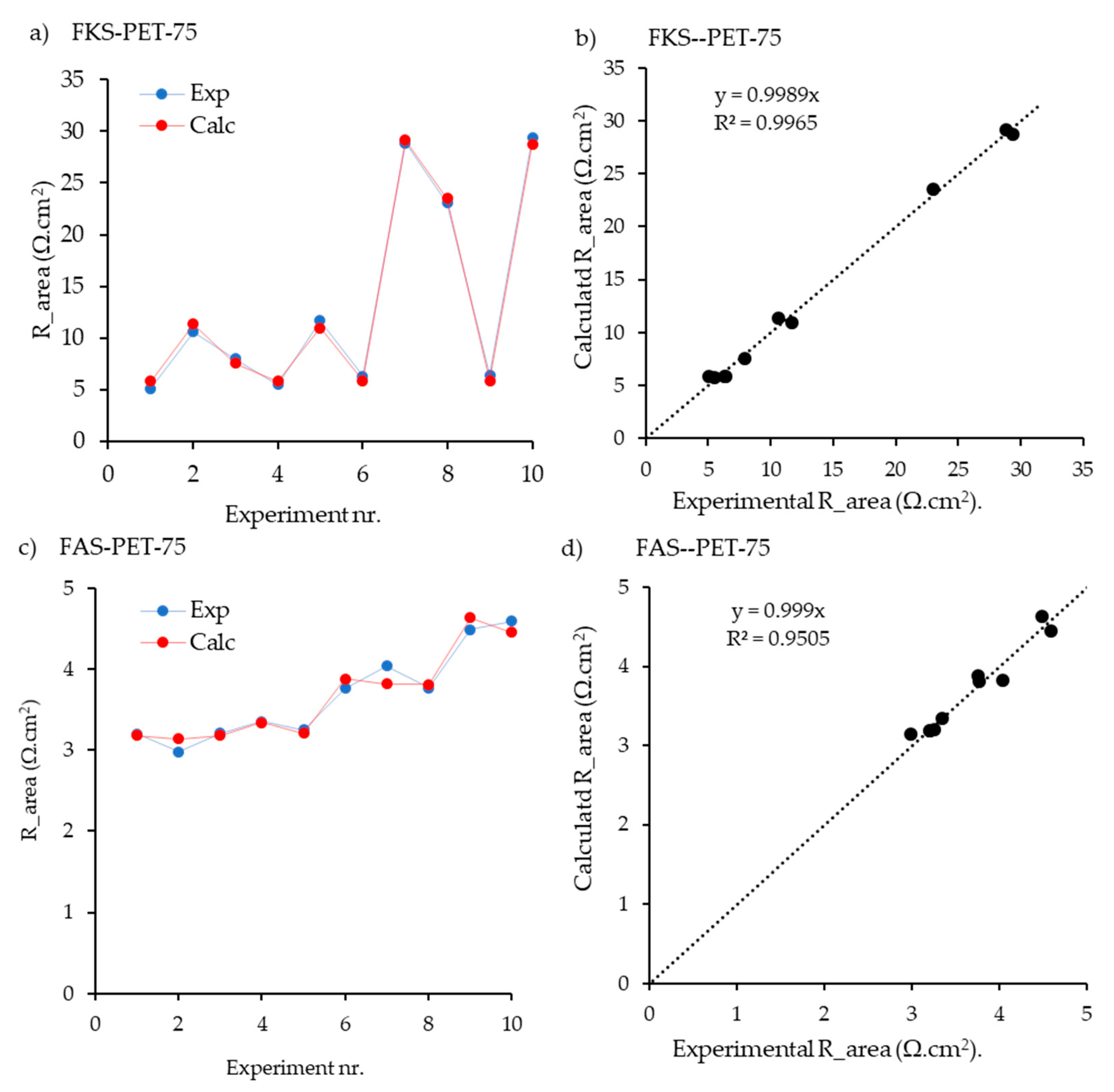
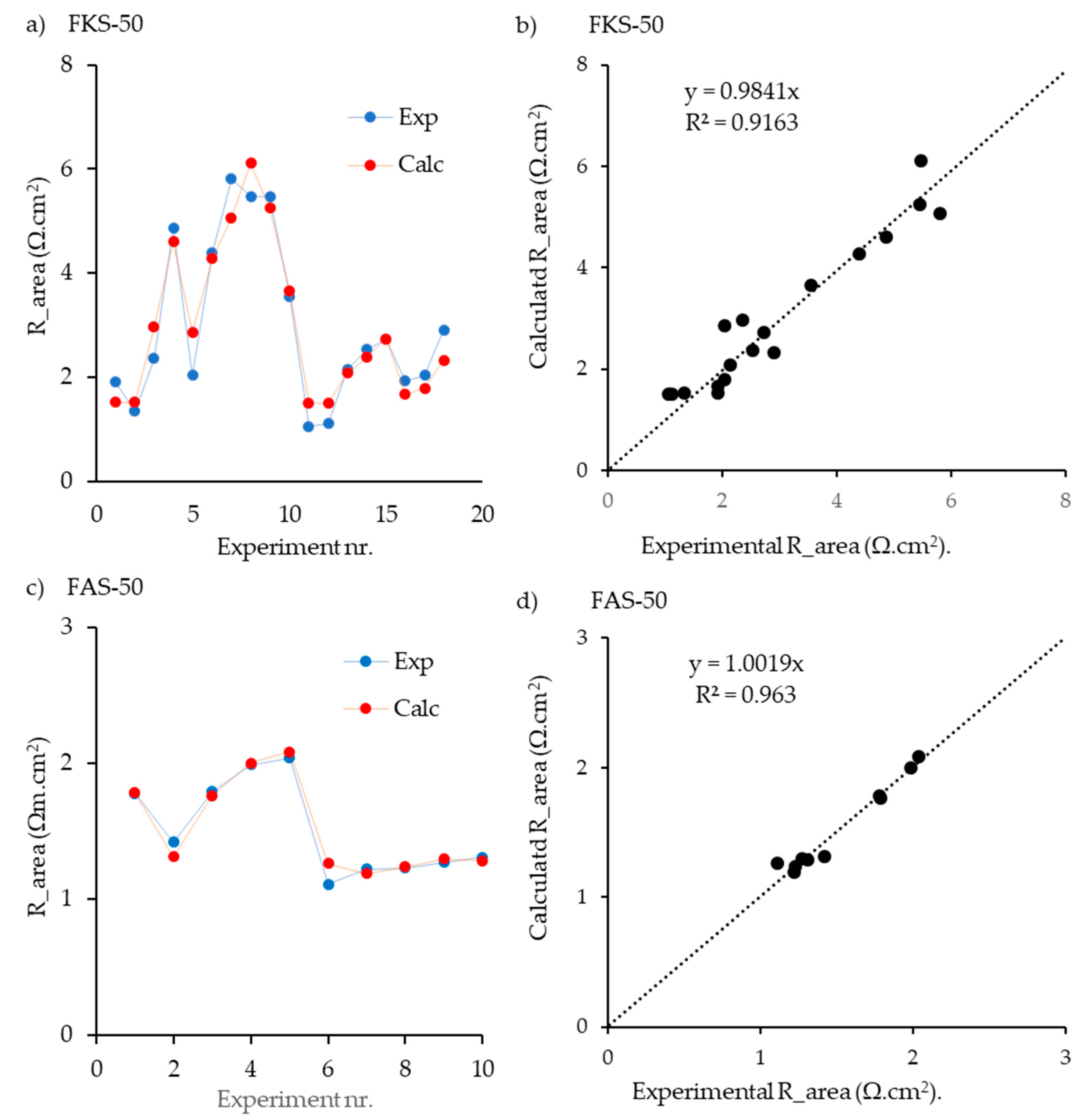
4.1. Estimation of Membrane Resistance
4.2. Application of the Ion Transport Model
| Exp. | Membrane | Type | CD (eq./L) | Ref. | Method | Salts Employed | n | k | R2 | R2adj. | Normalizad Mobility in the Gel Phase | Ratio Counter-Ion Mobility in the Gel Phase | Ratio Diffusion Constants in the Gel Phase | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NaCl | MgCl2 | CaCl2 | Na2SO4 | MgSO4 | Na+ | Mg2+ | Ca2+ | Cl− | SO42− | Na+/Mg2+ | Na+/Ca2+ | Cl−/SO42− | Na+/Ca2+ | Cl−/SO42− | Na+/Ca2+ | ||||||||||
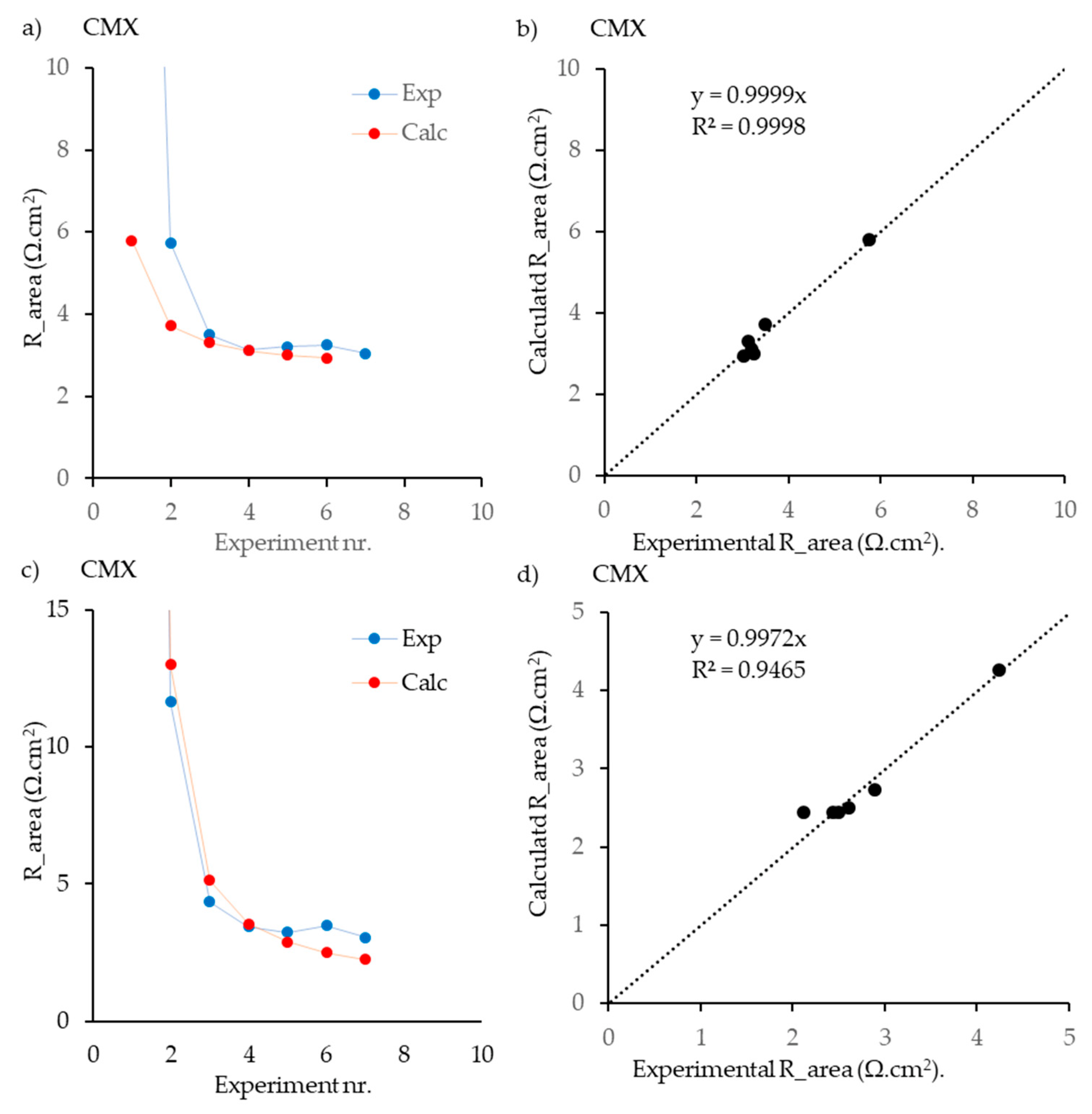
| a | CMX | CEM | 9 | [33] | AC | + | − | − | − | − | 7 | 3 | 0.999 | 0.999 | 0.976 | − | − | 0.024 | - | - | - | − | − | − | − |
| b | CMX | CEM | 9 | [33] | DC | + | − | − | − | − | 7 | 3 | 0.999 | 0.999 | 1 | − | − | 0 | - | - | - | − | − | − | − |
| c | FKS-PET-75 | CEM | 5.5 | This work | EIS | + | + | + | + | − | 10 | 6 | 0.997 | 0.99 | 0.771 | 0.085 | 0.116 | 0.029 | 0 | 9.1 | 6.7 | − | 18.2 | 13.4 | − |
| d | FAS-PET-75 | AEM | 9 | This work | EIS | + | + | + | + | − | 10 | 6 | 0.953 | 0.859 | 0.22 | 0.754 | 0 | 0.014 | 0.011 | - | - | 1.3 | − | − | 2.6 |
| e | FKS-50 | CEM | 8.7 | [22] | EIS | + | + | + | − | − | 18 | 5 | 0.9233 | 0.891 | 0.679 | 0.151 | 0.17 | 0 | - | 4.5 | 4 | - | 9 | 8 | − |
| f | FAS-50 | AEM | 10.3 | [22] | EIS | + | − | − | + | − | 10 | 4 | 0.964 | 0.935 | 0.844 | − | − | 0.098 | 0.059 | − | − | 1.7 | − | − | 3.3 |
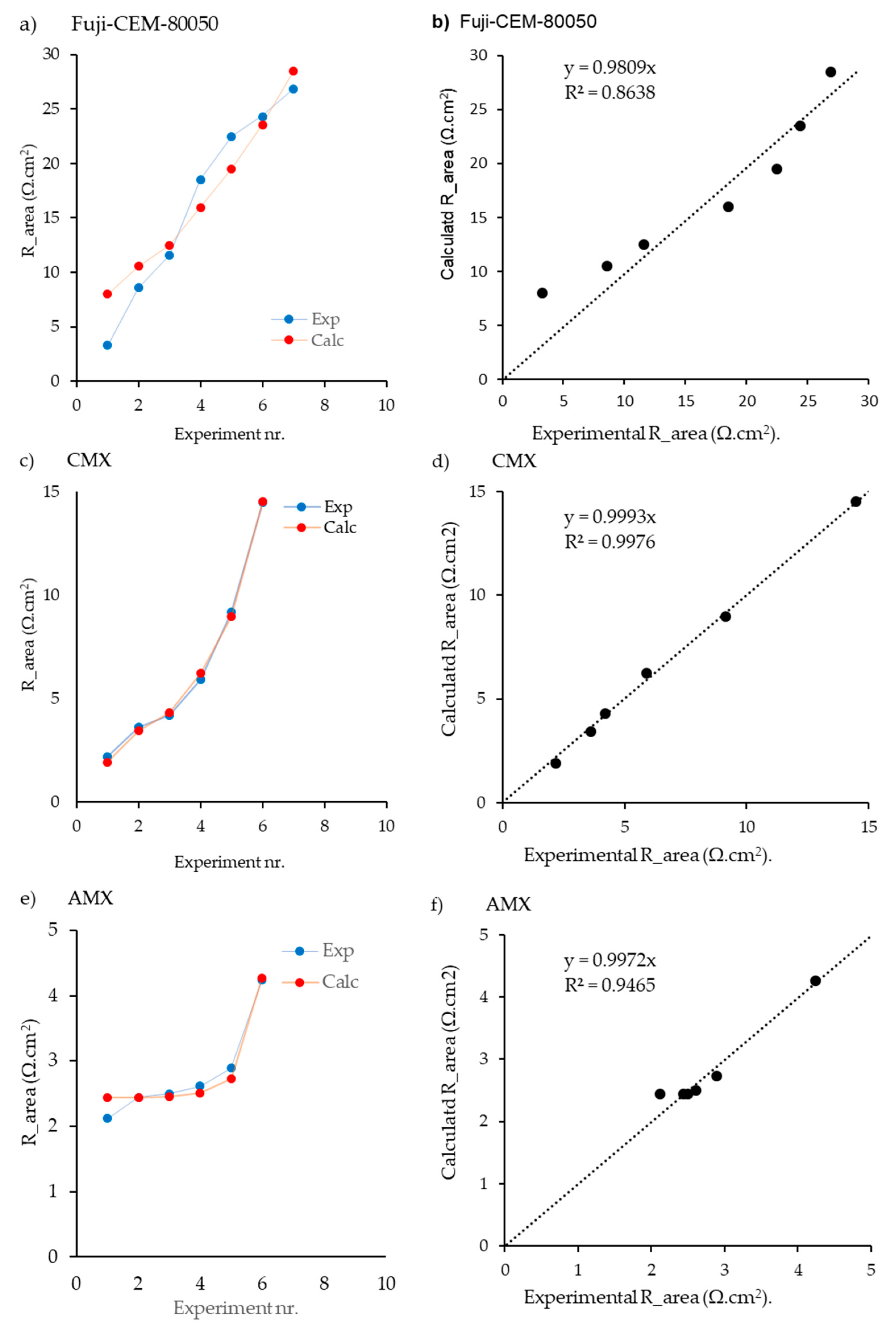
| g | Fuji-CEM-80050 | CEM | 2.4 | [15] | EIS | + | + | − | − | − | 7 | 4 | 0.922 | 0.767 | 0.635 | 0 | − | 0.365 | - | ∞ | − | − | ∞ | − | − |
| h | CMX | CEM | 9 | [18] | NR | + | − | − | − | + | 6 | 5 | 0.998 | − | 0.315 | 0.033 | − | 0 | 0.652 | 9.5 | − | − | 19 | − | − |
| i | AMX | AEM | 7.8 | [18] | NR | + | − | − | − | + | 6 | 5 | 0.95 | − | 0.994 | 0 | − | 0.006 | 0 | − | − | ∞ | − | − | ∞ |
4.2.1. Fumatech Membranes
4.2.2. Results with Neosepta CMX with AC and DC
4.2.3. Results with Fuji-CEM-80050, Neasepta CMX, and Neosepta AMX
4.3. Gross Power Density
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman | |
| A | Membrane areas (cm2) |
| C | Concentration (eq/L) |
| CD | Membrane charge density (eq/L) |
| D | Diffusion constant in H2O (m2/s) |
| Đ | Diffusion constant in gel phase (m2/s) |
| d | Membrane thickness (cm) |
| F | Faraday constant (96,485 C∙mol−1) |
| IEC | Ion exchange capacity (meq/g dry membrane) |
| SD | Membrane swelling degree (−) |
| k | Boltzmann constant (1.381 × 10−23 J/K) |
| K | Donnan equilibrium constant (−) |
| Rarea | Membrane area resistance (Ω∙m2) |
| Rfgel | Resistance factor of the gel part |
| Rfsol | Resistance factor of the solution part |
| Rgel | Resistance of the gel part (Ω) |
| Rmem | Resistance of the membrane (Ω) |
| Rsol | Resistance of the solution part (Ω) |
| Rspec | Specific resistance (Ω∙m) |
| Q | Ion charge (C) |
| T | Temperature (K) |
| z | Ionic valence |
| Greek | |
| φ | Relative ionic mobility (−) |
| κ | Conductivity (S/m) |
| λ | Ionic mobility (m2∙s−1∙V−1) |
| ρ | Density of the dry membrane (kg/L) |
| Sub- and super-scripts | |
| gel | Gel phase |
| sol | Solution phase |
| i | Ionic species i |
| co | Co-ions |
| ct | Counter-ions |
| Acronyms | |
| AEM | Anion exchange membrane |
| AC | Alternating current |
| CEM | Cation exchange membrane |
| DC | Direct current |
| EIS | Electrochemical impedance spectrometry |
| GPD | Gross power density |
| HCS | High-concentration solution |
| IEM | Ion exchange membranes |
| LCS | Low-concentration solution |
| RED | Reverse electrodialysis |
References
- Gierke, T.D.; Munn, G.E.; Wilson, F.C. The morphology in Nafion perfluorinated membrane products, as determined by wide-and small-angle X-ray studies. J. Polym. Sci. 1981, 19, 1687–1704. [Google Scholar] [CrossRef]
- Kreuer, K. On the development of proton conducting polymer membranes for hydrogen and methanol fuel cells. J. Membr. Sci. 2001, 185, 29–39. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V. Effect of structural membrane inhomogeneity on transport properties. J. Membr. Sci. 1933, 79, 181–198. [Google Scholar] [CrossRef]
- Berezina, N.; Gnusin, N.; Dyomina, O.; Timofeyev, S. Water electrotransport in membrane systems. Experiment and model description. J. Membr. Sci. 1994, 86, 207–229. [Google Scholar] [CrossRef]
- Sarapulova, V.; Shkorkina, I.; Mareev, S.; Pismenskaya, N.; Kononenko, N.; Larchet, C.; Dammak, L.; Nikonenko, V. Transport Characteristics of Fujifilm Ion-Exchange Membranes as Compared to Homogeneous Membranes AMX and CMX and to Heterogeneous Membranes MK-40 and MA-41. Membranes 2019, 9, 84. [Google Scholar] [CrossRef]
- Sarapulova, V.; Pismenskaya, N.; Titorova, V.; Sharafan, M.; Wang, Y.; Xu, T.; Zhang, Y.; Nikonenko, V. Transport characteristics of CJMAED homogeneous anion exchange membranes in sodium chloride and sodium sulfate solutions. Int. J. Mol. Sci. 2021, 22, 1415. [Google Scholar] [CrossRef]
- Sarapulova, V.V.; Titorova, V.D.; Nikonenko, V.V.; Pismenskaya, N.D. Transport Characteristics of Homogeneous and Heterogeneous Ion-Exchange Membranes in Sodium Chloride, Calcium Chloride, and Sodium Sulfate Solutions. Membr. Membr. Technol. 2019, 1, 168–182. [Google Scholar] [CrossRef]
- Veerman, J. The Effect of the NaCl bulk concentration on the resistance of ion exchange membranes—Measuring and modeling. Energies 2020, 13, 1946. [Google Scholar] [CrossRef]
- Abidin, M.N.Z.; Nasef, M.M.; Veerman, J. Towards the development of new generation of ion exchange mem-branes for reverse electrodialysis: A review. Desalination 2022, 537, 115854. [Google Scholar] [CrossRef]
- Imai, N.; Onishi, T. Analytical solution of Poisson-Boltzmann equation for two-dimensional nany-center problem. J. Chem. Phys. 1958, 30, 1115–1116. [Google Scholar] [CrossRef]
- Kamcev, J.; Paul, D.R.; Manning, G.S.; Freeman, B.D. Ion diffusion coefficients in ion exchange membranes: Significance of counterion condensation. Macromolecules 2018, 51, 5519–5529. [Google Scholar] [CrossRef]
- Oh, Y.; Jeong, Y.; Han, S.-J.; Kim, C.S.; Kim, H.; Han, J.-H.; Hwang, K.-S.; Jeong, N.; Park, J.S.; Chae, S.C. Effects of divalent cations on electrical membrane resistance in reverse electrodialysis for salinity power generation. Ind. Eng. Chem. Res. 2018, 57, 15803–15810. [Google Scholar] [CrossRef]
- Post, J.W.; Hamelers, H.V.M.; Buisman, C.J.N. Influence of multivalent ions on power production from mixing salt and fresh water with a reverse electrodialysis system. J. Membr. Sci. 2009, 330, 65–72. [Google Scholar] [CrossRef]
- Vermaas, D.A.; Veerman, J.; Saakes, M.; Nijmeijer, K. Influence of multivalent ions on renewable energy generation in reverse electrodialysis. Energy Environ. Sci. 2014, 7, 1434–1445. [Google Scholar] [CrossRef]
- Avci, A.H.; Sarkar, P.; Tufa, R.A.; Messana, D.; Argurio, P.; Fontananova, E.; Di Profio, G.; Curcio, E. Effect of Mg2+ ions on energy generation by reverse electrodialysis. J. Membr. Sci. 2016, 520, 499–506. [Google Scholar] [CrossRef]
- Moreno, J.; Díez, V.; Saakes, M.; Nijmeijer, K. Mitigation of the effects of multivalent ion transport in reverse electrodialysis. J. Membr. Sci. 2018, 550, 155–162. [Google Scholar] [CrossRef]
- Rijnaarts, H.H.M.; Huerta, T.E.; Van Baak, W.; Nijmeijer, K. Effect of divalent cations on RED performance and cation exchange membrane selection to enhance power densities. Environ. Sci. Technol. 2017, 51, 13028–13035. [Google Scholar] [CrossRef]
- Kuno, M.; Yasukawa, M.; Kakihana, Y.; Higa, M. The effect of divalent ions on reverse electrodialysis power generation system. Bull. Soc. Sea Water Sci. Jpn. 2017, 71, 350–351. [Google Scholar]
- Pintossi, D.; Chen, C.; Saakes, M.; Nijmeijer, K.; Borneman, Z. Influence of sulfate on anion exchange membranes in reverse electrodialysis. NPJ Clean Water 2020, 3, 29. [Google Scholar] [CrossRef]
- Pintossi, D.; Simoes, C.; Saakes, M.; Borneman, Z.; Nijmeijer, K. Predicting reverse electrodialysis performance in the presence of divalent ions for renewable energy generation. Energy Convers. Manag. 2021, 243, 114369. [Google Scholar] [CrossRef]
- Veerman, J. Concepts and misconceptions concerning the influence of divalent ions on the performance of reverse electrodialysis using natural waters. Membranes 2023, 13, 69. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Coma, L.; Ortiz-Martínez, V.M.; Carmona, J.; Palacio, L.; Prádanos, P.; Fallanza, M.; Ortiz, A.; Ibañez, R.; Ortiz, I. Modeling the influence of divalent ions on membrane resistance and electric power in reverse electrodialysis. J. Membr. Sci. 2019, 592, 117385. [Google Scholar] [CrossRef]
- Soldatov, V.; Pristavko, S.; Zelenkovskii, V.; Kosandrovich, E. Hydration of ion exchangers: Thermodynamics and quantum chemistry calculations. React. Funct. Polym. 2013, 73, 737–744. [Google Scholar] [CrossRef]
- Soldatov, V.; Zelenkovskii, V.; Kosandrovich, E. Hydration of ion exchangers: Thermodynamics and quantum chemistry calculations. II an improved variant of the predominant hydrates model. React. Funct. Polym. 2016, 102, 147–155. [Google Scholar] [CrossRef]
- Soldatov, V.; Zelenkovskii, V.; Kosandrovich, E. Hydration of ion exchangers: Thermodynamics and quantum chemistry calculations. III. The state of the proton and water molecules in hydrogen form of sulfostyrene ion exchangers. React. Funct. Polym. 2016, 102, 156–164. [Google Scholar] [CrossRef]
- Helfferich, F.G. Ion Exchange; McGraw-Hill: New York, NY, USA, 1962; ASIN B0000CLGWI. [Google Scholar]
- Soldatov, V.S.; Kosandrovich, E.G.; Bezyazychnaya, T.V. Quantum chemical evidence of a fundamental difference between hydrations and ion exchange selectivities of sodium and potassium ions on carboxylic and sulfonic acid cation exchangers. J. Struct. Chem. 2020, 61, 1898–1909. [Google Scholar] [CrossRef]
- Shaposhnik, V.A.; Butyrskaya, E.V. Computer simulation of cation-exchange membrane structure: An elementary act of hydrated ion transport. Russ. J. Electrochem. 2004, 40, 767–770. [Google Scholar] [CrossRef]
- Badessa, T.; Shaposhnik, V. The electrodialysis of electrolyte solutions of multi-charged cations. J. Membr. Sci. 2016, 498, 86–93. [Google Scholar] [CrossRef]
- Badessa, T.S.; Shaposhnik, V.A.; Nartova, M.R. Transport of multi-charged cations through cation exchange membrane by electrodialysis. Сoрбциoнные И Хрoматoграфические Прoцессы (Sorpt. Chromatogr. Process.) 2015, 15, 450–455. [Google Scholar]
- Luo, T.; Roghmans, F.; Wessling, M. Ion mobility and partition determine the counter-ion selectivity of ion exchange membranes. J. Membr. Sci. 2020, 597, 117645. [Google Scholar] [CrossRef]
- Tedesco, M.; Hamelers, H.V.M.; Biesheuvel, P.M. Nernst-Planck transport theory for (reverse) electrodialysis: I. Effect of co-ion transport through the membranes. J. Membr. Sci. 2016, 510, 370–381. [Google Scholar] [CrossRef]
- Galama, A.H.; Vermaas, D.A.; Veerman, J.; Saakes, M.; Rijnaarts, H.H.M.; Post, J.W.; Nijmeijer, K. Membrane resistance: The effect of salinity gradients over a cation exchange membrane. J. Membr. Sci. 2014, 467, 279–291. [Google Scholar] [CrossRef]
- Geise, G.M.; Curtis, A.J.; Hatzell, M.C.; Hickner, M.A.; Logan, B.E. Salt concentration differences alter membrane resistance in reverse electrodialysis stacks. Environ. Sci. Technol. Lett. 2014, 1, 36–39. [Google Scholar] [CrossRef]
- Ortiz-Martínez, V.M.; Gómez-Coma, L.; Tristán, C.; Pérez, G.; Fallanza, M.; Ortiz, A.; Ibañez, R.; Ortiz, I. A comprehensive study on the effects of operation variables on reverse electrodialysis performance. Desalination 2020, 482, 114389. [Google Scholar] [CrossRef]
- Ortiz-Imedio, R.; Gómez-Coma, L.; Fallanza, M.; Ortiz, A.; Ibañez, R.; Ortiz, I. Comparative performance of salinity gradient power-reverse electrodialysis under different operating conditions. Desalination 2019, 457, 8–21. [Google Scholar] [CrossRef]
- Gómez-Coma, L.; Ortiz-Martínez, V.M.; Fallanza, M.; Ortiz, A.; Ibañez, R.; Ortiz, I. Blue energy for sustainable water reclamation in WWTPs. J. Water Process. Eng. 2020, 33, 101020. [Google Scholar] [CrossRef]
- Gómez-Coma, L.; Abarca, J.A.; Fallanza, M.; Ortiz, A.; Ibañez, R.; Ortiz, I. Optimum recovery of saline gradient power using reversal electrodialysis: Influence of the stack components. J. Water Process. Eng. 2022, 48, 102816. [Google Scholar] [CrossRef]
- Available online: https://www.priyamstudycentre.com/2021/07/ionic-mobility.html (accessed on 15 July 2022).
- Moore, W.J. Physical Chemistry; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1974; ISBN 0-582-44234-6. [Google Scholar]
- Available online: https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/adjusted-r2/ (accessed on 15 July 2022).
- Sarapulova, V.; Pismenskaya, N.; Butylskii, D.; Titorova, V.; Wang, Y.; Xu, T.; Zhang, Y.; Nikonenko, V. Transport and Electrochemical Characteristics of CJMCED Homogeneous Cation Exchange Membranes in Sodium Chloride, Calcium Chloride, and Sodium Sulfate Solutions. Membranes 2020, 10, 165. [Google Scholar] [CrossRef]
- Technical Data Sheet Fumasep FKS-50. Available online: https://www.fuelcellstore.com/spec-sheets/fumasep-fks-50-technical-specifications.pdf (accessed on 15 July 2022).
- Długołęcki, P.; Nymeijer, K.; Metz, S.; Wessling, M. Current status of ion exchange membranes for power generation from salinity gradients. J. Membr. Sci. 2008, 319, 214–222. [Google Scholar] [CrossRef]
- Luo, T.; Abdu, S.; Wessling, M. Selectivity of ion exchange membranes: A review. J. Membr. Sci. 2018, 555, 429–454. [Google Scholar] [CrossRef]
- Hong, J.G.; Zhang, W.; Luo, J.; Chen, Y. Modeling of power generation from the mixing of simulated saline and freshwater with a reverse electrodialysis system: The effect of monovalent and multivalent ions. Appl. Energy 2013, 110, 244–251. [Google Scholar] [CrossRef]
- Besha, A.T.; Tsehaye, M.T.; Aili, D.; Zhang, W.; Tufa, R.A. Design of Monovalent Ion Selective Membranes for Reducing the Impacts of Multivalent Ions in Reverse Electrodialysis. Membranes 2020, 10, 7. [Google Scholar] [CrossRef] [PubMed]
- Luque Di Salvo, J.; Cosenza, A.; Tamburini, A.; Micale, G.; Cipollina, A. Long-run operation of a reverse electrodialysis system fed with wastewaters. J. Environ. Manag. 2018, 217, 871–887. [Google Scholar] [CrossRef] [PubMed]
- Vanoppen, M.; Gutierrez, V.V.T.L.; Roman, M.; Croué, L.J.P.; Verbeken, K.; Philips, J.; Verliefde, A.R.D. Secondary treated domestic wastewater in reverse electrodialysis: What is the best pre-treatment? Sep. Purif. Technol. 2019, 218, 25–42. [Google Scholar] [CrossRef]
- Kingsbury, R.S.; Liu, F.; Zhu, S.; Boggs, C.; Armstrong, M.D.; Call, D.F.; Coronell, O. Impact of natural organic matter and inorganic solutes on energy recovery from five real salinity gradients using reverse electrodialysis. J. Membr. Sci. 2017, 541, 621–632. [Google Scholar] [CrossRef]
- Available online: https://www.fuelcellstore.com/fuel-cell-components/membranes (accessed on 24 January 2023).

| Cation | λ (m2∙s−1∙V−1) | Anion | λ (m2∙s−1∙V−1) |
|---|---|---|---|
| Na+ | 5.20 × 10−8 | Cl− | 7.90 × 10−8 |
| Mg2+ | 5.50 × 10−8 | SO42− | 8.27 × 10−8 |
| Ca2+ | 6.16 × 10−8 |
| Experiment | M | Membrane Resistance (Ω·cm2) | |||||
|---|---|---|---|---|---|---|---|
| No. | NaCl | MgCl2 | CaCl2 | Na2SO4 | FKS-PET-75 | FAS-PET-75 | |
| HCS | 1 | 0.5 | 0 | 0 | 0 | 5.09 | 3.20 |
| 2 | 0.49 | 0.06 | 0 | 0 | 10.58 | 2.98 | |
| 3 | 0.49 | 0 | 0.011 | 0 | 7.97 | 3.21 | |
| 4 | 0.49 | 0 | 0 | 0.032 | 5.49 | 3.35 | |
| 5 | 0.49 | 0.06 | 0.011 | 0.032 | 11.69 | 3.25 | |
| LCS | 6 | 0.02 | 0 | 0 | 0 | 6.33 | 3.76 |
| 7 | 0.0176 | 0.0024 | 0 | 0 | 28.86 | 4.04 | |
| 8 | 0.0185 | 0 | 0.002 | 0 | 23.05 | 3.77 | |
| 9 | 0.0186 | 0 | 0 | 0.0014 | 6.40 | 4.49 | |
| 10 | 0.0172 | 0.0024 | 0.002 | 0.0014 | 29.39 | 4.59 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veerman, J.; Gómez-Coma, L.; Ortiz, A.; Ortiz, I. Resistance of Ion Exchange Membranes in Aqueous Mixtures of Monovalent and Divalent Ions and the Effect on Reverse Electrodialysis. Membranes 2023, 13, 322. https://doi.org/10.3390/membranes13030322
Veerman J, Gómez-Coma L, Ortiz A, Ortiz I. Resistance of Ion Exchange Membranes in Aqueous Mixtures of Monovalent and Divalent Ions and the Effect on Reverse Electrodialysis. Membranes. 2023; 13(3):322. https://doi.org/10.3390/membranes13030322
Chicago/Turabian StyleVeerman, Joost, Lucía Gómez-Coma, Alfredo Ortiz, and Inmaculada Ortiz. 2023. "Resistance of Ion Exchange Membranes in Aqueous Mixtures of Monovalent and Divalent Ions and the Effect on Reverse Electrodialysis" Membranes 13, no. 3: 322. https://doi.org/10.3390/membranes13030322
APA StyleVeerman, J., Gómez-Coma, L., Ortiz, A., & Ortiz, I. (2023). Resistance of Ion Exchange Membranes in Aqueous Mixtures of Monovalent and Divalent Ions and the Effect on Reverse Electrodialysis. Membranes, 13(3), 322. https://doi.org/10.3390/membranes13030322








