Investigation of Calcium and Magnesium Removal by Donnan Dialysis According to the Doehlert Design for Softening Different Water Types
Abstract
1. Introduction
2. Experiment
2.1. Reagents and Methods
2.2. Membranes
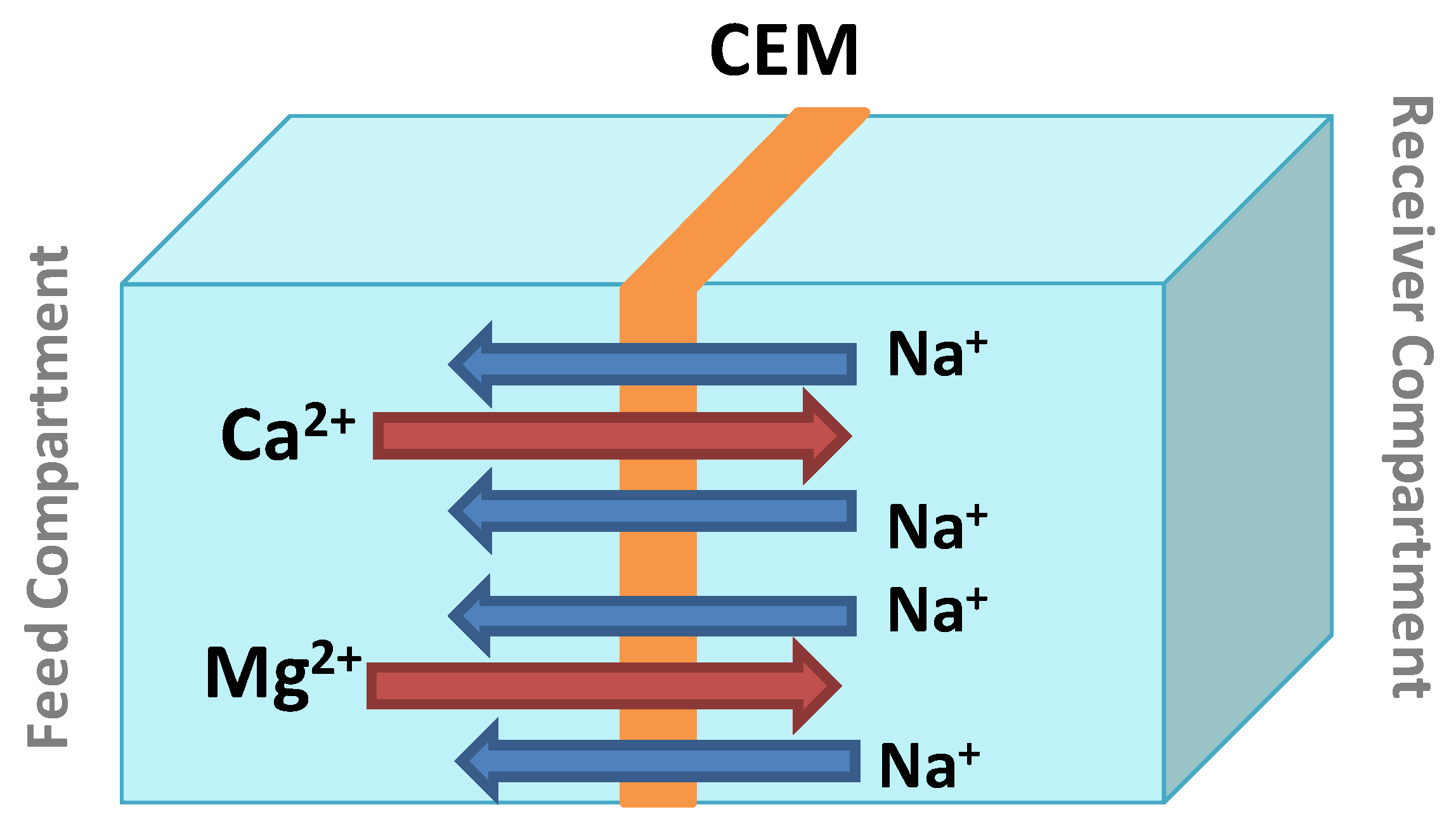
2.3. Donnan Dialysis (DD)
2.4. Optimization Software
3. Results and Discussion
3.1. The Preliminary Study
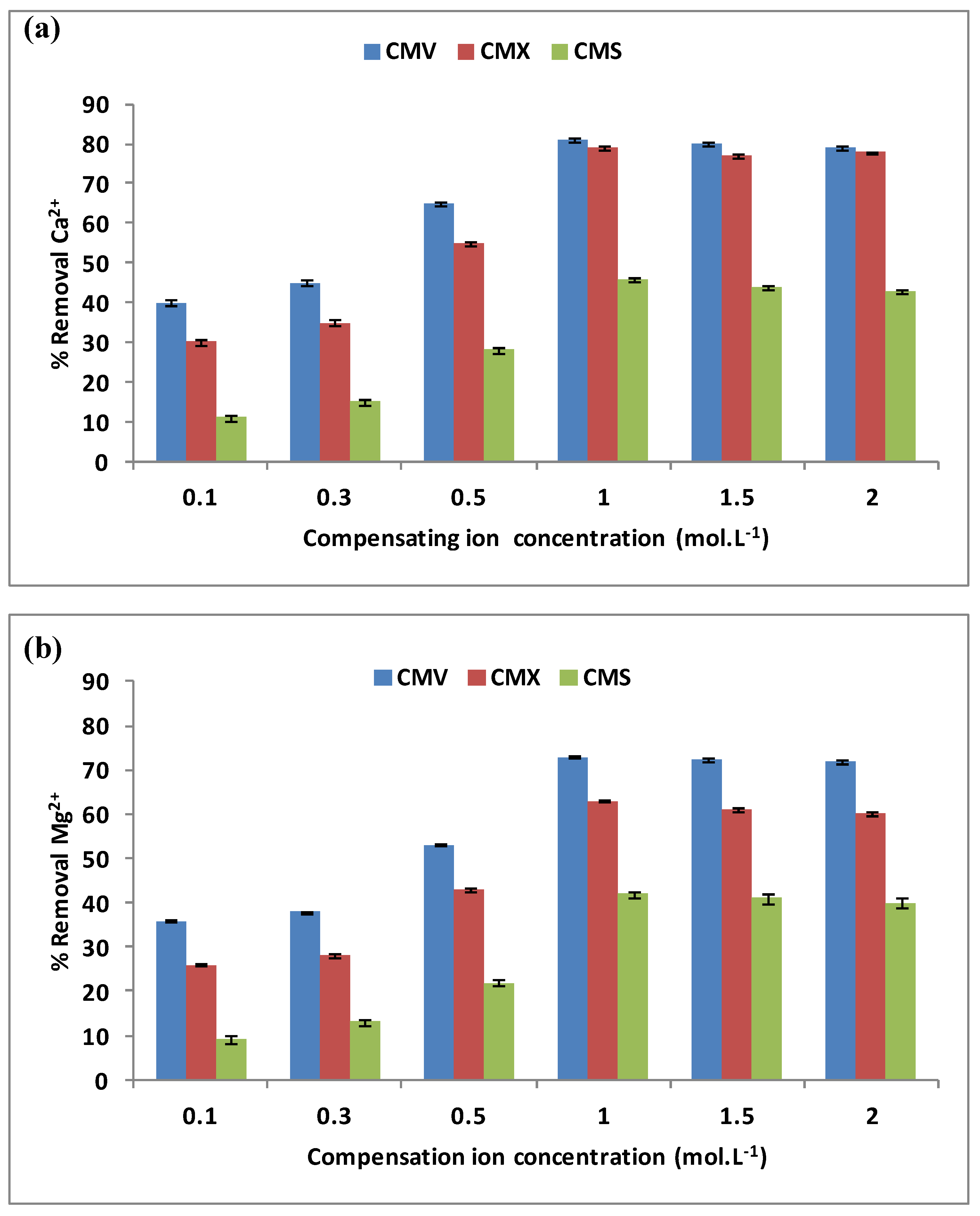
3.1.1. The Compensating Ion Effects
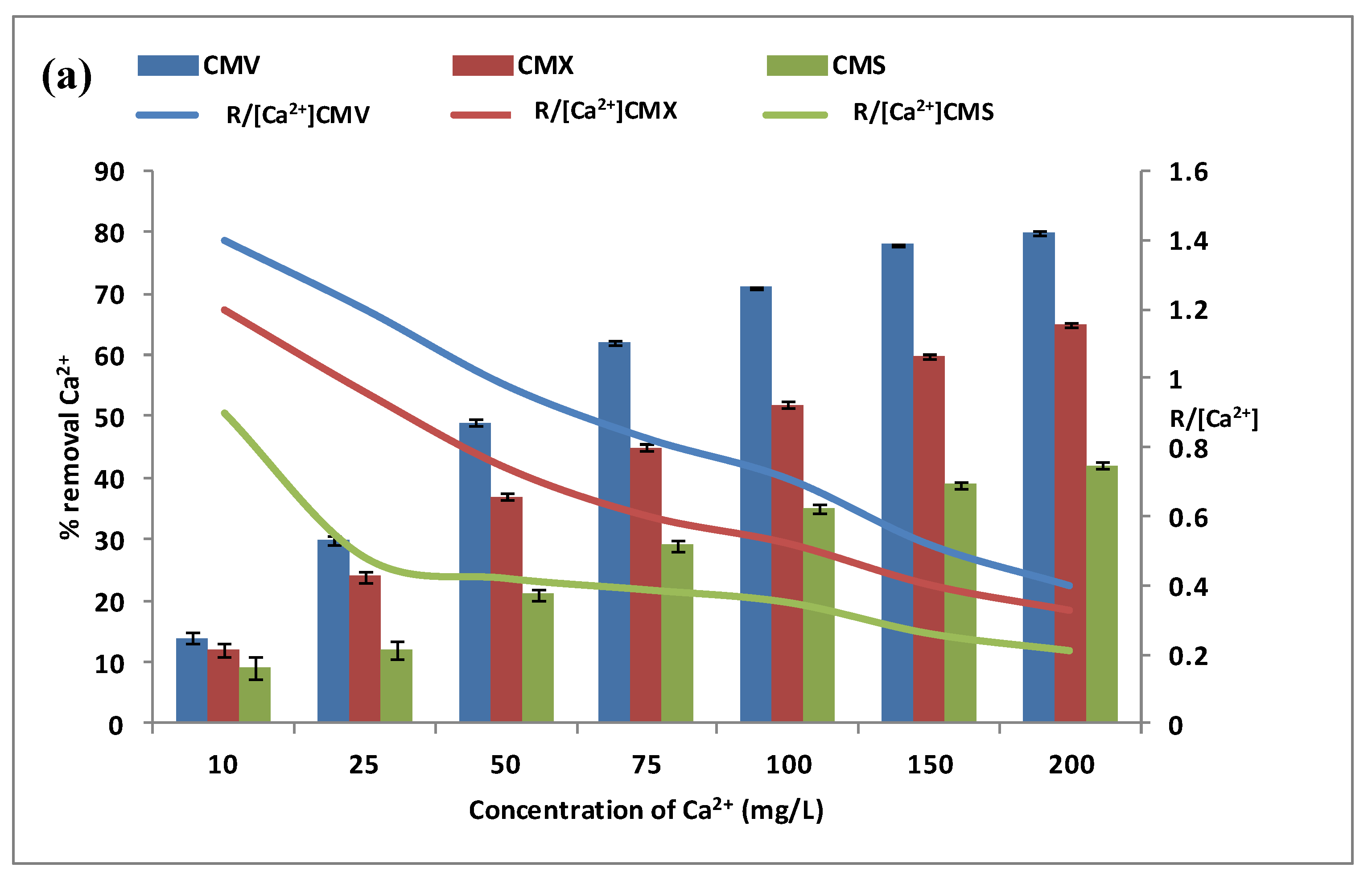
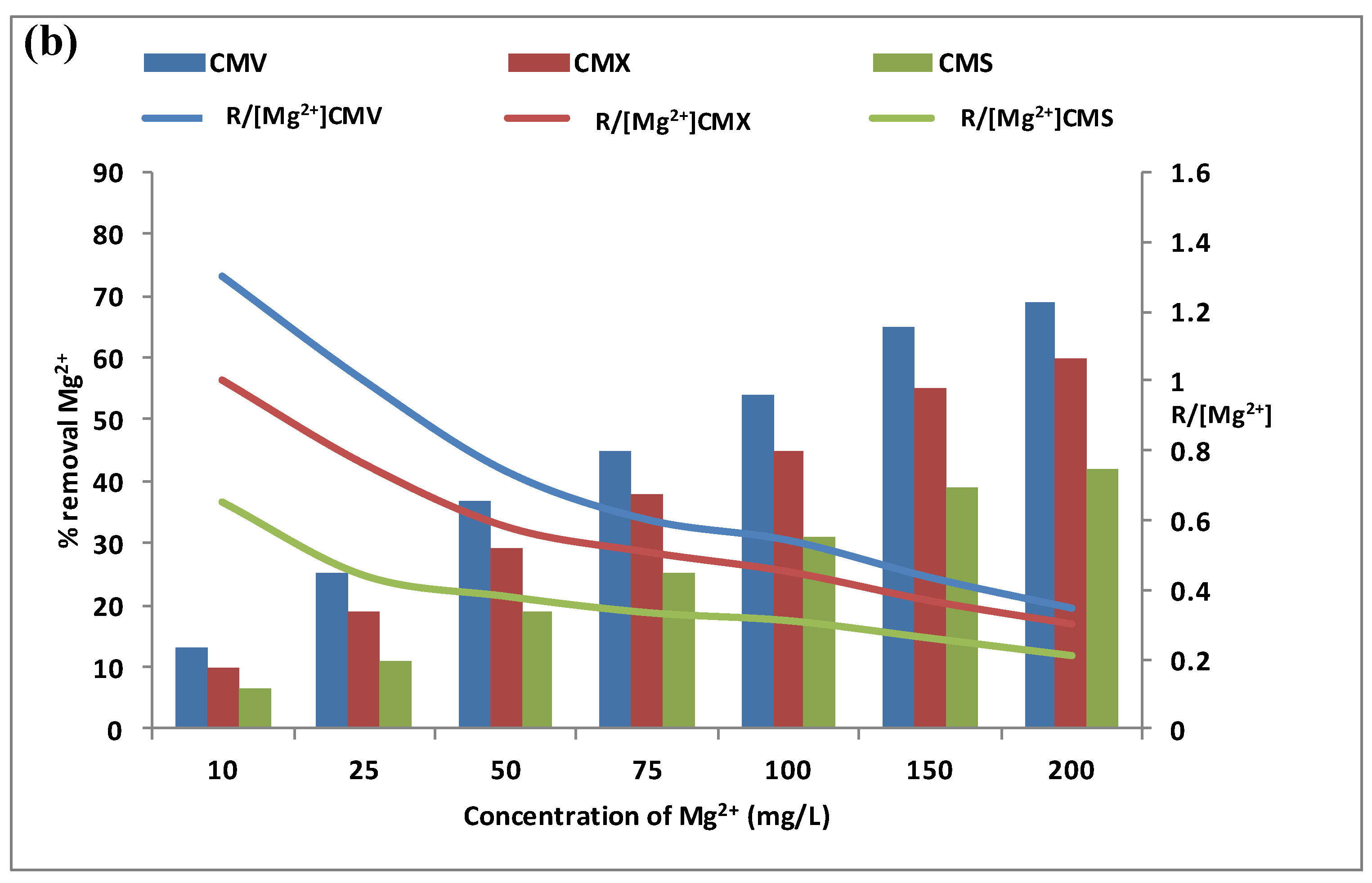
3.1.2. Effect of Calcium and Magnesium Concentrations in the Feed Compartment
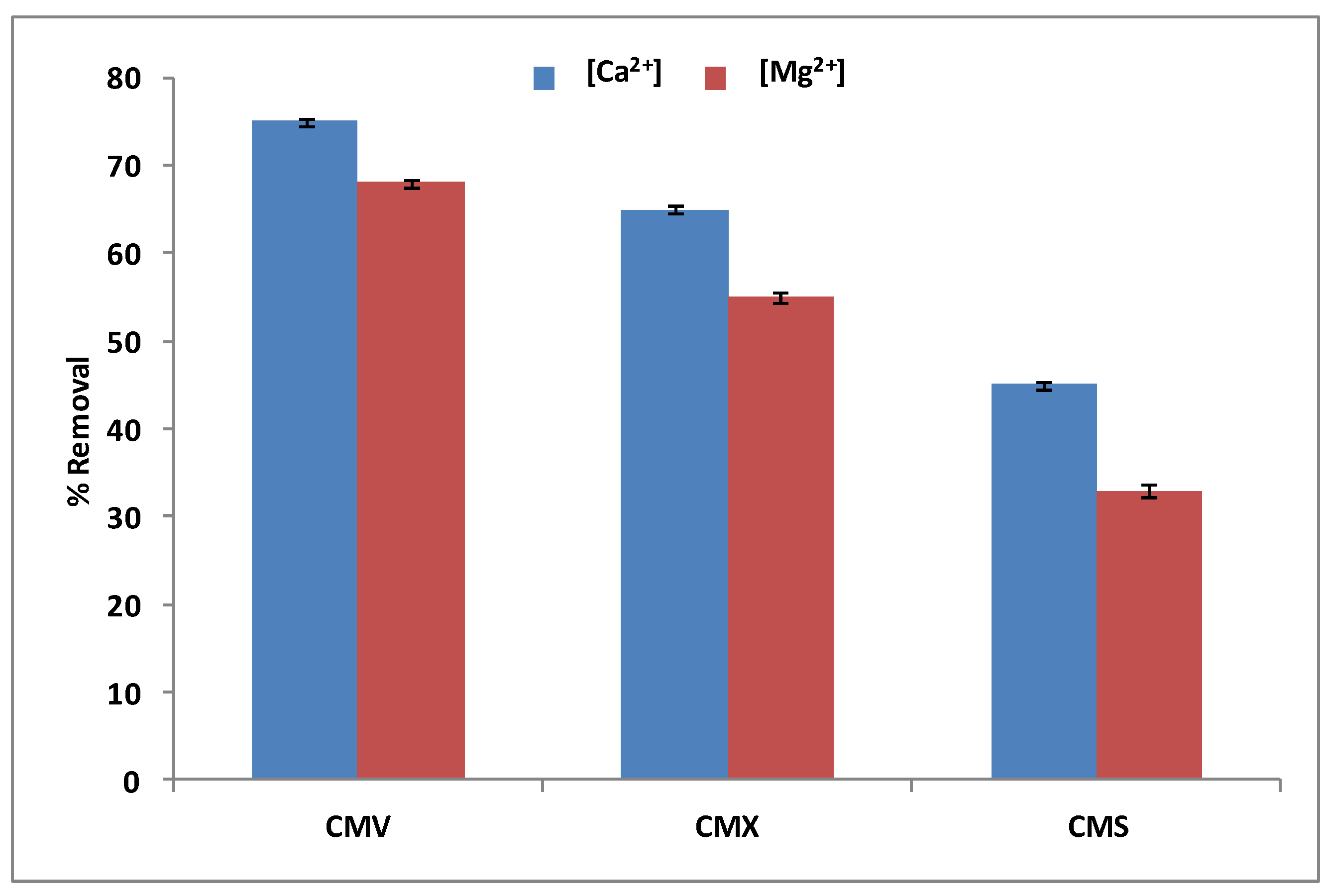
3.1.3. Membrane Selection
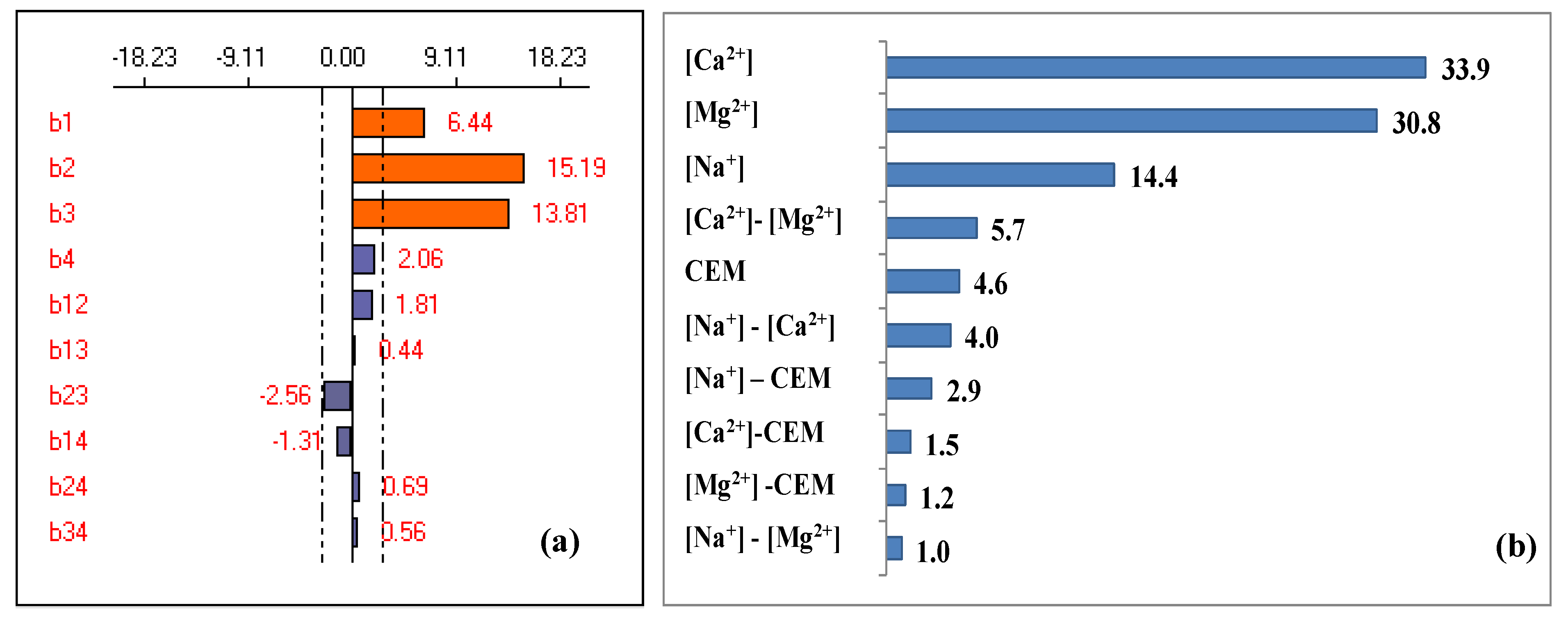
3.2. Full Factorial Design
3.3. Response Surface Methodology According to Doehlert
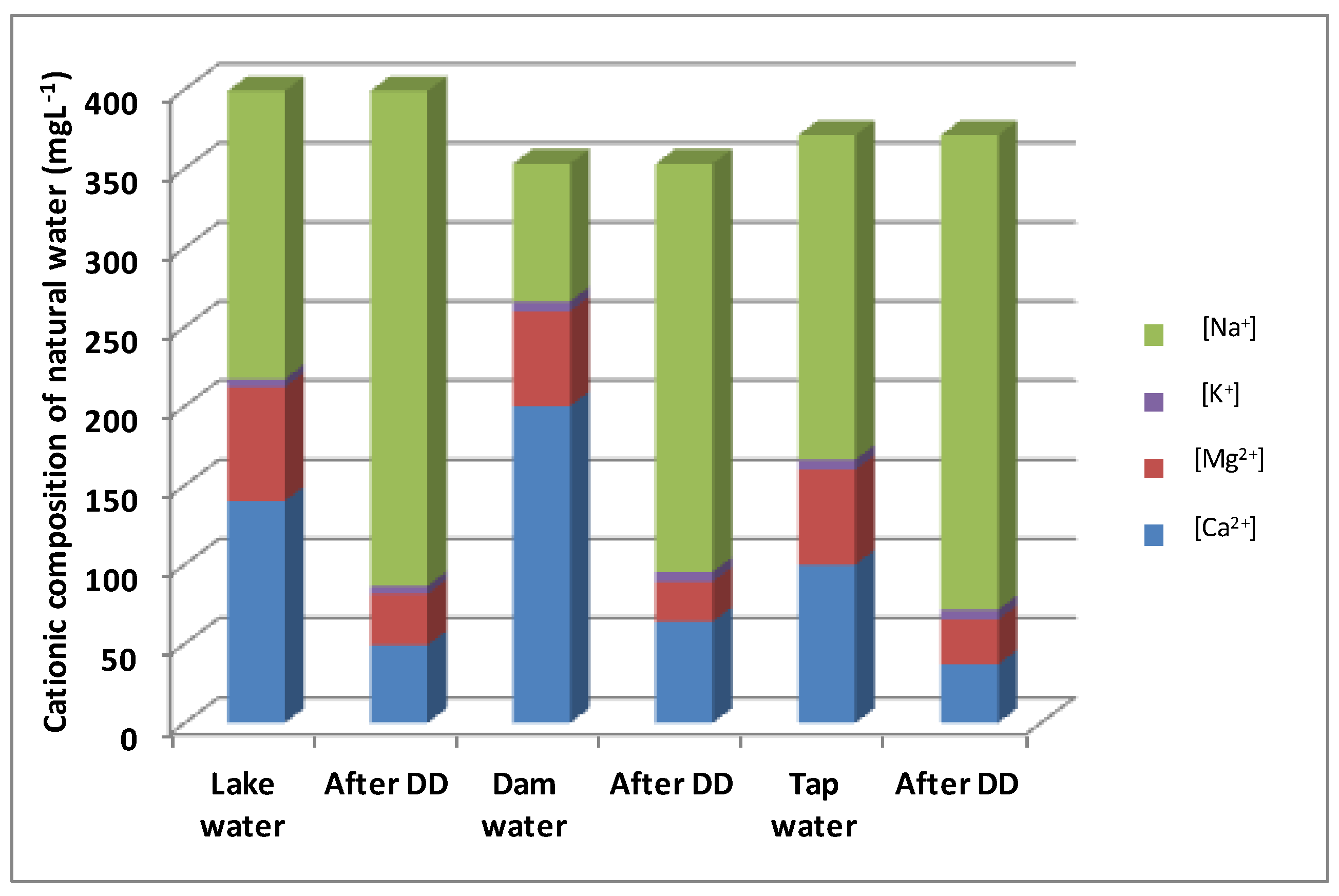
3.4. Application of Different Water Types
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ben Abdallah, S. The water resources and water management regimes in Tunisia. In Agricultural Water Management, Proceedings of the A Workshop in Tunisia; Series: Strengthening Science-Based Decision Making in Developing Countries; National Academies Press: Washington, DC, USA, 2007; pp. 81–87. [Google Scholar]
- World Health Organization. Calcium and Magnesium in Drinking-Water: Public Health Significance; World Health Organization: Geneva, Switzerland, 2009. [Google Scholar]
- World Health Organization. Hardness in Drinking-Water; World Health Organization: Geneva, Switzerland, 2010. [Google Scholar]
- Kozisek, F. Regulations for calcium, magnesium or hardness in drinking water in the European Union member states. Regul. Toxicol. Pharmacol. 2020, 112, 104589–104597. [Google Scholar] [CrossRef] [PubMed]
- Navalon, S.; Alvaro, M.; Garcia, H. Ca2+ and Mg2+ present in hard waters enhance trihalomethane formation. J. Hazard. Mater. 2009, 169, 901–906. [Google Scholar] [CrossRef] [PubMed]
- Nerbrand, C.; Agréus, L.; Lenner, R.A.; Nyberg, P.; Svärdsudd, K. The influence of calcium and magnesium in drinking water and diet on cardiovascular risk factors in individuals living in hard and soft water areas with differences in cardiovascular mortality. BMC Public Health 2003, 3, 21–30. [Google Scholar] [CrossRef] [PubMed]
- Kang, K.C.; Linga, P.; Park, K.N.; Choi, S.J.; Lee, J.D. Seawater desalination by gas hydrate process and removal characteristics of dissolved ions (Na+, K+, Mg2+, Ca2+, B3+, Cl−, SO42−). Desalination 2014, 353, 84–90. [Google Scholar] [CrossRef]
- Theiss, F.L.; Ayoko, G.A.; Frost, R.L. Synthesis of layered double hydroxides containing Mg2+, Zn2+, Ca2+ and Al3+ layer cations by co-precipitation methods—A review. Appl. Surf. Sci. 2016, 383, 200–213. [Google Scholar] [CrossRef]
- Silva, R.D.R.; Rodrigues, R.T.; Azevedo, A.C.; Rubio, J. Calcium and magnesium ion removal from water feeding a steam generator by chemical precipitation and flotation with micro and nanobubbles. Environ. Technol. 2020, 41, 2210–2218. [Google Scholar] [CrossRef]
- Hasson, D.; Lumelsky, V.; Greenberg, G.; Pinhas, Y.; Semiat, R. Development of the electrochemical scale removal technique for desalination applications. Desalination 2008, 230, 329–342. [Google Scholar] [CrossRef]
- Yu, Y.; Jin, H.; Meng, P.; Guan, Y.; Shao, S.; Chen, X. Electrochemical water softening using air-scoured washing for scale detachment. Sep. Purif. Technol. 2018, 191, 216–224. [Google Scholar] [CrossRef]
- Hamdona, S.K.; Tadros, H.R.Z.; Mabrouk, D.M.; Refaat, H.M. Removal of water hardness and some inorganic pollutants using nano marine algae extract embedded in waste polystyrene. Int. J. Sci. Res. 2022, 12, 67–75. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, Z.; Yang, L.; Wang, M. Effective Removal of calcium and magnesium ions from water by a novel alginate–citrate composite aerogel. Gels 2021, 7, 125. [Google Scholar] [CrossRef]
- Amarasooriya, A.A.G.D.; Kawakami, T. Removal of fluoride, hardness and alkalinity from groundwater by electrolysis, Groundw. Sustain. Dev. 2019, 9, 100231–100242. [Google Scholar] [CrossRef]
- Chebotareva, R.D.; Remez, S.V.; Bashtan, S.Y. Water softening and sisinfection using an electrolysis unit with a filtering cartridge. J. Water Chem. Technol. 2020, 42, 54–59. [Google Scholar] [CrossRef]
- Nielsen, E.N.; Merkel, A.; Yazdi, S.R.; Ahrné, L. The effect of acid whey composition on the removal of calcium and lactate during electrodialysis. Int. Dairy J. 2021, 117, 104985–104993. [Google Scholar] [CrossRef]
- Kabay, N.; Demircioglu, M.; Ersöz, E.; Kurucaovali, I. Removal of calcium and magnesium hardness by electrodialysis. Desalination 2002, 149, 343–349. [Google Scholar] [CrossRef]
- Walha, K.; Amar, R.B.; Firdaous, L.; Quéméneur, F.; Jaouen, P. Brackish groundwater treatment by nanofiltration, reverse osmosis and electrodialysis in Tunisia: Performance and cost comparison. Desalination 2007, 207, 95–106. [Google Scholar] [CrossRef]
- Schaep, J.; Van der Bruggen, B.; Uytterhoeven, S.; Croux, R.; Vandecasteele, C.; Wilms, D.; Van Houtte, E.; Vanlerberghe, F. Removal of hardness from groundwater by nanofiltration. Desalination 1998, 119, 295–301. [Google Scholar] [CrossRef]
- Izadpanah, A.A.; Javidnia, A. The ability of a nanofiltration membrane to remove hardness and ions from diluted Seawater. Water 2012, 4, 283–294. [Google Scholar] [CrossRef]
- Bekri-Abbes, I.; Bayoudh, S.; Baklouti, M. The removal of hardness of water using sulfonated waste plastic. Desalination 2008, 222, 81–86. [Google Scholar] [CrossRef]
- Vanoppen, M.; Stoffels, G.; Demuytere, C.; Bleyaert, W.; Verliefde, A.R.D. Increasing RO efficiency by chemical-free ion-exchange and Donnan dialysis: Principles and practical implications. Water Res. 2015, 80, 59–70. [Google Scholar] [CrossRef]
- Gueccia, R.; Alhadidi, A.M.M.; Cipollina, A.; Micale, G. Donnan dialysis for tap-water softening. Desalination Water Treat. 2020, 192, 19–32. [Google Scholar] [CrossRef]
- Turek, M.; Bandura-Zalska, B.; Dydo, P. Boron removal by Donnan dialysis. Desalination Water Treat. 2009, 10, 53–59. [Google Scholar] [CrossRef]
- Hamouda, S.B.; Touati, K.; Amor, M.B. Donnan dialysis as membrane process for nitrate removal from drinking water: Membrane structure effect. Arab. J. Chem. 2017, 10, S287–S292. [Google Scholar] [CrossRef]
- Hichour, M.; Persin, F.; Sandeaux, J.; Gavach, C. Fluoride removal from waters by Donnan dialysis. Sep. Purif. Technol. 2000, 18, 1–11. [Google Scholar] [CrossRef]
- Dieye, A.; Larchet, C.; Auclair, B.; Mar-Diop, C. Elimination des fluorures par la dialyse ionique croisée. Eur. Polym. J. 1998, 34, 67–75. [Google Scholar] [CrossRef]
- Trifi, I.M.; Trifi, B.; Djamel, A.; Hamrouni, B. Simultaneous removal of nitrate and nitrite by Donnan Dialysis. Environ. Eng. Manag. J. 2021, 20, 6973–6983. [Google Scholar] [CrossRef]
- Trifi, I.M.; Chaabane, L.; Dammak, L.; Baklouti, L.; Hamrouni, B. Response Surface Methodology for Boron Removal by Donnan Dialysis: Doehlert Experimental Design. Membranes 2021, 11, 731. [Google Scholar] [CrossRef]
- Marzouk, I.; Dammak, L.; Chaabane, L.; Hamrouni, B. Optimization of chromium (VI) removal by Donnan dialysis. Am. J. Analyt. Chem. 2013, 4, 306–313. [Google Scholar] [CrossRef]
- Marzouk, I.; Chaabane, L.; Dammak, L.; Hamrouni, B. Application of Donnan dialysis coupled to adsorption onto activated alumina for chromium (VI) removal. Am. J. Analyt. Chem. 2013, 4, 420–425. [Google Scholar] [CrossRef]
- Trifi, I.M.; Trifi, B.; Ayed, S.B.; Hamrouni, B. Removal of phosphate by Donnan dialysis coupled to adsorption onto alginate calcium beads. Water Sci. Technol. 2019, 80, 117–125. [Google Scholar] [CrossRef]
- Wisniewski, J.; Kabsch-Korbutowicz, M. Elimination of selected anions and cations from water by means of the Donnan Dialysis. Environ. Prot. Eng. 2017, 43, 189–205. [Google Scholar] [CrossRef]
- Bup, D.N.; Abi, C.F.; Tenin, D.; Kapseu, C.; Tchiegang, C. Optimisation of the cooking process of sheanut kernels (vitellaria paradoxa gaertn.) using the Doehlert experimental design. Food Bioproc. Technol. 2012, 5, 108–117. [Google Scholar] [CrossRef]
- Rangaiah, G.P.; Feng, Z.; Hoadley, A.F. Multi-Objective Optimization Applications in Chemical Process Engineering: Tutorial and Review. Processes 2020, 8, 508. [Google Scholar] [CrossRef]
- Ouejhani, A.; Hellal, F.; Dachraoui, M.; Lalleve, G.; Fauvarque, J.F. Application of Doehlert matrix to the study of electrochemical oxidation of Cr(III) to Cr(VI) in order to recover chromium from wastewater tanning bath. J. Hazard. Mater. 2008, 157, 423–431. [Google Scholar] [CrossRef] [PubMed]
- French Standard NF X 45-200; Membranes Polymers Échangeuse d’Ions. AFNOR: Paris, France, 1995.
- Gnusin, N.P.; Zabolotzki, V.I.; Meshechkov, A.I. Development of the generalized conductance principle to the description of transfer phenomena in disperse systems under the acting of different forces. Russ. J. Phys. Chem. 1980, 54, 1518–1522. [Google Scholar]
- Zabolotsky, V.I.; Nikonenko, V.V. Effect of structural membrane inhomogeneity on transport properties. J. Membr. Sci. 1993, 79, 181–198. [Google Scholar] [CrossRef]
- Gnusin, N.P.; Berezina, N.P.; Kononenko, N.A.; Dyomina, O.A. Transport structural parameters to characterize ion exchange membranes. J. Membr. Sci. 2004, 243, 301–310. [Google Scholar] [CrossRef]
- Amor, Z.; Barioub, B.; Mameri, N.; Taky, M.; Nicolas, S.; Elmidaoui, A. Fluoride removal Corn brackish water by electrodialysis. Desalination 2001, 133, 215–223. [Google Scholar] [CrossRef]
- Han, L.; Galier, S.; Roux-de Balmann, H. Ion hydration number and electro osmosis during electrodialysis of mixed salt solution. Desalination 2015, 373, 38–46. [Google Scholar] [CrossRef]
- Ji, Y.; Geise, G.M. The Role of Experimental Factors in Membrane Permselectivity Measurements. Ind. Eng. Chem. Res. 2017, 56, 7559–7566. [Google Scholar] [CrossRef]
- Karpenko-Jereb, L.V.; Berezina, N.P. Determination of structural, selective, electrokinetic and percolation characteristics of ion-exchange membranes from conductive data. Desalination 2009, 245, 587–596. [Google Scholar] [CrossRef]
- Choi, J.H.; Kim, S.H.; Moon, S.H. Heterogeneity of Ion-Exchange Membranes: The Effects of Membrane Heterogeneity on Transport Properties. J. Colloid Interface Sci. 2001, 241, 120–126. [Google Scholar] [CrossRef]
- Kariduraganavar, M.Y.; Kittur, A.A.; Kulkarni, S.S. Ion Exchange Technology I; Springer: Berlin/Heidelberg, Germany, 2012; Chapter 7; pp. 233–276. [Google Scholar] [CrossRef]
- Garcia-Vasquez, W.; Ghalloussi, R.; Dammak, L.; Larchet, C.; Nikonenko, V.; Grande, D. Structure and properties of heterogeneous and homogeneous ion-exchange membranes subjected to ageing in sodium hypochlorite. J. Membr. Sci. 2014, 452, 104–116. [Google Scholar] [CrossRef]
- Bdiri, M.; Dammak, L.; Larchet, C.; Hellal, F.; Porozhnyy, M.; Nevakshenova, E.; Pismenskaya, N.; Nikonenko, V. Characterization and cleaning of anion-exchange membranes used in electrodialysis of polyphenol-containing food industry solutions; comparison with cation-exchange membranes. Sep. Purif. Technol. 2019, 210, 636–650. [Google Scholar] [CrossRef]
- Schönbächler, M.; Fehr, M.A. 15.7—Basics of Ion Exchange Chromatography for Selected Geological Applications. In Treatise on Geochemistry, 2nd ed.; Heinrich, D., Holland, K., Turekian, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 123–146. [Google Scholar] [CrossRef]
- Strathmann, H. Ion-Exchange Membrane Separation Processes, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Rottiers, T.; De Staelen, J.; Van der Bruggen, B.; Pinoy, L. Permselectivity of cation-exchange membranes between different cations in aqueous alcohol mixtures. Electrochim. Acta 2016, 192, 489–496. [Google Scholar] [CrossRef]
- Goupy, J.; Greighton, L. Introduction to Design of Experiments (Introduction Aux Plans D’experiences), 3rd ed.; Dunod: Paris, France, 2006. [Google Scholar]
- Lundstedt, T.; Seifert, E.; Abramo, L.; Thelin, B.; Nyström, Å.; Pettersen, J.; Bergman, R. Experimental design and optimization, Chemometr. Intell. Lab. Syst. 1998, 42, 3–40. [Google Scholar] [CrossRef]
- Trifi, B.; Bouallegue, M.C.; Trifi, I.M. Application of response surface methodology for optimization of methyl red adsorption by orange peels. Desalination Water Treat. 2019, 154, 369–375. [Google Scholar] [CrossRef]
- Antony, J. Design of Experiments for Engineers and Scientists; Butterworth-Heinemann: New York, NY, USA, 2003. [Google Scholar]
- Doehlert, D.H. Uniform shell designs. Appl. Stat. 1970, 19, 231–239. [Google Scholar] [CrossRef]
- Design of Experiments in Protein Production and Purification Design of Experiments, 1st ed.; GE Healthcare Life Sciences: Uppsala, Sweden, 2014.
- Wiśniewski, J.; Różańska, A. Donnan dialysis for hardness removal from water before electrodialytic desalination. Desalination 2007, 212, 251–260. [Google Scholar] [CrossRef]
- Veerman, J. Concepts and Misconceptions Concerning the Influence of Divalent Ions on the Performance of Reverse Electrodialysis Using Natural Waters. Membranes 2023, 13, 69. [Google Scholar] [CrossRef] [PubMed]
- Saracco, G. Transport properties of monovalent-ion-permselective membranes. Chem. Emfineering Sci. 1997, 52, 3019–3031. [Google Scholar] [CrossRef]
- Firdaous, L.; Malériat, J.-P.; Schlumpf, J.-P.; Quéméneur, F. Transfer of monovalent and divalent cations in salt solutions by electrodialysis. Sep. Sci. Technol. 2007, 42, 931–948. [Google Scholar] [CrossRef]

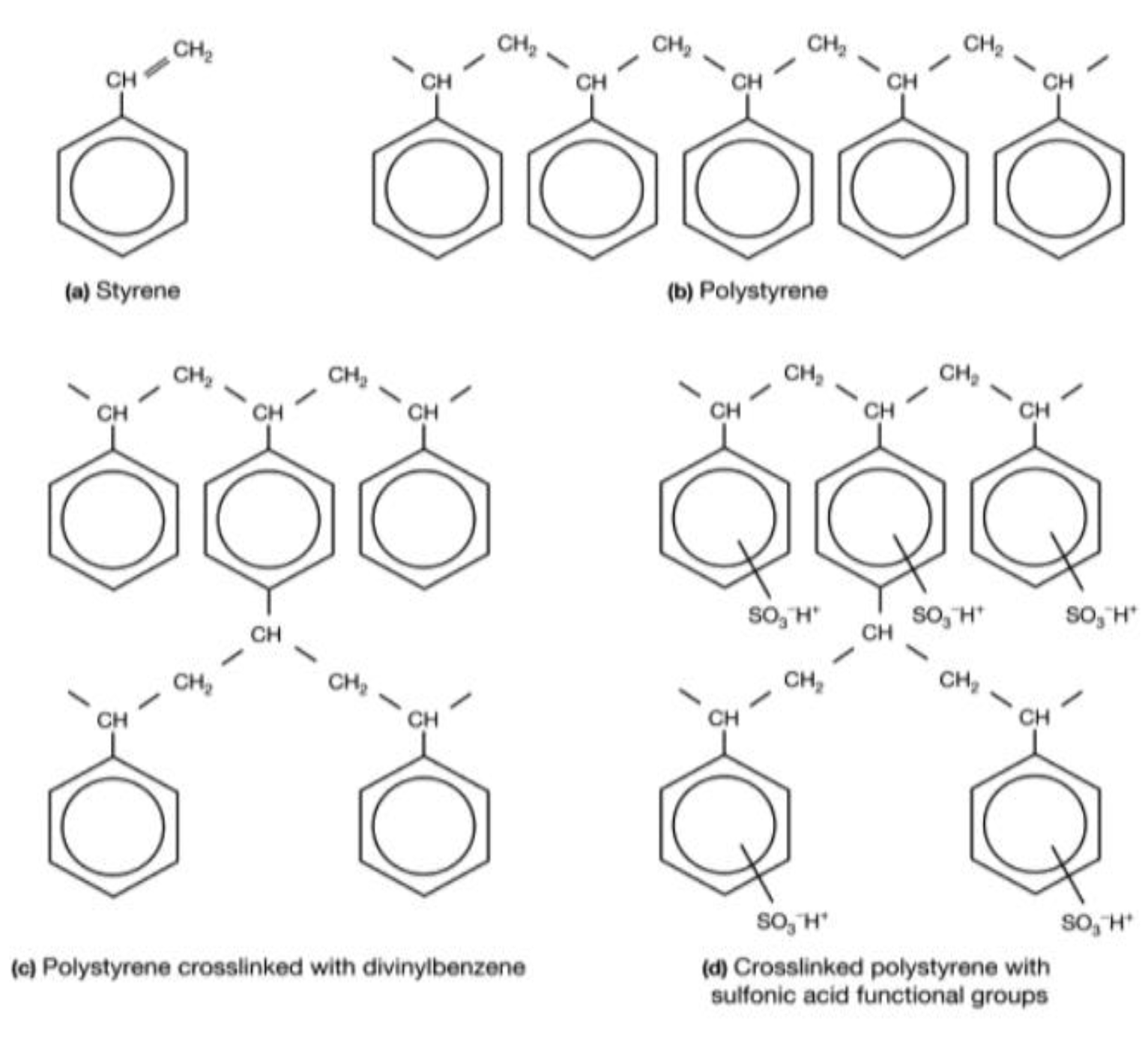

| Membranes | Selemion® CMV | Neosepta® CMX | Neosepta® CMS | |||
|---|---|---|---|---|---|---|
| Type | Homogeneous | Homogeneous | Homogeneous, but treated on the surface to be selective to monovalent cations. | |||
| Structure property | Styrene (PS/DVB) | Styrene (PS/DVB) | Styrene (PS/DVB) & two thin positively charged electrolyte layers (unknown nature) | |||
| Frame backing | PVC | PVC | PVC | |||
| Charged group | Sulfonate | Sulfonate | Sulfonate | |||
| Exchange Capacity (meq.g−1) a | 2.5 | 1.9 | 2.3 | |||
| Transport number | Na+, Ca2+ or Mg2+ | t > 0.92 | Na+ Ca2+ + Mg2+ | t > 0.70 t > 0.28 | Na+ Ca2+ + Mg2+ | t > 0.97 t ~ 0.10 |
| Water Content (%) a | 39 | 22 | 29 | |||
| Inter-gel fraction (f2) in NaCl | 0.06 | 0.06–0.10 | 0.13 | |||
| Permselectivity (%) | 99 | 98 | 97 | |||
| Thickness (μm) a | 130 | 170 | 150 | |||
| Factors | Symbol | Range and Levels | |
|---|---|---|---|
| Coded Variable X1 | [Na+] | −1 | 1 |
| Concentration of Na+ (mol·L−1) | 0.5 | 1.5 | |
| Coded Variable X2 | [Ca2+] | −1 | 1 |
| Concentration of calcium (mg·L−1) | 10 | 100 | |
| Coded Variable X3 | [Mg2+] | −1 | 1 |
| Concentration of magnesium (mg·L−1) | 10 | 100 | |
| Coded Variable X4 | CEM | −1 | 1 |
| Type of cation-exchange membranes | CMX | CMV | |
| N° | X1 | X2 | X3 | X4 | [Na+] | [Ca2+] | [Mg2+] | CEM | Y3(%)exp | Y3(%)cal |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −1 | −1 | −1 | −1 | 0.5 | 10 | 10 | CMX | 15.0 | 14.3 |
| 2 | +1 | −1 | −1 | −1 | 1.5 | 10 | 10 | CMX | 42.0 | 42.7 |
| 3 | −1 | +1 | −1 | +1 | 0.5 | 100 | 10 | CMX | 45.0 | 45.3 |
| 4 | +1 | +1 | −1 | +1 | 1.5 | 100 | 10 | CMX | 68.0 | 67.7 |
| 5 | −1 | −1 | +1 | +1 | 0.5 | 10 | 100 | CMX | 44.0 | 42.7 |
| 6 | +1 | −1 | +1 | +1 | 1.5 | 10 | 100 | CMX | 62.0 | 63.3 |
| 7 | −1 | +1 | +1 | −1 | 0.5 | 100 | 100 | CMX | 60.0 | 61.7 |
| 8 | +1 | +1 | +1 | −1 | 1.5 | 100 | 100 | CMX | 78.0 | 76.3 |
| 9 | −1 | −1 | −1 | +1 | 0.5 | 10 | 10 | CMV | 19.0 | 22.0 |
| 10 | +1 | −1 | −1 | +1 | 1.5 | 10 | 10 | CMV | 60.0 | 57.0 |
| 11 | −1 | +1 | −1 | +1 | 0.5 | 100 | 10 | CMV | 52.0 | 49.5 |
| 12 | +1 | +1 | −1 | +1 | 1.5 | 100 | 10 | CMV | 76.0 | 78.5 |
| 13 | −1 | −1 | +1 | +1 | 0.5 | 10 | 100 | CMV | 51.0 | 50.0 |
| 14 | +1 | −1 | +1 | +1 | 1.5 | 10 | 100 | CMV | 76.0 | 76.9 |
| 15 | −1 | +1 | +1 | +1 | 0.5 | 100 | 100 | CMV | 65.0 | 65.5 |
| 16 | +1 | +1 | +1 | +1 | 1.5 | 100 | 100 | CMV | 86.9 | 86.4 |
| Factors | Range and Levels | ||||||
|---|---|---|---|---|---|---|---|
| Coded Variable X1 | −1 | −0.5 | 0 | 0.5 | 1 | ||
| Concentration of Mg2+ (mg·L−1) | 10 | 33 | 55 | 78 | 100 | ||
| Coded Variable X2 | −0.866 | −0.577 | −0.287 | 0 | 0.287 | 0.577 | 0.866 |
| Concentration of Ca2+ (mg·L−1) | 16 | 29 | 42 | 55 | 68 | 81 | 94 |
| Coded Variable X3 | −0.816 | 0 | 0.816 | ||||
| Concentration of Na+ (mg·L−1) | 0.55 | 0.75 | 0.95 | ||||
| N° | X1 | X2 | X3 | [Mg2+] | [Ca2+] | [Na+] | Y3(%)Exp | Y3(%)Cal |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.0 | 0.000 | 0.000 | 100 | 55 | 0.75 | 77.3 | 77.8 |
| 2 | −1.0 | 0.000 | 0.000 | 10 | 55 | 0.75 | 71.5 | 70.9 |
| 3 | 0.5 | 0.866 | 0.000 | 78 | 94 | 0.75 | 88.4 | 86.1 |
| 4 | −0.5 | −0.866 | 0.000 | 33 | 16 | 0.75 | 16.1 | 18.4 |
| 5 | 0.5 | −0.866 | 0.000 | 78 | 16 | 0.75 | 21.1 | 20.0 |
| 6 | −0.5 | 0.866 | 0.000 | 33 | 94 | 0.75 | 79.7 | 80.8 |
| 7 | 0.5 | 0.287 | 0.816 | 78 | 68 | 0.95 | 79.9 | 81.7 |
| 8 | −0.5 | −0.287 | −0.816 | 33 | 42 | 0.55 | 55.9 | 54.1 |
| 9 | 0.5 | −0.287 | −0.816 | 78 | 42 | 0.55 | 60.1 | 60.7 |
| 10 | 0.0 | 0.577 | −0.816 | 55 | 81 | 0.55 | 82.6 | 84.5 |
| 11 | −0.5 | 0.287 | 0.816 | 33 | 68 | 0.95 | 82.6 | 81.4 |
| 12 | 0.0 | −0.577 | 0.816 | 55 | 29 | 0.95 | 45.5 | 43.7 |
| 13 | 0.0 | 0.000 | 0.000 | 55 | 55 | 0.75 | 74.2 | 74.2 |
| 14 | 0.0 | 0.000 | 0.000 | 55 | 55 | 0.75 | 74.2 | 74.2 |
| 15 | 0.0 | 0.000 | 0.000 | 55 | 55 | 0.75 | 74.2 | 74.2 |
| Source Model | Degree of Freedom | Sum of Square | Mean of Square | F-Value | Ftable (α = 5%) | p-Value |
|---|---|---|---|---|---|---|
| Regression | 9 | 6831.47 | 759.05 | 158.79 | 4.77 | 0.000015 |
| Residual | 5 | 23.94 | 4.78 | |||
| Total | 14 | 6855.42 |
| Lake Water | Dam Water | Tap Water | |
|---|---|---|---|
| Turbidity (NTU) | 9.40 | 39.59 | 221.14 |
| Conductivity (µs/cm) | 1603 | 1368 | 1615 |
| pH | 7.72 | 7.72 | 7.65 |
| Temperature (°C) | 18.2 | 17.5 | 15.9 |
| Salinity | 0.8 | 0.7 | 0.8 |
| TDS (mg·L−1) | 854 | 722 | 891 |
| Ca2+ (mg·L−1) | 140 | 200 | 100 |
| Mg2+ (mg·L−1) | 72 | 60 | 60 |
| Na+ (mg·L−1) | 181.9 | 86.9 | 204.9 |
| K+ (mg·L−1) | 5.1 | 6.2 | 6.2 |
| Cl− (mg·L−1) | 369.2 | 177.5 | 475.7 |
| SO42− (mg·L−1) | 0.302 | 0.316 | 0.230 |
| HCO3− (mg·L−1) | 488 | 305 | 396 |
| Ca2+ Removal (%) | 65 | 68 | 63 |
| Mg2+ Removal (%) | 55 | 58 | 53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marzouk-Trifi, I.; Baklouti, L.; Dammak, L. Investigation of Calcium and Magnesium Removal by Donnan Dialysis According to the Doehlert Design for Softening Different Water Types. Membranes 2023, 13, 203. https://doi.org/10.3390/membranes13020203
Marzouk-Trifi I, Baklouti L, Dammak L. Investigation of Calcium and Magnesium Removal by Donnan Dialysis According to the Doehlert Design for Softening Different Water Types. Membranes. 2023; 13(2):203. https://doi.org/10.3390/membranes13020203
Chicago/Turabian StyleMarzouk-Trifi, Ikhlass, Lassaad Baklouti, and Lasâad Dammak. 2023. "Investigation of Calcium and Magnesium Removal by Donnan Dialysis According to the Doehlert Design for Softening Different Water Types" Membranes 13, no. 2: 203. https://doi.org/10.3390/membranes13020203
APA StyleMarzouk-Trifi, I., Baklouti, L., & Dammak, L. (2023). Investigation of Calcium and Magnesium Removal by Donnan Dialysis According to the Doehlert Design for Softening Different Water Types. Membranes, 13(2), 203. https://doi.org/10.3390/membranes13020203







