Prediction of Flux and Rejection Coefficients in the Removal of Emerging Pollutants Using a Nanofiltration Membrane
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Chemicals
- Magnesium chloride hexahydrate, MgCl2 6H2O, 203.30 g/mol, supplied by Panreac (Barcelona, Spain).
- Conductivity standards (147 µS/cm, 1288 mS/cm at 25 °C) were provided by CRISON (Barcelona, Spain).
- Carbamazepine C15H12N2O, 236.27 g/mol, supplied by Sigma-Aldrich (St. Louis, MO, USA).
- Ketoprofen, C16H14O3, 254.28 g/mol (≥98%), supplied by Sigma-Aldrich.
- Bisphenol A, C15H16O2, 228.29 g/mol (≥99%), supplied by Sigma-Aldrich.
- Sodium hydroxide, NaOH, 40.00 g/mol, supplied by Honeywell (Charlotte, NC, USA).
- Absolute ethanol, CH3CH2OH, 46.07 g/mol, supplied by Panreac.
- Distilled water.
2.1.2. Membrane
2.1.3. Equipment
- Experimental system
- Analysis equipment
2.2. Methods
2.2.1. Operational Procedure
2.2.2. Analytical Method
- (a)
- Assays with distilled water. The permeate mass is obtained using the OHAUS SP2001 balance, and its volume is measured with a graduated cylinder, similarly carried out for each assay permeate.
- (b)
- Assays with MgCl2. The concentration of magnesium chloride in the permeate, reject, and feeding samples is determined by measuring their conductivity with the CRISON EC-Meter GLP 31 conductivity meter. Before conducting the measurements, a calibration curve is prepared.
- (c)
- Assays with emerging contaminants. The concentrations of carbamazepine, ketoprofen, and bisphenol A in the permeate, reject, and feeding samples are determined by measuring their absorbance in the Evolution 300 spectrophotometer at the wavelength of maximum absorbance (λm) for each compound. In the conducted assays, the feeding solution contained only one contaminant. Individual calibration curves were constructed for each compound before analysing the samples. To perform this, the absorption spectra of each contaminant were determined to find a wavelength, λm, at which the light absorption by the contaminant is noticeable.
2.3. Experimental Series
- (1)
- Experimental series for the initial membrane characterization: This series consists of two assays. In the first assay, the feeding tank is filled with distilled water to determine the membrane solvent permeability. In the second assay, a 1 g/L solution of MgCl2 is introduced to determine the membrane rejection coefficient towards saline solutions.
- (2)
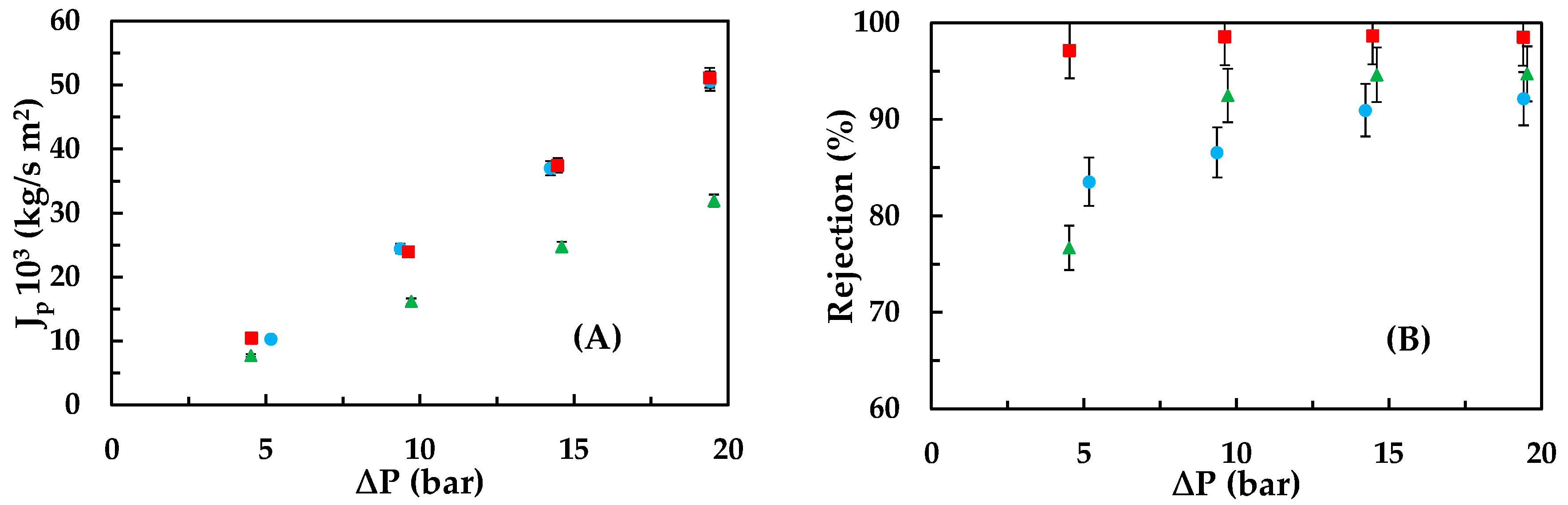
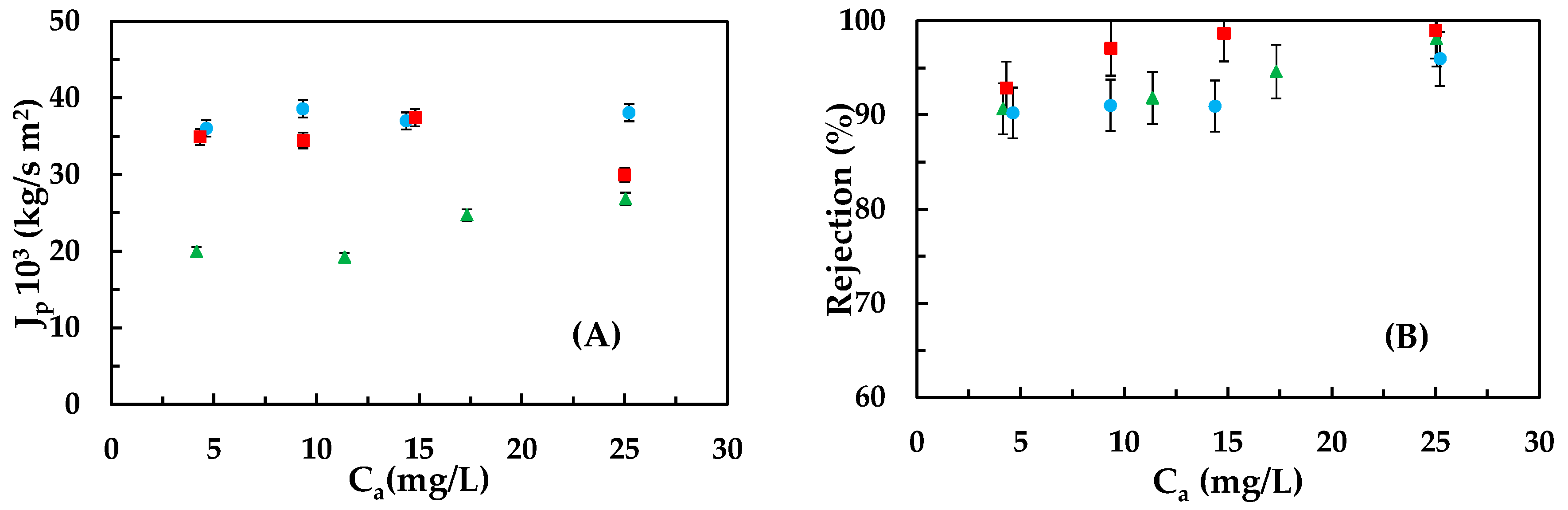
- Experimental series to determine the membrane behaviour towards the three emerging contaminants: This series comprises 12 assays. For each compound, four assays are conducted, where, in each one, the feeding concentration is kept constant at 5, 10, 15, and 25 ppm while the pressure varies from 5 to 20 bar. The experimental conditions tested—temperature 20 ± 1 °C; range of pressures; and concentrations—were selected taking into account other previous works [21].
- (3)
- Experimental series for the final membrane characterization: This series includes the same assays as the first experimental series, but they are conducted after the experimentation with the emerging contaminants has been completed. This is to account for the possibility that the contaminants may have affected the membrane, altering its permeability and rejection properties.
3. Results
3.1. Initial Membrane Characterisation
3.2. Emerging Pollutants Removal: Carbamazepine, Ketoprofen, and Bisphenol A
3.3. Fouling
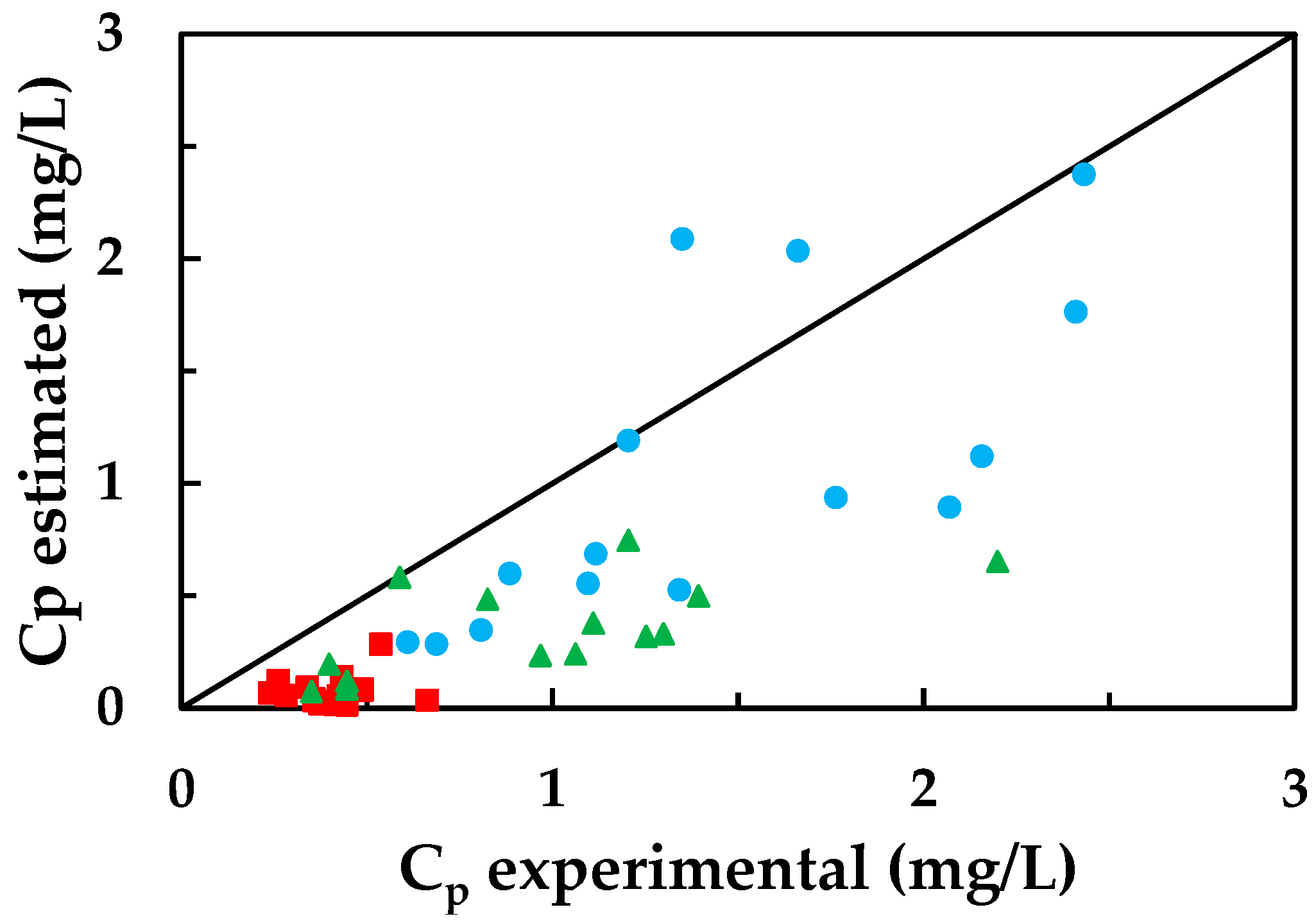
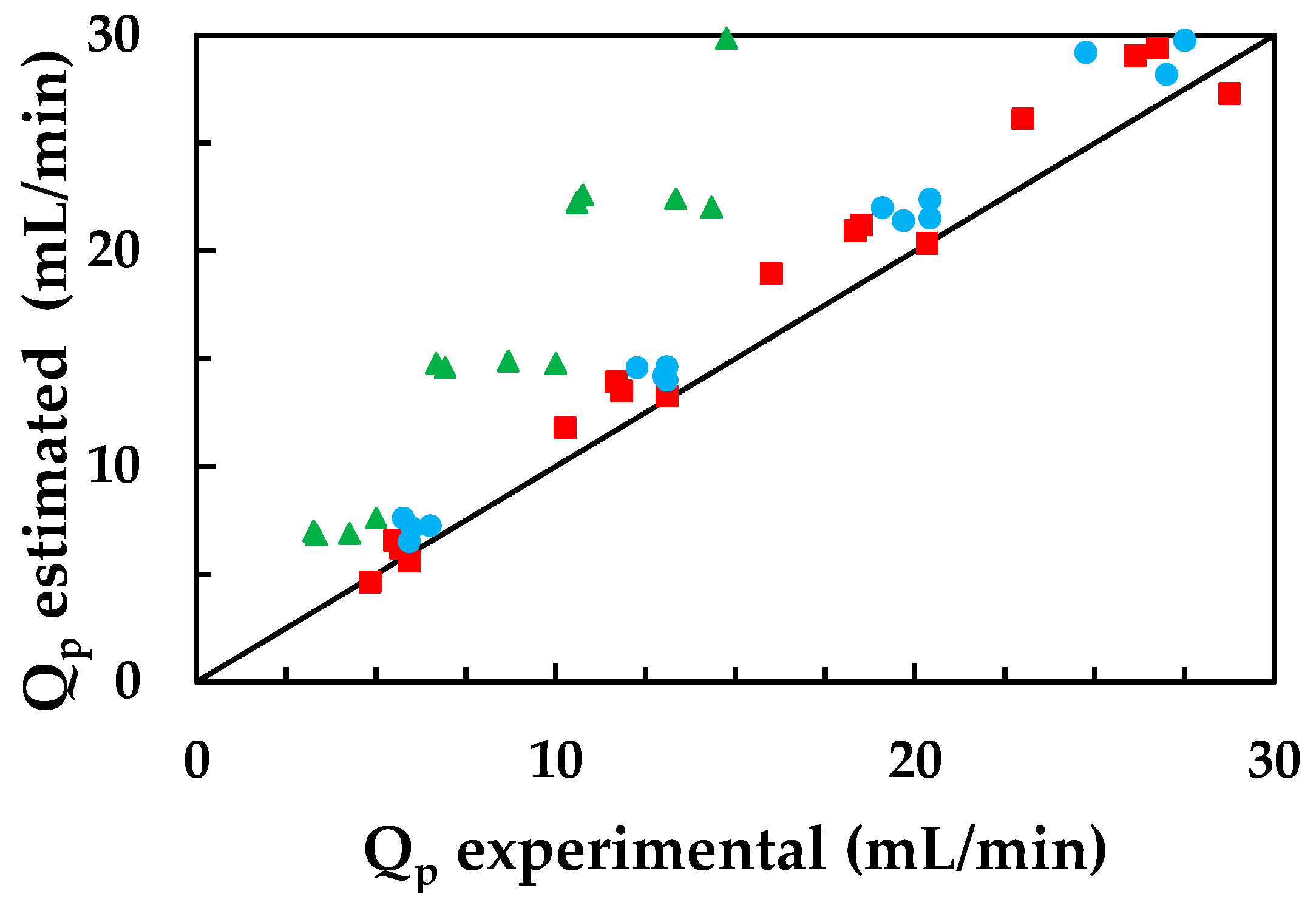
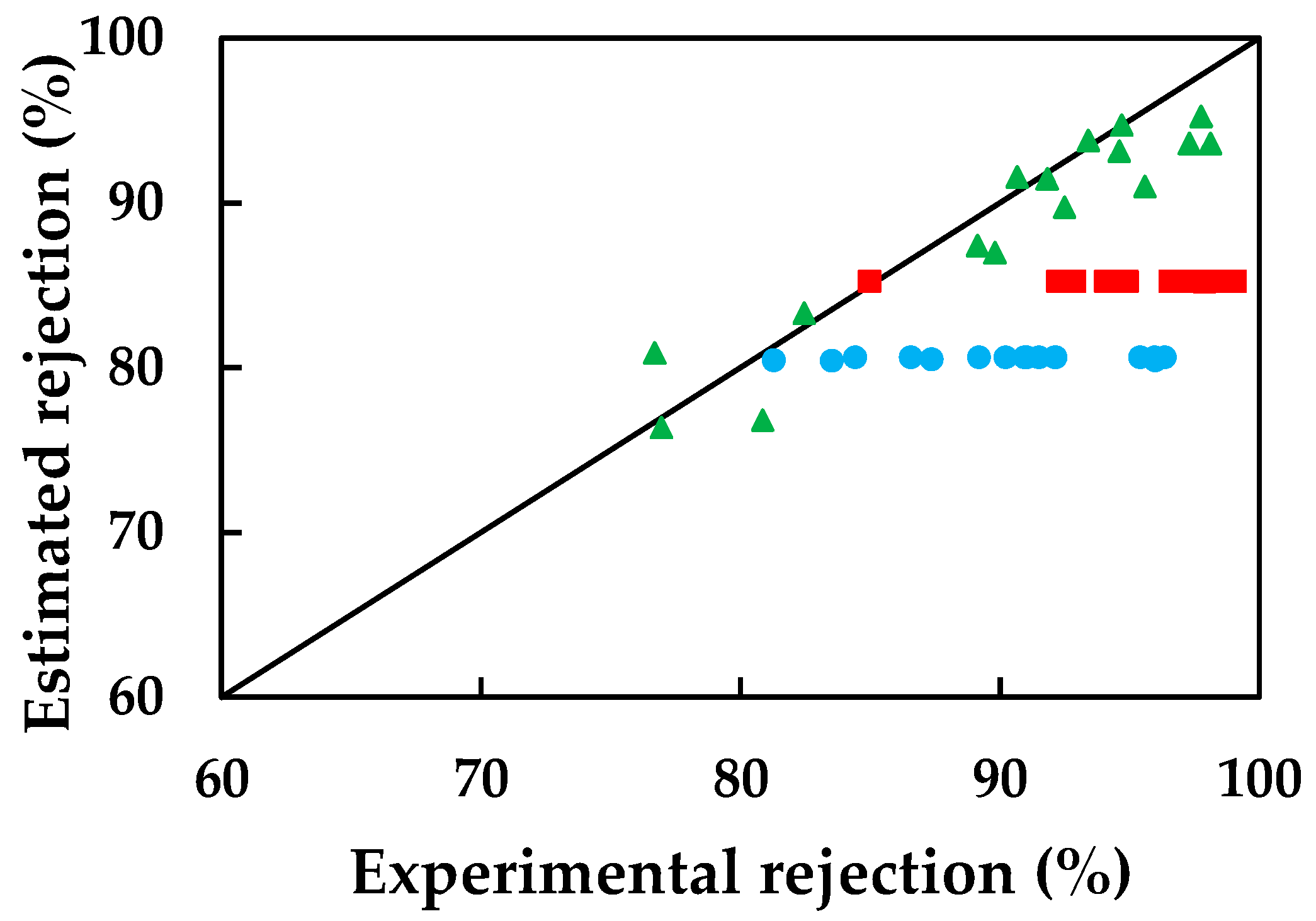
3.4. Application of Mathematical Models
3.4.1. Simplified Solution-Diffusion Model
3.4.2. Simplified Model of Spiegler-Kedem-Katchalsky (SKK)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Halden, R.U. Epistemology of Contaminants of Emerging Concern and Literature Meta-Analysis. J. Hazard. Mater. 2015, 282, 2–9. [Google Scholar] [CrossRef]
- Snyder, S.; Westerhoff, P.; Yoon, Y.; Sedlak, D. Pharmaceuticals, personal care products, and endocrine disruptors in water: Implications for the water industry. Environ. Eng. Sci. 2003, 20, 449–469. [Google Scholar] [CrossRef]
- Yangali-Quintanilla, V.; Maeng, S.K.; Fujioka, T.; Kennedy, M.; Amy, G. Proposing nanofiltration as acceptable barrier for organic contaminants in water reuse. J. Membr. Sci. 2010, 362, 334–345. [Google Scholar] [CrossRef]
- Fonseca Couto, C.; Lange, L.C.; Santos Amaral, M.C. A Critical Review on Membrane Separation Processes Applied to Remove Pharmaceutically Active Compounds from Water and Wastewater. J. Water Process Eng. 2018, 26, 156–175. [Google Scholar] [CrossRef]
- Giacobbo, A.; Bernardes, A.M. Membrane Separation Process in Wastewater and Water Purification. Membranes 2022, 12, 259. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Zhang, T.; Li, X. Performance of Nanofiltration Membrane in Rejecting Trace Organic Compounds: Experiment and Model Prediction. Desalination 2015, 370, 7–16. [Google Scholar] [CrossRef]
- Vasantha Raman, N.; Dubey, A.; Millar, E.; Nava, V.; Leoni, B.; Gallego, I. Monitoring Contaminants of Emerging Concern in Aquatic Systems through the Lens of Citizen Science. Sci. Total Environ. 2023, 874, 162527. [Google Scholar] [CrossRef] [PubMed]
- Van der Bruggen, B.; Schaep, J.; Wilms, D.; Vandecasteele, C. Influence of molecular size, polarity and charge on the retention of organic molecules by nanofiltration. J. Membr. Sci. 1999, 156, 29–41. [Google Scholar] [CrossRef]
- Meschke, K.; Hansen, N.; Hofmann, R.; Haseneder, R.; Repke, J.U. Influence of process parameters on separation performance of strategic elements by polymeric nanofiltration membranes. Sep. Purif. Technol. 2020, 235, 116186. [Google Scholar] [CrossRef]
- Meschke, K.; Hansen, N.; Hofmann, R.; Haseneder, R.; Repke, J.U. Characterization and performance evaluation of polymeric nanofiltration membranes for the separation of strategic elements from aqueous solutions. J. Membr. Sci. 2018, 546, 246–257. [Google Scholar] [CrossRef]
- Garcia-Ivars, J.; Durá-María, J.; Moscardó-Carreño, C.; Carbonell-Alcaina, C.; Alcaina-Miranda, M.-I.; Iborra-Clar, M.-I. Rejection of trace pharmaceutically active compounds present in municipal wastewaters using ceramic fine ultrafiltration membranes: Effect of feed solution pH and fouling phenomena. Sep. Purif. Technol. 2017, 175, 58–71. [Google Scholar] [CrossRef]
- Childress, A.E.; Elimelech, M. Relating nanofiltration membrane performance to membrane charge (electrokinetic) characteristics. Environ. Sci. Technol. 2000, 34, 3710–3716. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Liu, Y.; Hou, L. Removal of PhACs and Their Impacts on Membrane Fouling in NF/RO Membrane Filtration of Various Matrices. J. Membr. Sci. 2018, 548, 439–448. [Google Scholar] [CrossRef]
- Licona, K.P.M.; Geaquinto, L.D.O.; Nicolini, J.V.; Figueiredo, N.G.; Chiapetta, S.C.; Habert, A.C.; Yokoyama, L. Assessing Potential of Nanofiltration and Reverse Osmosis for Removal of Toxic Pharmaceuticals from Water. J. Water Process Eng. 2018, 25, 195–204. [Google Scholar] [CrossRef]
- Nghiem, L.D.; Schäfer, A.I.; Elimelech, M. Role of Electrostatic Interactions in the Retention of Pharmaceutically Active Contaminants by a Loose Nanofiltration Membrane. J. Membr. Sci. 2006, 286, 52–59. [Google Scholar] [CrossRef]
- Marchetti, P.; Jimenez-Solomon, M.F.; Szekely, G.; Livingston, G. Molecular separation with organic solvent nanofiltration: A critical review. Chem. Rev. 2014, 114, 10735–10806. [Google Scholar] [CrossRef]
- Alfa Laval. Membrana Plana de Nanofiltración: Ficha del Producto. Available online: https://urlzs.com/8ESAV (accessed on 8 May 2022).
- Oatley, D.L.; Llenas, L.; Pérez, R.; Williams, P.M.; Martínez-Lladó, X.; Rovira, M. Review of the dielectric properties of nanofiltration membranes and verification of the single oriented layer approximation. Adv. Colloid Interface Sci. 2012, 173, 1–11. [Google Scholar] [CrossRef]
- Ge, S.; Feng, L.; Zhang, L.; Xu, Q.; Yang, Y.; Wang, Z.; Kim, K.-H. Rejection rate and mechanisms of drugs in drinking water by nanofiltration technology. Environ. Eng. Res. 2017, 22, 329–338. [Google Scholar] [CrossRef]
- Schaefer, A.; Nghiem, L.D.; Oschmann, N. Bisphenol A retention in the direct ultrafiltration of greywater. J. Membr. Sci. 2006, 283, 233–243. [Google Scholar] [CrossRef]
- Hidalgo, A.M.; León, G.; Murcia, M.D.; Gómez, M.; Gómez, E.; Gómez, J.L. Using pressure driven membrane processes to remove emerging pollutants from aqueous solutions. Int. J. Environ. Res. Public Health 2021, 18, 4036. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wei, J.; Wang, C.; Wang, W. Comparison of phenol removal in synthetic wastewater by NF or RO membranes. Desalin. Water. Treat. 2010, 22, 211–219. [Google Scholar] [CrossRef]
- Hidalgo, A.M.; León, G.; Gómez, M.; Murcia, M.D.; Gómez, E.; Macario, J.A. Removal of Different Dye Solutions: A Comparison Study Using a Polyamide Nf Membrane. Membranes 2020, 10, 408. [Google Scholar] [CrossRef] [PubMed]
- Kabbani, H.M.; Al-Hindi, M.; Ayoub, G.M.; Ahmad, M. The effects of salt concentration on the rejection of pharmaceutically active compounds by nanofiltration membranes. J. Sustain. Dev. Energy Water Environ. Syst. 2021, 9, 1080356. [Google Scholar] [CrossRef]
- PubChem. «Carbamazepine». Available online: https://urlzs.com/bqSGC (accessed on 8 May 2022).
- PubChem. «Ketoprofen». Available online: https://urlzs.com/rbi3P (accessed on 8 May 2022).
- PubChem. «Bisphenol A». Available online: https://urlzs.com/pJWft (accessed on 8 May 2022).
- Xie, M.; Price, W.E.; Nghiem, L.D. Rejection of pharmaceutically active compounds by forward osmosis: Role of solution pH and membrane orientation. Sep. Purif. Technol. 2012, 93, 107–114. [Google Scholar] [CrossRef]
- Siraki, A.G.; Chevaldina, T.; O’Brien, P.J. Application of quantitative structure-toxicity relationships for acute NSAID cytotoxicity in rat hepatocytes. Chem. Biol. Interact. 2005, 151, 177–191. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.-B.; Tang, C.-C.; Liu, X.-Y.; Shi, F.-J.; Song, X.-R.; Tian, Y.; Li, Z.-S. Transportation characteristics of bisphenol A on ultrafiltration membrane with low molecule weight cut-off. Desalination 2015, 362, 18–25. [Google Scholar] [CrossRef]
- Yangali-Quintanilla, V.; Sadmani, A.; McConville, M.; Kennedy, M.; Amy, G. Rejection of pharmaceutically active compounds and endocrine disrupting compounds by clean and fouled nanofiltration membranes. Water Res. 2009, 43, 2349–2362. [Google Scholar] [CrossRef]
- Giacobbo, A.; Pasqualotto, I.F.; Machado Filho, R.C.d.C.; Minhalma, M.; Bernardes, A.M.; de Pinho, M.N. Ultrafiltration and Nanofiltration for the Removal of Pharmaceutically Active Compounds from Water: The Effect of Operating Pressure on Electrostatic Solute—Membrane Interactions. Membranes 2023, 13, 743. [Google Scholar] [CrossRef]
- da Trindade, C.D.M.; Giacobbo, A.; Ferreira, V.G.; Rodrigues, M.A.S.; Bernardes, A.M. Membranes Separation Processes Applied to the Treatment of Effluents from Nanoceramic Coating Operations. Desalin. Water Treat. 2015, 55, 28–38. [Google Scholar] [CrossRef]
- Tanninen, J.; Platt, S.; Weis, A.; Nyström, M. Long-term acid resistance and selectivity of NF membranes in very acidic conditions. J. Membr. Sci. 2004, 240, 11–18. [Google Scholar] [CrossRef]
- Zhang, Y.; Causserand, C.; Aimar, P.; Cravedi, J.P. Removal of bisphenol A by a nanofiltration membrane in view of drinking water production. Water Res. 2006, 40, 3793–3799. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Gao, N. Bisphenol A removal by nanofiltration process. Adv. Mater. Res. 2010, 113–116, 1648–1652. [Google Scholar] [CrossRef]
- Yüksel, S.; Kabay, N.; Yüksel, M. Removal of bisphenol A (BPA) from water by various nanofiltration (NF) and reverse osmosis (RO) membranes. J. Hazard. Mater. 2013, 263, 307–310. [Google Scholar] [CrossRef] [PubMed]
- Soltanieh, M.; Gill, W.N. Review of reverse osmosis membranes and transport models. Chem. Eng. Commun. 1981, 12, 279–363. [Google Scholar] [CrossRef]
- Hidalgo, A.M.; León, G.; Gómez, M.; Murcia, M.D.; Barbosa, D.S.; Blanco, P. Application of the solution-diffusion model for the removal of atrazine using a nanofiltration membrane. Desalin. Water Treat. 2013, 51, 2244–2252. [Google Scholar] [CrossRef]
- Bódalo, A.; Gómez, J.L.; Gómez, E.; León, G.; Tejera, M. Reduction of sulphate content in aqueous solutions by reverse osmosis using cellulose acetate membranes. Desalination 2004, 162, 55–60. [Google Scholar] [CrossRef]
- Hidalgo, A.M.; Gómez, M.; Murcia, M.D.; Gómez, E.; León, G.; Sánchez, A. Removal of Anilinic Compounds Using the NF-97 Membrane: Application of the Solution-Diffusion and SKK Models. Sep. Sci. Technol. 2016, 51, 2429–2439. [Google Scholar] [CrossRef]
- Koter, S. Determination of the Parameters of the Spiegler-Kedem-Katchalsky Model for Nanofiltration of Single Electrolyte Solutions. Desalination 2006, 198, 335–345. [Google Scholar] [CrossRef]
- Nair, R.R.; Protasova, E.; Strand, S.; Bilstad, T. Implementation of Spiegler–Kedem and Steric Hindrance Pore Models for Analyzing Nanofiltration Membrane Performance for Smart Water Production. Membranes 2018, 8, 78. [Google Scholar] [CrossRef]
- Wu, F.; Feng, L.; Zhang, L. Rejection Prediction of Isopropylantipyrine and Antipyrine by Nanofiltration Membranes Based on the Spiegler-Kedem-Katchalsky Model. Desalination 2015, 362, 11–17. [Google Scholar] [CrossRef]
| Characteristics | Technical Specifications |
|---|---|
| Manufacturer | Alfa Laval |
| Name | NF99HF |
| Type | Thin-layer composite polyester |
| Composition | Polyamide |
| MWCO (Molecular Weight Cut-Off) (Da) | ≥200 b |
| pH Range | 3–10 |
| Maximum Temperature (°C) | 50 |
| Maximum Pressure (bar) | 55 |
| MgSO4 Rejection (%) | ≥98 |
| Isoelectric Point (pH) | 4.12–4.42 a |
| Effective Pore Radius (nm) | 0.43 a |
| Contact Angle (°) | 34.5 ± 4.2 c |
| Effective Surface Area (m2) | 0.0028 |
| Aw | Temperature (°C) | ΔP (bar) | Flat Sheet Membrane Module Used | Reference | |
|---|---|---|---|---|---|
| (s/m) | (L/m2·h bar) | ||||
| 6.175 × 10−8 | 22.230 | - | 10–25 | INDEVEN with tangential filtration | [21] |
| 2.961 × 10−8 | 10.661 | 25 | 5–30 | Alfa Laval Lab M20 with tangential filtration | [22] |
| 4.788 × 10−8 | 17.237 | 15.8–18.1 | 10–30 | INDEVEN with tangential filtration | [23] |
| 3.035 × 10−8 | 10.927 | 19.7–20.5 | 5–20 | Triple System Model F1 with tangential filtration | Experimental |
| Emerging Pollutant | Carbamazepine | Ketoprofen | Bisphenol A |
|---|---|---|---|
| Molecular structure | 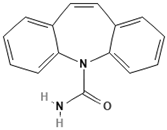 | 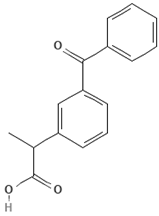 | 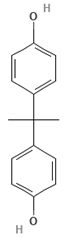 |
| Chemical formula | C15H12N2O | C16H14O3 | C15H16O2 |
| Molecular weight (g/mol) | 236.7 | 254.28 | 228.29 |
| Solubility in water (mg/L) | 18 | 51 | 120 |
| Dissociation constant | pKa = 13.9 | pKa = 3.98 | pKa = 9.6 |
| Charge at pH 7 | Neutral a | Negative b | Neutral a |
| log KOW | 2.45 | 3.12 | 3.32 |
| Dipole moment (D) | 3.6 c,f | 4.37 d | 2.13 f |
| Stokes radius (nm) | 0.37 c | - | 0.5 e |
| Emerging Pollutant | Membrane | Experimental Conditions | Rejection(%) | Jp (kg/m2s) | Reference |
|---|---|---|---|---|---|
| Carbamazepine | NF270 | Ca = 10 ppm ∆P = 10 bar | 70–80 | - | [24] |
| Carbamazepine | NF270 | Ca = 200 ppb TMP = 5 bar | 80 | - | [19] |
| Ketoprofen | NF270 | Ca = 200 ppb TMP = 5 bar | 93 | - | [19] |
| Bisphenol A | NF90 | Ca = 50 ppm ∆P = 10 bar | 98 | - | [37] |
| Bisphenol A | NF270 | Ca = 50 ppm ∆P = 10 bar | 80 | - | [37] |
| Bisphenol A | Desal5DK | Ca = 1 ppb TMP = 20 bar | 90–50 | - | [35] |
| Bisphenol A | NF | Ca = 0.5–3 ppm ∆P = 4 bar | 90–81 | - | [36] |
| Carbamazepine | NF99HF | Ca = 9.3 ppm ∆P = 9.7 bar | 89.2 | 24.3 | This work |
| Bisphenol A | NF99HF | Ca = 4.2 ppm ∆P = 4.5 bar | 77 | 5.8 | This work |
| Ketoprofen | NF99HF | Ca = 4.3 ppm ∆P = 4.5 bar | 85 | 9.9 | Thiswork |
| ΔP (bar) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| Fp (%) | 48.3 | 40.5 | 37.2 | 35.5 |
| Fs (%) | 64.7 | 41.7 | 42.7 | 49.2 |
| Carbamazepine | Ketoprofen | Bisphenol A | |
|---|---|---|---|
| Bs (m/s) | 3.998 × 10−6 | 3.155 × 10−7 | 7.712 × 10−7 |
| R2 | 0.771 | 0.421 | 0.774 |
| Ψ (m2/s2) | 8.876 × 105 | 7.537 × 106 | 5.657 × 106 |
| R2 | 0.004 | 0.684 | 0.362 |
| Coefficients | Carbamazepine | Ketoprofen | Bisphenol A |
|---|---|---|---|
| Ps (m/s) | 1.368 × 10−6 | 5.647 × 10−8 | 1.472 × 10−6 |
| σ | 0.841 | 0.930 | 0.987 |
| R2 | 0.832 | 0.617 | 0.418 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hidalgo, A.M.; Gómez, M.; Murcia, M.D.; Gómez, E.; León, G.; Alfaro, I. Prediction of Flux and Rejection Coefficients in the Removal of Emerging Pollutants Using a Nanofiltration Membrane. Membranes 2023, 13, 868. https://doi.org/10.3390/membranes13110868
Hidalgo AM, Gómez M, Murcia MD, Gómez E, León G, Alfaro I. Prediction of Flux and Rejection Coefficients in the Removal of Emerging Pollutants Using a Nanofiltration Membrane. Membranes. 2023; 13(11):868. https://doi.org/10.3390/membranes13110868
Chicago/Turabian StyleHidalgo, Asunción M., María Gómez, María D. Murcia, Elisa Gómez, Gerardo León, and Irene Alfaro. 2023. "Prediction of Flux and Rejection Coefficients in the Removal of Emerging Pollutants Using a Nanofiltration Membrane" Membranes 13, no. 11: 868. https://doi.org/10.3390/membranes13110868
APA StyleHidalgo, A. M., Gómez, M., Murcia, M. D., Gómez, E., León, G., & Alfaro, I. (2023). Prediction of Flux and Rejection Coefficients in the Removal of Emerging Pollutants Using a Nanofiltration Membrane. Membranes, 13(11), 868. https://doi.org/10.3390/membranes13110868








