Permeate Flux Enhancement in Air Gap Membrane Distillation Modules with Inserting Λ-Ribs Carbon-Fiber Open Slots
Abstract
1. Introduction
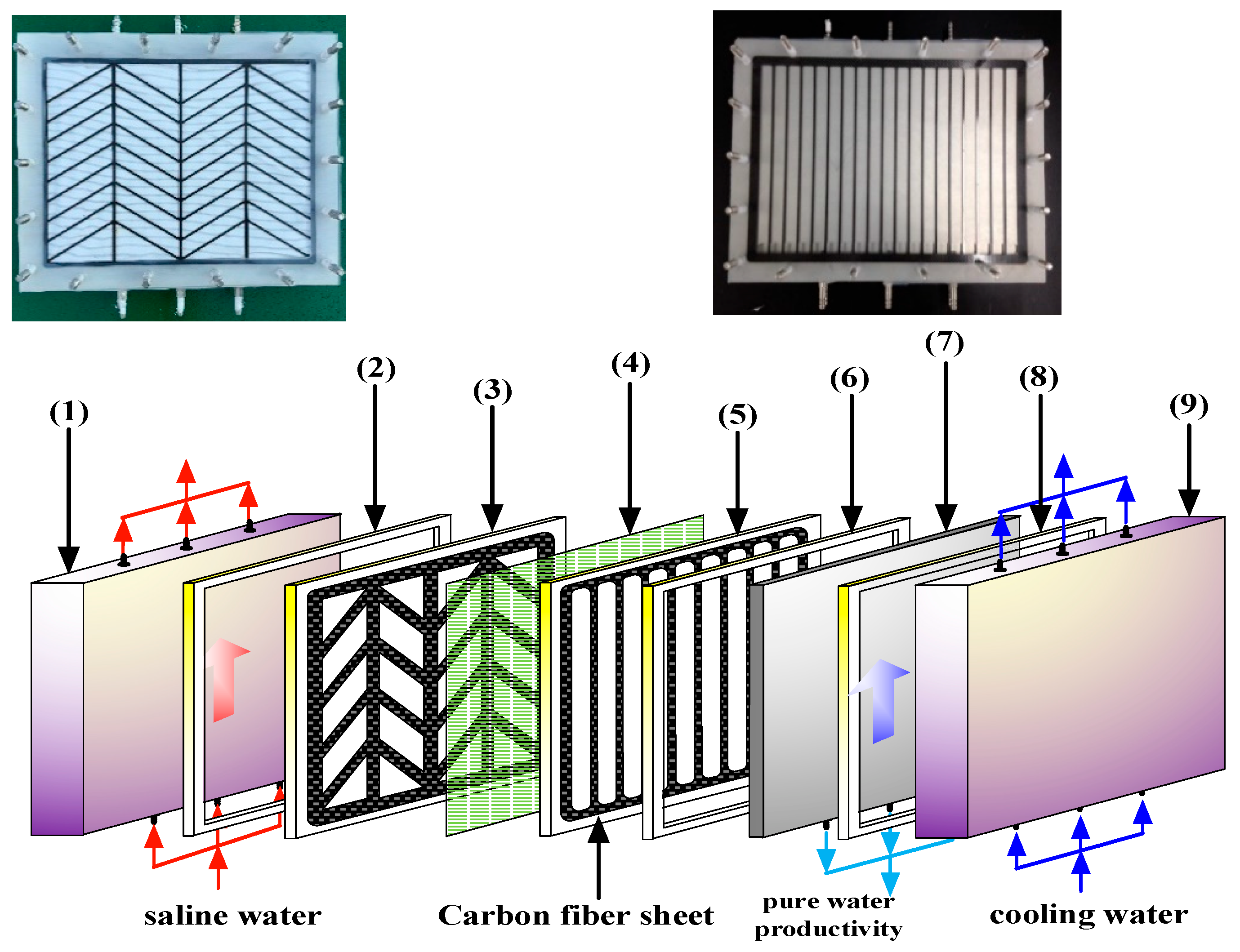
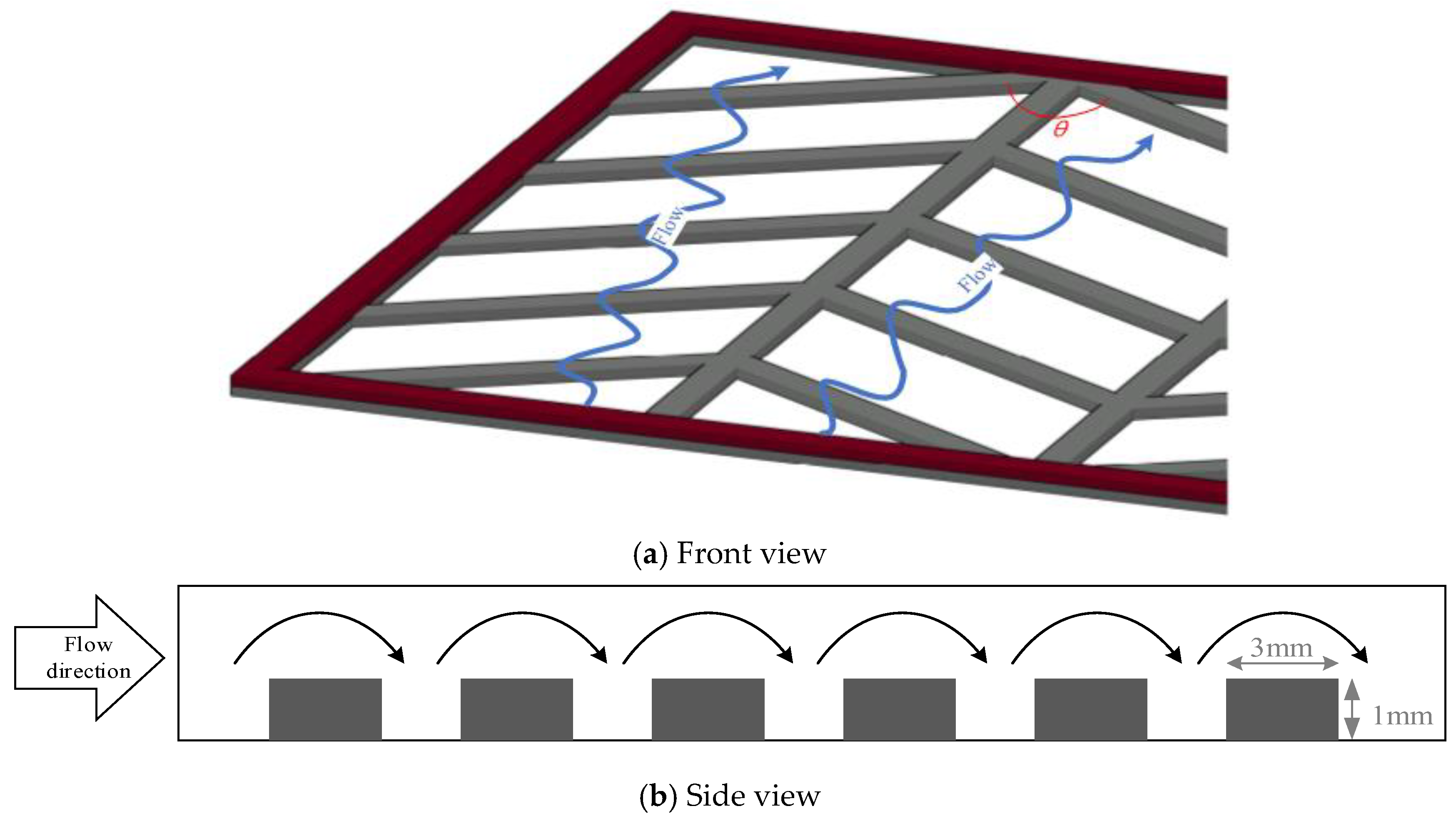
2. Experimental Apparatus and Procedure
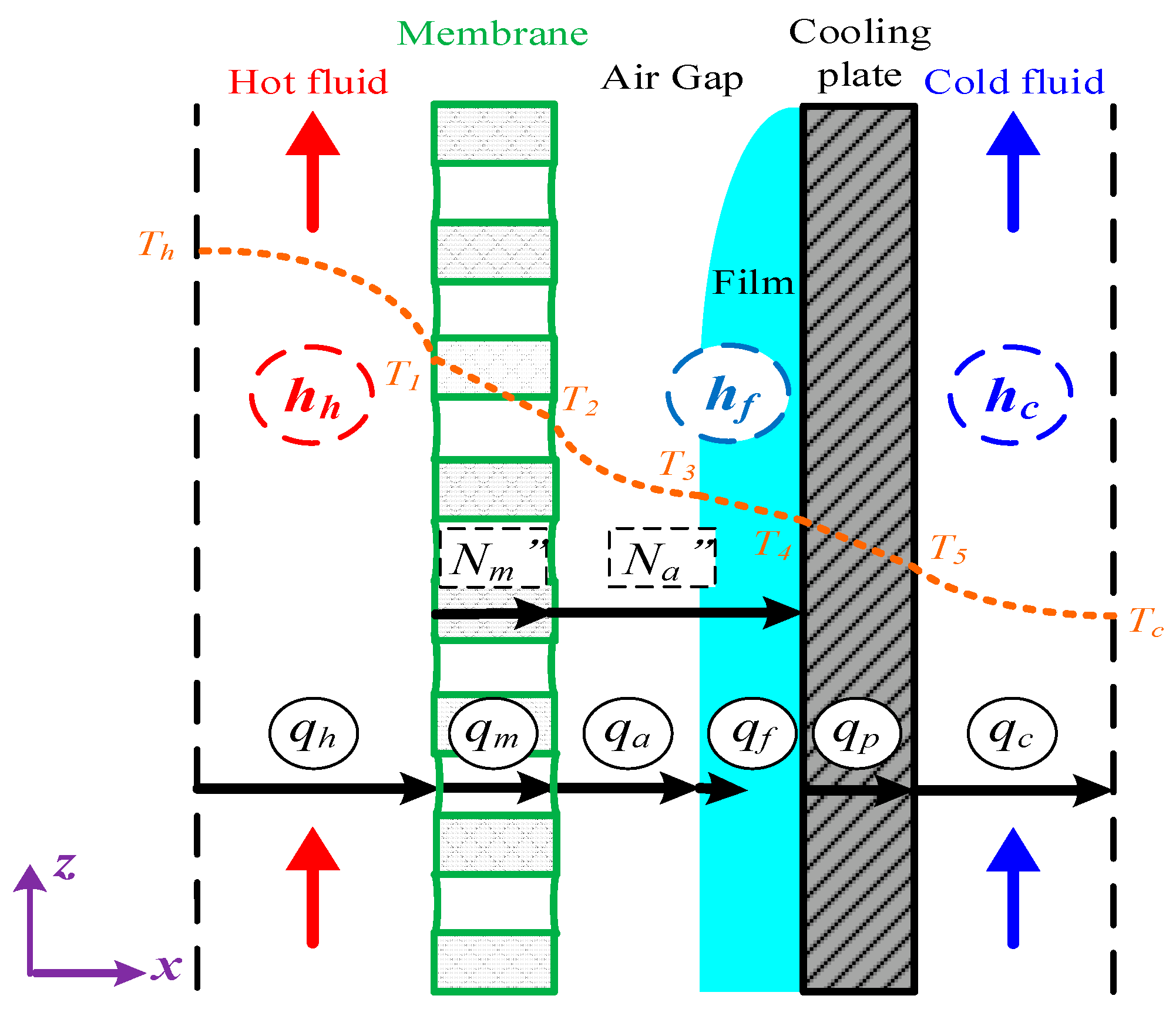
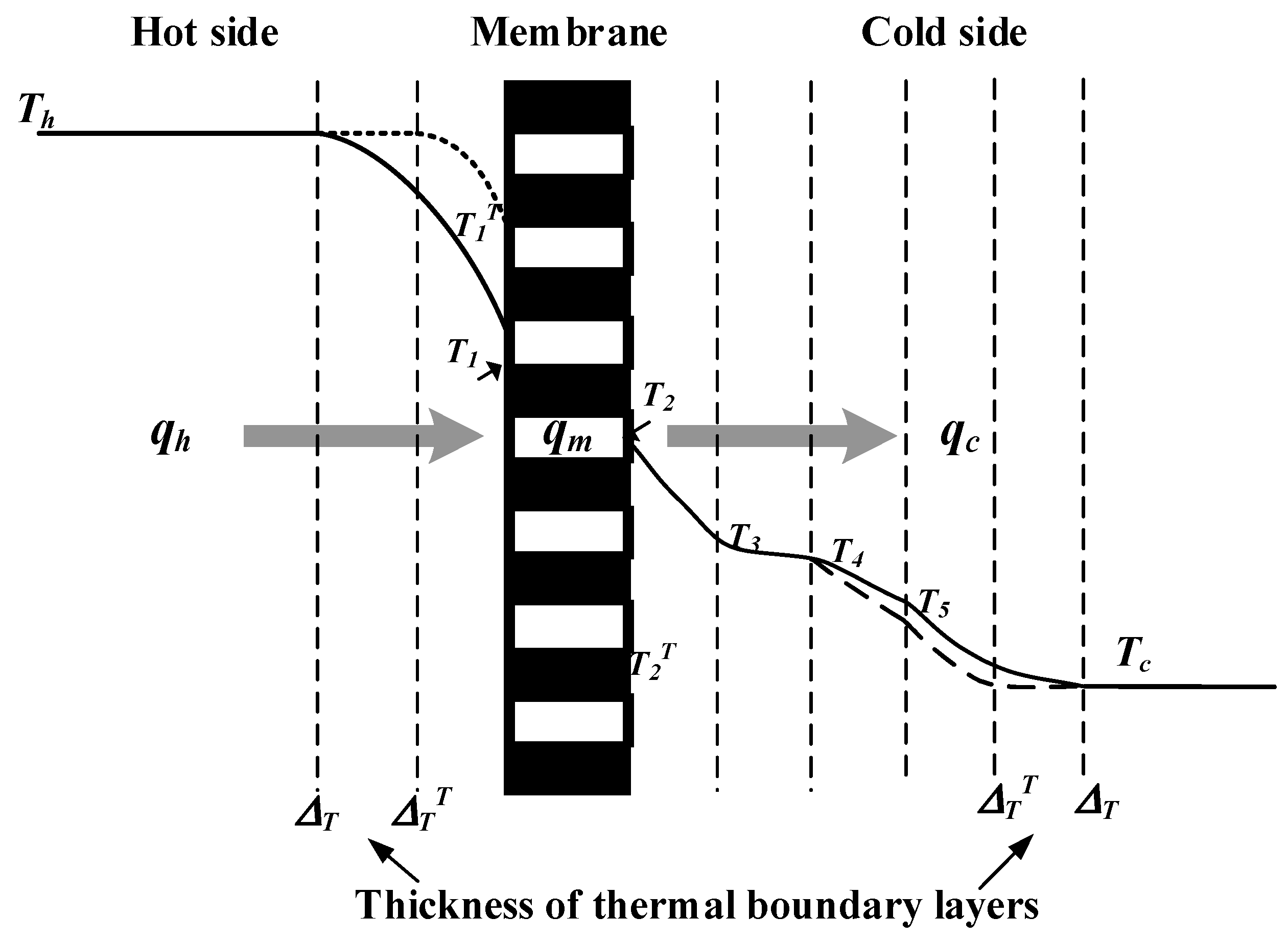
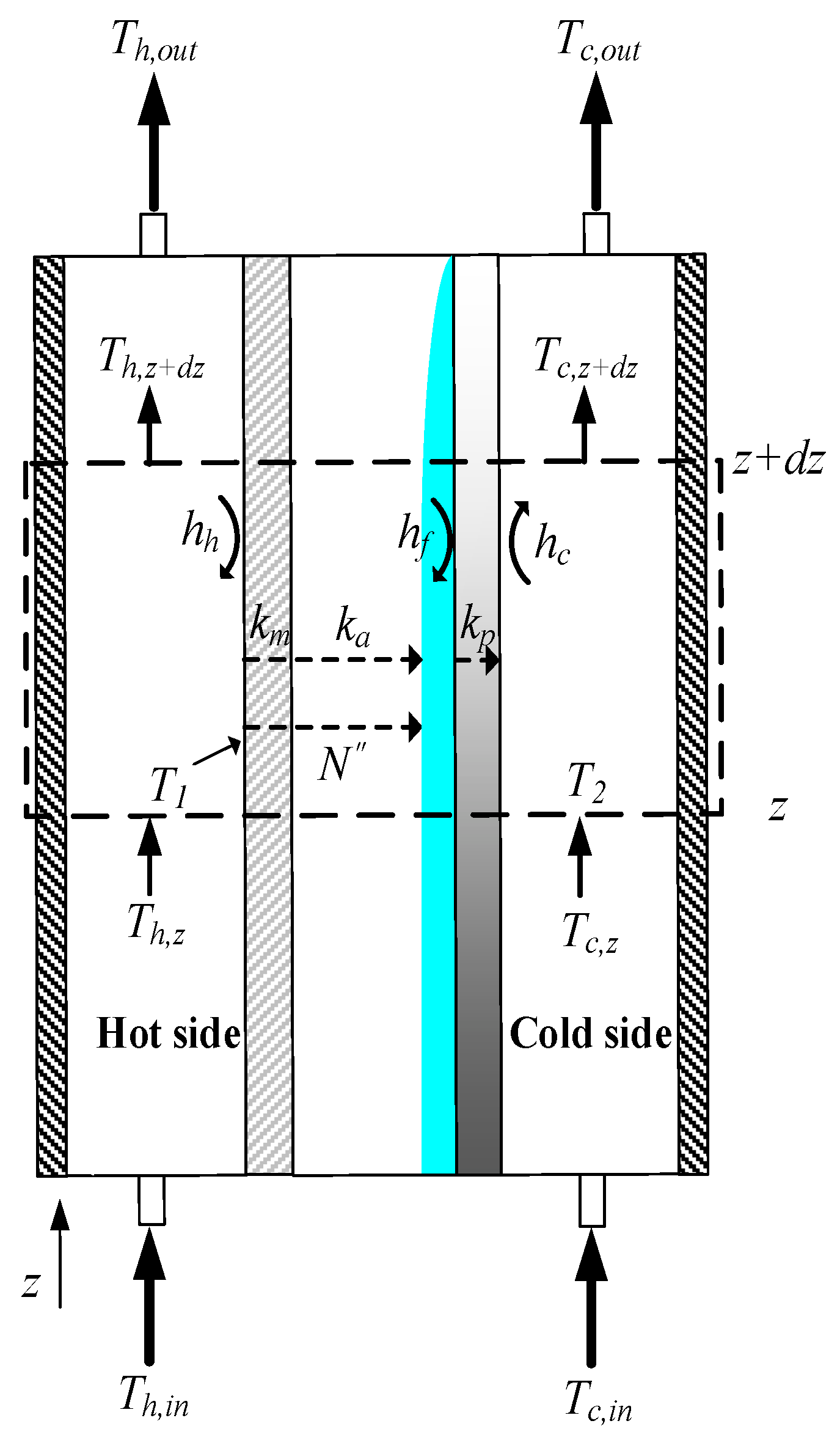
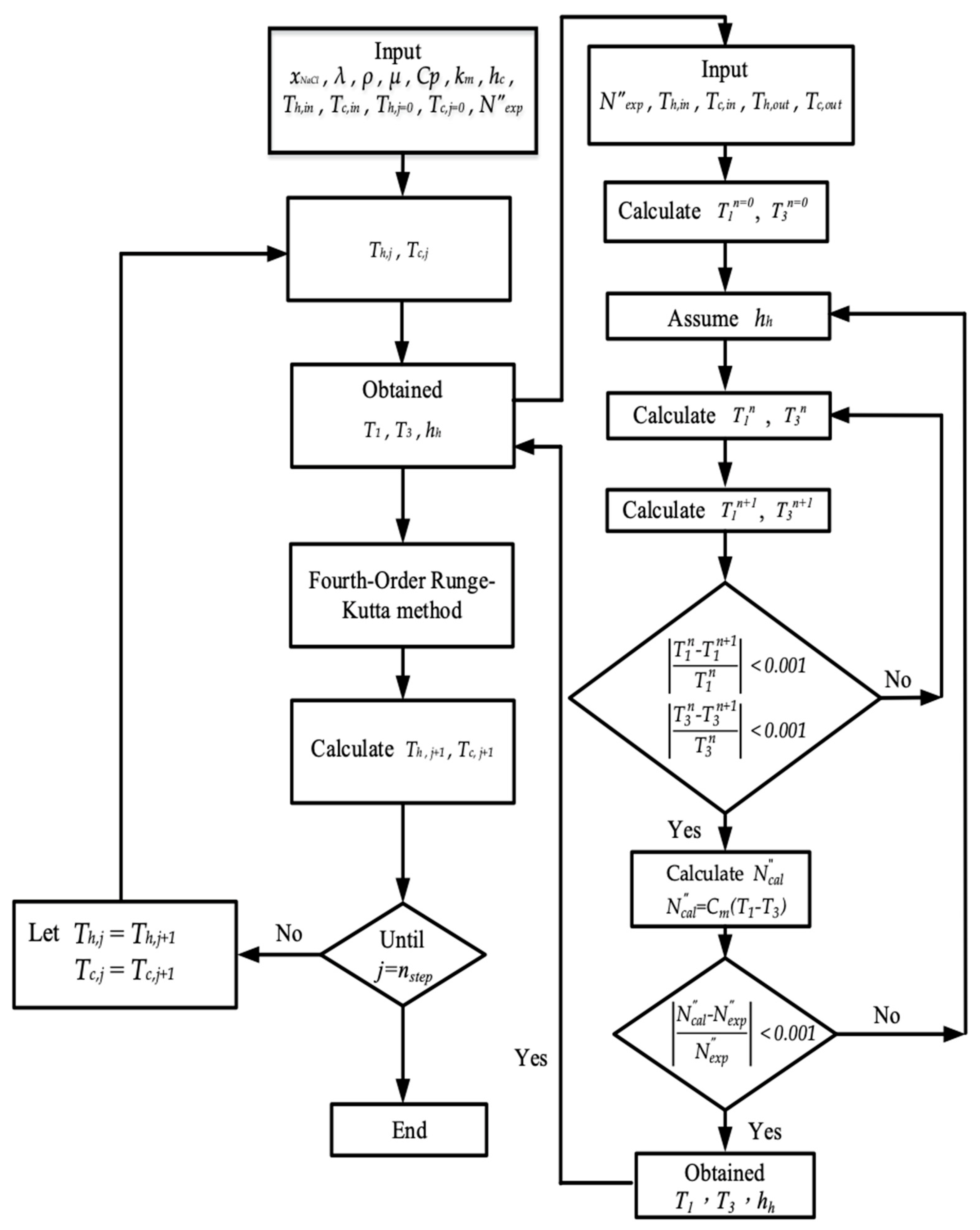
3. Theoretical Modeling of Mass and Heat Transfer in AGMD Modules
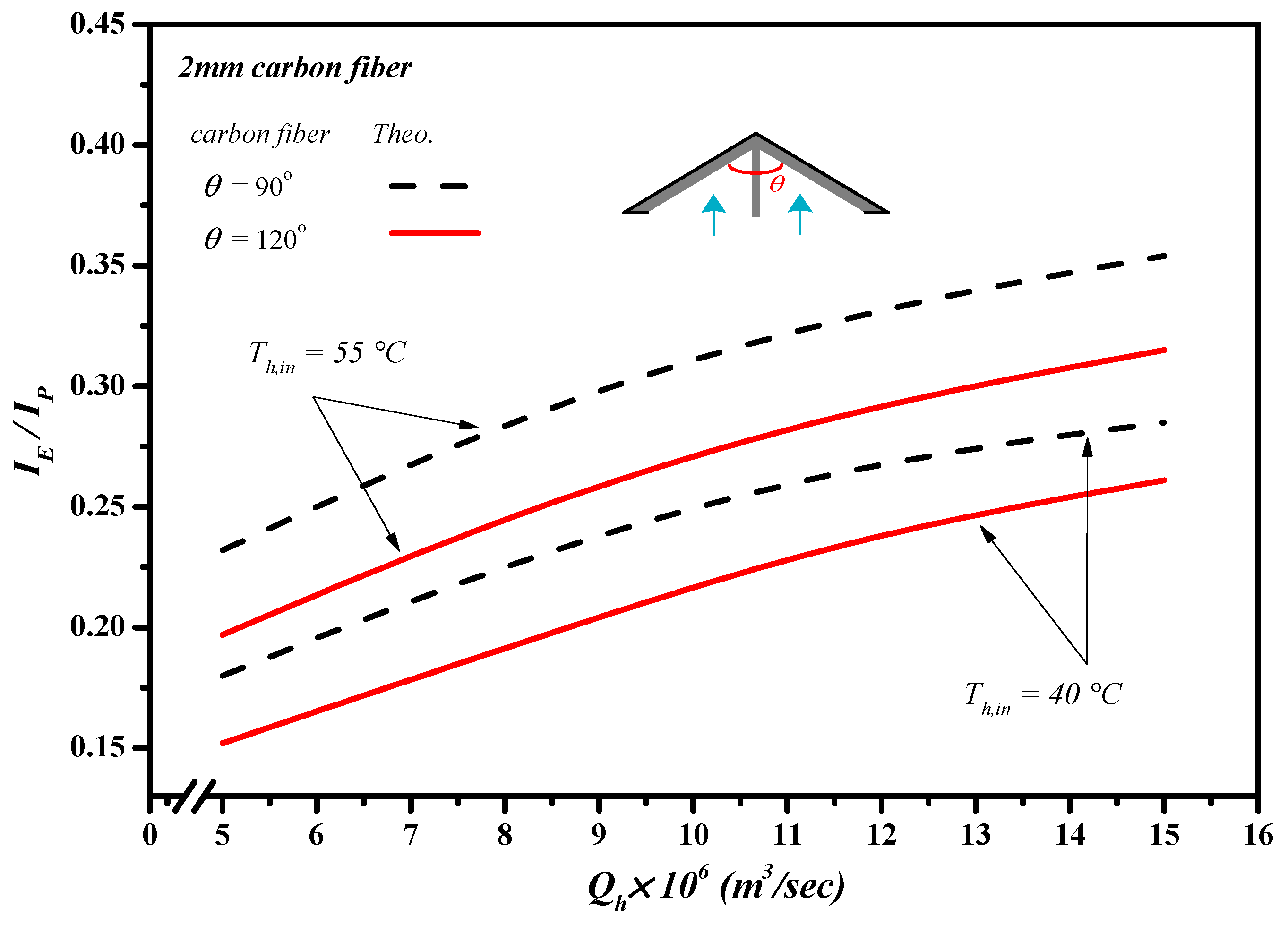
4. Permeate Flux Enhancement and Power Consumption Increment
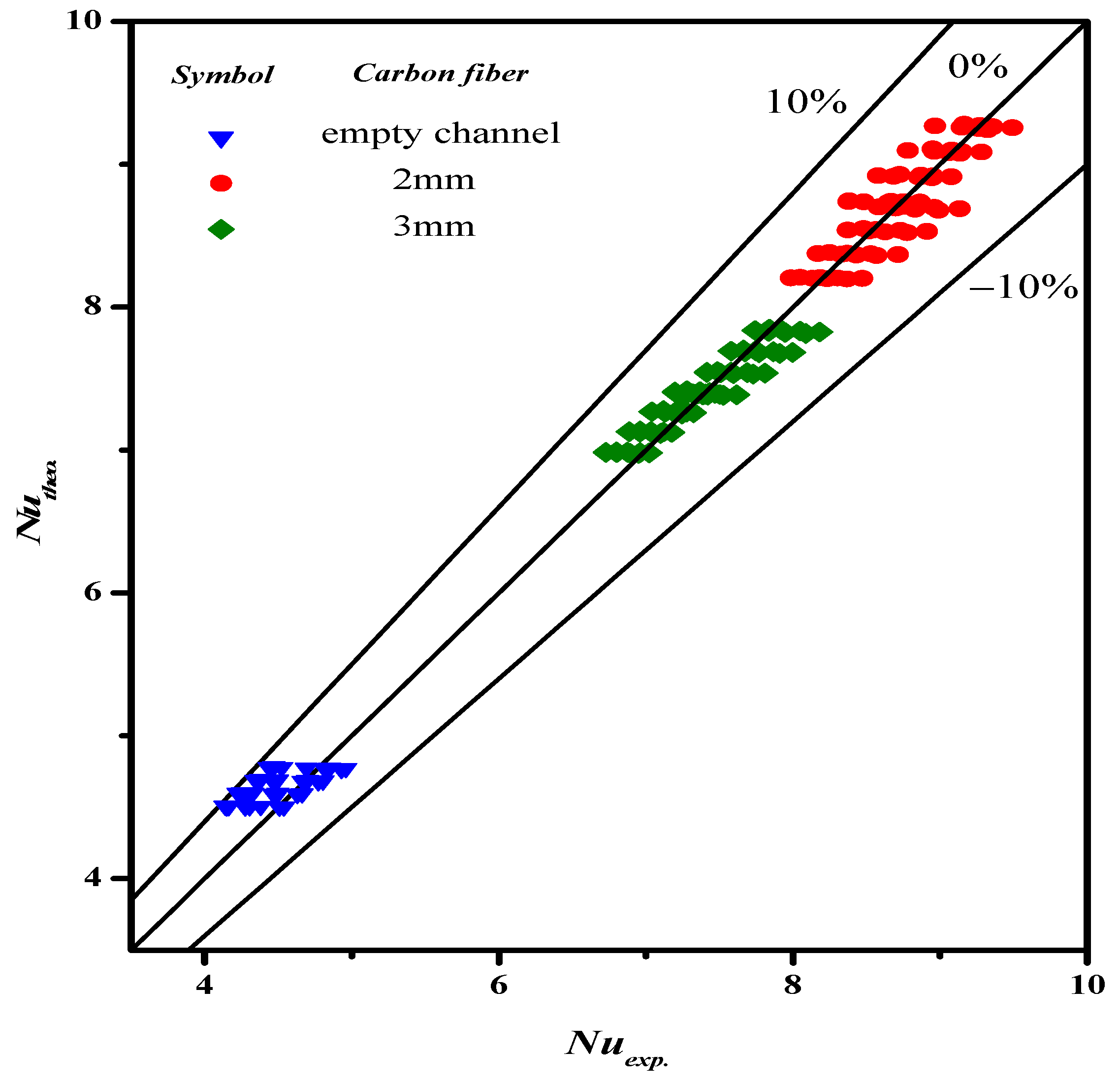
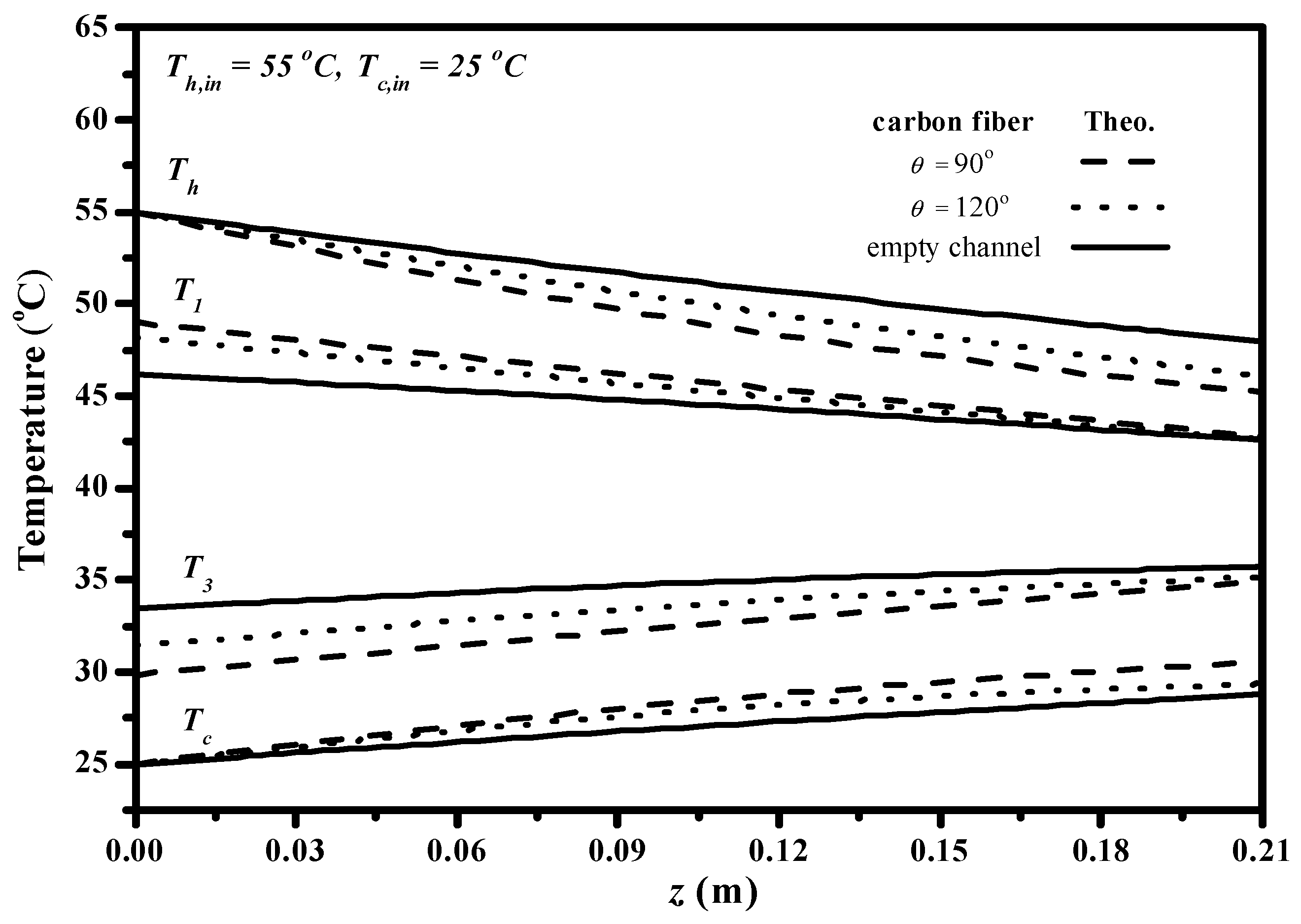
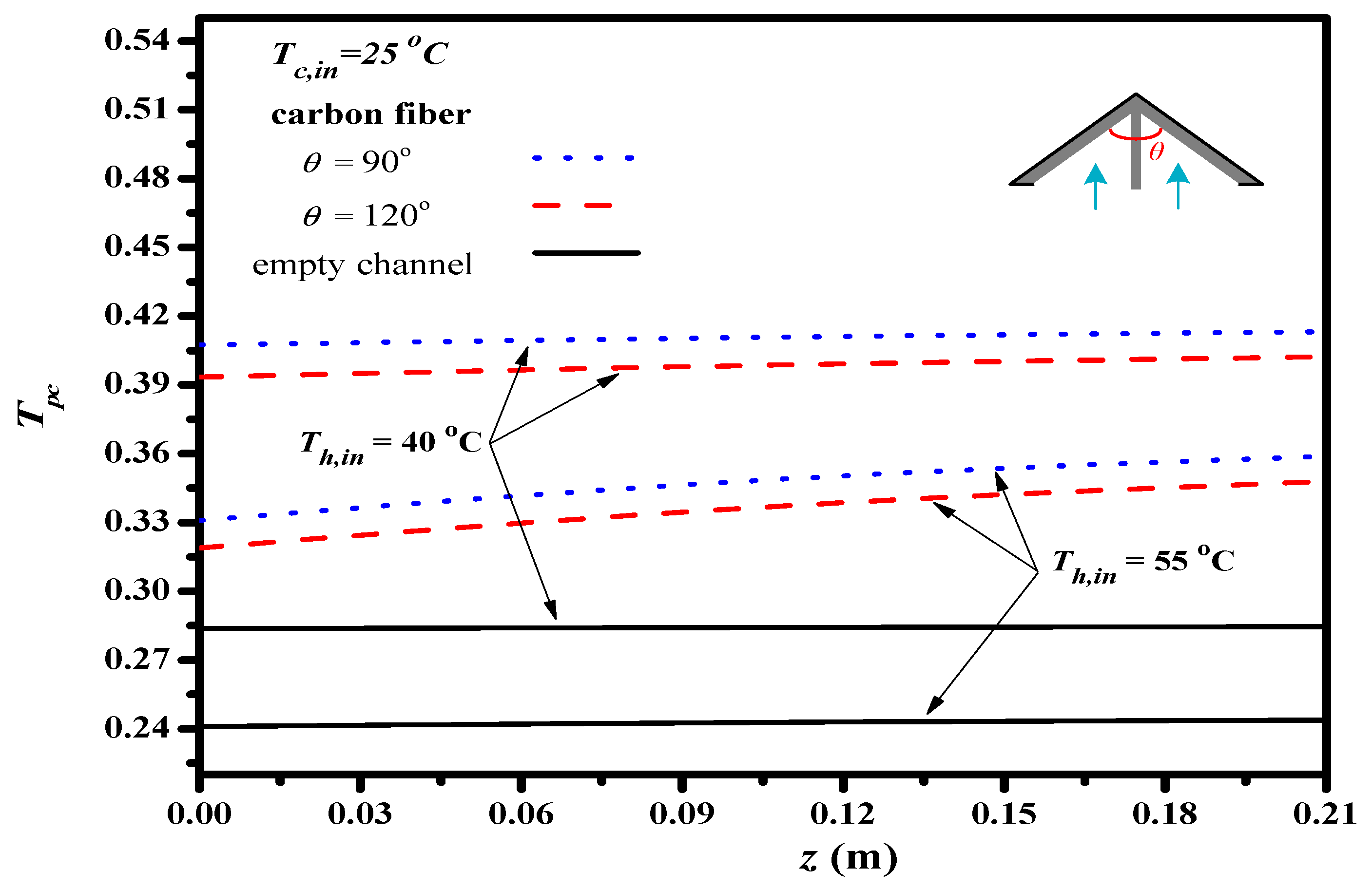
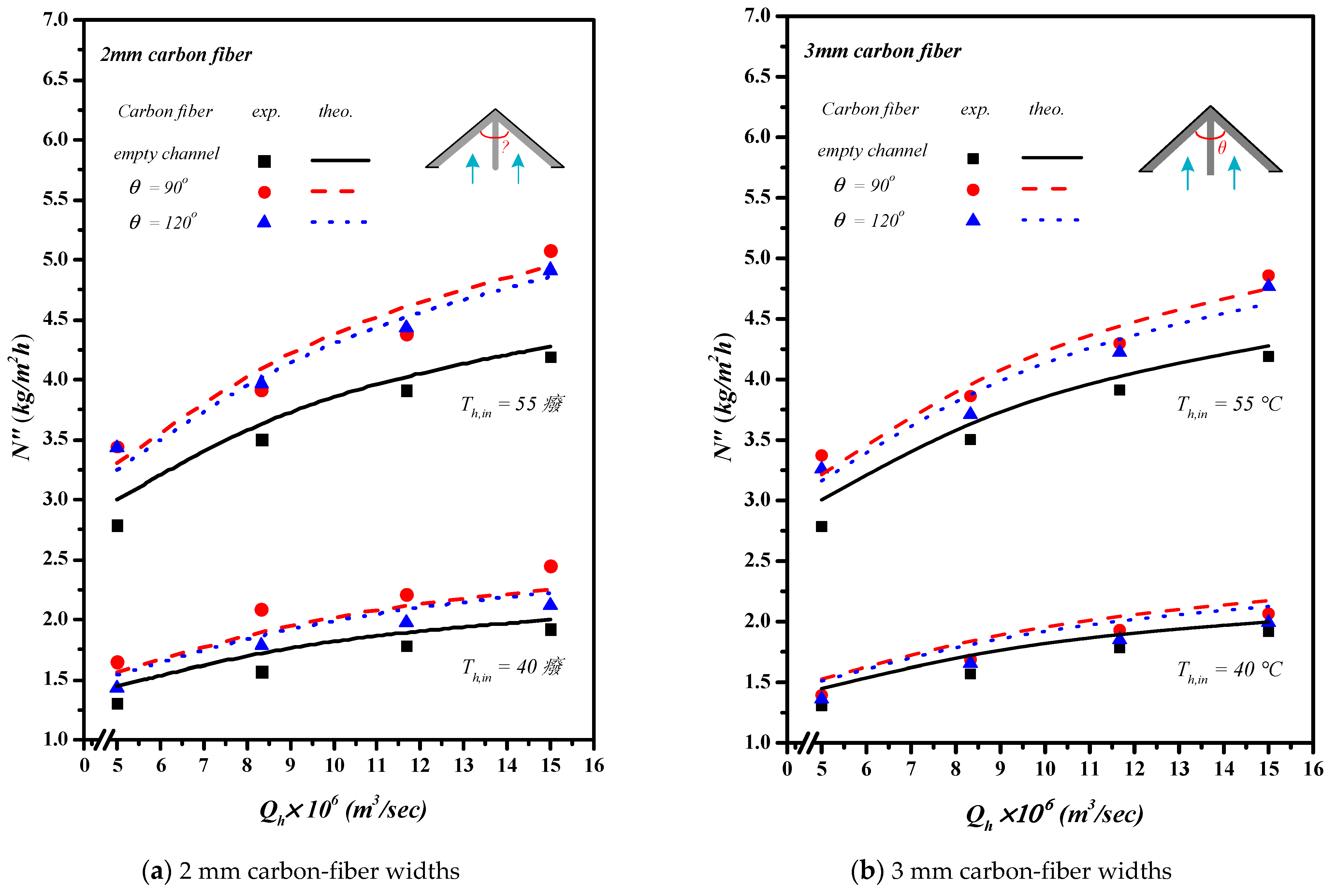
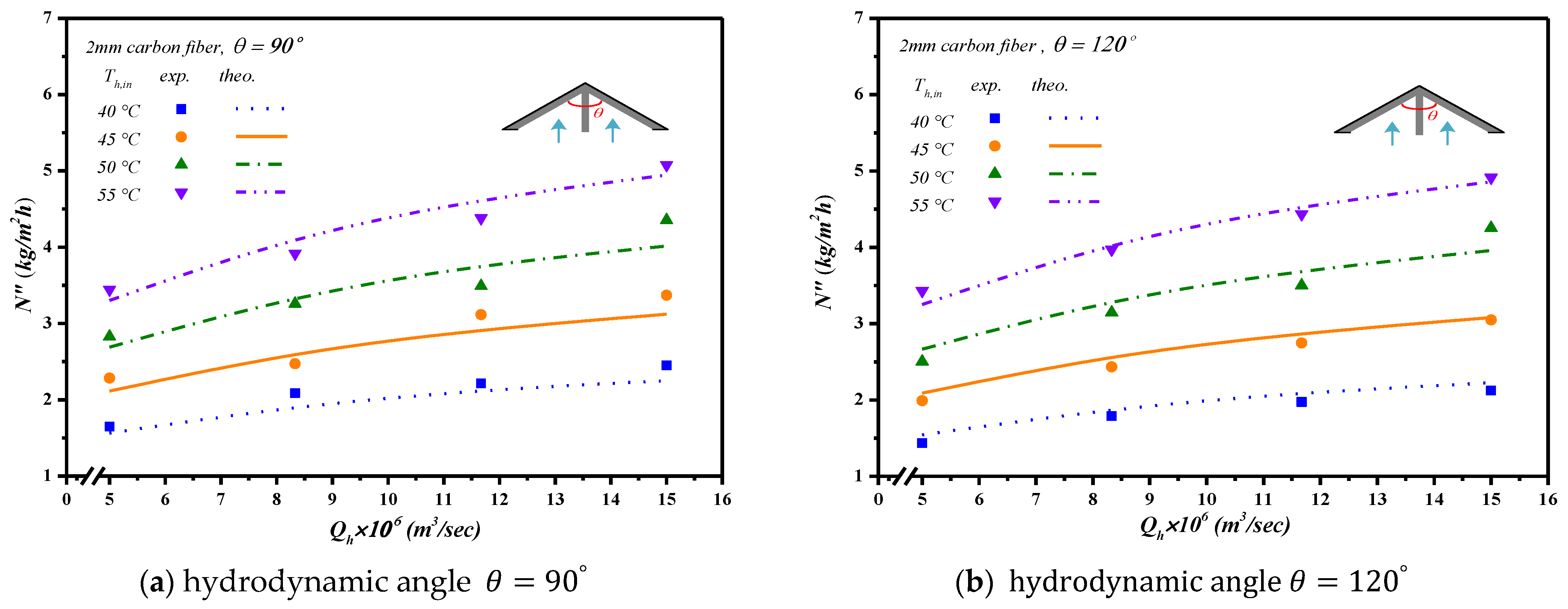
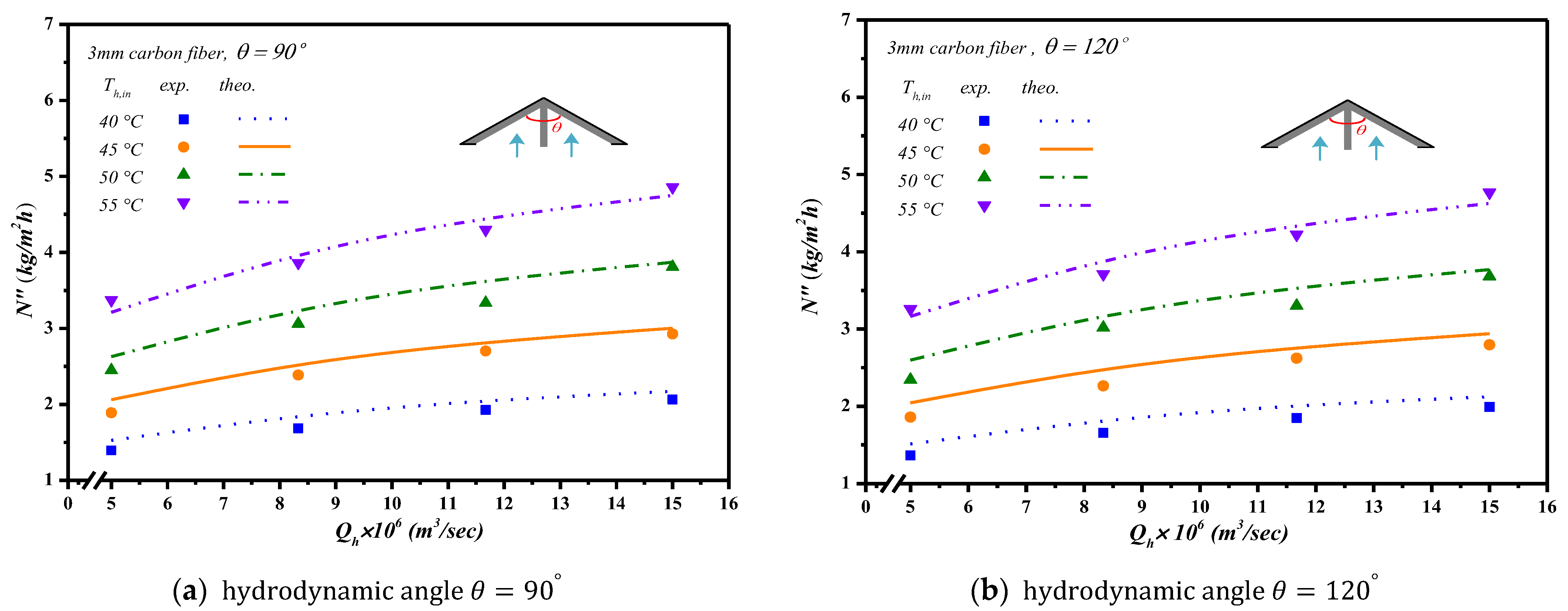
5. Results and Discussion
6. Conclusions
- The permeate flux increases with decreasing hydrodynamic angle and carbon-fiber width in the AGMD module by inserting -ribs carbon-fiber open slots.
- The permeate flux enhancement increases with the increase of the volumetric flow rate by inserting -ribs carbon-fiber open slots where the enhancement of the AGMD module using 2 mm open slots is higher than that of the 3 mm one.
- The higher the inlet saline feed temperature yields, the higher the permeate flux enhancement.
- A higher permeate flux enhancement was found in the module with inserting -ribs carbon-fiber open slots compared to that in the empty-channel module under both the smaller hydrodynamic angle and carbon-fiber width.
- The higher ratio of was achieved for the module by inserting -ribs carbon-fiber open slots, and was operated under both the higher saline feed flow rate and inlet saline feed temperature, and both the smaller carbon-fiber width and hydrodynamic angle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| membrane area (m2) | |
| water activity in NaCl solution | |
| heat capacity of cold fluid (J kg−1K−1) | |
| heat capacity of hot fluid (J kg−1K−1) | |
| mass transfer coefficient of air gap region (kg m−2 Pa−1 s−1) | |
| mass transfer coefficient of membrane (kg m−2 Pa−1 s−1) | |
| overall mass transfer coefficient of membrane (kg m−2 Pa−1 s−1) | |
| thickness of empty channel (m) | |
| equivalent hydraulic diameter of empty channel (m) | |
| equivalent hydraulic diameter of hot side (m) | |
| equivalent hydraulic diameter of cold side (m) | |
| E | deviation of experimental results from the theoretical predictions |
| Fanning friction factor | |
| convection coefficient of cold stream (W m−2 K−1) | |
| convection coefficient of saline stream (W m−2 K−1) | |
| hydraulic dissipate energy (J kg−1), | |
| thermal convection coefficient of membrane (W m−2 K−1) | |
| increased percentage of permeate flux | |
| raised percentage of hydraulic loss | |
| axial distance (m) | |
| thermal conductivity of the air gap (W m−1 K−1) | |
| thermal conductivity of the membrane (W m−1 K−1) | |
| thermal conductivity coefficient of aqueous solution (W m−1 K−1) | |
| thermal conductivity coefficient of the vapor in the membrane pore (W m−1 K−1) | |
| thermal conductivity coefficient of the solid membrane material (W m−1 K−1) | |
| thermal conductivity of the membrane (W m−1 K−1) | |
| thermal conductivity of cooling plate (W m−1 K−1) | |
| friction loss of conduits (J kg−1) | |
| molecular weight of water (kg mol−1) | |
| mass flow rate (kg s−1) | |
| permeate flux (kg m−2 s−1) | |
| Nusselt number | |
| enhanced Nusselt number with inserting turbulence promoter | |
| Nusselt number for laminar flow | |
| pressure (Pa) | |
| saturation vapor pressure in the saline feed stream (Pa) | |
| saturation vapor pressure in the hot feed flow side (Pa) | |
| saturated vapor pressure of pure water (Pa) | |
| Prandtl number | |
| heat transfer flux (W) | |
| heat transfer rate (W/m2) | |
| volumetric flow rate (m3 s−1) | |
| gas constant (8.314 J mol−1 K−1) | |
| Reynolds number | |
| radius of membrane pore (m) | |
| temperature (°C) | |
| mean temperature in membrane (°C) | |
| temperature polarization coefficients | |
| average velocity (m s−1) | |
| -ribs carbon-fiber width | |
| natural log mean mole fraction of air | |
| liquid mole fraction of NaCl | |
| liquid mole fraction of water | |
| axial coordinate along the flow direction (m) | |
| Greek letters | |
| heat-transfer enhancement factor | |
| aspect ratio of the channel | |
| vapor pressure difference of membrane (Pa) | |
| thickness of membrane (µm) | |
| membrane porosity | |
| channel voidage | |
| latent heat of water (J/kg) | |
| fluid viscosity (kg s−1 m−1) | |
| density (kg m−3) | |
| temperature polarization coefficients | |
| Subscripts | |
| 1 | on membrane surface in cold feed side |
| 2 | on membrane surface in hot feed side |
| a | in the air gap |
| c | in the cold feed flow channel |
| f | in the condensate film |
| h | in the hot feed flow channel |
| m | in the membrane |
| p | in the cooling plate |
| carbon fiber | inserting -ribs carbon-fiber open slots |
| empty | module with inserting nylon fiber as supporters |
| exp | experimental results |
| in | at the inlet |
| lam | module with empty channel |
| out | at the outlet |
| theo | theoretical predictions |
| Superscripts | |
| E | the channel with inserting -ribs carbon-fiber open slots |
References
- Alkhudhiri, A.; Darwish, N.; Hilal, N. Treatment of saline solutions using Air Gap Membrane Distillation: Experimental study. Desalination 2013, 323, 2–7. [Google Scholar] [CrossRef]
- Elhenawy, Y.; Elminshawy, N.A.S.; Bassyouni, M.; Alhathal Alanezi, A.; Drioli, E. Experimental and theoretical investigation of a new air gap membrane distillation module with a corrugated feed channel. J. Membr. Sci. 2020, 594, 117461. [Google Scholar] [CrossRef]
- Dehesa-Carrasco, U.; Perez-Rabago, C.A.; Arancibia-Bulnes, C.A. Experimental evaluation and modeling of internal temperatures in an air gap membrane distillation unit. Desalination 2013, 326, 47–54. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation. II. direct contact MD. J. Membr. Sci. 1996, 120, 123–133. [Google Scholar] [CrossRef]
- Alklaibi, A.M.; Lior, N. Membrane-distillation desalination: Status and potential. Desalination 2005, 171, 111–131. [Google Scholar] [CrossRef]
- Olatunji, S.O.; Camacho, L.M. Heat and Mass Transport in Modeling Membrane Distillation Configurations: A Review. Front. Energy Res. 2018, 6, 130. [Google Scholar] [CrossRef]
- Al-Obaidani, S.; Curcio, E.; Macedonio, F.; Di Profio, G.; Al-Hinai, H.; Drioli, E. Potential of membrane distillation in sea-water desalination: Thermal efficiency, sensitivity study and cost estimation. J. Membr. Sci. 2008, 323, 85–98. [Google Scholar] [CrossRef]
- Schofield, R.; Fane, A.; Fell, C. Heat and mass transfer in membrane distillation. J. Membr. Sci. 1987, 33, 299–313. [Google Scholar] [CrossRef]
- Martinez-Diez, L.; Vázquez-González, M. Effects of polarization on mass transport through hydrophobic porous membranes. Ind. Eng. Chem. Res. 1998, 37, 4128–4135. [Google Scholar] [CrossRef]
- Alkhudhiri, A.; Darwish, N.; Hilal, N. Membrane distillation: A compressive review. Desalination 2012, 287, 2–18. [Google Scholar] [CrossRef]
- Gryta, M.; Tomaszewska, M.; Grzechulska, J.; Morawski, A. Membrane distillation of NaCl solution containing natural organic matter. J. Membr. Sci. 2001, 181, 279–287. [Google Scholar] [CrossRef]
- Drioli, E.; Ali, A.; Macedonio, F. Membrane distillation: Recent developments and perspectives. Desalination 2015, 356, 56–84. [Google Scholar] [CrossRef]
- Chang, H.; Hsu, J.-A.; Chang, C.-L.; Ho, C.-D.; Cheng, T.-W. Simulation study of transfer characteristics for spacer-filled membrane distillation desalination modules. Appl. Energy 2015, 185, 2045–2057. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A. Effects of net-type spacers on heat and mass transfer in direct contact mem-brane distillation and comparison with ultrafiltration studies. J. Membr. Sci. 2003, 217, 193–206. [Google Scholar] [CrossRef]
- Santos, J.; Geraldes, V.; Velizarov, S.; Crespo, J. Investigation of flow patterns and mass transfer in membrane module channels filled with flow-aligned spacers using computational fluid dynamics (CFD). J. Membr. Sci. 2007, 305, 103–117. [Google Scholar] [CrossRef]
- Ho, C.; Chang, H.; Chang, C.; Huang, C. Theoretical and experimental studies of performance enhancement with roughened surface in direct contact membrane distillation desalination. J. Membr. Sci. 2013, 433, 160–166. [Google Scholar] [CrossRef]
- Yang, X.; Yu, H.; Wang, R.; Fane, A.G. Analysis of the effect of turbulence promoters in hollow fiber membrane distillation modules by computational fluid dynamic (CFD) simulations. J. Membr. Sci. 2012, 415–416, 758–769. [Google Scholar] [CrossRef]
- Singh, D.; Sirkar, K.K. Desalination by air gap membrane distillation using a two hollow-fiber-set membrane module. J. Membr. Sci. 2012, 421–422, 172–179. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Fane, A.G.; Wiley, D.E. Spacer characterization and pressure drop modelling in spacer-filled channels for ultrafiltration. J. Membr. Sci. 1994, 87, 79–98. [Google Scholar] [CrossRef]
- Ho, C.-D.; Chen, L.; Lai, J.-Y.; Ng, C.A. Theoretical and experimental studies of direct contact membrane distillation modules with inserting W-shaped carbon-fiber spacers. Desalin. Water Treat. 2017, 71, 32–44. [Google Scholar] [CrossRef]
- Yang, X.; Wang, R.; Fane, A.G. Novel designs for improving the performance of hollow fiber membrane distillation modules. J. Membr. Sci. 2011, 384, 52–62. [Google Scholar] [CrossRef]
- Dong, Y.; Dai, X.; Zhao, L.; Gao, L.; Xie, Z.; Zhang, J. Review of Transport Phenomena and Popular Modelling Approaches in Membrane Distillation. Membranes 2021, 11, 122. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-G.; Kim, Y.-D.; Kim, W.-S.; Francis, L.; Amy, G.; Ghaffour, N. Performance modeling of direct contact membrane distillation (DCMD) seawater desalination process using a commercial composite membrane. J. Membr. Sci. 2015, 478, 85–95. [Google Scholar] [CrossRef]
- Lawson, K.; Lloyd, D. Membrane distillation. J. Membr. Sci. 1997, 124, 1–25. [Google Scholar] [CrossRef]
- Schofield, R.W.; Fane, A.G.; Fell, C.J.D. Gas and vapor transport through microporous membranes. I. Knudsen-Poiseuille transition. J. Membr. Sci. 1990, 53, 159–171. [Google Scholar] [CrossRef]
- Iversen, S.; Bhatia, V.; Dam-Johansen, K.; Jonsson, G. Characterization of microporous membranes for use in membrane contactors. J. Membr. Sci. 1997, 130, 205–217. [Google Scholar] [CrossRef]
- Izquierdo-Gil, M.; Garcia-Payo, M.; Pineda, C.F. Air gab membrane distillation of sucrose aqueous solutions. J. Membr. Sci. 1999, 155, 291–307. [Google Scholar] [CrossRef]
- Warner, S.B. Fiber Science; Princeton-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Ho, C.D.; Chen, L.; Lim, J.W.; Lin, P.-H.; Lu, P.-T. Distillate flux enhancement of direct contact membrane distillation modules with inserting cross-diagonal carbon-fiber spacers. Membranes 2021, 11, 973. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A. Heat transport and membrane distillation coefficients in direct contact membrane distillation. J. Membr. Sci. 2003, 212, 177–193. [Google Scholar] [CrossRef]
- Welty, J.R.; Wicks, C.E.; Wilson, R.E. Fundamentals of Momentum, Heat, and Mass Transfer, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Kakac, S.; Shah, R.K.; Aung, W. Handbook of Single-Phase Convective Heat Transfer; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Shakaib, M.; Hasani, S.; Ahmed, I.; Yunus, R.M. A CFD study on the effect of spacer orientation on temperature polarization in membrane distillation modules. Desalination 2012, 284, 332–340. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]





| Empty Channel | 2 mm | 3 mm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 40 | 6.67 | 0.40 | 0.43 | 7.80 | 0.43 | 6.42 | 0.42 | 5.37 | 0.42 | 4.35 |
| 8.33 | 0.48 | 0.53 | 10.2 | 0.52 | 8.40 | 0.52 | 6.85 | 0.51 | 5.11 | |
| 11.7 | 0.53 | 0.59 | 11.9 | 0.58 | 10.3 | 0.57 | 8.01 | 0.56 | 5.94 | |
| 15.0 | 0.55 | 0.63 | 12.7 | 0.62 | 11.4 | 0.60 | 8.77 | 0.59 | 6.35 | |
| 45 | 6.67 | 0.54 | 0.59 | 8.28 | 0.58 | 7.07 | 0.57 | 5.66 | 0.57 | 4.77 |
| 8.33 | 0.66 | 0.73 | 10.7 | 0.72 | 9.19 | 0.71 | 7.66 | 0.70 | 5.62 | |
| 11.7 | 0.72 | 0.81 | 12.7 | 0.80 | 11.0 | 0.78 | 8.91 | 0.77 | 6.66 | |
| 15.0 | 0.76 | 0.87 | 13.9 | 0.86 | 12.4 | 0.83 | 9.48 | 0.82 | 7.20 | |
| 50 | 6.67 | 0.69 | 0.75 | 8.74 | 0.74 | 7.76 | 0.73 | 6.26 | 0.72 | 5.00 |
| 8.33 | 0.84 | 0.94 | 11.5 | 0.92 | 10.1 | 0.91 | 8.56 | 0.89 | 6.09 | |
| 11.7 | 0.92 | 1.05 | 14.0 | 1.03 | 11.8 | 1.01 | 10.0 | 0.99 | 7.21 | |
| 15.0 | 0.97 | 1.12 | 14.8 | 1.10 | 13.1 | 1.08 | 10.6 | 1.05 | 7.68 | |
| 55 | 6.67 | 0.83 | 0.92 | 9.93 | 0.90 | 8.23 | 0.89 | 6.96 | 0.88 | 5.30 |
| 8.33 | 1.02 | 1.15 | 12.7 | 1.13 | 10.6 | 1.12 | 9.02 | 1.09 | 6.68 | |
| 11.7 | 1.12 | 1.29 | 14.6 | 1.26 | 12.4 | 1.24 | 10.5 | 1.21 | 7.72 | |
| 15.0 | 1.19 | 1.37 | 15.6 | 1.35 | 13.6 | 1.32 | 11.0 | 1.29 | 8.16 | |
| 2 mm | 3 mm | ||||
|---|---|---|---|---|---|
| 40 | 6.67 | 0.18 | 0.15 | 0.13 | 0.11 |
| 8.33 | 0.23 | 0.20 | 0.16 | 0.13 | |
| 11.7 | 0.27 | 0.24 | 0.19 | 0.15 | |
| 15.0 | 0.29 | 0.26 | 0.21 | 0.16 | |
| 45 | 6.67 | 0.19 | 0.17 | 0.14 | 0.12 |
| 8.33 | 0.25 | 0.22 | 0.18 | 0.14 | |
| 11.7 | 0.29 | 0.26 | 0.21 | 0.17 | |
| 15.0 | 0.31 | 0.28 | 0.22 | 0.18 | |
| 50 | 6.67 | 0.20 | 0.19 | 0.15 | 0.13 |
| 8.33 | 0.27 | 0.24 | 0.20 | 0.15 | |
| 11.7 | 0.32 | 0.28 | 0.24 | 0.18 | |
| 15.0 | 0.33 | 0.30 | 0.25 | 0.19 | |
| 55 | 6.67 | 0.23 | 0.20 | 0.17 | 0.14 |
| 8.33 | 0.29 | 0.25 | 0.22 | 0.17 | |
| 11.7 | 0.33 | 0.29 | 0.25 | 0.19 | |
| 15.0 | 0.35 | 0.32 | 0.26 | 0.20 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, C.-D.; Chen, L.; Yang, Y.-L.; Chen, S.-T.; Lim, J.W.; Chen, Z.-Z. Permeate Flux Enhancement in Air Gap Membrane Distillation Modules with Inserting Λ-Ribs Carbon-Fiber Open Slots. Membranes 2023, 13, 66. https://doi.org/10.3390/membranes13010066
Ho C-D, Chen L, Yang Y-L, Chen S-T, Lim JW, Chen Z-Z. Permeate Flux Enhancement in Air Gap Membrane Distillation Modules with Inserting Λ-Ribs Carbon-Fiber Open Slots. Membranes. 2023; 13(1):66. https://doi.org/10.3390/membranes13010066
Chicago/Turabian StyleHo, Chii-Dong, Luke Chen, Yan-Ling Yang, Shih-Ting Chen, Jun Wei Lim, and Zheng-Zhong Chen. 2023. "Permeate Flux Enhancement in Air Gap Membrane Distillation Modules with Inserting Λ-Ribs Carbon-Fiber Open Slots" Membranes 13, no. 1: 66. https://doi.org/10.3390/membranes13010066
APA StyleHo, C.-D., Chen, L., Yang, Y.-L., Chen, S.-T., Lim, J. W., & Chen, Z.-Z. (2023). Permeate Flux Enhancement in Air Gap Membrane Distillation Modules with Inserting Λ-Ribs Carbon-Fiber Open Slots. Membranes, 13(1), 66. https://doi.org/10.3390/membranes13010066









