Abstract
Chabazite (CHA)-type zeolite membranes are a potential material for CO2 separations because of their small pore aperture, large pore volume, and low aluminum content. In this study, the permeation and separation properties were evaluated using a molecular simulation technique with a focus on improving the CO2 separation performance. The adsorption isotherms of CO2 and CH4 on CHA-type zeolite with Si/Al = 18.2 were predicted by grand canonical Monte Carlo, and the diffusivities in zeolite micropores were simulated by molecular dynamics. The CO2 separation performance of the CHA-type zeolite membrane was estimated by a Maxwell–Stefan equation, accounting for mass transfer through the support tube. The results indicated that the permeances of CO2 and CH4 were influenced mainly by the porosity of the support, with the CO2 permeance reduced due to preferential adsorption with increasing pressure drop. In contrast, it was important for estimation of the CH4 permeance to predict the amounts of adsorbed CH4. Using molecular simulation and the Maxwell–Stefan equation is shown to be a useful technique for estimating the permeation properties of zeolite membranes, although some problems such as predicting accurate adsorption terms remain.
1. Introduction
Zeolite membranes separate via molecular sieving and selective adsorption, which makes them a promising candidate technology for energy-efficient separations. Geus et al. successfully formed polycrystalline MFI-type zeolite layer on a porous substrate and investigated the permeation properties of hydrocarbons [1,2,3,4,5]. In the 1990s, Kita and coworkers developed a commercially available LTA-type zeolite membrane and applied it to dehydration of ethanol [6,7,8].
Although it is well known that polymeric membranes are currently employed [9,10,11,12], zeolite membranes exhibit excellent dehydration performance. FAU, DDR, AEI, and CHA-type zeolite membranes show high CO2 separation performance [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Kusakabe et al. developed the FAU-type zeolite membranes, and the influence of the membrane composition and cations species on the adsorption and diffusion properties of CO2 in the zeolite were investigated to improve the CO2 separation performance [13,14,15,16]. As a result, the CO2 permeance and CO2/N2 permeance ratio were ca. 10−6 mol m−2 s−1 Pa−1 and 40–100, respectively. Noble and coworkers investigated a SAPO-34 membrane and applied it to CO2 separation from CH4 [17,18,19]. The CO2 permeance and CO2/CH4 permeance ratio were ca. 10−6 mol m−2 s−1 Pa−1 and 80–170, respectively. DDR-type zeolite membranes [20,21] exhibited a higher CO2/CH4 permeance ratio of 200–2000, although the CO2 permeance was lower than those of FAU and CHA-type zeolite membranes. Recently, we have developed a high-silica CHA-type zeolite membrane (Si/Al = 18) for CO2 separation [26,27,28]. The CO2 permeance and CO2/CH4 permeance ratio were ca. 5 × 10−7 mol m−2 s−1 Pa−1 and 200, respectively. This is important for improving the CO2 separation performance to understand the permeation mechanisms in zeolite membranes.
There are many reports about the permeation and separation mechanisms in zeolite membranes [3,4,5,14,15,16]. Since CO2 and hydrocarbon molecules adsorb onto zeolite strongly, the adsorbed molecules move to a neighboring adsorption site according to the concentration gradient across the membrane. The permeation phenomenon due to the surface diffusion is quantitatively described by the Maxwell–Stefan equation [3,4,5]. Many studies have predicted the permeation and separation properties of zeolite membranes from the adsorption and diffusion properties of single gases. Bakker et al. checked that the equation is suitable for expression of the single gas permeation properties through a silicalite-1 membrane [4]. Additionally, van den Broeke et al. applied the equation to separation of binary hydrocarbon mixtures [5], and the gas permeation properties for binary mixtures could be described using the adsorption and diffusion parameters obtained by single component gases.
The permeation and separation properties of zeolite membranes are explained by adsorption of molecules on zeolite and diffusion in zeolite channels. Both the adsorption and diffusion properties can be predicted by molecular simulation such as grand canonical Monte Carlo and molecular dynamics, respectively [29,30,31,32,33,34]. Vujic et al. reported the potential parameters applicable to many zeolites [33].
In this study, the CO2 separation performances of CHA-type zeolite membranes with Si/Al = 18 were predicted using the molecular simulation technique and Maxwell–Stefan equation to understand the permeation behavior in CHA-type zeolite membranes.
2. Theory
2.1. Molecular Simulation
The interaction between adsorbate and adsorbent atoms is described as the sum of interactions between bonded and nonbonded atoms as [33]:
The interaction between bonded atoms is calculated as the sum of bond-stretching and angle-bending as:
where kb and kθ are the force constants for bond-stretching and angle-bending, respectively. The interaction between nonbonded atom pair is calculated as the sum of van der Waals and coulomb interactions as:
where the depth of interaction ϕij and zero-interaction distance σij for the pair of different atoms are calculated as:
When two atoms are in the same structure and separated by three covalent bonds (known as a 1–4 interaction), the interaction is treated as a nonbonded interaction with scaling factor of 0.5. Nonbonded interactions are ignored for directly bonded atoms (1–2 interaction) and two atoms separated by two bonds (1–3 interaction) since they are included in the bond-stretching and angle-bending interactions.
2.2. Gas permeation through Zeolite Layer
Zeolite membranes are often prepared on porous supports, as shown in Figure 1. The molecules are transferred by the concentration gradient across the membrane.
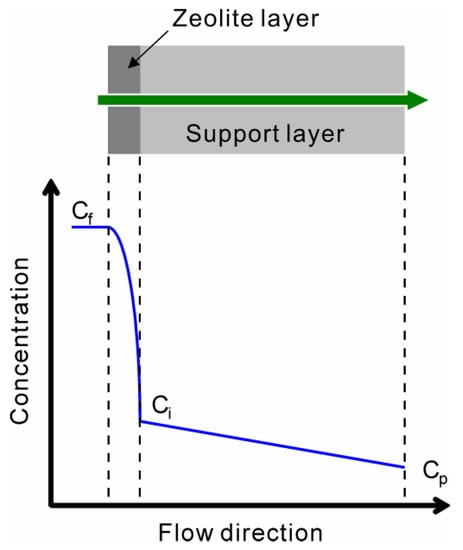
Figure 1.
Schematic illustration of concentration gradient across the zeolite membrane supported by porous substrate. Cf is the concentration in the feed, Cp is the concentration in the permeate, and Ci is the concentration at the interface of the zeolite and support layers.
In the zeolite layer, molecules adsorbed on the adsorption sites within zeolite channels, and then move to a neighboring site according to the concentration gradient. The permeation flux is described as [3,4,5]:
The elements of matrix B are calculated by:
where the mutual diffusivity can be approximated as:
When the adsorption isotherm is described by a Langmuir Equation (13), the elements of matrix Γ are described using Equation (14).
where δij = 1 for i = j, and δij = 0 for i ≠ j. The adsorption and diffusion parameters are summarized in Tables 2 and 3, respectively.
2.3. Mass Transfer in the Support Tube
In the porous support tube, the overall permeation flux is:
where L is the thickness of the support, and C is the concentration shown by:
where ε is the porosity of the support. The diffusivity in the porous support is estimated by the Fuller equation [4,35]:
where Mi is the molecular mass of component i and Vi is the diffusion volume of component i. The diffusion volumes of CO2 and CH4 were taken as 26.9 cm3 and 25.1 cm3, respectively [35].
3. Methods
3.1. Adsorption on Zeolites
The adsorption isotherms of CO2 and CH4 on the CHA-type zeolite were simulated by a grand canonical Monte Carlo (GCMC) technique using software (Biovia, Materials Studio 2021 Sorption). For the GCMC simulation, fugacity was applied to the canonical ensemble, and the number and location of molecules with the lowest potential energy were calculated probabilistically. The cutoff distance of the van der Waals interaction was 1.25 nm, and the Ewald summation method was used for the integration of the coulomb interaction. The total number of Monte Carlo cycles were 106, and the average of the final 105 steps were used as the simulation result. The fugacity was assumed to be equal to the pressure in this study since the difference between fugacity and pressure is less than 5% below 1 MPa.
Figure 2 shows the atomistic models of CO2, CH4, and CHA-type zeolite. The model of the CO2 molecule reported by Harris et al. [36] was used. This model can describe the gas–liquid coexistence curve including the critical point region. The carbon atom was connected to two oxygen atoms by chemical bonds 0.1149 nm long, and the bond-stretching was ignored (kb = 0). The original angle of O=C=O was 180°, and the force constant was kθ = 1236 kJ mol−1 rad−2. For CH4, the model reported by Siepman et al. [37] was used. The carbon atom was connected to four hydrogen atoms with bond lengths of 0.11 nm, and each H-C-H angle was 109.5°. Although the bond-stretching and angle-bending are ignored in this model (kb = kθ = 0), the gas–liquid coexistence curve can be expressed. The crystal structure of the CHA-type zeolite was imported from the IZA zeolite database [38]. The CHA-type zeolite model with a composition of Si91Al5Na5O192 was prepared by substituting Si atoms with Al atoms followed by introduction of Na+ cations by GCMC simulation. Table 1 lists the non-bonding interaction parameters for CO2, CH4, and zeolite. Vujic et al. reported that the adsorption of gases such as CO2 on CHA-type zeolite can be predicted with high accuracy by using these parameters [33].
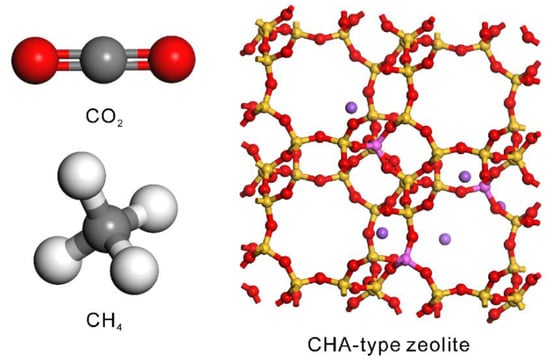
Figure 2.
Atomistic models of CO2, CH4, and CHA-type zeolite used in this study.

Table 1.
Nonbonding interaction parameters of CH4, CO2, and zeolite.
3.2. Diffusion in Zeolite
The self-diffusivities of CH4 and CO2 in CHA-type zeolite channels were also simulated by a molecular dynamic technique (Biovia, Materials Studio 2021 Forcite Plus). CH4 and CO2 molecules were adsorbed at 1 MPa by GCMC, and the molecular dynamic simulation was conducted with a time step of 2 fs. The total simulation time was 1 ns, and the mean square displacement every 10 ps was plotted against the simulation time. The self-diffusivity was calculated using the slope by the Einstein equation. The procedure was repeated 5 times and the average value taken as the diffusivity.
4. Results and Discussion
4.1. Adsorption Isotherms
Figure 3 shows the adsorption isotherms of CO2 and CH4 on the CHA-type zeolite with Si/Al = 18.2 at 253–473 K. The amounts of adsorbed CO2 at 253 K increased significantly at low pressures and was 6.0 mol kg−1 at 100 kPa. At higher pressures, in contrast, the increment became small, with 7.1 mol kg−1 adsorbed at 1000 kPa. This isotherm is typical for adsorption in micropores, and the relationship is described by the Langmuir equation (Equation (13)). The adsorption isotherms of CO2 became linear as temperature increased. A similar trend was observed for CH4. The estimated isotherms were calculated for each temperature using the simulated points by Equation (13) and are shown as lines in Figure 3. The agreement between simulated points and estimated isotherm suggests the Langmuir equation is applicable at 253–473 K. Furthermore, the adsorption isotherms of CO2 and CH4 on CHA-type zeolite have been reported by several groups [39,40] and our simulated isotherms agree well with their experimental data, which suggests that the potential parameters are reasonable for simulating the adsorption and diffusion behaviors of CO2 and CH4 for CHA-type zeolite.
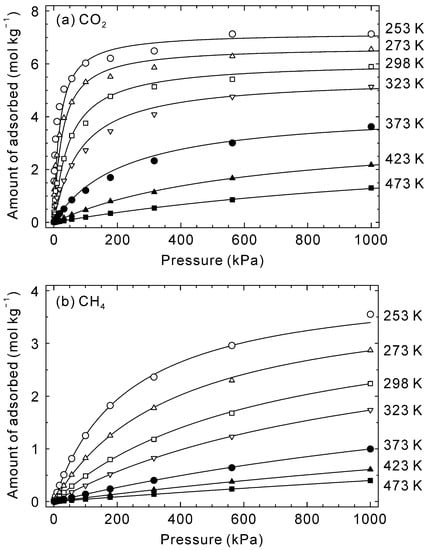
Figure 3.
Simulated adsorption isotherms of (a) CO2 and (b) CH4 on CHA-type zeolite with Si/Al = 18.2 at 253–473 K. Symbols describe the simulated data, and lines are calculated values by Equation (13) and Table 2.
Figure 4 shows the effect of temperature on the adsorption amounts at saturation and Langmuir constants of CO2 and CH4. Both the saturated adsorption amounts, a, and Langmuir constants, b, decreased with increasing temperature. An Arrhenius dependence was observed, as is typical for adsorption isotherms, with the temperature dependencies described by:
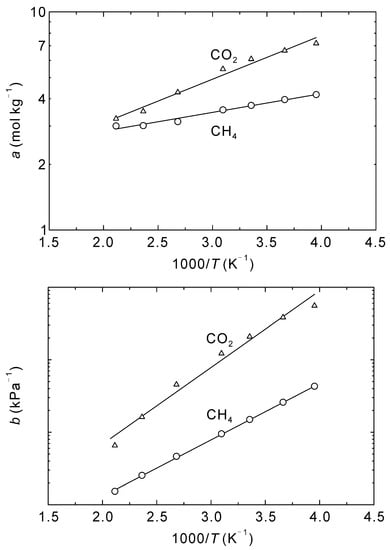
Figure 4.
Arrhenius plots of amount of adsorbed at saturation a and Langmuir constant b for CO2 and CH4 for the adsorption on CHA-type zeolite with Si/Al = 18.2.
The pre-exponential factors and activation energies are listed in Table 2. Assuming the heat of adsorption is equal to −(Ea + Eb), the heats of adsorption for CO2 and CH4 are 23.8 kJ mol−1 and 16.6 kJ mol−1, respectively. Maghsoudi et al. experimentally measured the heats of adsorption of CO2 and CH4 to be 21.0 kJ mol−1 and 17.1 kJ mol−1, respectively [40], which shows good agreement with the current work and further justifies the proposed methods for simulating the adsorption and diffusion behaviors of CO2 and CH4 in CHA-type zeolite.

Table 2.
Pre-exponential factors and activation energies of CO2 and CH4 for the adsorption on CHA-type zeolite with Si/Al = 18.2.
4.2. Diffusivities
Figure 5 shows the time courses in the mean square displacement of CO2 and CH4 at 298–473 K. Because the mean square displacements were linearly proportional to simulation time before 1 ns, longer diffusional times were not required. The diffusivities of CO2 and CH4 in the CHA-type zeolite were calculated as 1/6 of the slope [33], which resulted in temperature dependencies as reported in Figure 6. The diffusivities of CO2 and CH4 at 298 K were 3.9 × 10−10 m2 s−1 and 1.2 × 10−11 m2 s−1, respectively. The pore diameter of the CHA-type zeolite is 0.38 nm [38], which is identical to the molecular diameter of CH4 (0.38 nm [41]). In contrast, the molecular diameter of CO2 (0.33 nm [41]) is smaller than the pore diameter, which results in molecular sieving behavior with a CO2 diffusivity nearly an order of magnitude higher than CH4.
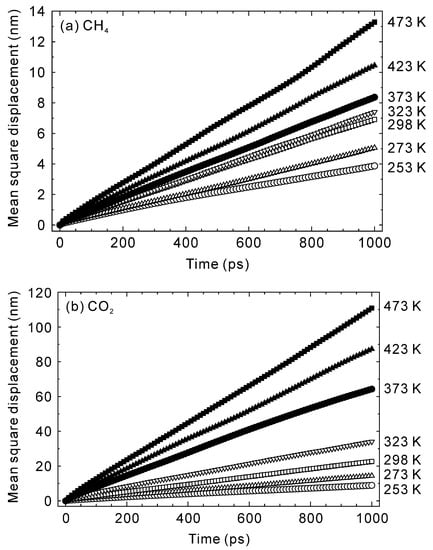
Figure 5.
Time courses in the mean square displacements of (a) CH4 and (b) CO2 at 253–473 K.
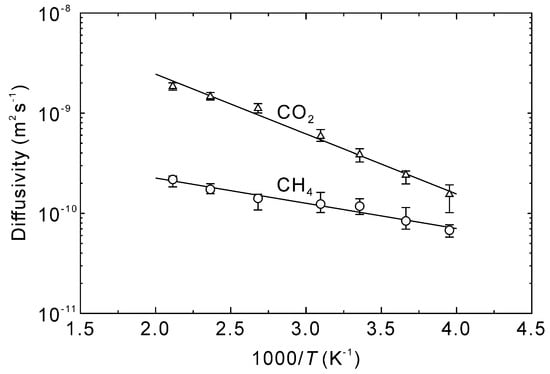
Figure 6.
Arrhenius plots of CO2 and CH4 diffusivities within the CHA-type zeolite channels.
Vujic et al. compared to the simulated CO2 diffusivities with those obtained by experiments [33], and the simulated diffusivities were twice higher than the experimental values for high silica zeolites. Krishna et al. [42] also simulated the diffusivities of CO2 and CH4 in all-silica CHA-type zeolite at 300 K. When the fugacities of CO2 and CH4 were 1 MPa, their diffusivities were ca. 4 × 10−10 m2 s−1 for CO2 and 8 × 10−11 m2 s−1 for CH4. The similarity in diffusivity measurements with the current work suggests aluminum and sodium do not have a significant effect on gas diffusivity. This is considered reasonable because only one aluminum and sodium atom are incorporated per cavity for a Si/Al ratio of 18.2, as shown in Figure 2.
The effect of temperature on the diffusivity is also described by the Arrhenius equation as follows:
The diffusivities at infinite temperature and activation energies of CO2 and CH4 are listed in Table 3. Sladek et al. [43] investigated the relationship between the diffusivity and heat of adsorption for physical and chemical adsorption species and concluded that the activation energy for diffusion was 0.45 times the heat of adsorption. This compares well with the current work wherein the activation energy of CO2 diffusivity is 0.48 times the heat of adsorption.

Table 3.
Diffusivities at infinite temperature and activation energies of CO2 and CH4 within CHA-type zeolite with Si/Al = 18.2.
4.3. CO2 Separation Performance
Figure 7 shows the influence of accounting the material transfer in porous support on the calculated permeation properties of CO2 and CH4 for the equimolar mixture at 323 K. When the polycrystalline zeolite layer was not supported by a substrate (self-standing membrane), the permeances of CO2 and CH4 were predicted to be 2.3 × 10−6 and 1.7 × 10−8 mol m−2 s−1 Pa−1, respectively. The permeances were reduced to 6.3 × 10−7 mol m−2 s−1 Pa−1 for CO2 and 5.0 × 10−9 mol m−2 s−1 Pa−1 for CH4 by supporting with the porous support (porosity = 35% and thickness = 0.3 mm). The reduction of CO2 permeance could be explained by the porosity of the support tube and pressure drop across the support (3.9 kPa). The calculated permeance of CO2 was almost identical to the experimental data [28]. However, the calculated CH4 permeance was higher than the experimental value. Since the amounts of adsorbed CO2 and CH4 were calculated using the extended Langmuir Equation (13) in this study, it is considered that the concentration gradient of CH4 across the polycrystalline zeolite layer was estimated to be high. As a result, the higher CH4 permeance was obtained compared to the experiment.
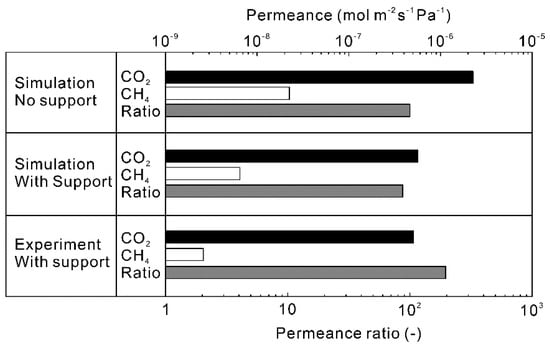
Figure 7.
Comparison of simulated permeation properties of the CHA-type zeolite membrane with Si/Al = 18.2 to experimental results [28]. The permeation properties were calculated at CO2 concentration = 50 vol%, total pressure = 300 kPa, and temperature = 323 K. The thickness of zeolite layer was 5 μm, and the pore size, porosity and thickness of the support tube were 150 nm, 35% and 0.3 mm [24].
Figure 8 shows the effect of temperature on the estimated permeation properties of CO2 and CH4 for an equimolar mixture. The permeances of CO2 and CH4 at 253 K were 3.3 × 10−7 and 1.8 × 10−9 mol m−2 s−1 Pa−1, respectively, with a resultant CO2/CH4 permeance ratio of 190. The CO2 permeance increased with increasing temperature until reaching a maximum at 323 K and then decreasing with further rising temperatures. As a result, the CO2 permeance decreased to 1.5 × 10−7 mol m−2 s−1 Pa−1 at 473 K, with the permeance ratio also decreasing to 38. Notably, the simulated permeances followed similar trends as the experimental data and the permeances at 473 K were nearly identical. This convergence is because the effect of preferential adsorption was marginal at 473 K compared to lower temperatures, which suggests accurate prediction of permeation properties requires accurate estimates of adsorption amounts.
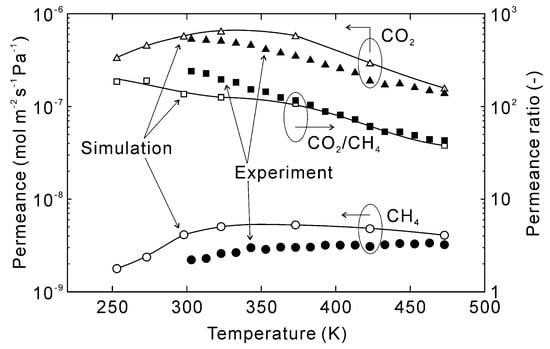
Figure 8.
Effect of temperature on the permeation properties of the CHA-type zeolite membrane with Si/Al = 18.2. The permeation properties were calculated at CO2 concentration = 50 vol% and total pressure = 300 kPa, experimental data were taken from [28].
Figure 9 shows the influence of the CO2 concentration on the permeation properties of CO2 and CH4 at 303 K. The pure gas CO2 permeance was estimated to be 3.8 × 10−7 mol m−2 s−1 Pa−1 and slightly increased with decreasing CO2 concentration until around 40%. However, below 40% CO2 the CO2 permeance increased significantly. This was due to a relative change in the permeance versus partial pressure difference between feed and permeate streams. At 40% CO2, the partial pressures of CO2 on the feed and permeate sides were 120 kPa and 96 kPa, respectively, with a permeate flux of 1.5 × 10−2 mol m−2 s−1. At 30% CO2 concentration, the partial pressures and permeate flux were 90 kPa, 84 kPa, and 6.0 × 10−3 mol m−2 s−1, respectively. This means the relative permeate flux at 30% CO2 compared to 40% CO2 was 1/2.5, whereas the partial pressure difference was 1/4. As a result, the CO2 permeance increased below 40% CO2. For all conditions, the estimated CH4 permeance was higher than the experimental data, as discussed in Figure 7 and Figure 8, which is the cause of the lower CO2/CH4 permeance ratio.
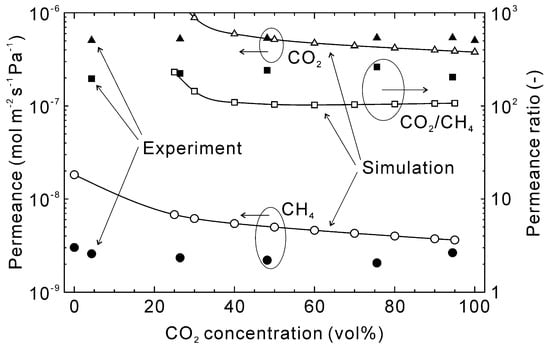
Figure 9.
Influence of the CO2 concentration on the permeation properties of the CHA-type zeolite membrane with Si/Al = 18.2 at 303 K. The permeation properties were calculated at the total pressure of 300 kPa, and experimental data were taken from [28].
Figure 10 shows the influence of the total pressure on the permeation properties of CO2 and CH4 at 303 K. When the total pressure was 200 kPa, the estimated permeances of CO2 and CH4 were 6.8 × 10−7 and 5.8 × 10−9 mol m−2 s−1 Pa−1, respectively, with a CO2/CH4 permeance ratio of 120. The permeances decreased with increasing total pressure and at 1000 kPa were 2.9 × 10−7 for CO2 and 2.4 × 10−9 mol m−2 s−1 Pa−1 for CH4. The decrease was calculated to be similar for both gases so the permeance ratio was nearly independent of total pressure.
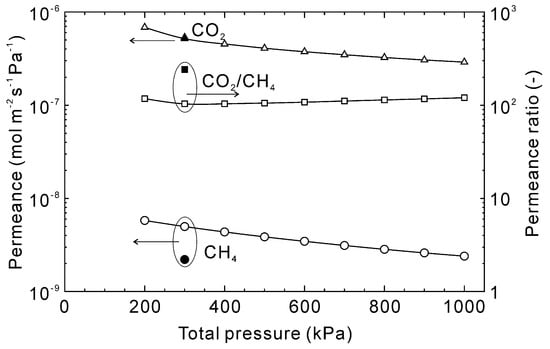
Figure 10.
Influence of total pressure on the permeation properties through the CHA-type zeolite membrane with Si/Al = 18.2 at 303 K. The permeation properties were calculated at a CO2 concentration of 50 vol%, and experimental data were taken from [28].
5. Conclusions
In this study, the permeation and separation properties of a CHA-type zeolite membrane were evaluated for improving the CO2 separation performance. The adsorption isotherms of CO2 and CH4 on CHA-type zeolite with Si/Al = 18.2 were predicted by grand canonical Monte Carlo, and the diffusivities in zeolite micropores were simulated by molecular dynamics. The CO2 separation performance of the CHA-type zeolite membrane was estimated by a Maxwell–Stefan equation, accounting for mass transfer through the support tube. In this study, the influences of the support tube, temperature, CO2 concentration, and total pressure on the permeation properties were calculated, and the estimated permeation properties were compared with experimental data [24]. The estimated CO2 permeance agreed well with the experimental results due to the inclusion of the effect of the support tube. However, the estimated CH4 permeance was slightly overestimated, suggesting that better predictions of the amount of adsorbed CH4 on both the sides of the membrane must be made to obtain more accurate results.
Author Contributions
Conceptualization, Y.H.; methodology, Y.H.; software, Y.H.; validation, Y.H.; formal analysis, Y.H.; investigation, M.N. and C.A.; resources, Y.H.; data curation, Y.H.; writing—original draft preparation, Y.H.; writing—review and editing, A.I. and S.-T.B.L.; visualization, Y.H.; supervision, Y.H.; project administration, Y.H.; funding acquisition, Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| a | Amount adsorbed at saturation (mol kg−1) |
| b | Langmuir constant (Pa−1) |
| B | Mobility as defined by Equation (11) |
| C | Concentration (mol m−3) |
| D | Diffusivity (m2 s−1) |
| E | Activation energy (kJ mol−1) |
| J | Permeation flux (mol m−2 s−1 Pa−1) |
| kb | Force constant for bond-stretching (kJ mol−1 m−2) |
| kθ | Force constant for angle-bending (kJ mol−1 rad−2) |
| L | Thickness (m) |
| M | Molecular mass (g mol−1) |
| p | Partial pressure (Pa) |
| Q | Partial atomic charge (e) |
| q | Amount of adsorbed (mol kg−1) |
| r | Distance (m) |
| R | Gas constant (=8.314 J K−1 mol−1) |
| T | Temperature (K) |
| V | Diffusion volume (cm3) |
| Symbols | |
| Γ | Thermodynamic factor defined by Equation (14) |
| δ | Kronecker delta (dimensionless) |
| ε | Porosity (dimensionless) |
| ε0 | Vacuum permittivity (=8.85 × 10−12 F m−1) |
| Φ | Interaction potential energy (kJ mol−1) |
| ϕ | Depth of potential (kJ mol−1) |
| θ | Binding angle (rad) |
| Θ | Surface coverage (dimensionless) |
| ρ | Density of zeolite (kg m−3) |
| σ | Distance at zero-potential energy (m) |
References
- Geus, E.R.; den Ester, M.J.; van Bekkum, H. Synthesis and characterization of zeolite (MFI) membranes on porous ceramic supports. J. Chem. Soc. Faraday Trans. 1992, 80, 3101–3109. [Google Scholar] [CrossRef]
- Geus, E.R.; van Bekkum, H.; Bakker, W.J.W.; Moulijn, J.A. High-temperature stainless steel supported zeolite (MFI) membranes: Preparation, module construction, and permeation experiments. Microp. Mater. 1993, 1, 131–147. [Google Scholar] [CrossRef]
- Kapteijn, F.; Bakker, W.J.W.; Zheng, G.; Poppe, J.; Moulijn, J.A. Permeation and separation of light hydrocarbons through a silicalite-1 membrane: Application of the generalized Maxwell-Stefan equations. Chem. Eng. J. 1995, 57, 145–153. [Google Scholar]
- Bakker, W.J.W.; van den Broeke, L.P.J.; Kapteijn, F.; Moulijn, J.A. Temperature dependence of one-component permeation through a silicalite-1 membrane. AIChE J. 1997, 43, 2203–2214. [Google Scholar] [CrossRef]
- van den Broeke, L.P.J.; Bakker, W.J.W.; Kapteijn, F.; Moulijn, J.A. Binary permeation through a silicalite-1 membrane. AIChE J. 1999, 45, 976–985. [Google Scholar] [CrossRef]
- Okamoto, K.; Kita, H.; Horii, K.; Tanaka, K. Zeolite NaA membrane: Permeation single-gas permeation, and pervaporation and vapor permeation of water/organic liquid mixtures. Ind. Eng. Chem. Res. 2001, 40, 163–175. [Google Scholar] [CrossRef]
- Kondo, M.; Komori, M.; Kita, H.; Okamoto, K. Tubular-type pervaporation module with zeolite NaA membrane. J. Membr. Sci. 1997, 133, 133–141. [Google Scholar] [CrossRef]
- Morigami, Y.; Kondo, M.; Abe, J.; Kita, H.; Okamoto, K. The first large-scale pervaporation plant using tubular-type module with zeolite NaA membrane. Sep. Purif. Technol. 2001, 25, 251–260. [Google Scholar] [CrossRef]
- Parasetya, N.; Himma, N.F.; Sutrisna, P.D.; Wenten, I.G. A review on emerging organic-containing microporous material membranes for carbon capture and separation. Chem. Eng. Sci. 2020, 391, 123575. [Google Scholar] [CrossRef]
- Han, Y.; Ho, W.S.W. Polymeric membranes for CO2 separation and capture. J. Membr. Sci. 2021, 628, 119244. [Google Scholar] [CrossRef]
- Hu, L.; Clark, K.; Alebrahim, T.; Lin, H. Mixed matrix membranes for post-combustion carbon capture: From materials design to membrane engineering. J. Membr. Sci. 2022, 644, 120140. [Google Scholar] [CrossRef]
- Usman, M.; Khan, M.Y.; Anjum, T.; Khan, A.L.; Hoque, B.; Helal, A.; Hakeem, A.S.; Al-Maythalony, B.A. Controlled covalent functionalization of ZIF-90 for selective CO2 capture and separation. Membranes 2022, 12, 1055. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, Y.; Tanak, T.; Watanabe, K.; Jeong, B.H.; Kusakabe, K.; Morooka, S. Separation of CO2-CH4 and CO2-N2 systems using ion-exchanged FAU-type zeolite membranes with different Si/Al ratios. Korean J. Chem. Eng. 2002, 19, 309–313. [Google Scholar] [CrossRef]
- Kusakabe, K.; Kuroda, T.; Uchino, K.; Hasegawa, Y.; Morooka, S. Gas permeation properties of ion-exchanged faujasite-type zeolite membranes. AIChE J. 1999, 45, 1220–1226. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Watanabe, K.; Kusakabe, K.; Morooka, S. The separation of CO2 using T-type zeolite membranes ion-exchanged with alkali metal cations. Sep. Purif. Technol. 2001, 22–23, 319–325. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Kusakabe, K.; Morooka, S. Effect of temperature on the gas permeation properties of NaY-type zeolite formed on the inner surface of a porous support tube. Chem. Eng. Sci. 2001, 56, 4273–4281. [Google Scholar] [CrossRef]
- Poshusta, J.C.; Tuan, V.A.; Falconer, J.L.; Noble, R.D. Synthesis and permeation properties of SAPO-34 tubular membranes. Ind. Eng. Chem. Res. 1998, 37, 3924–3929. [Google Scholar] [CrossRef]
- Poshusta, J.C.; Tuan, V.A.; Pape, E.A.; Noble, R.D.; Falconer, J.L. Separation of light gas mixtures using SAPO-34 membranes. AIChE J. 2000, 46, 779–789. [Google Scholar] [CrossRef]
- Crreon, M.A.; Li, S.; Falconer, J.L.; Noble, R.D. Alumina-supported SAPO-34 membranes for CO2/CH4 separation. J. Am. Chem. Soc. 2008, 130, 5412–5413. [Google Scholar] [CrossRef]
- Tomita, T.; Nakayama, K.; Sakai, H. Gas separation characteristics of RRR type zeolite membrane. Micropor. Mesopor. Mater. 2004, 68, 71–75. [Google Scholar] [CrossRef]
- van den Bergh, J.; Zhu, W.; Gascon, J.; Moulijn, J.A.; Kapteijn, F. Separation and permeation characteristics of a DD3R zeolite membrane. J. Membr. Sci. 2008, 316, 35–45. [Google Scholar] [CrossRef]
- Wang, B.; Hu, N.; Wang, H.; Zheng, Y.; Zhou, R. Improved AlPO-18 membranes for light gas separation. J. Mater. Chem. A 2015, 3, 12205–12212. [Google Scholar] [CrossRef]
- Wang, B.; Gao, F.; Zhang, F.; Xing, W.; Zhou, R. Highly permeable and oriented AlPO-18 membrane prepared using directly synthesized nanosheets for CO2/CH4 separation. J. Mater. Chem. A 2019, 7, 13164–13172. [Google Scholar] [CrossRef]
- Zhan, T.; Wu, T.; Shi, Y.; Chen, X.; Li, Y.; Zhu, M.; Kumakiri, I.; Chen, X.; Kita, H. Influence of synthesis parameters on the preparation of AlPO-18 membranes by single DIPEA for CO2/CH4 separation. J. Membr. Sci. 2020, 601, 117853. [Google Scholar] [CrossRef]
- Imasaka, S.; Itakura, M.; Yano, K.; Fujita, S.; Okada, M.; Hasegawa, Y.; Abe, C.; Araki, S.; Yamamoto, H. Rapid preparation of high-silica CHA-type zeolite membranes and their separation properties. Sep. Purif. Technol. 2018, 199, 298–303. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Abe, C.; Ikeda, T.; Sato, K.; Imasaka, S.; Itakura, M.; Yano, K. Influence of the synthesis parameters on the morphology and dehydration performance of high-silica chabazite membranes. Adv. Porus Mater. 2016, 4, 134–143. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Abe, C.; Ikeda, A. Pervaporative dehydration of organic solvents using high-silica CHA-type zeolite membrane. Membranes 2021, 11, 229. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Abe, C.; Natsui, M.; Ikeda, A. Gas permeation properties of high-silica CHA-type zeolite membrane. Membranes 2021, 11, 249. [Google Scholar] [CrossRef]
- Talu, O.; Myers, A.L. Reference potentials for adsorption of helium, argon, methane, and krypton in high-silica zeolites. Colloids Surf. A 2001, 187–188, 83–93. [Google Scholar] [CrossRef]
- Bai, P.; Tsapatsis, M.; Siepmann, J.I. TraPPE-zeo: Transferable potentials for phase equilibria force field for all-silica zeolites. J. Phys. Chem. C 2013, 117, 24375–24387. [Google Scholar] [CrossRef]
- Rahmati, M.; Modarress, H. Selectivity of new siliceous zeolites for separation of methane and carbon dioxide by Monte Carlo simulation. Micropor. Mesopor. Mater. 2013, 176, 168–177. [Google Scholar] [CrossRef]
- Pham, T.D.; Xiong, R.; Dandler, S.I.; Lobo, R.F. Experimental and computational studies on the adsorption of CO2 and N2 on pure silica zeolites. Micropor. Mesopor. Mater. 2014, 185, 157–166. [Google Scholar] [CrossRef]
- Vujic, B.; Lyubartsev, A.P. Transferable forcefield for modelling of CO2, N2, O2, and Ar in all-silica and Na+ exchanged zeolites. Modelling Simul. Mater. Sci. Eng. 2016, 24, 045002. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Abe, C. Prediction of adsorption and diffusion behaviors of CO2 and CH4 in all-silica zeolites using molecular simulation. Membranes 2021, 11, 392. [Google Scholar] [CrossRef] [PubMed]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw Hill: New York, NY, USA, 2000. [Google Scholar]
- Harris, J.G.; Yung, K.H. Carbon dioxide’s liquid-vapor coexistence curve and critical properties as predicted by a simple molecular model. J. Phys. Chem. 1995, 99, 12021–12024. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Baerlocher, C.; McCusker, L.B.; Olson, D.H. Atlas of Zeolite Framework Types, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Pham, T.D.; Liu, Q.; Lobo, R.F. Carbon dioxide and nitrogen adsorption on cation exchanged SSZ-13 zeolites. Langmuir 2013, 29, 832–839. [Google Scholar] [CrossRef]
- Maghsoudi, H.; Soltanieh, M.; Bozorgzadeh, H.; Mohamadalizadeh, A. Adsorption isotherms and ideal selectivities of hydrogen sulfide and carbon dioxide over methane for the Si-CHA zeolite: Comparison of carbon dioxide and methane adsorption with the all-silica DD3R zeolite. Adsorption 2013, 19, 1045–1053. [Google Scholar] [CrossRef]
- Breck, D.W.D. Zeolite Molecular Sieves; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Krishna, R.; van Baten, J.M.; Garcia-Perez, E.; Calero, S. Diffusion of CH4 and CO2 in MFI, CHA and DDR zeolites. Chem. Phys. Lett. 2006, 429, 219–224. [Google Scholar] [CrossRef]
- Sladek, K.J.; Gilliland, E.R.; Baddour, R.F. Diffusion on surfaces. II. Correlation of diffusivities of physically and chemically adsorbed species. Ind. Eng. Chem. Fundam. 1974, 13, 100–105. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).