Comparison of Artificial Intelligence Control Strategies for a Peristaltically Pumped Low-Pressure Driven Membrane Process
Abstract
:1. Introduction
1.1. Modelling of Peristaltically Pumped Low-Pressure Driven Membrane Systems
1.2. Intelligent Control Approaches for Low-Pressure Membrane Systems
1.3. Selection of Study Case for Comparison of Control Approaches
2. Materials and Methods
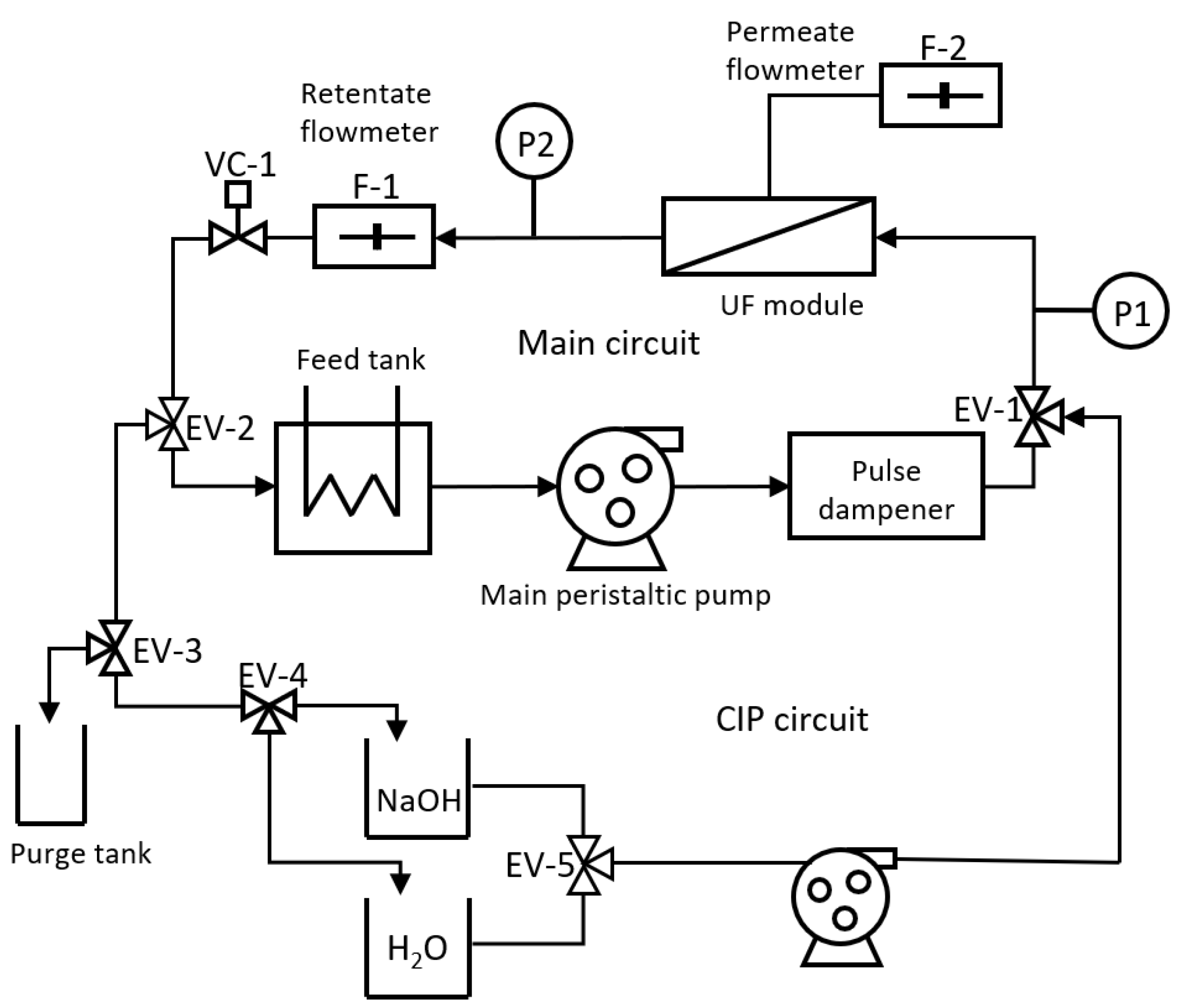
2.1. Experimental Setup
2.2. Experimental Conditions
2.3. Control Strategies
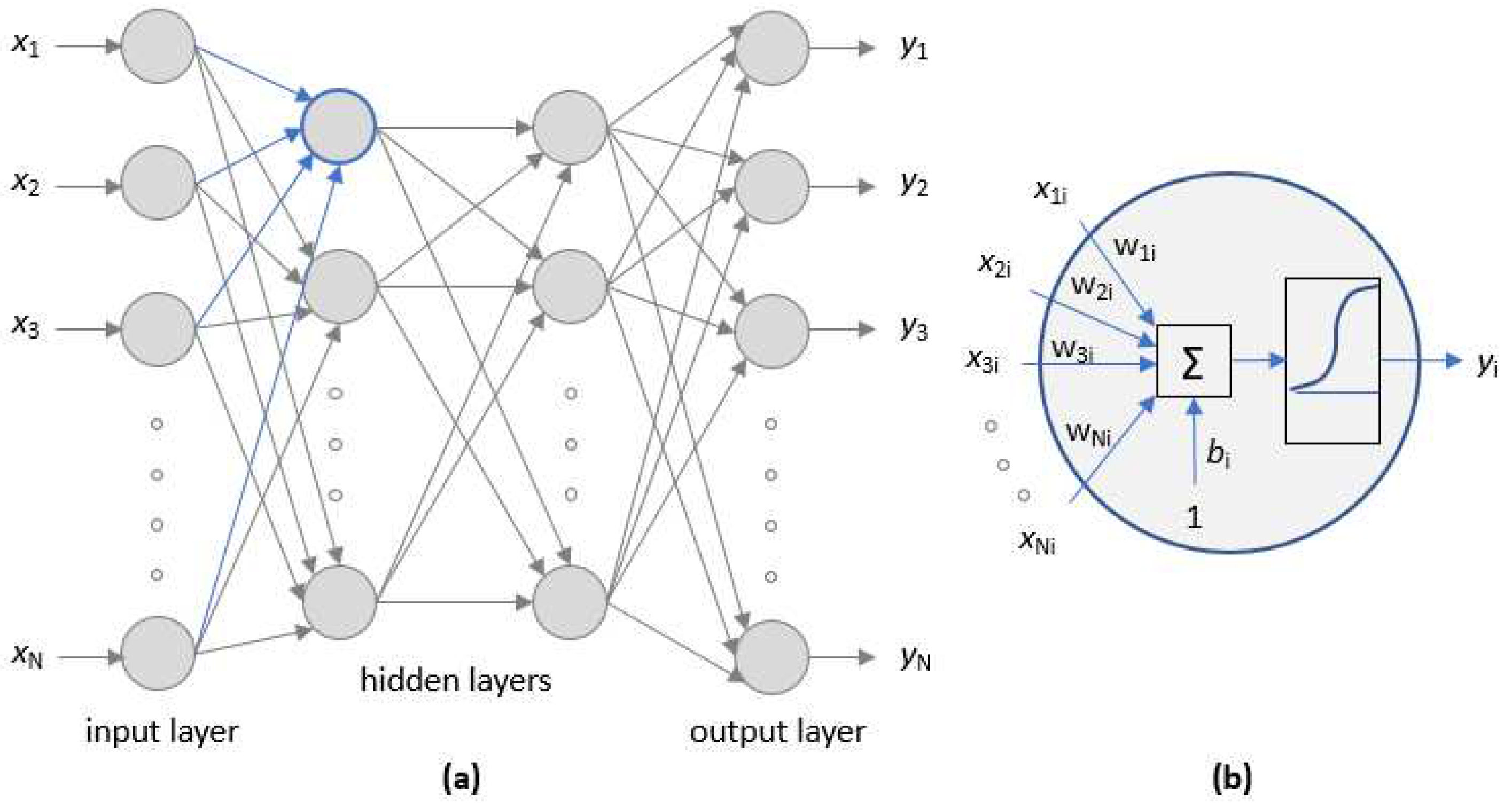
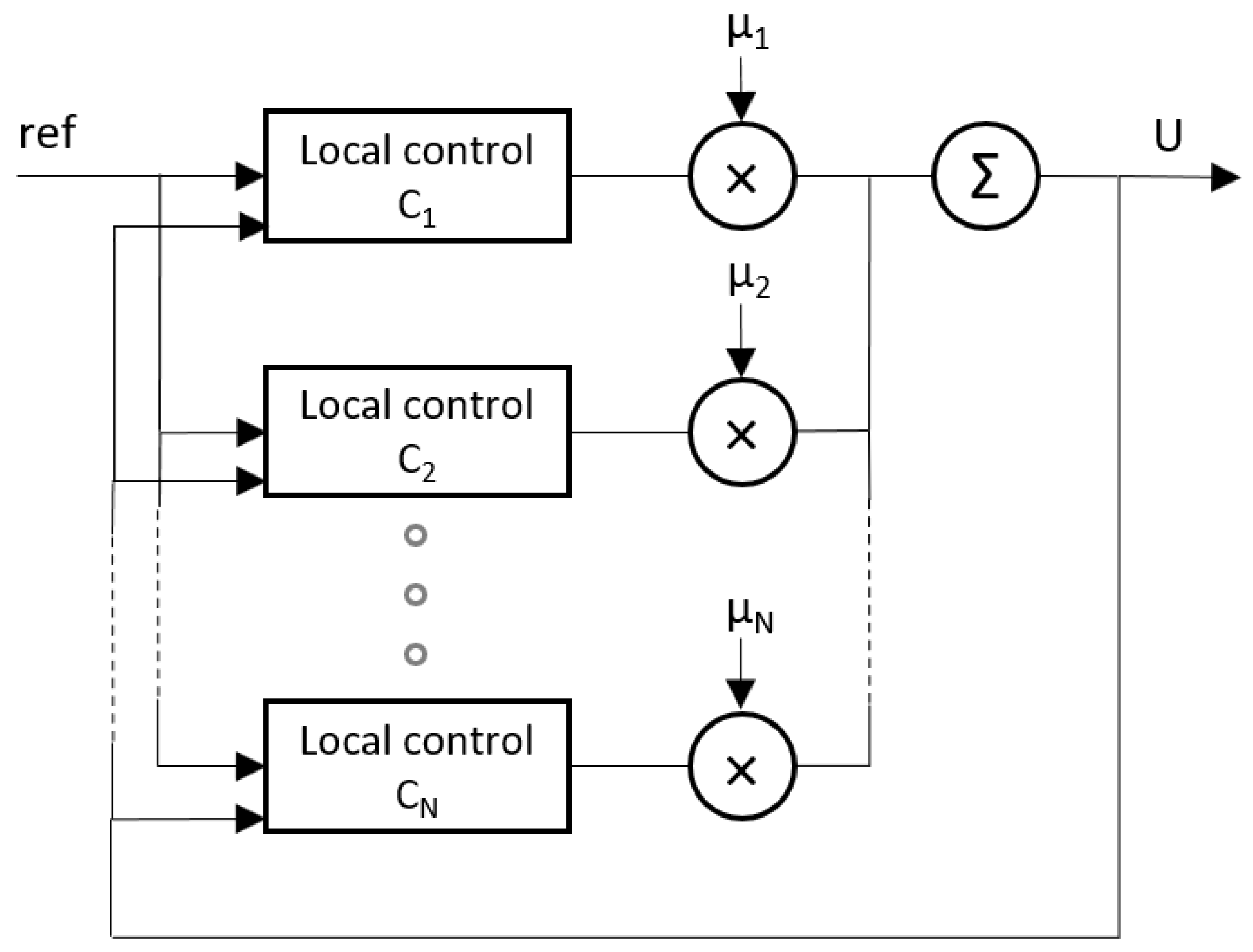
2.3.1. Control Based on Artificial Neural Networks (ANN)
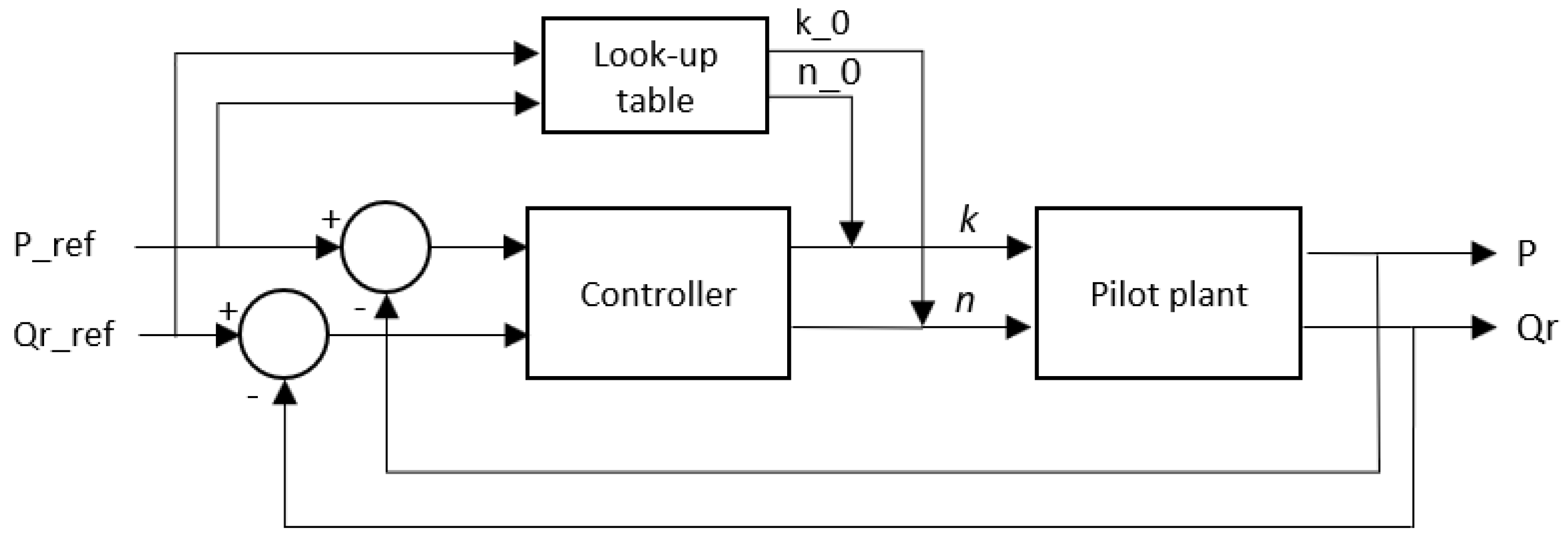
2.3.2. Expert Control Based on Fuzzy Logic
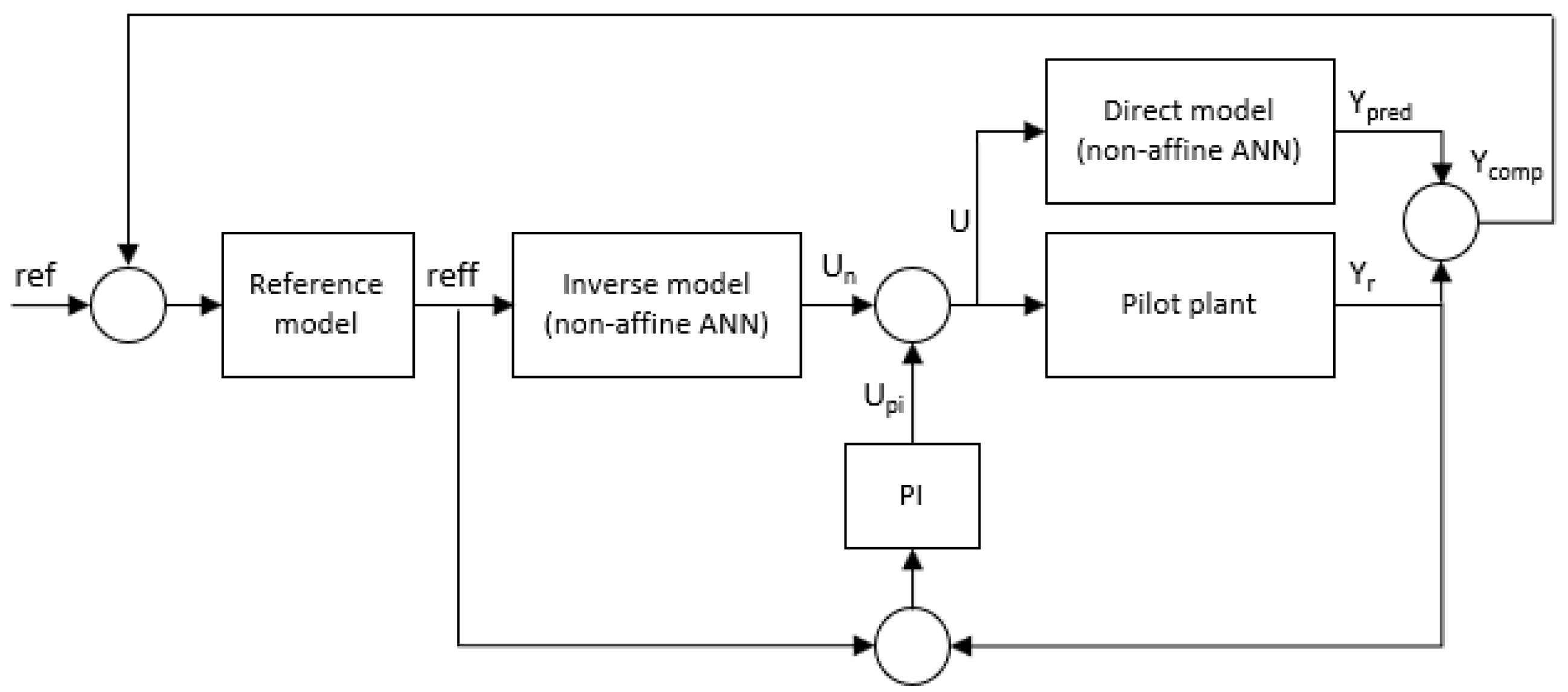
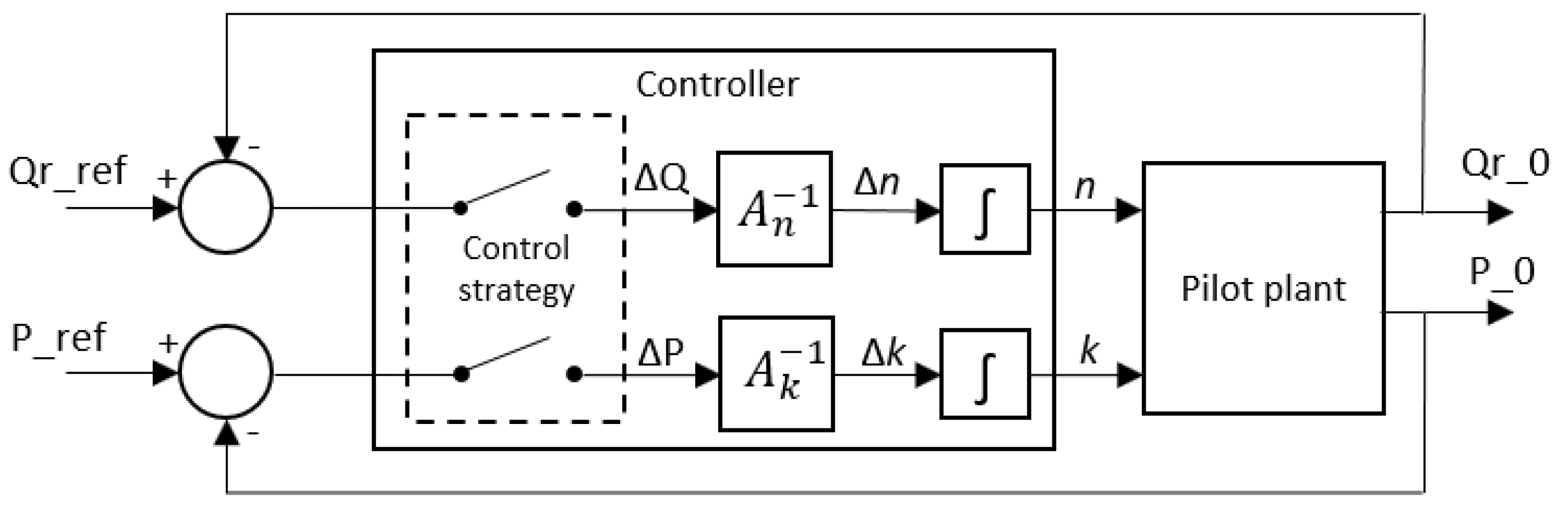
2.3.3. Control by Inverse Local Models
3. Results and Discussion
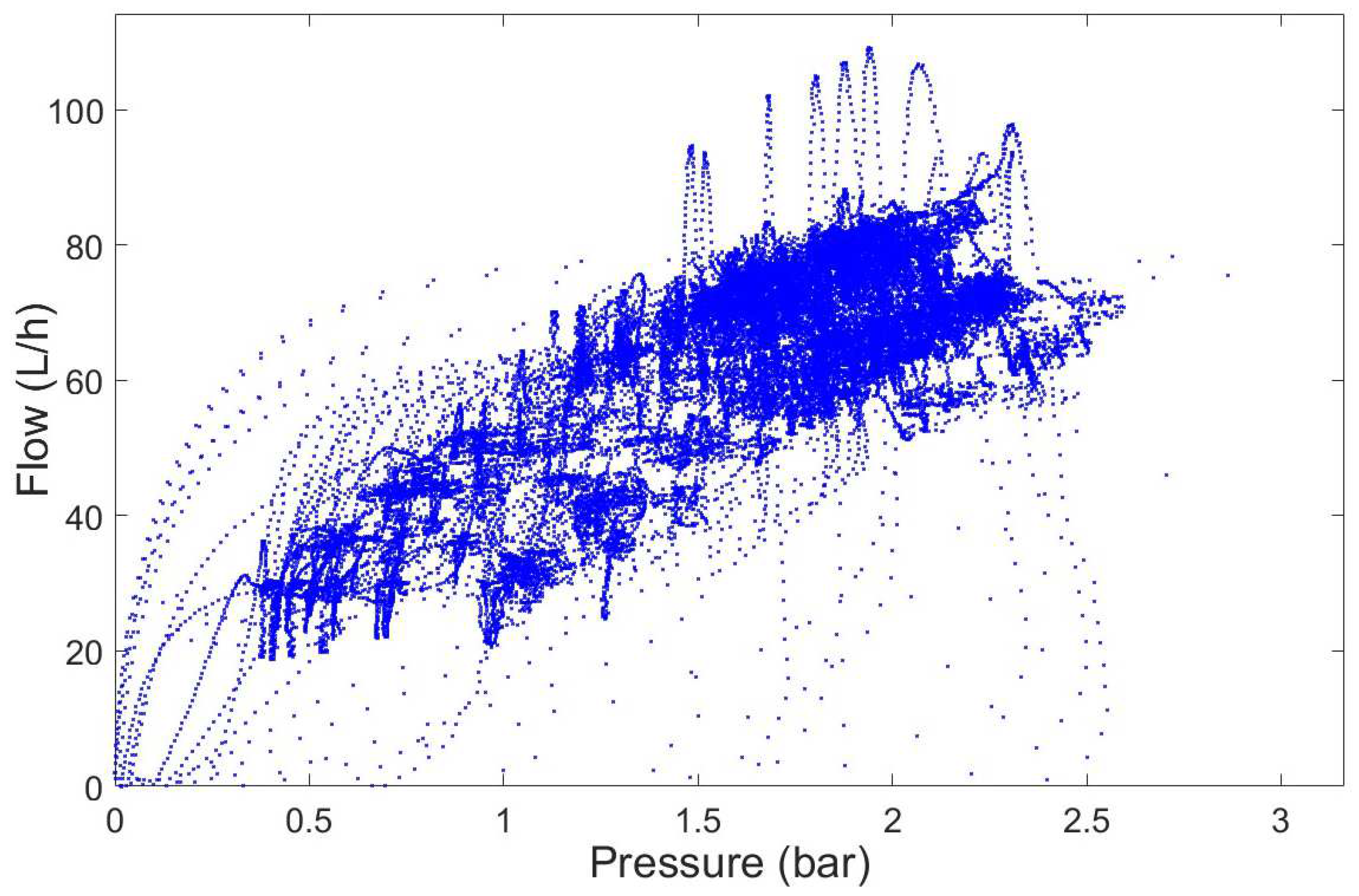
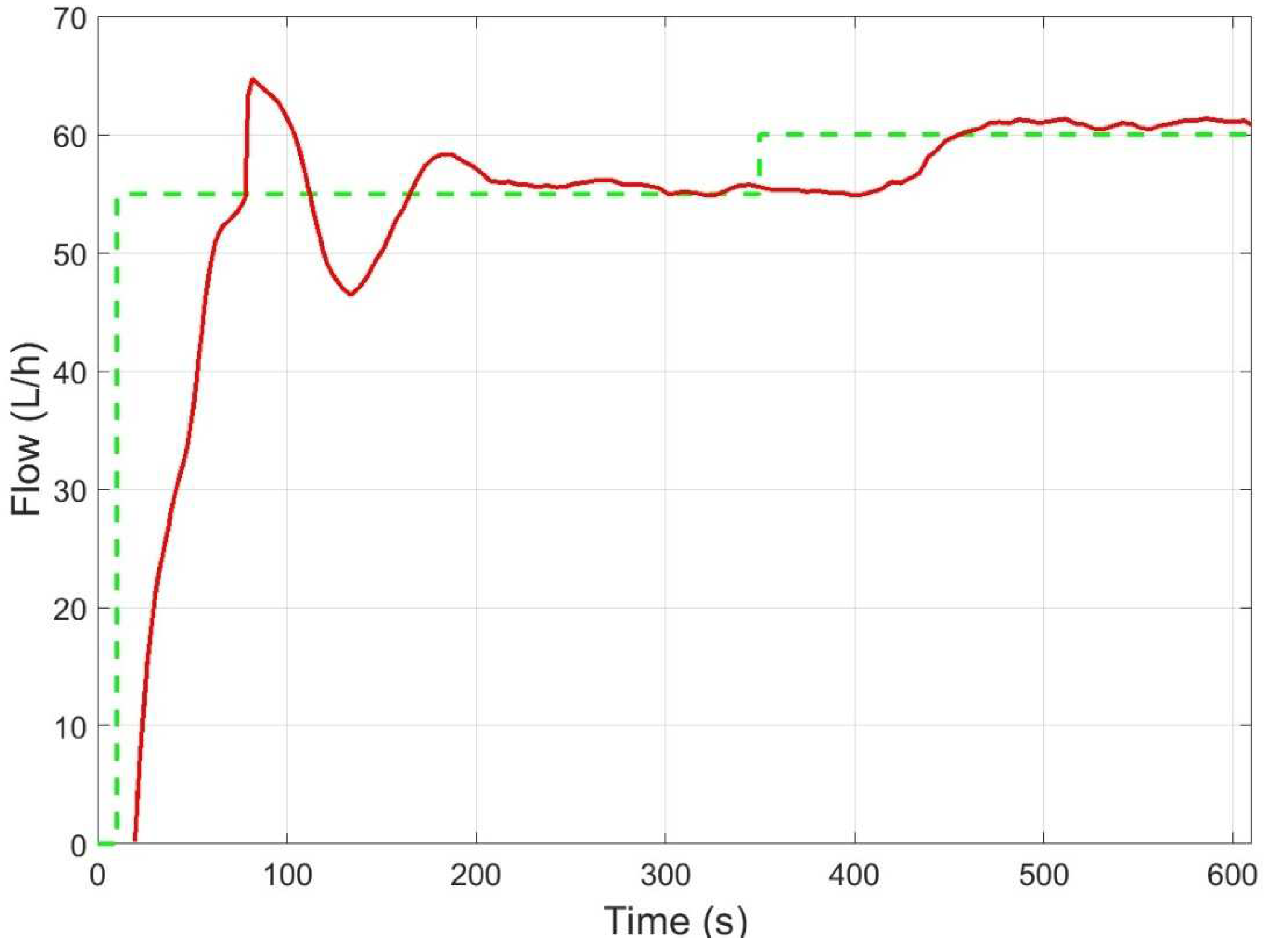
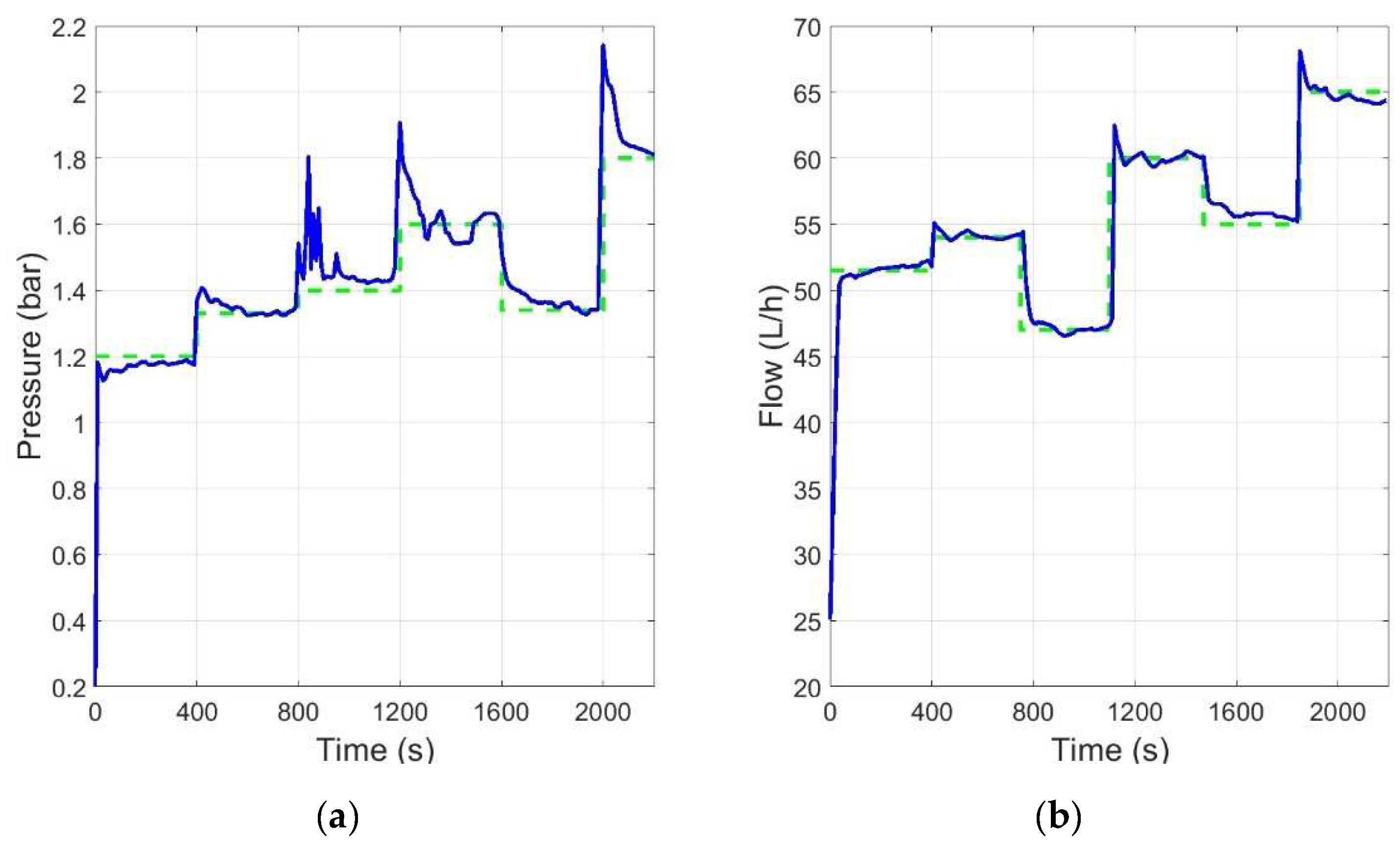
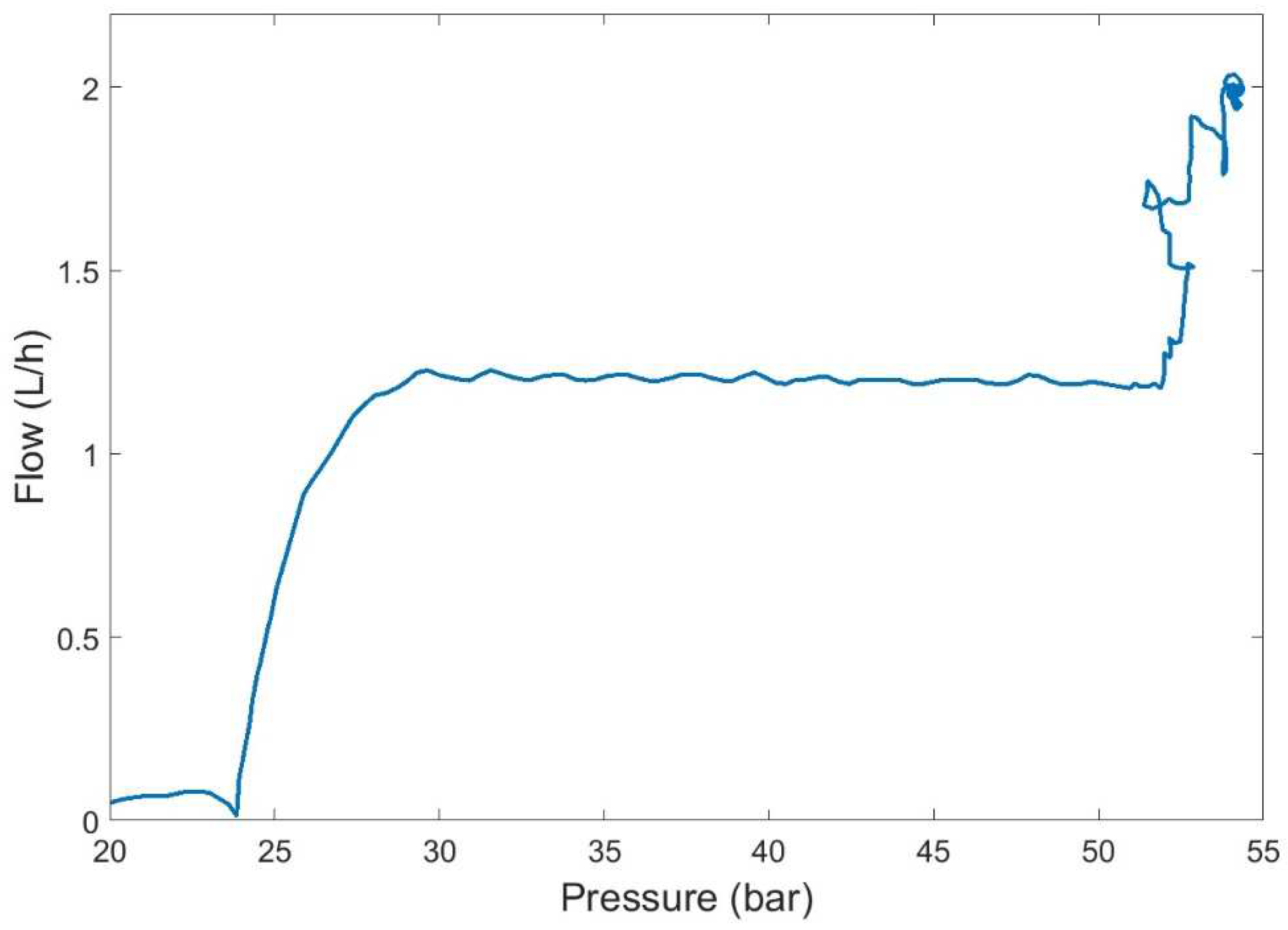
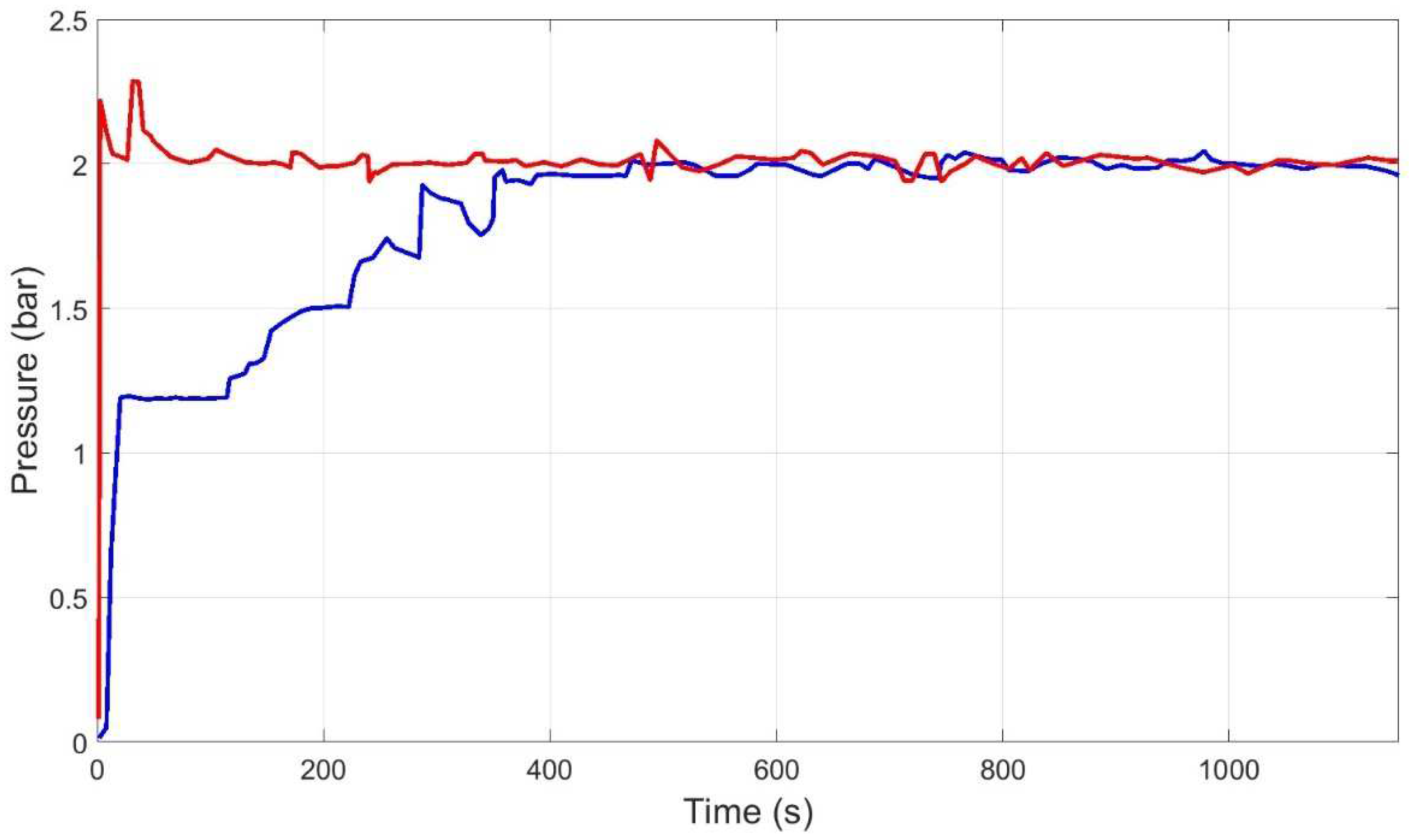
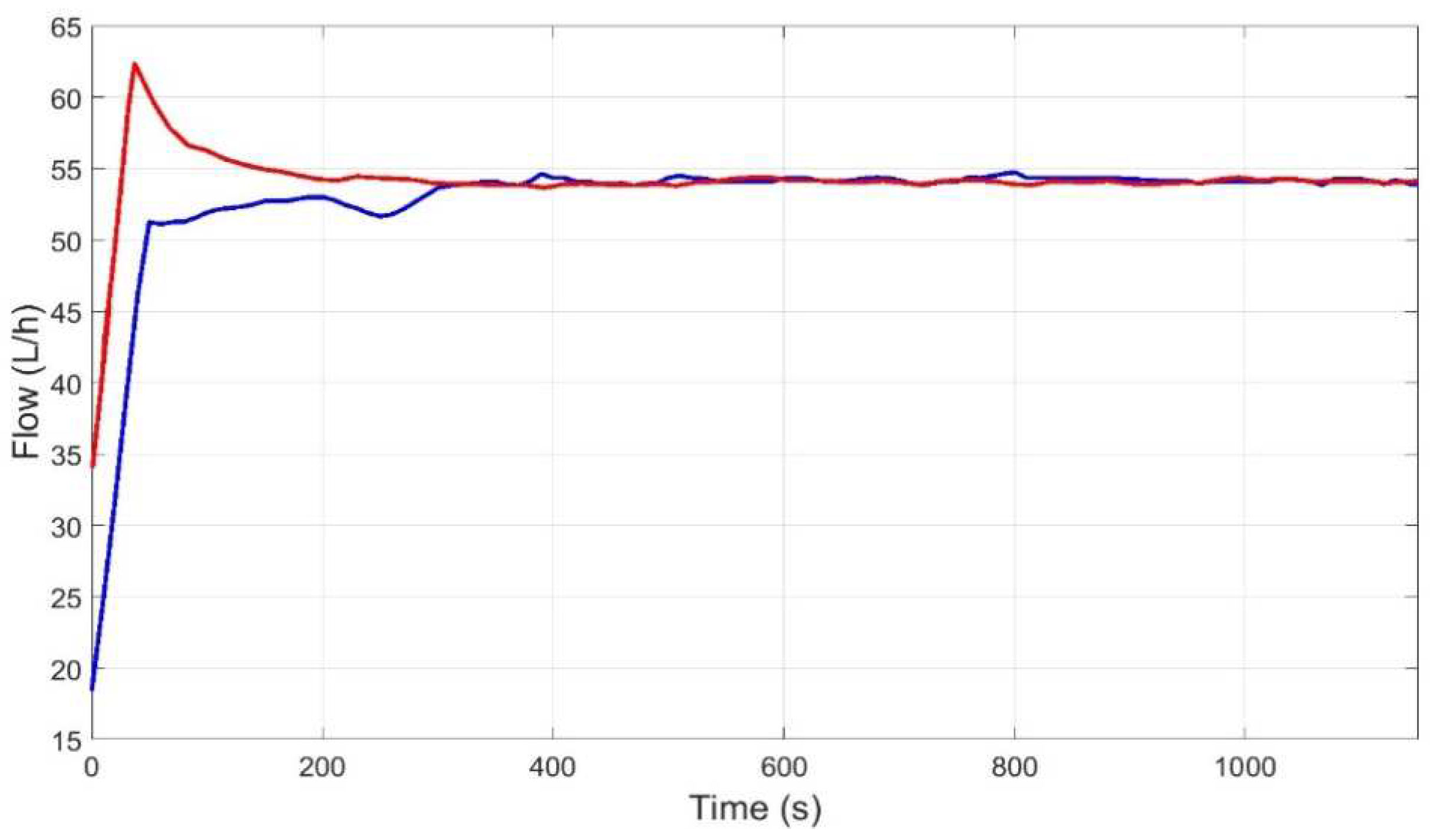
3.1. Control Based on Artificial Neural Networks
3.2. Expert Control Based on Fuzzy Logic
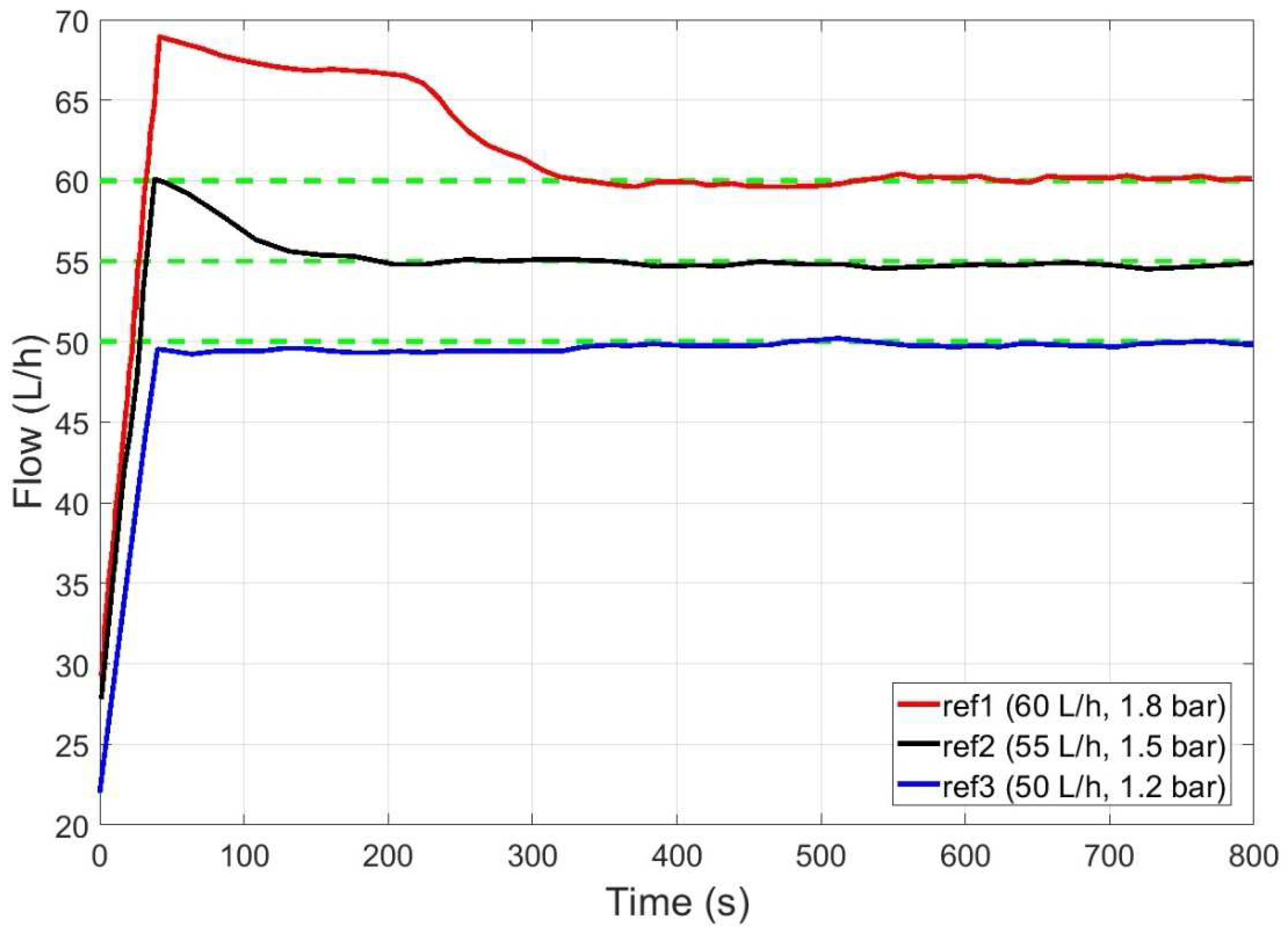
3.3. Control by Fuzzy-Integrated Inverse Local Models
- Reach Qr_ref using the pump speed control variable Vel, but with the solenoid valve fully open (for security reasons)
- If more pressure is needed, then close the solenoid valve by controlling the valve opening %Ev to reach P_ref
- The last action will decrease the flow. Then reach again Qr_ref using the pump speed control variable Vel.
- Follow the last two steps until both references (P_ref, Qr_ref) are obtained.
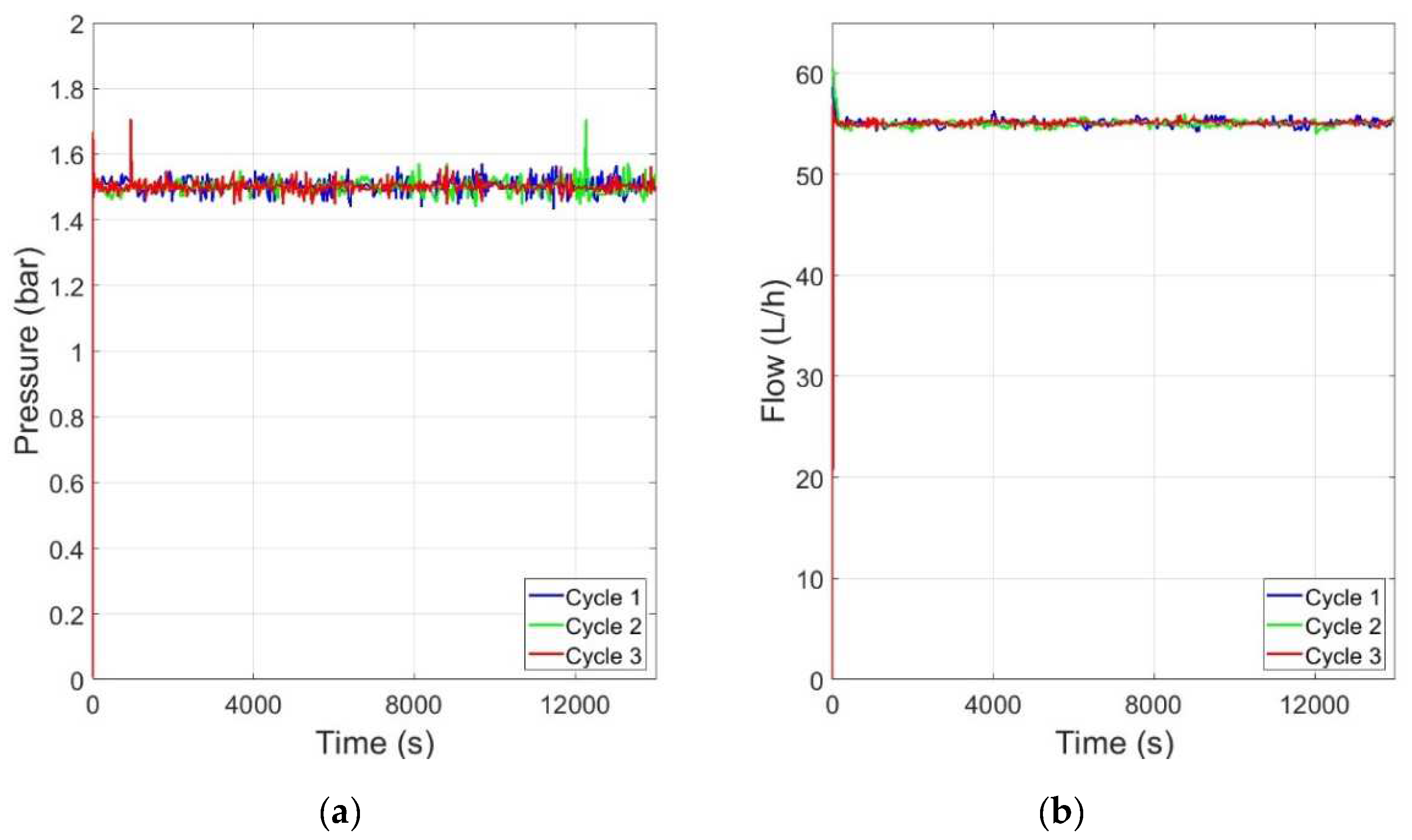
3.4. Discussion of the Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ozgun, H.; Tao, Y.; Ersahin, M.E.; Zhou, Z.; Gimenez, J.B.; Spanjers, H.; van Lier, J.B. Impact of Temperature on Feed-Flow Characteristics and Filtration Performance of an Upflow Anaerobic Sludge Blanket Coupled Ultrafiltration Membrane Treating Municipal Wastewater. Water Res. 2015, 83, 71–83. [Google Scholar] [CrossRef] [PubMed]
- Muñoz Sierra, J.D.; Oosterkamp, M.J.; Wang, W.; Spanjers, H.; van Lier, J.B. Comparative Performance of Upflow Anaerobic Sludge Blanket Reactor and Anaerobic Membrane Bioreactor Treating Phenolic Wastewater: Overcoming High Salinity. Chem. Eng. J. 2019, 366, 480–490. [Google Scholar] [CrossRef]
- Düppenbecker, B.; Engelhart, M.; Cornel, P. Fouling Mitigation in Anaerobic Membrane Bioreactor Using Fluidized Glass Beads: Evaluation Fitness for Purpose of Ceramic Membranes. J. Memb. Sci. 2017, 537, 69–82. [Google Scholar] [CrossRef]
- Armignacco, P.; Garzotto, F.; Bellini, C.; Neri, M.; Lorenzin, A.; Sartori, M.; Ronco, C. Pumps in Wearable Ultrafiltration Devices: Pumps in Wuf Devices. Blood Purif. 2015, 39, 115–124. [Google Scholar] [CrossRef]
- Liu, Y.; Faria, M.; Leonard, E. Spallation of Small Particles from Peristaltic Pump Tube Segments. Artif. Organs. 2017, 41, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Deiringer, N.; Friess, W. Proteins on the Rack: Mechanistic Studies on Protein Particle Formation During Peristaltic Pumping. J. Pharm. Sci. 2022, 111, 1370–1378. [Google Scholar] [CrossRef]
- Kazemi, A.S.; Patterson, B.; LaRue, R.J.; Papangelakis, P.; Yoo, S.M.; Ghosh, R.; Latulippe, D.R. Microscale Parallel-Structured, Cross-Flow Filtration System for Evaluation and Optimization of the Filtration Performance of Hollow-Fiber Membranes. Sep. Purif. Technol. 2019, 215, 299–307. [Google Scholar] [CrossRef]
- Yuan, P.; Le, Z.; Zhong, L.; Huang, C. Dynamic Dialysis: An Efficient Technique for Large-Volume Sample Desalting. Prep. Biochem. Biotechnol. 2015, 45, 588–595. [Google Scholar] [CrossRef]
- McIntyre, M.P.; van Schoor, G.; Uren, K.R.; Kloppers, C.P. Modelling the Pulsatile Flow Rate and Pressure Response of a Roller-Type Peristaltic Pump. Sens. Actuators A Phys. 2021, 325, 112708. [Google Scholar] [CrossRef]
- Gendy, M.E.L.; Anwar Bég, O.; Kadir, A.; Islam, M.N.; Tripathi, D. CFD Simulation and Visualization of Netonian and Non-Newtonian Transport in a Peristaltic Micro-Pump. J. Mech. Med. Biol. 2021, 21, 2150058. [Google Scholar] [CrossRef]
- Medvedev, A.; Hillerström, G. External Model Control of a Peristaltic Pump. IFAC Proc. Vol. 1994, 27, 517–522. [Google Scholar] [CrossRef]
- van der Bruggen, B. Microfiltration, Ultrafiltration, Nanofiltration, Reverse Osmosis, and Forward Osmosis. Fundam. Modeling Membr. Syst. Membr. Process Perform. 2018, 2016, 25–70. [Google Scholar] [CrossRef]
- Iritani, E.; Katagiri, N. Developments of Blocking Filtration Model in Membrane Filtration. KONA Powder Part. J. 2016, 2016, 179–202. [Google Scholar] [CrossRef]
- Kecili, K.; Habarou, H.; Suty, H.; Croué, J.P.; Pontié, M. Approche Analytique Intégrée Du Colmatage de Membranes MF–UF Par Les Matières Organiques Naturelles (MON). Partie 1: Caractérisations in Situ et Modèles de Colmatage. Comptes Rendus Chim. 2006, 9, 1178–1191. [Google Scholar] [CrossRef]
- Sreedhar, N.; Mavukkandy, M.O.; Aminabhavi, T.M.; Hong, S.; Arafat, H.A. Fouling Mechanisms in Ultrafiltration under Constant Flux: Effect of Feed Spacer Design. Chem. Eng. J. 2022, 446, 136563. [Google Scholar] [CrossRef]
- Winzeler, H.B.; Belfort, G. Enhanced Performance for Pressure-Driven Membrane Processes: The Argument for Fluid Instabilities. J. Memb. Sci. 1993, 80, 35–47. [Google Scholar] [CrossRef]
- Flendrig, J.G.; Carpay, W.M.; Dekkers, W.T. The Accurate Control of Ultrafiltration. Artif. Organs. 1978, 2, 144–146. [Google Scholar] [CrossRef]
- Roberts, M.; Winney, R.J. Errors in Fluid Balance with Pump Control of Continuous Hemodialysis. Int. J. Artif. Organs. 1992, 15, 99–102. [Google Scholar] [CrossRef]
- Morales, E.O.; Polycarpou, M.M.; Member, S.; Hemasilpin, N.; Bissler, J.J. Hierarchical Adaptive and Supervisory Control of Continuous Venovenous Hemofiltration. IEEE Trans. Control. Syst. Technol. 2001, 9, 445–457. [Google Scholar] [CrossRef]
- Niu, C.; Li, X.; Dai, R.; Wang, Z. Artificial Intelligence-Incorporated Membrane Fouling Prediction for Membrane-Based Processes in the Past 20 Years: A Critical Review. Water Res. 2022, 216, 118299. [Google Scholar] [CrossRef]
- Jawad, J.; Hawari, A.H.; Javaid Zaidi, S. Artificial Neural Network Modeling of Wastewater Treatment and Desalination Using Membrane Processes: A Review. Chem. Eng. J. 2021, 419, 129540. [Google Scholar] [CrossRef]
- Zhou, Y.; Khan, B.; Gu, H.; Christofides, P.D.; Cohen, Y. Modeling UF Fouling and Backwash in Seawater RO Feedwater Treatment Using Neural Networks with Evolutionary Algorithm and Bayesian Binary Classification. Desalination 2021, 513, 115129. [Google Scholar] [CrossRef]
- Ibáñez, R.; Almécija, C.; Guadix, A.; Guadix, E.M. Modelling the Ultrafiltration of Protein Solutions by Artificial Neural Networks. In Artificial Neural Networks (Mathematics Research Developments); Nova Science Publishers, Inc.: New York, NY, USA, 2011; pp. 361–384. ISBN 9781617615535. [Google Scholar]
- Corbatón-Báguena, M.-J.; Vincent-Vela, M.-C.; Gozálvez-Zafrilla, J.-M.; Álvarez-Blanco, S.; Lora-García, J.; Catalán-Martínez, D. Comparison between Artificial Neural Networks and Hermia’s Models to Assess Ultrafiltration Performance. Sep. Purif. Technol. 2016, 170, 434–444. [Google Scholar] [CrossRef]
- Yusuf, Z.; Wahab, N.A.; Sudin, S. Soft Computing Techniques in Modelling of Membrane Filtration System: A Review. Desalination Water Treat 2019, 161, 144–155. [Google Scholar] [CrossRef]
- Yuan, W.; Kocic, A.; Zydney, A.L. Analysis of Humic Acid Fouling during Microfiltration Using a Pore Blockage–Cake Filtration Model. J. Memb. Sci. 2002, 198, 51–62. [Google Scholar] [CrossRef]
- Yuan, W.; Zydney, A.L. Effects of Solution Environment on Humic Acid Fouling during Microfiltration. Desalination 1999, 122, 63–76. [Google Scholar] [CrossRef]
- Yuan, W.; Zydney, A.L. Humic Acid Fouling during Microfiltration. J. Memb. Sci. 1999, 157, 1–12. [Google Scholar] [CrossRef]
- Gruskevica, K.; Mezule, L. Cleaning Methods for Ceramic Ultrafiltration Membranes Affected by Organic Fouling. Membranes 2021, 11, 131. [Google Scholar] [CrossRef]
- Alresheedi, M.T.; Barbeau, B.; Basu, O.D. Comparisons of NOM Fouling and Cleaning of Ceramic and Polymeric Membranes during Water Treatment. Sep. Purif. Technol. 2019, 209, 452–460. [Google Scholar] [CrossRef]
- Narendra, K.S.; Parthasarathy, K. Identification and Control of Dynamical Systems Using Neural Networks. IEEE Trans. Neural Netw. 1990, 1, 4–27. [Google Scholar] [CrossRef] [Green Version]
- Zadeh, L.A. Fuzzy Sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Albertos, P.; Olivares, M.; Sala, A. Fuzzy Logic Based Look-up Table Controller with Generalization. Proc. Am. Control. Conf. 2000, 3, 1949–1953. [Google Scholar] [CrossRef]
- Murray-Smith, R.; Johansen, T.A. The Operating Regime Approach to Nonlinear Modelling and Control; Taylor and Francis: London, UK, 2020; pp. 3–72. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer: New York, NY, USA, 1981. [Google Scholar]
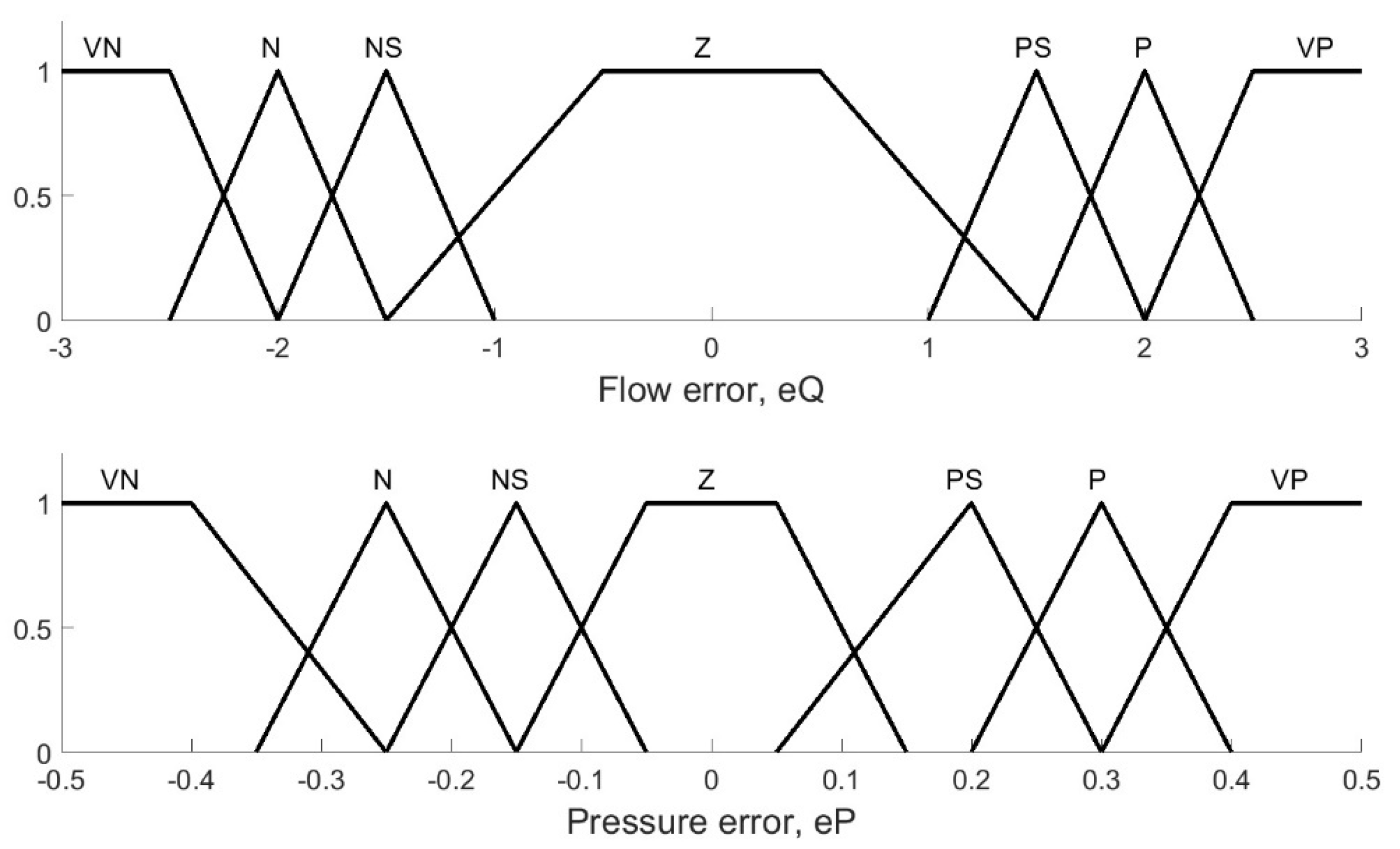
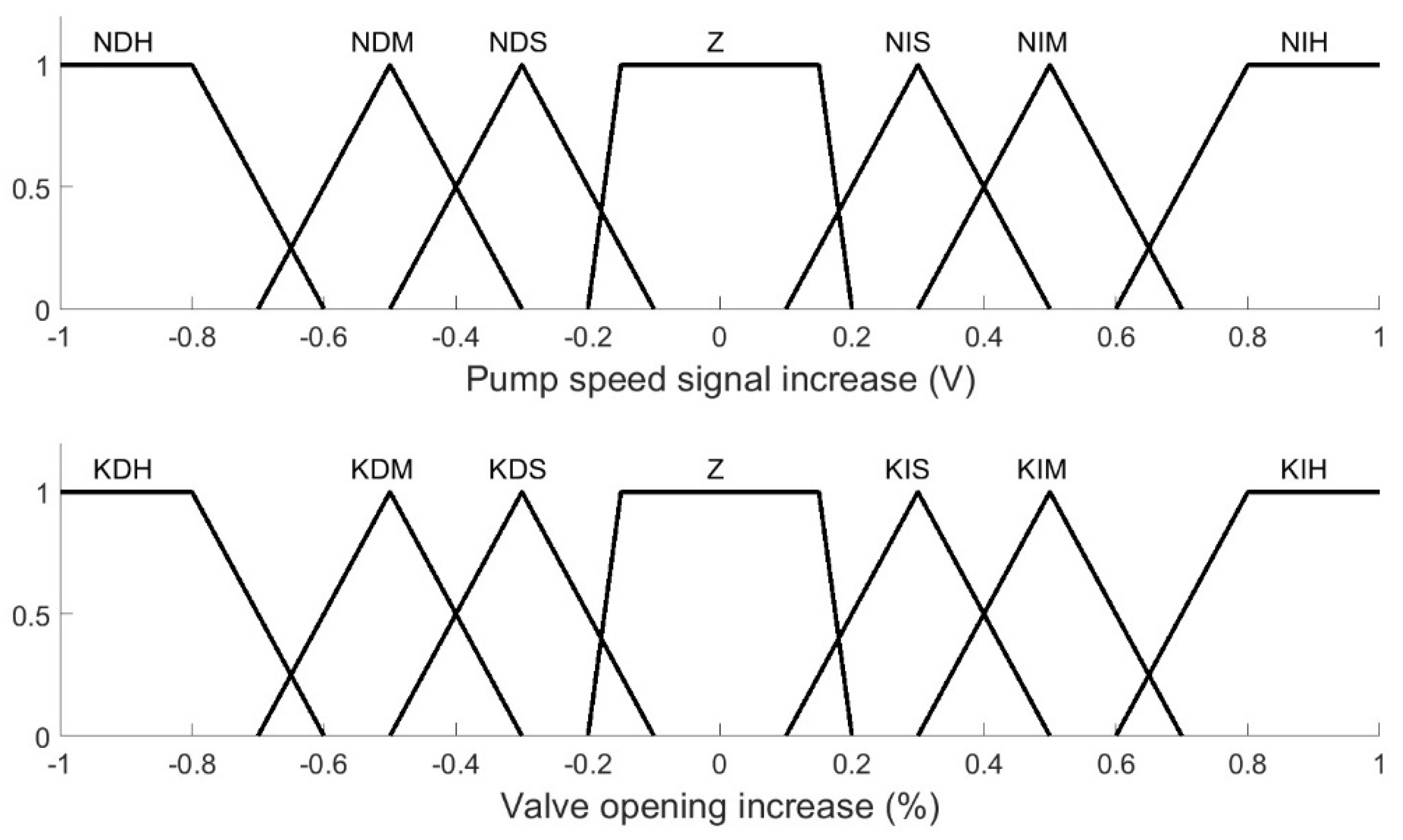
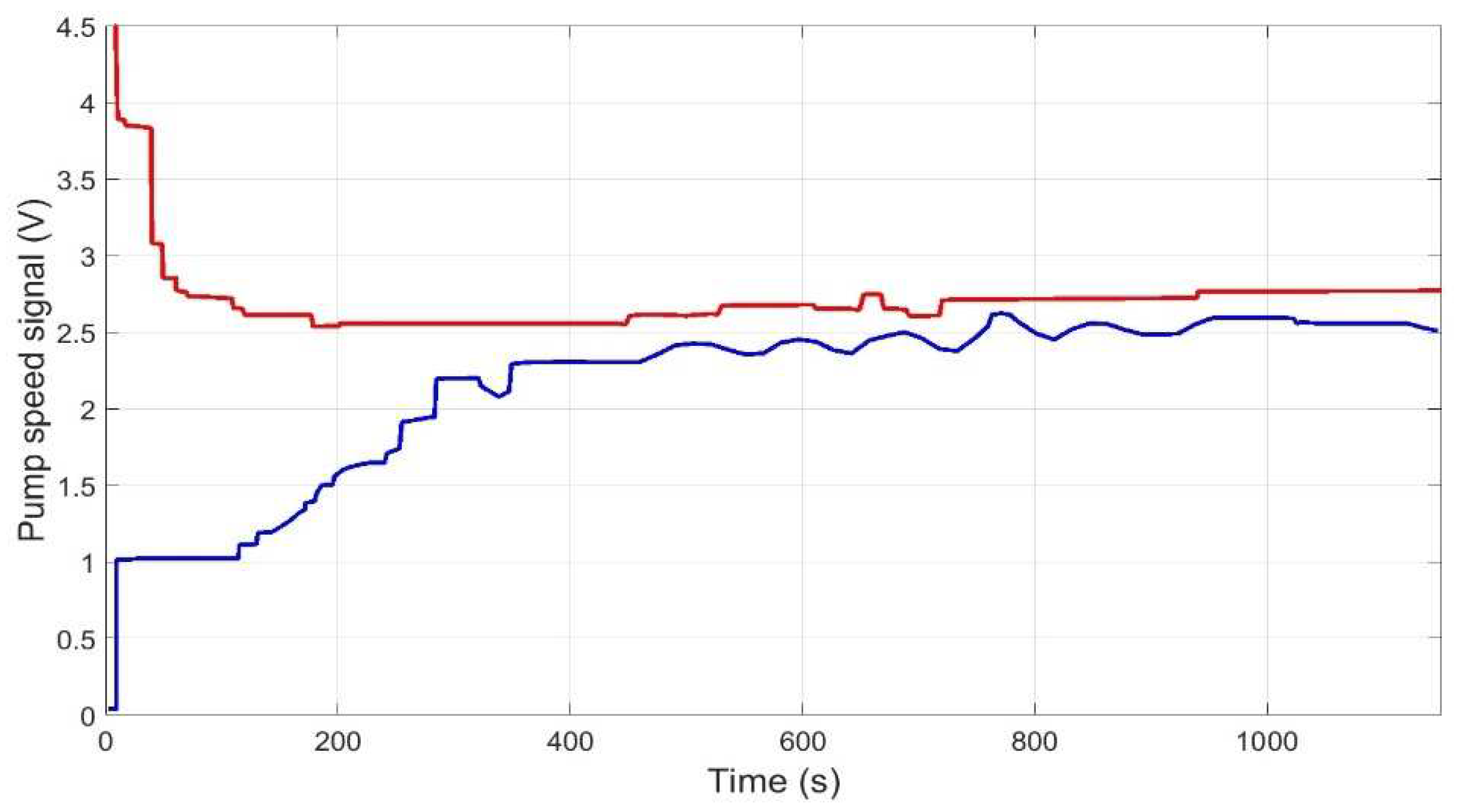
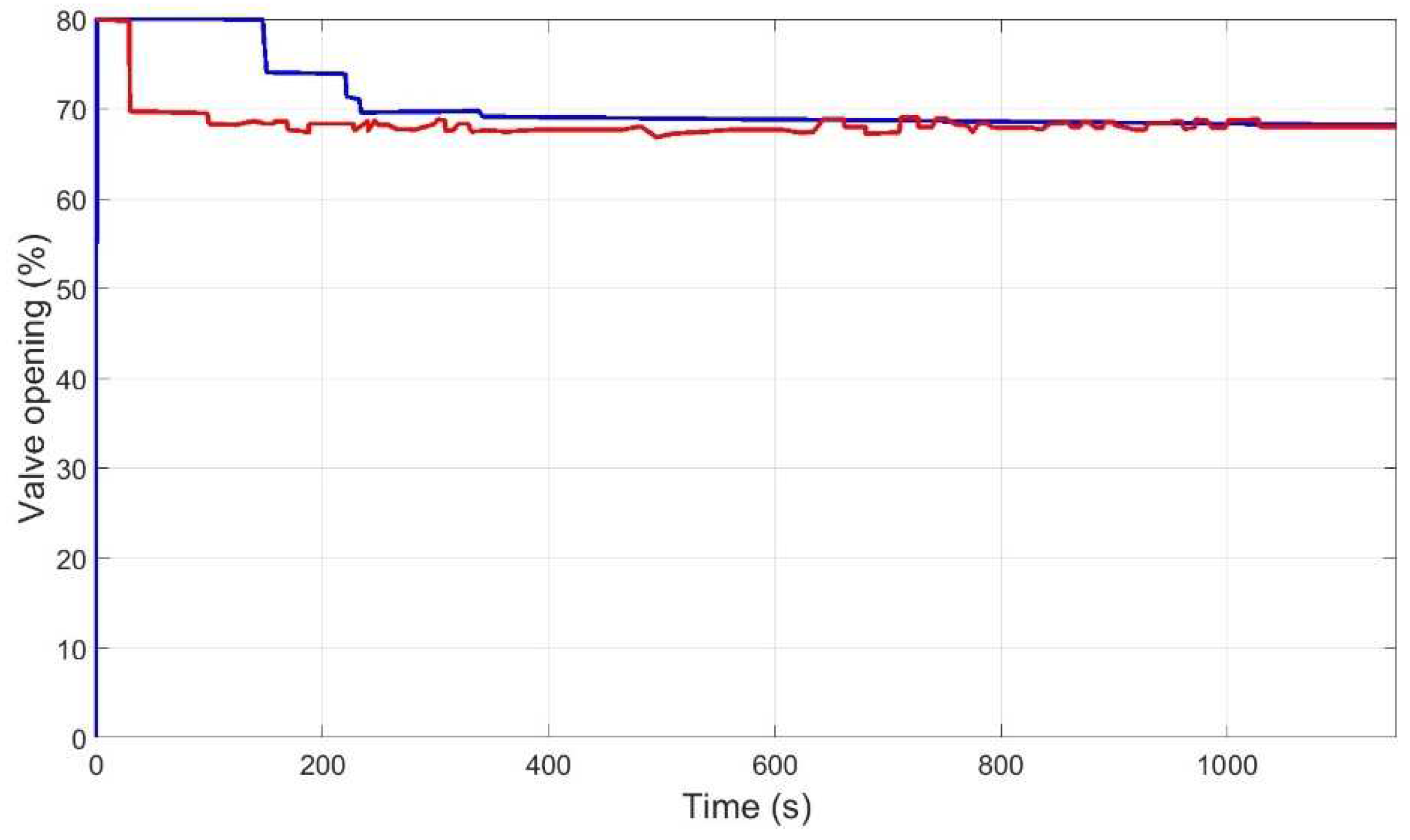
| Pump Speed | Valve Opening | |
|---|---|---|
| increase (high) | NIH | KIH |
| increase (medium) | NIM | KIM |
| increase (slight) | NIS | KIS |
| decrease (slight) | NDS | KDS |
| decrease (medium) | NDM | KDM |
| decrease (high) | NDH | KDH |
| eQ/eP | VN | N | NS | Z | PS | P | VP |
|---|---|---|---|---|---|---|---|
| VN | NDH | KDM NDM | NDM | KDM NDS | NIS | KDM | KDM NIM |
| N | NDH | NDM | NDM | KDM | KDS NIS | KDM | KDM NIS |
| NS | NDM | NDM | NDS | KDS | KIS | KIM | NIM |
| Z | KIS | NDM | KIS | - | KDS | NIM | NIM KDS |
| PS | KIM | KIM | KIS | KIS | KDS NIS | NIM | NIM |
| P | KIH | KIM | KIM | KIM | NIM | NIM | NIM |
| VP | KIH | KIS NDS | KIS | KIS NIS | KDS | KDS | NIH |
| Controller | Modelling | Control | Robustness |
|---|---|---|---|
| Local models | Few data required | Slow, precise | High. Some problems in different functioning points |
| Expert control | Only models look-up-table | Sharp, fast, precise | Pondering problems in different working areas |
| Artificial neural networks | Many data required | Slow, precision achieved by PI controller | Limited. The models do not cover all areas |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díez, J.-L.; Masip-Moret, V.; Santafé-Moros, A.; Gozálvez-Zafrilla, J.M. Comparison of Artificial Intelligence Control Strategies for a Peristaltically Pumped Low-Pressure Driven Membrane Process. Membranes 2022, 12, 883. https://doi.org/10.3390/membranes12090883
Díez J-L, Masip-Moret V, Santafé-Moros A, Gozálvez-Zafrilla JM. Comparison of Artificial Intelligence Control Strategies for a Peristaltically Pumped Low-Pressure Driven Membrane Process. Membranes. 2022; 12(9):883. https://doi.org/10.3390/membranes12090883
Chicago/Turabian StyleDíez, José-Luis, Vicente Masip-Moret, Asunción Santafé-Moros, and José M. Gozálvez-Zafrilla. 2022. "Comparison of Artificial Intelligence Control Strategies for a Peristaltically Pumped Low-Pressure Driven Membrane Process" Membranes 12, no. 9: 883. https://doi.org/10.3390/membranes12090883
APA StyleDíez, J.-L., Masip-Moret, V., Santafé-Moros, A., & Gozálvez-Zafrilla, J. M. (2022). Comparison of Artificial Intelligence Control Strategies for a Peristaltically Pumped Low-Pressure Driven Membrane Process. Membranes, 12(9), 883. https://doi.org/10.3390/membranes12090883







