1. Introduction
The lack of fresh water resources is an indisputable fact, and desalination technology is an effective strategy to solve this problem [
1,
2]. At present, among many seawater desalination technologies, multistage flash (MSF), and reverse osmosis seawater (SWRO) desalination are the most effectively and widely technologies used in practice. However, with the increased requirement of cost-saving and wastewater discharge reduction, new challenges are presented to improve seawater desalination process [
3]. Since the MSF technique [
4,
5] can get a large amount of higher quality fresh water from low-grade energy and its concentration is significantly lower than that of the SWRO technique, the good complementary characteristics of these two techniques become an attractive direction to improve the overall profits for freshwater achievement with lower operational costs. At present, the MSF technology and SWRO technology are relatively mature, and there are some studies about the hybrid thermal-membrane desalination technology, but the detailed research on the optimal structure of the hybrid system is relatively novel and deficient [
6]. Since both the SWRO desalination and the MSF desalination are energy-intensive technologies, most new studies are focused on the couple of desalination technique with the energy-driven system. For example, Khan et al. [
7,
8] carried out fruitful work on the desalination system coupled with nuclear power. In their studies, a techno-economic analysis of a nuclear power plant coupled with RO or MED or RO + MED and even RO + MSF systems were assessed in detail. With the consideration of environmental impact, they also built a simulation model for calculation and assessment of the socio-economic and environmental impacts of a nuclear desalination system.
In many regions where there are no renewable energies or nuclear energy available, the hybrid desalination technologies for full utilization of energy and cost saving were also studied by researchers. Kuenstle et al. [
9] proposed a design concept for a combined MSF-RO and power plant system. They evaluated its economic benefits, and concluded that the combined system has lower water production costs than a single MSF system. Al-marafie [
10] carried out the economic comparison between MSF and MSF-RO seawater desalination systems—the results showed that the MSF-RO system has more advantageous than MSF. In addition, the author proposed that replacement of the local traditional desalination system with the MSF-RO system has better application prospects. Awerbuch et al. [
11] studied the SWRO desalination system and MSF-RO hybrid seawater desalination system, and designed two MSF-RO and one MSF-RO-VEC seawater desalination systems with different coupling structures. In the same year, Awerbuch et al. [
12] designed a hybrid system, analyzed the characteristics of the MSF desalination system and RO desalination system, and after 1987, the authors still affirmed the advantages of the MSF-RO seawater desalination system and gave a structure diagram of the initially designed hybrid system. In the same year, Al-Mutaz et al. [
13] designed a relatively simple MSF-RO system and established the system model. However, it has not been verified and simulated, and the subsequent system optimization work has not been carried out. El-Sayed et al. [
14] designed the MSF-RO experimental device and analyzed and studied the experimental data. After 1800 h of experimental testing, the experimental data proved the superiority of the MSF-RO system in terms of desalination rate, fresh water output, and energy conservation. However, this conclusion can only be regarded as a qualitative background, not enough to draw a specific conclusion, and further research is needed. However, at least based on our literature knowledge, the above work did not carry detailed model-based numerical analysis on the optimal design and operation of systems. A reasonable and accurate mathematical model, which can fully describe the important process parameters and their influences, is very important for the study of the subsequent system. Most of the above research work affirms the superiority of the MSF-RO system, but at least based on our literature knowledge, the above work does not carry out detailed model-based numerical analysis for optimal system design and operation.
For the detailed quantitative analysis and performance prediction requirement to guide the hybrid system’s application, a series of modeling, simulation, and optimization works have been carried out at home and abroad. The relevant characteristics of the hot-film hybrid system is deeply understood by using the calculation tool. Cardona et al. [
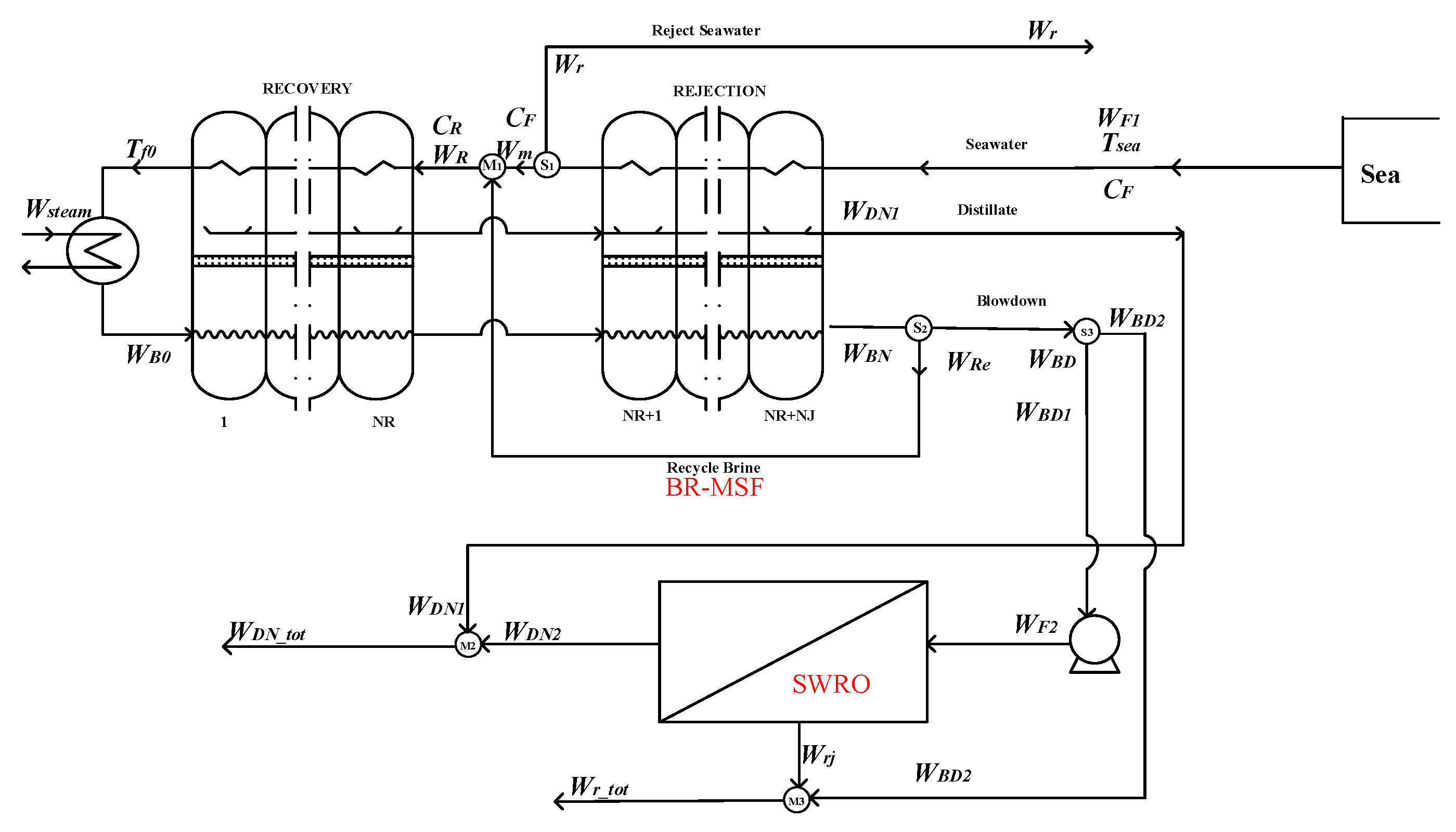
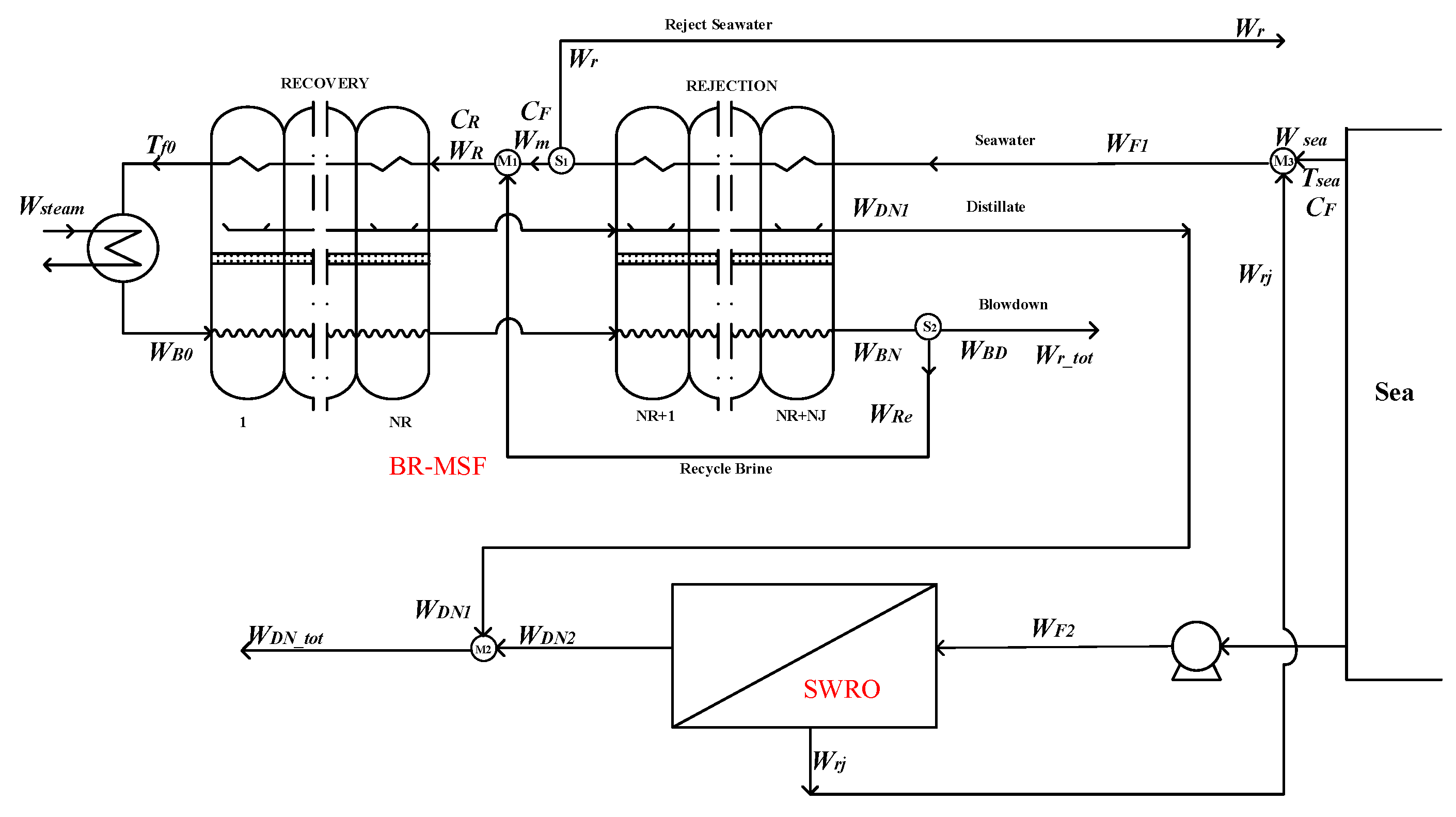
15] studied the changes in energy saving and water production cost after the integration of the MSF system and RO system. Based on the established water production model, the levels of energy consumption and water production before and after the system integration were obtained, which emphasized the advantages of MSF-RO in energy saving. Helal et al. [
16,
17,
18] established seven different coupling forms of the MSF-RO seawater desalination system, in addition to a two-stage SWRO seawater desalination system model and a BR-MSF seawater desalination model. Finally, various schemes are compared and evaluated, and it is concluded that through integrating MSF with the SWRO technique, the water production cost of the system can be reduced by 17% to 24%. Marcovecchio et al. [
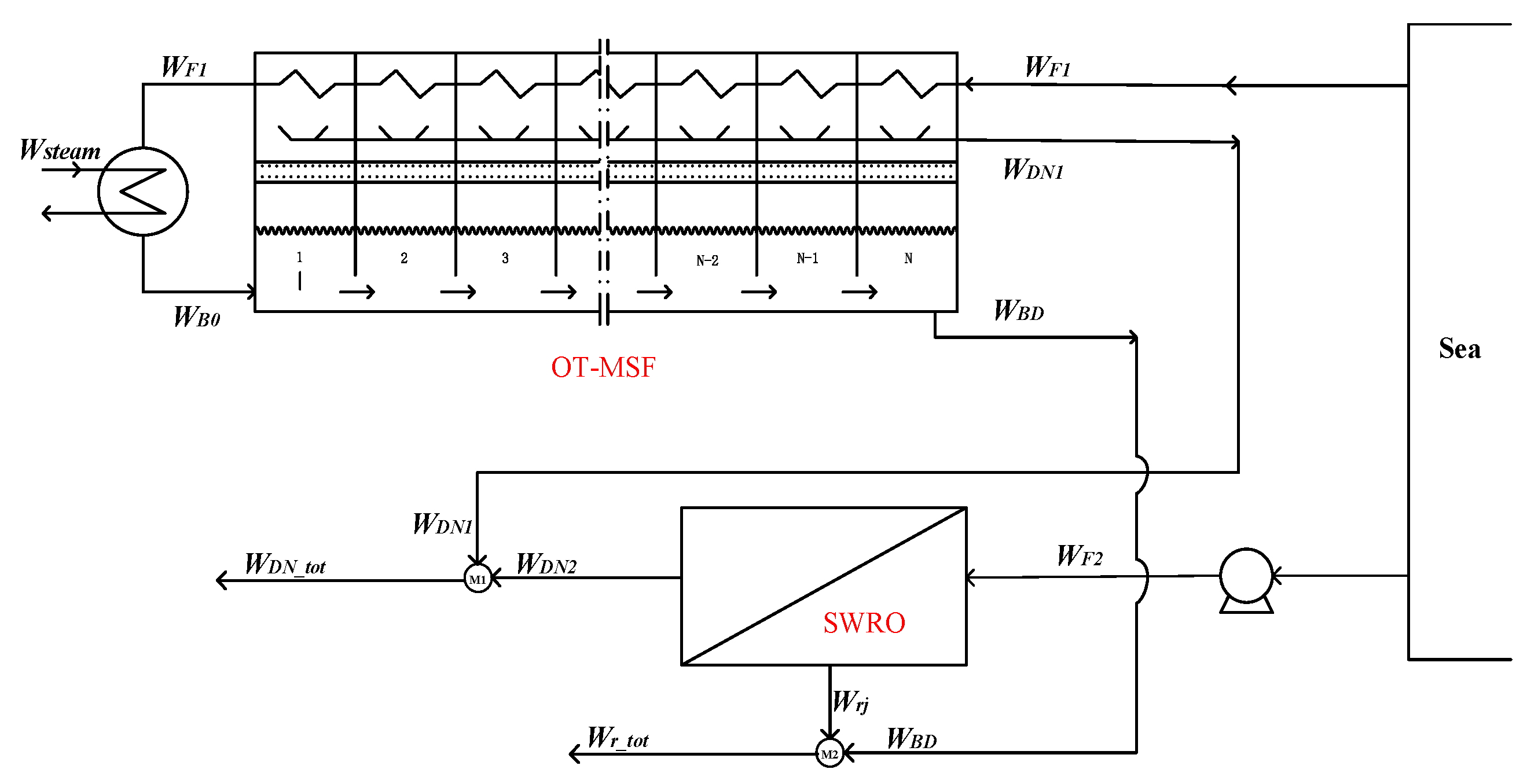
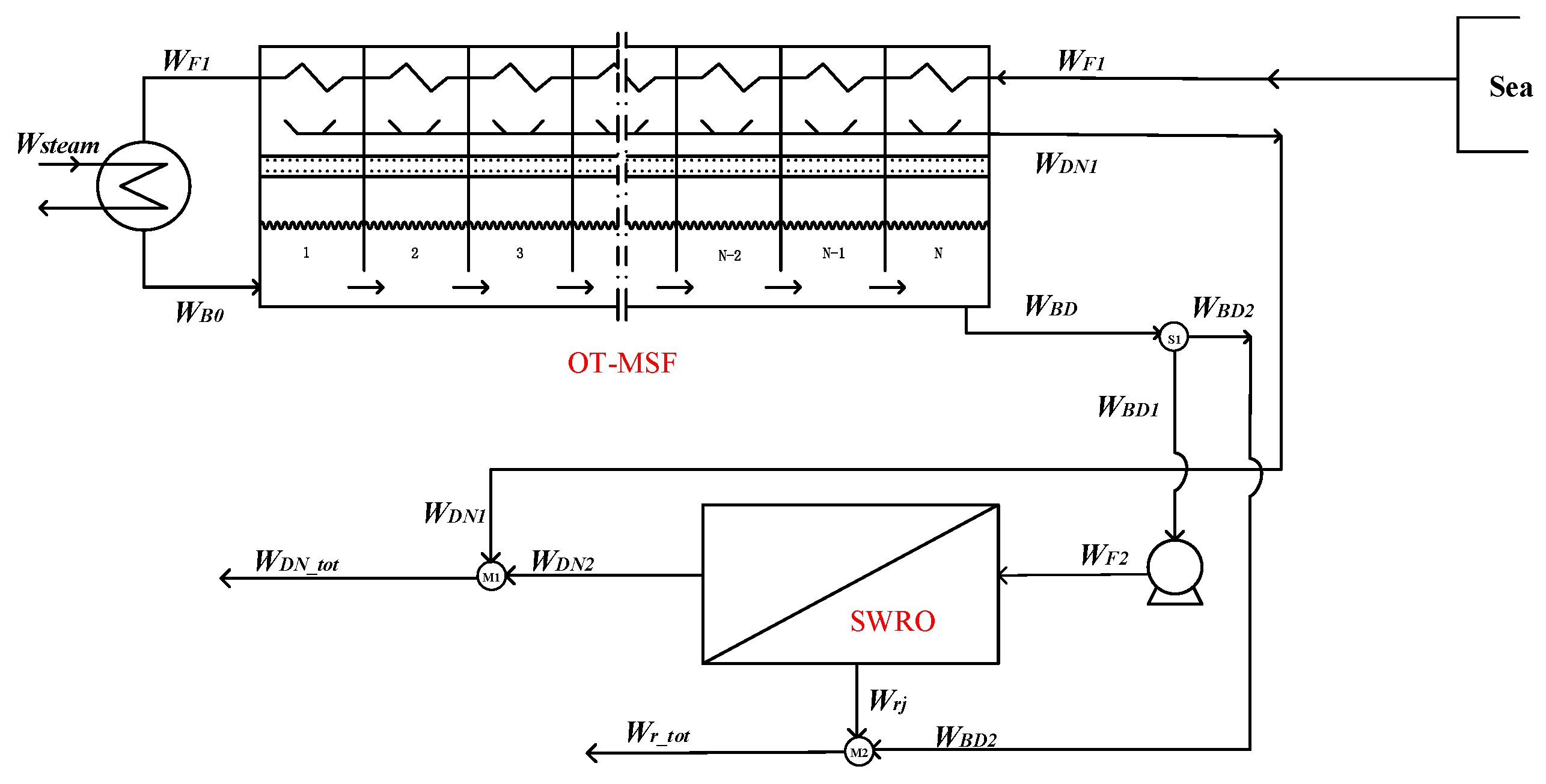
19] established a simple hybrid MSF-RO desalination system with reference to the work of Helal and others, taking the highest daily fresh water output as the optimization goal and solving it. The MSF part of the model was the OT-MSF seawater desalination system, which had a simple structure. Only the discharge of the MSF system and the feed of the RO system are coupled, and the coupling mode is relatively single. Vince et al. [
20] established a super-model of the MSF-RO seawater desalination system, and proposed a method of optimization problem decomposition and realization of multiobjective optimization. This method combined process modeling and process integration technology with advanced mathematical solving tools to simultaneously optimize the configuration and operation of the integrated desalination system. Moreover, this method has been verified in the model established in this paper. Abdulrahim et al. [
21] used the first and second laws of thermodynamics to conduct a rigorous modeling and simulation study on the hybrid MSF-RO system. The results showed that the performance of the MSF-RO integrated system had been enhanced. The study considered four optimization goals, namely the maximum fresh water production, the minimum water production cost, the maximum gain ratio, and the minimum exergy damage rate; and the genetic algorithm was used to optimize the multiobjectives to make this system meet the requirements.
Wu et al. [
22] adopted the concept of hybrid nodes and distribution nodes, and established a superstructure model of the MSF and RO seawater desalination system. Regarding the water production ratio as an optimization variable of the integrated system, an improved genetic algorithm was used to get the optimal solution. Malik et al. [
23] used the Aspen custom modeling tool (ACM, V8.4.) to model and simulate MSF, RO, and MSF-RO respectively. The author took the lowest economic objective function as the optimization goal, and optimized the system operating conditions and process design variables. However, in his study, only one simple MSF-RO coupled structure was considered. For application intention, Boushi [
24] studied two system transformation schemes for the current status of the MSF plant in Al Taweelah A2 in Abu Dhabi, UAE. Based on practical data and the performance model of MSF, RO, and MSF-RO systems, the techno-economics and environmental impact were analyzed. To realize detailed numerical calculations and global optimization for a more complex system, Bandi et al. [
25] used differential evolution algorithm (DE) to globally optimize the MSF-RO desalination system with five different MSF-RO alternative mixing schemes. The results showed that the DE algorithm was suitable for the solving optimization problems of the more complex MSF-RO system. The given system and algorithm can be used to estimate the flowrate, the salt content of blowdown brine, circulating brine flowrate, the salt content, and condensate flowrate.
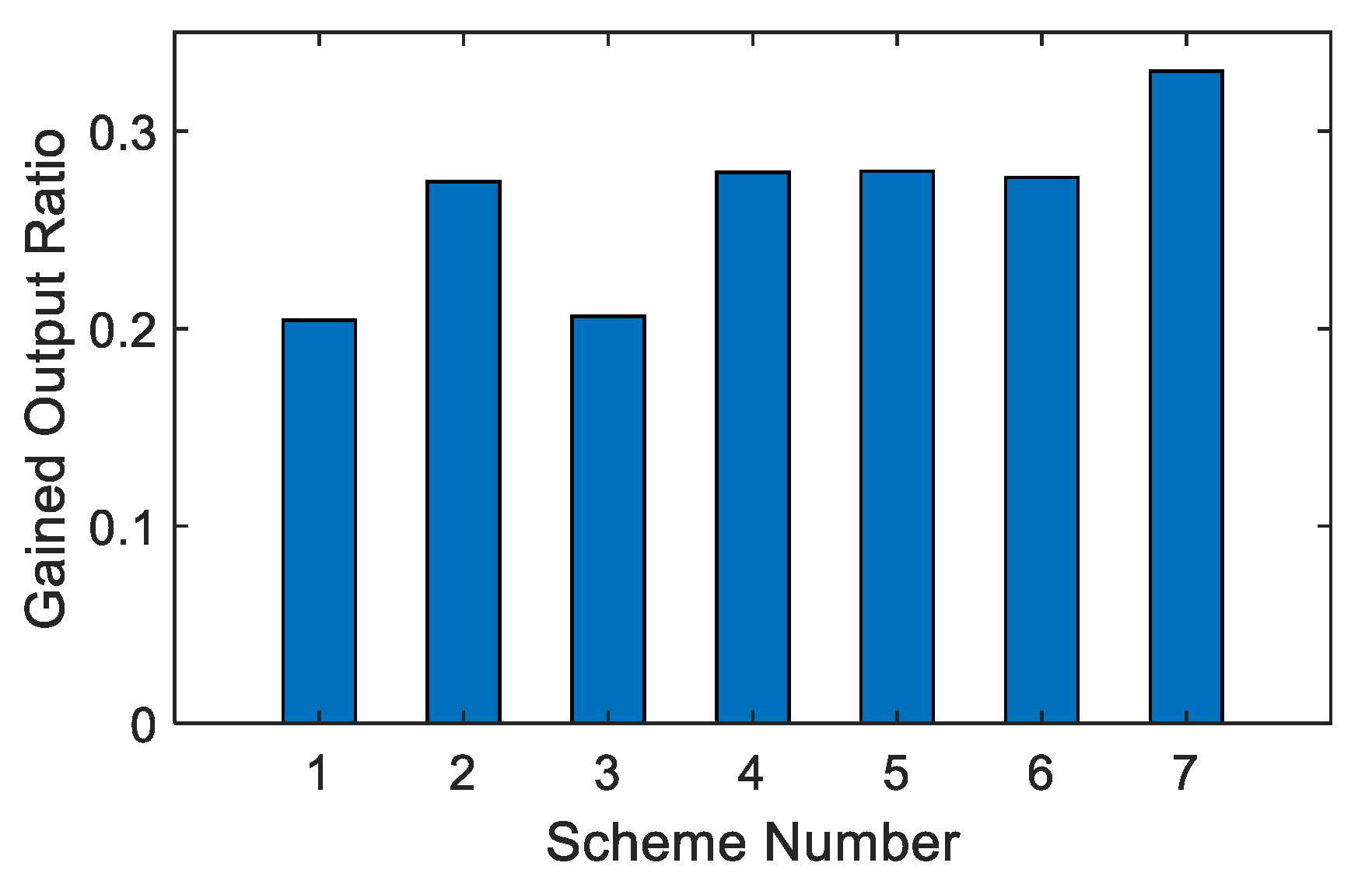
The above studies have confirmed the advantages and prospects of the MSF-RO system, and carried out relevant work in the aspect of optimal control. However, there are still some works that should be done for better guiding the structural and operational optimization of the MSF-RO system, especially in the plants who need to upgrade their RO or MSF system and achievement better operational profits. In this work, based on our earlier studies of full-scale detailed mechanism models of SWRO and MSF systems, detailed structural optimizations of the MSF-RO system under certain operational conditions and with techno-economics indexes are studied. After establishing the complete mechanism models of MSF and SWRO systems, according to the different feeding, mixture, and separation forms of the MSF-RO system, seven structural combination forms are designed and modeled for numerical calculation, and furthermore, the economic and performance equations are established for comparative analysis end scheme evaluation. Our work is helpful to guide structural optimization and detailed quantitative analysis of the MSF-RO system.
3. Operation Economics and Evaluation Index of the MSF-RO System
3.1. Operational Economic Model of the SWRO System
The economic model discussed in this article is an hourly operating cost model, and the investment cost is ignored due to the unequal years of plant service life. The operation cost of the SWRO system mainly includes the following seven parts:
Preliminary energy consumption cost OCIP;
Chemical cost OCCH;
Operating energy consumption cost OCEN;
Reverse osmosis membrane replacement cost OCMER;
Maintenance cost OCMN;
Labor costs OCLB1;
Wastewater management cost OCWS1.
The relevant expression of the corresponding operation cost of each part is as follows:
The preliminary energy consumption cost of SWRO system refers to the energy consumption cost of water intake and pretreatment. Pin refers to the outlet pressure of the water intake pump, which is 5 bar; WF2 is the feed water flowrate; Pelc is the price of electricity; PLF is the load factor, which is 0.9; is the motor efficiency, which is 0.85.
The cost of chemical agents mainly includes various acid reagents, scale inhibitors, flocculants, and other additives that change the water hardness.
OCEN:
where
Pf denotes the feed water pressure, which is 65 bar;
refers to the high-pressure pump efficiency, which is 0.85;
is the mechanical efficiency of the variable frequency drive, which is 0.94;
Pr is the outlet pressure of concentrated brine;
Wrj refers to the concentrated brine outlet flowrate;
is the booster pump mechanical efficiency, which is 0.8.
OCMER:
where
PriME is the unit price of the RO membrane, 6200 CNY/group;
MOD refers to the total number of RO membranes used in the system;
represents the replacement rate of membrane modules, which is 0.3.
The maintenance cost of the SWRO system is composed of the maintenance cost of conventional equipment OCMNCON and the cleaning and maintenance cost of reverse osmosis membrane module OCMNCL. Ncl is the number of membrane module cleanings in a membrane replacement cycle; Xmr is the membrane replacement cycle; OCOT is the cost of chemicals in membrane cleaning; OCPC is the system startup and shutdown costs incurred by the cleaning operation.
OCLB1:
NLB refers to the number of labors.
WDN2 represents the water production of the SWRO system, and
NP refers to the number of pressure vessels in the system.
OCWS2:
where
Wrj is the blowdown water from the SWRO system.
This article studies the operation plan of the system within the day, and the cost of RO membrane cleaning can be ignored. Therefore, Equation (36) can be rewritten as Equation (41) as shown:
The total cost of SWRO system can be formulated as follows:
3.2. Operational Economic Model of MSF System
Likewise, the economic model of the MSF seawater desalination system is only for the hourly operating cost model. It mainly includes the following six parts, namely:
Heating steam, OCST;
System power consumption cost, OCEL;
Maintenance cost, OCMT;
Pretreatment cost, OCPR;
Maintenance cost, OCMN;
Labor costs, OCLB2;
Wastewater management cost, OCWS2;
The relevant expression of the corresponding operation cost of each part is as follows:
The MSF system economic model can be seen from Gao et al. [
31], and the corresponding reference is the data in the paper by Wade et al. [
37] in 2001. Taking into account the US dollar inflation, the GDP deflator is used for conversion. Areppim website provides a dollar conversion calculator for each year based on the GDP deflator, and the dollar in 2001 is equivalent to
$1.45 in 2021. Based on the exchange rate between USD and RMB at 6.4525, the economic model of MSF seawater desalination system is synthesized, as shown in the following formulas.
The specific cost of the above six parts, which make up the total hourly operational costs of the MSF system can be expressed as:
3.3. Evaluation Indicators and Economic Model Verification
The economic model of MSF-RO system is composed of the economic model of MSF system and SWRO system. In order to evaluate the economy of the hybrid model, the economic models of the OT-MSF system and the SWRO system need to be verified respectively. For the MSF system, the OT-MSF system is selected for economic model verification. This study only discusses the case that the seawater temperature is 25 °C and the electricity price is 0.67 CNY/KW h. The verification premises of the economic model of MSF-RO hybrid system are as follows:
The feed seawater flowrate of the OT-MSF system and the SWRO system are both 1.203 × 107 kg/h = 1.203 × 104 m3/h.
The heating steam temperature is 97 °C.
The feed seawater concentration of the OT-MSF system is 5.7% = 57 kg/m3, and the feed seawater concentration of the SWRO system is 30 kg/m3. Because the pretreatment requirements of the system are inconsistent, the feed seawater concentrations of MSF system and RO system are different.
The unit price of single RO membrane of SWRO system is 6200 CNY.
Substitute the above parameters into the SWRO system economic model, and the IPOPT and CONOPT solver of the GAMS platform is called for simulation [
38]. The SWRO system water production and system cost ratio are shown in
Table 1 and
Table 2. And the cost analysis is shown in
Figure 8.
The above parameters were substituted into the OT-MSF system economic model, and simulated on the GAMS platform. The OT-MSF system water production and system cost ratio are shown in
Table 3 and
Table 4. The cost analysis is shown in
Figure 9.
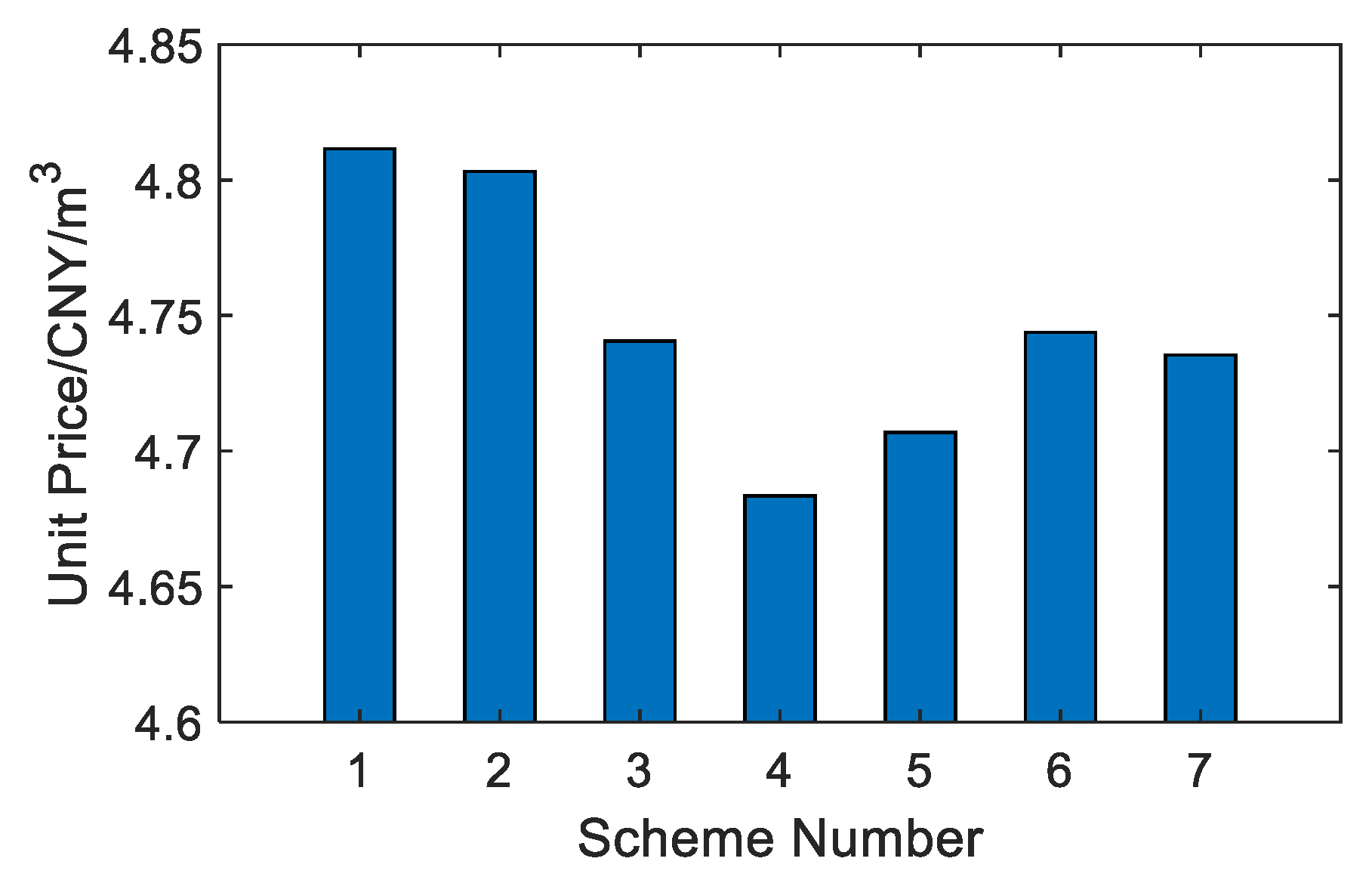
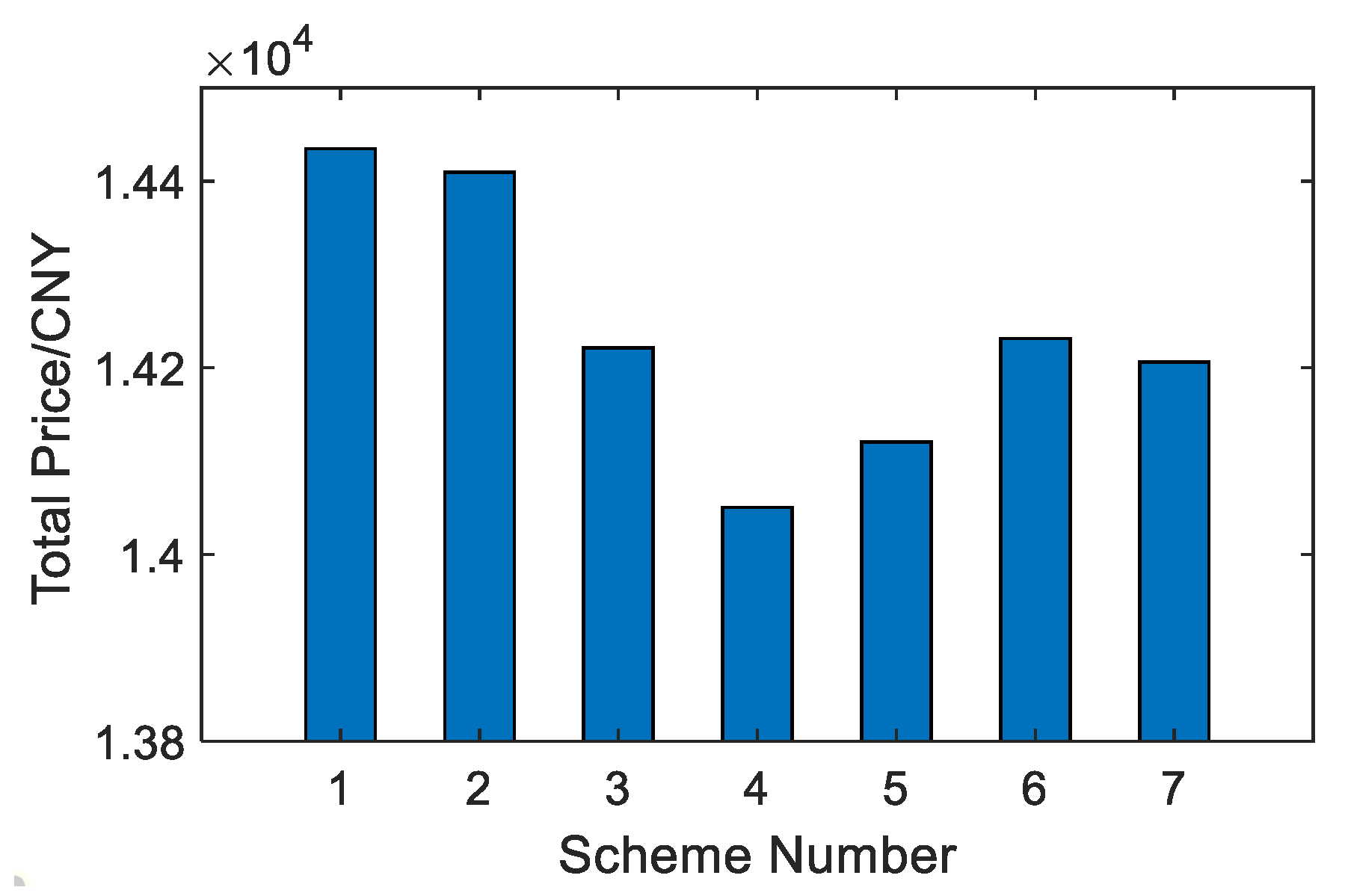
Under the same water intake flowrate conditions, the total price and cost ratio of the water production cost of SWRO and MSF systems can be obtained, respectively. For the SWRO system, the unit price of water production is 3.51 CNY/m
3, and for the OT-MSF system, the unit price of water production is 7.63 CNY/m
3. The ratio of the MSF system to the SWRO system’s water price is 0.4594, and Fan [
39] et al.’s statistical result ratio is 0.4600. Therefore, it is proved that the economic model designed in this study can reflect the economic situation of the system and it can be used for analysis and research. It can be seen from
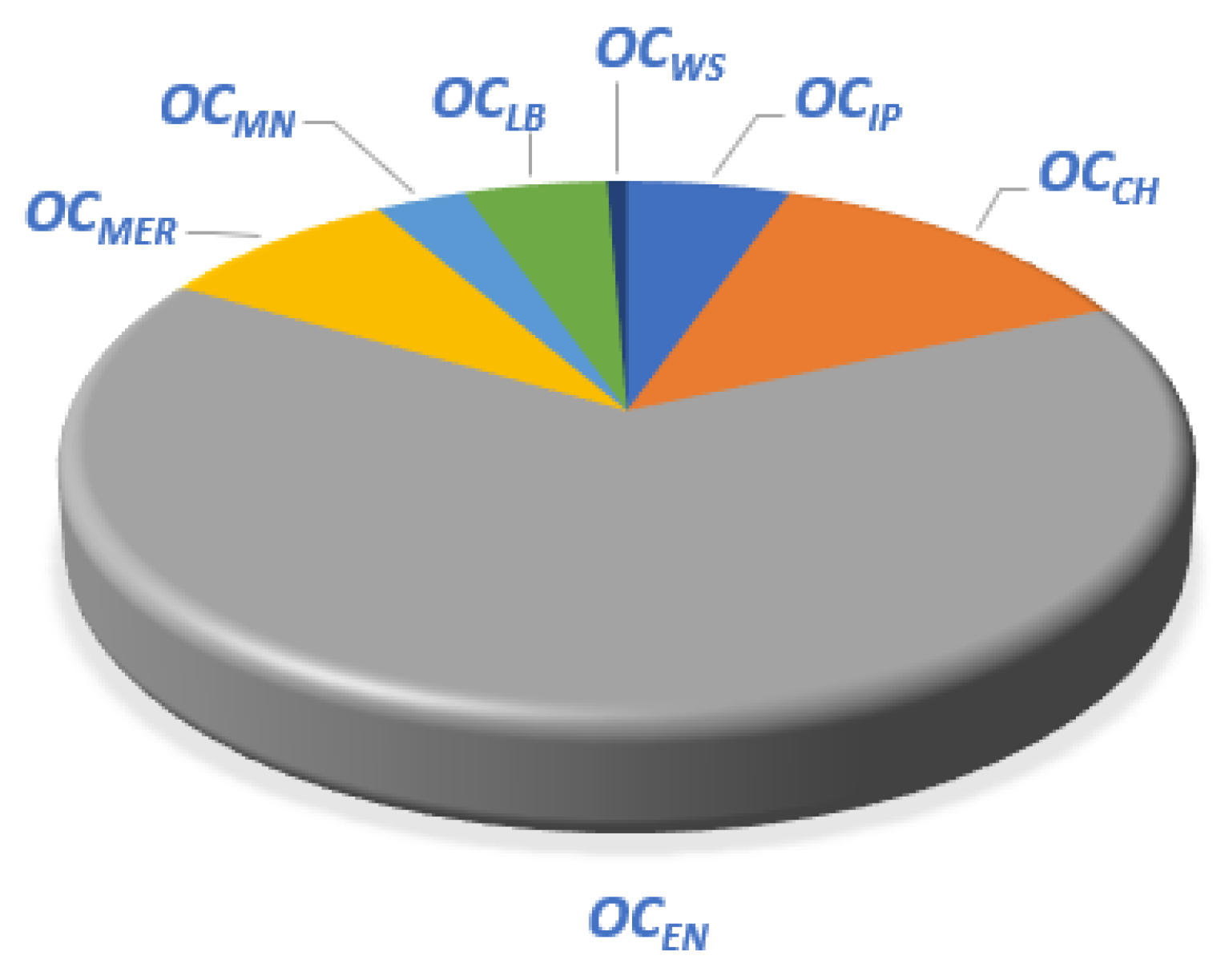
Figure 8 that in the cost of SWRO, the
OCEN accounts for the highest proportion of the overall cost, exceeding 50% of the overall cost, and the remaining costs account for a small proportion. It can be seen from
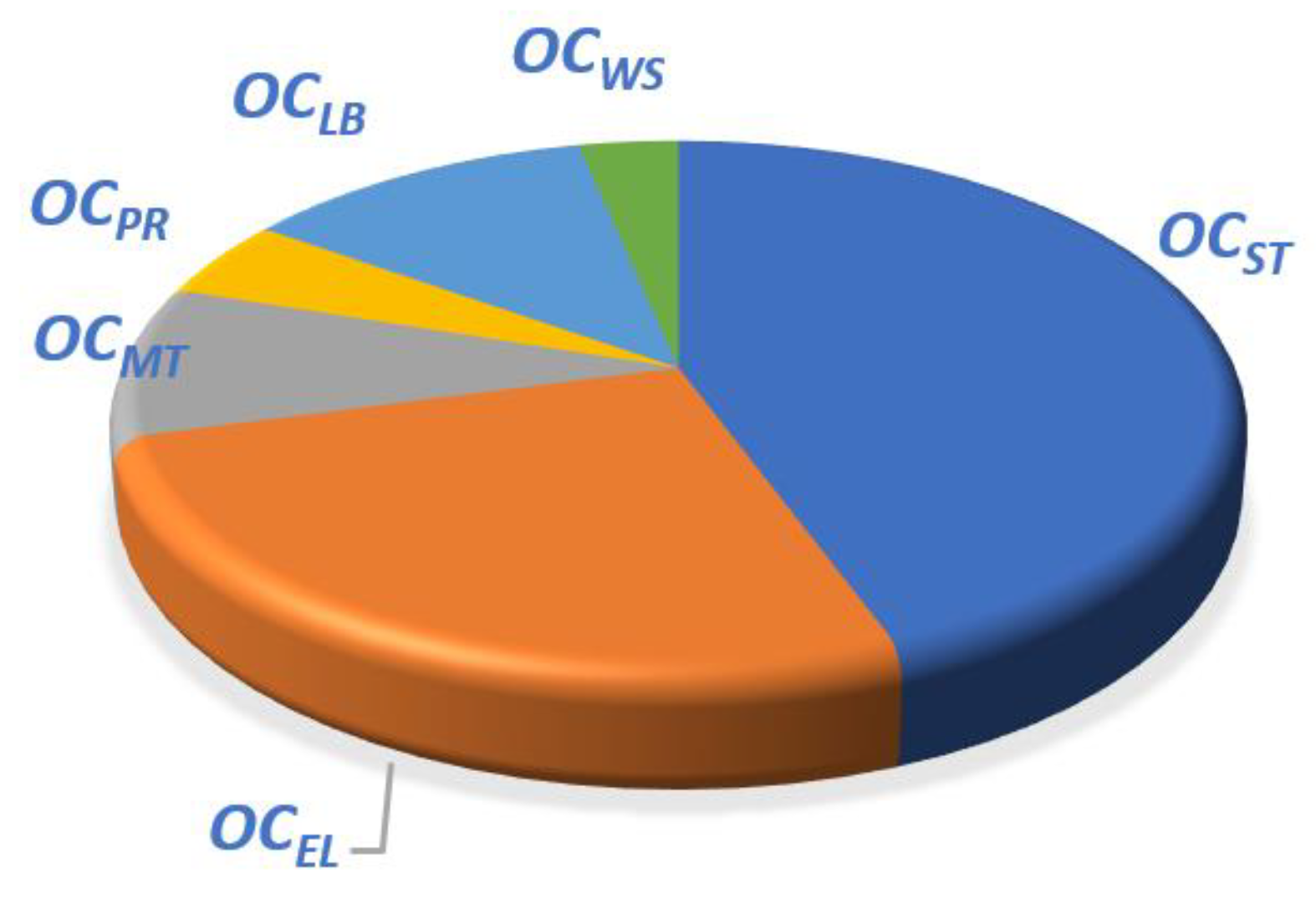
Figure 9 that among the OT-MSF costs, the
OCST accounts for the highest proportion of the overall cost, followed by the system power consumption cost, and the remaining costs account for a relatively low proportion. On the whole, the operation cost of SWRO and MSF system is 1:2, and both account for the highest proportion in the power consumption of the two processes.