1. Introduction
With the advancement of industrialization and urbanization, the discharge of wastewater has become increasingly uncontrolled, resulting in a series of environmental problems and a global water shortage. As water usage is a key operational aspect of most industrial processes, the generation of a large amount of industrial wastewater is inevitable [
1,
2]. With the significant increase in the world’s energy consumption, in order to meet the demand for increasing electricity consumption, coal-fired power plants have been intensively utilized [
3]. Water is an essential and fundamental resource in thermal power plants with various uses: as a make-up for boiler feed water, in the cooling of bearings and equipment, and in various plant services. Nowdays, China has formed a coal-based energy production structure with oil, natural gas, electricity, and other energies complementing each other. Coal-based electricity accounts for about 90% of energy production [
4]. Therefore, a large amount of water is used in coal-fired power plants in China. It has become very important to treat and reuse the wastewater from coal-fired power plants, especially in Central and Western China, due to water shortages.
Compared with seawater, wastewater from coal-fired power plants has a high pH and COD (chemical oxygen demand) and a complex water quality, which make treatment and reuse very difficult [
5]. Coal-fired power plants’ wastewater is mainly divided into two categories: saline wastewater and organic wastewater [
6]. Saline wastewater comes from recycling systems, such as circulating water systems and chemical water station drainage, mainly containing inorganic salts, such as Cl
−, SO
42−, Na
+, and Ca
2+. Based on TDS, it can be classified into low-saline and high-salt water. The TDS of low-saline water is usually less than 10,000 mg/L and that of high-salt water is usually 10,000~20,000 mg/L. The organic wastewater produced by coal-fired power plants comes from gasification process wastewater, coal-water slurry, and black water of dry coal-pulverized entrained flow gasification, etc. It mainly contains phenol, naphthalene, anthracene, and thiophene. These are all refractory organics with poor biodegradability and are highly difficult to treat, requiring biochemical treatment. Saline water makes up a large share of wastewater in coal-fired power plants, and thus more efforts should be made to desalinate and reuse the wastewater.
So far, the desalination methods for saline wastewater treatment from coal-fired power plants mainly include membrane technology and thermal technology. Among them, membrane technology mainly includes microfiltration (MF), ultrafiltration (UF), nanofiltration (NF), and reverse osmosis (RO), etc. Thermal technology mainly includes multi-stage flash (MSF), multiple effect distillation (MED), and vapor compression (VC), etc. [
7,
8,
9]. Reverse osmosis (RO) technology is extensively adopted in the treatment of wastewater from coal-fired power plants due to the advantages of high efficiency, simple operation, and maintenance of biological activity [
10,
11]. However, the operational efficiency of RO-based desalination systems is greatly affected by the feeding conditions of wastewater [
12]. Therefore, it is of great significance to study the inherent operating characteristics of RO-based wastewater desalination systems so as to take effective measures to reduce the energy consumption and operational costs of these systems. For this reason, a mechanistic model is required to simulate and study the RO-based desalination process, at the same time enabling the operational optimization of the process.
Reverse osmosis seawater (SWRO) desalination is a typical resource treatment method of concentrated brine desalination. Malek et al. [
13] established a model of a large-scale seawater desalination plant, including seawater intake and a pretreatment model, a high-pressure pump model, an energy recovery system model, and an RO process model. Based on these models, a replacement plan for membrane elements, system investment cost, and operating cost were provided, and an economic analysis was also carried out. Based on the solution–diffusion theory, Al-Bastaki et al. [
14] established a mechanistic model of hollow fiber RO membranes, which considered the effects of pressure drops and concentration polarization. Considering the complex spatiotemporal variability of the membrane modules in the RO process, Karabelas et al. [
15] proposed a “scale separation” global structured modeling method to develop a comprehensive SWRO system model. Al-Enezi et al. [
16] gave the main structure of the RO system, which mainly includes one-stage, two-stage, and two-pass RO devices, and analyzed the effect of feed concentration and temperature on the salt rejection rate of the RO system. Oh et al. [
17] gave a system model of SWRO based on solution–diffusion theory and studied the relationship between recovery rate and permeate flux and other performance aspects of the RO system. Kaghazchi et al. [
18] presented an RO system mechanistic model of two desalination plants in the Persian Gulf region and analyzed the influence of operating parameters on system performance. Lu et al. [
19] established a mathematical model of the desalination process unit, predicted the impact of operating parameters on the RO process under different conditions through simulation analysis, and gave the relevant economic model.
Using a detailed mathematical model of the RO-based desalination process, the optimized operation could be obtained by solving its corresponding optimization problem. In 2005, Marcovecchio et al. [
20] established the mechanistic model of the hollow fiber membrane system and the economic model of the RO system, discretized the model by using the PR algorithm, and finally solved the optimization problem by GAMS. In 2007, Luo et al. [
21] used the average value of the parameters of the membrane element model simplification of the differential solution operation. In 2013, Kim et al. [
22] transformed the implicit mathematical model of the desalination process into an explicit model by converting the exponential function into a second-order polynomial and tested the accuracy, rapidity, and robustness of this method. In 2017, Gong et al. [
23] used the finite element configuration method to discretize the differential equations in the membrane RO process model and optimized the solution by GAMS. In 2021, Blechschmidt et al. [
24] used neural networks to solve the differential equations; this method is significant for RO system performance research.
In addition to using mechanistic modeling to analyze the RO process, some researchers have proposed a new method in recent years. In 2021, Cai et al. [
25] used artificial neural network (ANN) and multilinear regression (MLR) techniques to model industrial RO concentrate processing. The performance of the models in predicting total organic carbon removal and sludge production in reverse osmosis concentrate treatment was evaluated and the ANN model’s predictive accuracy was validated. In 2021, Wang et al. [
26] developed an ion transport model for RO, referred to as the solution–friction model, by rigorously considering the mechanisms of partitioning and the interactions among water, salt ions, and the membrane. Ion transport through the membrane is described by the extended Nernst–Planck equation, with the consideration of frictions between species. The model is validated using experimental measurements of salt rejection and permeate water flux in a lab-scale, cross-flow RO setup. Lastly, the pressure drop distribution across the membrane was analyzed by means of a framework. Bonny et al. [
27] suggested a novel and efficient approach to determining transmembrane pressure using Deep Reinforcement Learning (DRL) and used a Deep Deterministic Policy Gradient (DDPG) agent to adjust the pressure across a membrane.
The above studies provide strong support for the modeling and solution of the RO process of membrane desalination, but most studies are mainly aimed at the desalination process of seawater or specific brines. It is known that there are few studies on modeling the wastewater treatment process of coal-fired power plants. Cai, Bonny, Salgado-Reyna, and Al-Obaidi et al. [
25,
27,
28,
29] used intelligent algorithms to model and analyze the RO process. These excellent studies used intelligent algorithms for research analysis; unfortunately, there may be some uncertainty in the analytic process. In this study, a mechanistic modeling method is applied to the treatment of coal-fired power plant wastewater so that the internal operation of the RO membrane can be seen intuitively. Most studies which establish mechanistic modeling are mainly aimed at the desalination process of seawater or specific brines, and there are few studies on the treatment of coal-fired power plant wastewater. Hence, a further improvement of the above models is required before they can be used for the simulation and operational optimization of the membrane treatment process of coal-fired power plant wastewater. Similarly, this study of coal-fired power plant wastewater treatment is relevant to the study of actual plants.
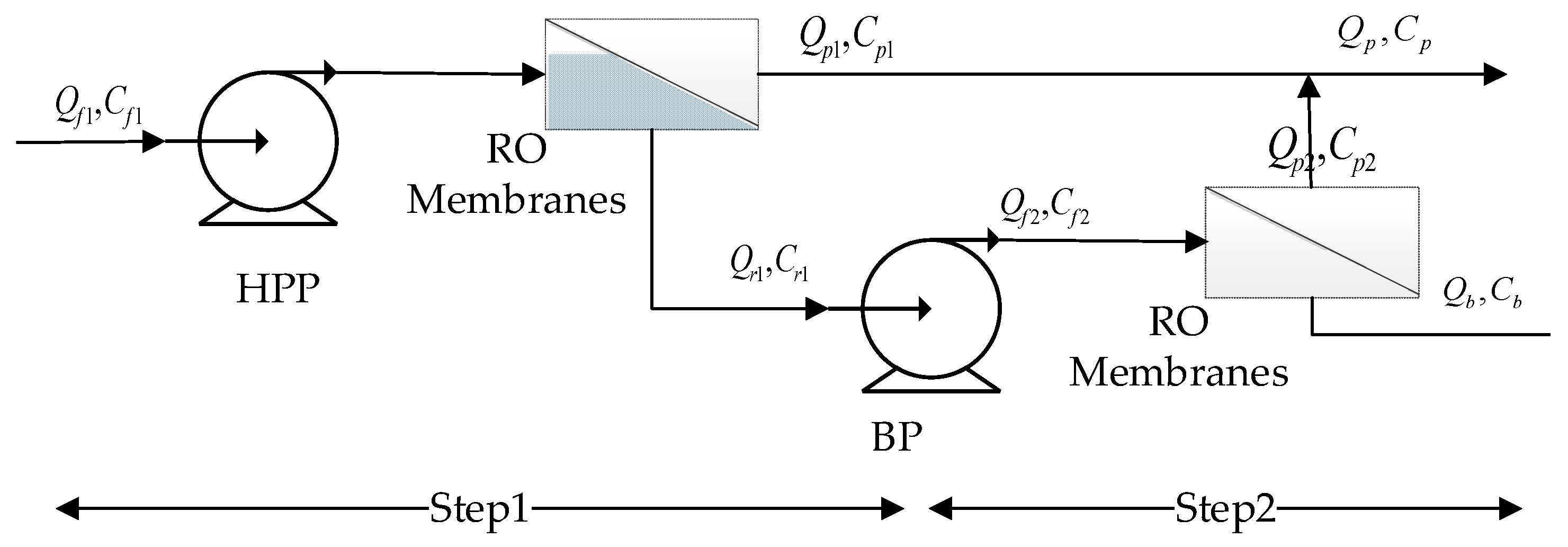
Therefore, in order to realize the efficient operation of coal-fired power plant wastewater treatment processes, this paper establishes a mechanistic model of an RO-based desalination system for coal-fired power plant wastewater treatment based on the theory of dissolution and diffusion, energy conservation, and material conservation. Then, aiming at the mismatch of model parameters, the parameters of the model are identified to obtain an accurate coal-fired power plant wastewater membrane treatment process model. Finally, the whole process is simulated and optimized to obtain the production process state and to determine mutual influence relationships, as well as the optimal operation strategy, so as to realize the optimal operation of the production process for the membrane treatment of coal-fired power plant wastewater.
6. Conclusions
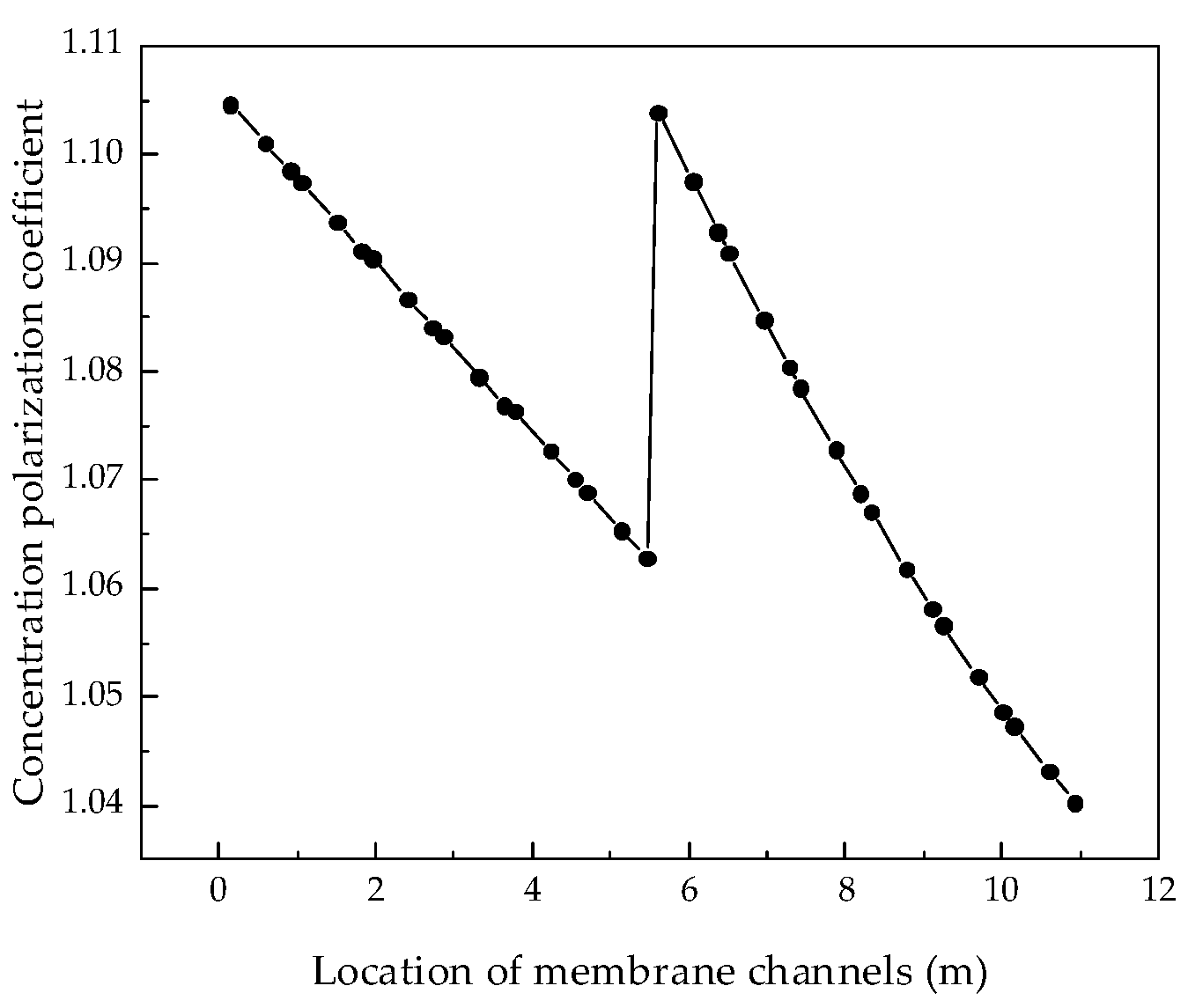
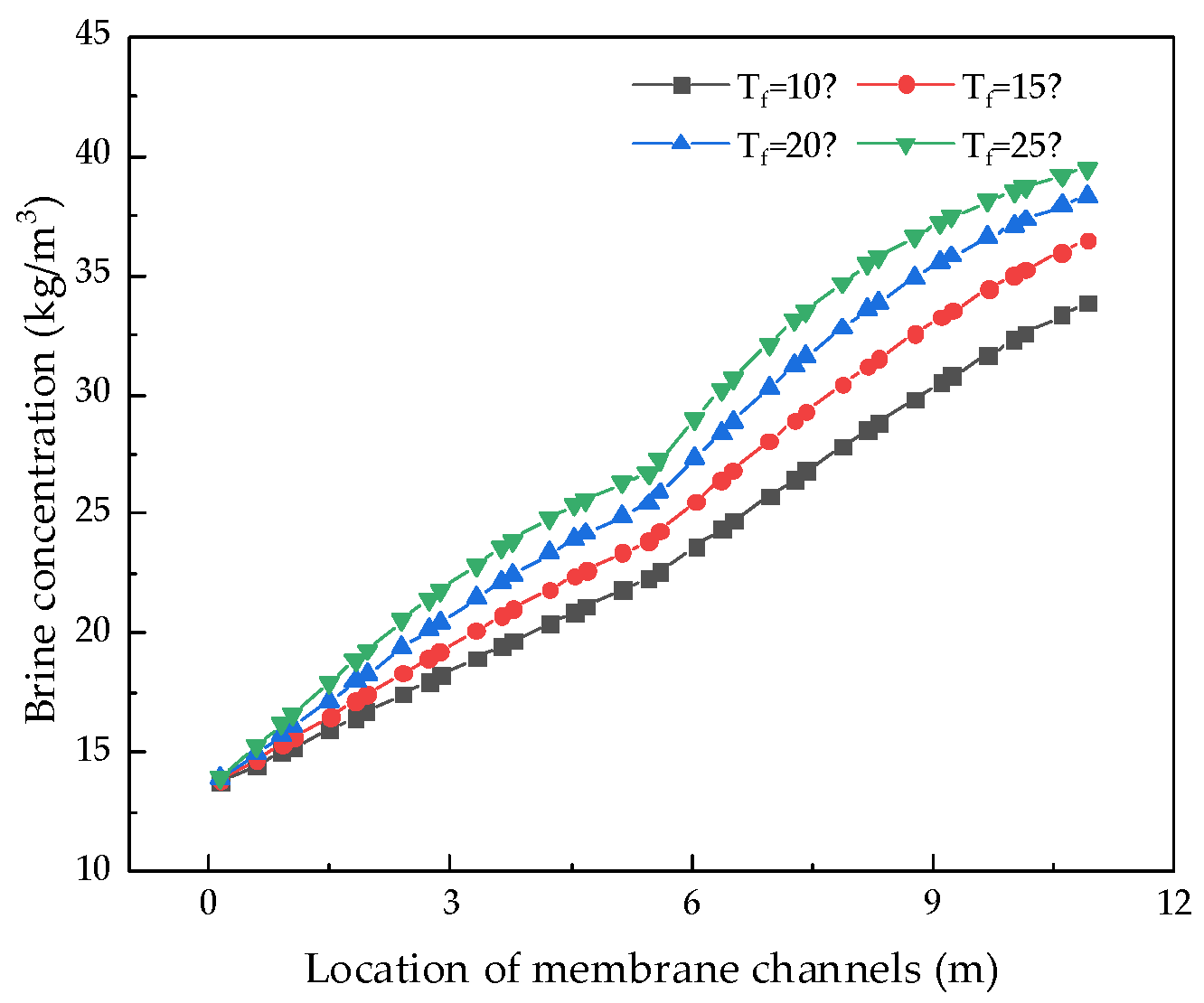
RO technology is important not only for seawater desalination but also for coal-fired power plant wastewater treatment. In this paper, a coal-fired power plant system in Inner Mongolia was taken as an example to study the simulation and optimization of the membrane treatment process of coal-fired power plant wastewater. Firstly, based on the solution–diffusion theory, pressure drop, and osmotic concentration polarization phenomena, a mechanistic model equation of the RO process of coal-fired power plant wastewater treatment was completed by drawing on the seawater desalination process. Through the correction of model parameters, a system model suitable for coal-fired power plant wastewater treatment was obtained. Secondly, in view of the opaqueness of the resource treatment process, a simulation analysis of the coal-fired power plant wastewater treatment process was carried out and internal data for the coal-fired power plant wastewater RO treatment process were obtained, realizing the transparent management of the system. Finally, an optimization analysis of the coal-fired power plant wastewater treatment system was carried out.
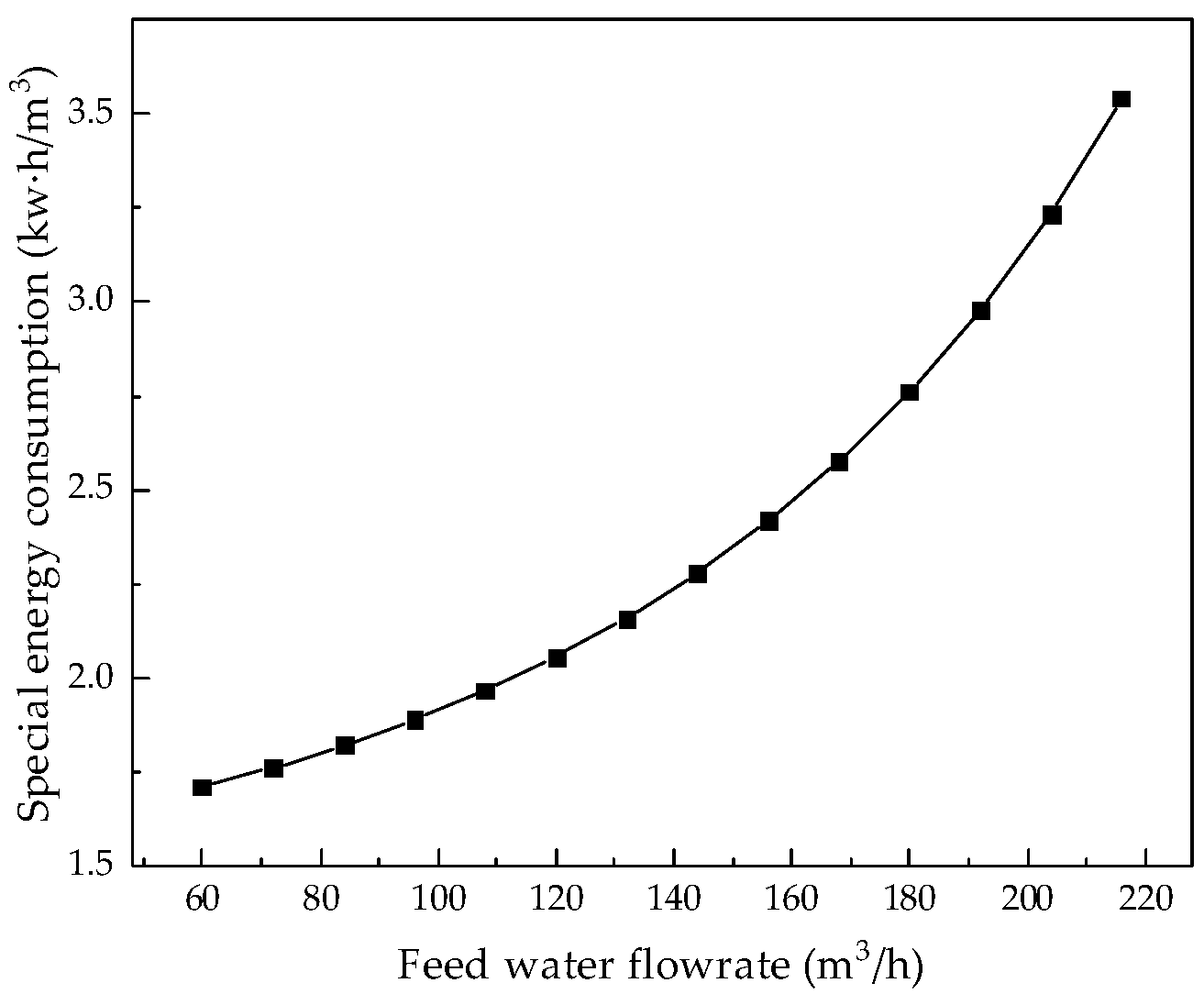
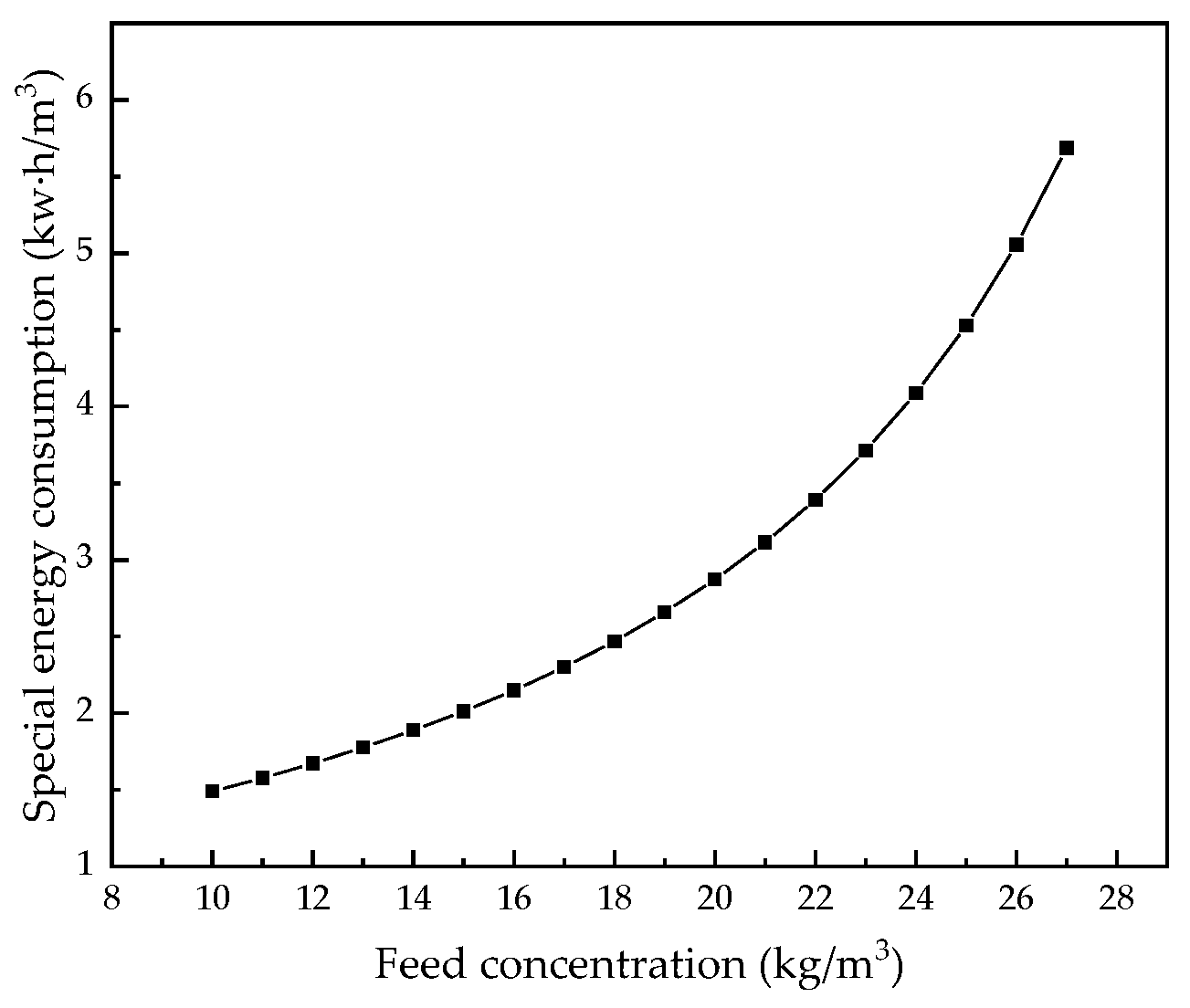
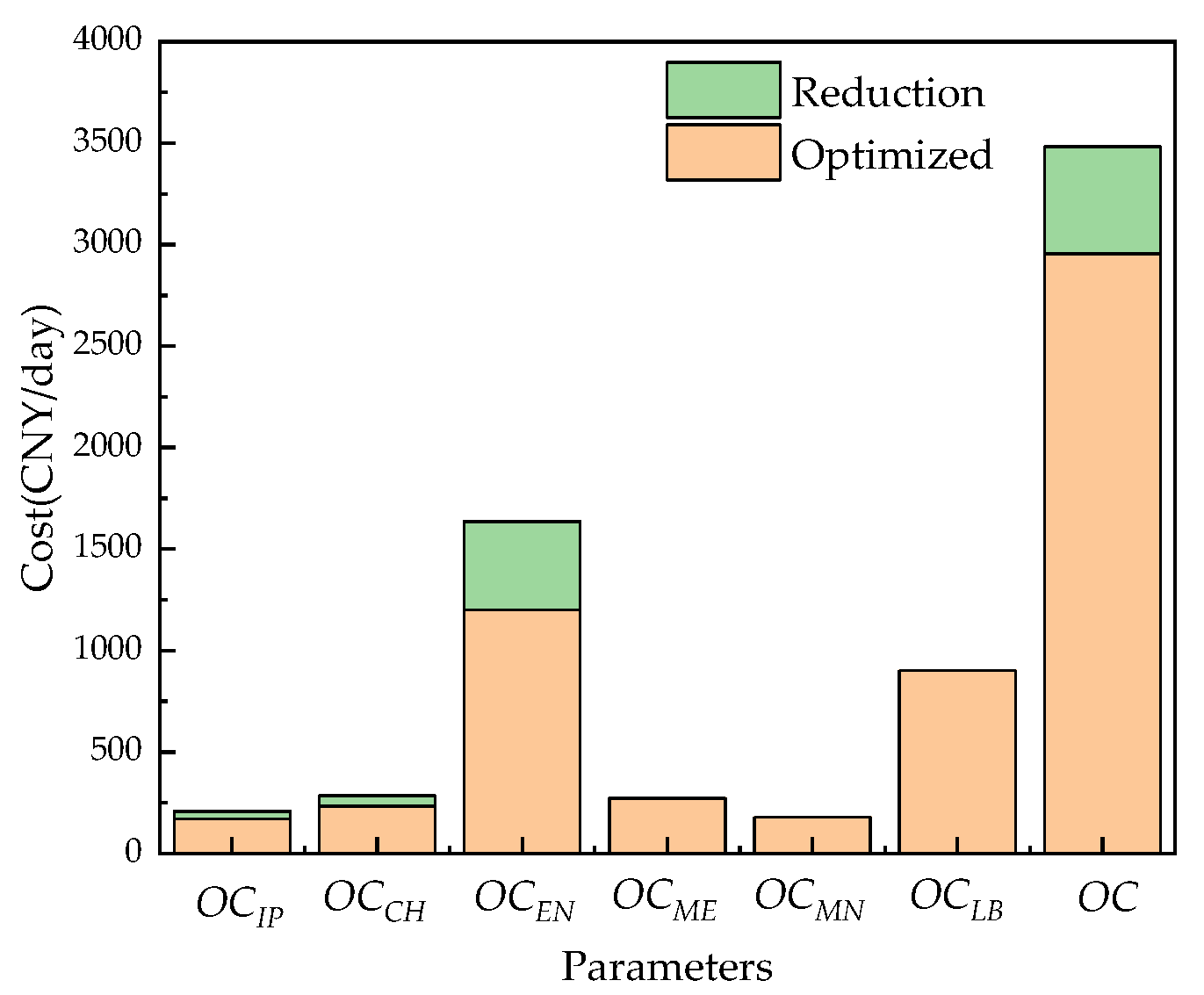
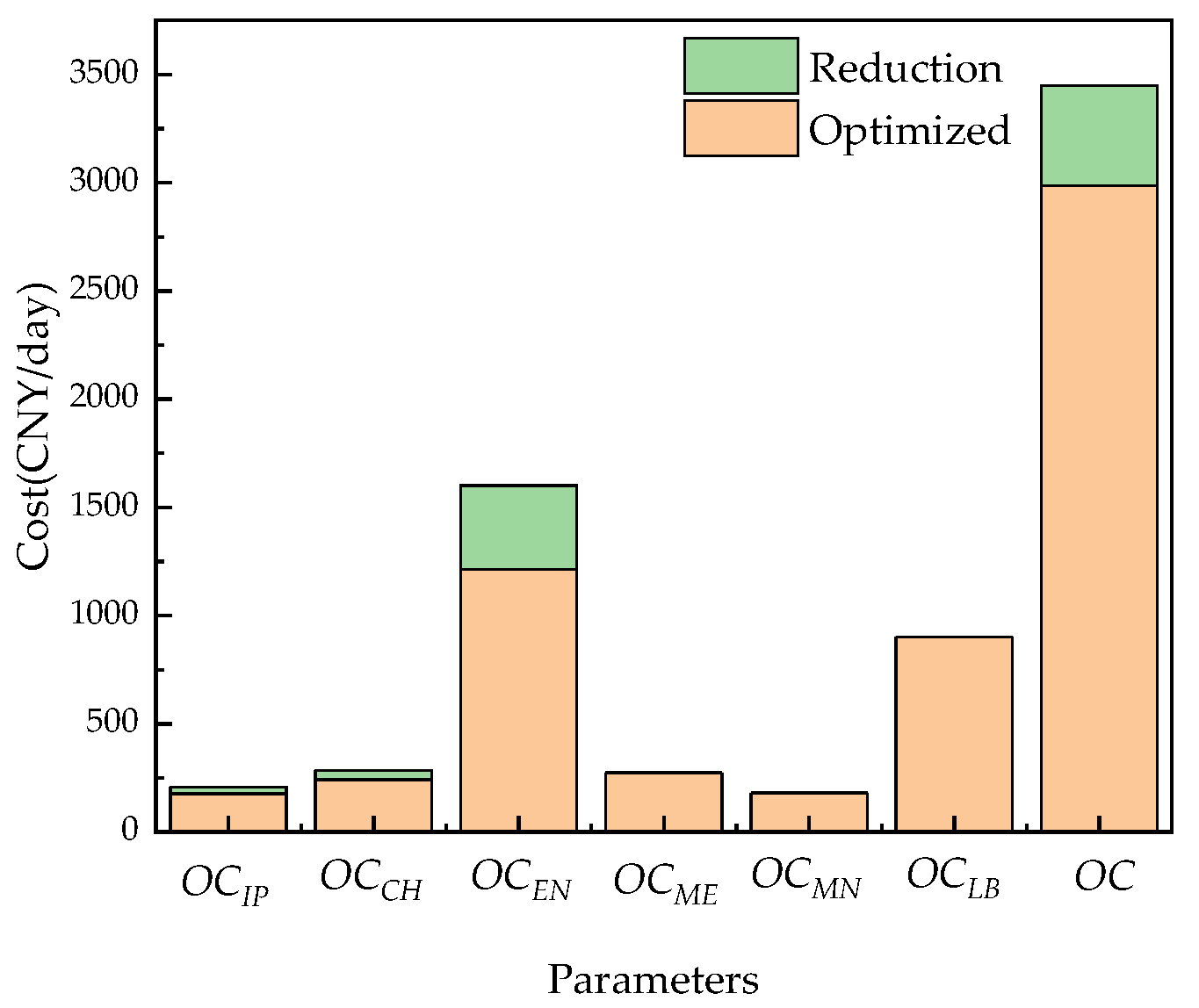
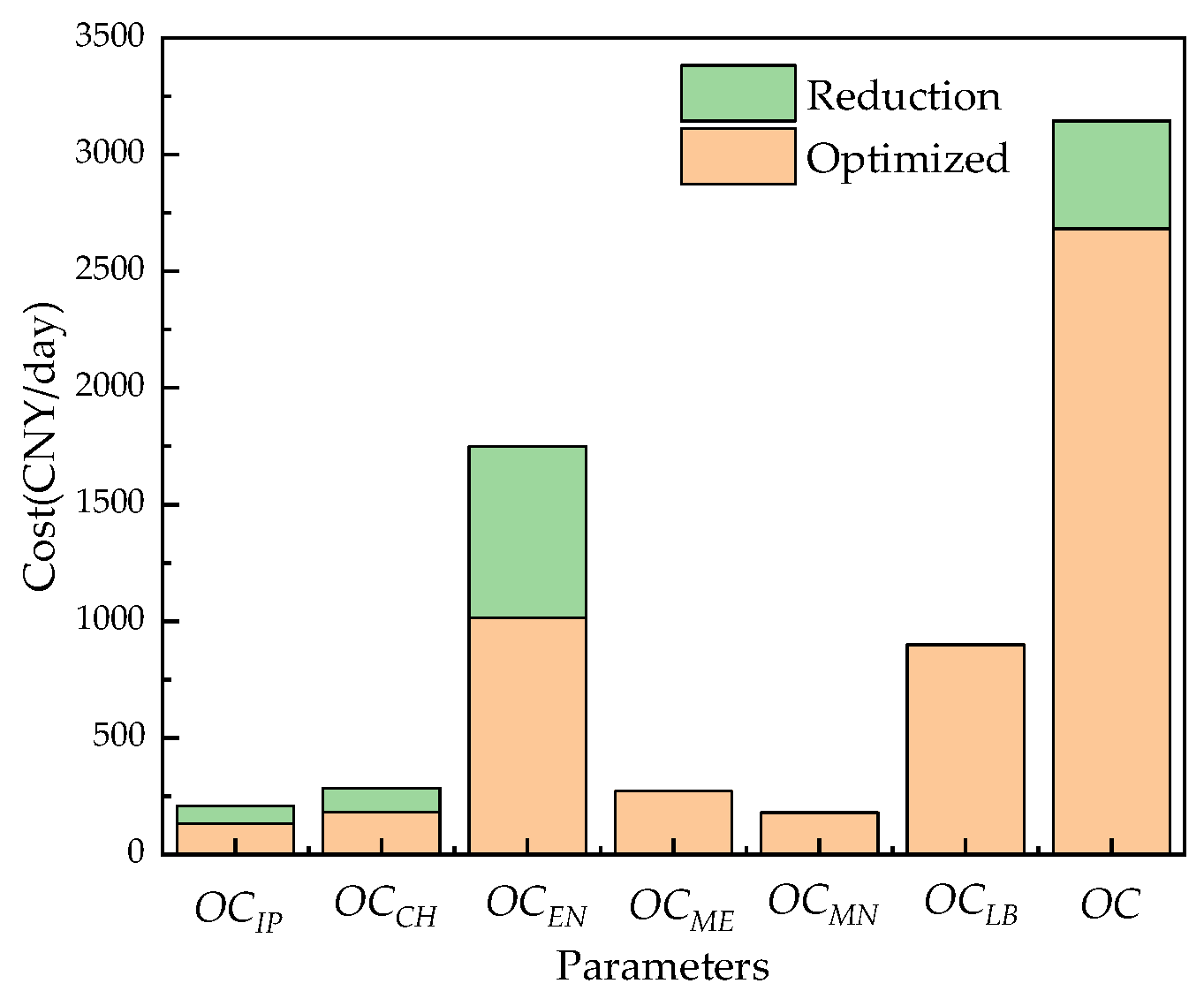
Focusing on the problem of high energy consumption in the resource treatment of coal-fired power plant wastewater by the RO process, an optimization and analysis of a coal-fired power plant wastewater RO treatment system was carried out. To begin with, an optimization analysis of three different working conditions was performed, with the lowest specific energy consumption as the optimization goal. The water recovery rate was increased by 11.2%, 9.0%, and 20.7%, and the specific energy consumption was decreased by 23.6%, 18.6%, and 42.6%, respectively, which fully proved the effectiveness of the optimization strategy. Afterwards, taking the lowest average daily operating cost as the optimization goal, the same three working conditions were analyzed. The average daily operating costs of the system were reduced by 526.9 CNY/day, 462.4 CNY/day, and 911.1 CNY/day, which also proved the effectiveness of the optimization strategy. Therefore, the simulation and optimization research on the recycling process of coal-fired power plant wastewater presented here can promote the treatment of coal-fired power plant wastewater and is significant for the development of zero-emission coal-fired power plant wastewater treatment systems.