Effect of Membrane Orientation and Concentration of Draw Solution on the Behavior of Commercial Osmotic Membrane in a Novel Dynamic Forward Osmosis Tests
Abstract
:1. Introduction
2. Theoretical Background
2.1. Reverse Osmosis
2.2. Forward Osmosis
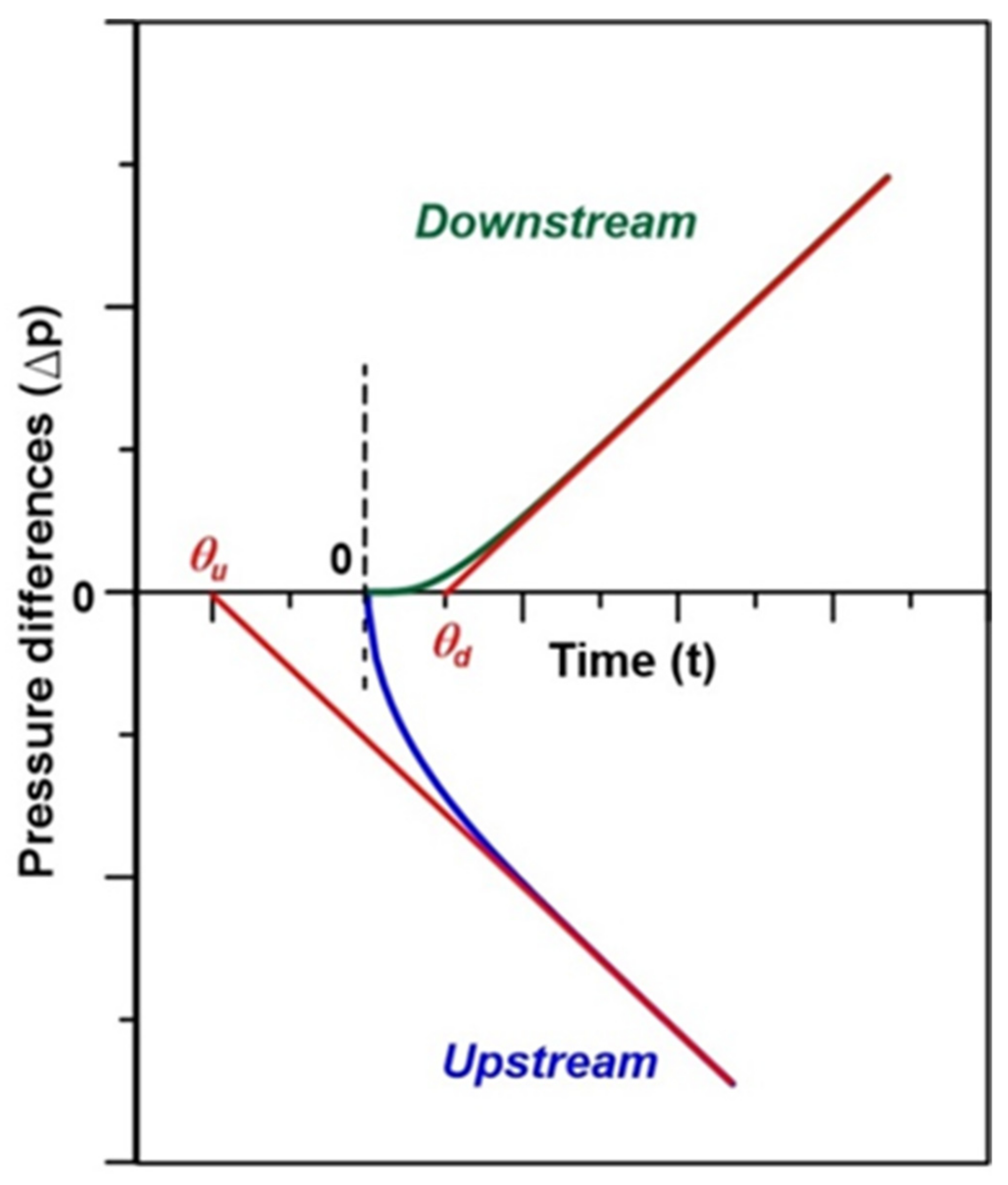
2.3. Time-Lag Method
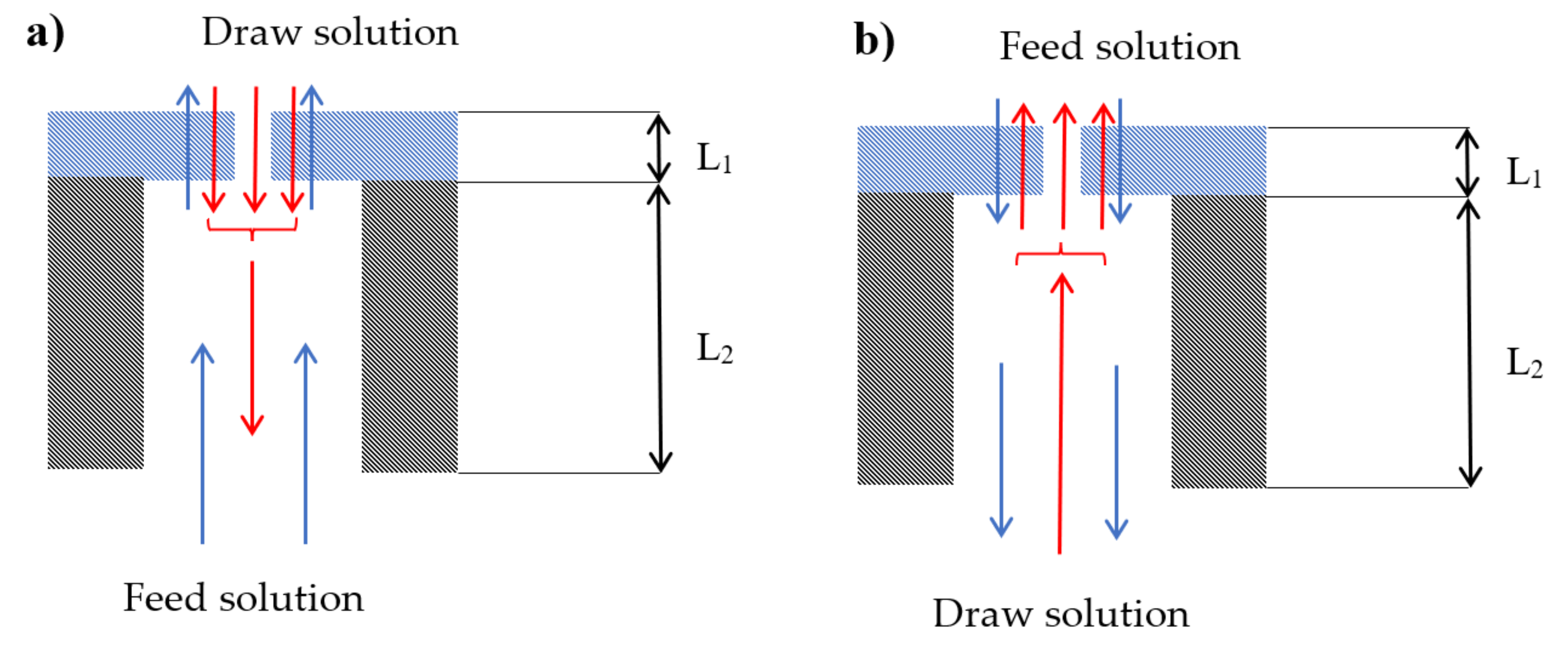
3. Materials and Methods
4. Results and Discussion
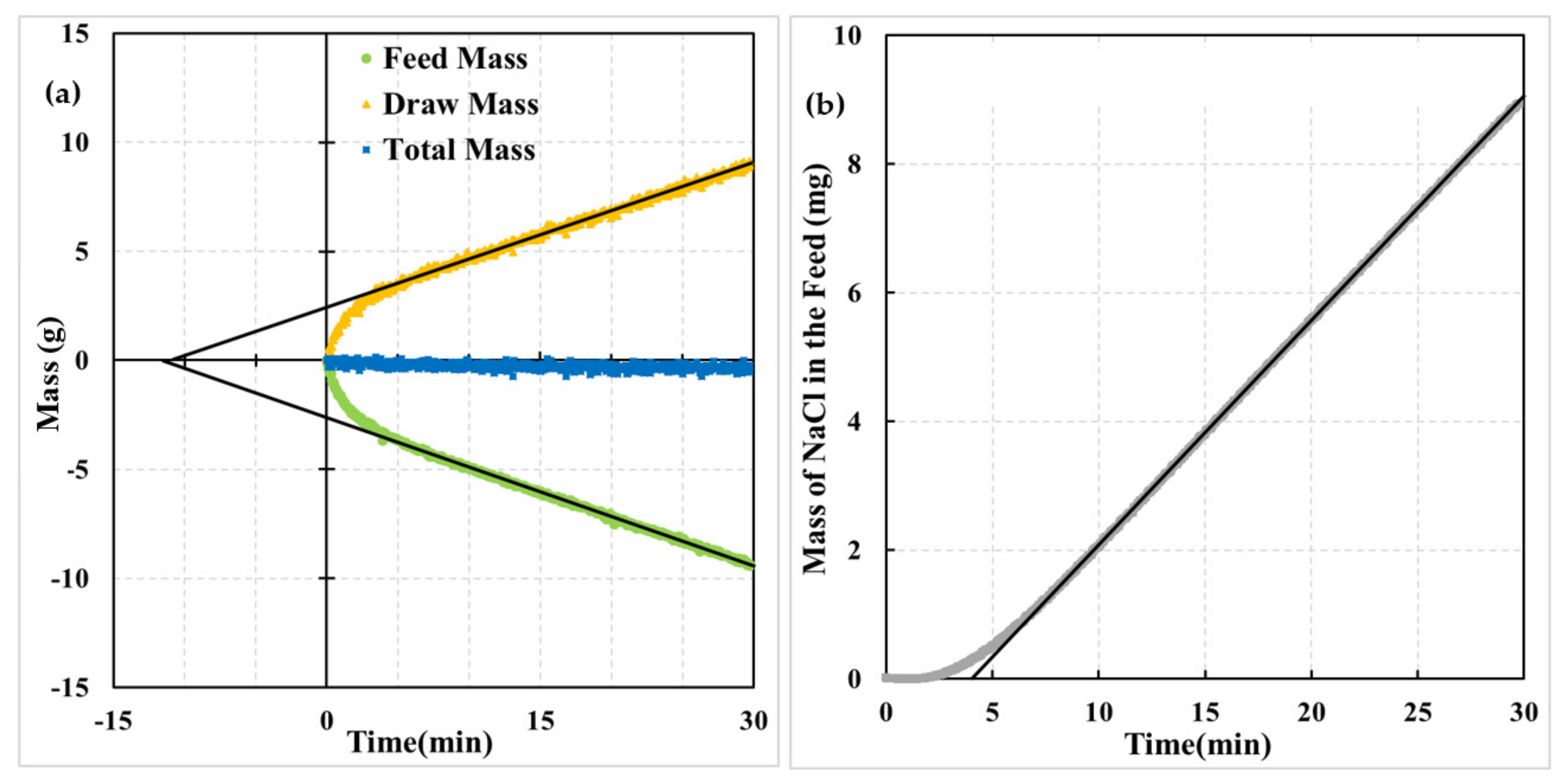
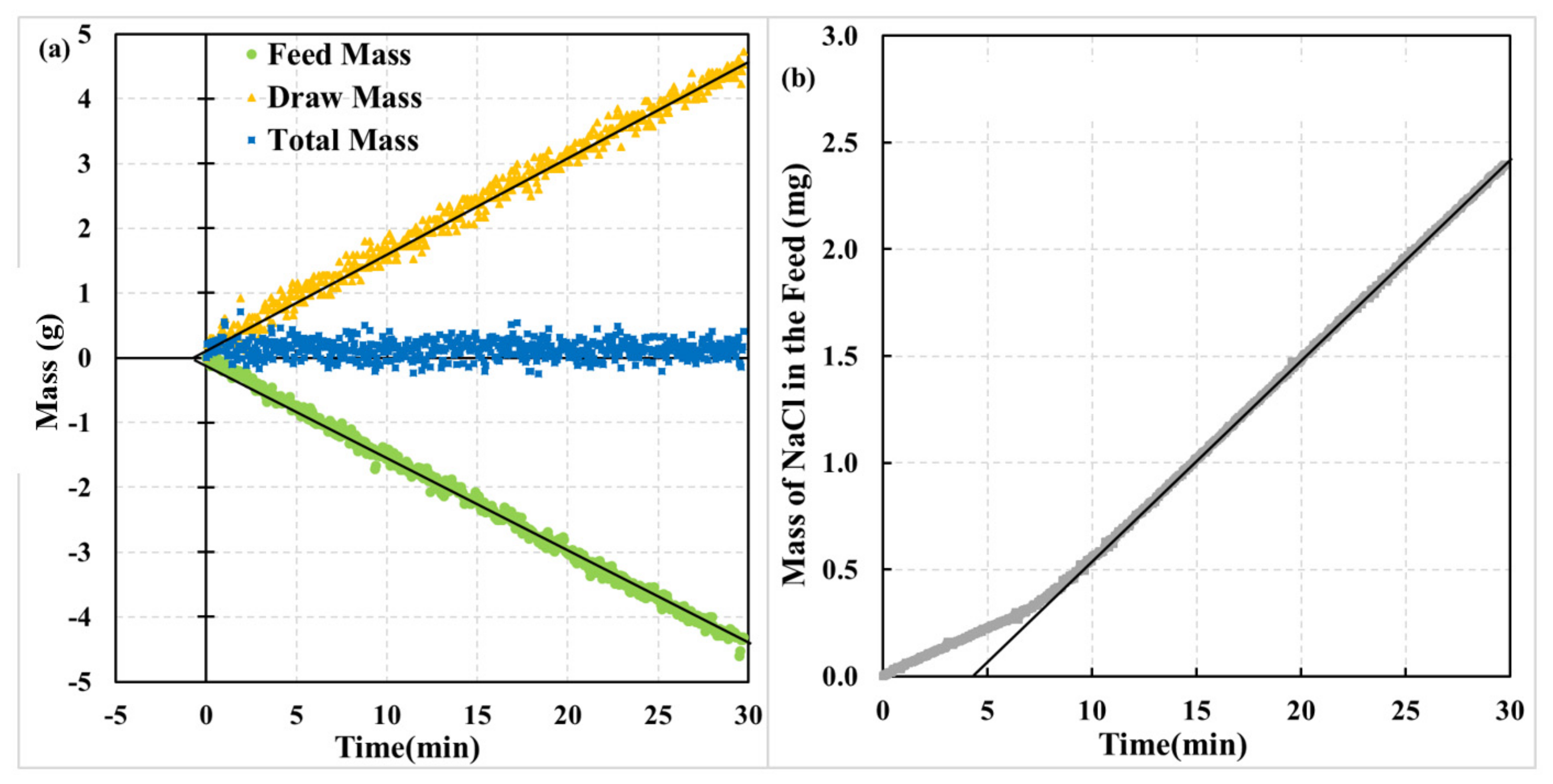
4.1. Effect of Membrane Orientation
4.2. Physical Interpretation of Dynamic Experiments
4.3. The Effect of Draw Solution Concentration
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Suwaileh, W.; Pathak, N.; Shon, H.; Hilal, N. Forward osmosis membranes and processes: A comprehensive review of research trends and future outlook. Desalination 2020, 485, 114455. [Google Scholar] [CrossRef]
- Wang, Y.-N.; Goh, K.; Li, X.; Setiawan, L.; Wang, R. Membranes and processes for forward osmosis-based desalination: Recent advances and future prospects. Desalination 2017, 434, 81–99. [Google Scholar] [CrossRef]
- Ang, W.L.; Mohammad, A.W.; Johnson, D.; Hilal, N. Forward osmosis research trends in desalination and wastewater treatment: A review of research trends over the past decade. J. Water Process Eng. 2019, 31, 100886. [Google Scholar] [CrossRef]
- Ang, W.L.; Mohammad, A.W.; Johnson, D.; Hilal, N. Unlocking the application potential of forward osmosis through integrated/hybrid process. Sci. Total Environ. 2019, 706, 136047. [Google Scholar] [CrossRef] [Green Version]
- Haupt, A.; Lerch, A. Forward Osmosis Application in Manufacturing Industries: A Short Review. Membranes 2018, 8, 47. [Google Scholar] [CrossRef] [Green Version]
- Cath, T.Y.; Childress, A.E.; Elimelech, M. Forward osmosis: Principles, applications, and recent developments. J. Membr. Sci. 2006, 281, 70–87. [Google Scholar] [CrossRef]
- Xu, W.; Chen, Q.; Ge, Q. Recent advances in forward osmosis (FO) membrane: Chemical modifications on membranes for FO processes. Desalination 2017, 419, 101–116. [Google Scholar] [CrossRef]
- Manickam, S.S.; McCutcheon, J.R. Understanding mass transfer through asymmetric membranes during forward osmosis: A historical perspective and critical review on measuring structural parameter with semi-empirical models and characterization approaches. Desalination 2017, 421, 110–126. [Google Scholar] [CrossRef]
- Loeb, S. Effect of porous support fabric on osmosis through a Loeb-Sourirajan type asymmetric membrane. J. Membr. Sci. 1997, 129, 243–249. [Google Scholar] [CrossRef]
- Cath, T.Y.; Elimelech, M.; McCutcheon, J.R.; McGinnis, R.L.; Achilli, A.; Anastasio, D.; Brady, A.R.; Childress, A.E.; Farr, I.V.; Hancock, N.T.; et al. Standard Methodology for Evaluating Membrane Performance in Osmotically Driven Membrane Processes. Desalination 2013, 312, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.; Lee, S.; Hong, S. A novel analysis of reverse draw and feed solute fluxes in forward osmosis membrane process. Desalination 2014, 352, 128–135. [Google Scholar] [CrossRef]
- Tiraferri, A.; Yip, N.Y.; Straub, A.; Castrillón, S.R.-V.; Elimelech, M. A method for the simultaneous determination of transport and structural parameters of forward osmosis membranes. J. Membr. Sci. 2013, 444, 523–538. [Google Scholar] [CrossRef]
- Bilad, M.; Qing, L.; Fane, A.G. Non-linear least-square fitting method for characterization of forward osmosis membrane. J. Water Process Eng. 2018, 25, 70–80. [Google Scholar] [CrossRef]
- Kim, J.; Kim, B.; Kim, D.I.; Hong, S. Evaluation of apparent membrane performance parameters in pressure retarded osmosis processes under varying draw pressures and with draw solutions containing organics. J. Membr. Sci. 2015, 493, 636–644. [Google Scholar] [CrossRef]
- Bui, N.-N.; Arena, J.T.; McCutcheon, J.R. Proper accounting of mass transfer resistances in forward osmosis: Improving the accuracy of model predictions of structural parameter. J. Membr. Sci. 2015, 492, 289–302. [Google Scholar] [CrossRef] [Green Version]
- Martin, J.T.; Kolliopoulos, G.; Papangelakis, V.G. An improved model for membrane characterization in forward osmosis. J. Membr. Sci. 2019, 598, 117668. [Google Scholar] [CrossRef]
- Kim, B.; Gwak, G.; Hong, S. Review on methodology for determining forward osmosis (FO) membrane characteristics: Water permeability (A), solute permeability (B), and structural parameter (S). Desalination 2017, 422, 5–16. [Google Scholar] [CrossRef]
- Barrer, R.M.; Rideal, E.K. Permeation, diffusion and solution of gases in organic polymers. Trans. Faraday Soc. 1939, 35, 628–643. [Google Scholar] [CrossRef]
- Lashkari, S.; Kruczek, B. Effect of resistance to gas accumulation in multi-tank receivers on membrane characterization by the time lag method. Analytical approach for optimization of the receiver. J. Membr. Sci. 2010, 360, 442–453. [Google Scholar] [CrossRef]
- Bai, D.; Asempour, F.; Kruczek, B. Can the time-lag method be used for the characterization of liquid permeation membranes? Chem. Eng. Res. Des. 2020, 162, 228–237. [Google Scholar] [CrossRef]
- Al-Ismaily, M.; Wijmans, J.; Kruczek, B. A shortcut method for faster determination of permeability coefficient from time lag experiments. J. Membr. Sci. 2012, 423–424, 165–174. [Google Scholar] [CrossRef]
- Ismail, A.F.; Matsuura, T. Progress in transport theory and characterization method of Reverse Osmosis (RO) membrane in past fifty years. Desalination 2017, 434, 2–11. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Johnson, D.J.; Suwaileh, W.A.; Mohammad, A.W.; Hilal, N. Osmotic’s potential: An overview of draw solutes for forward osmosis. Desalination 2018, 434, 100–120. [Google Scholar] [CrossRef] [Green Version]
- Yip, N.Y.; Tiraferri, A.; Phillip, W.A.; Schiffman, J.D.; Elimelech, M. High Performance Thin-Film Composite Forward Osmosis Membrane. Environ. Sci. Technol. 2010, 44, 3812–3818. [Google Scholar] [CrossRef]
- Wu, H. Gas Membrane Characterization via the Time-Lag Method for Neat and Mixed-Matrix Membranes. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2020. [Google Scholar]
- Fraga, S.; Monteleone, M.; Lanč, M.; Esposito, E.; Fuoco, A.; Giorno, L.; Pilnáček, K.; Friess, K.; Carta, M.; McKeown, N.; et al. A novel time lag method for the analysis of mixed gas diffusion in polymeric membranes by on-line mass spectrometry: Method development and validation. J. Membr. Sci. 2018, 561, 39–58. [Google Scholar] [CrossRef]
- Al-Qasas, N.; Thibault, J.; Kruczek, B. A new characterization method of membranes with nonlinear sorption isotherm systems based on continuous upstream and downstream time-lag measurements. J. Membr. Sci. 2017, 542, 91–101. [Google Scholar] [CrossRef]
- Shaffer, D.L.; Werber, J.R.; Jaramillo, H.; Lin, S.; Elimelech, M. Forward Osmosis: Where Are We Now? Desalination 2015, 356, 271–284. [Google Scholar] [CrossRef]
- Ghanbari, M.; Emadzadeh, D.; Lau, W.; Riazi, H.; Almasi, D.; Ismail, A.F. Minimizing structural parameter of thin film composite forward osmosis membranes using polysulfone/halloysite nanotubes as membrane substrates. Desalination 2016, 377, 152–162. [Google Scholar] [CrossRef]
- Wang, K.Y.; Chung, T.-S.; Amy, G. Developing thin-film-composite forward osmosis membranes on the PES/SPSf substrate through interfacial polymerization. AIChE J. 2011, 58, 770–781. [Google Scholar] [CrossRef]
- Li, X.; Wang, K.Y.; Helmer, B.; Chung, N.T.-S. Thin-Film Composite Membranes and Formation Mechanism of Thin-Film Layers on Hydrophilic Cellulose Acetate Propionate Substrates for Forward Osmosis Processes. Ind. Eng. Chem. Res. 2012, 51, 10039–10050. [Google Scholar] [CrossRef]
- Qasim, M.; Badrelzaman, M.; Darwish, N.N.; Darwish, N.A.; Hilal, N. Reverse osmosis desalination: A state-of-the-art review. Desalination 2019, 459, 59–104. [Google Scholar] [CrossRef] [Green Version]
- Bilad, M.R.; Declerck, P.; Piasecka, A.; Vanysacker, L.; Yan, X.; Vankelecom, I.F. Development and validation of a high-throughput membrane bioreactor (HT-MBR). J. Membr. Sci. 2011, 379, 146–153. [Google Scholar] [CrossRef]

| Componet | Description | Supplier |
|---|---|---|
| V1–V4 | On/off valves, 4757K18 | McMaster-Carr, USA |
| V5–V8 | Diverting ball valves, 4757K62 | McMaster-Carr, USA |
| FM1, FM2 | 0–4 LPM flowmeters | Blue-White Indust., USA |
| PG1, PG2 | 0–3 psig pressure gauges | McMaster-Carr, USA |
| B1, B2 | 0.01 g resolution balances, 6202-1S | Entris Precision, Germany |
| P1, P2 | Centrifugal pumps P1 and P2, TE-3-MD-HC | Little Giant Co., USA |
| T-C | Conductivity/temperature meter, CON2700 | Oakton Instruments, USA |
| Concentration Draw Solution (M) | Orientation | Membrane | Water Transport | Salt Transport | ||
|---|---|---|---|---|---|---|
| Flux 1 (L/m2·h) | Time Lag 1 (min) | Flux (g/m2·h) | Time Lag (min) | |||
| 1 | AL-DS | M1 | 5.11 | −9.58 | 7.08 | 3.50 |
| M2 | 6.65 | −9.27 | 6.79 | 3.58 | ||
| M3 | 4.02 | −14.61 | 8.27 | 4.30 | ||
| Average | 5.26 | −11.15 | 7.38 | 3.79 | ||
| 1 | AL-FS | M4 | 4.08 | −0.15 | 2.39 | 4.83 |
| M5 | 3.57 | −0.35 | 2.75 | 2.93 | ||
| M6 | 4.19 | −1.72 | 2.03 | 5.23 | ||
| Average | 3.98 | −0.74 | 2.38 | 4.33 | ||
| 2 | AL-DS | M7 | 6.41 | −11.92 | 12.50 | 4.16 |
| M8 | 5.40 | −26.12 | 7.54 | 7.58 | ||
| M9 | 4.80 | −18.65 | 12.55 | 4.97 | ||
| Average | 5.43 | −18.90 | 10.86 | 5.56 | ||
| 2 | AL-FS | M10 | 3.83 | −0.69 | 3.23 | 4.82 |
| M11 | 4.61 | 0.07 | 3.07 | 4.91 | ||
| M12 | 4.27 | −0.79 | 3.24 | 4.18 | ||
| Average | 4.24 | −0.47 | 3.18 | 4.63 | ||
| 4 | AL-DS | M13 | 7.35 | −25.81 | 10.50 | 8.26 |
| M14 | 6.06 | −15.17 | 27.84 | 3.92 | ||
| M15 | 5.86 | −19.09 | 22.10 | 5.37 | ||
| Average | 6.42 | −20.03 | 20.12 | 5.85 | ||
| 4 | AL-FS | M16 | 5.61 | −0.57 | 1.33 2 | 0.79 2 |
| M17 | 5.41 | −0.18 | 5.96 | 4.77 | ||
| M18 | 5.83 | 0.47 | 4.21 | 4.00 | ||
| Average | 5.62 | −0.09 | 5.09 | 4.39 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, D.; Kruczek, B. Effect of Membrane Orientation and Concentration of Draw Solution on the Behavior of Commercial Osmotic Membrane in a Novel Dynamic Forward Osmosis Tests. Membranes 2022, 12, 385. https://doi.org/10.3390/membranes12040385
Bai D, Kruczek B. Effect of Membrane Orientation and Concentration of Draw Solution on the Behavior of Commercial Osmotic Membrane in a Novel Dynamic Forward Osmosis Tests. Membranes. 2022; 12(4):385. https://doi.org/10.3390/membranes12040385
Chicago/Turabian StyleBai, Du, and Boguslaw Kruczek. 2022. "Effect of Membrane Orientation and Concentration of Draw Solution on the Behavior of Commercial Osmotic Membrane in a Novel Dynamic Forward Osmosis Tests" Membranes 12, no. 4: 385. https://doi.org/10.3390/membranes12040385
APA StyleBai, D., & Kruczek, B. (2022). Effect of Membrane Orientation and Concentration of Draw Solution on the Behavior of Commercial Osmotic Membrane in a Novel Dynamic Forward Osmosis Tests. Membranes, 12(4), 385. https://doi.org/10.3390/membranes12040385






