The Influence of Concentration and Temperature on the Membrane Resistance of Ion Exchange Membranes and the Levelised Cost of Hydrogen from Reverse Electrodialysis with Ammonium Bicarbonate
Abstract
1. Introduction
2. Theory and Background
Effect of Solution Concentration, IEM Thickness and Operating Temperature on Membrane Resistance
3. Materials and Methods
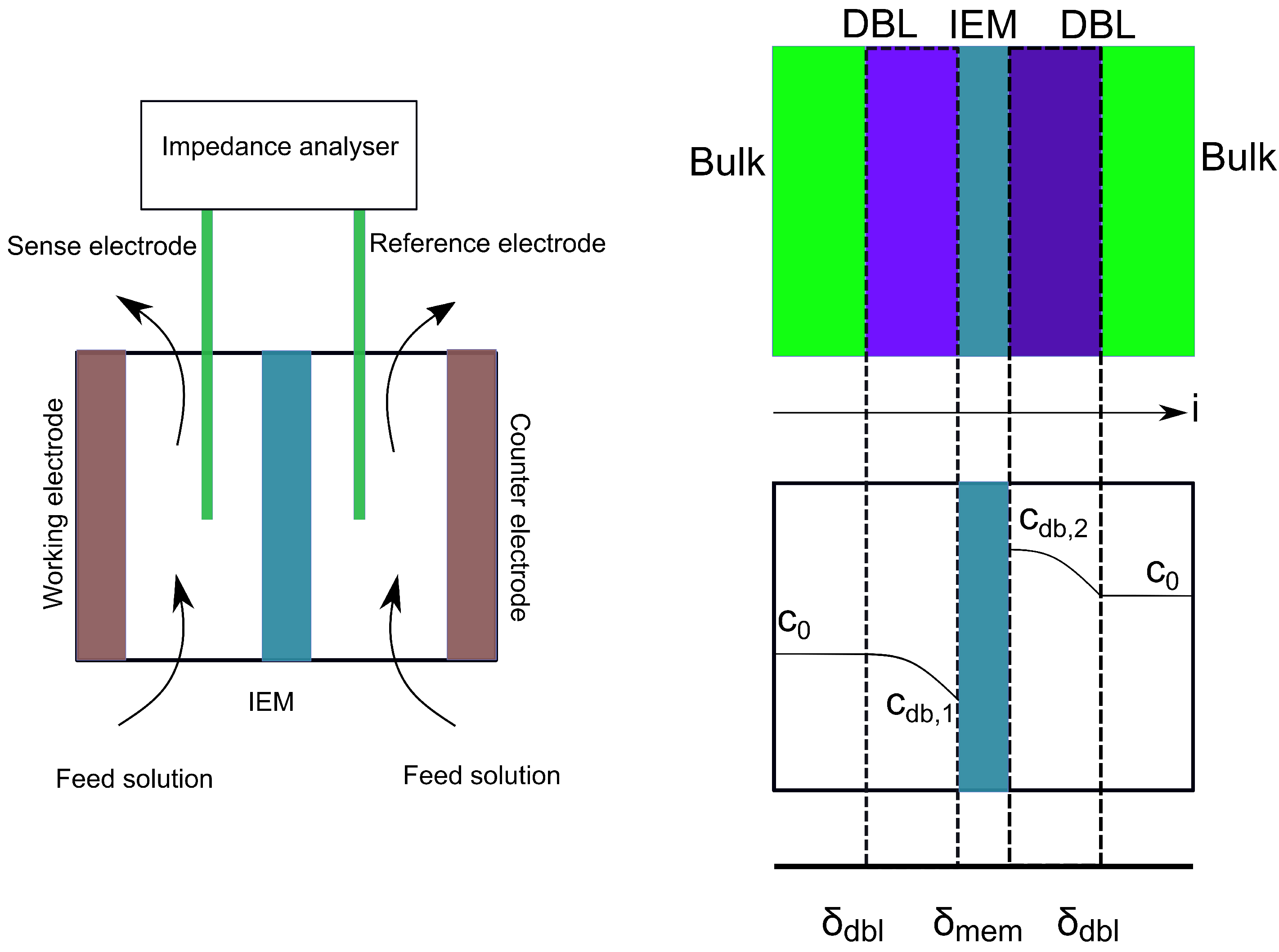
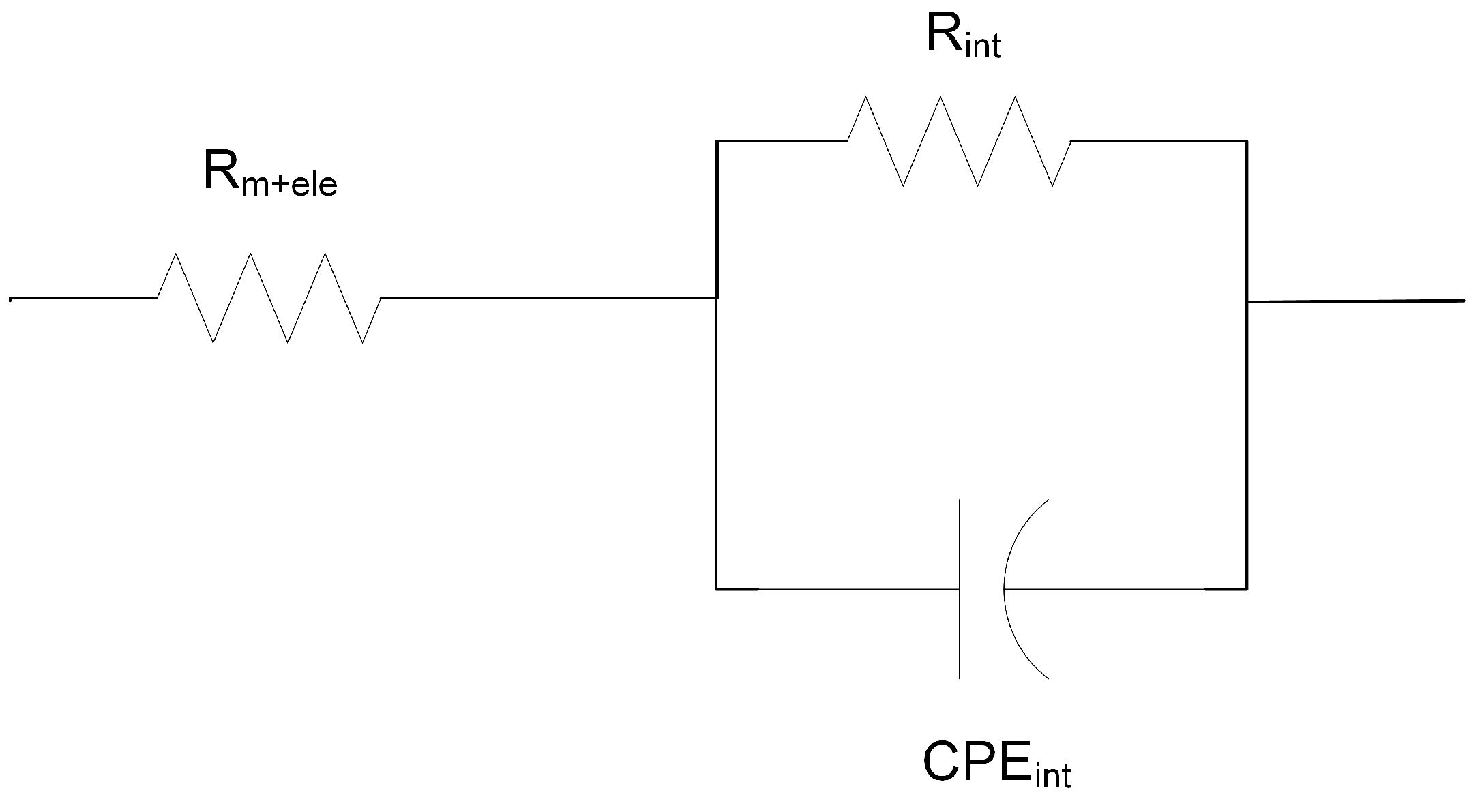
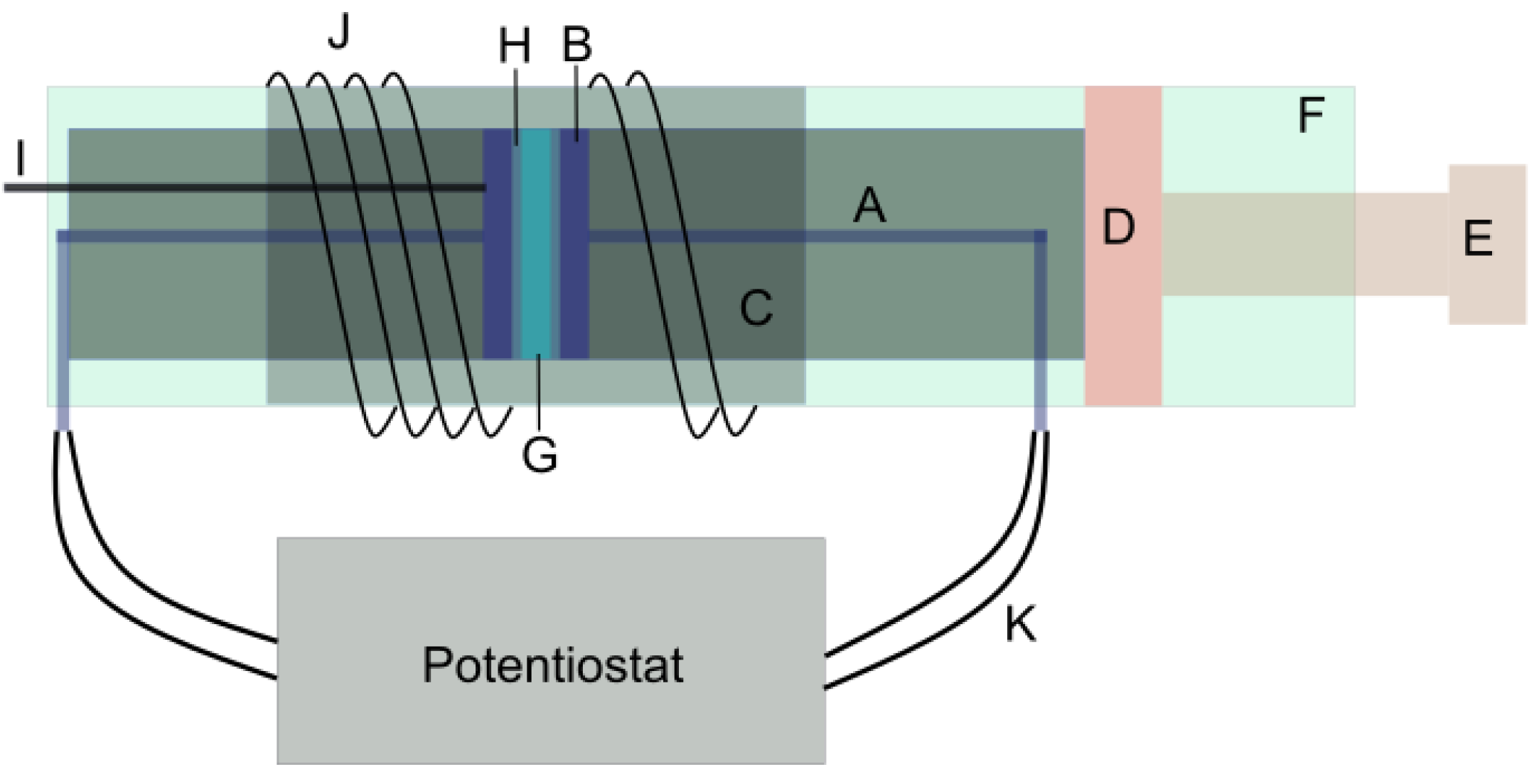
3.1. Membrane Resistivity Measurements
3.1.1. Membrane Equilibration
3.1.2. Electrode Preparation
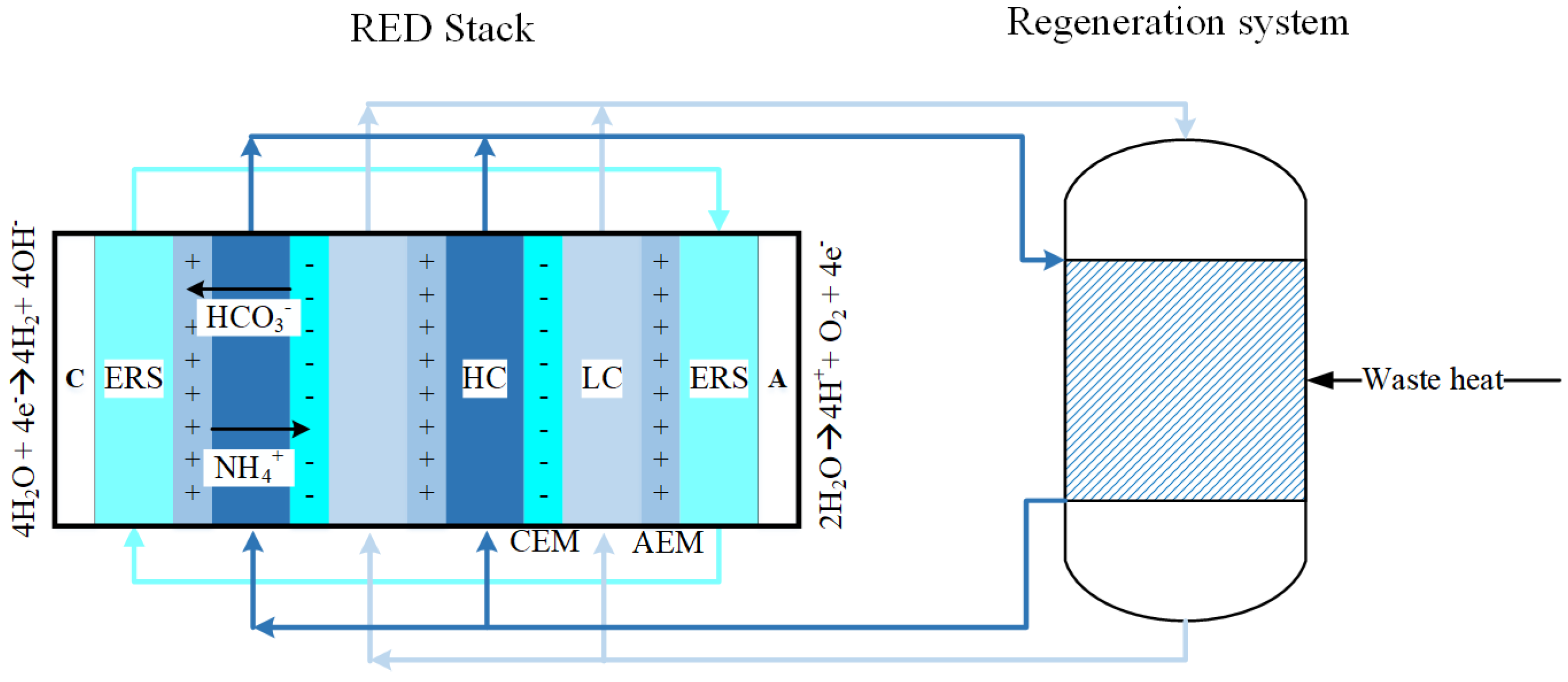
3.2. Thermodynamic Model for the RED System
3.2.1. Hydrogen Production
3.2.2. Waste Heat/Regeneration System
3.2.3. Levelised Cost of Hydrogen
4. Results and Discussion
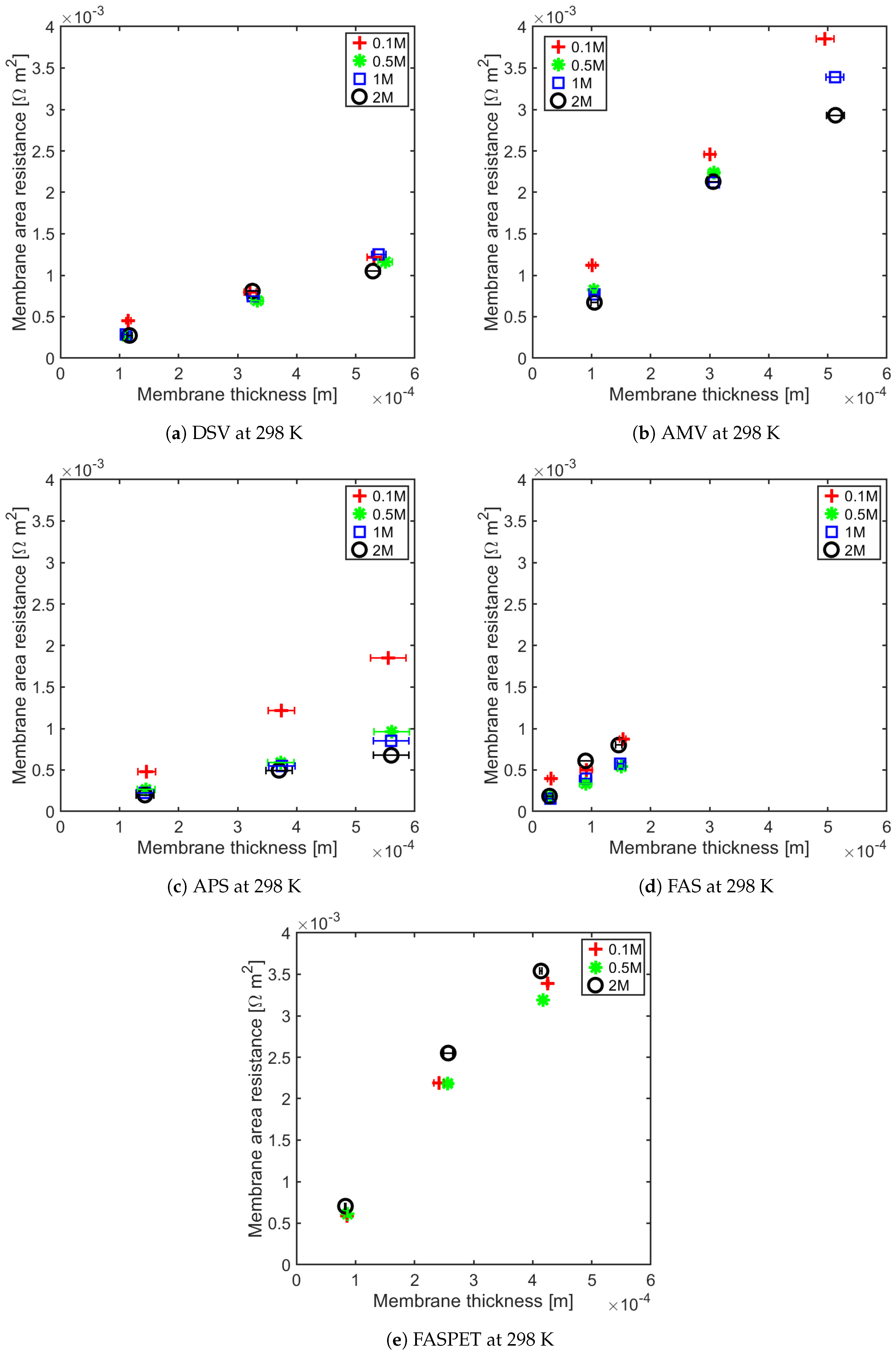
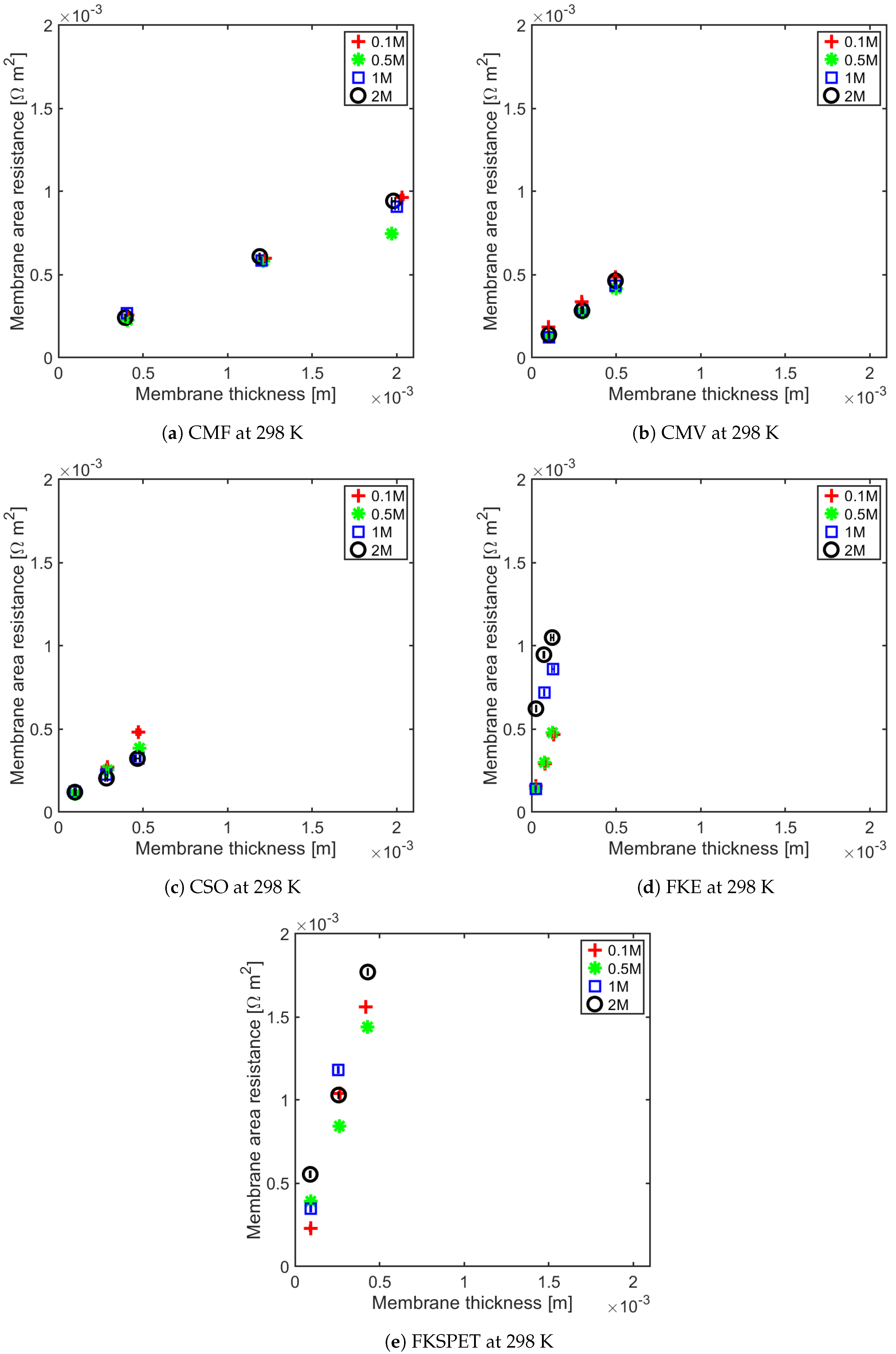
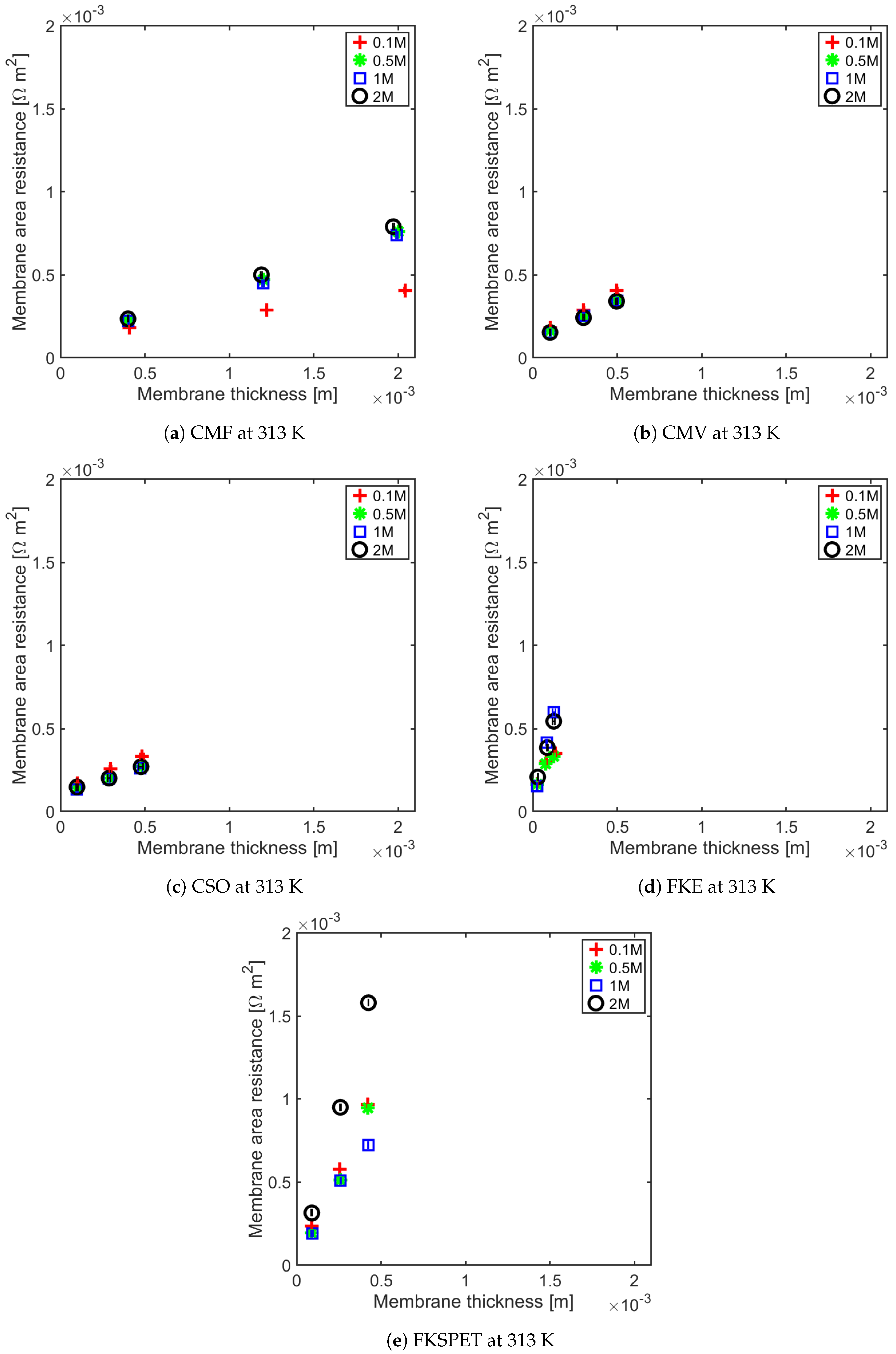
4.1. Influence of Thickness on Membrane Resistance and Membrane Resistance at Elevated Temperature
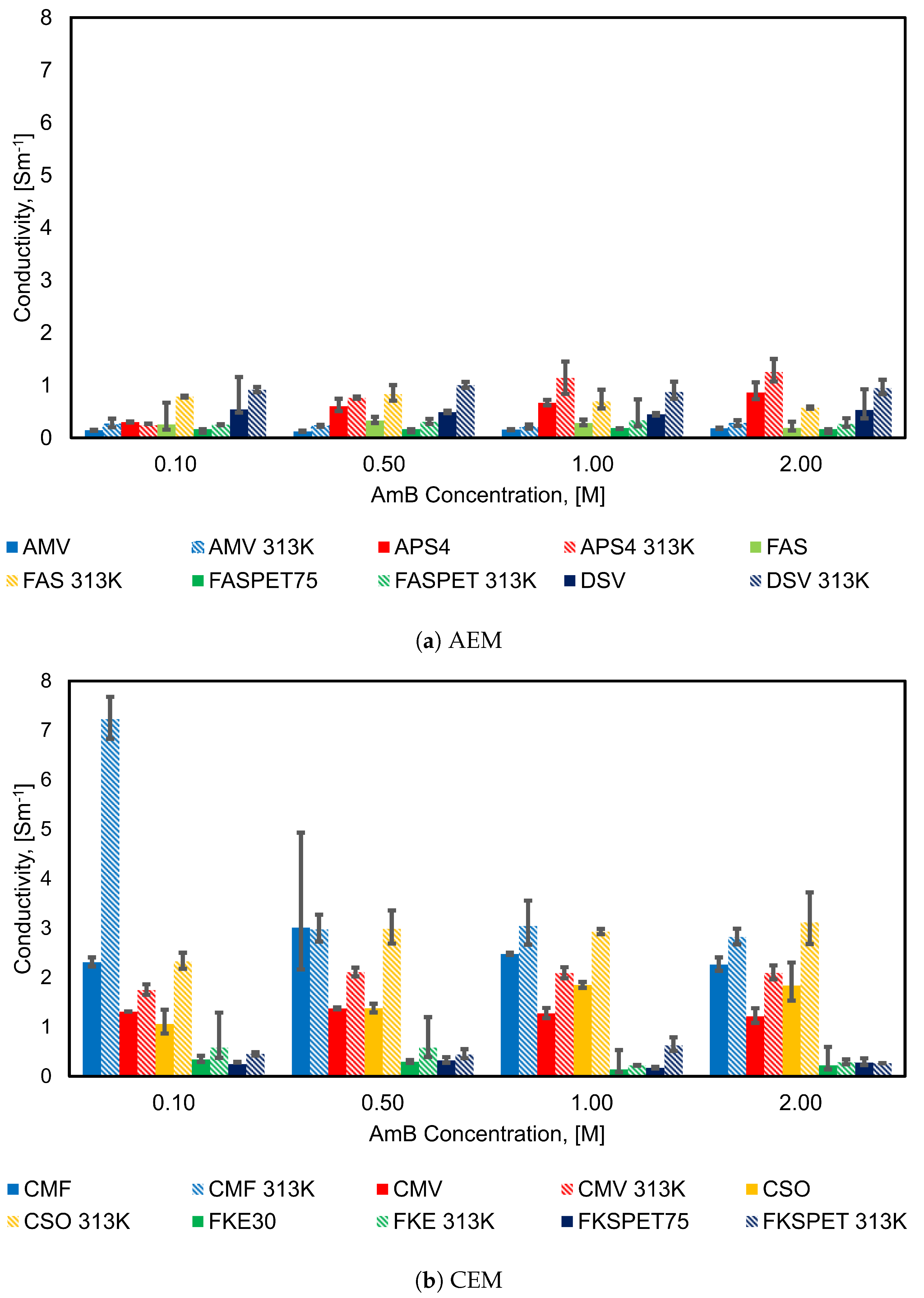
4.2. Influence of Concentration on Membrane Conductivity
4.3. Influence of Membrane Resistance on H Production rate and Specific Waste Heat Required Q
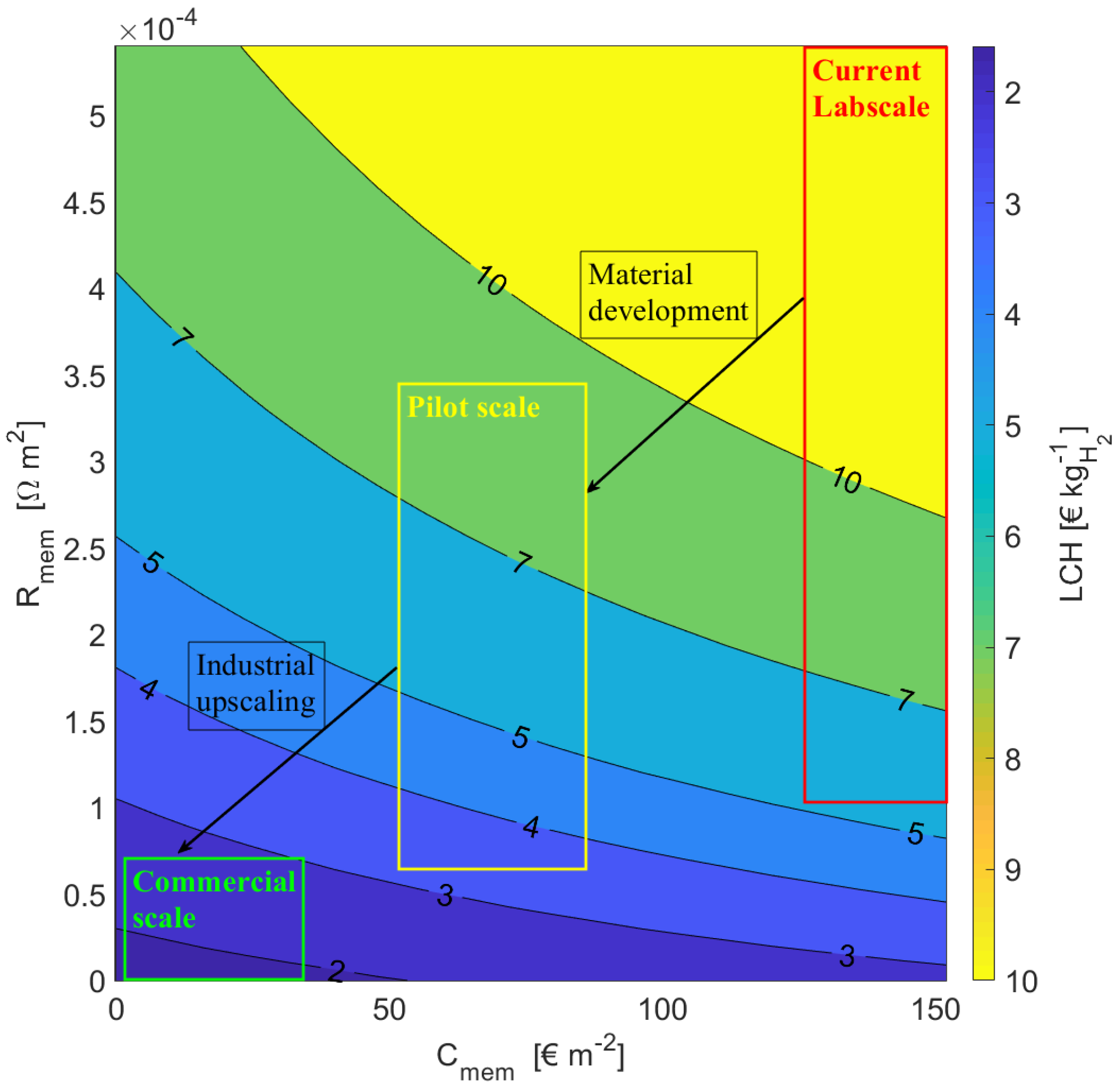
4.4. Influence of R on and LCH
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Regression Coefficients
| IEM | Concentration (M) | Regression (R = a· Thickness + b) |
|---|---|---|
| DSV | 0.1 0.5 1 2 | (1.85 ± 0.22) × +2.26 × 10 ± 8.26 × 10 (2.04 ± 0.10) × +2.92 × 10 ± 4.04 × 10 (2.24 ± 0.12) × +2.91 × 10 ± 4.30 × 10 (1.89 ± 0.80) × +1.01 × 10 ± 2.94 × 10 |
| AMV | 0.1 0.5 1 2 | (6.94 ± 0.2) × +4.04 × 10 ± 6.79 × 10 (7.98 ± 1.06) × −7.64 × 10 ± 4.06 × 10 (6.45 ± 0.28) × +1.07 × 10 ± 3.06 × 10 (5.52 ± 0.36) × +2.10 × 10 ± 2.54 × 10 |
| APS | 0.1 0.5 1 2 | (3.34 ± 0.12) × +1.55 × 10 ± 1.56 × 10 (1.52 ± 0.12) × +4.05 × 10 ± 4.68 × 10 (1.50 ± 0.12) × +1.19 × 10 ± 4.82 × 10 (1.10 ± 0.14) × +6.98 × 10 ± 5.70 × 10 |
| FAS30 | 0.1 0.5 1 2 | (3.96 ± 2.46) × +2.27 × 10 ± 2.56 × 10 (3.01 ± 0.52) × +8.04 × 10 ± 5.32 × 10 (3.54 ± 0.66) × +5.74 × 10 ± 6.70 × 10 (5.29 ± 2.04) × +6.54 × 10 ± 2.06 × 10 |
| FASPET | 0.1 0.5 1 2 | (8.23 ± 2.14) × −5.79 × 10 ± 6.14 × 10 (7.81 ± 1.74) × +1.10 × 10 ± 4.98 × 10 (5.69 ± 0.28) × +1.02 × 10 ± 8.14 × 10 (8.45 ± 0.90) × − 4.28 × 10 ± 2.76 × 10 |
| IEM | Concentration (M) | Regression (R = a· Thickness + b) |
|---|---|---|
| CMV | 0.1 0.5 1 2 | (0.76 ± 0.00) × +1.09 × 10 ± 5.64 × 10 (0.73 ± 0.00) × +5.07 × 10 ± 3.32 × 10 (0.79 ± 0.06) × +4.66 × 10 ± 2.16 × 10 (0.82 ± 0.10) × +4.90 × 10 ± 3.34 × 10 |
| CMF | 0.1 0.5 1 2 | (0.43 ± 0.02) × +8.07 × 10 ± 2.44 × 10 (0.43 ± 0.01) × +5.20 × 10 ± 1.47 × 10 (0.40 ± 0.00) × +1.02 × 10 ± 4.88 × 10 (0.44 ± 0.02) × +7.25 × 10 ± 3.58 × 10 |
| CSO | 0.1 0.5 1 2 | (0.95 ± 0.20) × +2.15 × 10 ± 6.72 × 10 (0.73 ± 0.04) × +3.81 × 10 ± 1.50 × 10 (0.54 ± 0.02) × +7.02 × 10 ± 5.72 × 10 (0.54 ± 0.10) × +6.18 × 10 ± 3.50 × 10 |
| FKE | 0.1 0.5 1 2 | (2.93 ± 0.52) × +7.47 × 10 ± 4.64 × 10 (3.36 ± 0.32) × +5.58 × 10 ± 2.80 × 10 (7.02 ± 5.06) × +4.18 × 10 ± 4.46 × 10 (4.45 ± 2.76) × +5.45 × 10 ± 2.32 × 10 |
| FKSPET | 0.1 0.5 1 2 | (4.66 ± 0.00) × −1.98 × 10 ± 0.00 (3.11 ± 0.54) × +7.76 × 10 ± 1.60 × 10 (5.70 ± 0.58) × − 2.18 × 10 ± 1.68 × 10 (3.57 ± 0.86) × +1.89 × 10 ± 2.52 × 10 |
| IEM | Concentration (M) | Regression (R = a· Thickness + b) |
|---|---|---|
| DSV | 0.1 0.5 1 2 | (1.10 ± 0.06) × +1.15 × 10 ± 2.36 × 10 (1.00 ± 0.06) × +9.51 × 10 ± 2.04 × 10 (1.14 ± 0.20) × +9.04 × 10 ± 7.68 × 10 (1.05 ± 0.14) × +8.30 × 10 ± 5.64 × 10 |
| AMV | 0.1 0.5 1 2 | (3.85 ± 1.12) × +6.46 × 10 ± 3.98 × 10 (5.34 ± 1.06) × −1.33 × 10 ± 3.24 × 10 (4.79 ± 0.86) × −1.52 × 10 ± 3.06 × 10 (3.69 ± 0.72) × −3.94 × 10 ± 2.54 × 10’ |
| APS | 0.1 0.5 1 2 | (3.75 ± 0.06) × +1.30 × 10 ± 1.80 × 10 (1.15 ± 0.02) × +7.86 × 10 ± 8.68 × 10 (1.15 ± 0.16) × +3.79 × 10 ± 6.12 × 10 (0.86 ± 0.08) × +8.04 × 10 ± 2.86 × 10 |
| FAS30 | 0.1 0.5 1 2 | (1.28 ± 0.04) × +1.28 × 10 ± 3.40 × 10 (1.21 ± 0.22) × +1.65 × 10 ± 2.24 × 10 (1.44 ± 0.34) × +7.11 × 10 ± 3.70 × 10 (1.74 ± 0.06) × +1.10 × 10 ± 6.82 × 10 |
| FASPET | 0.1 0.5 1 2 | (4.01 ± 0.18) × − 2.56 × 10 ± 5.10 × 10 (3.29 ± 0.52) × +1.49 × 10 ± 1.50 × 10 (2.99 ± 1.62) × +2.05 × 10 ± 4.78 × 10 (3.75 ± 1.06) × − 1.24 × 10 ± 3.12 × 10 |
| IEM | Concentration (M) | Regression (R = a· Thickness + b) |
|---|---|---|
| CMV | 0.1 0.5 1 2 | (0.57 ± 0.04) × +1.20 × 10 ± 1.07 × 10 (0.47 ± 0.02) × +1.13 × 10 ± 6.84 × 10 (0.48 ± 0.02) × +1.06 × 10 ± 8.76 × 10 (0.48 ± 0.04) × +1.02 × 10 ± 1.09 × 10 |
| CMF | 0.1 0.5 1 2 | (0.14 ± 0.00) × +1.23 × 10 ± 1.03 × 10 (0.34 ± 0.04) × +8.09 × 10 ± 4.20 × 10 (0.33 ± 0.04) × +7.76 × 10 ± 6.42 × 10 (0.35 ± 0.02) × +8.92 × 10 ± 2.66 × 10 |
| CSO | 0.1 0.5 1 2 | (0.43 ± 0.02) × +1.27 × 10 ± 4.97 × 10 (0.33 ± 0.04) × +1.08 × 10 ± 1.23 × 10 (0.34 ± 0.00) × +9.98 × 10 ± 2.04 × 10 (0.32 ± 0.06) × +1.14 × 10 ± 1.71 × 10 |
| FKE | 0.1 0.5 1 2 | (1.72 ± 0.94) × +1.34 × 10 ± 8.64 × 10 (1.71 ± 0.88) × +1.34 × 10 ± 7.44 × 10 (4.47 ± 0.14) × +4.30 × 10 ± 1.26 × 10 (3.51 ± 0.60) × +9.97 × 10 ± 5.26 × 10 |
| FKSPET | 0.1 0.5 1 2 | (0.79 ± 0.44) × − 2.03 × 10 ± 4.84 × 10 (2.27 ± 0.46) × − 3.25 × 10 ± 1.32 × 10 (1.60 ± 0.34) × +6.02 × 10 ± 9.74 × 10 (3.79 ± 0.04) × − 2.85 × 10 ± 1.05 × 10 |
| IEM at 298 K | Concentration [M] 0.10 | 0.50 | 1.00 | 2.00 |
|---|---|---|---|---|
| AMV | 0.14 | 0.13 | 0.16 | 0.18 |
| APS | 0.30 | 0.61 | 0.67 | 0.87 |
| FAS | 0.25 | 0.33 | 0.28 | 0.19 |
| FASPET | 0.16 | 0.16 | 0.18 | 0.16 |
| DSV | 0.54 | 0.49 | 0.45 | 0.53 |
| CMF | 2.31 | 3.01 | 2.48 | 2.26 |
| CMV | 1.31 | 1.37 | 1.27 | 1.21 |
| CSO | 1.06 | 1.38 | 1.85 | 1.84 |
| FKE | 0.34 | 0.30 | 0.14 | 0.22 |
| FKSPET | 0.24 | 0.32 | 0.18 | 0.28 |
| IEM at 313 K | Concentration [M] 0.10 | 0.50 | 1.00 | 2.00 |
|---|---|---|---|---|
| AMV | 0.26 | 0.23 | 0.21 | 0.27 |
| APS | 0.24 | 0.76 | 1.14 | 1.25 |
| FAS | 0.78 | 0.83 | 0.69 | 0.57 |
| FASPET | 0.25 | 0.30 | 0.33 | 0.27 |
| DSV | 0.91 | 1.00 | 0.88 | 0.95 |
| CMF | 7.23 | 2.98 | 3.05 | 2.82 |
| CMV | 1.75 | 2.11 | 2.09 | 2.09 |
| CSO | 2.33 | 2.99 | 2.93 | 3.12 |
| FKE | 0.58 | 0.59 | 0.22 | 0.29 |
| FKSPET | 0.45 | 0.44 | 0.62 | 0.26 |
References
- Burheim, O. Engineering Energy Storage; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Giacalone, F.; Vassallo, F.; Griffin, L.; Ferrari, M.C.; Micale, G.; Scargiali, F.; Tamburini, A.; Cipollina, A. Thermolytic reverse electrodialysis heat engine: Model development, integration and performance analysis. Energy Convers. Manag. 2019, 189, 1–13. [Google Scholar] [CrossRef]
- Luo, Y.; Guo, J.; Wang, C.; Chu, D. Fuel cell durability enhancement by crosslinking alkaline anion exchange membrane electrolyte. Electrochem. Commun. 2012, 16, 65–68. [Google Scholar] [CrossRef]
- Nam, J.Y.; Cusick, R.D.; Kim, Y.; Logan, B.E. Hydrogen generation in microbial reverse-electrodialysis electrolysis cells using a heat-regenerated salt solution. Environ. Sci. Technol. 2012, 46, 5240–5246. [Google Scholar] [CrossRef]
- Kwon, K.; Park, B.H.; Kim, D.H.; Kim, D. Parametric study of reverse electrodialysis using ammonium bicarbonate solution for low-grade waste heat recovery. Energy Convers. Manag. 2015, 103, 104–110. [Google Scholar] [CrossRef]
- Cusick, R.D.; Kim, Y.; Logan, B.E. Energy Capture fromThermolytic Solutions in Microbial Reverse-Electrodialysis Cells. Science 2012, 335, 1474–1478. [Google Scholar] [CrossRef]
- Logan, B.E.; Elimelech, M. Membrane-based processes for sustainable power generation using water. Nature 2012, 488, 313–319. [Google Scholar] [CrossRef] [PubMed]
- Micari, M.; Cipollina, A.; Giacalone, F.; Kosmadakis, G.; Papapetrou, M.; Zaragoza, G.; Micale, G.; Tamburini, A. Towards the first proof of the concept of a Reverse ElectroDialysis—Membrane Distillation Heat Engine. Desalination 2019, 453, 77–88. [Google Scholar] [CrossRef]
- Kwon, K.; Park, B.H.; Kim, D.H.; Kim, D. Comparison of spacer-less and spacer-filled reverse electrodialysis. J. Renew. Sustain. Energy 2017, 9, 044502. [Google Scholar] [CrossRef]
- Bevacqua, M.; Tamburini, A.; Papapetrou, M.; Cipollina, A.; Micale, G.; Piacentino, A. Reverse electrodialysis with NH4HCO3-water systems for heat-to-power conversion. Energy 2017, 137, 1293–1307. [Google Scholar] [CrossRef]
- Güler, E.; Elizen, R.; Vermaas, D.a.; Saakes, M.; Nijmeijer, K. Performance-determining membrane properties in reverse electrodialysis. J. Membr. Sci. 2013, 446, 266–276. [Google Scholar] [CrossRef]
- Galama, A.H.; Hoog, N.A.; Yntema, D.R. Method for determining ion exchange membrane resistance for electrodialysis systems. Desalination 2016, 380, 1–11. [Google Scholar] [CrossRef]
- Geise, G.M.; Hickner, M.A.; Logan, B.E. Ammonium Bicorbonate Transport in anion exchange membranes for salinity gradient energy. ACS Macro Lett. 2013, 2, 814–817. [Google Scholar] [CrossRef]
- Hong, J.G.; Zhang, B.; Glabman, S.; Uzal, N.; Dou, X.; Zhang, H.; Wei, X.; Chen, Y. Potential ion exchange membranes and system performance in reverse electrodialysis for power generation: A review. J. Membr. Sci. 2015, 486, 71–88. [Google Scholar] [CrossRef]
- Geise, G.M.; Hickner, M.A.; Logan, B.E. Ionic resistance and permselectivity tradeoffs in anion exchange membranes. ACS Appl. Mater. Interfaces 2013, 5, 10294–10301. [Google Scholar] [CrossRef]
- Kamcev, J.; Sujanani, R.; Jang, E.S.; Yan, N.; Moe, N.; Paul, D.R.; Freeman, B.D. Salt concentration dependence of ionic conductivity in ion exchange membranes. J. Membr. Sci. 2018, 547, 123–133. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Kozmai, A.E. Electrical equivalent circuit of an ion-exchange membrane system. Electrochim. Acta 2011, 56, 1262–1269. [Google Scholar] [CrossRef]
- Park, J.S.; Choi, J.H.; Woo, J.J.; Moon, S.H. An electrical impedance spectroscopic (EIS) study on transport characteristics of ion-exchange membrane systems. J. Colloid Interface Sci. 2006, 300, 655–662. [Google Scholar] [CrossRef]
- Długołȩcki, P.; Ogonowski, P.; Metz, S.J.; Saakes, M.; Nijmeijer, K.; Wessling, M. On the resistances of membrane, diffusion boundary layer and double layer in ion exchange membrane transport. J. Membr. Sci. 2010, 349, 369–379. [Google Scholar] [CrossRef]
- Zhang, W.; Ma, J.; Wang, P.; Wang, Z.; Shi, F.; Liu, H. Investigations on the interfacial capacitance and the diffusion boundary layer thickness of ion exchange membrane using electrochemical impedance spectroscopy. J. Membr. Sci. 2016, 502, 37–47. [Google Scholar] [CrossRef]
- Tufa, R.A.; Pawlowski, S.; Veerman, J.; Bouzek, K.; Fontananova, E.; di Profio, G.; Velizarov, S.; Goulão Crespo, J.; Nijmeijer, K.; Curcio, E. Progress and prospects in reverse electrodialysis for salinity gradient energy conversion and storage. Appl. Energy 2018, 225, 290–331. [Google Scholar] [CrossRef]
- Galama, A.H.; Vermaas, D.A.; Veerman, J.; Saakes, M.; Rijnaarts, H.H.; Post, J.W.; Nijmeijer, K. Membrane resistance: The effect of salinity gradients over a cation exchange membrane. J. Membr. Sci. 2014, 467, 279–291. [Google Scholar] [CrossRef]
- Veerman, J.; Saakes, M.; Metz, S.J.; Harmsen, G.J. Reverse electrodialysis: Performance of a stack with 50 cells on the mixing of sea and river water. J. Membr. Sci. 2009, 327, 136–144. [Google Scholar] [CrossRef]
- Kim, K.S.; Ryoo, W.; Chun, M.S.; Chung, G.Y. Simulation of enhanced power generation by reverse electrodialysis stack module in serial configuration. Desalination 2013, 318, 79–87. [Google Scholar] [CrossRef]
- Mei, Y.; Tang, C.Y. Recent developments and future perspectives of reverse electrodialysis technology: A review. Desalination 2017, 425, 156–174. [Google Scholar] [CrossRef]
- Raka, Y.D.; Karoliussen, H.; Lien, K.M. Odne Stokke Burheim. Opportunities and challenges for thermally driven hydrogen production using reverse electrodialysis system. Int. J. Hydrog. Energy 2020, 5, 1212–1225. [Google Scholar] [CrossRef]
- Nazemi, M.; Zhang, J.; Hatzell, M.C. Harvesting Natural Salinity Gradient Energy for Hydrogen Production Through Reverse Electrodialysis Power Generation. J. Electrochem. Energy Convers. Storage 2017, 14, 020702. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, C.; Zhang, Y.; Wang, Y.; Xu, T. Storable hydrogen production by Reverse Electro-Electrodialysis (REED). J. Membr. Sci. 2017, 544, 397–405. [Google Scholar] [CrossRef]
- Millet, P.; Grigoriev, S. Water Electrolysis Technologies. In Renewable Hydrogen Technologies: Production, Purification, Storage, Applications and Safety; Elsevier Science: Amsterdam, The Netherlands, 2013; pp. 19–41. [Google Scholar] [CrossRef]
- Buttler, A.; Spliethoff, H. Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: A review. Renew. Sustain. Energy Rev. 2018, 82, 2440–2454. [Google Scholar] [CrossRef]
- Minke, C.; Turek, T. Economics of vanadium redox flow battery membranes. J. Power Sources 2015, 286, 247–257. [Google Scholar] [CrossRef]
- Krakhella, K.W.; Morales, M.; Bock, R.; Seland, F.; Burheim, O.S.; Einarsrud, K.E. Electrodialytic energy storage system: Permselectivity, stack measurements and life-cycle analysis. Energies 2020, 13, 1247. [Google Scholar] [CrossRef]

| IEM | Type | Thickness m | Fixed Charge Group | Material | Counter-ion | Permselectivity | Resistance m | IEC meq g | SD (wt) meq g | Ref |
|---|---|---|---|---|---|---|---|---|---|---|
| FKE | CEM | 28–33 | -SO | - | H | 0.965–0.986 | 1.6–2.46 | 1.35–1.36 | 12–27 | [21] |
| FKSPET | CEM | 74–87 | -SO | - | H | >0.95 | 2.5 | 1–1.25 | - | * |
| FAS | AEM | 27–33 | - | - | Br | 0.894–0.9 | 1.03–2 | 1.1–1.85 | 8–19 | [14,21] |
| FASPET | AEM | 72–85 | - | - | Br | >0.9 | <3 | 1–1.5 | - | * |
| DSV | AEM | 95–121 | - | Cl | 0.899 | 2.3 | 1.89 | 28 | [21] | |
| AMV | AEM | 110–150 | -N(CH) | PS/DVB/CMS | Cl | 0.873–0.96 | 2.8–3.15 | 1.78–1.9 | 17–19.8 | [14,21,25] |
| CMV | CEM | 101–150 | - | PS/DVB | Na | 0.91–0.988 | 1.03–1.1 | 2–2.4 | 20–30 | [14,21,25] |
| CSO | CEM | 100 | - | PS/DVB | Na | 0.923–0.97 | 2.29–3 | 1.04 | 16 | [25] |
| CMF | CEM | 440 | - | - | H | > 0.95 | 2.5 | - | - | * |
| APS | AEM | 138–150 | -N(CH) | PS/DVB/CMS | SO | 0.884 | 0.68–0.7 | 0.29 | 147 | [21,25] |
| Parameter | Value | Unit |
|---|---|---|
| Electrode Area | 3.14 | cm |
| Pre-step Voltage | 0 vs. | V |
| Pre-step Delay Time | 0.5 | s |
| Step 1 Voltage | −2.5 | V |
| Step 1 Time | 200 | s |
| Step 2 Voltage | 0.1 | V |
| Step 2 Time | 5 | s |
| Max Current | 200 | mA |
| Limit I | 200 | mA cm |
| Equil. Time | 5 | s |
| Ion | NH | HCO |
|---|---|---|
| Hydrated radius [nm] | 0.331 | 0.439 |
| Charge density [mC cm] | 1.05 | 0.45 |
| Average polarisability [a.u] | 7.91 | 23.7 |
| Ionic mobility [cmVs] | 7.71 × 10 | 4.59 × 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raka, Y.D.; Bock, R.; Karoliussen, H.; Wilhelmsen, Ø.; Stokke Burheim, O. The Influence of Concentration and Temperature on the Membrane Resistance of Ion Exchange Membranes and the Levelised Cost of Hydrogen from Reverse Electrodialysis with Ammonium Bicarbonate. Membranes 2021, 11, 135. https://doi.org/10.3390/membranes11020135
Raka YD, Bock R, Karoliussen H, Wilhelmsen Ø, Stokke Burheim O. The Influence of Concentration and Temperature on the Membrane Resistance of Ion Exchange Membranes and the Levelised Cost of Hydrogen from Reverse Electrodialysis with Ammonium Bicarbonate. Membranes. 2021; 11(2):135. https://doi.org/10.3390/membranes11020135
Chicago/Turabian StyleRaka, Yash Dharmendra, Robert Bock, Håvard Karoliussen, Øivind Wilhelmsen, and Odne Stokke Burheim. 2021. "The Influence of Concentration and Temperature on the Membrane Resistance of Ion Exchange Membranes and the Levelised Cost of Hydrogen from Reverse Electrodialysis with Ammonium Bicarbonate" Membranes 11, no. 2: 135. https://doi.org/10.3390/membranes11020135
APA StyleRaka, Y. D., Bock, R., Karoliussen, H., Wilhelmsen, Ø., & Stokke Burheim, O. (2021). The Influence of Concentration and Temperature on the Membrane Resistance of Ion Exchange Membranes and the Levelised Cost of Hydrogen from Reverse Electrodialysis with Ammonium Bicarbonate. Membranes, 11(2), 135. https://doi.org/10.3390/membranes11020135







