Effects of Membrane Structure on Oil–Water Separation by Smoothed Particle Hydrodynamics
Abstract
:1. Introduction
2. Governing Equation and SPH Model
2.1. Governing Equation
| Symbol | Description |
|---|---|
| The density of oil and water phases | |
| Time | |
| The fluid velocity | |
| FS | The surface tension force |
| g | The gravity acceleration |
| peq | The equilibrium pressure |
| neq | The equilibrium number density |
| p | The system pressure |
| n | The number density |
| The pressures of oil phase | |
| The pressures of water phase | |
| The viscous stress tensor of oil phase | |
| The viscous stress tensor of water phase | |
| The oil surface coefficient | |
| The water surface coefficient | |
| The equilibrium contact angle | |
| The field function | |
| The mass function of particle b | |
| The density function of particle b | |
| The field function of particle b | |
| h | The smooth length |
| The distance between two particles | |
| W | The kernel function |
| The kernel normalization factor in different dimensions | |
| The strength coefficient of the interaction force between particle a in α phase and particle b in β phase | |
| The unit normal vector on the solid particle j | |
| The prescribed acceleration for solid particle | |
| The number of fluid particles | |
| The number of solid particles |
2.2. SPH Model
3. Results and Discussion
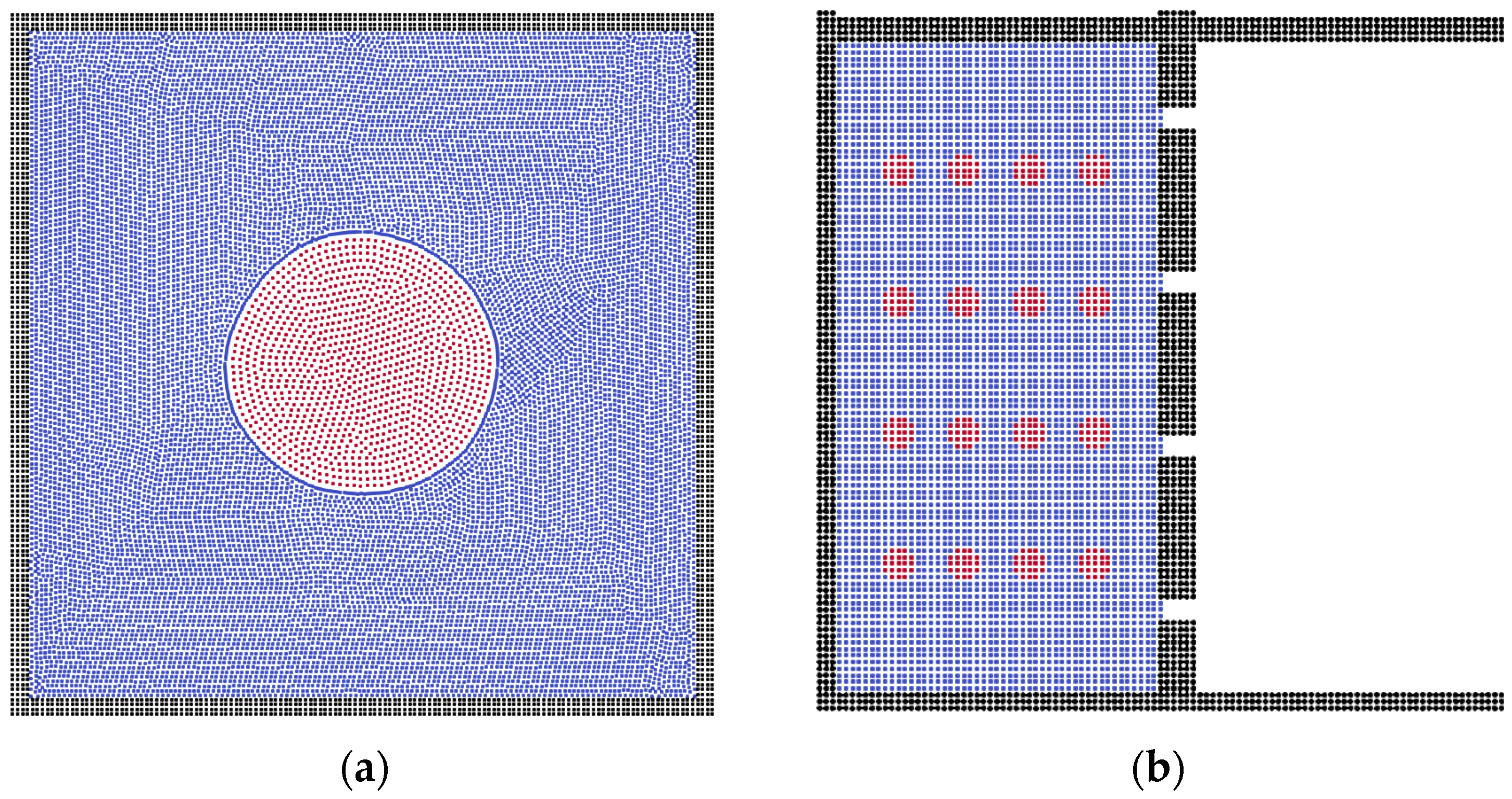
3.1. Scheme Validation
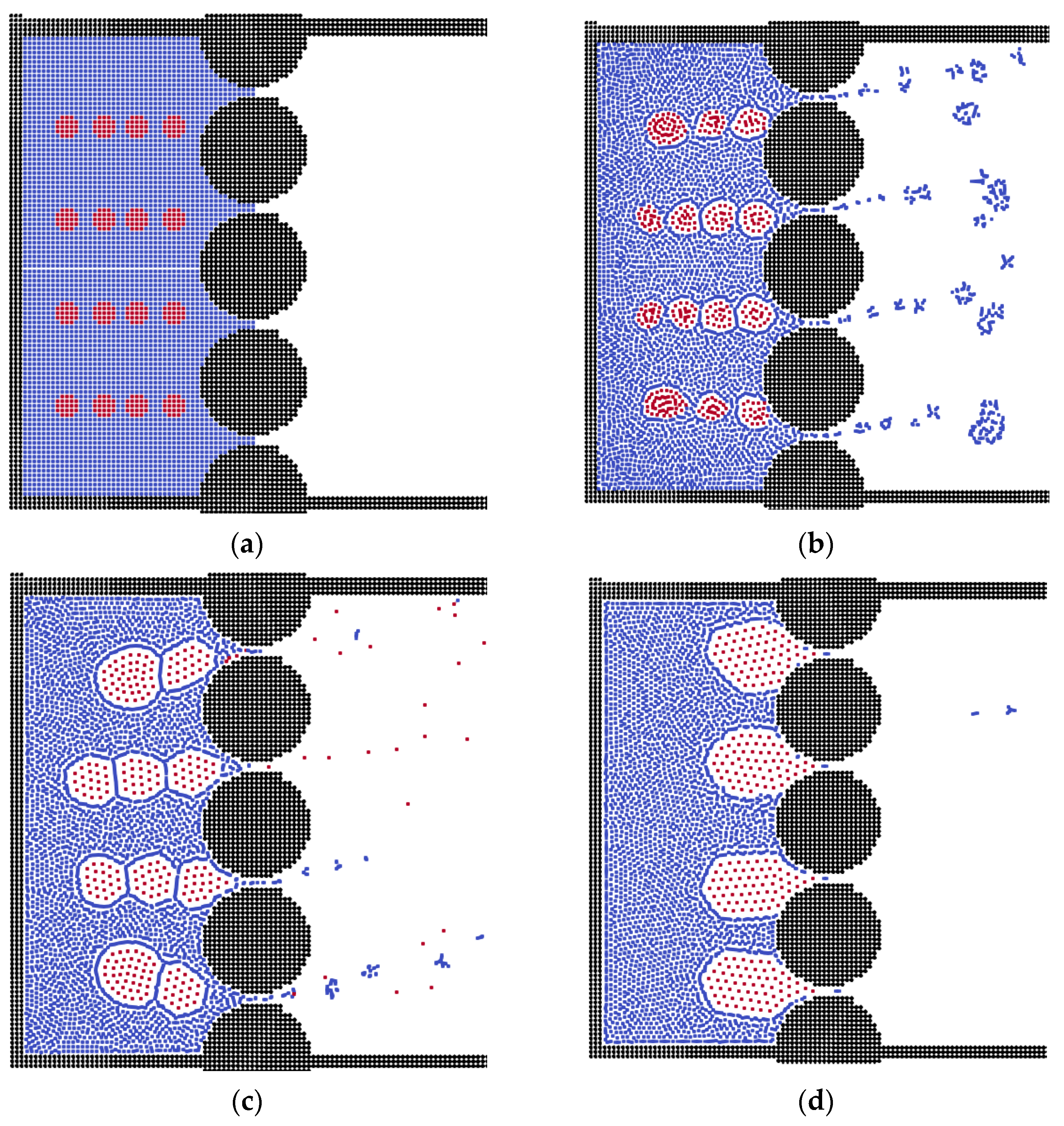
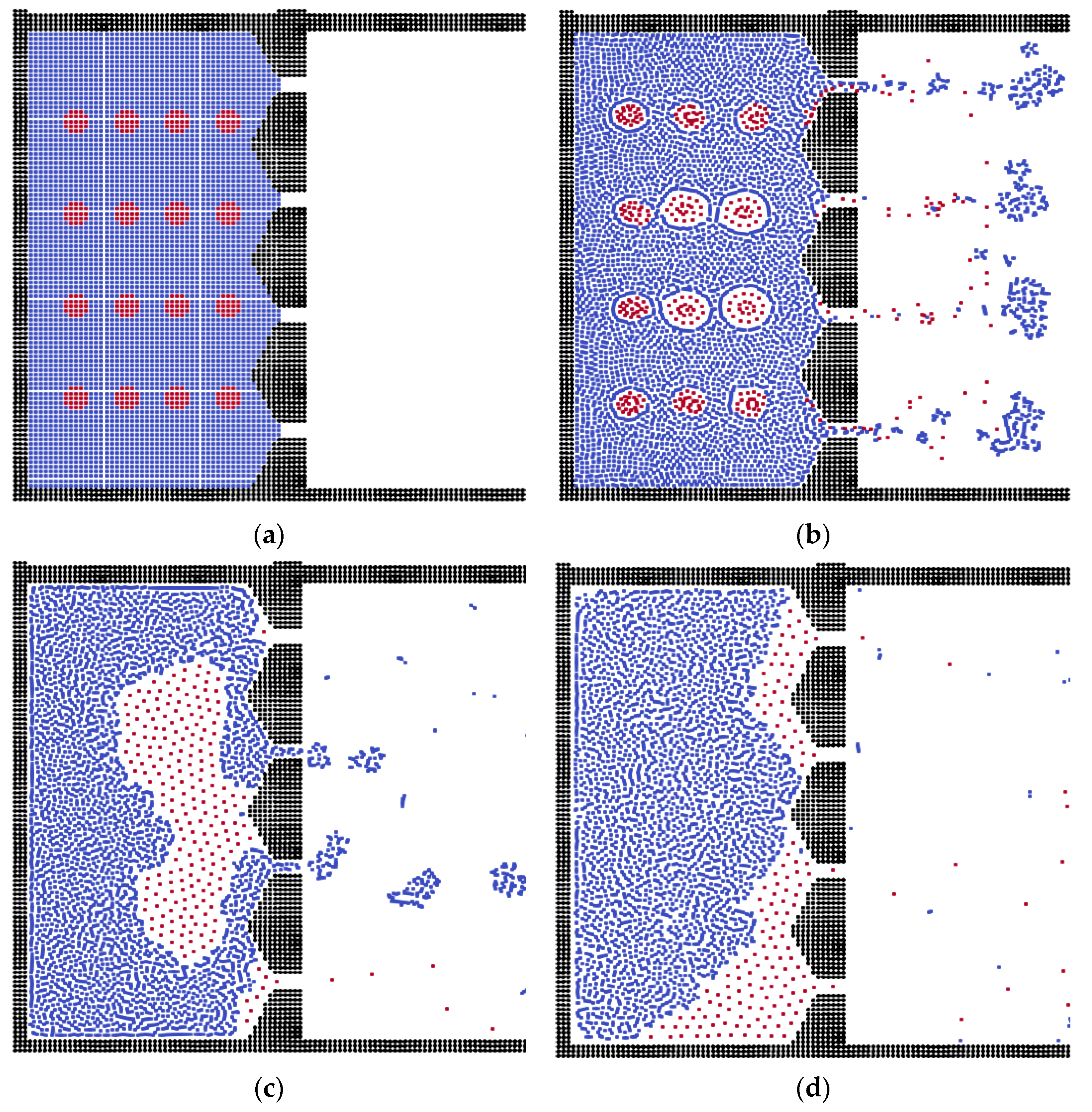
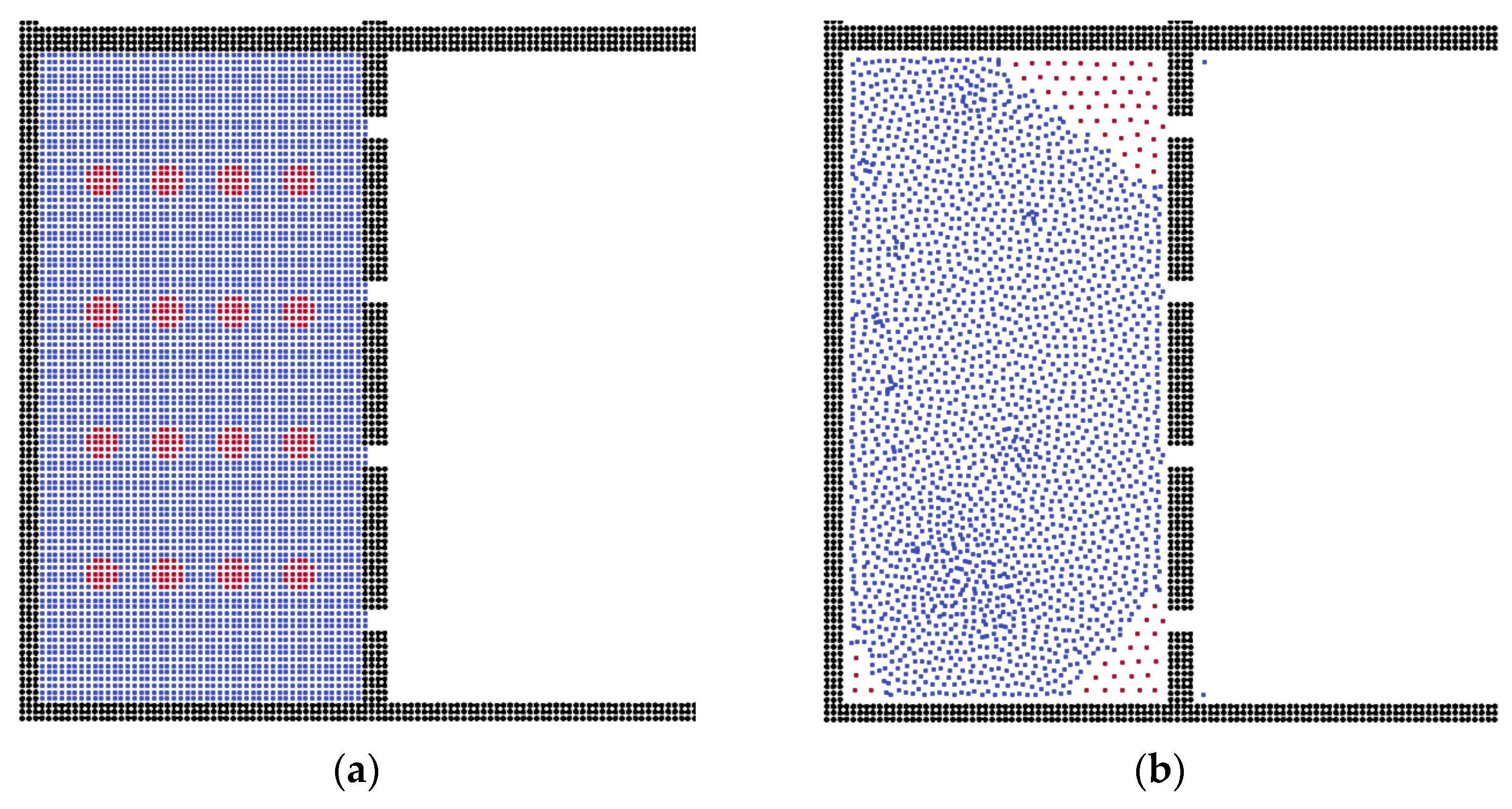
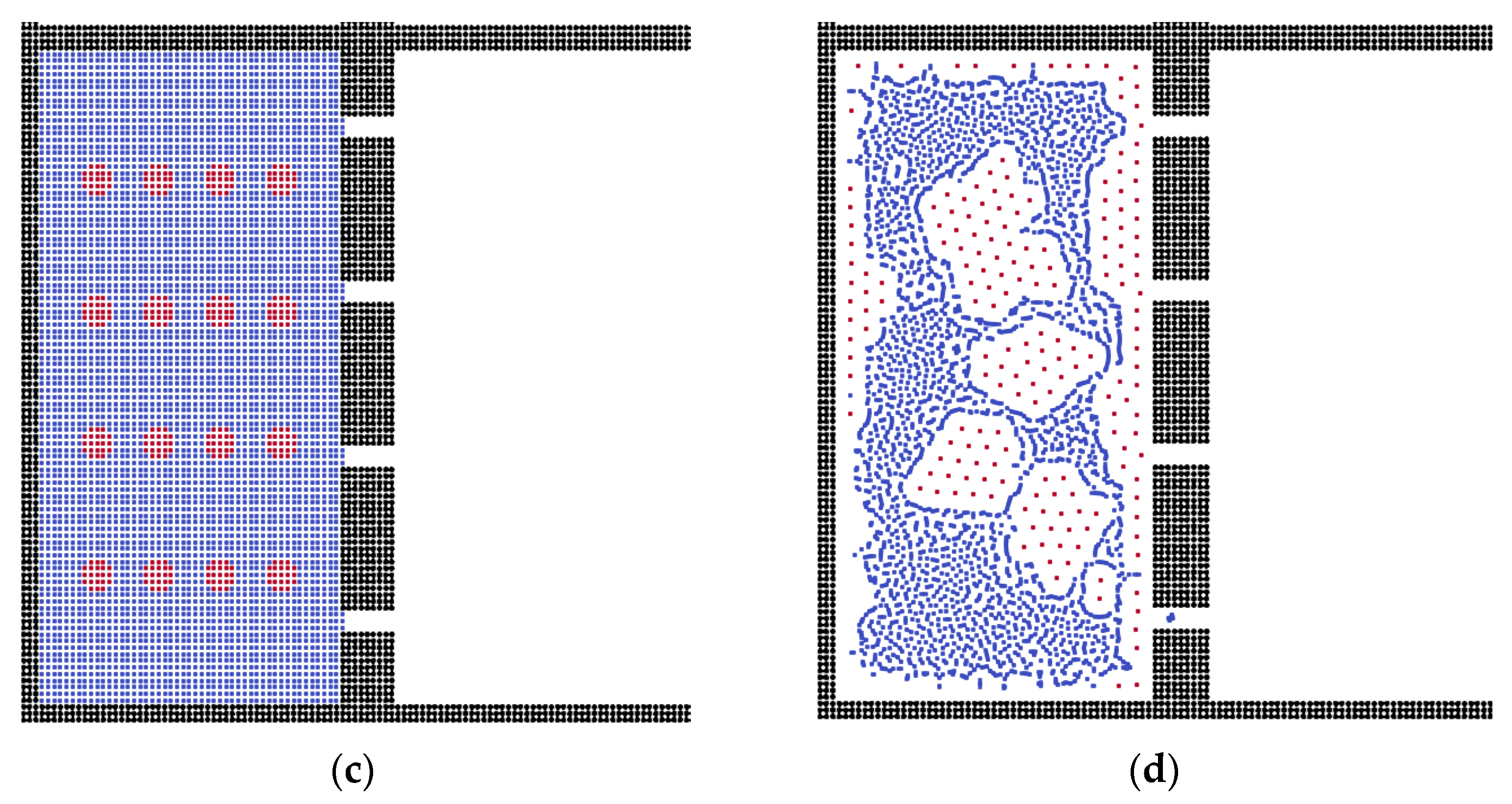
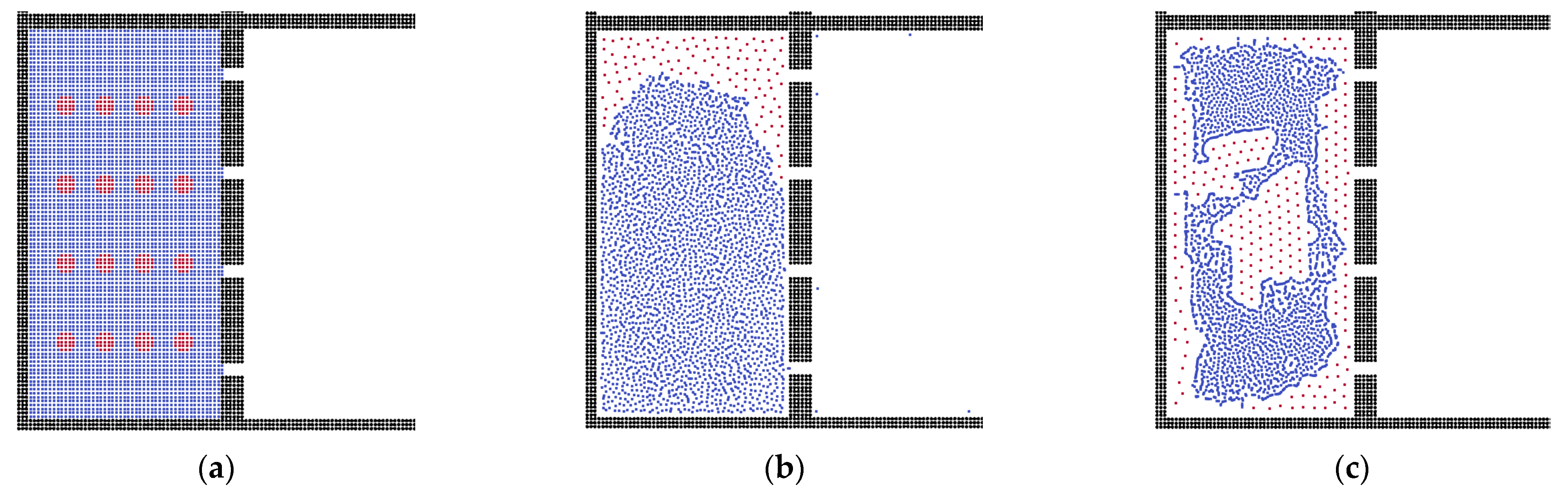
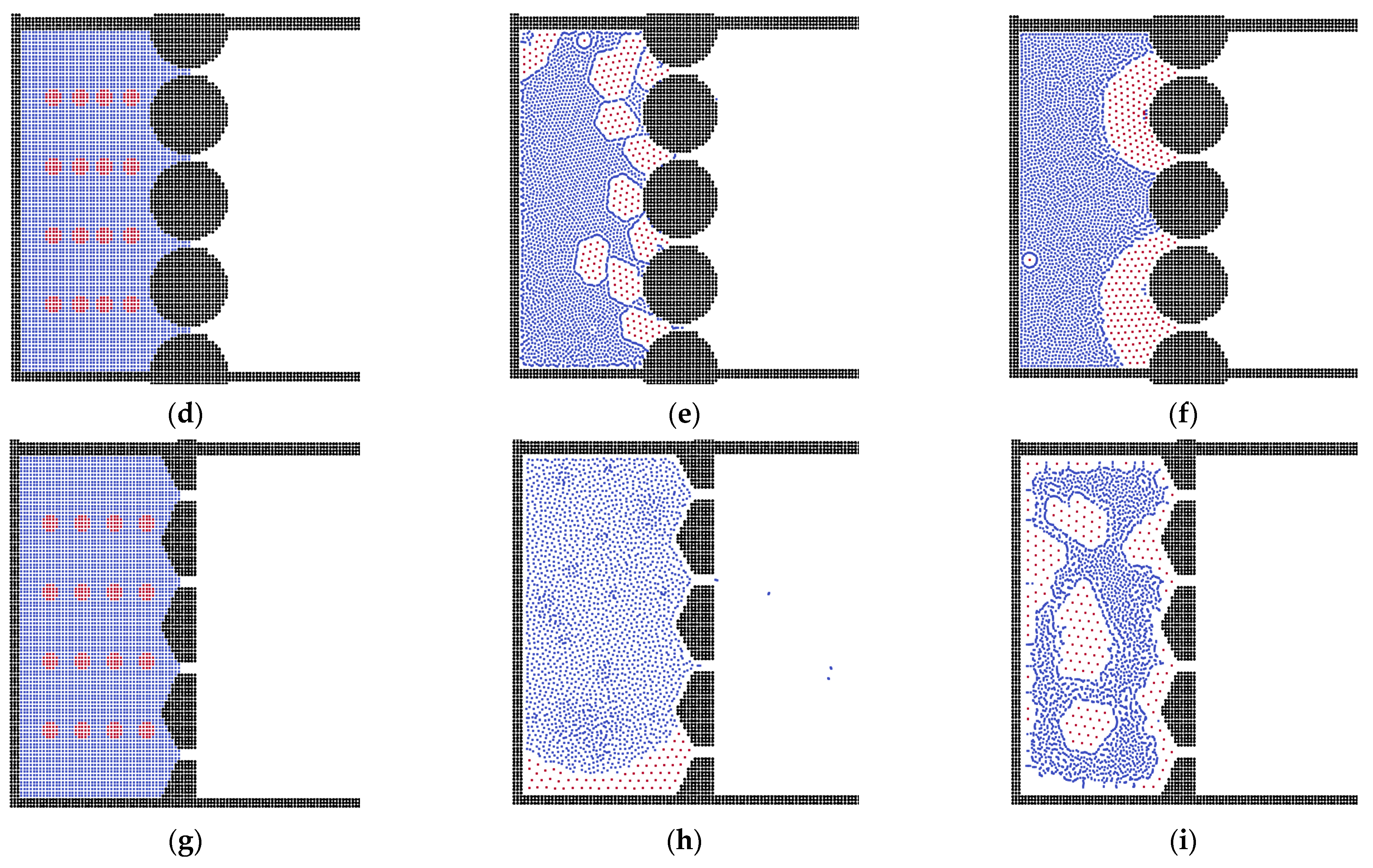
3.2. The Effects of Membrane Structures
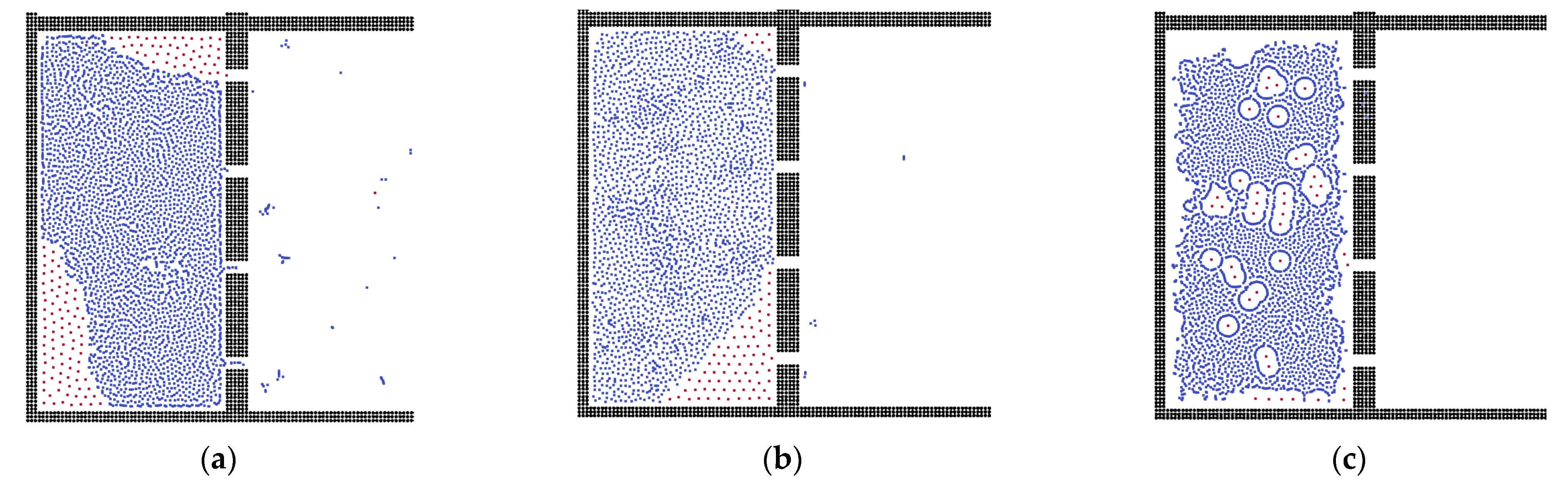
3.3. Oil Properties on the Separation Behavior
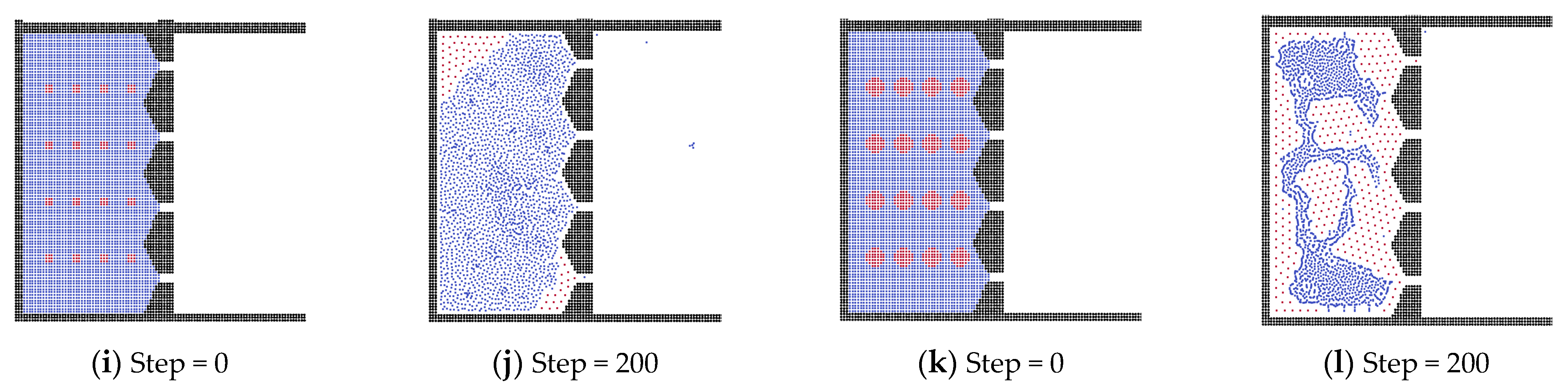
3.4. Analysis of External Force and State of Liquid
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Yao, J.; Wang, C.; Gao, Y.; Zhang, Q.; An, S.; Song, W. New pore space characterization method of shale matrix formation by considering organic and inorganic pores. J. Nat. Gas Sci. Eng. 2015, 27, 496–503. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Yao, J.; Iglauer, S.; Luquot, L.; Zhang, K.; Sun, H.; Zhang, L.; Song, W.; Wang, Z. Dynamic pore-scale dissolution by CO2-saturated brine in carbonates: Impact of homogeneous versus fractured versus vuggy pore structure. Water Resour. Res. 2020, 56, e2019WR026112. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Sun, S. Phase equilibrium calculations in shale gas reservoirs. Capillarity 2019, 2, 8–16. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.; Hajibeygi, H.; Yao, J.; Hassanizadeh, M. Advances in porous media science and engineering from InterPore2020 perspective. Adv. Geo-Energy Res. 2020, 4, 352–355. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, S. A coupled Lattice Boltzmann approach to simulate gas flow and transport in shale reservoirs with dynamic sorption. Fuel 2019, 246, 196–203. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, S.; Song, H. Flow mechanism and simulation approaches for shale gas reservoirs: A review. Transp. Porous Media 2019, 126, 655–681. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Kou, J.; Sun, S.; Zhang, T. Fully mass-conservative IMPES schemes for incompressible two-phase flow in porous media. Comput. Methods Appl. Mech. Eng. 2019, 350, 641–663. [Google Scholar] [CrossRef]
- Dawson, C.; Sun, S.; Wheeler, M.F. Compatible algorithms for coupled flow and transport. Comput. Methods Appl. Mech. Eng. 2004, 193, 2565–2580. [Google Scholar] [CrossRef]
- Moortgat, J.; Sun, S.; Firoozabadi, A. Compositional modeling of three-phase flow with gravity using higher-order finite element methods. Water Resour. Res. 2011, 47, W0551. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Li, Y.; Li, Y.; Sun, S.; Gao, X. A self-adaptive deep learning algorithm for accelerating multi-component flash calculation. Comput. Methods Appl. Mech. Eng. 2020, 369, 113207. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, S. Thermodynamics-Informed Neural Network (TINN) for Phase Equilibrium Calculations Considering Capillary Pressure. Energies 2021, 14, 7724. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, Y.; Blunt, M.J.; Yao, J.; Cai, J. Advances in multiscale numerical and experimental approaches for multiphysics problems in porous media. Adv. Geo-Energy Res. 2021, 5, 233–238. [Google Scholar] [CrossRef]
- Hua, J.; Stene, J.F.; Lin, P. Numerical simulation of 3D bubbles rising in viscous liquids using a front tracking method. J. Comput. Phys. 2008, 227, 3358–3382. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Tan, H.H.; Zhang, B. A high-resolution characteristics-based implicit dual time-stepping VOF method for free surface flow simulation on unstructured grids. J. Comput. Phys. 2002, 183, 233–273. [Google Scholar] [CrossRef]
- Li, H.; Yap, Y.; Lou, J.; Shang, Z. Numerical modelling of three-fluid flow using the level-set method. Chem. Eng. Sci. 2015, 126, 224–236. [Google Scholar] [CrossRef]
- Bui, H.H.; Fukagawa, R.; Sako, K.; Ohno, S. Lagrangian meshfree particles method (SPH) for large deformation and failure flows of geomaterial using elastic–plastic soil constitutive model. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1537–1570. [Google Scholar] [CrossRef]
- Kong, J.; Li, K. Oil removal from oil-in-water emulsions using PVDF membranes. Sep. Purif. Technol. 1999, 16, 83–93. [Google Scholar] [CrossRef]
- Abadi, S.R.H.; Sebzari, M.R.; Hemati, M.; Rekabdar, F.; Mohammadi, T. Ceramic membrane performance in microfiltration of oily wastewater. Desalination 2011, 265, 222–228. [Google Scholar] [CrossRef]
- Cheryan, M.; Rajagopalan, N. Membrane processing of oily streams. Wastewater treatment and waste reduction. J. Membr. Sci. 1998, 151, 13–28. [Google Scholar] [CrossRef]
- Padaki, M.; Murali, R.S.; Abdullah, M.S.; Misdan, N.; Moslehyani, A.; Kassim, M.; Hilal, N.; Ismail, A. Membrane technology enhancement in oil–water separation. A review. Desalination 2015, 357, 197–207. [Google Scholar] [CrossRef]
- Singh, V.; Purkait, M.; Das, C. Cross-flow microfiltration of industrial oily wastewater: Experimental and theoretical consideration. Sep. Sci. Technol. 2011, 46, 1213–1223. [Google Scholar] [CrossRef]
- Wang, H.; Yuan, X.; Liang, H.; Chai, Z.; Shi, B. A brief review of the phase-field-based lattice Boltzmann method for multiphase flows. Capillarity 2019, 2, 33–52. [Google Scholar] [CrossRef] [Green Version]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Amicarelli, A.; Albano, R.; Mirauda, D.; Agate, G.; Sole, A.; Guandalini, R. A Smoothed Particle Hydrodynamics model for 3D solid body transport in free surface flows. Comput. Fluids 2015, 116, 205–228. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G.; Lam, K.; Zong, Z. Smoothed particle hydrodynamics for numerical simulation of underwater explosion. Comput. Mech. 2003, 30, 106–118. [Google Scholar] [CrossRef]
- Mayrhofer, A.; Laurence, D.; Rogers, B.; Violeau, D. DNS and LES of 3-D wall-bounded turbulence using smoothed particle hydrodynamics. Comput. Fluids 2015, 115, 86–97. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- He, M.; Khayyer, A.; Gao, X.; Xu, W.; Liu, B. Theoretical method for generating solitary waves using plunger-type wavemakers and its Smoothed Particle Hydrodynamics validation. Appl. Ocean Res. 2021, 106, 102414. [Google Scholar] [CrossRef]
- Crespo, A.; Altomare, C.; Domínguez, J.; González-Cao, J.; Gómez-Gesteira, M. Towards simulating floating offshore oscillating water column converters with smoothed particle hydrodynamics. Coast. Eng. 2017, 126, 11–26. [Google Scholar] [CrossRef]
- Chen, Y.-k.; Meringolo, D.D.; Liu, Y. SPH study of wave force on simplified superstructure of open-type sea access road. Ocean Eng. 2022, 249, 110869. [Google Scholar] [CrossRef]
- Yang, Q.; Yao, J.; Huang, Z.; Asif, M. A comprehensive SPH model for three-dimensional multiphase interface simulation. Comput. Fluids 2019, 187, 98–106. [Google Scholar] [CrossRef]
- Yang, Q.; Yao, J.; Huang, Z.; Zhu, G.; Liu, L.; Song, W. Pore-scale investigation of petro-physical fluid behaviours based on multiphase SPH method. J. Pet. Sci. Eng. 2020, 192, 107238. [Google Scholar] [CrossRef]
- Fatehi, R.; Manzari, M. A consistent and fast weakly compressible Smoothed Particle Hydrodynamics with a new wall boundary condition. Int. J. Numer. Methods Fluids 2012, 68, 905–921. [Google Scholar] [CrossRef]
- Fatehi, R.; Manzari, M. A remedy for numerical oscillations in weakly compressible smoothed particle hydrodynamics. Int. J. Numer. Methods Fluids 2011, 67, 1100–1114. [Google Scholar] [CrossRef]
- He, X.; Luo, L.-S. Lattice Boltzmann model for the incompressible Navier–Stokes equation. J. Stat. Phys. 1997, 88, 927–944. [Google Scholar] [CrossRef]
- Mohd-Yusof, J. Combined immersed-boundary/B-spline methods for simulations of flow in complex geometries. Cent. Turbul. Res. Annu. Res. Briefs 1997, 161, 317–327. [Google Scholar]
- Tartakovsky, A.M.; Meakin, P. Pore scale modeling of immiscible and miscible fluid flows using smoothed particle hydrodynamics. Adv. Water Resour. 2006, 29, 1464–1478. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Panchenko, A. Pairwise force smoothed particle hydrodynamics model for multiphase flow: Surface tension and contact line dynamics. J. Comput. Phys. 2016, 305, 1119–1146. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Chiu, M.-S.; Weng, C.-N. Derivation of the generalized Young-Laplace equation of curved interfaces in nanoscaled solids. J. Appl. Phys. 2006, 100, 074308. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Cao, G. Effectiveness of the Young-Laplace equation at nanoscale. Sci. Rep. 2016, 6, 1–10. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Violeau, D.; Rogers, B.D. Smoothed particle hydrodynamics (SPH) for free-surface flows: Past, present and future. J. Hydraul. Res. 2016, 54, 1–26. [Google Scholar] [CrossRef]
- Zhu, Y.; Fox, P.J. Simulation of pore-scale dispersion in periodic porous media using smoothed particle hydrodynamics. J. Comput. Phys. 2002, 182, 622–645. [Google Scholar] [CrossRef]
- Price, D.J. Smoothed particle hydrodynamics and magnetohydrodynamics. J. Comput. Phys. 2012, 231, 759–794. [Google Scholar] [CrossRef] [Green Version]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Zhu, Y.; Fox, P.J.; Morris, J.P. A pore-scale numerical model for flow through porous media. Int. J. Numer. Anal. Methods Geomech. 1999, 23, 881–904. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Trask, N.; Pan, K.; Jones, B.; Pan, W.; Williams, J.R. Smoothed particle hydrodynamics and its applications for multiphase flow and reactive transport in porous media. Comput. Geosci. 2016, 20, 807–834. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Yang, Y.; Sun, S.; Yao, J.; Kou, J. Flow Behaviors of Shale Oil in Kerogen Slit by Molecular Dynamics Simulation. Chem. Eng. J. 2022, 434, 134682. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Yao, J.; Kou, J.; Li, Z.; Wu, T.; Zhang, K.; Zhang, L.; Sun, H. Adsorption behaviors of shale oil in kerogen slit by molecular simulation. Chem. Eng. J. 2020, 387, 124054. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Y.; Yang, Y.; Mei, Q.; Yang, S.; Wang, C. Multicomponent Shale Oil Flow in Real Kerogen Structures via Molecular Dynamic Simulation. Energies 2020, 13, 3815. [Google Scholar] [CrossRef]
- Ko, S.; Prigiobbe, V.; Huh, C.; Bryant, S.; Bennetzen, M.V.; Mogensen, K. Accelerated Oil Droplet Separation from Produced Water Using Magnetic Nanoparticles. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014; OnePetro: Richardson, TX, USA, 2014. [Google Scholar]
- Finborud, A.; Faucher, M.; Sellman, E. New Method for Improving Oil Droplet Growth for Separation Enhancement. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999; OnePetro: Richardson, TX, USA, 1999. [Google Scholar]
- Dmitrieva, E.S.; Anokhina, T.S.; Novitsky, E.G.; Volkov, V.V.; Borisov, I.L.; Volkov, A.V. Polymeric Membranes for Oil-Water Separation: A Review. Polymers 2022, 14, 980. [Google Scholar] [CrossRef]
- Wang, Y.; Kang, Y.; Wang, D.; You, L.; Chen, M.; Yan, X. Liquid phase blockage in micro-nano capillary pores of tight condensate reservoirs. Capillarity 2022, 5, 12–22. [Google Scholar] [CrossRef]


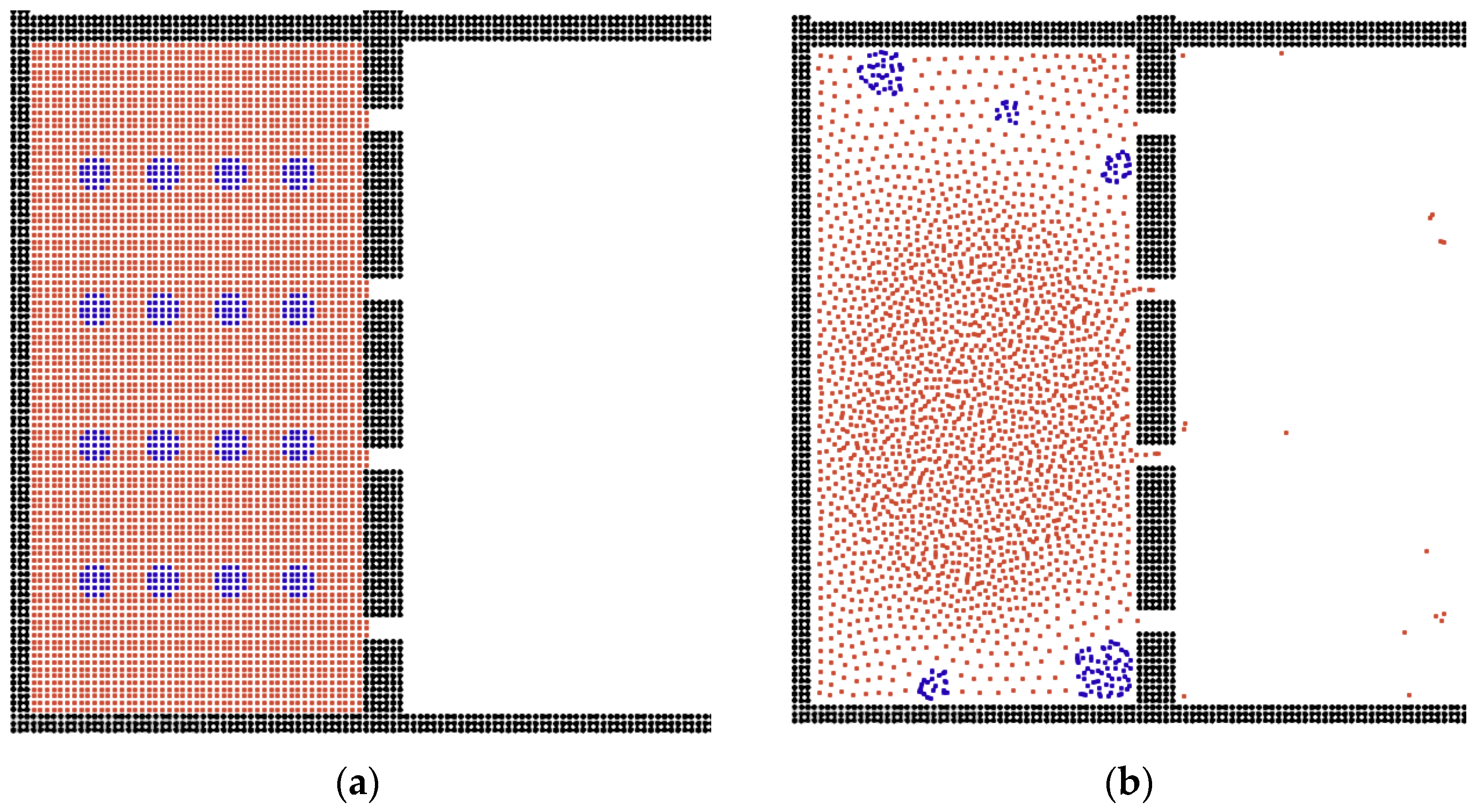
| Pore Size | Thickness | Droplet Size | Viscosity | External Force | |
|---|---|---|---|---|---|
| Flat | ↑ | ↓ | ↑ | ↓ | ↑ |
| Triangular | ↑ | ↔ | ↔ | ↓ | ↑ |
| Sphere | ↑ | ↔ | ↓ | ↓ | ↑ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Xie, X.; Meng, Q.; Sun, S. Effects of Membrane Structure on Oil–Water Separation by Smoothed Particle Hydrodynamics. Membranes 2022, 12, 387. https://doi.org/10.3390/membranes12040387
Liu J, Xie X, Meng Q, Sun S. Effects of Membrane Structure on Oil–Water Separation by Smoothed Particle Hydrodynamics. Membranes. 2022; 12(4):387. https://doi.org/10.3390/membranes12040387
Chicago/Turabian StyleLiu, Jie, Xiaoping Xie, Qingbang Meng, and Shuyu Sun. 2022. "Effects of Membrane Structure on Oil–Water Separation by Smoothed Particle Hydrodynamics" Membranes 12, no. 4: 387. https://doi.org/10.3390/membranes12040387
APA StyleLiu, J., Xie, X., Meng, Q., & Sun, S. (2022). Effects of Membrane Structure on Oil–Water Separation by Smoothed Particle Hydrodynamics. Membranes, 12(4), 387. https://doi.org/10.3390/membranes12040387









