Fabrication of Polyamide-6 Membranes—The Effect of Gelation Time towards Their Morphological, Physical and Transport Properties
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials
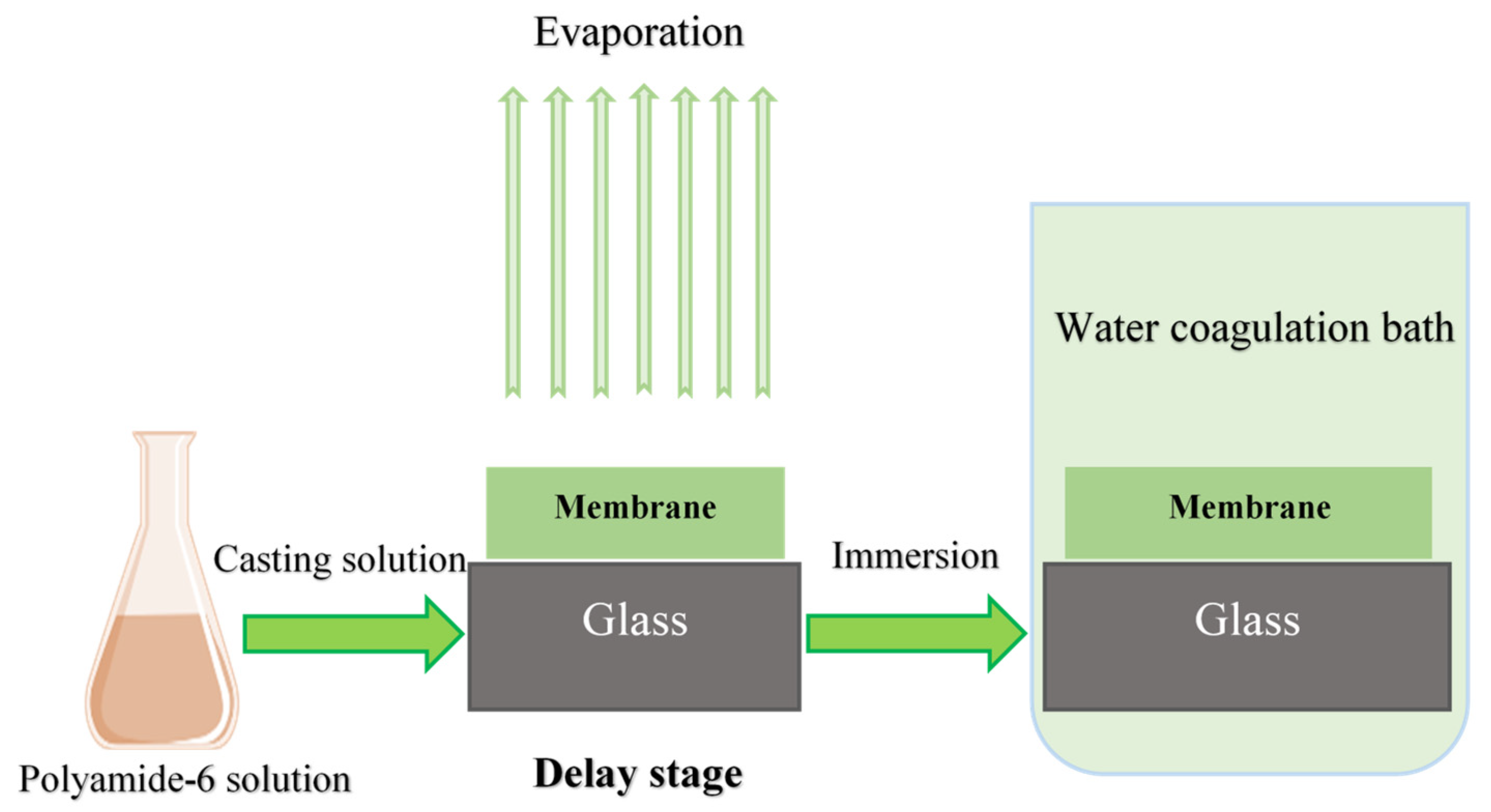
2.2. Membrane Fabrication
3. Characterization of PA6 Membranes
3.1. Scanning Electron Microscopy
3.2. Atomic Force Microscopy
- f(x,y): surface relative to the center plane,
- Lx and Ly: dimensions of the surface.
- Zi: the current height value,
- Zave: the average height,
- Np: number of points in a given area.
3.3. Thickness Measurements
3.4. Contact Angle Measurement
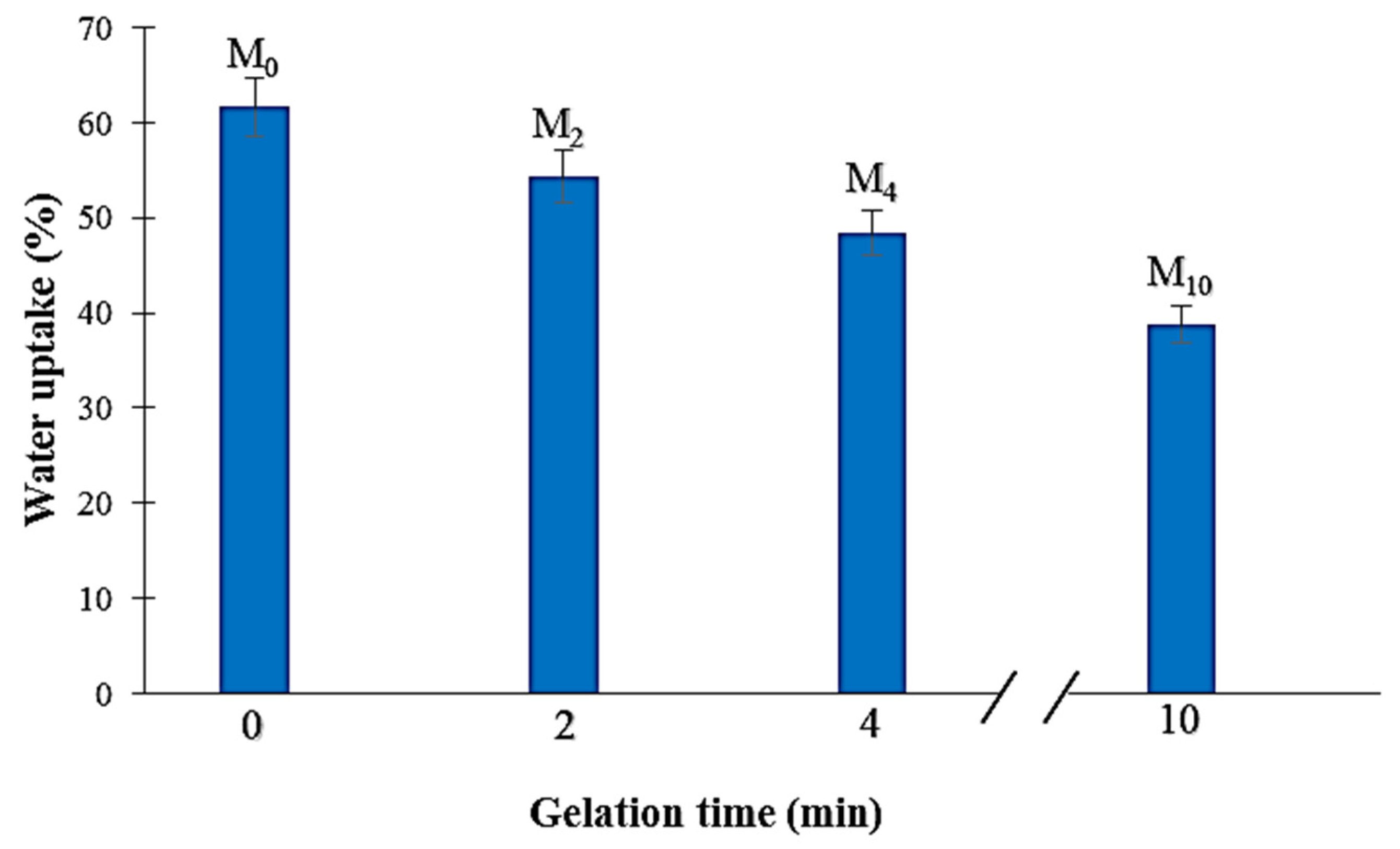
3.5. Water Uptake (WU)
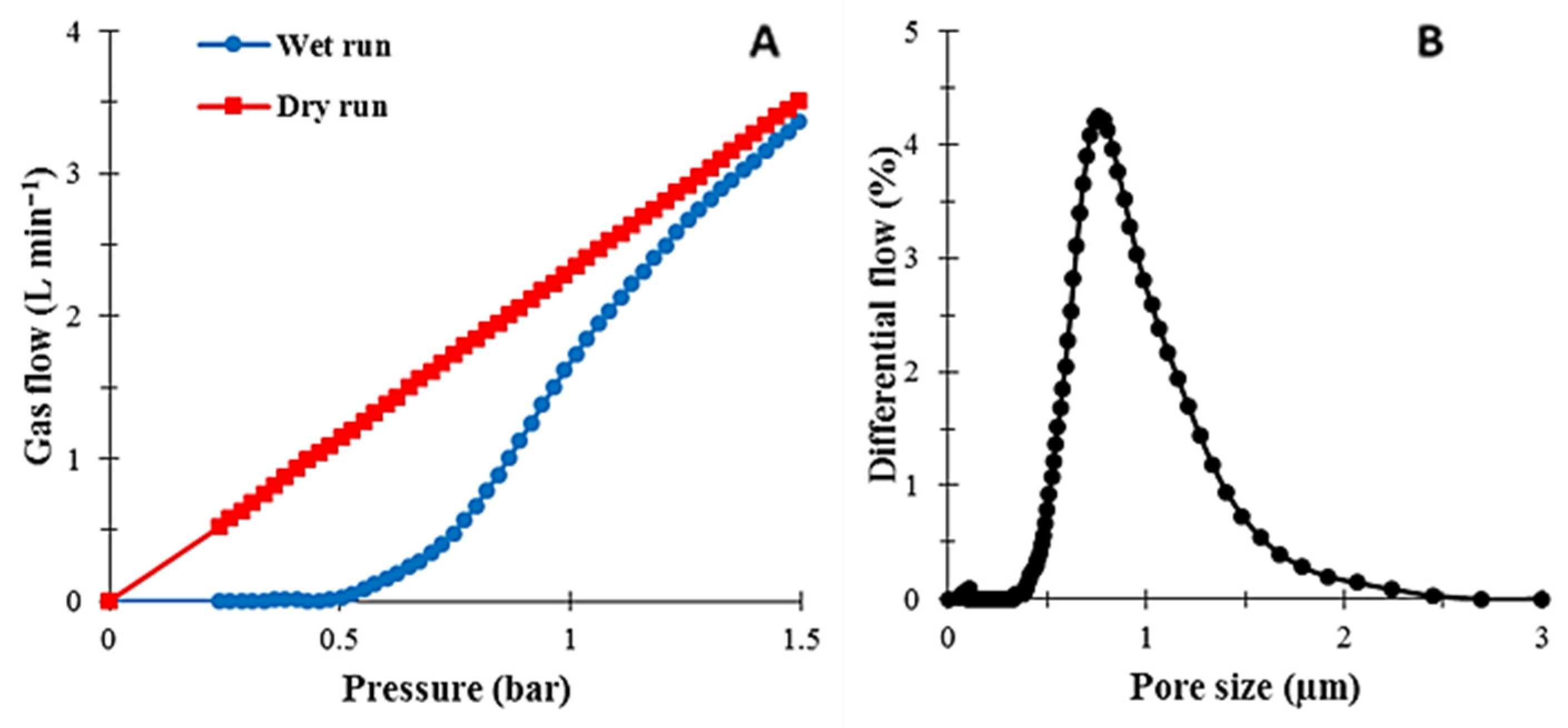
3.6. Mean Pore Size and Porosity Measurements
3.7. Mechanical Resistance
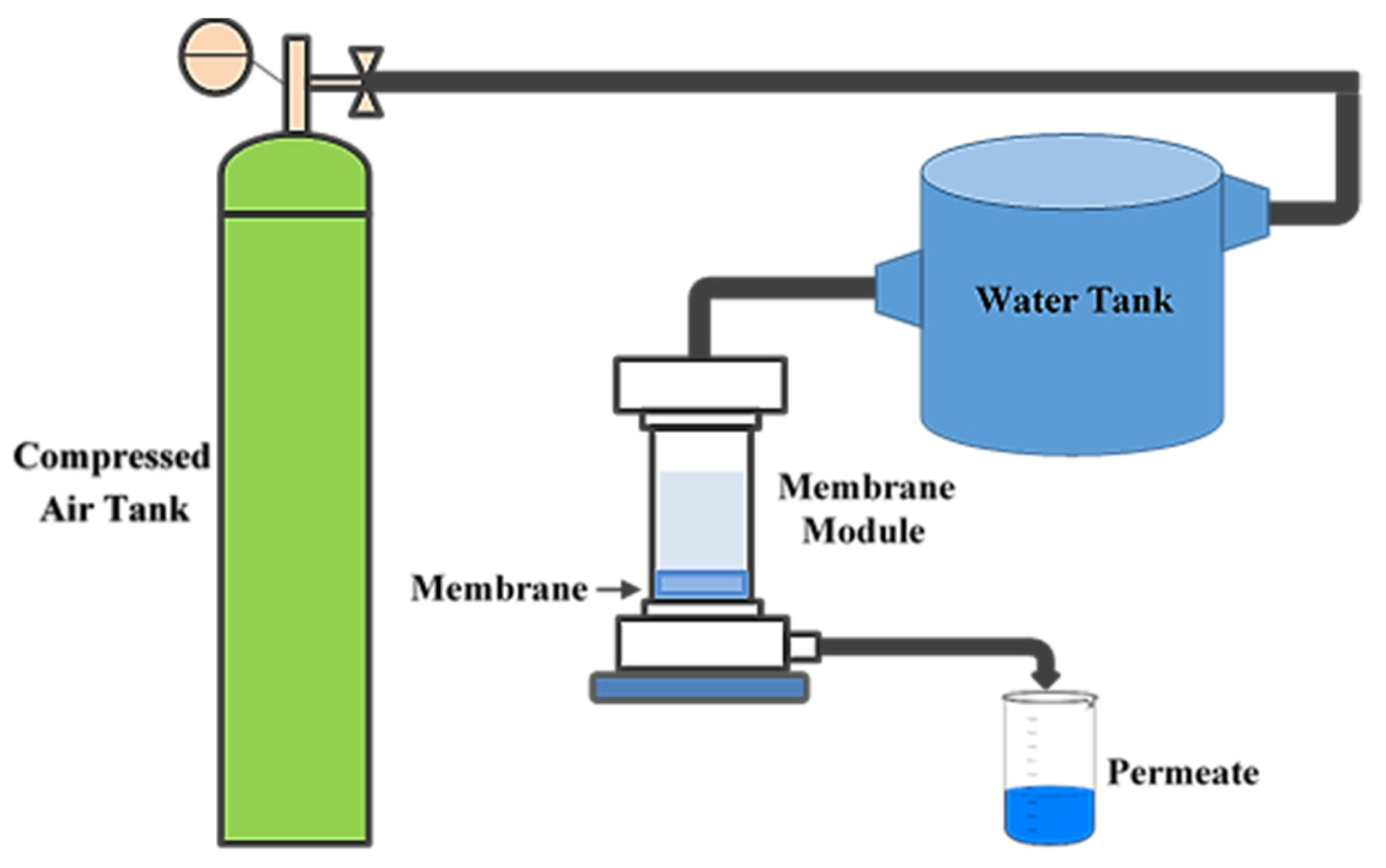
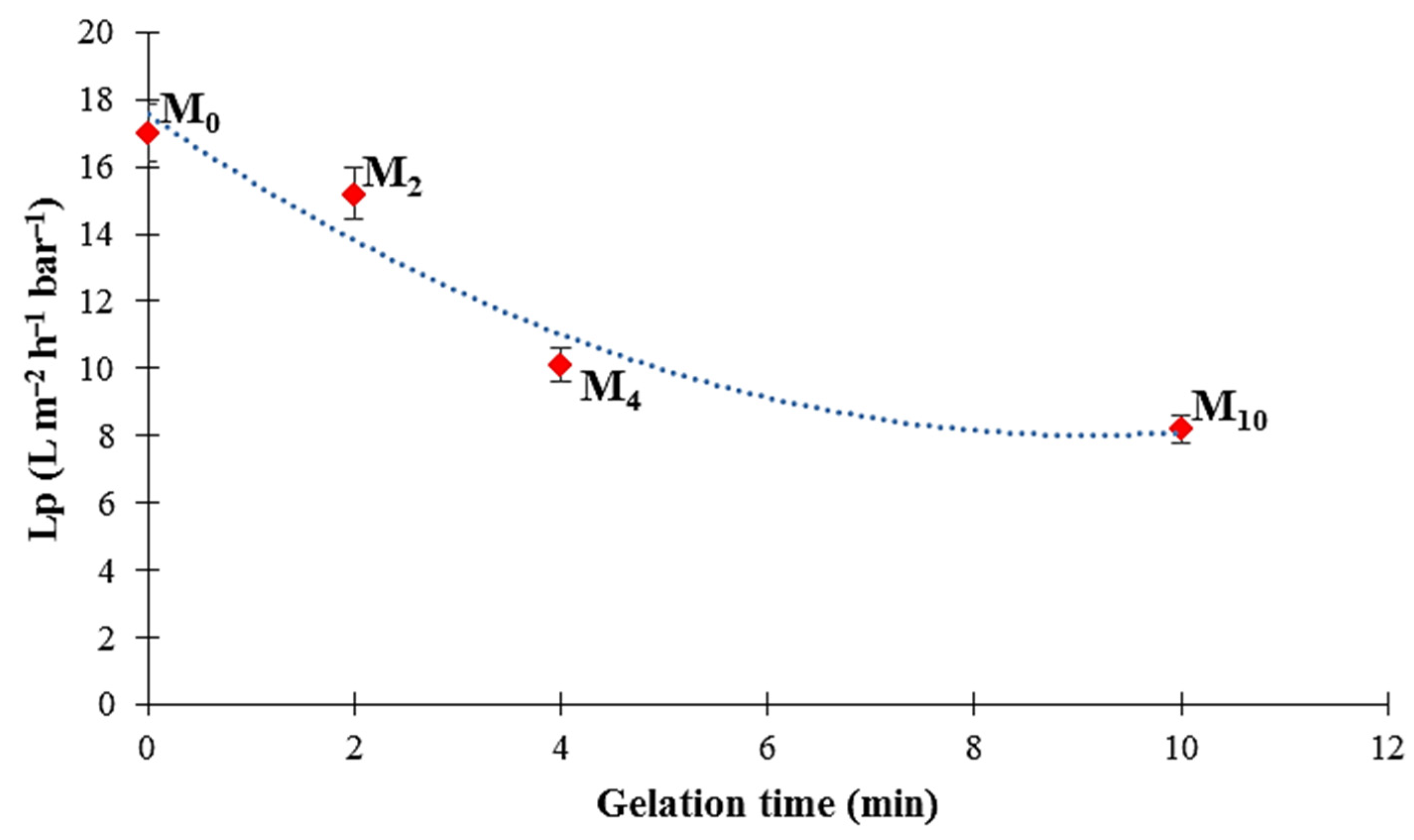
3.8. Membrane Filtration Performance
4. Results and Discussion
4.1. Scanning Electron Microscopy
4.2. Atomic Force Microscopy
4.3. Thickness Measurements
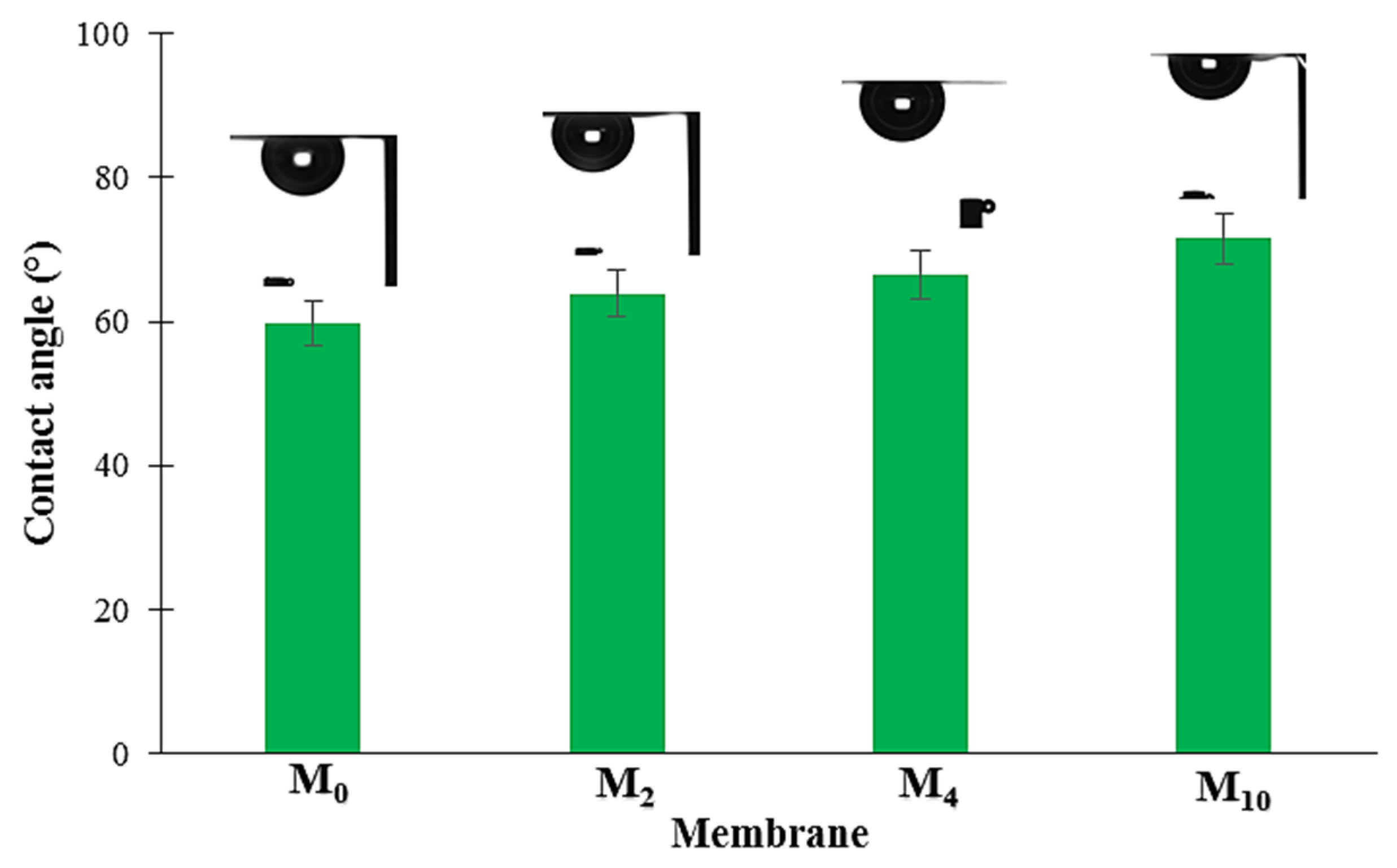
4.4. Contact Angle Measurement
4.5. Water Uptake (WU)
4.6. Mean Pore Size and Porosity Measurements
4.7. Mechanical Strength
4.8. Membrane Filtration Performance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Ra (nm) | Average roughness |
| AFM | Atomic force microscopy |
| CA (deg) | Contact angle |
| Td (µm) | Dry thickness |
| MPS (µm) | Mean pore size |
| Lp (L m−2 h−1 bar−1) | Membrane hydrodynamic permeability |
| NP | Nanoparticle |
| PA6 | Polyamide-6 |
| PEG | Polyethylene glycol |
| ε (%) | Porosity |
| RH (%) | Relative humidity |
| Rq (nm) | Root mean square |
| SEM | Scanning electron microscopy |
| WU (%) | Water uptake |
| Tw (µm) | Wet thickness |
References
- Baker, R.W. Membrane Technology and Applications, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Pal, P. Chapter 2—Introduction to membrane-based technology applications. In Membrane-Based Technologies for Environmental Pollution Control, 1st ed.; Pal, P., Ed.; Butterworth-Heinemann: Oxford, UK, 2020; pp. 71–100. [Google Scholar]
- Cassano, A.; Basile, A. 7—Integrating different membrane operations and combining membranes with conventional separation techniques in industrial processes. In Handbook of Membrane Reactors; Basile, A., Ed.; Woodhead Publishing: Sawston, UK, 2013; Volume 2, pp. 296–343. [Google Scholar]
- Vigneswaran, C.; Ananthasubramanian, M.; Kandhavadivu, P. 5—Enzymes in textile effluents. In Bioprocessing of Textiles; Vigneswaran, C., Ananthasubramanian, M., Kandhavadivu, P., Eds.; Woodhead Publishing India: Delhi, India, 2014; pp. 251–298. [Google Scholar]
- Mulder, M.; Mulder, J. Basic Principles of Membrane Technology, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Ray, P.; Singh, P.S.; Polisetti, V. 2—Synthetic polymeric membranes for the removal of toxic pollutants and other harmful contaminants from water. In Removal of Toxic Pollutants Through Microbiological and Tertiary Treatment; Shah, M.P., Ed.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 43–99. [Google Scholar]
- Kovaleva, O.; Lazarev, S.; Kovalev, S. Effect of transmembrane pressure on microfiltration concentration of yeast biomass. Pet. Chem. 2017, 57, 974–982. [Google Scholar] [CrossRef]
- Vieira, A.H.; Balthazar, C.F.; Guimaraes, J.T.; Rocha, R.S.; Pagani, M.M.; Esmerino, E.A.; Silva, M.C.; Raices, R.S.; Tonon, R.V.; Cabral, L.M. Advantages of microfiltration processing of goat whey orange juice beverage. Food Res. Int. 2020, 132, 109060. [Google Scholar] [CrossRef] [PubMed]
- Hartinger, M.; Heidebrecht, H.-J.; Schiffer, S.; Dumpler, J.; Kulozik, U. Milk protein fractionation by means of spiral-wound microfiltration membranes: Effect of the pressure adjustment mode and temperature on flux and protein permeation. Foods 2019, 8, 180. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Severcan, S.S.; Uzal, N.; Kahraman, K. Clarification of pomegranate juice using PSF microfiltration membranes fabricated with nano TiO2 and Al2O3. J. Food Processing Preserv. 2020, 44, e14559. [Google Scholar] [CrossRef]
- Han, Q.; Lay, H.T.; Li, W.; Chew, J.W. Effect of initial particle deposition rate on cake formation during dead-end microfiltration. J. Membr. Sci. 2021, 618, 118672. [Google Scholar] [CrossRef]
- Mazerolle, D.; Bronson, B.; Kruczek, B. Experimental Evaluation and Empirical Modeling of Cross-Flow Microfiltration for Solids and Ash Removal from Fast Pyrolysis Bio-Oil. Energy Fuels 2020, 34, 11014–11025. [Google Scholar] [CrossRef]
- Iritani, E.; Katagiri, N.; Sawada, D. Simultaneous Evaluation of Mechanism and Degree of Fouling from Limited Flux Decline Data in Dead-End Microfiltration. J. Chem. Eng. Jpn. 2018, 51, 507–517. [Google Scholar] [CrossRef]
- Cogan, N.; Hussaini, M.; Chellam, S. Uncertainty propagation in a model of dead-end bacterial microfiltration using fuzzy interval analysis. J. Membr. Sci. 2018, 546, 215–224. [Google Scholar] [CrossRef]
- Diagne, F.; Malaisamy, R.; Boddie, V.; Holbrook, R.D.; Eribo, B.; Jones, K.L. Polyelectrolyte and Silver Nanoparticle Modification of Microfiltration Membranes To Mitigate Organic and Bacterial Fouling. Environ. Sci. Technol. 2012, 46, 4025–4033. [Google Scholar] [CrossRef]
- Homem, N.C.; de Camargo Lima Beluci, N.; Amorim, S.; Reis, R.; Vieira, A.M.S.; Vieira, M.F.; Bergamasco, R.; Amorim, M.T.P. Surface modification of a polyethersulfone microfiltration membrane with graphene oxide for reactive dyes removal. Appl. Surf. Sci. 2019, 486, 499–507. [Google Scholar] [CrossRef]
- Liu, Z.-M.; Xu, Z.-K.; Wang, J.-Q.; Wu, J.; Fu, J.-J. Surface modification of polypropylene microfiltration membranes by graft polymerization of N-vinyl-2-pyrrolidone. Eur. Polym. J. 2004, 40, 2077–2087. [Google Scholar] [CrossRef]
- Liu, Z.-M.; Xu, Z.-K.; Wan, L.-S.; Wu, J.; Ulbricht, M. Surface modification of polypropylene microfiltration membranes by the immobilization of poly(N-vinyl-2-pyrrolidone): A facile plasma approach. J. Membr. Sci. 2005, 249, 21–31. [Google Scholar] [CrossRef]
- Yan, M.-G.; Liu, L.-Q.; Tang, Z.-Q.; Huang, L.; Li, W.; Zhou, J.; Gu, J.-S.; Wei, X.-W.; Yu, H.-Y. Plasma surface modification of polypropylene microfiltration membranes and fouling by BSA dispersion. Chem. Eng. J. 2008, 145, 218–224. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, B.; Fu, Z.; Li, J.; Yu, M.; Li, L.; Li, J. Poly(vinyl alcohol) modification of poly(vinylidene fluoride) microfiltration membranes for oil/water emulsion separation via an unconventional radiation method. J. Membr. Sci. 2021, 619, 118792. [Google Scholar] [CrossRef]
- Vankelecom, I.; De Smet, K.; Gevers, L.; Jacobs, P. Nanofiltration Membrane Materials and Preparation, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2005; p. 31. [Google Scholar]
- Ismail, A.F.; Yean, L.P. Review on the development of defect-free and ultrathin-skinned asymmetric membranes for gas separation through manipulation of phase inversion and rheological factors. J. Appl. Polym. Sci. 2003, 88, 442–451. [Google Scholar] [CrossRef]
- Li, D.; Chung, T.-S.; Ren, J.; Wang, R. Thickness dependence of macrovoid evolution in wet phase-inversion asymmetric membranes. Ind. Eng. Chem. Res. 2004, 43, 1553–1556. [Google Scholar] [CrossRef]
- Fan, S.-C.; Wang, Y.-C.; Li, C.-L.; Lee, K.-R.; Liaw, D.-J.; Huang, H.-P.; Lai, J.-Y. Effect of coagulation media on membrane formation and vapor permeation performance of novel aromatic polyamide membrane. J. Membr. Sci. 2002, 204, 67–79. [Google Scholar] [CrossRef]
- See-Toh, Y.H.; Ferreira, F.C.; Livingston, A.G. The influence of membrane formation parameters on the functional performance of organic solvent nanofiltration membranes. J. Membr. Sci. 2007, 299, 236–250. [Google Scholar] [CrossRef]
- Paulsen, F.G.; Shojaie, S.S.; Krantz, W.B. Effect of evaporation step on macrovoid formation in wet-cast polymeric membranes. J. Membr. Sci. 1994, 91, 265–282. [Google Scholar] [CrossRef]
- Vandezande, P.; Li, X.; Gevers, L.E.; Vankelecom, I.F. High throughput study of phase inversion parameters for polyimide-based SRNF membranes. J. Membr. Sci. 2009, 330, 307–318. [Google Scholar] [CrossRef]
- Ceynowa, J.; Adamczak, P. Enzyme membrane based upon polyamide-6 for oil hydrolysis. J. Appl. Polym. Sci. 1992, 46, 749–755. [Google Scholar] [CrossRef]
- Hołda, A.K.; Aernouts, B.; Saeys, W.; Vankelecom, I.F. Study of polymer concentration and evaporation time as phase inversion parameters for polysulfone-based SRNF membranes. J. Membr. Sci. 2013, 442, 196–205. [Google Scholar] [CrossRef]
- Singh, S.; Khulbe, K.; Matsuura, T.; Ramamurthy, P. Membrane characterization by solute transport and atomic force microscopy. J. Membr. Sci. 1998, 142, 111–127. [Google Scholar] [CrossRef]
- Baek, Y.; Kang, J.; Theato, P.; Yoon, J. Measuring hydrophilicity of RO membranes by contact angles via sessile drop and captive bubble method: A comparative study. Desalination 2012, 303, 23–28. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, M.; Shen, P.; Uytterhoeven, C.; Mamrol, N.; Shen, J.; Gao, C.; Van der Bruggen, B. Composite anti-scaling membrane made of interpenetrating networks of nanofibers for selective separation of lithium. J. Membr. Sci. 2021, 618, 118668. [Google Scholar] [CrossRef]
- Letellier, P.; Mayaffre, A.; Turmine, M. Drop size effect on contact angle explained by nonextensive thermodynamics. Young’s equation revisited. J. Colloid Interface Sci. 2007, 314, 604–614. [Google Scholar] [CrossRef]
- Kubiak, K.J.; Wilson, M.C.T.; Mathia, T.G.; Carval, P. Wettability versus roughness of engineering surfaces. Wear 2011, 271, 523–528. [Google Scholar] [CrossRef] [Green Version]
- George, J.E.; Chidangil, S.; George, S.D. Recent progress in fabricating superaerophobic and superaerophilic surfaces. Adv. Mater. Interfaces 2017, 4, 1601088. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Moradi, F.; Farahani, S.K.; Bandehali, S.; Parvizian, F.; Ebrahimi, M.; Shen, J. Carbon nanofibers/chitosan nanocomposite thin film for surface modification of poly (ether sulphone) nanofiltration membrane. Mater. Chem. Phys. 2021, 269, 124720. [Google Scholar] [CrossRef]
- da Trindade, L.G.; Borba, K.M.; Zanchet, L.; Lima, D.W.; Trench, A.B.; Rey, F.; Diaz, U.; Longo, E.; Bernardo-Gusmao, K.; Martini, E.M. SPEEK-based proton exchange membranes modified with MOF-encapsulated ionic liquid. Mater. Chem. Phys. 2019, 236, 121792. [Google Scholar] [CrossRef]
- Kujawski, W.; Adamczak, P.; Narebska, A. A Fully Automated System for the Determination of Pore Size Distribution in Microfiltration and Ultrafiltration Membranes. Sep. Sci. Technol. 1989, 24, 495–506. [Google Scholar] [CrossRef]
- Szczerbińska, J.; Kujawski, W.; Arszyńska, J.M.; Kujawa, J. Assessment of air-gap membrane distillation with hydrophobic porous membranes utilized for damaged paintings humidification. J. Membr. Sci. 2017, 538, 1–8. [Google Scholar] [CrossRef]
- Hernández, A.; Calvo, J.I.; Prádanos, P.; Tejerina, F. Pore size distributions in microporous membranes. A critical analysis of the bubble point extended method. J. Membr. Sci. 1996, 112, 1–12. [Google Scholar] [CrossRef]
- Kujawa, J.; Chrzanowska, E.; Kujawski, W. Transport properties and fouling issues of membranes utilized for the concentration of dairy products by air-gap membrane distillation and microfiltration. Chem. Pap. 2019, 73, 565–582. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Xiu, R.; Lu, S.; Xu, X.; Yang, S.; Xiang, Y. Submicro-pore containing poly(ether sulfones)/polyvinylpyrrolidone membranes for high-temperature fuel cell applications. J. Mater. Chem. A 2015, 3, 8847–8854. [Google Scholar] [CrossRef]
- Jakubowska, E.; Gierszewska, M.; Nowaczyk, J.; Olewnik-Kruszkowska, E. Physicochemical and storage properties of chitosan-based films plasticized with deep eutectic solvent. Food Hydrocoll. 2020, 108, 106007. [Google Scholar] [CrossRef]
- Gierszewska, M.; Jakubowska, E.; Olewnik-Kruszkowska, E. Effect of chemical crosslinking on properties of chitosan-montmorillonite composites. Polym. Test. 2019, 77, 105872. [Google Scholar] [CrossRef]
- da Trindade, L.G.; Zanchet, L.; Souza, J.C.; Leite, E.R.; Martini, E.M.A.; Pereira, E.C. Enhancement of sulfonated poly (ether ether ketone)-based proton exchange membranes doped with different ionic liquids cations. Ionics 2020, 26, 5661–5672. [Google Scholar] [CrossRef]
- Yang, J.; Che, Q.; Zhou, L.; He, R.; Savinell, R.F. Studies of a high temperature proton exchange membrane based on incorporating an ionic liquid cation 1-butyl-3-methylimidazolium into a Nafion matrix. Electrochim. Acta 2011, 56, 5940–5946. [Google Scholar] [CrossRef]
- Hong, J.; He, Y. Effects of nano sized zinc oxide on the performance of PVDF microfiltration membranes. Desalination 2012, 302, 71–79. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, F.; Zhang, X.; Zhang, H.; Li, Y.; Li, J. Ionic liquid grafted polyamide 6 as porous membrane materials: Enhanced water flux and heavy metal adsorption. Appl. Surf. Sci. 2019, 481, 1435–1441. [Google Scholar] [CrossRef]
- Shin, S.-J.; Kim, J.-P.; Kim, H.-J.; Jeon, J.-H.; Min, B.-R. Preparation and characterization of polyethersulfone microfiltration membranes by a 2-methoxyethanol additive. Desalination 2005, 186, 1–10. [Google Scholar] [CrossRef]
- Ferreira, A.M.; Roque, É.B.; Fonseca, F.V.d.; Borges, C.P. High flux microfiltration membranes with silver nanoparticles for water disinfection. Desalination Water Treat. 2015, 56, 3590–3598. [Google Scholar] [CrossRef]
- Fontão, N.C.; Wilhelm, M.; Rezwan, K. Asymmetric polysiloxane-based SiOC membranes produced via phase inversion tape casting process. Mater. Des. 2021, 198, 109328. [Google Scholar] [CrossRef]
- Woo, S.H.; Park, J.; Min, B.R. Relationship between permeate flux and surface roughness of membranes with similar water contact angle values. Sep. Purif. Technol. 2015, 146, 187–191. [Google Scholar] [CrossRef]







| Membrane | Gelation Time (min) |
|---|---|
| M0 | 0 |
| M2 | 2 |
| M4 | 4 |
| M10 | 10 |
| Membrane | Gelation Time (min) | Ra (nm) | Rq (nm) |
|---|---|---|---|
| M0 | 0 | 154 ± 22 | 200 ± 34 |
| M2 | 2 | 155 ± 32 | 195 ± 42 |
| M4 | 4 | 166 ± 28 | 203 ± 31 |
| M10 | 10 | 189 ± 53 | 240 ± 59 |
| Membrane | Gelation Time (min) | Thickness (µm) | Thickness Change (%) | ||
|---|---|---|---|---|---|
| Wet | Dry | Measured by SEM | |||
| M0 | 0 | 162 ± 8 | 150 ± 7 | 153 | 8 |
| M2 | 2 | 150 ± 7 | 141 ± 15 | 145 | 6 |
| M4 | 4 | 141 ± 7 | 134 ± 7 | 137 | 5 |
| M10 | 10 | 124 ± 7 | 120 ± 16 | 119 | 3 |
| Membrane | Porosity (%) | Mean Pore Size (µm) * | Minimum Pore Size (µm) * | Maximum Pore Size (µm) * | Bubble Point Pressure (bar) * |
|---|---|---|---|---|---|
| M0 | 72 ± 2 | 0.710 ± 0.060 | 0.166 | 2.832 | 0.226 |
| M2 | 59 ± 1 | 0.563 ± 0.036 | 0.364 | 1.449 | 0.442 |
| M4 | 54 ± 2 | 0.468 ± 0.023 | 0.223 | 1.036 | 0.618 |
| M10 | 39 ± 4 | 0.234 ± 0.019 | 0.153 | 0.960 | 0.667 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebrahimi, M.; Kujawski, W.; Fatyeyeva, K. Fabrication of Polyamide-6 Membranes—The Effect of Gelation Time towards Their Morphological, Physical and Transport Properties. Membranes 2022, 12, 315. https://doi.org/10.3390/membranes12030315
Ebrahimi M, Kujawski W, Fatyeyeva K. Fabrication of Polyamide-6 Membranes—The Effect of Gelation Time towards Their Morphological, Physical and Transport Properties. Membranes. 2022; 12(3):315. https://doi.org/10.3390/membranes12030315
Chicago/Turabian StyleEbrahimi, Mohammad, Wojciech Kujawski, and Kateryna Fatyeyeva. 2022. "Fabrication of Polyamide-6 Membranes—The Effect of Gelation Time towards Their Morphological, Physical and Transport Properties" Membranes 12, no. 3: 315. https://doi.org/10.3390/membranes12030315
APA StyleEbrahimi, M., Kujawski, W., & Fatyeyeva, K. (2022). Fabrication of Polyamide-6 Membranes—The Effect of Gelation Time towards Their Morphological, Physical and Transport Properties. Membranes, 12(3), 315. https://doi.org/10.3390/membranes12030315








