Mass Transport of Dye Solutions through Porous Membrane Containing Tannic Acid/Fe3+ Selective Layer
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Preparation of Tannic Acid/Fe3+ Selective Layer
2.3. Membrane Characterization
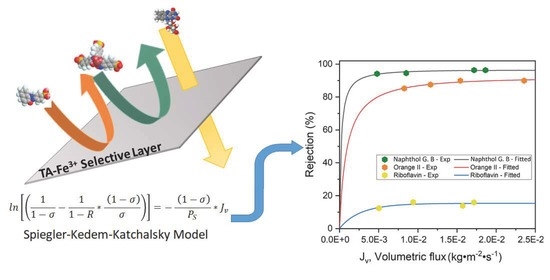
2.4. Fitting/Prediction of Dye Rejection with Spiegler–Kedem–Katchalsky Model
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Feed solute concentration (kg·m−3) | |
| Permeate solute concentration (kg·m−3) | |
| Retentate solute concentration (kg·m−3) | |
| Logarithmic mean concentration of solute between the feed and permeate (kg·m−3) | |
| Permeate flux (kg·m−2·s−1) | |
| Solute flux (kg·m−2·s−1) | |
| Solvent permeability constant (m·s−1) | |
| Solute permeability constant (m·s−1) | |
| R | Membrane rejection (%) |
| Rfitted | Membrane rejection calculated (%) |
| Robs | Membrane rejection experimental (%) |
| ΔP | Transmembrane pressure (bar) |
| Δπ | Osmotic pressure (bar) |
| σ | Reflection coefficient |
References
- Kadhim, R.J.; Al-Ani, F.H.; Al-shaeli, M.; Alsalhy, Q.F.; Figoli, A. Removal of dyes using graphene oxide (go) mixed matrix membranes. Membranes 2020, 10, 366. [Google Scholar] [CrossRef] [PubMed]
- Sachdeva, S.; Kumar, A. Separation of dyes using composite carbon membranes. Aiche J. 2009, 55, 1712–1722. [Google Scholar] [CrossRef]
- Majewska-Nowak, K. Ultrafiltration of dye solutions in the presence of cationic and anionic surfactants. Env. Prot. Eng. 2009, 35, 111–121. [Google Scholar]
- Koyuncu, I.; Topacik, D.; Yuksel, E. Reuse of reactive dyehouse wastewater by nanofiltration: Process water quality and economical implications. Sep. Purif. Technol. 2004, 36, 77–85. [Google Scholar] [CrossRef]
- Uzal, N.; Yilmaz, L.; Yetis, U. Nanofiltration and reverse osmosis for reuse of indigo dye rinsing waters. Sep. Sci. Technol. 2010, 45, 331–338. [Google Scholar] [CrossRef]
- Van der Bruggen, B.; Daems, B.; Wilms, D.; Vandecasteele, C. Mechanisms of retention and flux decline for the nanofiltration of dye baths from the textile industry. Sep. Purif. Technol. 2001, 22, 519–528. [Google Scholar] [CrossRef]
- Yen, H.Y.; Kang, S.F.; Yang, M.H. Separation of textile effluents by polyamide membrane for reuse. Polym. Test. 2002, 21, 539–543. [Google Scholar] [CrossRef]
- Bielska, M.; Prochaska, K. Dyes separation by means of cross-flow ultrafiltration of micellar solutions. Dye. Pigment. 2007, 74, 410–415. [Google Scholar] [CrossRef]
- Ghadhban, M.Y.; Majdi, H.S.; Rashid, K.T.; Alsalhy, Q.F.; Lakshmi, D.S.; Salih, I.K.; Figoli, A. Removal of dye from a leather tanning factory by flat-sheet blend ultrafiltration (uf) membrane. Membranes 2020, 10, 47. [Google Scholar] [CrossRef] [Green Version]
- Oyarce, E.; Roa, K.; Boulett, A.; Sotelo, S.; Cantero-Lopez, P.; Sanchez, J.; Rivas, B.L. Removal of dyes by polymer-enhanced ultrafiltration: An overview. Polymers 2021, 13, 3450. [Google Scholar] [CrossRef]
- Zhang, Z.; Rahman, M.M.; Abetz, C.; Bajer, B.; Wang, J.; Abetz, V. Quaternization of a polystyrene-block-poly(4-vinylpyridine) isoporous membrane: An approach to tune the pore size and the charge density. Macromol. Rapid Commun. 2019, 40, 1800729. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Li, B.; Huang, W.; Lin, C.; Li, G.; Ren, H.; Wu, Y.; Chen, S.; Zhang, W.; Ma, H. Highly crystalline ionic covalent organic framework membrane for nanofiltration and charge-controlled organic pollutants removal. Sep. Purif. Technol. 2021, 256, 117787. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, L.; Zhao, H.; Li, B.; Ma, H. A two-dimensional cationic covalent organic framework membrane for selective molecular sieving. J. Mater. Chem. A 2018, 6, 13331–13339. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Y.; Xing, Z.; Zhao, M.; Fu, Y.; Wang, S.; Wu, Y.; Zeng, J.; Li, X.; Ma, H. Ionic cof composite membranes for selective perfluoroalkyl substances separation. Macromol. Rapid Commun. 2022, 2200718. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Rahman, M.M.; Abetz, C.; Hohme, A.L.; Sperling, E.; Abetz, V. Chemically tailored multifunctional asymmetric isoporous triblock terpolymer membranes for selective transport. Adv. Mater. 2020, 32, e1907014. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Rahman, M.M.; Abetz, C.; Abetz, V. High-performance asymmetric isoporous nanocomposite membranes with chemically-tailored amphiphilic nanochannels. J. Mater. Chem. A 2020, 8, 9554–9566. [Google Scholar] [CrossRef]
- Mohammad, A.W.; Teow, Y.H.; Ang, W.L.; Chung, Y.T.; Oatley-Radcliffe, D.L.; Hilal, N. Nanofiltration membranes review: Recent advances and future prospects. Desalination 2015, 356, 226–254. [Google Scholar] [CrossRef]
- Spiegler, K.S.; Kedem, O. Thermodynamics of hyperfiltration (reverse osmosis): Criteria for efficient membranes. Desalination 1966, 1, 311–326. [Google Scholar] [CrossRef]
- Wu, F.; Feng, L.; Zhang, L.Q. Rejection prediction of isopropylantipyrine and antipyrine by nanofiltration membranes based on the spiegler-kedem-katchalsky model. Desalination 2015, 362, 11–17. [Google Scholar] [CrossRef]
- Wu, J.J. On the application of the spiegler-kedem model to forward osmosis. BMC Chem. Eng. 2019, 1, 15. [Google Scholar] [CrossRef]
- Agboola, O.; Maree, J.; Kolesnikov, A.; Mbaya, R.; Sadiku, R. Theoretical performance of nanofiltration membranes for wastewater treatment. Environ. Chem. Lett. 2015, 13, 37–47. [Google Scholar] [CrossRef]
- Ormerod, D.; Buekenhoudt, A.; Bongers, B.; Baramov, T.; Hassfeld, J. From reaction solvent to crystallization solvent, membrane assisted reaction workup and interpretation of membrane performance results by application of spiegler-kedem theory. Org. Process Res. Dev. 2017, 21, 2060–2067. [Google Scholar] [CrossRef]
- Nayak, V.; Cuhorka, J.; Mikulasek, P. Separation of drugs by commercial nanofiltration membranes and their modelling. Membranes 2022, 12, 528. [Google Scholar] [CrossRef] [PubMed]
- Schirg, P.; Widmer, F. Characterization of nanofiltration membranes for the separation of aqueous dye-salt solutions. Desalination 1992, 89, 89–107. [Google Scholar] [CrossRef]
- Hidalgo, A.M.; Leon, G.; Gomez, M.; Murcia, M.D.; Gomez, E.; Macario, J.A. Removal of different dye solutions: A comparison study using a polyamide nf membrane. Membranes 2020, 10, 408. [Google Scholar] [CrossRef]
- Wu, H.; Xie, J.; Mao, L. One-pot assembly tannic acid-titanium dual network coating for low-pressure nanofiltration membranes. Sep. Purif. Technol. 2020, 233, 116051. [Google Scholar] [CrossRef]
- Fan, L.; Ma, Y.; Su, Y.; Zhang, R.; Liu, Y.; Zhang, Q.; Jiang, Z. Green coating by coordination of tannic acid and iron ions for antioxidant nanofiltration membranes. RSC Adv. 2015, 5, 107777–107784. [Google Scholar] [CrossRef]
- You, F.; Xu, Y.; Yang, X.; Zhang, Y.; Shao, L. Bio-inspired Ni2+-polyphenol hydrophilic network to achieve unconventional high-flux nanofiltration membranes for environmental remediation. Chem. Commun. 2017, 53, 6128–6131. [Google Scholar] [CrossRef]
- Kim, H.J.; Kim, D.G.; Yoon, H.; Choi, Y.S.; Yoon, J.; Lee, J.C. Polyphenol/FeIII complex coated membranes having multifunctional properties prepared by a one-step fast assembly. Adv. Mater. Interfaces 2015, 2, 1500298. [Google Scholar] [CrossRef]
- Song, Y.Z.; Kong, X.; Yin, X.; Zhang, Y.; Sun, C.C.; Yuan, J.J.; Zhu, B.; Zhu, L.P. Tannin-inspired superhydrophilic and underwater superoleophobic polypropylene membrane for effective oil/water emulsions separation. Colloids Surf. A Physicochem. Eng. Asp. 2017, 522, 585–592. [Google Scholar] [CrossRef]
- Fang, X.F.; Wei, S.H.; Liu, S.; Li, R.; Zhang, Z.Y.; Liu, Y.B.; Zhang, X.R.; Lou, M.M.; Chen, G.; Li, F. Metal-coordinated nanofiltration membranes constructed on metal ions blended support toward enhanced dye/salt separation and antifouling performances. Membranes 2022, 12, 340. [Google Scholar] [CrossRef] [PubMed]
- Ejima, H.; Richardson, J.J.; Liang, K.; Best, J.P.; Van Koeverden, M.P.; Such, G.K.; Cui, J.; Caruso, F. One-step assembly of coordination complexes. Science 2013, 341, 154–157. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Chen, Y.; Tran, T.T.; Zhang, G. Facile and rapid assembly of high-performance tannic acid thin-film nanofiltration membranes via Fe3+ intermediated regulation and coordination. Sep. Purif. Technol. 2021, 260, 118228. [Google Scholar] [CrossRef]
- Yan, W.; Shi, M.; Dong, C.; Liu, L.; Gao, C. Applications of tannic acid in membrane technologies: A review. Adv. Colloid Interface Sci. 2020, 284, 102267. [Google Scholar] [CrossRef]
- Fievet, P.; Labbez, C.; Szymczyk, A.; Vidonne, A.; Foissy, A.; Pagetti, J. Electrolyte transport through amphoteric nanofiltration membranes. Chem. Eng. Sci. 2002, 57, 2921–2931. [Google Scholar] [CrossRef]
- Fang, J.; Deng, B.L. Rejection and modeling of arsenate by nanofiltration: Contributions of convection, diffusion and electromigration to arsenic transport. J. Membr. Sci. 2014, 453, 42–51. [Google Scholar] [CrossRef]
- Ma, X.; Chen, P.L.; Zhou, M.; Zhong, Z.X.; Zhang, F.; Xing, W.H. Tight ultrafiltration ceramic membrane for separation of dyes and mixed salts (both NaCl/Na2SO4) in textile wastewater treatment. Ind. Eng. Chem. Res. 2017, 56, 7070–7079. [Google Scholar] [CrossRef]
- Peng, L.E.; Yao, Z.; Chen, J.; Guo, H.; Tang, C.Y. Highly selective separation and resource recovery using forward osmosis membrane assembled by polyphenol network. J. Membr. Sci. 2020, 611, 118305. [Google Scholar] [CrossRef]







| Dye | σ | PS (m/s) |
|---|---|---|
| Riboflavin | 0.153822 | 2.57 × 10−6 |
| Orange II | 0.911965 | 8.83 × 10−7 |
| Naphthol Green B | 0.962552 | 2.04 × 10−7 |
| Dye | σ | PS (m/s) |
|---|---|---|
| Riboflavin | 0.187374 | 2.92 × 10−6 |
| Orange II | 0.909181 | 2.65 × 10−7 |
| Naphthol Green B | 0.954968 | 1.04 × 10−8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kinfu, H.H.; Rahman, M.M.; Cevallos-Cueva, N.; Abetz, V. Mass Transport of Dye Solutions through Porous Membrane Containing Tannic Acid/Fe3+ Selective Layer. Membranes 2022, 12, 1216. https://doi.org/10.3390/membranes12121216
Kinfu HH, Rahman MM, Cevallos-Cueva N, Abetz V. Mass Transport of Dye Solutions through Porous Membrane Containing Tannic Acid/Fe3+ Selective Layer. Membranes. 2022; 12(12):1216. https://doi.org/10.3390/membranes12121216
Chicago/Turabian StyleKinfu, Hluf Hailu, Md. Mushfequr Rahman, Nicolás Cevallos-Cueva, and Volker Abetz. 2022. "Mass Transport of Dye Solutions through Porous Membrane Containing Tannic Acid/Fe3+ Selective Layer" Membranes 12, no. 12: 1216. https://doi.org/10.3390/membranes12121216
APA StyleKinfu, H. H., Rahman, M. M., Cevallos-Cueva, N., & Abetz, V. (2022). Mass Transport of Dye Solutions through Porous Membrane Containing Tannic Acid/Fe3+ Selective Layer. Membranes, 12(12), 1216. https://doi.org/10.3390/membranes12121216