Minimizing Specific Energy Consumption of Electrochemical Hydrogen Compressor at Various Operating Conditions Using Pseudo-2D Model Simulation
Abstract
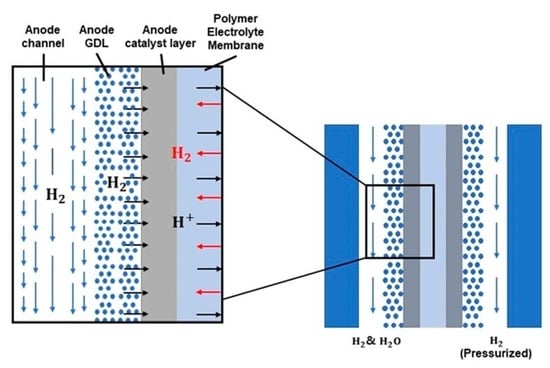
1. Introduction
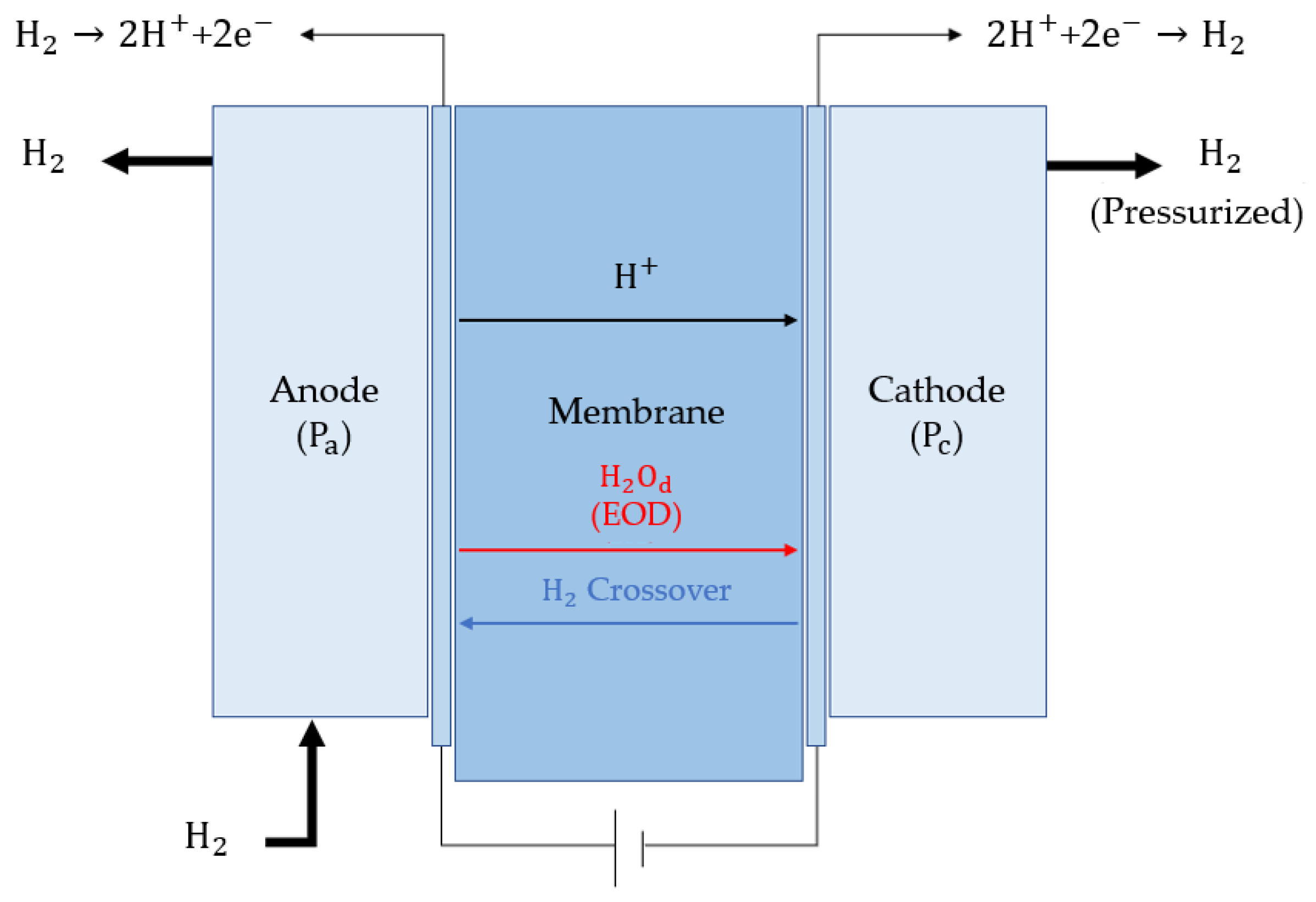
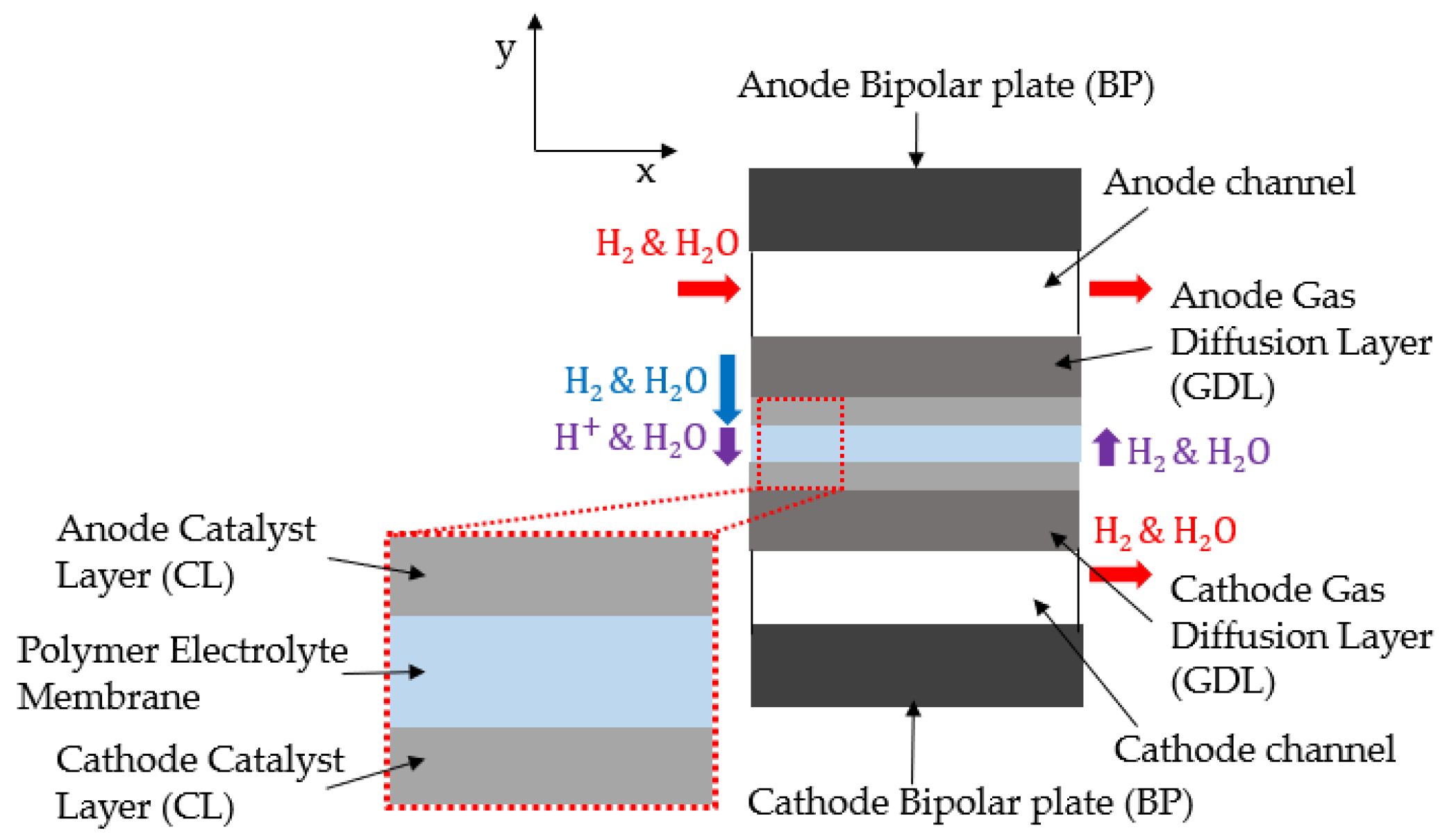
2. Mathematical Model
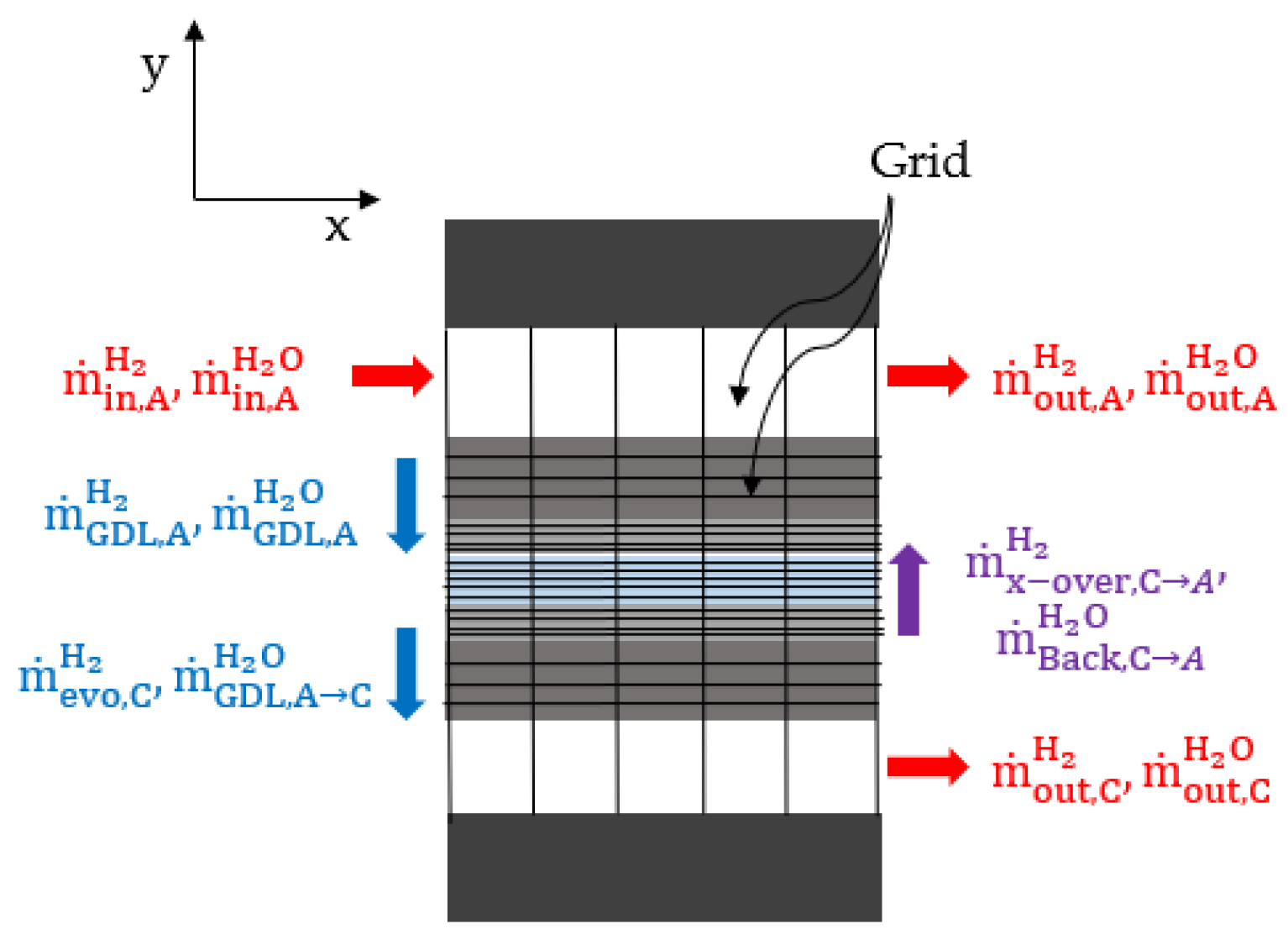
2.1. Mass Balance
2.2. Gas Diffusion Layer Modeling
2.3. Overpotential Modeling
2.4. Polymer Electrolyte Membrane Modeling
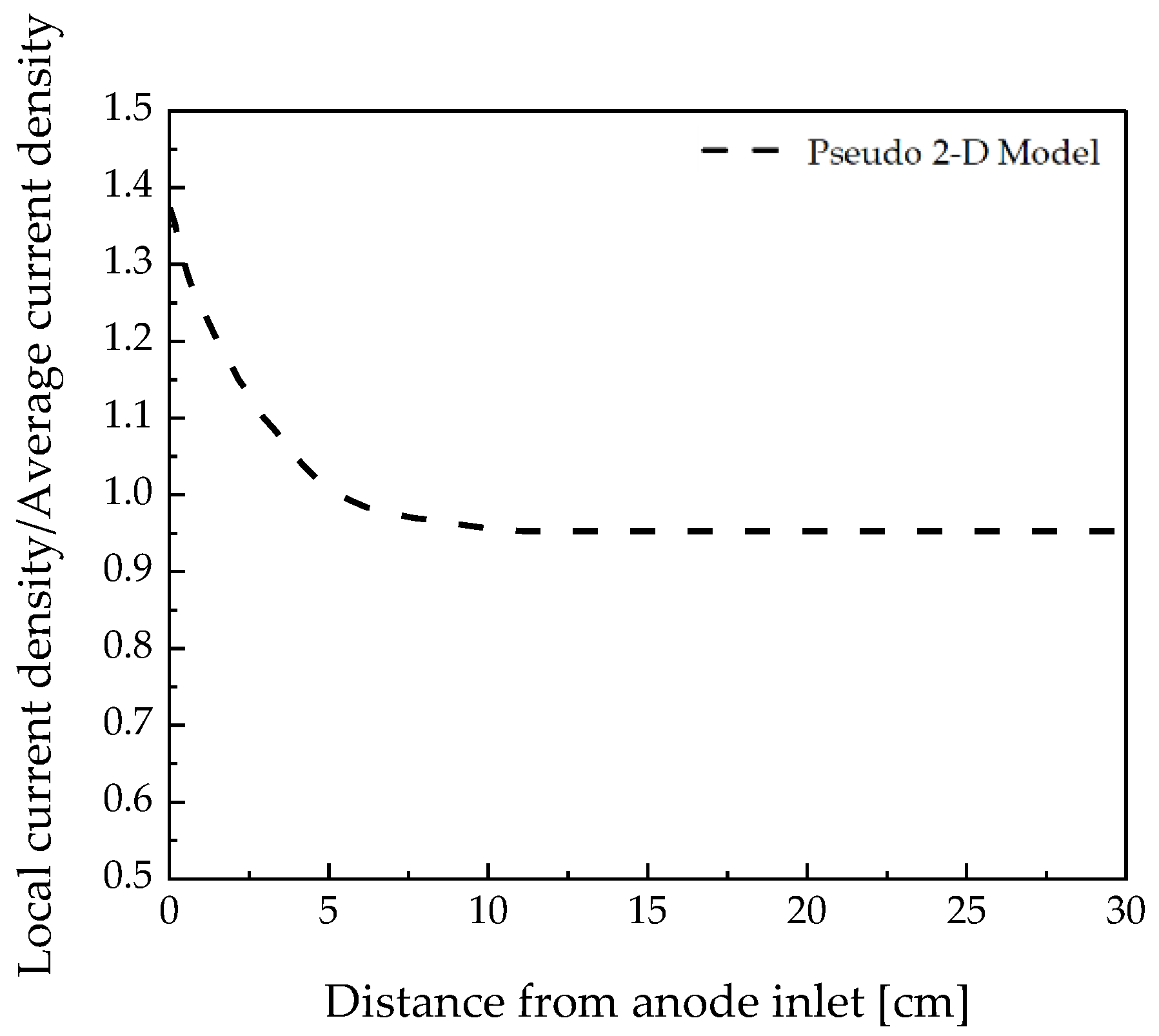
2.5. Validation of Modeling
3. Results and Discussion
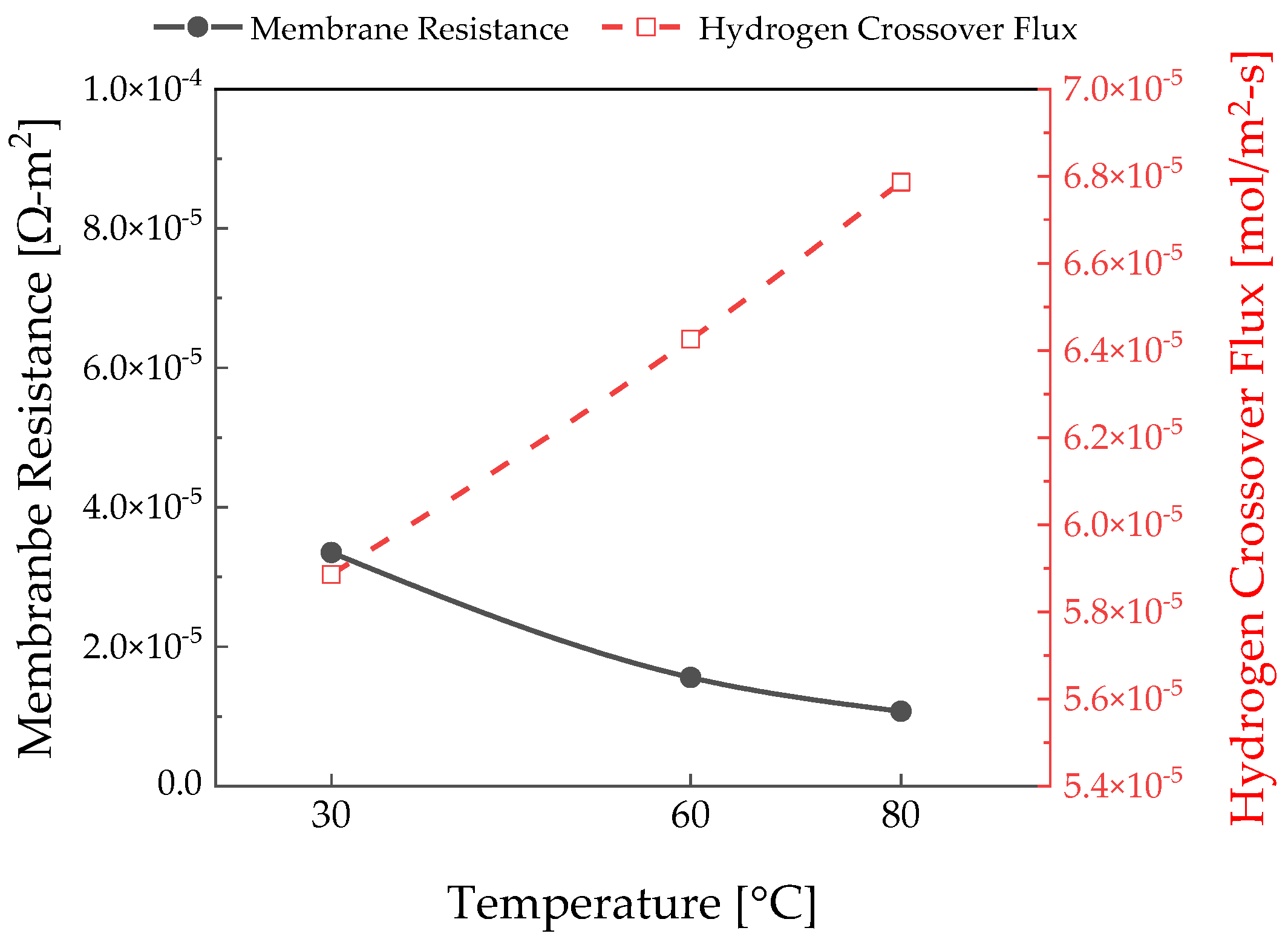
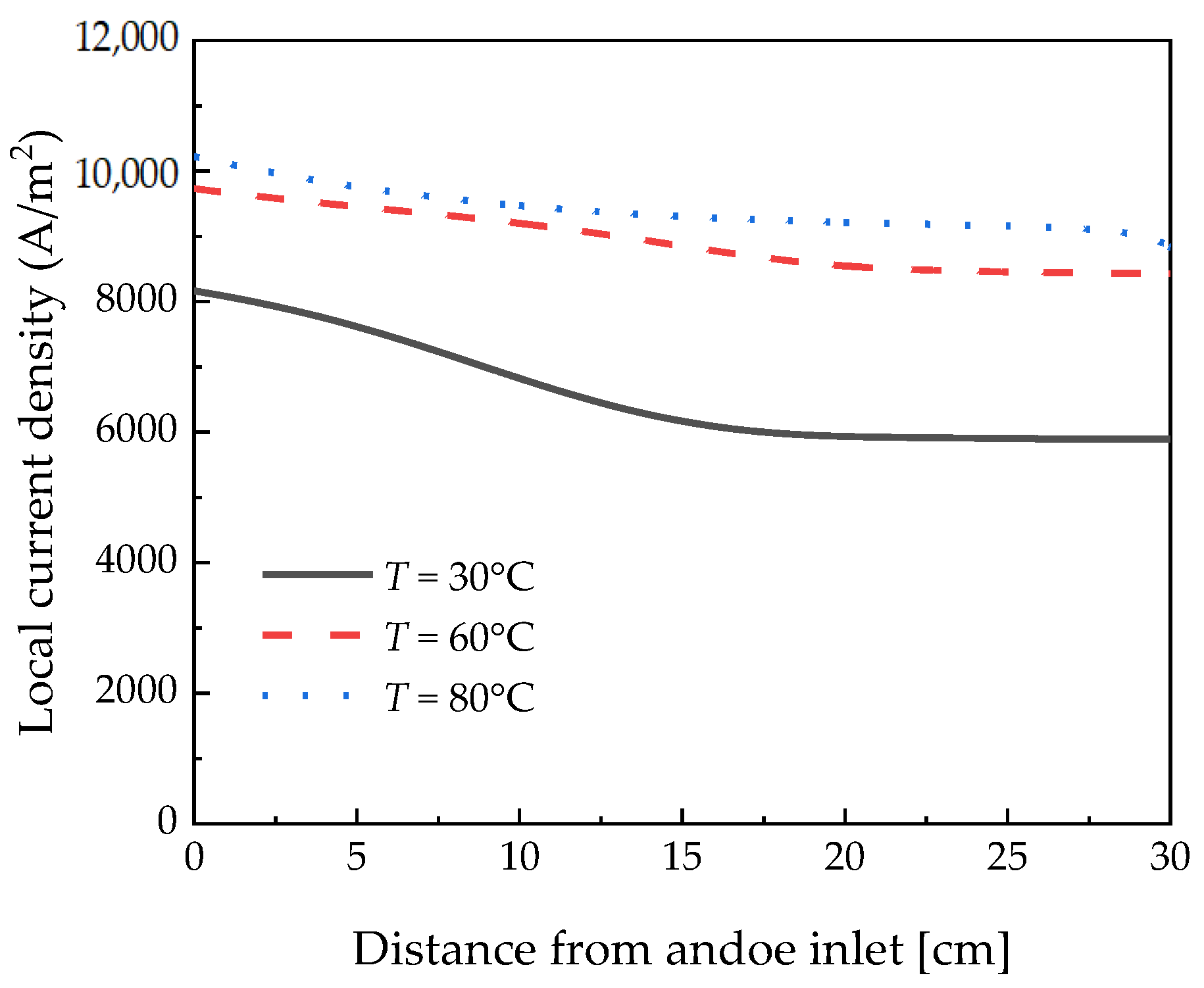
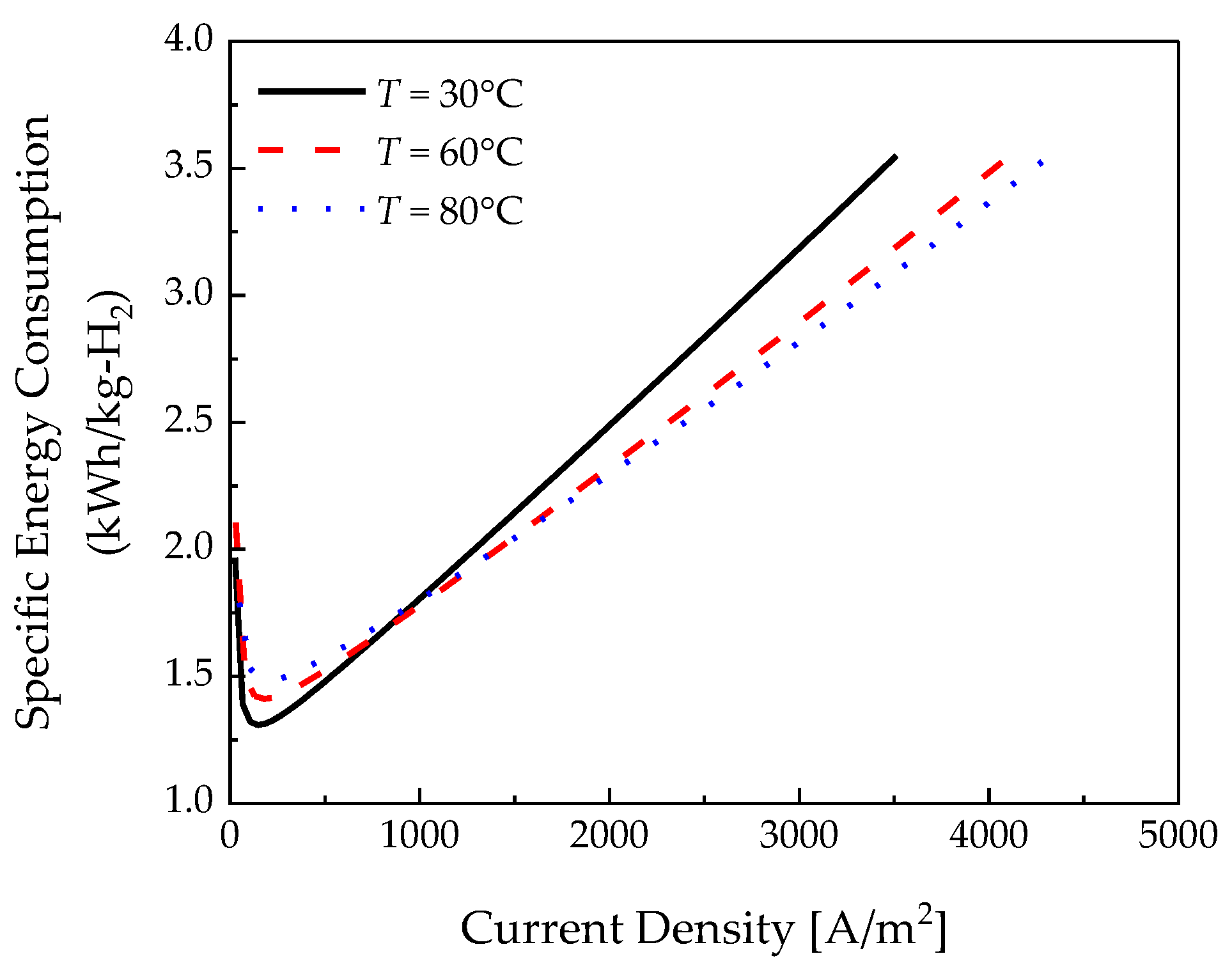
3.1. Temperature Effects
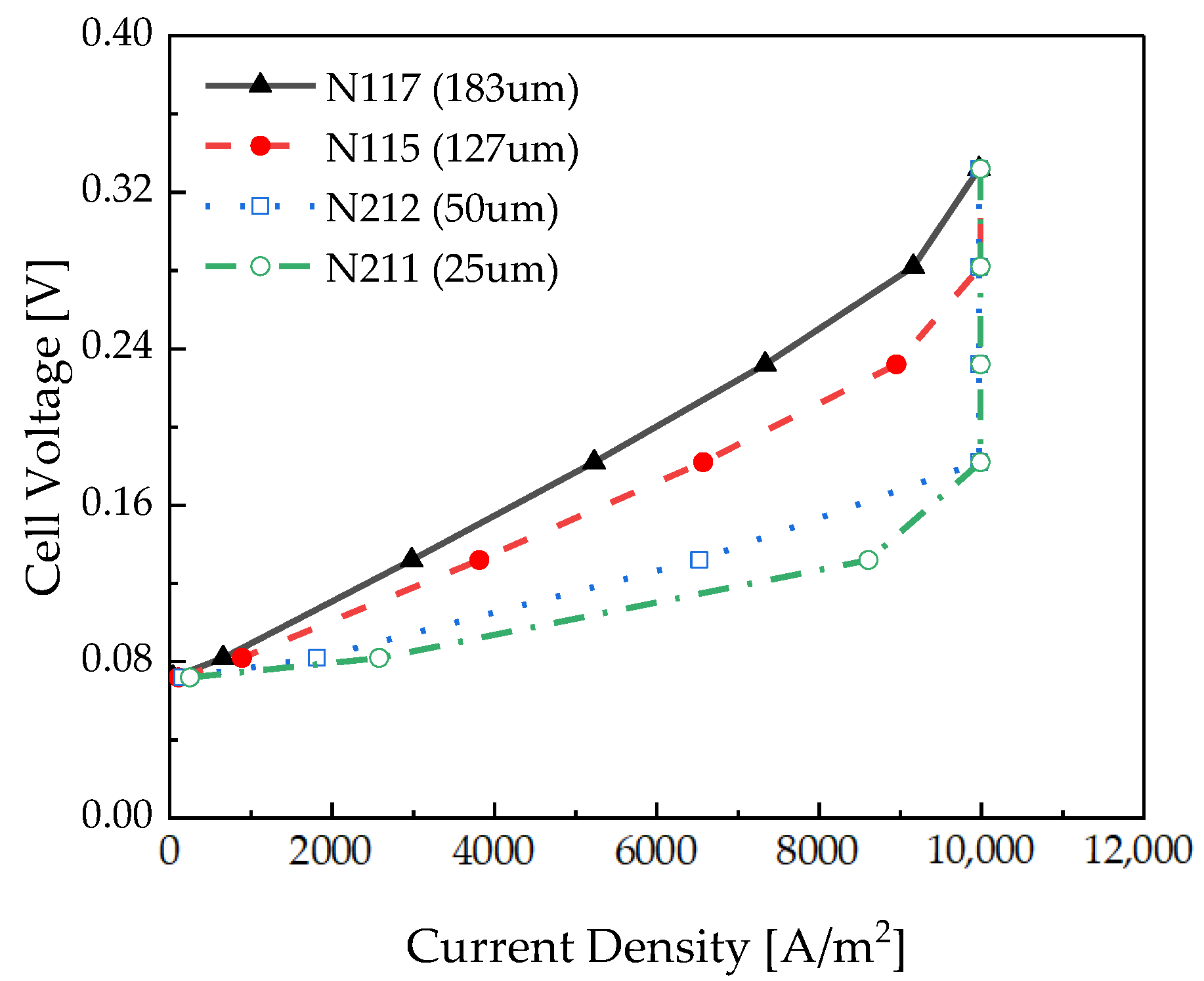
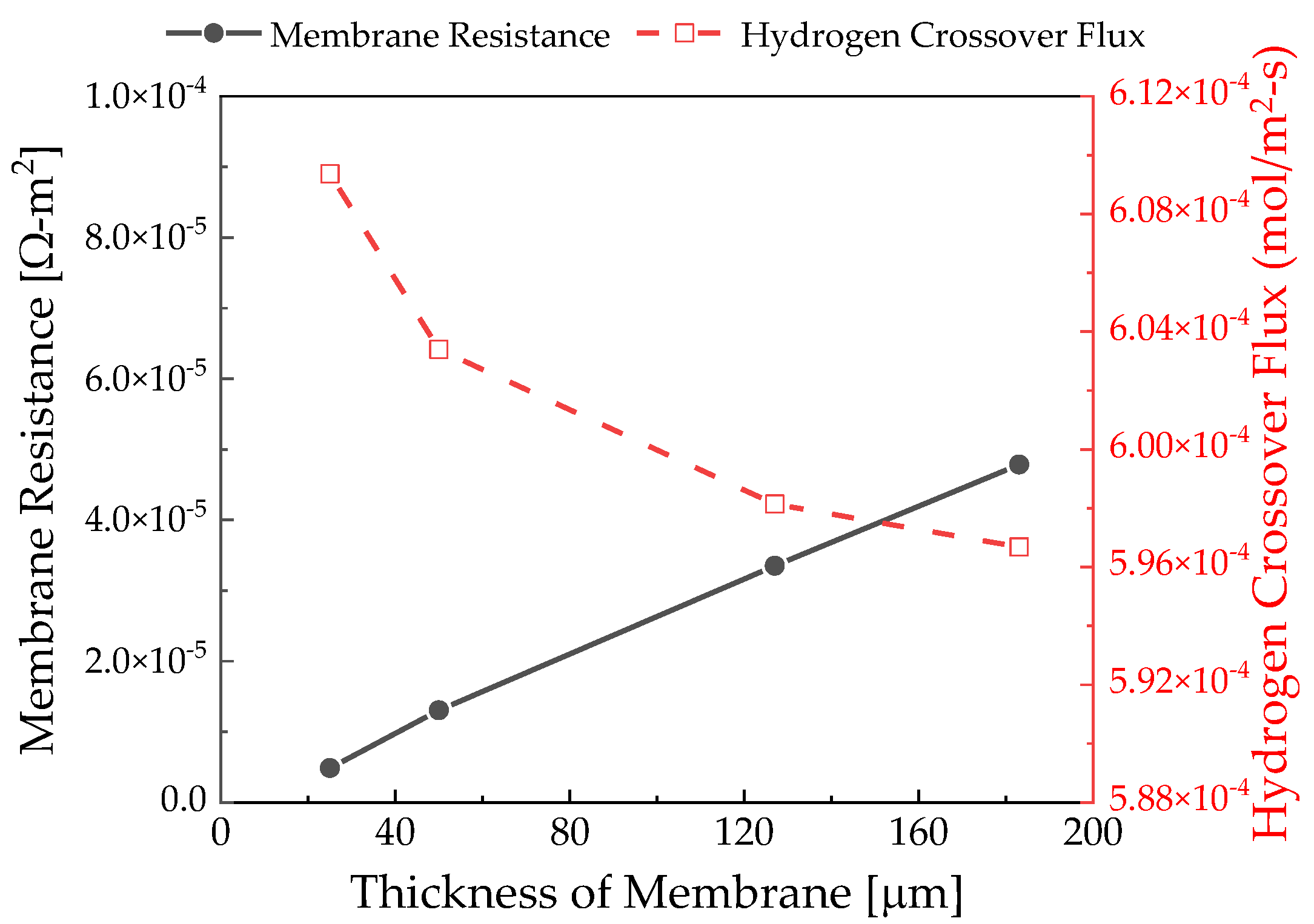
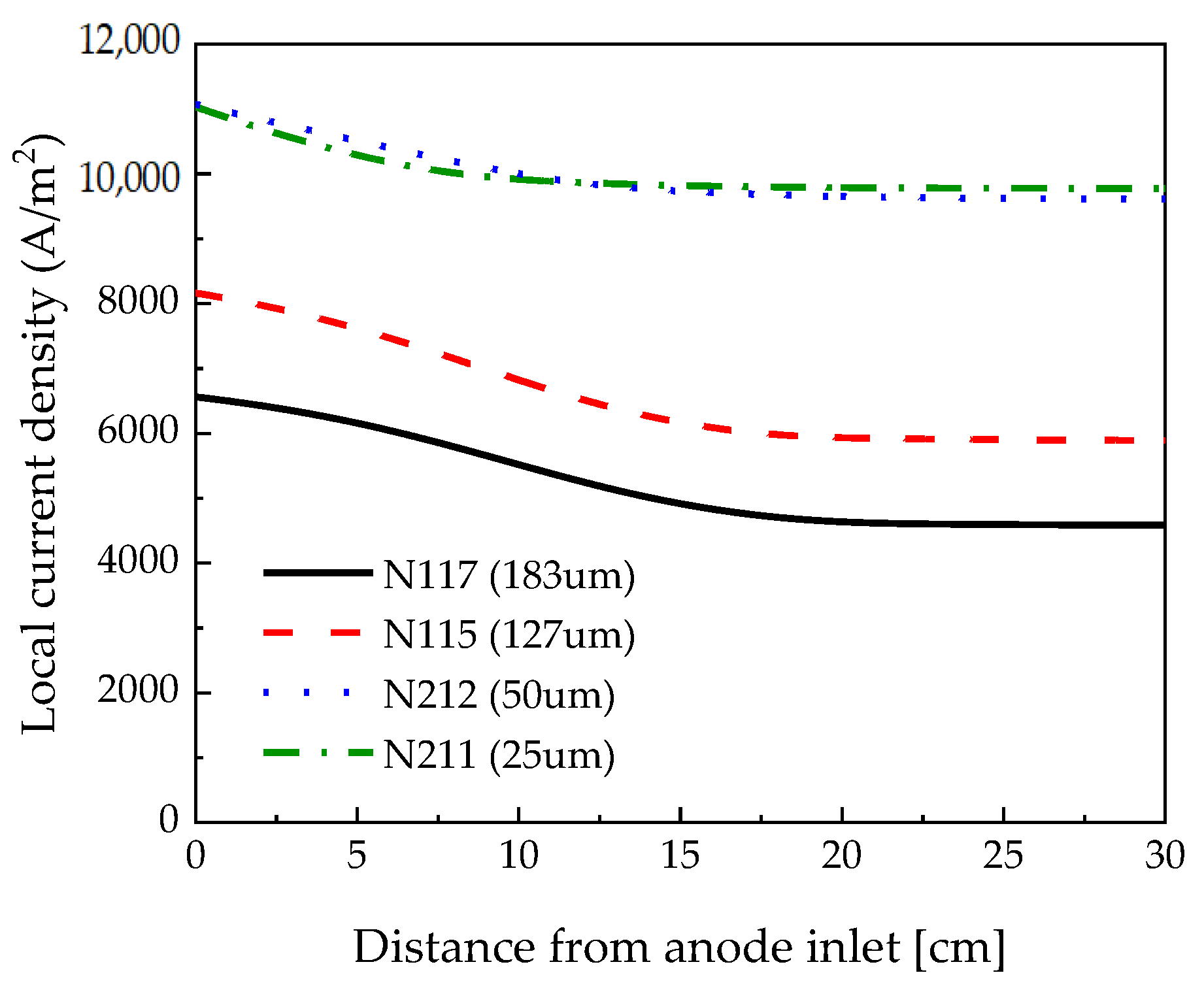
3.2. Membrane Thickness Effects
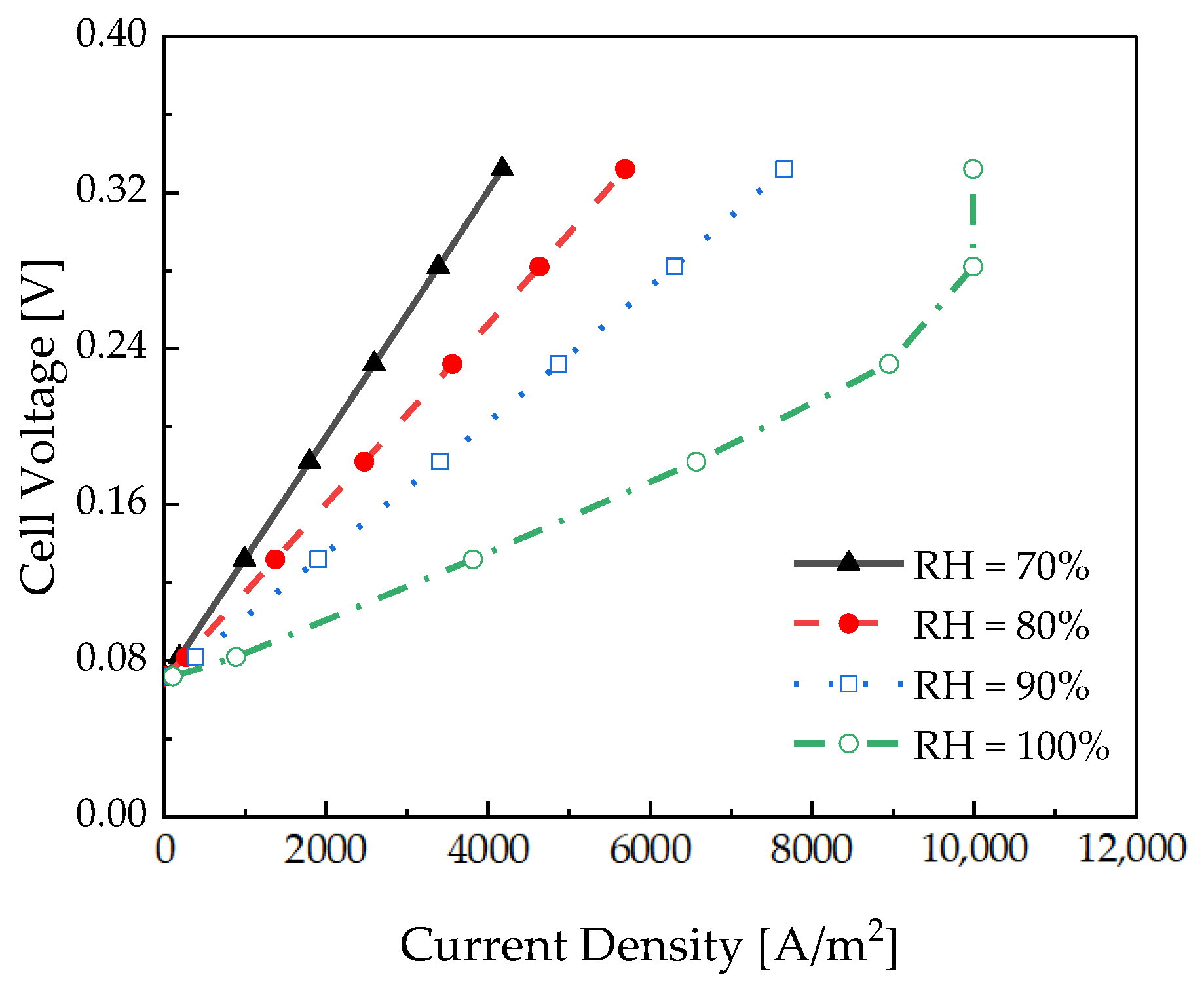
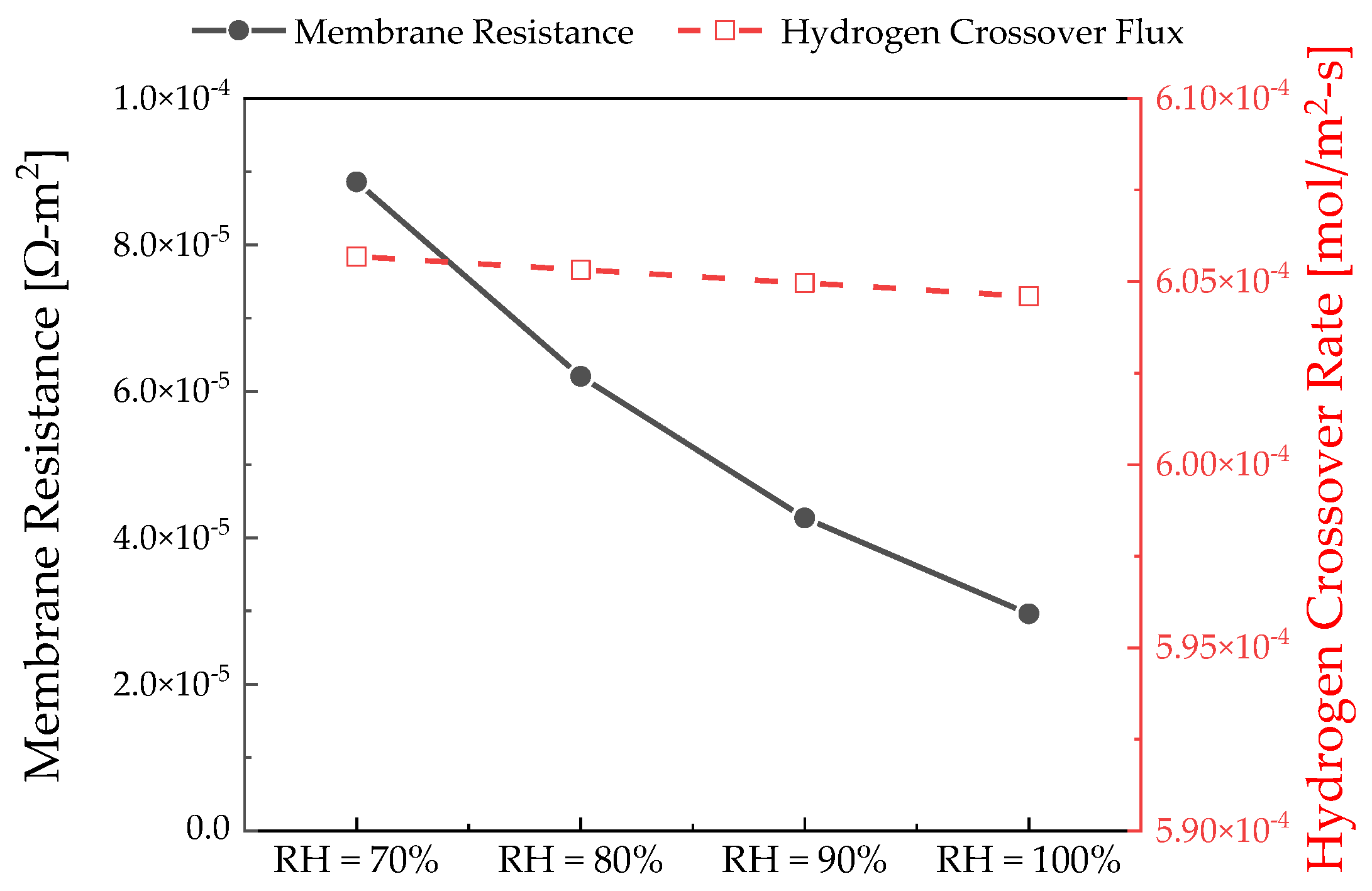
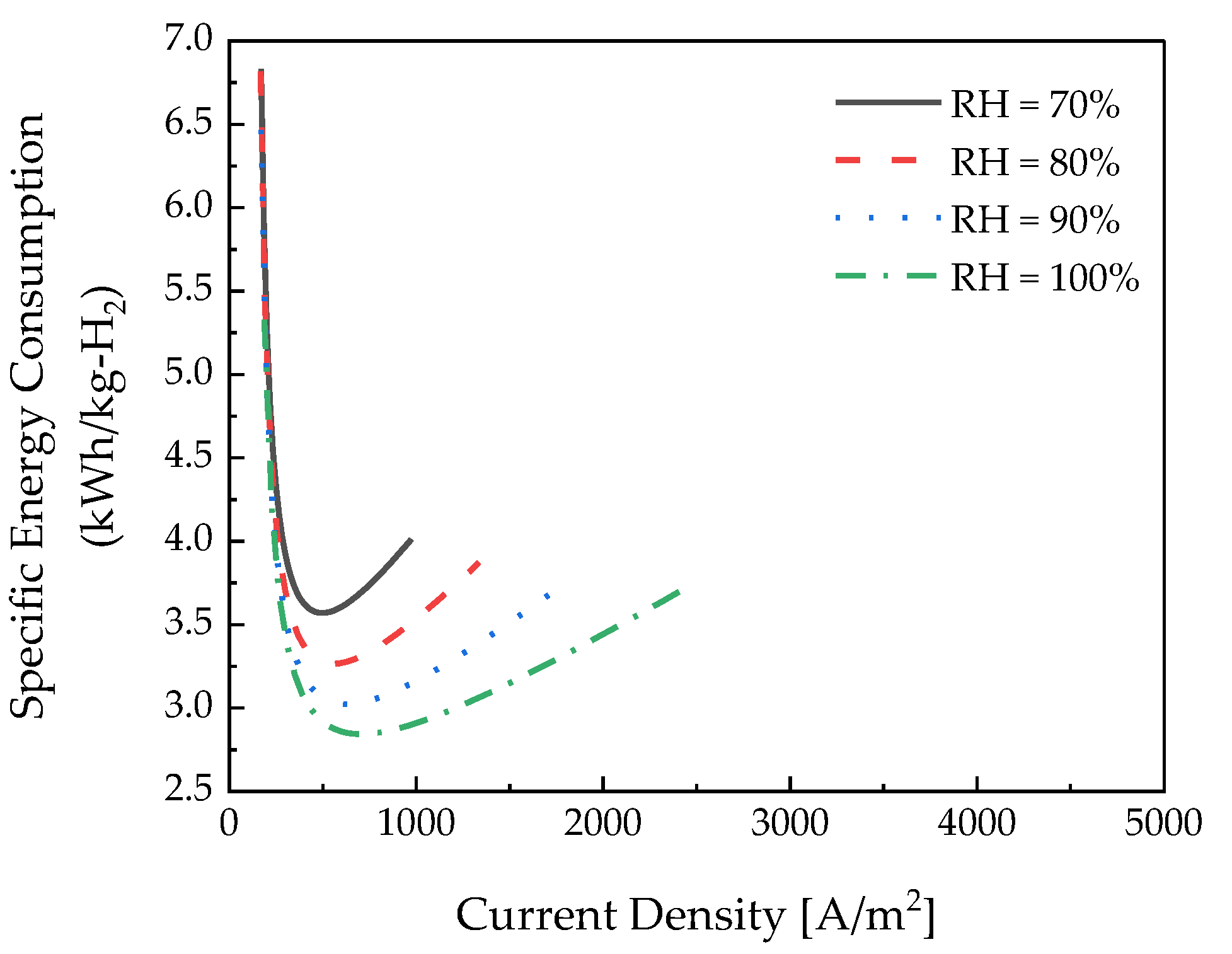
3.3. Relative Humidity Effects
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| List of symbols | |
| a | Activity/- |
| ASR | Area-specific resistance/ |
| Binary diffusivity/ | |
| Water diffusivity/ | |
| E | Cell voltage/V |
| F | Faraday constant/ |
| i | Current density/ |
| J | Water flux considering electroosmotic drag and back diffusion/mol |
| K | Kinetic constant/ |
| Mass flow rate/ | |
| M | Equivalent weight of membrane/ |
| Number of electrons in hydrogen | |
| Hydrogen crossover flux/mol | |
| Molar flux/ | |
| Pressure/bar | |
| Power/ | |
| Ideal gas constant/ | |
| t | Thickness/mm |
| Temperature/K | |
| Mole fraction/- | |
| Greek letters | |
| Transfer coefficient/- | |
| Porosity/- | |
| Density/ | |
| Subscripts and superscripts | |
| act | Activation losses |
| amb | Ambient |
| Anode | |
| Anode to cathode | |
| Back diffusion | |
| BP | Bipolar plate |
| Cathode | |
| Cathode to anode | |
| Cons | Consumption |
| drag | Drag coefficient |
| evo | Evolution |
| e | Electron |
| GDL | Gas diffusion layer |
| Hydrogen | |
| Water | |
| Inlet | |
| mem | Polymer electrolyte membrane |
| Nernst | Nernst potential |
| Outlet | |
| ohmic | Ohmic losses |
| o | Oxidation of hydrogen |
| Prod | Production |
| r | Reduction of hydrogen |
| sa | Chemical species of a |
| sb | Chemical species of b |
| s | Surface |
| SAT | Saturation |
| Total | Applied voltage to the EHC |
| Hydrogen crossover | |
References
- Marciuš, D.; Kovač, A.; Firak, M. Electrochemical hydrogen compressor: Recent progress and challenges. Int. J. Hydrogen Energy 2022, 47, 24179–24193. [Google Scholar] [CrossRef]
- Bethoux, O. Hydrogen fuel cell road vehicles: Stat of the art and perspectives. Energies 2020, 13, 5843. [Google Scholar] [CrossRef]
- Zou, J.; Han, N.; Yan, J.; Feng, Q.; Wang, Y.; Zhao, Z.; Fan, J.; Zeng, L.; Li, H.; Wang, H. Electrochemical Compression Technologies for High-Pressure Hydrogen: Current Status, Challenges and Perspective. Electrochem. Energy Rev. 2020, 3, 690–729. [Google Scholar] [CrossRef]
- Sdanghi, G.; Maranzana, G.; Celzard, A.; Fierro, V. Towards Non-Mechanical Hybrid Hydrogen Compression for Decentralized Hydrogen Facilities. Energies 2020, 13, 3145. [Google Scholar] [CrossRef]
- Wiebe, W.; Unwerth, T.V.; Schmitz, S. Hydrogen pump for hydrogen recirculation in fuel cell vehicles. E3S Web Conf. 2020, 155, 01001. [Google Scholar] [CrossRef]
- Scheepers, F.; Stähler, M.; Stähler, A.; Rauls, E.; Müller, M.; Carmo, M.; Lehnert, W. Improving the Efficiency of PEM Electrolyzers through Membrane-Specific Pressure Optimization. Energies 2020, 13, 612. [Google Scholar] [CrossRef]
- Lim, D.K.; Plymill, A.B.; Paik, H.; Qian, X.; Zecevic, S.; Chisholm, C.R.; Haile, S.M. Solid Acid Electrochemical Cell for the Production of Hydrogen from Ammonia. Joule 2020, 4, 2338–2347. [Google Scholar] [CrossRef]
- Schorer, L.; Schmitz, S.; Weber, A. Membrane based purification of hydrogen system (MEMPHYS). Int. J. Hydrogen Energy 2019, 44, 12708–12714. [Google Scholar] [CrossRef]
- Durmus, G.N.B.; Colpan, C.O.; Devrim, Y. A review on the development of the electrochemical hydrogen compressors. J. Power Sources 2021, 494, 229743. [Google Scholar] [CrossRef]
- Bouwman, P. Electrochemical Hydrogen Compression (EHC) solutions for hydrogen infrastructure. Fuel Cells Bull. 2014, 2014, 12–16. [Google Scholar] [CrossRef]
- Sdanghi, G.; Maranzana, G.; Celzard, A.; Fierro, V. Review of the current technologies and performances of hydrogen compression for stationary and automotive applocations. Renew. Sustain. Energy Rev. 2019, 102, 150–170. [Google Scholar] [CrossRef]
- Sdanghi, G.; Dillet, J.; Didierjean, S.; Fierro, V.; Maranzana, G. Feasibility of Hydrogen Compression in an Electrochemical System: Focus on Water Transport Mechanisms. Fuel Cells 2020, 20, 370–380. [Google Scholar] [CrossRef]
- Hao, Y.; Nakajima, H.; Yoshizumi, H.; Inada, A.; Sasaki, K.; Ito, K. Characterization of an electrochemical hydrogen pump with internal humidifier and dead-end anode channel. Int. J. Hydrogen Energy 2016, 41, 13879–13887. [Google Scholar] [CrossRef]
- Chouhan, A.; Bahar, B.; Prasad, A.K. Effect of back-diffusion on the performance of an electrochemical hydrogen compressor. Int. J. Hydrogen Energy 2020, 45, 10991–10999. [Google Scholar] [CrossRef]
- Ströbel, R.; Oszcipok, M.; Fasil, M.; Rohland, B.; Jörissen, L.; Garche, J. The compression of hydrogen in an electrochemical cell based on a PE fuel cell design. J. Power Sources 2002, 105, 208–215. [Google Scholar] [CrossRef]
- Grigoriev, S.; Shtatniy, I.; Millet, P.; Porembsky, V.; Fateev, V. Description and characterization of an electrochemical hydrogen compressor/concentrator based on solid polymer electrolyte technology. Int. J. Hydrogen Energy 2011, 36, 4148–4155. [Google Scholar] [CrossRef]
- Casati, C.; Longhi, P.; Zanderighi, L.; Bianchi, F. Some fundamental aspects in electrochemical hydrogen purification/compression. J. Power Sources 2008, 180, 103–113. [Google Scholar] [CrossRef]
- Pineda-Delgado, J.L.; Menchaca-Rivera, J.A.; Pérez-Robles, J.F.; Aviles-Arellano, L.M.; Chávez-Ramirez, A.U.; de Jesús Hernández-Cortes, R.; Rivera, J.G.; Rivas, S. Energetic evaluations of an electrochemical hydrogen compressor. J. Energy Storage 2022, 55, 105675. [Google Scholar] [CrossRef]
- Toghyani, S.; Baniasadi, E.; Afshari, E.; Javani, N. Performance analysis and exergoeconomic assessment of a proton exchange membrane compressor for electrochemical hydrogen storage. Int. J. Hydrogen Energy 2020, 45, 34993–35005. [Google Scholar] [CrossRef]
- Nordio, M.; Rizzi, F.; Manzolini, G.; Mulder, M.; Raymakers, L.; Annaland, M.V.S.; Gallucci, F. Experimental and modelling study of an electrochemical hydrogen compressor. Chem. Eng. J. 2019, 369, 432–442. [Google Scholar] [CrossRef]
- Kim, M.S.; Kim, J.; Kim, S.Y.; Chu, C.H.; Rho, K.H.; Kim, M.; Kim, D.K. Parametric study on the performance of electrochemical hydrogen compressors. Renew. Energy 2022, 199, 1176–1188. [Google Scholar] [CrossRef]
- O’Hayre, R.; Colella, W.; Cha, S.-W.; Prinz, F.B. Fuel Cell Fundamentals, 2nd ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Sdanghi, G.; Dillet, J.; Didierjean, S.; Fierro, V.; Maranzana, G. Operating heterogeneities in a PEM Electrochemical Hydrogen Compressor. In Proceedings of the 8th International Conference on Fundamentals and Development of Fuel Cells, Nantes, France, 12–14 February 2019. [Google Scholar]
- Pierson, H.O. Handbook of Carbon, Graphite, Diamonds and Fullerenes: Processing, Properties and Applications, 1st ed.; William Andrew: Norwich, NY, USA, 1994. [Google Scholar]
- Schweiss, R.; Meiser, C.; Damjanovic, T.; Galbiati, I.; Haak, N. SIGRACET® Gas Diffusion Layers for PEM Fuel Cells, Electrolyzers and Batteries (White Paper); SGL Group: Bavaria, Germany, 2016. [Google Scholar]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Olesen, A.C. Macroscopic Modeling of Transport Phenomena in Direct Methanol Fuel Cells; Department of Energy Technology, Aalborg University: Aalborg, Denmark, 2013. [Google Scholar]
- Baik, K.D.; Hong, B.K.; Kim, M.S. Effects of operating parameters on hydrogen crossover rate through Nafion® membranes in polymer electrolyte membrane fuel cells. Renew. Energy 2013, 57, 234–239. [Google Scholar] [CrossRef]
- Yuan, X.Z.; Zhang, S.; Wang, H.; Wu, J.; Sun, J.C.; Hiesgen, R.; Friedrich, K.A.; Schulze, M.; Haug, A. Degradation of a polymer exchange membrane fuel cell stack with Nafion® membrane of different thicknesses: Part I. In situ diagnosis. J. Power Sources 2010, 195, 7594–7599. [Google Scholar] [CrossRef]



| Parameter | Units | Value |
|---|---|---|
| Faraday constant (F) | C/mol | 96,485.332 |
| Gas constant (R) | J/mol∙K | 8.3144 |
| Equivalent weight of membrane () | kg/kmol | 1100 [22] |
| Dry density of membrane () | 1970 [22] | |
| Channel length () | mm | 300 [23] |
| Thickness of bipolar plate () | mm | 1 |
| Through-plane electrical conductivity of bipolar plate () | S/m | 3.3 [24] |
| Thickness of gas diffusion layer () | m | 325 [25] |
| Through-plane electrical conductivity of gas diffusion layer () | S/m | 220 [25] |
| Gas diffusion layer porosity () | - | 0.5 [25] |
| Polymer electrolyte membrane thickness () | m | 25, 50, 127, 183 |
| Parameter | Units | Value |
|---|---|---|
| Operating temperature (T) | °C | 30, 60, 80 |
| Operating pressure (P) | bar | 100 |
| Relative humidity (RH) | % | 100, 90, 80, 70 |
| Flow rate | sccm | 41.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.; Gong, M.; Lee, J.; Na, Y. Minimizing Specific Energy Consumption of Electrochemical Hydrogen Compressor at Various Operating Conditions Using Pseudo-2D Model Simulation. Membranes 2022, 12, 1214. https://doi.org/10.3390/membranes12121214
Kim C, Gong M, Lee J, Na Y. Minimizing Specific Energy Consumption of Electrochemical Hydrogen Compressor at Various Operating Conditions Using Pseudo-2D Model Simulation. Membranes. 2022; 12(12):1214. https://doi.org/10.3390/membranes12121214
Chicago/Turabian StyleKim, Changhyun, Myungkeun Gong, Jaewon Lee, and Youngseung Na. 2022. "Minimizing Specific Energy Consumption of Electrochemical Hydrogen Compressor at Various Operating Conditions Using Pseudo-2D Model Simulation" Membranes 12, no. 12: 1214. https://doi.org/10.3390/membranes12121214
APA StyleKim, C., Gong, M., Lee, J., & Na, Y. (2022). Minimizing Specific Energy Consumption of Electrochemical Hydrogen Compressor at Various Operating Conditions Using Pseudo-2D Model Simulation. Membranes, 12(12), 1214. https://doi.org/10.3390/membranes12121214