On the Choice of Different Water Model in Molecular Dynamics Simulations of Nanopore Transport Phenomena
Abstract
1. Introduction
2. Methods and Model
3. Cumulative Molecule Passage and Occupancy
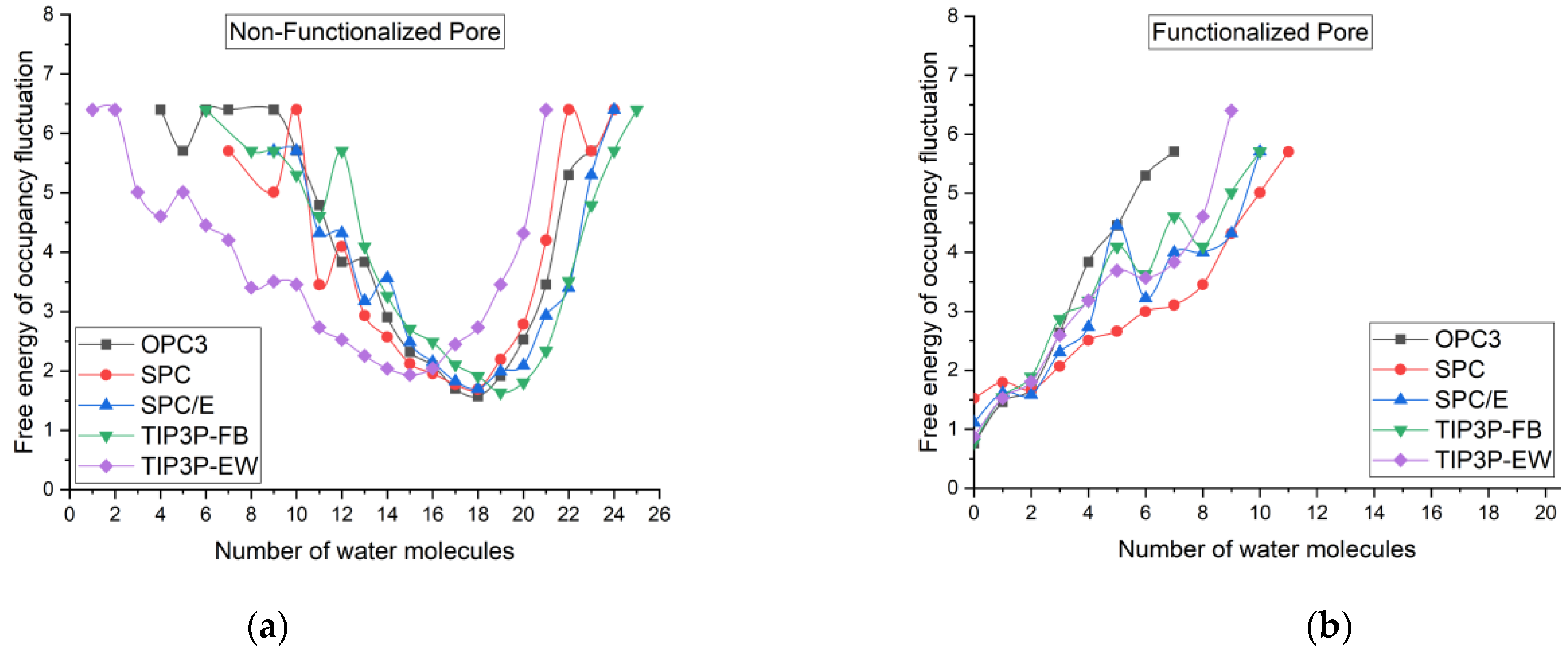
4. Free Energy of Occupancy Fluctuations
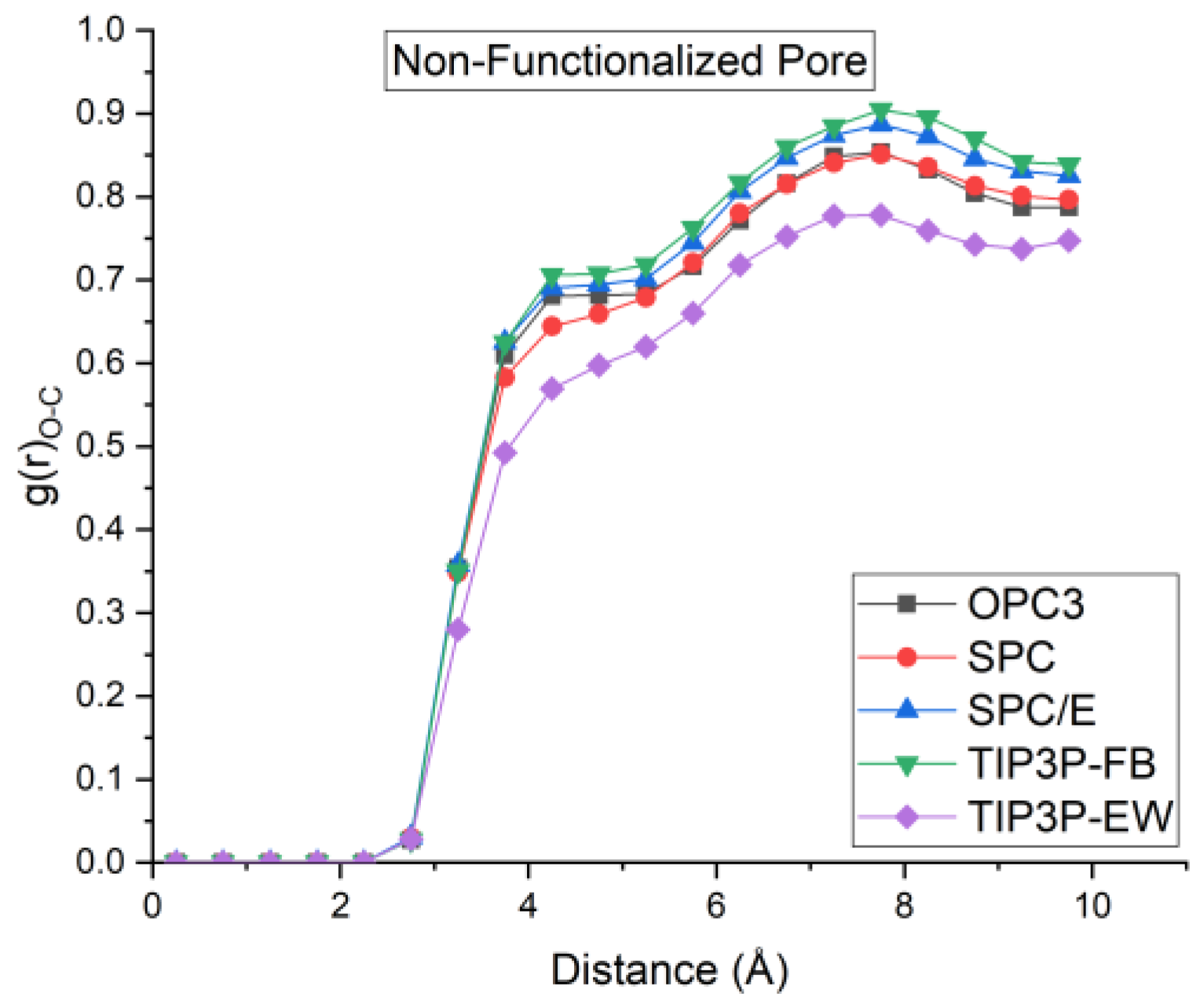
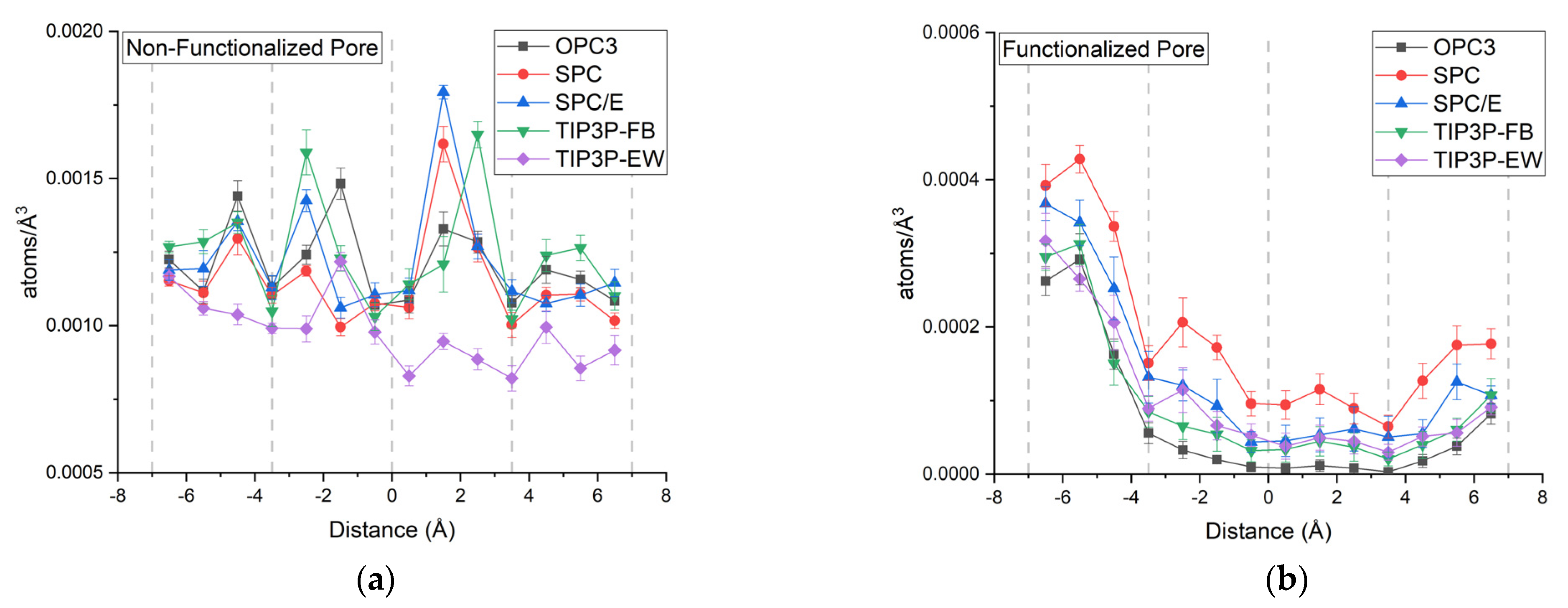
5. Radial Distribution Function and Density
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Santhosh, C.; Velmurugan, V.; Jacob, G.; Jeong, S.K.; Grace, A.N.; Bhatnagar, A. Role of Nanomaterials in Water Treatment Applications: A Review. Chem. Eng. J. 2016, 306, 1116–1137. [Google Scholar] [CrossRef]
- Carpenter, A.W.; de Lannoy, C.-F.; Wiesner, M.R. Cellulose Nanomaterials in Water Treatment Technologies. Environ. Sci. Technol. 2015, 49, 5277–5287. [Google Scholar] [CrossRef]
- Cohen-Tanugi, D.; Grossman, J.C. Water Desalination across Nanoporous Graphene. Nano Lett. 2012, 12, 3602–3608. [Google Scholar] [CrossRef]
- Daer, S.; Kharraz, J.; Giwa, A.; Hasan, S.W. Recent Applications of Nanomaterials in Water Desalination: A Critical Review and Future Opportunities. Desalination 2015, 367, 37–48. [Google Scholar] [CrossRef]
- Qu, X.; Alvarez, P.J.J.; Li, Q. Applications of Nanotechnology in Water and Wastewater Treatment. Water Res. 2013, 47, 3931–3946. [Google Scholar] [CrossRef] [PubMed]
- Savage, N.; Diallo, M.S. Nanomaterials and Water Purification: Opportunities and Challenges. J. Nanoparticle Res. 2005, 7, 331–342. [Google Scholar] [CrossRef]
- Corry, B. Designing Carbon Nanotube Membranes for Efficient Water Desalination. J. Phys. Chem. B 2008, 112, 1427–1434. [Google Scholar] [CrossRef]
- Spiegler, K.S.; El-Sayed, Y.M. The Energetics of Desalination Processes. Desalination 2001, 134, 109–128. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Suk, M.E.; Aluru, N.R. Water Transport through Ultrathin Graphene. J. Phys. Chem. Lett. 2010, 1, 1590–1594. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, X. Pyridinic Nitrogen Doped Nanoporous Graphene as Desalination Membrane: Molecular Simulation Study. J. Membr. Sci. 2015, 496, 108–117. [Google Scholar] [CrossRef]
- Kommu, A.; Namsani, S.; Singh, J.K. Removal of Heavy Metal Ions Using Functionalized Graphene Membranes: A Molecular Dynamics Study. RSC Adv. 2016, 6, 63190–63199. [Google Scholar] [CrossRef]
- Balme, S.; Picaud, F.; Manghi, M.; Palmeri, J.; Bechelany, M.; Cabello-Aguilar, S.; Abou-Chaaya, A.; Miele, P.; Balanzat, E.; Janot, J.M. Ionic Transport through Sub-10 Nm Diameter Hydrophobic High-Aspect Ratio Nanopores: Experiment, Theory and Simulation. Sci. Rep. 2015, 5, 10135. [Google Scholar] [CrossRef]
- Kale, S.; Herzfeld, J. Natural Polarizability and Flexibility via Explicit Valency: The Case of Water. J. Chem. Phys. 2012, 136, 084109. [Google Scholar] [CrossRef]
- Tu, Y.; Laaksonen, A. The Electronic Properties of Water Molecules in Water Clusters and Liquid Water. Chem. Phys. Lett. 2000, 329, 283–288. [Google Scholar] [CrossRef]
- Stillinger, F.H. Water Revisited. Science 1980, 209, 451–457. [Google Scholar] [CrossRef]
- Izadi, S.; Onufriev, A.V. Accuracy Limit of Rigid 3-Point Water Models. J. Chem. Phys. 2016, 145, 074501. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Hermans, J. Interaction Models for Water in Relation to Protein Hydration. In Intermolecular Forces, Proceedings of the Fourteenth Jerusalem Symposium on Quantum Chemistry and Biochemistry Held in Jerusalem, Israel, April 13–16, 1981; Pullman, B., Ed.; Springer: Dordrecht, The Netherlands, 1981; pp. 331–342. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Kadaoluwa Pathirannahalage, S.; Meftahi, N.; Elbourne, A.; Besford, A.; McConville, C.; Padua, A.; Winkler, D.; Gomes, M.; Greaves, T.; Le, T.; et al. Systematic Comparison of the Structural and Dynamic Properties of Commonly Used Water Models for Molecular Dynamics Simulations; ACS Publications: Washington, DC, USA, 2021. [Google Scholar] [CrossRef]
- Sengupta, A.; Li, Z.; Song, L.F.; Li, P.; Merz, K.M. Parameterization of Monovalent Ions for the OPC3, OPC, TIP3P-FB, and TIP4P-FB Water Models. J. Chem. Inf. Model. 2021, 61, 869–880. [Google Scholar] [CrossRef]
- Sahu, S.; Zwolak, M. Ionic Selectivity and Filtration from Fragmented Dehydration in Multilayer Graphene Nanopores. Nanoscale 2017, 9, 11424–11428. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liu, B.; Wu, M.-S.; Zhou, K.; Law, A. Transport of Salty Water through Graphene Bilayer in an Electric Field: A Molecular Dynamics Study. Comput. Mater. Sci. 2017, 131, 100–107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, Y.; Yang, R.; Zhao, N.; Liu, W.; Zhuang, W.; Lu, X. Molecular Insights into Multilayer 18-Crown-6-like Graphene Nanopores for K+/Na+ Separation: A Molecular Dynamics Study. Carbon 2018, 144, 32–42. [Google Scholar] [CrossRef]
- Yang, J.; Shen, Z.; He, J.; Li, Y. Efficient Separation of Small Organic Contaminants in Water Using Functionalized Nanoporous Graphene Membranes: Insights from Molecular Dynamics Simulations. J. Membr. Sci. 2021, 630, 119331. [Google Scholar] [CrossRef]
- Soleimani, E.; Foroutan, M. Multilayer Graphene with a Rippled Structure for Water Desalination. J. Mol. Liq. 2018, 265, 208–215. [Google Scholar] [CrossRef]
- Pan, J.; Xiao, S.; Zhang, Z.; Wei, N.; He, J.; Zhao, J. Nanoconfined Water Dynamics in Multilayer Graphene Nanopores. J. Phys. Chem. C 2020, 124, 17819–17828. [Google Scholar] [CrossRef]
- Suk, M.E.; Aluru, N.R. Molecular and Continuum Hydrodynamics in Graphene Nanopores. RSC Adv. 2013, 3, 9365–9372. [Google Scholar] [CrossRef]
- Cicero, G.; Grossman, J.C.; Schwegler, E.; Gygi, F.; Galli, G. Water Confined in Nanotubes and between Graphene Sheets: A First Principle Study. J. Am. Chem. Soc. 2008, 130, 1871–1878. [Google Scholar] [CrossRef]
- Konatham, D.; Yu, J.; Ho, T.A.; Striolo, A. Simulation Insights for Graphene-Based Water Desalination Membranes. Langmuir 2013, 29, 11884–11897. [Google Scholar] [CrossRef]
- Falk, K.; Sedlmeier, F.; Joly, L.; Netz, R.R.; Bocquet, L. Molecular Origin of Fast Water Transport in Carbon Nanotube Membranes: Superlubricity versus Curvature Dependent Friction. Nano Lett. 2010, 10, 4067–4073. [Google Scholar] [CrossRef]
- Mejri, A.; Mazouzi, K.; Herlem, G.; Picaud, F.; Hennequin, T.; Palmeri, J.; Manghi, M. Molecular Dynamics Investigations of Ionic Conductance at the Nanoscale: Role of the Water Model and Geometric Parameters. J. Mol. Liq. 2022, 351, 118575. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, S.; Mi, B.; Wang, J.; Ding, J. Surface Slip on Rotating Graphene Membrane Enables the Temporal Selectivity That Breaks the Permeability-Selectivity Trade-Off. Sci. Adv. 2020, 6, eaba9471. [Google Scholar] [CrossRef]
- Zhao, S.; Jiang, C.; Fan, J.-C.; Hong, S.; Mei, P.; Yao, R.; Liu, Y.; Zhang, S.; Li, H.; Zhang, H.; et al. Hydrophilicity Gradient in Covalent Organic Frameworks for Membrane Distillation. Nat. Mater. 2021, 20, 1551–1558. [Google Scholar] [CrossRef] [PubMed]
- Prasad, K.V.; Kannam, S.K.; Hartkamp, R.; Sathian, S.P. Water Desalination Using Graphene Nanopores: Influence of the Water Models Used in Simulations. Phys. Chem. Chem. Phys. 2018, 20, 16005–16011. [Google Scholar] [CrossRef]
- Wang, L.-P.; Martinez, T.J.; Pande, V.S. Building Force Fields: An Automatic, Systematic, and Reproducible Approach. J. Phys. Chem. Lett. 2014, 5, 1885–1891. [Google Scholar] [CrossRef] [PubMed]
- Price, D.J.; Brooks, C.L. A Modified TIP3P Water Potential for Simulation with Ewald Summation. J. Chem. Phys. 2004, 121, 10096–10103. [Google Scholar] [CrossRef]
- OneAngstrom; SAMSON: Zorah, Nahal Sorek, 2020.
- Bitzek, E.; Koskinen, P.; Gähler, F.; Moseler, M.; Gumbsch, P. Structural Relaxation Made Simple. Phys. Rev. Lett. 2006, 97, 170201. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A Reactive Potential for Hydrocarbons with Intermolecular Interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles; CRC Press: Boca Raton, FL, USA, 1988. [Google Scholar]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The Nose–Hoover Thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Chogani, A.; Moosavi, A.; Bagheri Sarvestani, A.; Shariat, M. The Effect of Chemical Functional Groups and Salt Concentration on Performance of Single-Layer Graphene Membrane in Water Desalination Process: A Molecular Dynamics Simulation Study. J. Mol. Liq. 2020, 301, 112478. [Google Scholar] [CrossRef]
- Hummer, G.; Rasaiah, J.C.; Noworyta, J.P. Water Conduction through the Hydrophobic Channel of a Carbon Nanotube. Nature 2001, 414, 188–190. [Google Scholar] [CrossRef]
- Robinson, F.; Shahbabaei, M.; Kim, D. Deformation Effect on Water Transport through Nanotubes. Energies 2019, 12, 4424. [Google Scholar] [CrossRef]
- Robinson, F.; Park, C.; Kim, M.; Kim, D. Defect Induced Deformation Effect on Water Transport through (6, 6) Carbon Nanotube. Chem. Phys. Lett. 2021, 778, 138632. [Google Scholar] [CrossRef]
- Azamat, J.; Khataee, A.; Joo, S.W.; Yin, B. Removal of Trihalomethanes from Aqueous Solution through Armchair Carbon Nanotubes: A Molecular Dynamics Study. J. Mol. Graph. Model. 2015, 57, 70–75. [Google Scholar] [CrossRef]
- Abbaspour, M.; Akbarzadeh, H.; Abroodi, M. A New and Accurate Expression for the Radial Distribution Function of Confined Lennard-Jones Fluid in Carbon Nanotubes. RSC Adv. 2015, 5, 95781–95787. [Google Scholar] [CrossRef]
- Liu, L.; Patey, G.N. Simulations of Water Transport through Carbon Nanotubes: How Different Water Models Influence the Conduction Rate. J. Chem. Phys. 2014, 141, 18C518. [Google Scholar] [CrossRef]
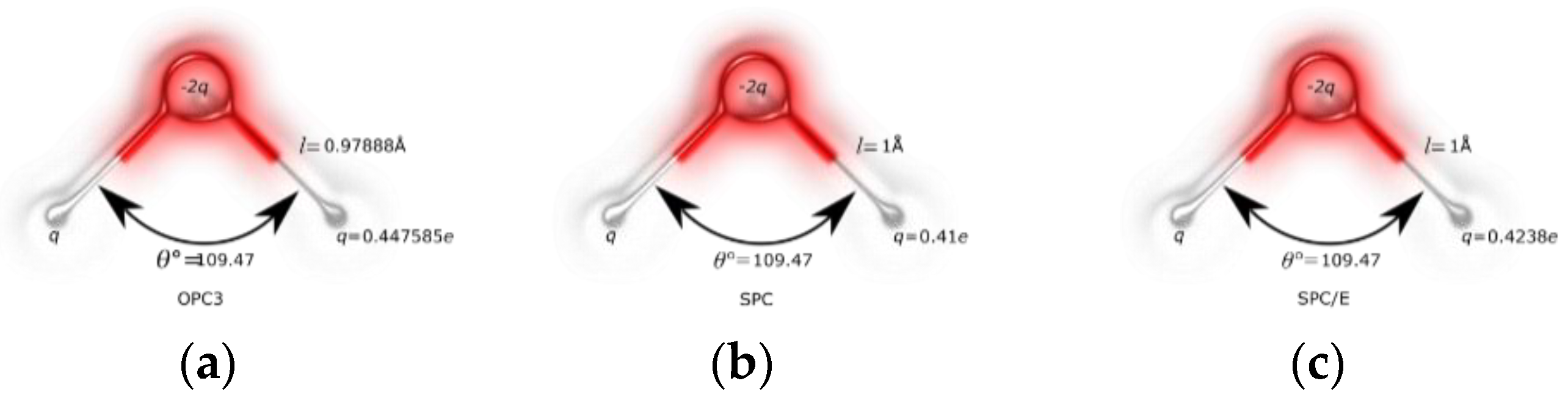
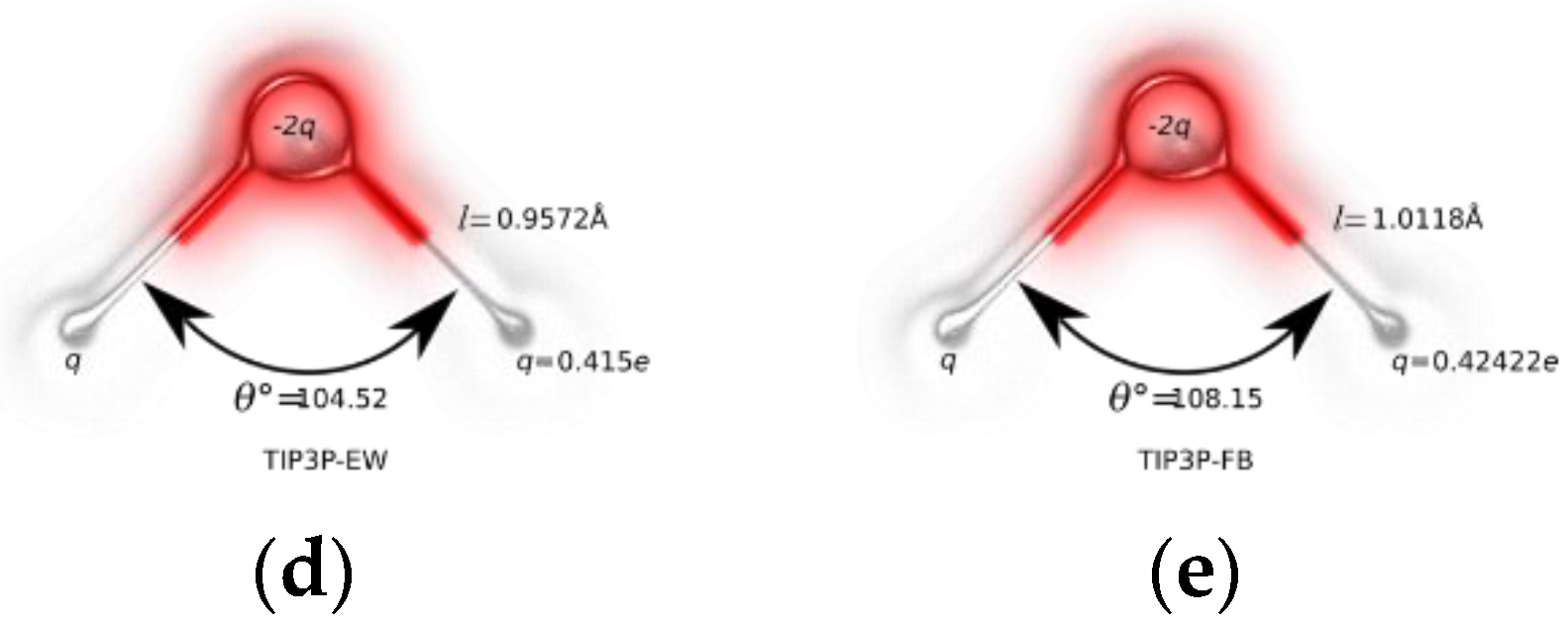


| Water Model | σO (Å) | εO (kcal/mol) | qH (e) | qO (e) |
|---|---|---|---|---|
| SPC | 3.16557 | 0.1554 | 0.41 | −0.82 |
| SPC/E | 3.16557 | 0.1554 | 0.4238 | −0.8476 |
| TIP3P-FB | 3.178 | 0.15587 | 0.41722 | −0.84844 |
| TIP3P-EW | 3.188 | 0.102 | 0.415 | −0.83 |
| OPC3 | 3.17427 | 0.1634 | 0.447585 | −0.89517 |
| Number of Water Molecules | Number of Occurrences | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Non-Functionalized Pore | Functionalized Pore | |||||||||
| OPC3 | SPC | SPC/E | TIP3P-FB | TIP3P-EW | OPC3 | SPC | SPC/E | TIP3P-FB | TIP3P-EW | |
| 0 | 0 | 0 | 0 | 0 | 0 | 282 | 131 | 197 | 275 | 250 |
| 1 | 0 | 0 | 0 | 0 | 1 | 140 | 100 | 119 | 128 | 130 |
| 2 | 0 | 0 | 0 | 0 | 1 | 111 | 113 | 123 | 91 | 99 |
| 3 | 0 | 0 | 0 | 0 | 4 | 43 | 76 | 60 | 34 | 45 |
| 4 | 1 | 0 | 0 | 0 | 6 | 13 | 49 | 39 | 25 | 25 |
| 5 | 2 | 0 | 0 | 0 | 4 | 7 | 42 | 7 | 10 | 15 |
| 6 | 1 | 0 | 0 | 1 | 7 | 3 | 30 | 24 | 16 | 17 |
| 7 | 1 | 2 | 0 | 0 | 9 | 2 | 27 | 11 | 6 | 13 |
| 8 | 0 | 0 | 0 | 2 | 20 | 0 | 19 | 11 | 10 | 6 |
| 9 | 1 | 4 | 2 | 2 | 18 | 0 | 8 | 8 | 4 | 1 |
| 10 | 2 | 1 | 2 | 3 | 19 | 0 | 4 | 2 | 2 | 0 |
| 11 | 5 | 19 | 8 | 6 | 39 | 0 | 2 | 0 | 0 | 0 |
| 12 | 13 | 10 | 8 | 2 | 48 | 0 | 0 | 0 | 0 | 0 |
| 13 | 13 | 32 | 25 | 10 | 63 | 0 | 0 | 0 | 0 | 0 |
| 14 | 33 | 46 | 17 | 23 | 78 | 0 | 0 | 0 | 0 | 0 |
| 15 | 59 | 72 | 50 | 40 | 87 | 0 | 0 | 0 | 0 | 0 |
| 16 | 74 | 85 | 70 | 50 | 78 | 0 | 0 | 0 | 0 | 0 |
| 17 | 110 | 102 | 97 | 73 | 52 | 0 | 0 | 0 | 0 | 0 |
| 18 | 125 | 111 | 110 | 89 | 39 | 0 | 0 | 0 | 0 | 0 |
| 19 | 89 | 67 | 82 | 117 | 19 | 0 | 0 | 0 | 0 | 0 |
| 20 | 48 | 37 | 74 | 99 | 8 | 0 | 0 | 0 | 0 | 0 |
| 21 | 19 | 9 | 32 | 58 | 1 | 0 | 0 | 0 | 0 | 0 |
| 22 | 3 | 1 | 20 | 18 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 | 2 | 2 | 3 | 5 | 0 | 0 | 0 | 0 | 0 | 0 |
| 24 | 0 | 1 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 25 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, C.; Robinson, F.; Kim, D. On the Choice of Different Water Model in Molecular Dynamics Simulations of Nanopore Transport Phenomena. Membranes 2022, 12, 1109. https://doi.org/10.3390/membranes12111109
Park C, Robinson F, Kim D. On the Choice of Different Water Model in Molecular Dynamics Simulations of Nanopore Transport Phenomena. Membranes. 2022; 12(11):1109. https://doi.org/10.3390/membranes12111109
Chicago/Turabian StylePark, Chulwoo, Ferlin Robinson, and Daejoong Kim. 2022. "On the Choice of Different Water Model in Molecular Dynamics Simulations of Nanopore Transport Phenomena" Membranes 12, no. 11: 1109. https://doi.org/10.3390/membranes12111109
APA StylePark, C., Robinson, F., & Kim, D. (2022). On the Choice of Different Water Model in Molecular Dynamics Simulations of Nanopore Transport Phenomena. Membranes, 12(11), 1109. https://doi.org/10.3390/membranes12111109





