An Assessment on Average Pressure Drop and Dust-Holding Capacity of Hollow-Fiber Membranes in Air Filtration
Abstract
:1. Introduction
2. Analysis on Average Pressure Drop of Air Filters
3. Materials and Methods
3.1. Hollow-Fiber Membrane Bundles
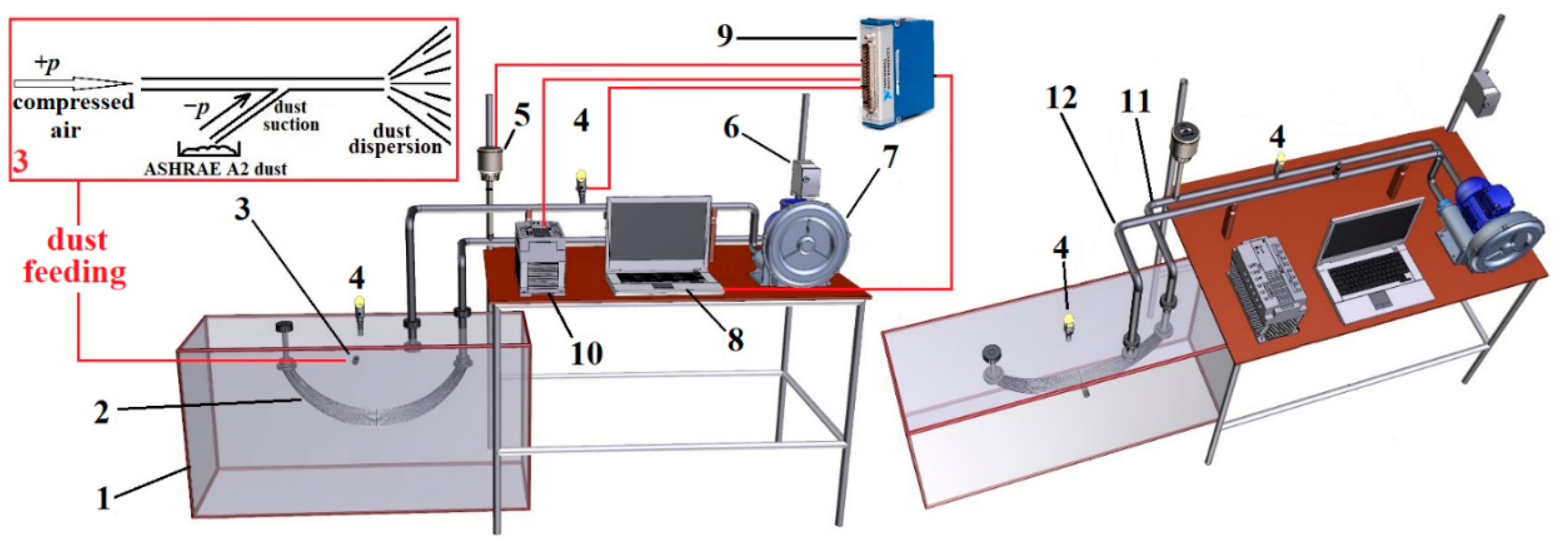
3.2. Experimental Setup
3.3. Dust Supply Scheme
4. Results and Discussion
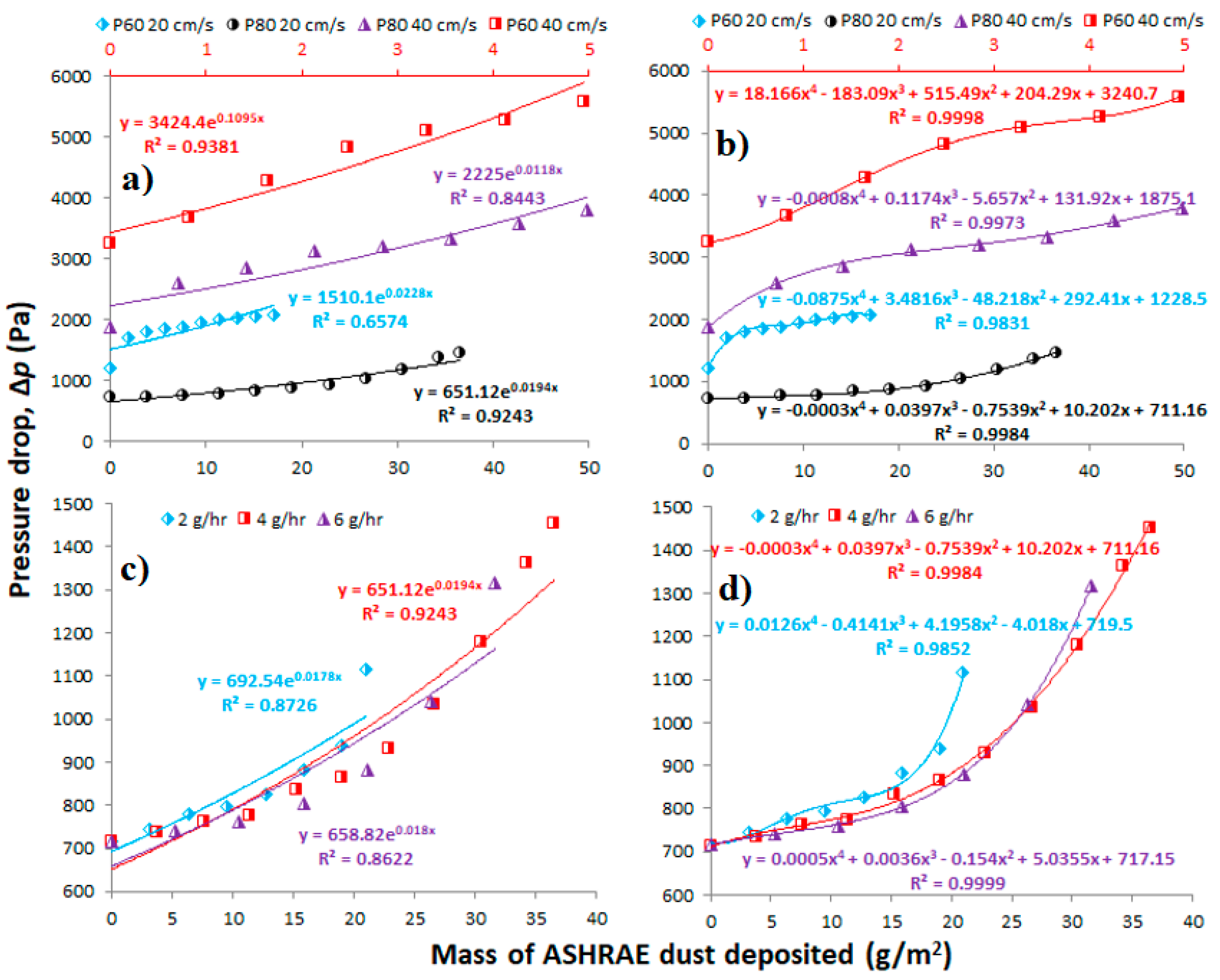
4.1. Experimental Data
4.2. Average Pressure Drop
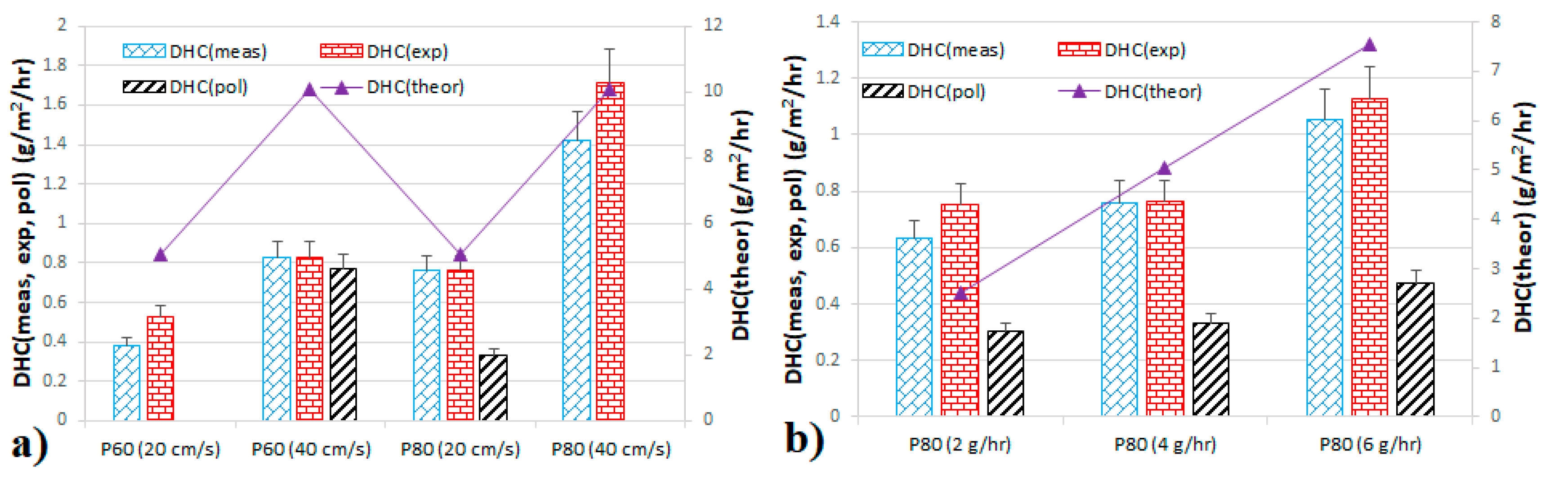
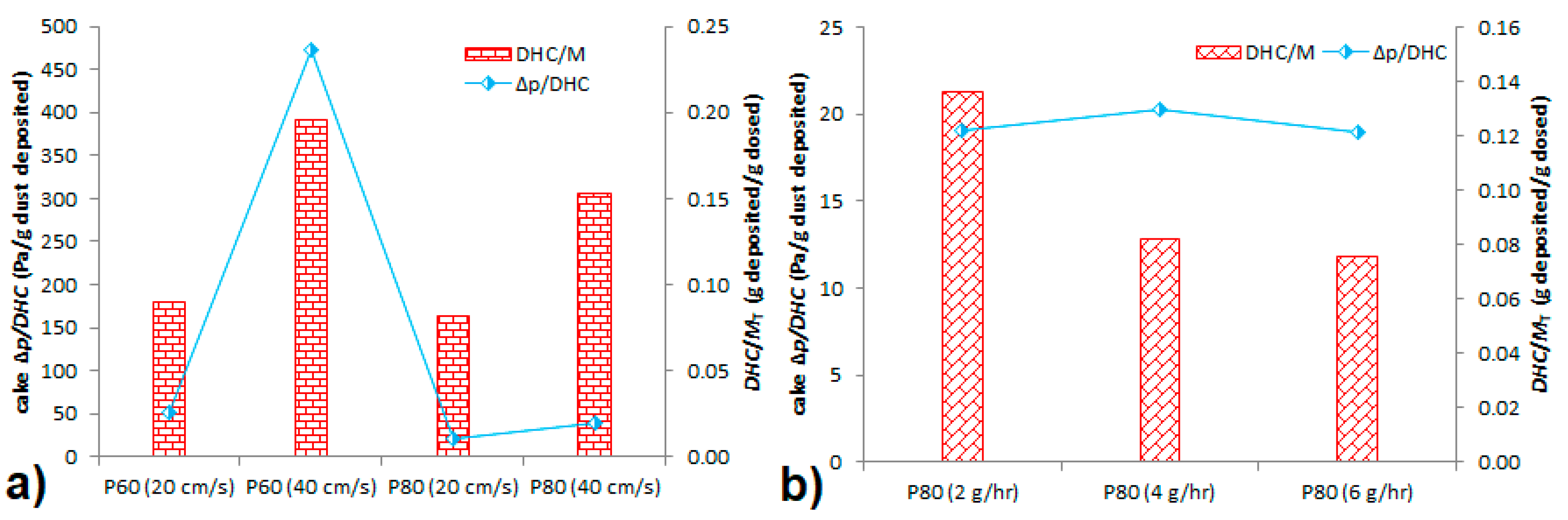
4.3. Dust-Holding Capacity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | a curve fitting parameter |
| A | membrane surface area |
| Ar | Archimedes number |
| b | a curve fitting parameter |
| B | a constant in relationship for pressure drop at filter exchange |
| Cup | upstream particle concentration |
| dp | particle diameter |
| D | discriminant |
| DHC | dust-holding capacity |
| DHCmeas | experimentally measured dust-holding capacity |
| DHCexp | dust-holding capacity from exponential fit |
| DHCpol | dust-holding capacity from polynomial fit |
| DHCtheor | theoretical dust-holding capacity |
| g | gravitational acceleration |
| H | humidity |
| K | constant describing dust and/or filter type |
| m | dust accumulation in filter |
| mHFM | instantaneous mass of dust deposited on HFM |
| mload | dust loading rate |
| m(t) | mass of dust on filter at a given time |
| M | final dust loading |
| MT | total amount of dust dosed to the chamber |
| ∆p(m) | pressure drop as a function of dust load |
| ∆p(t) | pressure drop as a function of time |
| ∆pavg | average pressure drop |
| ∆pc-o | pressure drop at change out of the filter |
| ∆pf | final pressure drop |
| ∆pi | initial pressure drop |
| Q | air flowrate |
| Re | Reynolds number |
| t | instant time of filtration |
| tf | final time of filtration |
| T | temperature |
| v | curve fitting parameter |
| x | curve fitting parameter |
| y | curve fitting parameter |
| z | curve fitting parameter |
| η | filtration efficiency |
| µ | fluid viscosity |
| νp | sedimentation velocity |
| ξ | friction coefficient |
| ρ | fluid density |
| ρp | particle density |
References
- Chen, J.; Brager, G.S.; Augenbroe, G.; Song, X. Impact of Outdoor Air Quality on the Natural Ventilation Usage of Commercial Buildings in the US. Appl. Energy 2019, 235, 673–684. [Google Scholar] [CrossRef]
- Yu, B.F.; Hu, Z.B.; Liu, M.; Yang, H.L.; Kong, Q.X.; Liu, Y.H. Review of Research on Air-Conditioning Systems and Indoor Air Quality Control for Human Health. Int. J. Refrig. 2009, 32, 3–20. [Google Scholar] [CrossRef]
- Bulejko, P. An Analysis on Energy Demands in Airborne Particulate Matter Filtration Using Hollow-Fiber Membranes. Energy Rep. 2021, 7, 2727–2736. [Google Scholar] [CrossRef]
- Leung, W.W.-F.; Hau, C.W.-Y. A Model of Backpulse and Backblow Cleaning of Nanofiber Filter Loaded with Nano-Aerosols. Sep. Purif. Technol. 2016, 169, 171–178. [Google Scholar] [CrossRef]
- Leung, W.W.-F.; Hau, C.W.Y. Skin Layer in Cyclic Loading-Cleaning of a Nanofiber Filter in Filtering Nano-Aerosols. Sep. Purif. Technol. 2017, 188, 367–378. [Google Scholar] [CrossRef] [PubMed]
- Bulejko, P.; Krištof, O.; Dohnal, M.; Svěrák, T. Fine/Ultrafine Particle Air Filtration and Aerosol Loading of Hollow-Fiber Membranes: A Comparison of Mathematical Models for the Most Penetrating Particle Size and Dimensionless Permeability with Experimental Data. J. Membr. Sci. 2019, 592, 117393. [Google Scholar] [CrossRef]
- Bulejko, P. Numerical Comparison of Prediction Models for Aerosol Filtration Efficiency Applied on a Hollow-Fiber Membrane Pore Structure. Nanomaterials 2018, 8, 447. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.-Y.; Yu, L.E.; Chung, T.-S. Effects of Relative Humidity, Particle Hygroscopicity, and Filter Hydrophilicity on Filtration Performance of Hollow Fiber Air Filters. J. Membr. Sci. 2020, 595, 117561. [Google Scholar] [CrossRef]
- Bulejko, P.; Krištof, O.; Svěrák, T. Experimental and Modeling Study on Fouling of Hollow-Fiber Membranes by Fine Dust Aerosol Particles. J. Membr. Sci. 2020, 616, 118562. [Google Scholar] [CrossRef]
- Bulejko, P.; Svěrák, T.; Dohnal, M.; Pospíšil, J. Aerosol Filtration Using Hollow-Fiber Membranes: Effect of Permeate Velocity and Dust Amount on Separation of Submicron TiO2 Particles. Powder Technol. 2018, 340, 344–353. [Google Scholar] [CrossRef]
- Xu, H.; Jin, W.; Wang, F.; Li, C.; Wang, J.; Zhu, H.; Guo, Y. Preparation and Properties of PTFE Hollow Fiber Membranes for the Removal of Ultrafine Particles in PM2.5 with Repetitive Usage Capability. RSC Adv. 2018, 8, 38245–38258. [Google Scholar] [CrossRef]
- Sun, C.; Woodman, D. Delivering Sustainability Promise to HVAC Air Filtration-Part I: Classification of Energy Efficiency for Air Filters. ASHRAE Trans. 2009, 115, 581–585. [Google Scholar]
- Eurovent 4/21—2014: Calculation Method for the Energy Use Related to Air Filters in General Ventilation Systems—First Edition | Eurovent. Available online: https://eurovent.eu/?q=content/eurovent-421-2014-calculation-method-energy-use-related-air-filters-general-ventilation (accessed on 11 November 2020).
- Zhang, W.; Deng, S.; Wang, Y.; Lin, Z. Dust Loading Performance of the PTFE HEPA Media and Its Comparison with the Glass Fibre HEPA Media. Aerosol Air Qual. Res. 2018, 18, 1921–1931. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Tang, M.; Sun, Z.; Liang, Y.; Hu, J. Dust Loading Performance of a Novel Submicro-Fiber Composite Filter Medium for Engine. Materials 2018, 11, 2038. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, C. Delivering Sustainability Promise to HVAC Air Filtration: Part II: Life Cycle Sustainability of Air Filters. ASHRAE Trans. 2010, 116, 25–32. [Google Scholar]
- Montgomery, J.F.; Green, S.I.; Rogak, S.N.; Bartlett, K. Predicting the Energy Use and Operation Cost of HVAC Air Filters. Energy Build. 2012, 47, 643–650. [Google Scholar] [CrossRef]
- Zena Membranes s.r.O. Available online: www.zena-membranes.cz/ (accessed on 14 May 2021).
- Sverak, T.; Bulejko, P.; Ostrezi, J.; Kristof, O.; Kalivoda, J.; Kejik, P.; Mayerova, K.; Adamcik, M. Separation of Gaseous Air Pollutants Using Membrane Contactors. IOP Conf. Ser. Earth Environ. Sci. 2017, 92, 012061. [Google Scholar] [CrossRef] [Green Version]
- Kůdelová, T.; Bartuli, E.; Strunga, A.; Hvožďa, J.; Dohnal, M. Fully Polymeric Distillation Unit Based on Polypropylene Hollow Fibers. Polymers 2021, 13, 1031. [Google Scholar] [CrossRef] [PubMed]
- ASHRAE 52.2-2017. Method of Testing General Ventilation Air-Cleaning Devices for Removal Efficiency by Particle Size; (ANSI Approved); ASHRAE: Peachtree Corners, GA, USA, 2017. [Google Scholar]
- Bulejko, P.; Dohnal, M.; Pospíšil, J.; Svěrák, T. Air Filtration Performance of Symmetric Polypropylene Hollow-Fibre Membranes for Nanoparticle Removal. Sep. Purif. Technol. 2018, 197, 122–128. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.; Liu, X.; Liu, C. Performance Optimization of Airliner Cabin Air Filters. Build. Environ. 2021, 187, 107392. [Google Scholar] [CrossRef]
- Banik, R.; Das, P.; Ray, S.; Biswas, A. Prediction of Electrical Energy Consumption Based on Machine Learning Technique. Electr. Eng. 2020. [Google Scholar] [CrossRef]
- Maduna, L.; Patnaik, A. Textiles in Air Filtration. Text. Prog. 2017, 49, 173–247. [Google Scholar] [CrossRef]
- Azimi, P.; Stephens, B. HVAC Filtration for Controlling Infectious Airborne Disease Transmission in Indoor Environments: Predicting Risk Reductions and Operational Costs. Build. Environ. 2013, 70, 150–160. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Ou, Q.; Liu, J.; Liang, Y.; Pui, D.Y.H. Influence of Pre-Stage Filter Selection and Face Velocity on the Loading Characteristics of a Two-Stage Filtration System. Sep. Purif. Technol. 2019, 224, 227–236. [Google Scholar] [CrossRef]
- Walsh, D.C. Possibilities for the Design of Fibrous Filter Materials with Enhanced Dust Holding Capacity. J. Aerosol Sci. 1998, 29, S939–S940. [Google Scholar] [CrossRef]
- Chang, D.-Q.; Tien, C.-Y.; Peng, C.-Y.; Tang, M.; Chen, S.-C. Development of Composite Filters with High Efficiency, Low Pressure Drop, and High Holding Capacity PM2.5 Filtration. Sep. Purif. Technol. 2019, 212, 699–708. [Google Scholar] [CrossRef]
- Rebai, M.; Prat, M.; Meireles, M.; Schmitz, P.; Baclet, R. Clogging Modeling in Pleated Filters for Gas Filtration. Chem. Eng. Res. Des. 2010, 88, 476–486. [Google Scholar] [CrossRef]
- Shao, P.; Huang, R.Y.M. An Analytical Approach to the Gas Pressure Drop in Hollow Fiber Membranes. J. Membr. Sci. 2006, 271, 69–76. [Google Scholar] [CrossRef]
- Tang, M.; Chen, S.-C.; Chang, D.-Q.; Xie, X.; Sun, J.; Pui, D.Y.H. Filtration Efficiency and Loading Characteristics of PM2.5 through Composite Filter Media Consisting of Commercial HVAC Electret Media and Nanofiber Layer. Sep. Purif. Technol. 2018, 198, 137–145. [Google Scholar] [CrossRef]



| Hollow-Fiber Membrane | P60 | P80 |
|---|---|---|
| Fiber outer diameter (µm) | 300 | 620 |
| Number of fibers | 1380 | 300 |
| Active length (mm) | 730 | 730 |
| Surface area (m2) | 0.95 | 0.43 |
| Initial pressure drop (Pa m−2) | 1143 ± 13 | 307 ± 2 |
| Experiment | DHCmeas (g) | Δpi (Pa) | Δpf (Pa) | MT (g) | tf (h) | |
|---|---|---|---|---|---|---|
| 4 g/h | P60 (20 cm/s) | 16.2 | 1204 | 2072 | 180 | 45 |
| P60 (40 cm/s) | 4.7 | 3239 | 5581 | 24 | 6 | |
| P80 (20 cm/s) | 15.7 | 714 | 1453 | 192 | 48 | |
| P80 (40 cm/s) | 21.4 | 1870 | 3789 | 140 | 35 | |
| 20 cm/s | P80 (2 g/h) | 9.0 | 717 | 1115 | 66 | 33 |
| P80 (4 g/h) | 15.7 | 714 | 1453 | 192 | 48 | |
| P80 (6 g/h) | 13.6 | 717 | 1318 | 180 | 30 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulejko, P.; Krištof, O.; Dohnal, M. An Assessment on Average Pressure Drop and Dust-Holding Capacity of Hollow-Fiber Membranes in Air Filtration. Membranes 2021, 11, 467. https://doi.org/10.3390/membranes11070467
Bulejko P, Krištof O, Dohnal M. An Assessment on Average Pressure Drop and Dust-Holding Capacity of Hollow-Fiber Membranes in Air Filtration. Membranes. 2021; 11(7):467. https://doi.org/10.3390/membranes11070467
Chicago/Turabian StyleBulejko, Pavel, Ondřej Krištof, and Miroslav Dohnal. 2021. "An Assessment on Average Pressure Drop and Dust-Holding Capacity of Hollow-Fiber Membranes in Air Filtration" Membranes 11, no. 7: 467. https://doi.org/10.3390/membranes11070467
APA StyleBulejko, P., Krištof, O., & Dohnal, M. (2021). An Assessment on Average Pressure Drop and Dust-Holding Capacity of Hollow-Fiber Membranes in Air Filtration. Membranes, 11(7), 467. https://doi.org/10.3390/membranes11070467






