On the Role of Electrostatic Repulsion in Topological Defect-Driven Membrane Fission
Abstract
:1. Introduction
2. Topological Defects/Antidefects and Membrane Fission
3. Electrostatic Interaction between Charged Membrane Surfaces
3.1. Modified Langevin Poisson–Boltzmann Model
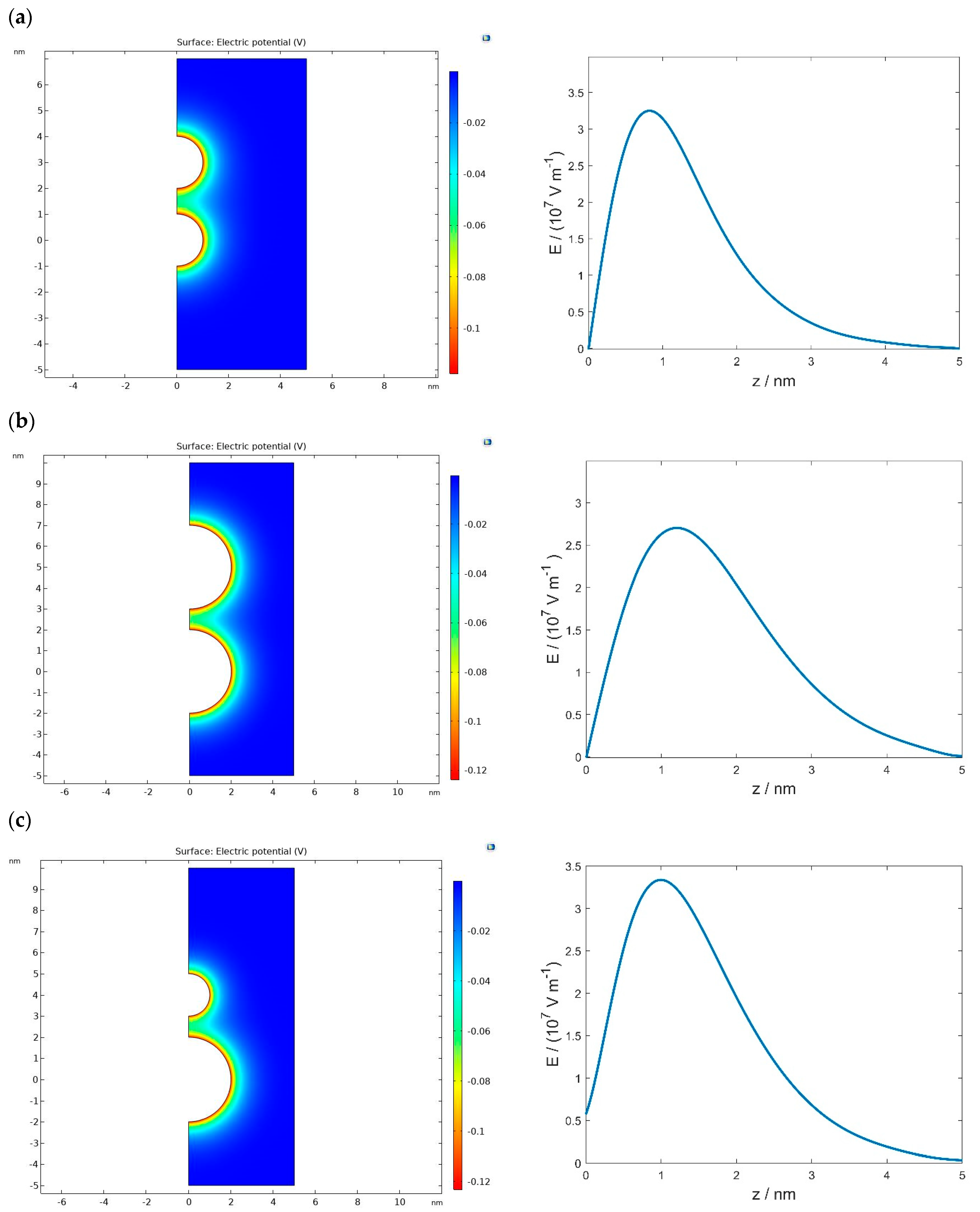
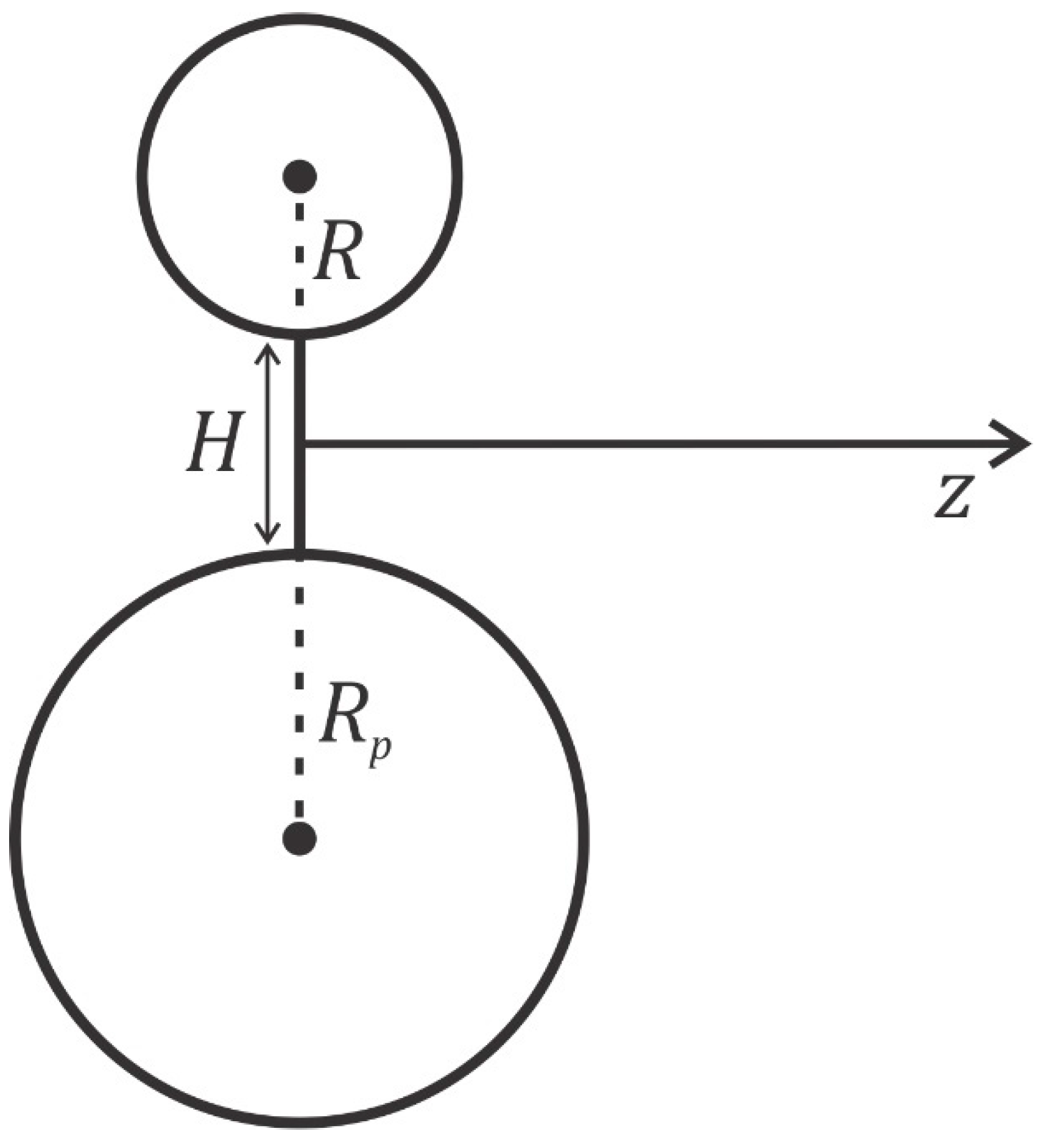
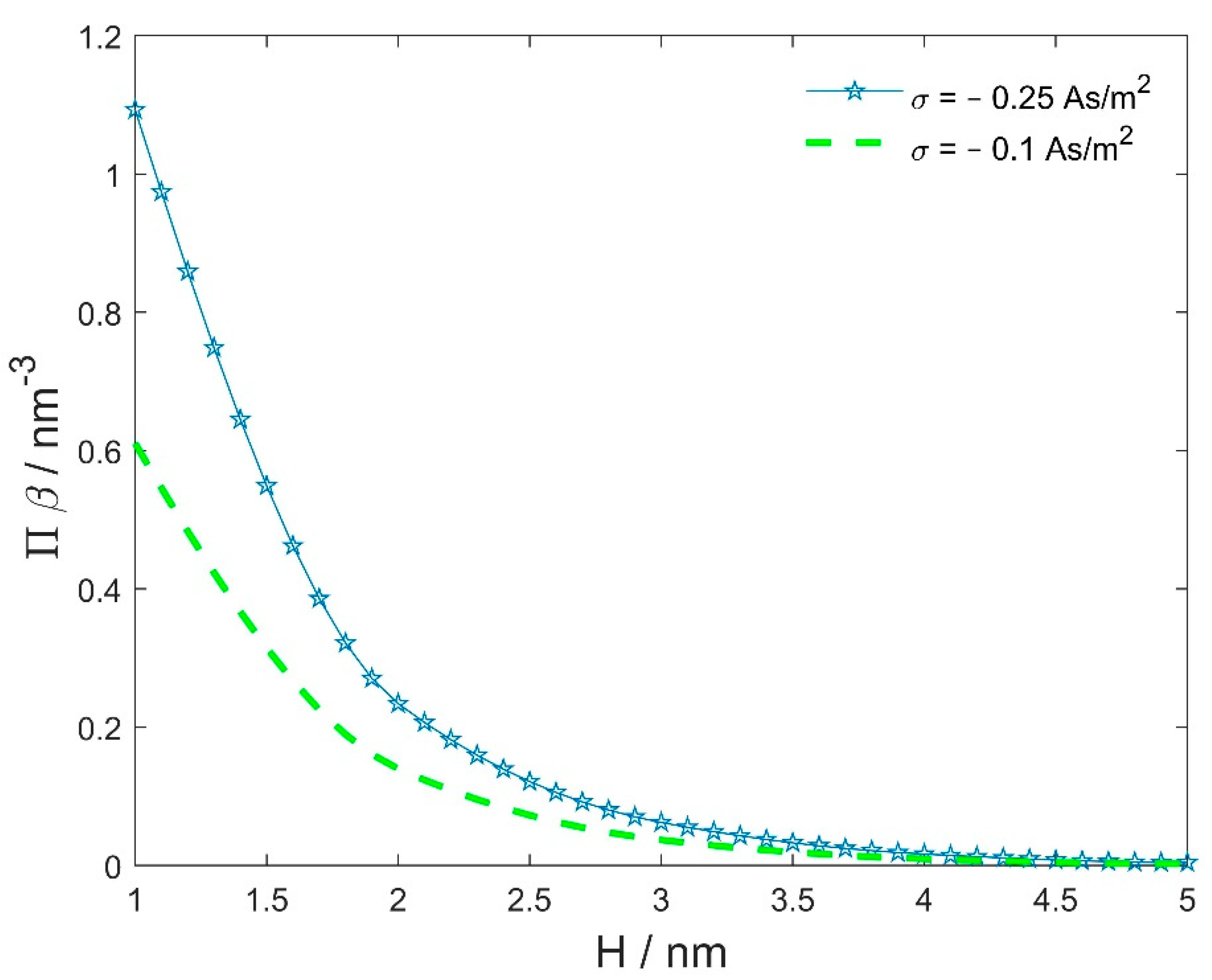
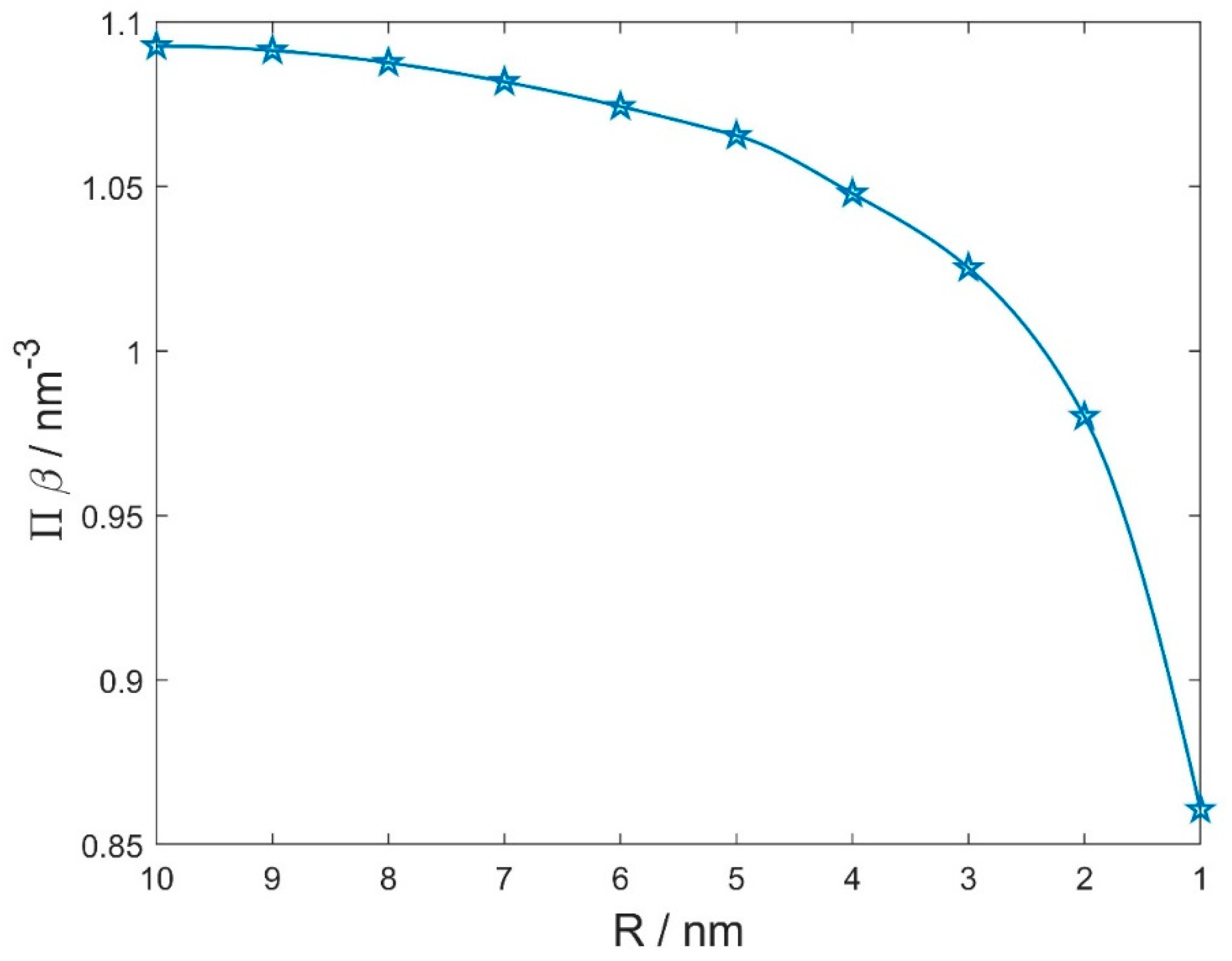
3.2. Osmotic Pressure between Two Charged Surfaces within a Modified Langevin Poisson–Boltzmann Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singer, S.J.; Nicolson, G.L. The fluid mosaic model of the structure of cell membranes. Science 1972, 175, 720–731. [Google Scholar] [CrossRef] [PubMed]
- Iglič, A.; Drobne, D.; Kralj-Iglic, V. Nanostructures in Biological Systems: Theory and Applications, 1st ed.; Pan/Jenny Stanford Publishing, Taylor and Francis: New York, NY, USA, 2015. [Google Scholar]
- Fošnarič, M.; Iglič, A.; May, S. Influence of rigid inclusions on the bending elasticity of a lipid membrane. Phys. Rev. E 2006, 74, 051503. [Google Scholar] [CrossRef] [Green Version]
- Kralj-Iglič, V.; Pocsfalvi, G.; Mesarec, L.; Šuštar, V.; Hägerstrand, H.; Iglič, A. Minimizing isotropic and deviatoric membrane energy–An unifying formation mechanism of different cellular membrane nanovesicle types. PLoS ONE 2020, 15, e0244796. [Google Scholar] [CrossRef]
- Kralj-Iglič, V.; Heinrich, V.; Svetina, S.; Žekš, B. Free energy of closed membrane with anisotropic inclusions. Eur. Phys. J. B-Cond. Matter Complex Syst. 1999, 10, 5–8. [Google Scholar] [CrossRef] [Green Version]
- Kralj-Iglič, V.; Svetina, S.; Žekš, B. Shapes of bilayer vesicles with membrane embedded molecules. Eur. Biophys. J. 1996, 24, 311–321. [Google Scholar] [CrossRef]
- Markin, V.S. Lateral organization of membranes and cell shapes. Biophys. J. 1981, 36, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Walani, N.; Torres, J.; Agrawal, A. Endocytic proteins drive vesicle growth via instability in high membrane tension environment. Proc. Natl. Acad. Sci. USA 2015, 112, E1423–E1432. [Google Scholar] [CrossRef] [Green Version]
- Gov, N.S. Guided by curvature: Shaping cells by coupling curved membrane proteins and cytoskeletal forces. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373, 20170115. [Google Scholar] [CrossRef] [PubMed]
- Fošnarič, M.; Penič, S.; Iglič, A.; Kralj-Iglič, V.; Drab, M.; Gov, N.S. Theoretical study of vesicle shapes driven by coupling curved proteins and active cytoskeletal forces. Soft Matter 2019, 15, 5319–5330. [Google Scholar] [CrossRef]
- Mesarec, L.; Góźdź, W.; Kralj, S.; Fošnarič, M.; Penič, S.; Kralj-Iglič, V.; Iglič, A. On the role of external force of actin filaments in the formation of tubular protrusions of closed membrane shapes with anisotropic membrane components. Eur. Biophys. J. 2017, 46, 705–718. [Google Scholar] [CrossRef]
- Hägerstrand, H.; Mrówczyńska, L.; Salzer, U.; Prohaska, R.; Michelsen, K.A.; Kralj-Iglič, V.; Iglič, A. Curvature-dependent lateral distribution of raft markers in the human erythrocyte membrane. Mol. Membr. Biol. 2006, 23, 277–288. [Google Scholar] [CrossRef] [PubMed]
- Kabaso, D.; Bobrovska, N.; Góźdź, W.; Gov, N.; Kralj-Iglič, V.; Veranič, P.; Iglič, A. On the role of membrane anisotropy and BAR proteins in the stability of tubular membrane structures. J. Biomech. 2012, 45, 231–238. [Google Scholar] [CrossRef]
- Liese, S.; Carlson, A. Membrane shape remodeling by protein crowding. Biophys. J. 2021. in print. [Google Scholar] [CrossRef] [PubMed]
- Mesarec, L.; Drab, M.; Penič, S.; Kralj-Iglič, V.; Iglič, A. On the role of curved membrane nanodomains and passive and active skeleton forces in the determination of cell shape and membrane budding. Int. J. Mol. Sci. 2021, 22, 2348. [Google Scholar] [CrossRef] [PubMed]
- Fischer, T.M. Bending stiffness of lipid bilayers. III. Gaussian curvature. J. Phys. II 1992, 2, 337–343. [Google Scholar] [CrossRef]
- Fischer, T.M. Bending stiffness of lipid bilayers. V. Comparison of two formulations. J. Phys. II 1993, 3, 1795–1805. [Google Scholar] [CrossRef] [Green Version]
- Fournier, J.B. Nontopological saddle-splay and curvature instabilities from anisotropic membrane inclusions. Phys. Rev. Lett. 1996, 76, 4436. [Google Scholar] [CrossRef]
- Safinya, C.R. Biomolecular materials: Structure, interactions and higher order self-assembly. Coll. Surf. A Physicochem. Eng. Asp. 1997, 128, 183–195. [Google Scholar] [CrossRef]
- Fournier, J.B.; Galatola, P. Bilayer membranes with 2D-nematic order of the surfactant polar heads. Braz. J. Phys. 1998, 28, 329–338. [Google Scholar] [CrossRef]
- Kralj-Iglič, V.; Babnik, B.; Gauger, D.R.; May, S.; Iglič, A. Quadrupolar ordering of phospholipid molecules in narrow necks of phospholipid vesicles. J. Stat. Phys. 2006, 125, 727–752. [Google Scholar] [CrossRef]
- Penič, S.; Mesarec, L.; Fošnarič, M.; Mrówczyńska, L.; Hägerstrand, H.; Kralj-Iglič, V.; Iglič, A. Budding and fission of membrane vesicles: A mini review. Front. Phys. 2020, 8, 342. [Google Scholar] [CrossRef]
- Mesarec, L.; Góźdź, W.; Iglič, A.; Kralj-Iglič, V.; Virga, E.G.; Kralj, S. Normal red blood cells’ shape stabilized by membrane’s in-plane ordering. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Mares, T.; Daniel, M.; Perutkova, S.; Perne, A.; Dolinar, G.; Iglic, A.; Rappolt, M.; Kralj-Iglic, V. Role of phospholipid asymmetry in the stability of inverted hexagonal mesoscopic phases. J. Phys. Chem. B 2008, 112, 16575–16584. [Google Scholar] [CrossRef]
- Mesarec, L.; Góźdź, W.; Iglič, A.; Kralj, S. Effective topological charge cancelation mechanism. Sci. Rep. 2016, 6, 1–12. [Google Scholar]
- Mesarec, L.; Iglič, A.; Kralj-Iglič, V.; Góźdź, W.; Virga, E.G.; Kralj, S. Curvature Potential Unveiled Topological Defect Attractors. Crystals 2021, 11, 539. [Google Scholar] [CrossRef]
- Vitelli, V.; Turner, A.M. Anomalous coupling between topological defects and curvature. Phys. Rev. Lett. 2004, 93, 215301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bowick, M.J.; Giomi, L. Two-dimensional matter: Order, curvature and defects. Adv. Phys. 2009, 58, 449–563. [Google Scholar] [CrossRef]
- Turner, A.M.; Vitelli, V.; Nelson, D.R. Vortices on curved surfaces. Rev. Mod. Phys. 2010, 82, 1301. [Google Scholar] [CrossRef] [Green Version]
- Kralj-Iglič, V.; Iglič, A.; Hägerstrand, H.; Peterlin, P. Stable tubular microexovesicles of the erythrocyte membrane induced by dimeric amphiphiles. Phys. Rev. E 2000, 61, 4230. [Google Scholar] [CrossRef] [Green Version]
- Penič, S.; Fošnarič, M.; Mesarec, L.; Iglič, A.; Kralj-Iglič, V. Active forces of myosin motors may control endovesiculation of red blood cells. Acta Chim. Slov. 2020, 67, 674–681. [Google Scholar] [CrossRef]
- Kralj, S.; Rosso, R.; Virga, E.G. Curvature control of valence on nematic shells. Soft Matter 2011, 7, 670–683. [Google Scholar] [CrossRef]
- Mesarec, L.; Kurioz, P.; Iglič, A.; Góźdź, W.; Kralj, S. Curvature-controlled topological defects. Crystals 2017, 7, 153. [Google Scholar] [CrossRef] [Green Version]
- Jesenek, D.; Perutková, Š.; Góźdź, W.; Kralj-Iglič, V.; Iglič, A.; Kralj, S. Vesiculation of biological membrane driven by curvature induced frustrations in membrane orientational ordering. Int. J. Nanomed. 2013, 8, 677–687. [Google Scholar] [CrossRef] [Green Version]
- Bowick, M.; Nelson, D.R.; Travesset, A. Curvature-induced defect unbinding in toroidal geometries. Phys. Rev. E 2004, 69, 041102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mermin, N.D. The topological theory of defects in ordered media. Rev. Mod. Phys. 1979, 51, 591. [Google Scholar] [CrossRef]
- Kurik, M.V.; Lavrentovich, O.D. Defects in liquid crystals: Homotopy theory and experimental studies. SvPhU 1988, 31, 196. [Google Scholar] [CrossRef]
- Kamien, R.D. The geometry of soft materials: A primer. Rev. Mod. Phys. 2002, 74, 953. [Google Scholar] [CrossRef] [Green Version]
- Helfrich, W. Elastic properties of lipid bilayers: Theory and possible experiments. Z. Naturforsch. C 1973, 28, 693–703. [Google Scholar] [CrossRef] [PubMed]
- Helfrich, W.; Prost, J. Intrinsic bending force in anisotropic membranes made of chiral molecules. Phys. Rev. A 1988, 38, 3065. [Google Scholar] [CrossRef] [PubMed]
- Stein, D.B.; De Canio, G.; Lauga, E.; Shelley, M.J.; Goldstein, R.E. Swirling Instability of the Microtubule Cytoskeleton. Phys. Rev. Lett. 2021, 126, 028103. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Elvati, P.; Majumder, S.; Wang, Y.; Liu, A.P.; Violi, A. Predicting the time of entry of nanoparticles in lipid membranes. ACS Nano 2019, 13, 10221–10232. [Google Scholar] [CrossRef]
- Kikuchi, H.; Yokota, M.; Hisakado, Y.; Yang, H.; Kajiyama, T. Polymer-stabilized liquid crystal blue phases. Nat. Mater. 2002, 1, 64–68. [Google Scholar] [CrossRef]
- Cordoyiannis, G.; Jampani, V.S.R.; Kralj, S.; Dhara, S.; Tzitzios, V.; Basina, G.; Nounesis, G.; Kutnjak, Z.; Tripathi, C.S.P.; Losada-Pérez, P. Different modulated structures of topological defects stabilized by adaptive targeting nanoparticles. Soft Matter 2013, 9, 3956–3964. [Google Scholar] [CrossRef]
- Pires, D.; Fleury, J.-B.; Galerne, Y. Colloid particles in the interaction field of a disclination line in a nematic phase. Phys. Rev. Lett. 2007, 98, 247801. [Google Scholar] [CrossRef] [PubMed]
- Gouy, M. Sur la constitution de la charge électrique à la surface d’un électrolyte. J. Phys. Theor. Appl. 1910, 9, 457–468. [Google Scholar] [CrossRef] [Green Version]
- Chapman, D.L.L.I. A contribution to the theory of electrocapillarity. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1913, 25, 475–481. [Google Scholar] [CrossRef] [Green Version]
- Freise, V. Zur theorie der diffusen doppelschicht. Z. Elektrochem. Ber. Bunsenges. Phys. Chem. 1952, 56, 822–827. [Google Scholar]
- Torrie, G.M.; Valleau, J.P. Electrical double layers. I. Monte Carlo study of a uniformly charged surface. J. Chem. Phys. 1980, 73, 5807–5816. [Google Scholar] [CrossRef]
- Kenkel, S.W.; Macdonald, J.R. A lattice model for the electrical double layer using finite-length dipoles. J. Chem. Phys. 1984, 81, 3215–3221. [Google Scholar] [CrossRef]
- Outhwaite, C.W.; Bhuiyan, L.B. A modified Poisson–Boltzmann equation in electric double layer theory for a primitive model electrolyte with size-asymmetric ions. J. Chem. Phys. 1986, 84, 3461–3471. [Google Scholar] [CrossRef]
- McLaughlin, S. The electrostatic properties of membranes. Ann. Rev. Biophys. Biophys. Chem. 1989, 18, 113–136. [Google Scholar] [CrossRef] [PubMed]
- Kralj-Iglič, V.; Iglič, A. A simple statistical mechanical approach to the free energy of the electric double layer including the excluded volume effect. J. Phys. II 1996, 6, 477–491. [Google Scholar] [CrossRef] [Green Version]
- Bivas, I. Electrostatic and mechanical properties of a flat lipid bilayer containing ionic lipids: Possibility for formation of domains with different surface charges. Coll. Surf. A Physicochem. Eng. Asp. 2006, 282, 423–434. [Google Scholar] [CrossRef]
- Gongadze, E.; Velikonja, A.; Perutkova, Š.; Kramar, P.; Maček-Lebar, A.; Kralj-Iglič, V.; Iglič, A. Ions and water molecules in an electrolyte solution in contact with charged and dipolar surfaces. Electrochim. Acta 2014, 126, 42–60. [Google Scholar] [CrossRef]
- Stern, O. Zur theorie der elektrolytischen doppelschicht. ZEAPC 1924, 30, 508–516. [Google Scholar]
- Bikerman, J.J. XXXIX. Structure and capacity of electrical double layer. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1942, 33, 384–397. [Google Scholar] [CrossRef]
- Wicke, E.; Eigen, M. Über den Einfluß des Raumbedarfs von Ionen in wäßriger Lösung auf ihre Verteilung in elektrischen Feld und ihre Aktivitätskoeffizienten. Z. Elektrochem. Ber. Bunsenges. Phys. Chem. 1952, 56, 551–561. [Google Scholar]
- Eigen, M.; Wicke, E. The thermodynamics of electrolytes at higher concentration. J. Phys. Chem. 1954, 58, 702–714. [Google Scholar] [CrossRef]
- Onsager, L. Electric moments of molecules in liquids. J. Am. Chem. Soc. 1936, 58, 1486–1493. [Google Scholar] [CrossRef]
- Booth, F. The dielectric constant of water and the saturation effect. J. Chem. Phys. 1951, 19, 391–394. [Google Scholar] [CrossRef]
- Outhwaite, C.W. A treatment of solvent effects in the potential theory of electrolyte solutions. Mol. Phys. 1976, 31, 1345–1357. [Google Scholar] [CrossRef]
- Outhwaite, C.W. Towards a mean electrostatic potential treatment of an ion-dipole mixture or a dipolar system next to a plane wall. Mol. Phys. 1983, 48, 599–614. [Google Scholar] [CrossRef]
- Iglič, A.; Gongadze, E.; Bohinc, K. Excluded volume effect and orientational ordering near charged surface in solution of ions and Langevin dipoles. Bioelectrochemistry 2010, 79, 223–227. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Kilic, M.S.; Storey, B.D.; Ajdari, A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface Sci. 2009, 152, 48–88. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gongadze, E.; Iglič, A. Asymmetric size of ions and orientational ordering of water dipoles in electric double layer model-an analytical mean-field approach. Electrochim. Acta 2015, 178, 541–545. [Google Scholar] [CrossRef]
- Gongadze, E.; Mesarec, L.; Kralj-Iglic, V.; Iglic, A. Asymmetric finite size of ions and orientational ordering of water in electric double layer theory within lattice model. Mini Rev. Med. Chem. 2018, 18, 1559–1566. [Google Scholar] [CrossRef] [Green Version]
- Iglič, A.; Gongadze, E.; Kralj-Iglič, V. Differential Capacitance of Electric Double Layer–Influence of Asymmetric Size of Ions, Thickness of Stern Layer and Orientational Ordering of Water Dipoles. Acta Chim. Slov. 2019, 66, 534–541. [Google Scholar] [CrossRef] [PubMed]
- Helmholtz, H.V. Ueber einige Gesetze der Vertheilung elektrischer Ströme in körperlichen Leitern, mit Anwendung auf die thierisch-elektrischen Versuche (Schluss.). Ann. Phys. 1853, 165, 353–377. [Google Scholar] [CrossRef] [Green Version]
- Helmholtz, H.V. Studien über electrische Grenzschichten. Ann. Phys. 1879, 243, 337–382. [Google Scholar] [CrossRef] [Green Version]
- Torrie, G.M.; Valleau, J.P. Electrical double layers. 4. Limitations of the Gouy-Chapman theory. J. Phys. Chem. 1982, 86, 3251–3257. [Google Scholar] [CrossRef]
- Nielaba, P.; Forstmann, F. Packing of ions near an electrolyte-electrode interface in the hnc/lmsa approximation to the rpm model. Chem. Phys. Lett. 1985, 117, 46–48. [Google Scholar] [CrossRef]
- Plischke, M.; Henderson, D. Pair correlation functions and density profiles in the primitive model of the electric double layer. J. Chem. Phys. 1988, 88, 2712–2718. [Google Scholar] [CrossRef]
- Kornyshev, A.A. Double-layer in ionic liquids: Paradigm change? J. Phys. Chem. B 2007, 111, 5545–5557. [Google Scholar] [CrossRef]
- Mier-y-Teran, L.; Suh, S.H.; White, H.S.; Davis, H.T. A nonlocal free-energy density-functional approximation for the electrical double layer. J. Chem. Phys. 1990, 92, 5087–5098. [Google Scholar] [CrossRef] [Green Version]
- Strating, P.; Wiegel, F.W. Effects of excluded volume on the electrolyte distribution around a charged sphere. J. Phys. A Math. Gen. 1993, 26, 3383. [Google Scholar] [CrossRef]
- Lee, J.W.; Nilson, R.H.; Templeton, J.A.; Griffiths, S.K.; Kung, A.; Wong, B.M. Comparison of molecular dynamics with classical density functional and Poisson–Boltzmann theories of the electric double layer in nanochannels. J. Chem. Theory Comput. 2012, 8, 2012–2022. [Google Scholar] [CrossRef] [PubMed]
- Quiroga, M.A.; Xue, K.-H.; Nguyen, T.-K.; Tułodziecki, M.; Huang, H.; Franco, A.A. A multiscale model of electrochemical double layers in energy conversion and storage devices. J. Electrochem. Soc. 2014, 161, E3302. [Google Scholar] [CrossRef]
- Bandopadhyay, A.; Shaik, V.A.; Chakraborty, S. Effects of finite ionic size and solvent polarization on the dynamics of electrolytes probed through harmonic disturbances. Phys. Rev. E 2015, 91, 042307. [Google Scholar] [CrossRef] [PubMed]
- Lian, C.; Liu, K.; Van Aken, K.L.; Gogotsi, Y.; Wesolowski, D.J.; Liu, H.L.; Jiang, D.E.; Wu, J.Z. Enhancing the capacitive performance of electric double-layer capacitors with ionic liquid mixtures. ACS Energy Lett. 2016, 1, 21–26. [Google Scholar] [CrossRef]
- Drab, M.; Kralj-Iglič, V. Diffuse electric double layer in planar nanostructures due to Fermi-Dirac statistics. Electrochim. Acta 2016, 204, 154–159. [Google Scholar] [CrossRef]
- Budkov, Y.A.; Kolesnikov, A.L.; Goodwin, Z.A.H.; Kiselev, M.G.; Kornyshev, A.A. Theory of electrosorption of water from ionic liquids. Electrochim. Acta 2018, 284, 346–354. [Google Scholar] [CrossRef]
- Budkov, Y.A. Nonlocal statistical field theory of dipolar particles in electrolyte solutions. J. Phys. Condens. Matter 2018, 30, 344001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dubtsov, A.V.; Pasechnik, S.V.; Shmeliova, D.V.; Saidgaziev, A.S.; Gongadze, E.; Iglič, A.; Kralj, S. Liquid crystalline droplets in aqueous environments: Electrostatic effects. Soft Matter 2018, 14, 9619–9630. [Google Scholar] [CrossRef] [PubMed]
- Gavish, N.; Elad, D.; Yochelis, A. From solvent-free to dilute electrolytes: Essential components for a continuum theory. J. Phys. Chem. Lett. 2018, 9, 36–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gavish, N. Poisson–Nernst–Planck equations with steric effects—Non-convexity and multiple stationary solutions. Phys. D Nonlinear Phenom. 2018, 368, 50–65. [Google Scholar] [CrossRef] [Green Version]
- Kruczek, J.; Chiu, S.-W.; Varma, S.; Jakobsson, E.; Pandit, S.A. Interactions of monovalent and divalent cations at palmitoyl-oleoyl-phosphatidylcholine interface. Langmuir 2019, 35, 10522–10532. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Tian, R.; Ding, W.; Wu, L.; Li, H. Role of ionic polarization and dielectric decrement in the estimation of surface potential of clay particles. Eur. J. Soil Sci. 2019, 70, 1073–1081. [Google Scholar] [CrossRef]
- May, S. Differential capacitance of the electric double layer: Mean-field modeling approaches. Curr. Opin. Electrochem. 2019, 13, 125–131. [Google Scholar] [CrossRef]
- Cruz, C.; Kondrat, S.; Lomba, E.; Ciach, A. Effect of proximity to ionic liquid-solvent demixing on electrical double layers. J. Mol. Liq. 2019, 294, 111368. [Google Scholar] [CrossRef]
- Guardiani, C.; Gibby, W.; Barabash, M.; Luchinsky, D.; Khovanov, I.; McClintock, P. Prehistory probability distribution of ionic transitions through a graphene nanopore. In Proceedings of the 25th International Conference on Noise and Fluctuations—ICNF 2019, Neuchatel, Switzerland, 18–21 June 2019. [Google Scholar]
- Khademi, M.; Barz, D.P.J. Structure of the electrical double layer revisited: Electrode capacitance in aqueous solutions. Langmuir 2020, 36, 4250–4260. [Google Scholar] [CrossRef] [PubMed]
- Kjellander, R.; Marčelja, S. Interaction of charged surfaces in electrolyte solutions. Chem. Phys. Lett. 1986, 127, 402–407. [Google Scholar] [CrossRef]
- Evans, D.F.; Wennerström, H. The Colloidal Domain: Where Physics, Chemistry, Biology, and Technology Meet, 2nd ed.; Wiley-VCH: New York, NY, USA, 1999. [Google Scholar]
- Butt, H.J.; Graf, K.; Kappl, M. Physics and Chemistry of Interfaces; Wiley-VCH: Weinheim, Germany, 2003. [Google Scholar]
- Bohinc, K.; Iglič, A.; May, S. Interaction between macroions mediated by divalent rod-like ions. EPL (Europhys. Lett.) 2004, 68, 494. [Google Scholar] [CrossRef] [Green Version]
- Urbanija, J.; Bohinc, K.; Bellen, A.; Maset, S.; Iglič, A.; Kralj-Iglič, V.; Sunil Kumar, P.B. Attraction between negatively charged surfaces mediated by spherical counterions with quadrupolar charge distribution. J. Chem. Phys. 2008, 129, 09B609. [Google Scholar] [CrossRef] [Green Version]
- Perutková, Š.; Frank, M.; Bohinc, K.; Bobojevič, G.; Zelko, J.; Rozman, B.; Kralj-Iglič, V.; Iglič, A. Interaction between equally charged membrane surfaces mediated by positively and negatively charged macro-ions. J. Membr. Biol. 2010, 236, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: London, UK, 2011. [Google Scholar]
- Velikonja, A.; Santhosh, P.B.; Gongadze, E.; Kulkarni, M.; Eleršič, K.; Perutkova, Š.; Kralj-Iglič, V.; Ulrih, N.P.; Iglič, A. Interaction between dipolar lipid headgroups and charged nanoparticles mediated by water dipoles and ions. Int. J. Mol. Sci. 2013, 14, 15312–15329. [Google Scholar] [CrossRef]
- Prasanna Misra, R.; Das, S.; Mitra, S.K. Electric double layer force between charged surfaces: Effect of solvent polarization. J. Chem. Phys. 2013, 138, 114703. [Google Scholar] [CrossRef] [PubMed]
- Gimsa, J.; Wysotzki, P.; Perutkova, Š.; Weihe, T.; Elter, P.; Marszałek, P.; Kralj-Iglič, V.; Müller, T.; Iglič, A. Spermidine-induced attraction of like-charged surfaces is correlated with the pH-dependent spermidine charge: Force spectroscopy characterization. Langmuir 2018, 34, 2725–2733. [Google Scholar] [CrossRef]
- Goršak, T.; Drab, M.; Križaj, D.; Jeran, M.; Genova, J.; Kralj, S.; Lisjak, D.; Kralj-Iglič, V.; Iglič, A.; Makovec, D. Magneto-mechanical actuation of barium-hexaferrite nanoplatelets for the disruption of phospholipid membranes. J. Colloid Interface Sci. 2020, 579, 508–519. [Google Scholar] [CrossRef] [PubMed]
- Gongadze, E.; van Rienen, U.; Kralj-Iglič, V.; Iglič, A. Langevin Poisson-Boltzmann equation: Point-like ions and water dipoles near a charged surface. Gen. Physiol. Biophys. 2011, 30, 130. [Google Scholar] [CrossRef]
- Drab, M.; Gongadze, E.; Kralj-Iglič, V.; Iglič, A. Electric double layer and orientational ordering of water dipoles in narrow channels within a modified Langevin Poisson-Boltzmann model. Entropy 2020, 22, 1054. [Google Scholar] [CrossRef]
- Abrashkin, A.; Andelman, D.; Orland, H. Dipolar Poisson-Boltzmann equation: Ions and dipoles close to charge interfaces. Phys. Rev. Lett. 2007, 99, 077801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Teschke, O.; Ceotto, G.; de Souza, E.F. Interfacial aqueous solutions dielectric constant measurements using atomic force microscopy. Chem. Phys. Lett. 2000, 326, 328. [Google Scholar] [CrossRef]
- De Souza, E.F.; Ceotto, G.; Teschke, O. Dielectric constant measurements of interfacial aqueous solutions using atomic force microscopy. J. Mol. Catal. A Chem. 2001, 167, 235. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gongadze, E.; Mesarec, L.; Kralj, S.; Kralj-Iglič, V.; Iglič, A. On the Role of Electrostatic Repulsion in Topological Defect-Driven Membrane Fission. Membranes 2021, 11, 812. https://doi.org/10.3390/membranes11110812
Gongadze E, Mesarec L, Kralj S, Kralj-Iglič V, Iglič A. On the Role of Electrostatic Repulsion in Topological Defect-Driven Membrane Fission. Membranes. 2021; 11(11):812. https://doi.org/10.3390/membranes11110812
Chicago/Turabian StyleGongadze, Ekaterina, Luka Mesarec, Samo Kralj, Veronika Kralj-Iglič, and Aleš Iglič. 2021. "On the Role of Electrostatic Repulsion in Topological Defect-Driven Membrane Fission" Membranes 11, no. 11: 812. https://doi.org/10.3390/membranes11110812
APA StyleGongadze, E., Mesarec, L., Kralj, S., Kralj-Iglič, V., & Iglič, A. (2021). On the Role of Electrostatic Repulsion in Topological Defect-Driven Membrane Fission. Membranes, 11(11), 812. https://doi.org/10.3390/membranes11110812









