Prediction of Membrane Failure in a Water Purification Plant Using Nonhomogeneous Poisson Process Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Membrane Filtration Plant and Membrane Failure Detection
2.2. Statistical Inference of Membrane Failure Process
2.2.1. Membrane Failure Data
2.2.2. Statistical Models for the Membrane Failure Process
- Power law model
- Log-linear model
2.2.3. Estimation of Model Parameter Distribution by the Bootstrap Method
2.3. Requirement for Membrane Filtration Performance
3. Results
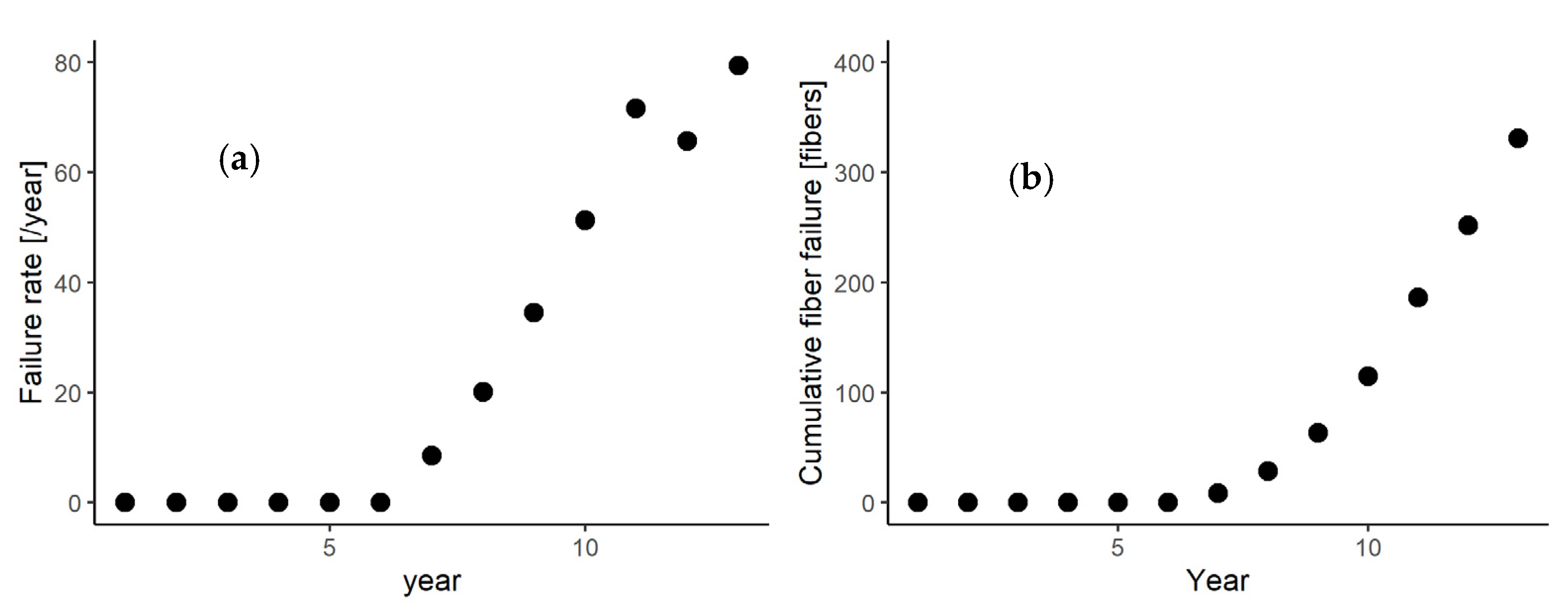
3.1. Membrane Fiber Failure in the Water Purification Plant
3.2. Application of Nonhomogeneous Poisson Process Models to Membrane Failure
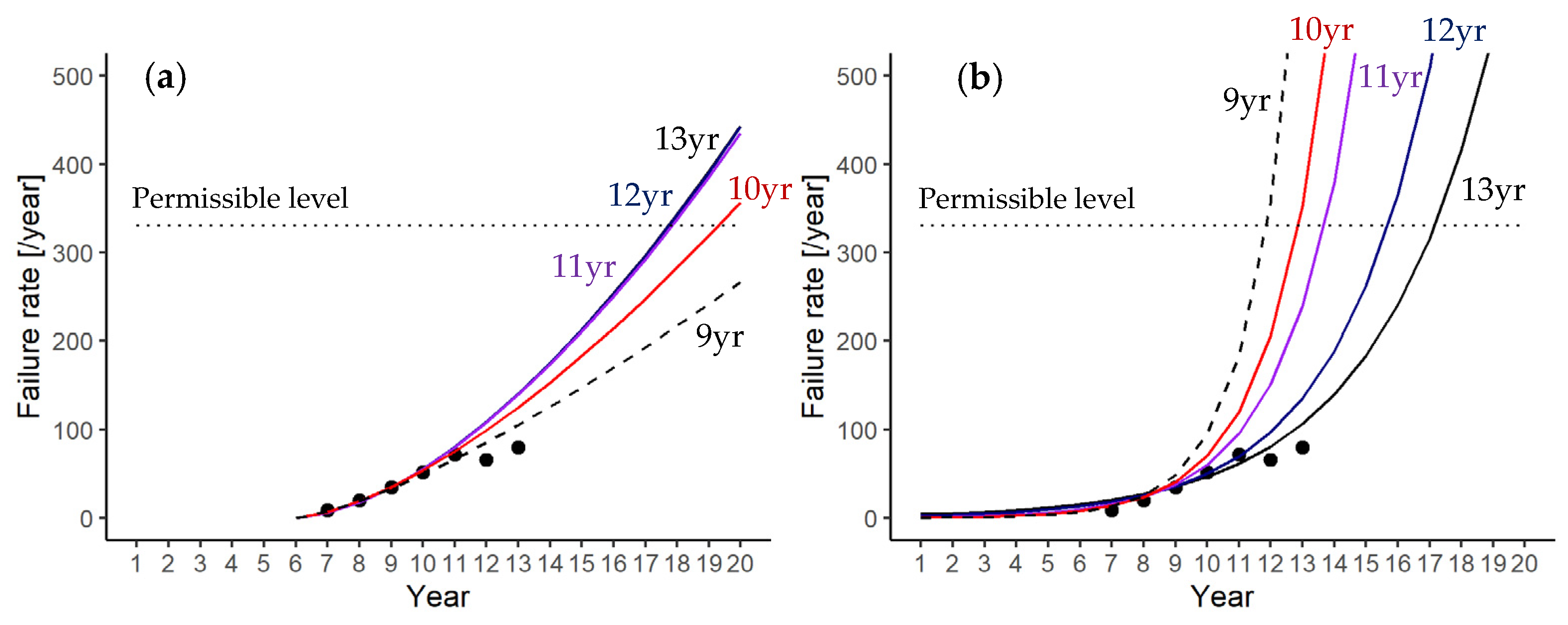
3.2.1. Membrane Failure Rates in the Water Purification Plant
- Power law model
- Log-linear model
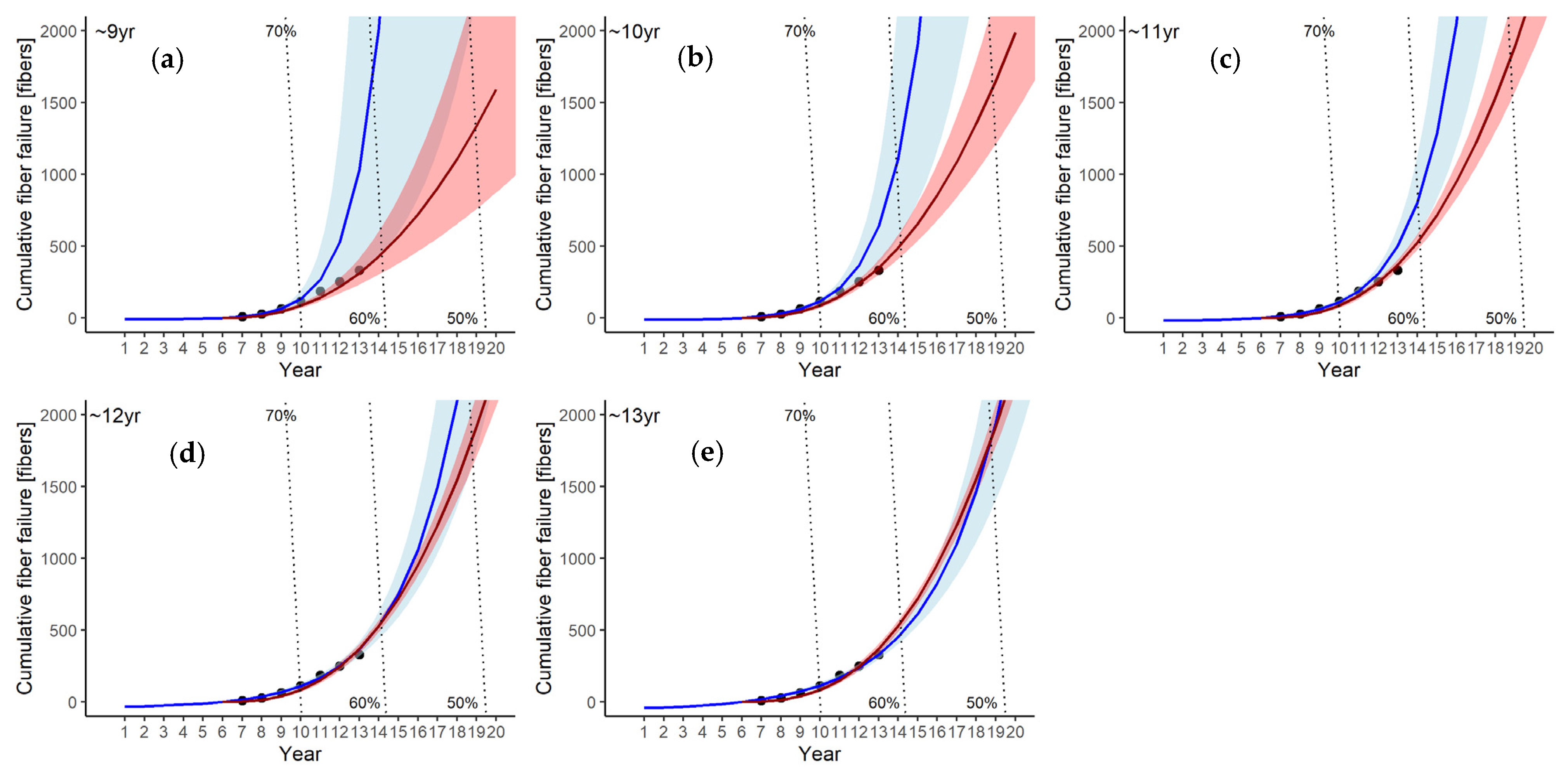
3.2.2. Cumulative Membrane Failure in the Water Purification Plant
- Power law model
- Log-linear model
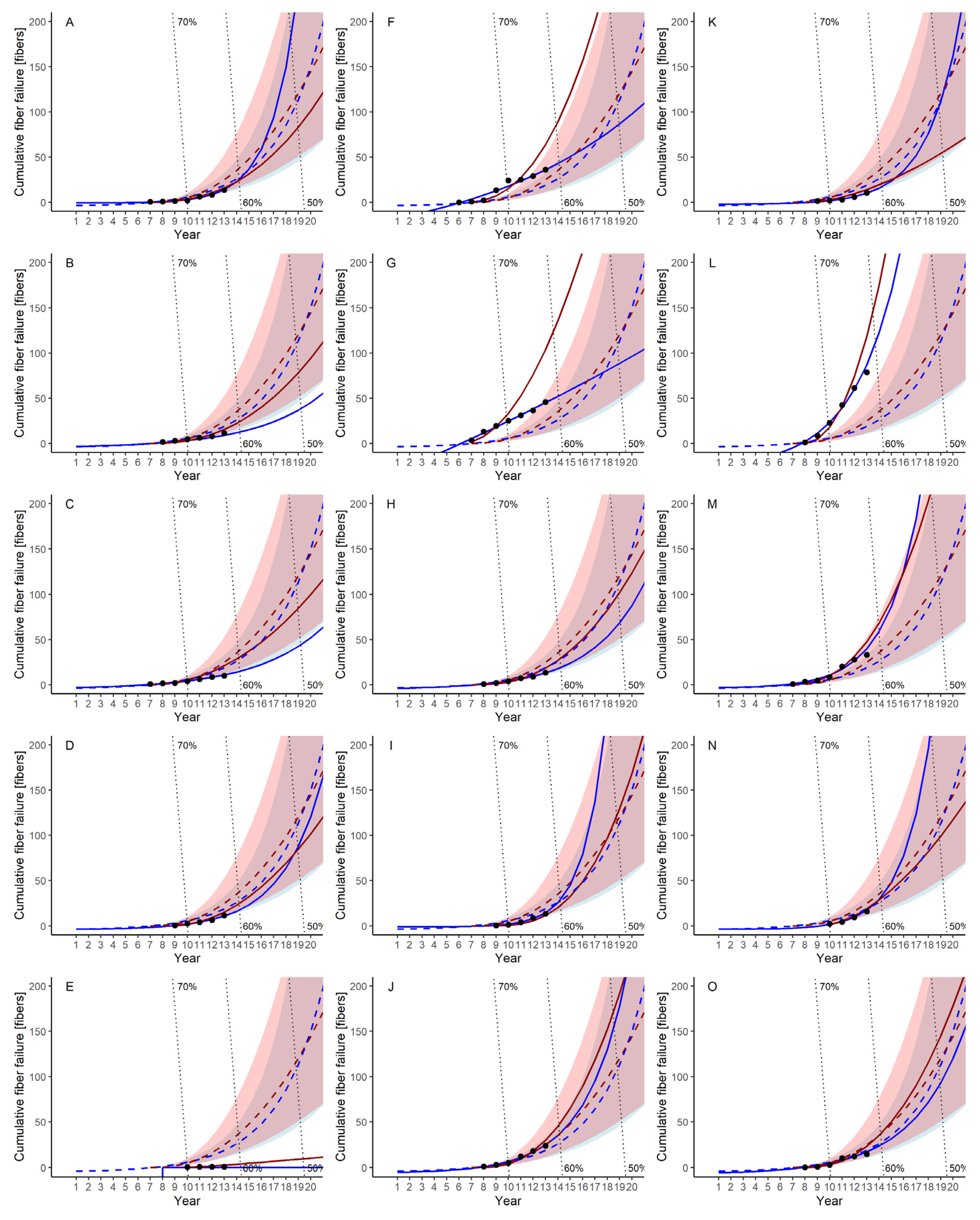
3.3. Failure Trends by Modules
3.3.1. Failure Rate and NHPP Model Fitting to Modules
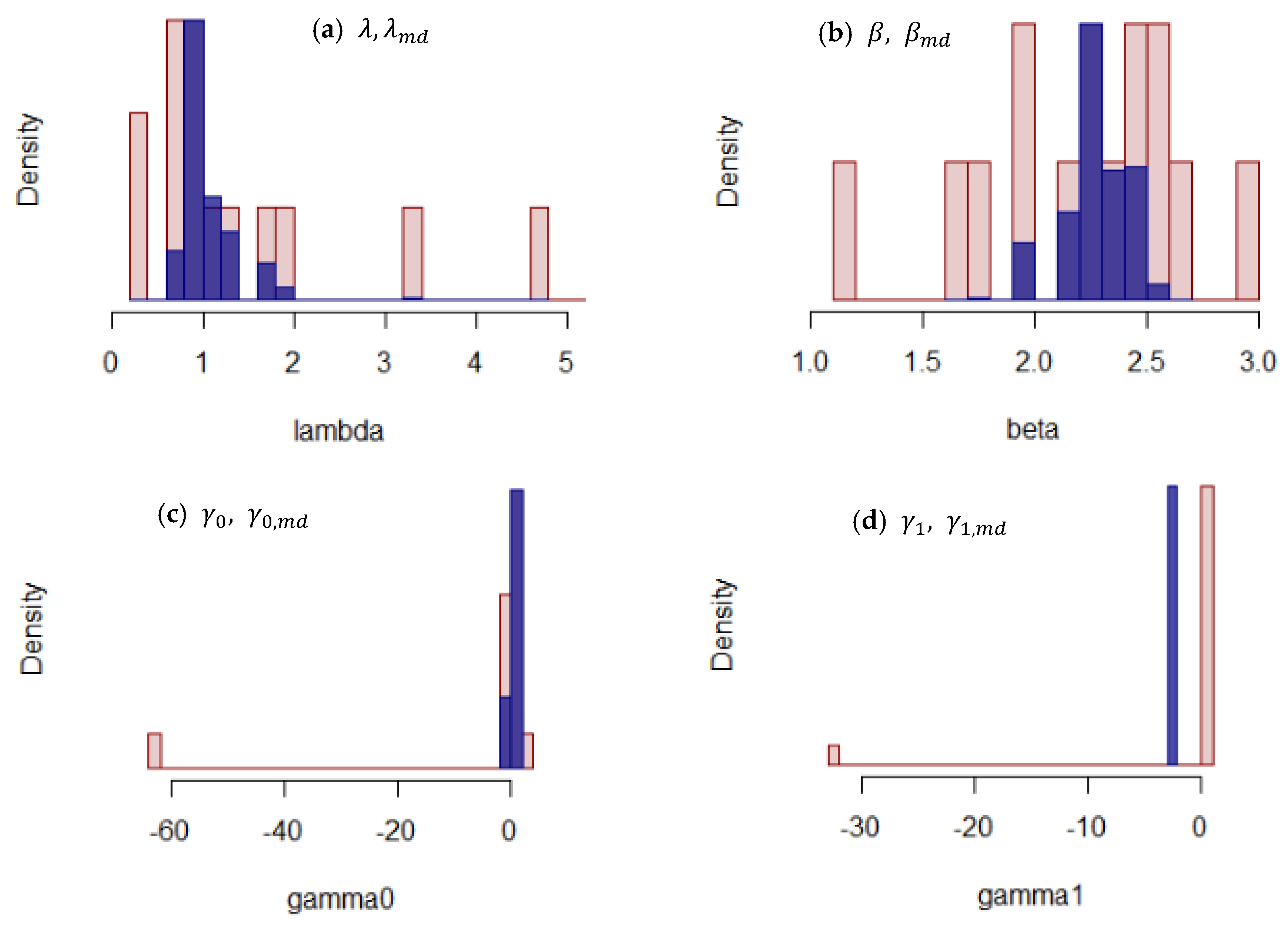
3.3.2. Bootstrap Estimation of Model Parameters
4. Discussion
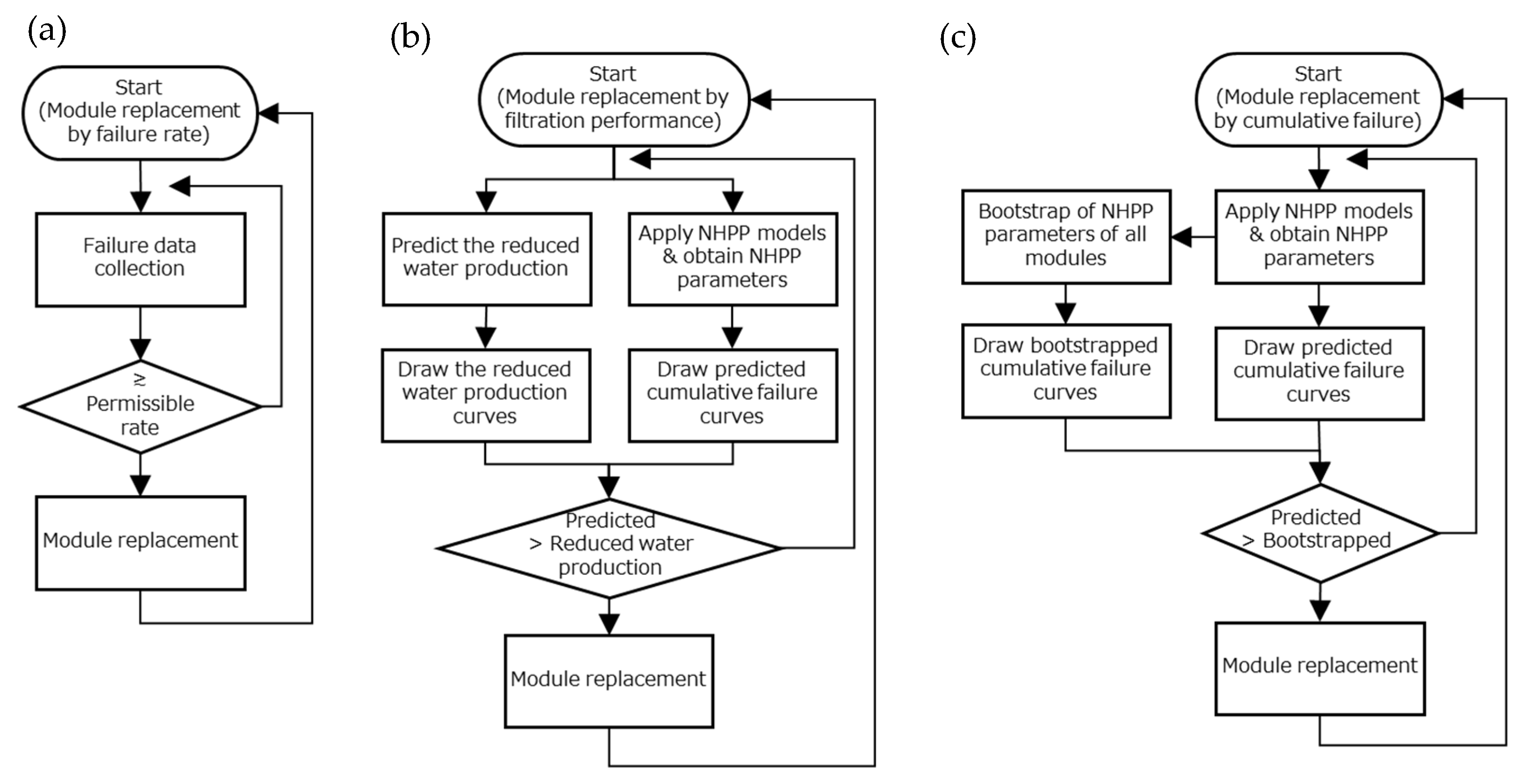
4.1. Criteria for Membrane Replacement
4.1.1. Replacement of the Membrane Module by Failure Rate
4.1.2. Replacement of the Membrane Module by Filtration Performance
4.2. Comparison between the Power Law and Log-Linear Models
4.3. Membrane Module Replacement Strategy
- (1)
- Estimate the NHPP model parameters for each module from the actual failure data, and draw the predicted cumulative failure curve from the estimated parameters of the NHPP models.
- (2)
- Obtain the bootstrapped median and its 95% confidence interval of model parameter for each module, and draw the bootstrapped cumulative failure curve with a confidence interval.
- (3)
- Compare the predicted cumulative failure curve and the bootstrapped cumulative failure curve, and select the modules to be replaced when the predicted curve is above the upper boundary of the confidence interval of the bootstrapped curve.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
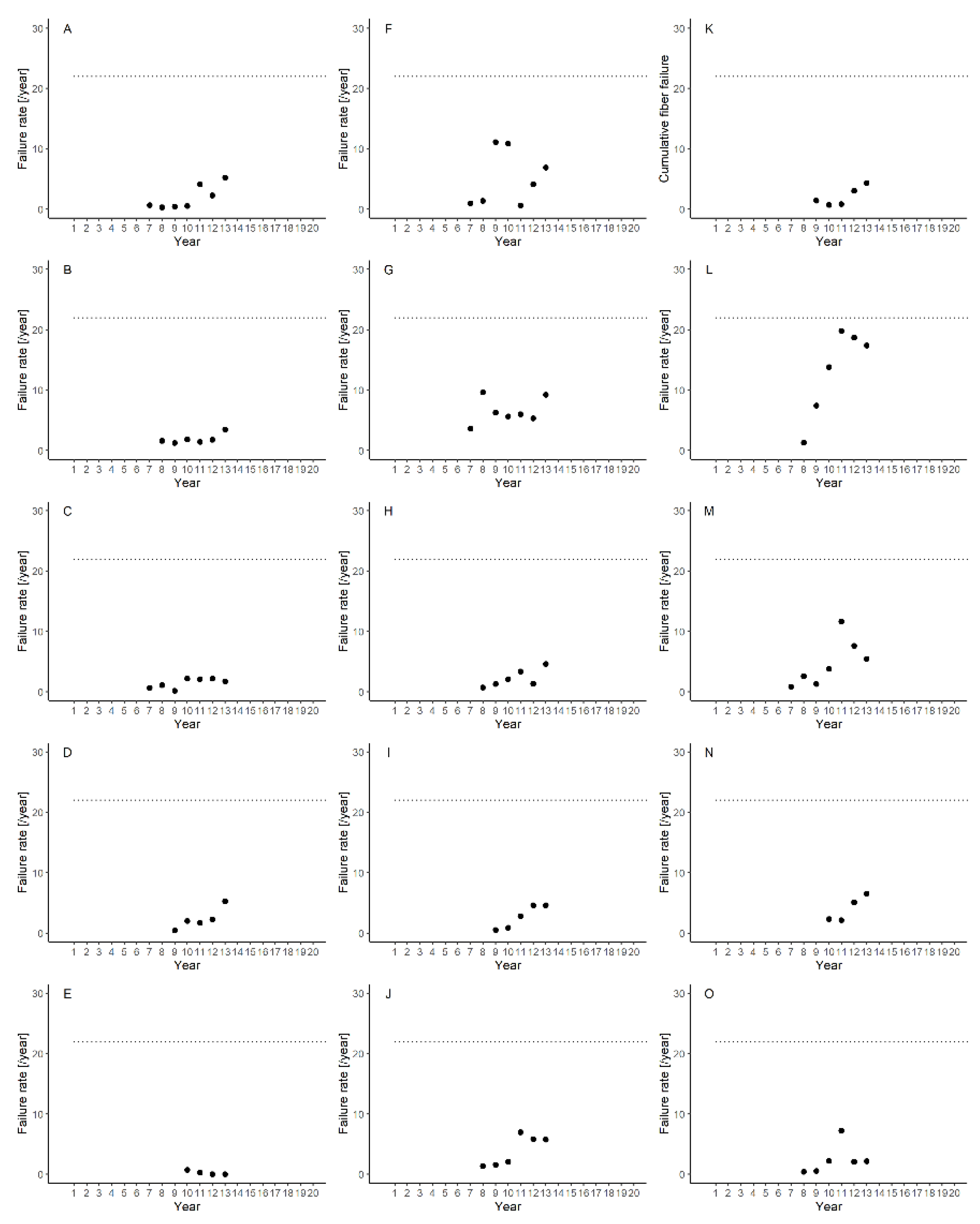
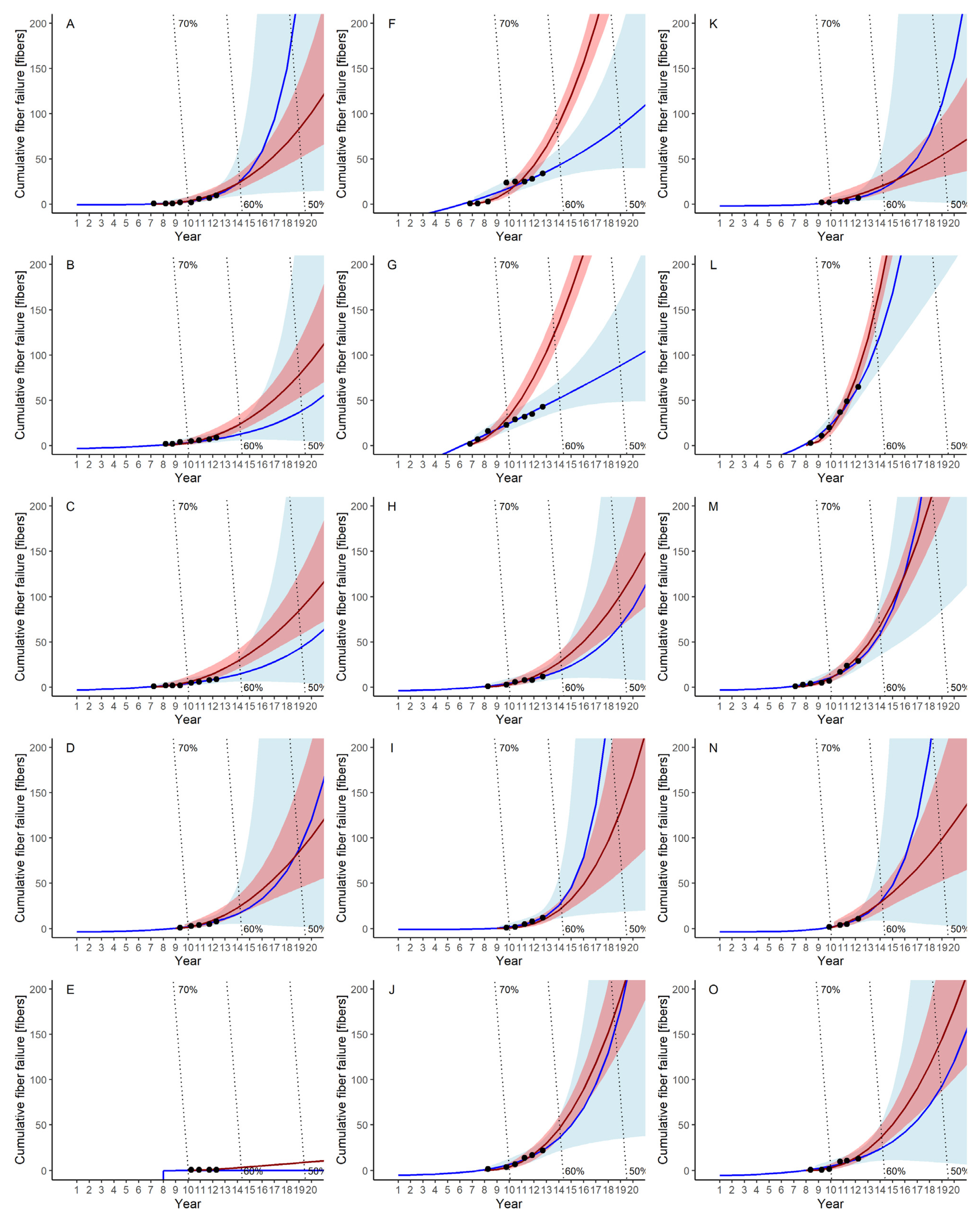
Appendix A. Failure Rate and Cumulative Failure of Each Module
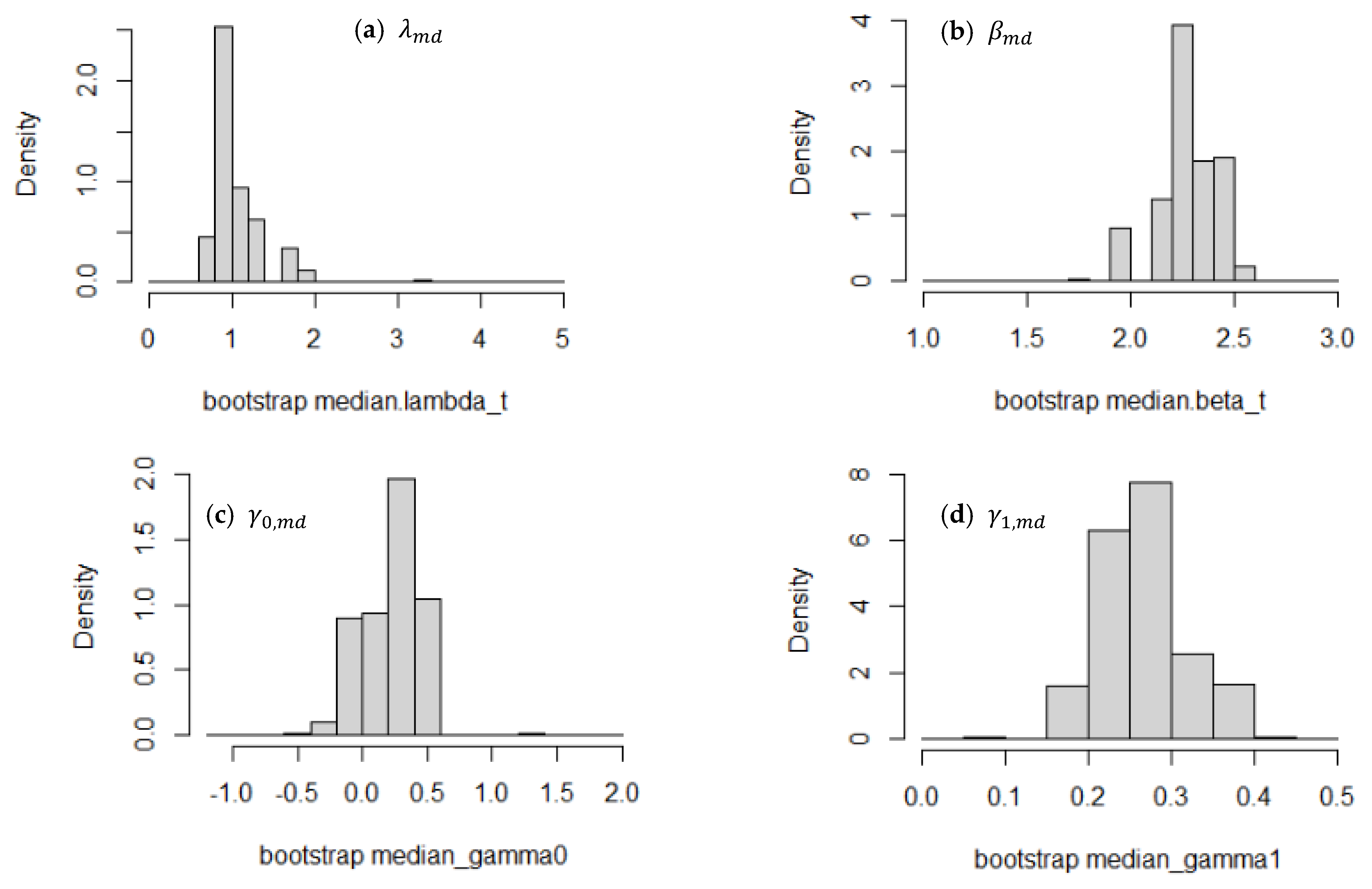
Appendix B. Distribution of Estimated Parameters

References
- Holloway, R.W.; Miller-Robbie, L.; Patel, M.; Stokes, J.R.; Munakata-Marr, J.; Dadakis, J.; Cath, T.Y. Life-cycle assessment of two potable water reuse technologies: MF/RO/UV-AOP treatment and hybrid osmotic membrane bioreactors. J. Memb. Sci. 2016, 507, 165–178. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.Y.; Yang, Z.; Guo, H.; Wen, J.J.; Nghiem, L.D.; Cornelissen, E. Potable Water Reuse through Advanced Membrane Technology. Environ. Sci. Technol. 2018, 52, 10215–10223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nunes, S.P.; Culfaz-Emecen, P.Z.; Ramon, G.Z.; Visser, T.; Koops, G.H.; Jin, W.; Ulbricht, M. Thinking the future of membranes: Perspectives for advanced and new membrane materials and manufacturing processes. J. Memb. Sci. 2020, 598, 117761. [Google Scholar] [CrossRef]
- Robinson, S.; Bérubé, P.R. Membrane ageing in full-scale water treatment plants. Water Res. 2020, 169, 115212. [Google Scholar] [CrossRef]
- Liu, C. Integrity Testing for Low-Pressure Membrane Systems; American Wter Works Association: Denver, CO, USA, 2012; ISBN 9781583217931. [Google Scholar]
- Lee, S.; Yamashita, N.; Tanaka, H. How Fiber Breakage Reduces Microorganism Removal in Ultrafiltration for Wastewater Reclamation. Food Environ. Virol. 2019, 11, 167–177. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Wyart, Y.; Perot, J.; Nauleau, F.; Moulin, P. Low-pressure membrane integrity tests for drinking water treatment: A review. Water Res. 2010, 44, 41–57. [Google Scholar] [CrossRef]
- Johnson, W.T. Automatic monitoring of membrane integrity in microfiltration systems. Desalination 1997, 113, 303–307. [Google Scholar] [CrossRef]
- Giglia, S.; Bohonak, D.; Greenhalgh, P.; Leahy, A. Measurement of pore size distribution and prediction of membrane filter virus retention using liquid-liquid porometry. J. Memb. Sci. 2015, 476, 399–409. [Google Scholar] [CrossRef]
- Panglisch, S.; Deinert, U.; Dautzenberg, W.; Kiepke, O.; Gimbel, R. Monitoring the integrity of capillary membranes by particle counters. Desalination 1998, 119, 65–72. [Google Scholar] [CrossRef]
- Naismith, J. Membrane integrity—Direct turbidity measurement of filtrate from MF membrane modules at an operating potable water treatment plant. Desalination 2005, 179, 25–30. [Google Scholar] [CrossRef]
- Krantz, W.B.; Lin, C.S.; Ching, P.; Sin, Y.; Yeo, A.; Fane, A.G. An Integrity Sensor for assessing the performance of low pressure membrane modules in the water industry. Desalination 2011, 283, 117–122. [Google Scholar] [CrossRef]
- US EPA. Membrane Filtration Guidance Manual; United States Environmental Protection Agency: Washington, DC, USA, 2005.
- Gere, A.R. Microfiltration operating costs. J. AWWA 1997, 89, 40–49. [Google Scholar] [CrossRef]
- Chellam, S.; Serra, C.A.; Wiesner, M.R. Estimating costs for integrated membrane systems: Despite greater NF fouling rates, life cycle costs for membrane facilities appear to be reduced when membranes are operated at higher permeate fluxes and feedwater recoveries. J. AWWA 1998, 90, 96–104. [Google Scholar] [CrossRef]
- Walker, T. Maintain Your Membranes to Know When To Replace Them. Opflow 2015, 41, 26–28. [Google Scholar] [CrossRef]
- O’Connell, P.M.; Winters, M. Making a Case for Membrane Replacement. Opflow 2019, 45, 18–22. [Google Scholar] [CrossRef]
- Zondervan, E.; Roffel, B. Modeling and optimization of membrane lifetime in dead-end ultra filtration. J. Memb. Sci. 2008, 322, 46–51. [Google Scholar] [CrossRef] [Green Version]
- Müller, N.; Handge, U.A.; Abetz, V. Physical ageing and lifetime prediction of polymer membranes for gas separation processes. J. Memb. Sci. 2016, 516, 33–46. [Google Scholar] [CrossRef]
- Plota, A.; Masek, A. Lifetime prediction methods for degradable polymeric materials—A short review. Materials 2020, 13, 4507. [Google Scholar] [CrossRef] [PubMed]
- Zondervan, E.; Zwijnenburg, A.; Roffel, B. Statistical analysis of data from accelerated ageing tests of PES UF membranes. J. Memb. Sci. 2007, 300, 111–116. [Google Scholar] [CrossRef]
- Gaudichet-Maurin, E.; Thominette, F. Ageing of polysulfone ultrafiltration membranes in contact with bleach solutions. J. Memb. Sci. 2006, 282, 198–204. [Google Scholar] [CrossRef]
- Pellegrin, B.; Prulho, R.; Rivaton, A.; Thérias, S.; Gardette, J.L.; Gaudichet-Maurin, E.; Causserand, C. Multi-scale analysis of hypochlorite induced PES/PVP ultrafiltration membranes degradation. J. Memb. Sci. 2013, 447, 287–296. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, S.Z.; Bérubé, P.R. Filtration and cleaning performances of PVDF membranes aged with exposure to sodium hypochlorite. Sep. Purif. Technol. 2018, 195, 253–259. [Google Scholar] [CrossRef]
- Mori, Y.; Ellingwood, B.R. Maintaining Reliability of Concrete Structures. II: Optimum Inspection/Repair. J. Struct. Eng. 1994, 120, 846–862. [Google Scholar] [CrossRef]
- Jia, G.; Gardoni, P. State-dependent stochastic models: A general stochastic framework for modeling deteriorating engineering systems considering multiple deterioration processes and their interactions. Struct. Saf. 2018, 72, 99–110. [Google Scholar] [CrossRef]
- Chen, Z. A new two-parameter lifetime distribution with bathtub shape or increasing failure rate function. Stat. Probab. Lett. 2000, 49, 155–161. [Google Scholar] [CrossRef]
- Boxall, J.B.; O’Hagan, A.; Pooladsaz, S.; Saul, A.J.; Unwin, D.M. Estimation of burst rates in water distribution mains. Proc. Inst. Civ. Eng. Water Manag. 2007, 160, 73–82. [Google Scholar] [CrossRef]
- Jiang, R.; Ji, P.; Xiao, X. Aging property of unimodal failure rate models. Reliab. Eng. Syst. Saf. 2003, 79, 113–116. [Google Scholar] [CrossRef]
- Slimacek, V.; Lindqvist, B.H. Nonhomogeneous Poisson process with nonparametric frailty. Reliab. Eng. Syst. Saf. 2016, 149, 14–23. [Google Scholar] [CrossRef]
- Mailhot, A.; Pelletier, G.; Noël, J.-F.; Villeneuve, J.-P. Modeling the evolution of the structural state of water pipe networks with brief recorded pipe break histories: Methodology and application. Water Resour. Res. 2000, 36, 3053–3062. [Google Scholar] [CrossRef]
- Wang, K.S.; Hsu, F.S.; Liu, P.P. Modeling the bathtub shape hazard rate function in terms of reliability. Reliab. Eng. Syst. Saf. 2002, 75, 397–406. [Google Scholar] [CrossRef]
- Ellingwood, B.R.; Mori, Y. Probabilistic methods for condition assessment and life prediction of concrete structures in nuclear power plants. Nucl. Eng. Des. 1993, 142, 155–166. [Google Scholar] [CrossRef]
- Crow, L.H. Evaluating the reliability of repairable systems. In Proceedings of the Annual Proceedings on Reliability and Maintainability Symposium, Los Angeles, CA, USA, 23–25 January 1990; pp. 275–279. [Google Scholar]
- Lee, L. Testing Adequacy of the Weibull and Log Linear Rate Models for a Poisson Process. Technometrics 1980, 22, 195–199. [Google Scholar] [CrossRef]
- Sonalkar, S.A.; Hao, P.; Lipscomb, G.G. Effect of Fiber Property Variation on Hollow Fiber Membrane Module Performance in the Production of a Permeate Product. Ind. Eng. Chem. Res. 2010, 49, 12074–12083. [Google Scholar] [CrossRef]
- Van Dyck, J.; Verdonck, T. Precision of power-law NHPP estimates for multiple systems with known failure rate scaling. Reliab. Eng. Syst. Saf. 2014, 126, 143–152. [Google Scholar] [CrossRef]
- Slimacek, V.; Lindqvist, B.H. Reliability of wind turbines modeled by a Poisson process with covariates, unobserved heterogeneity and seasonality. Wind Energy 2016, 19, 1991–2002. [Google Scholar] [CrossRef]
- Si, W.; Yang, Q.; Monplaisir, L.; Chen, Y. Reliability Analysis of Repairable Systems With Incomplete Failure Time Data. IEEE Trans. Reliab. 2018, 67, 1043–1059. [Google Scholar] [CrossRef]
- Muralidharan, K. Repairable System Modeling Using Power Law Process. Syst. Reliab. Manag. 2018, 79–101. [Google Scholar] [CrossRef]
- Bolker, B.; R Development Core Team; Giné-Vázquez, I. ‘bbmle’. 2020. Available online: https://cran.r-project.org/package=bbmle (accessed on 15 April 2021).
- Duane, J.T. Learning Curve Approach to Reliability Monitoring. IEEE Aerosp. Conf. Proc. 1964, 2, 563–566. [Google Scholar] [CrossRef]
- US EPA. Long Term 2 Enhanced Surface Water treatment Rule Toolbox Guidance Manual; United States Environmental Protection Agency: Washington, DC, USA, 2010.
- Cote, P.; Alam, Z.; Penny, J. Hollow fiber membrane life in membrane bioreactors (MBR). Desalination 2012, 288, 145–151. [Google Scholar] [CrossRef]
- Adham, S.; Hussain, A.; Minier-Matar, J.; Janson, A.; Sharma, R. Membrane applications and opportunities for water management in the oil & gas industry. Desalination 2018, 440, 2–17. [Google Scholar] [CrossRef]
| Operational Parameter | |
|---|---|
| Raw water | Stream water |
| Process flow | Intake → Receiving pond → Membrane filtration → Distribution pond |
| System | 3 trains (5 module/train) |
| Capacity | 350 m3/day |
| Filtration flux | 1.28 m3/m2/day |
| Membrane cleaning | Backwash: Once in 45 min (air 30 s + water 30 s) |
| Operating time | Chemical cleaning: every 6 to 9 months (acid, hypochlorite) |
| Specification | |
|---|---|
| Molecular weight cut off (MWCO) | 150,000 |
| Material | Polyacrylonitrile (PAN) |
| Filtration mode | Dead end mode (outside-in) |
| Length | ca. 1900 mm |
| Inner/outer diameter | 0.9 mm/1.25 mm |
| Number of membranes per module | ca. 5000 fibers |
| Years of Operation | Power Law Model | Log-Linear Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AIC | RMSE | AIC | RMSE | |||||||
| Failure Rate | Cumulative Failure | Failure Rate | Cumulative Failure | |||||||
| ~9 | 7.57 | 2.35 | −546 | 12.2 | 26.9 | 1.89 | 0.66 | −271 | 259.2 | 284.9 |
| ~10 | 6.58 | 2.51 | −1400 | 21.4 | 22.0 | 2.09 | 0.54 | −571 | 117.5 | 123.9 |
| ~11 | 5.68 | 2.64 | −2970 | 28.0 | 25.1 | 2.25 | 0.46 | −1038 | 69.3 | 66.8 |
| ~12 | 5.59 | 2.66 | −5248 | 28.4 | 25.5 | 2.58 | 0.33 | −1446 | 24.5 | 15.6 |
| ~13 | 5.57 | 2.66 | −8427 | 28.5 | 25.5 | 2.75 | 0.27 | −1977 | 13.4 | 11.2 |
| Module | Power Law Model | Log-Linear Model | ||||
|---|---|---|---|---|---|---|
| AIC | AIC | |||||
| A | 0.36 | 2.53 | −37.9 | −1.07 | 0.46 | 11.5 |
| B | 0.64 | 2.28 | −42.1 | −0.13 | 0.18 | 11.4 |
| C | 0.85 | 2.12 | −38.6 | −0.13 | 0.18 | 14.2 |
| D | 1.74 | 1.96 | −20.3 | 0.22 | 0.30 | 8.5 |
| E | 0.74 | 1.19 | − | −62.9 | −32.2 | 85.5 |
| F | 1.36 | 2.47 | −496.4 | 1.39 | 0.07 | −38.4 |
| G | 4.64 | 1.97 | −716.1 | 1.83 | 0.01 | −67.8 |
| H | 0.78 | 2.34 | −56.9 | 0.15 | 0.23 | 5.5 |
| I | 0.33 | 2.97 | −44.9 | −0.46 | 0.55 | −1.7 |
| J | 0.95 | 2.55 | −163.8 | 0.53 | 0.30 | −21.7 |
| K | 1.90 | 1.62 | −8.2 | −0.21 | 0.37 | 9.4 |
| L | 6.38 | 2.24 | −964.1 | 2.00 | 0.27 | −202.9 |
| M | 0.85 | 2.61 | −313.6 | 0.31 | 0.36 | −34.0 |
| N | 3.36 | 1.73 | −33.7 | 0.57 | 0.45 | 1.5 |
| O | 1.01 | 2.41 | −88.0 | 0.48 | 0.24 | 5.0 |
| Average | 1.73 | 2.20 | −3.83 | −1.88 | ||
| Median | 0.95 | 2.28 | 0.22 | 0.27 | ||
| Bootstrapped median (2.5%, 97.5%) | 0.95 (0.78, 1.90) | 2.28 (1.97, 2.47) | - | 0.26 (−0.21, 0.57) | 0.20 (0.18, 0.36) | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hashimoto, T.; Takizawa, S. Prediction of Membrane Failure in a Water Purification Plant Using Nonhomogeneous Poisson Process Models. Membranes 2021, 11, 800. https://doi.org/10.3390/membranes11110800
Hashimoto T, Takizawa S. Prediction of Membrane Failure in a Water Purification Plant Using Nonhomogeneous Poisson Process Models. Membranes. 2021; 11(11):800. https://doi.org/10.3390/membranes11110800
Chicago/Turabian StyleHashimoto, Takashi, and Satoshi Takizawa. 2021. "Prediction of Membrane Failure in a Water Purification Plant Using Nonhomogeneous Poisson Process Models" Membranes 11, no. 11: 800. https://doi.org/10.3390/membranes11110800
APA StyleHashimoto, T., & Takizawa, S. (2021). Prediction of Membrane Failure in a Water Purification Plant Using Nonhomogeneous Poisson Process Models. Membranes, 11(11), 800. https://doi.org/10.3390/membranes11110800








