Reasons for the Formation and Properties of Soliton-Like Charge Waves in Membrane Systems When Using Overlimiting Current Modes
Abstract
1. Introduction
2. Materials and Methods
Mathematical Model of One-Dimensional Non-Stationary Ion Transport in Membrane Systems
3. Results
3.1. Reasons for the Formation of a Local Maximum (Minimum) Space Charge in the Extended Space Charge Region (Extended SCR)
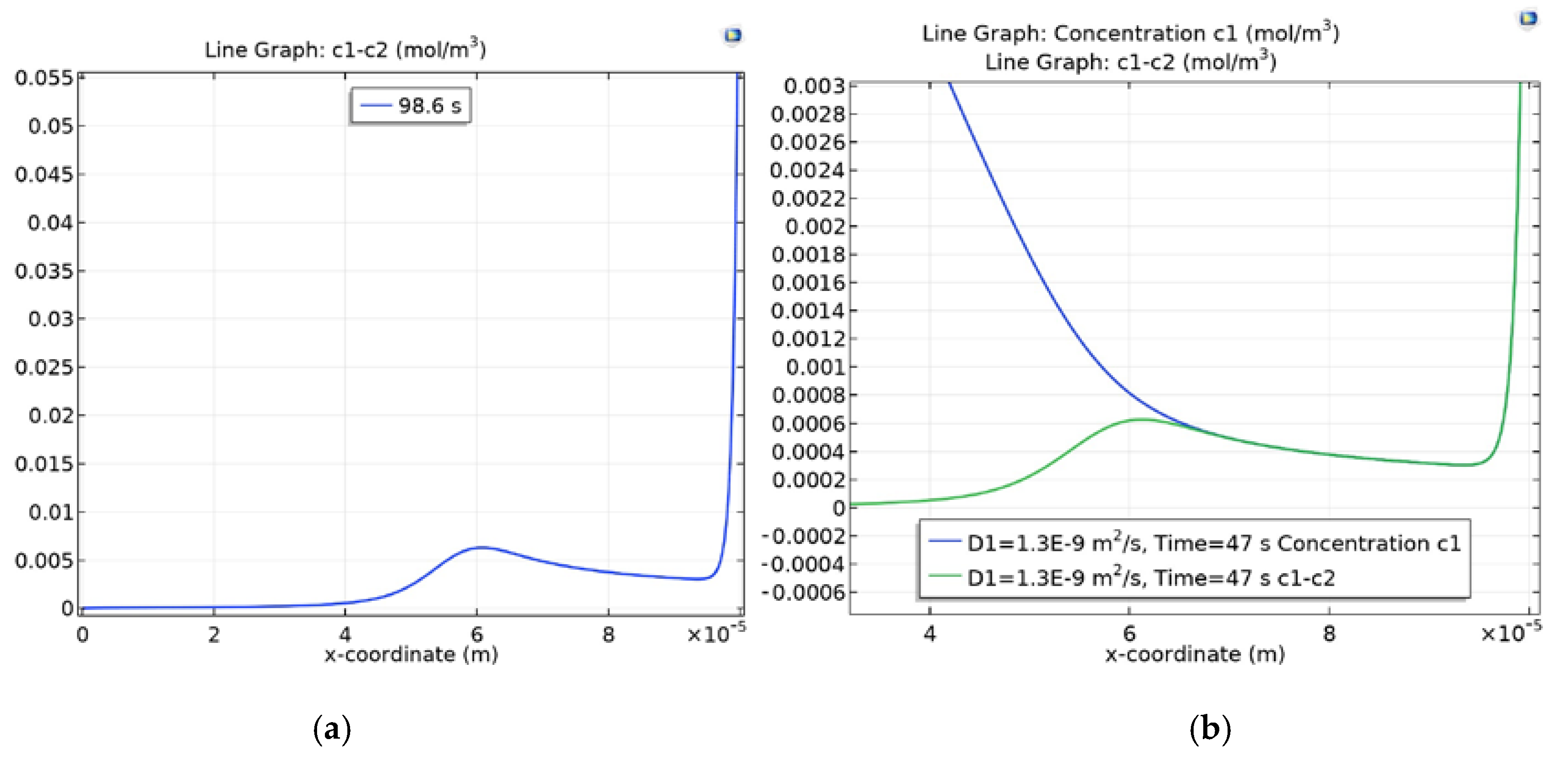
3.2. Dependence of the Local Maximum in the Diffusion Layer on the Boundary Concentration of
3.3. Soliton-like Charge Wave. Dependence of the Local Maximum (Minimum) Charge on the Growth Rate of the Potential Jump
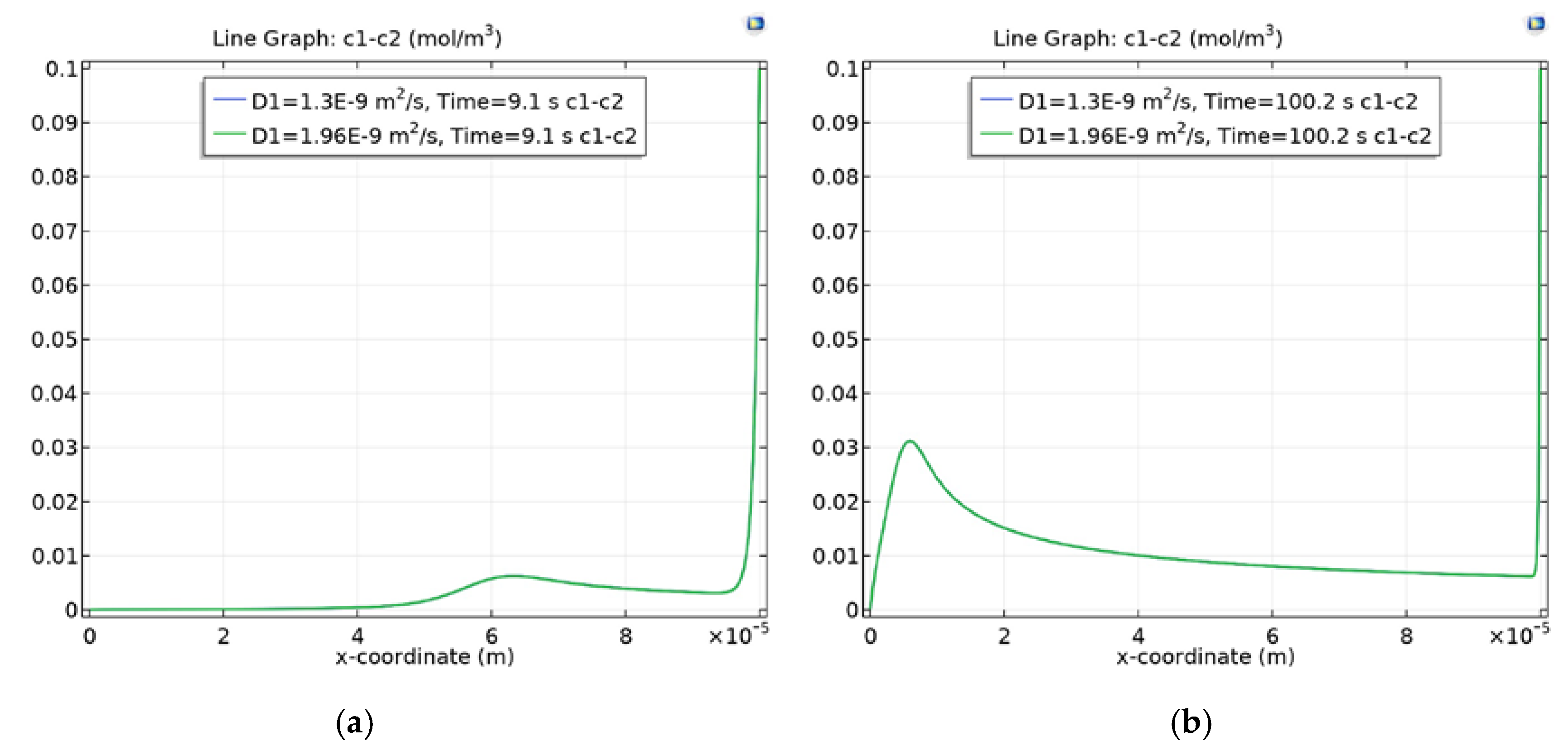
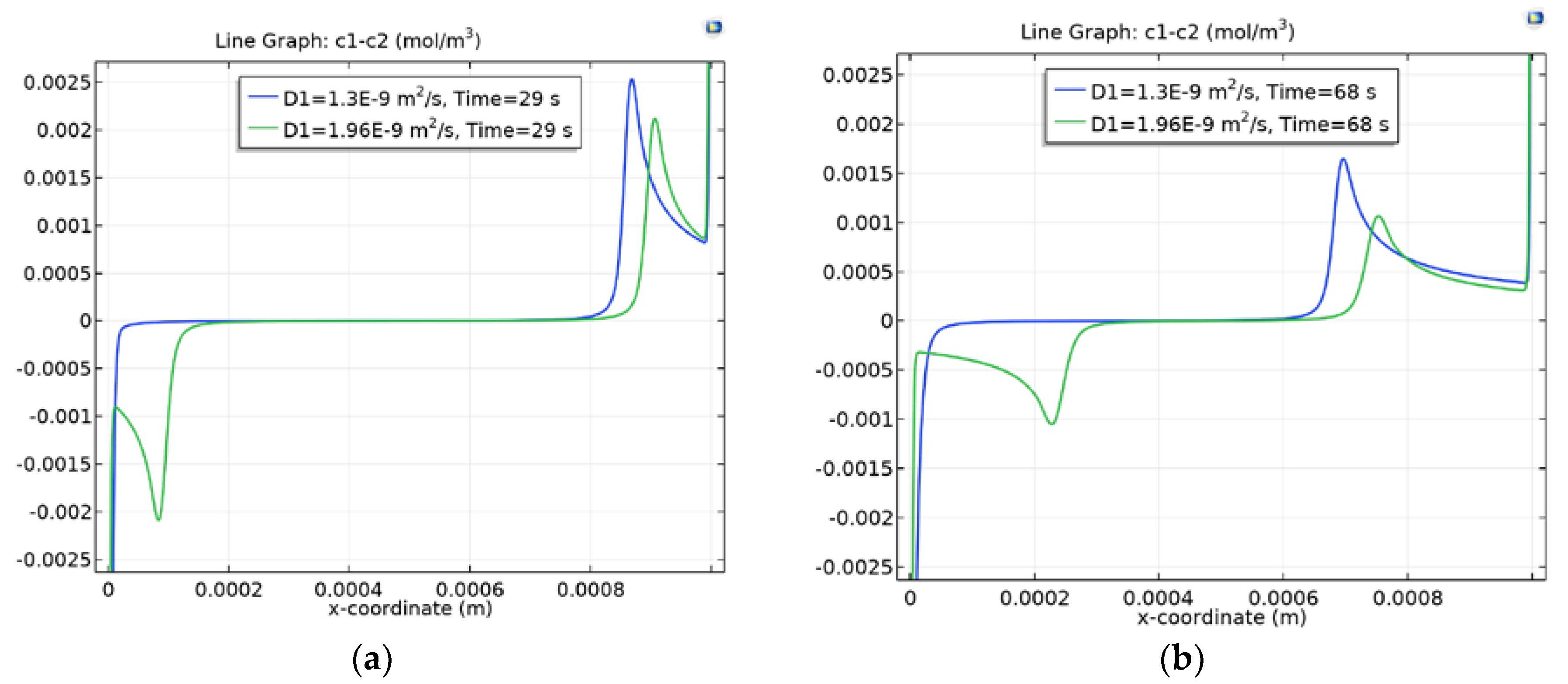
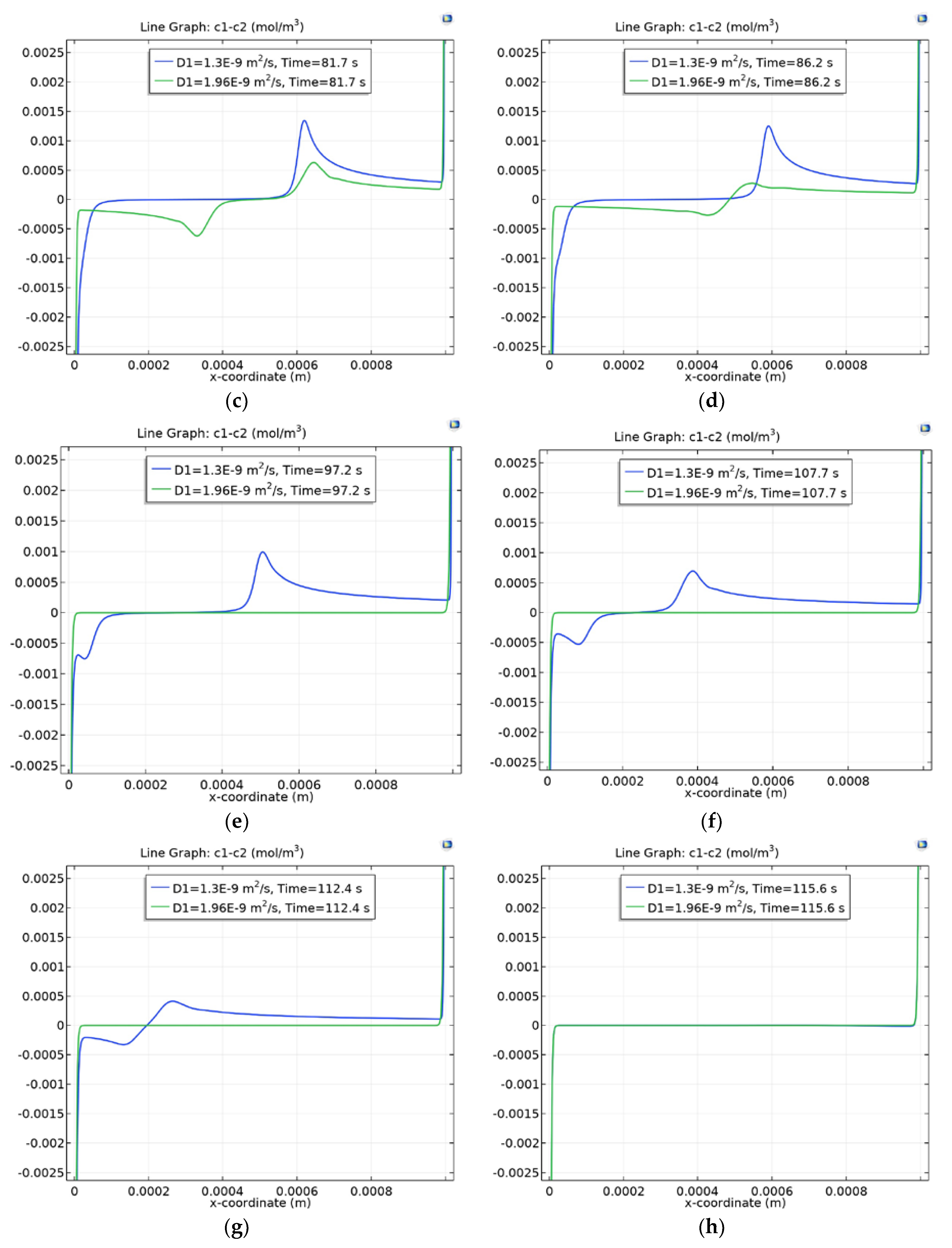
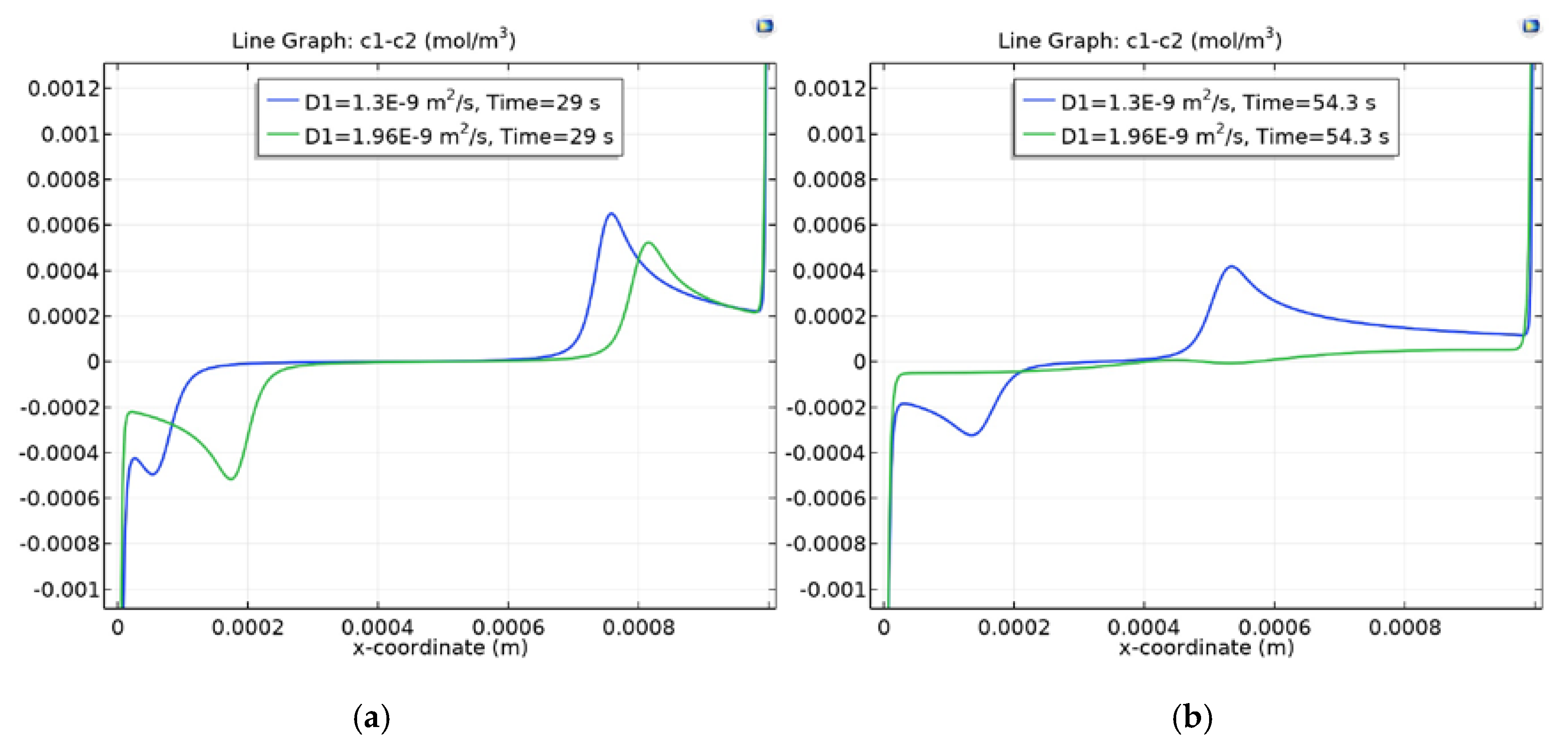
3.4. Dependence of Charge Waves on the Cation Diffusion Coefficient
3.4.1. Diffusion Layer
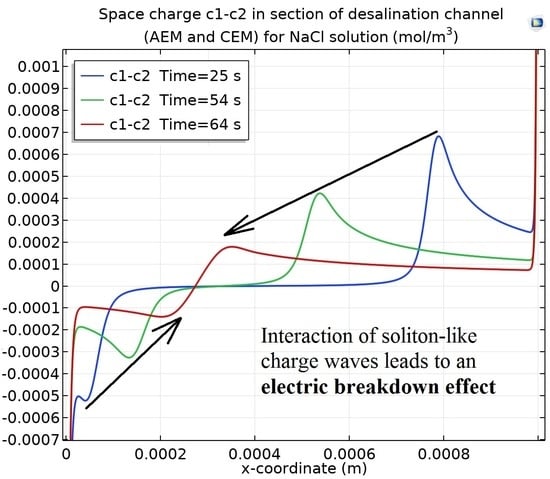
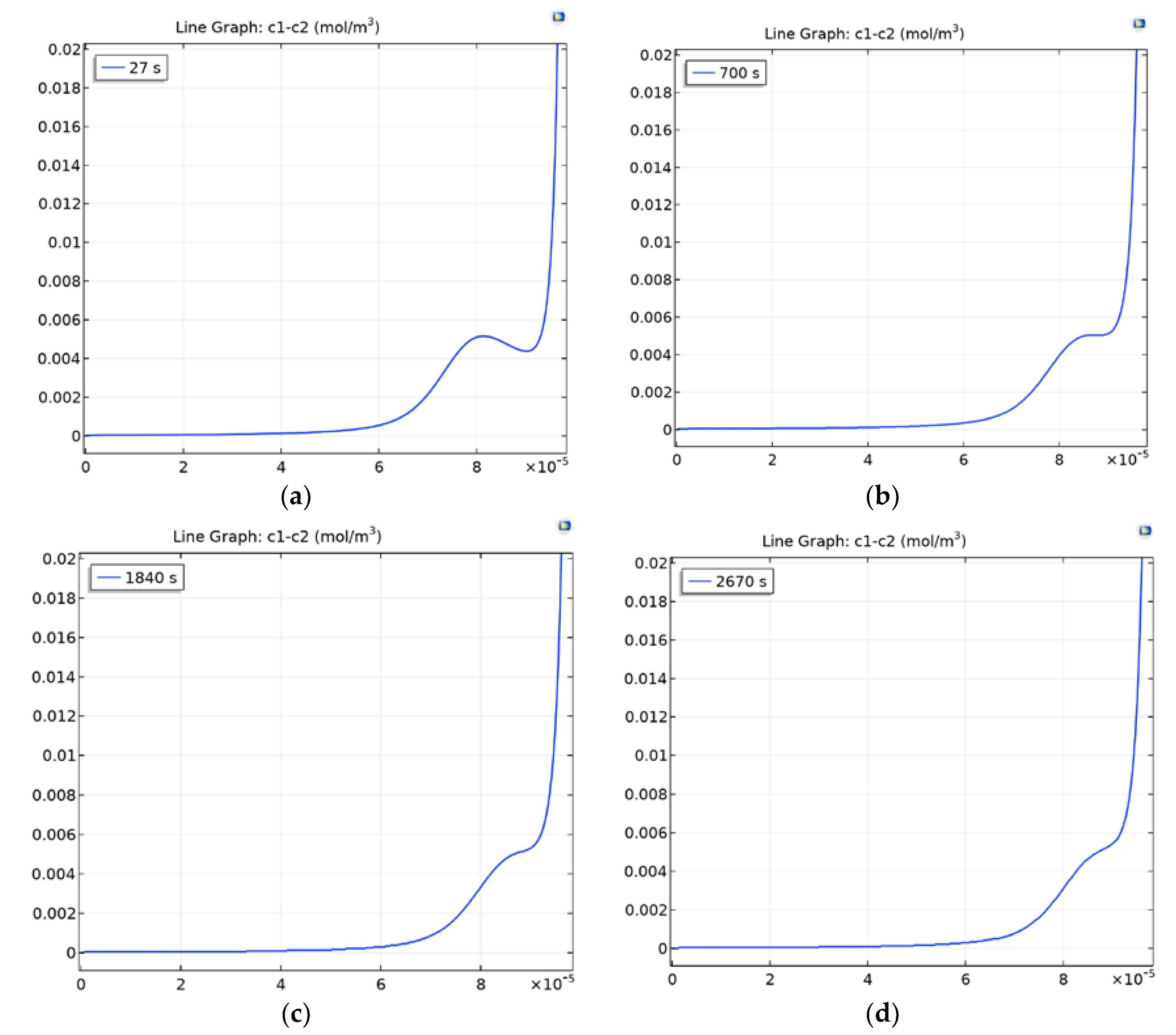
3.4.2. Section of the Desalination Channel
3.5. Dependence of Charge Waves on the Initial Concentration of
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tabani, H.; Khodaei, K.; Varanusupakul, P.; Alexovič, M. Gel electromembrane extraction: Study of various gel types and compositions toward diminishing the electroendosmosis flow. Microchem. J. 2020, 153, 104520. [Google Scholar] [CrossRef]
- Rubinshtein, I.; Zaltzman, B.; Prez, J.; Linder, C. Experimental verification of the electroosmotic mechanism for the formation of overlimiting current in a system with a cation-exchange electrodialysis membrane. Electrochemistry 2002, 38, 956–967. [Google Scholar]
- Nikonenko, V.; Kovalenko, A.V.; Urtenov, M.K.; Pismenskaya, N.D.; Han, J.; Sistat, P.; Pourcelly, G. Desalination at overlimiting currents: State-of-the-art and perspectives. Desalination 2014, 342, 85–106. [Google Scholar] [CrossRef]
- Urtenov, M.K.; Uzdenova, A.M.; Kovalenko, A.V.; Nikonenko, V.V.; Pismenskaya, N.D.; Vasil’eva, V.I.; Sistat, P.; Pourcelly, G. Basic mathematical model of overlimiting transfer enhanced by electroconvection in flow-through electrodialysis membrane cells. J. Membr. Sci. 2013, 447, 190. [Google Scholar] [CrossRef]
- Vasilieva, V.I.; Zhiltsova, A.V.; Malykhin, M.D.; Zabolotsky, V.I.; Lebedev, K.A.; Chermit, R.H.; Sharafan, M.V. Influence of the chemical nature of ionogenic groups of ion-exchange membranes on the size of the region of electroconvective instability in high-intensity current modes. Electrochemistry 2014, 50, 134. [Google Scholar]
- Vasilieva, V.I.; Shaposhnik, V.A.; Zabolotsky, V.I.; Lebedev, K.A.; Petrunya, I.P. Diffusive boundary layers at the ion exchange membrane/solution boundary under high-intensity electrodialysis regimes. Sorpt. Chromatogr. Process. 2005, 5, 111–127. [Google Scholar]
- Pismenskaya, N.D.; Nikonenko, V.V.; Belova, E.I.; Lopatkova, G.Y.; Sista, F.; Purseli, Z.; Larshe, K. Conjugate convection of a solution at the surface of ion-exchange membranes under intense current conditions. Electrochemistry 2007, 43, 325–343. [Google Scholar]
- Rubinstein, I.; Shtilman, L. Voltage against current curves of cation exchange membranes. J. Chem. Soc. Faraday Trans. 1979, 75, 231–246. [Google Scholar] [CrossRef]
- Urtenov, M.K.; Nikonenko, V.V. Analysis of electrodiffusion equations in decomposition form. Electrochemistry 1996, 32, 207–214. [Google Scholar]
- Nikonenko, V.V.; Zabolotsky, V.I.; Gnusin, N.P. Electric transfer of ions through a diffusive layer with disturbed electroneutrality. Electrochemistry 1989, 25, 301–306. [Google Scholar]
- Listovnichy, A.V. Concentration polarization of the ionite membrane-electrolyte solution system in the overlimiting mode. Electrochemistry 1991, 27, 316–323. [Google Scholar]
- Urtenov, M.A.K.; Nikonenko, V.V. Analysis of solutions for the boundary value problem for the Nernst-Planck-Poisson equations: The 1:1 electrolyte Case. Electrochemistry 1993, 29, 239–245. [Google Scholar]
- Zabolotsky, V.I.; Manzanares, H.A.; Mafe, S.; Nikonenko, V.V.; Lebedev, K.A. Accounting for electroneutrality violations in mathematical modeling of stationary ion transport through a three-layer membrane system. Electrochemistry 2002, 38, 921–929. [Google Scholar]
- Zabolotsky, V.I.; Manzanares, J.A.; Mafe, S.; Nikonenko, V.V.; Lebedev, K.A. Mathematical simulation of a stationary electrodiffusion kinetics in multilayer ion-exchange membrane systems with the help of the numerical shooting parallel method continued by parameters. Desalination 2002, 147, 387–392. [Google Scholar] [CrossRef]
- Manzanares, J.A.; Murphy, W.D.; Mafe, S.; Reiss, H. Numerical simulation of the non-equilibrium diffuse double layer in ion-exchange membranes. J. Phys. Chem. 1993, 97, 8524–8530. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V. Electrodialysis of dilute solutions of electrolytes. Some theoretical and applied aspects. Electrochemistry 1996, 32, 246–254. [Google Scholar]
- Urtenov, M.A.K.; Kirillova, E.V.; Seidova, N.M.; Nikonenko, V.V. Decoupling of the Nernst–Planck and Poisson Equations. Application to a Membrane System at Overlimiting Currents. J. Phys. Chem. 2007, 111, 14208–14222. [Google Scholar] [CrossRef] [PubMed]
- Uzdenova, A.; Kovalenko, A.V.; Urtenov, M.; Nikonenko, V. 1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode. Membranes 2018, 8, 84. [Google Scholar] [CrossRef] [PubMed]
- Deng, D.; Aouad, W.; Braff, W.A.; Schlumpberger, S.; Suss, M.E.; Bazant, M.Z. Water purification by shock electrodialysis: Deionization, filtration, separation, and disinfection. Desalination 2015, 357, 77–83. [Google Scholar] [CrossRef]
- Mani, A.; Bazant, M.Z. Deionization shocks in microstructures. Phys. Rev. E 2011, 84, 061504. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urtenov, M.; Chubyr, N.; Gudza, V. Reasons for the Formation and Properties of Soliton-Like Charge Waves in Membrane Systems When Using Overlimiting Current Modes. Membranes 2020, 10, 189. https://doi.org/10.3390/membranes10080189
Urtenov M, Chubyr N, Gudza V. Reasons for the Formation and Properties of Soliton-Like Charge Waves in Membrane Systems When Using Overlimiting Current Modes. Membranes. 2020; 10(8):189. https://doi.org/10.3390/membranes10080189
Chicago/Turabian StyleUrtenov, Makhamet, Natalia Chubyr, and Vitaly Gudza. 2020. "Reasons for the Formation and Properties of Soliton-Like Charge Waves in Membrane Systems When Using Overlimiting Current Modes" Membranes 10, no. 8: 189. https://doi.org/10.3390/membranes10080189
APA StyleUrtenov, M., Chubyr, N., & Gudza, V. (2020). Reasons for the Formation and Properties of Soliton-Like Charge Waves in Membrane Systems When Using Overlimiting Current Modes. Membranes, 10(8), 189. https://doi.org/10.3390/membranes10080189