Potentiodynamic and Galvanodynamic Regimes of Mass Transfer in Flow-Through Electrodialysis Membrane Systems: Numerical Simulation of Electroconvection and Current-Voltage Curve
Abstract
1. Introduction
- (1)
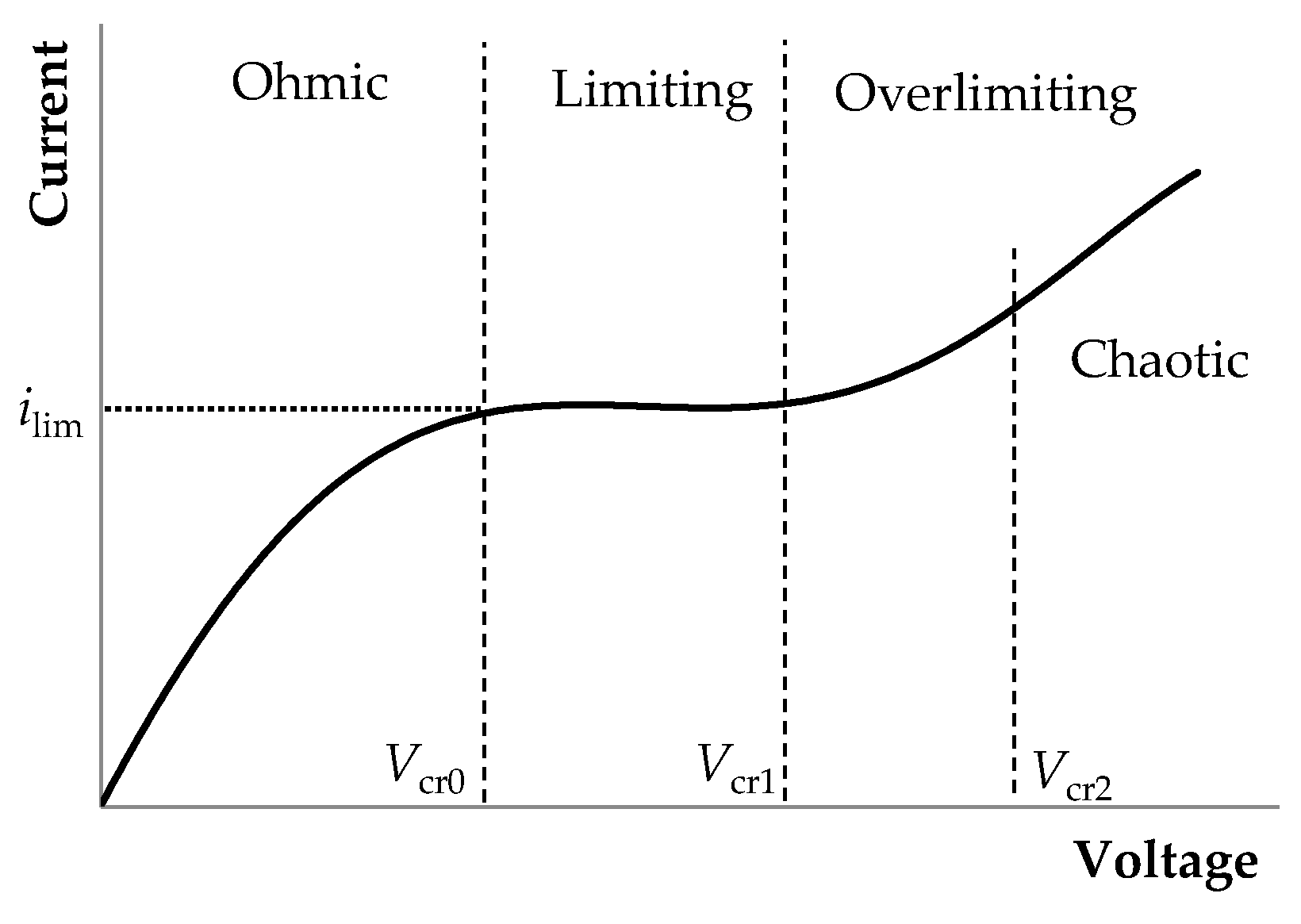
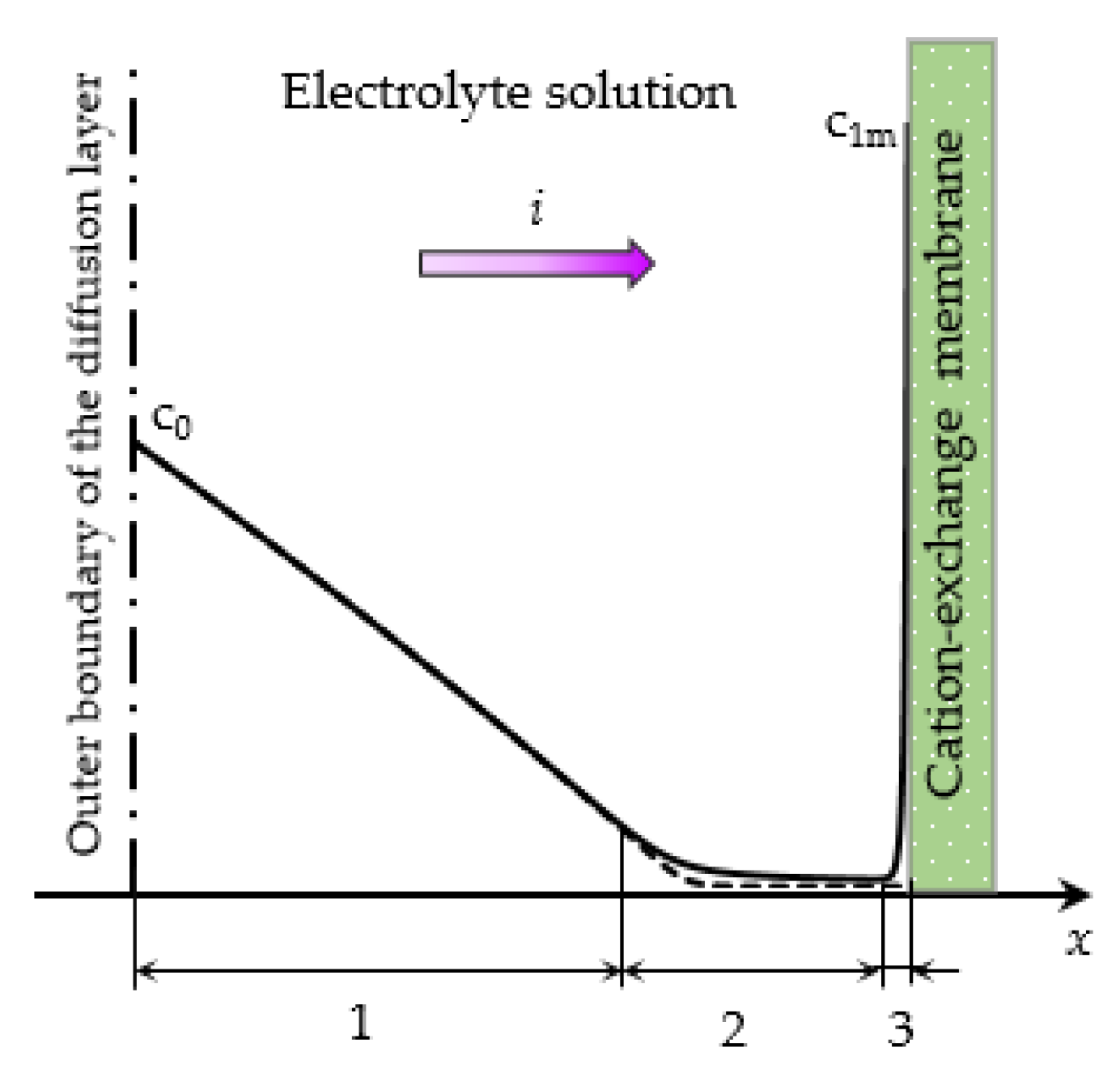
- The underlimiting current (ohmic behavior) is the initial linear region of the CVC, which is characterized by a rather high concentration of ions in the region near the membrane. When an electric current flows through the ion-exchange membrane, the ion concentration decreases on one side of the membrane and increases on the other due to the selective transfer of counterions in the membrane (ion concentration polarization). With the increase in the potential drop, almost complete depletion of ions in the region at the membrane surface in the channel of desalination and the transition of the system to the limiting state are observed [20,21].
- (2)
- (3)
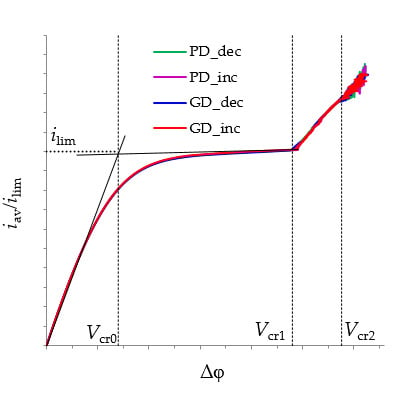
- The overlimiting current is the region of secondary current growth: with a further increase in the applied potential drop, the current takes on values greater than the limiting. The increase in the electric current essentially indicates an increase in the conductivity of the depleted region. For dilute electrolyte solutions, electroconvection is the main process that partially destroys the depleted region [7,8,9,10,11,12,13,14,15,16,17,18,19]. Electroconvection is the entrainment of liquid molecules by ions that form a space charge at the ion-selective surface under the influence of the electric force [24]. The intensity of electroconvection increases significantly with the passage of the overlimiting current when an extended macroscopic space charge region (SCR) is formed at the interface due to the polarization of the electric double layer (EDL) (Figure 2 and Figure 3).
2. Mathematical Models
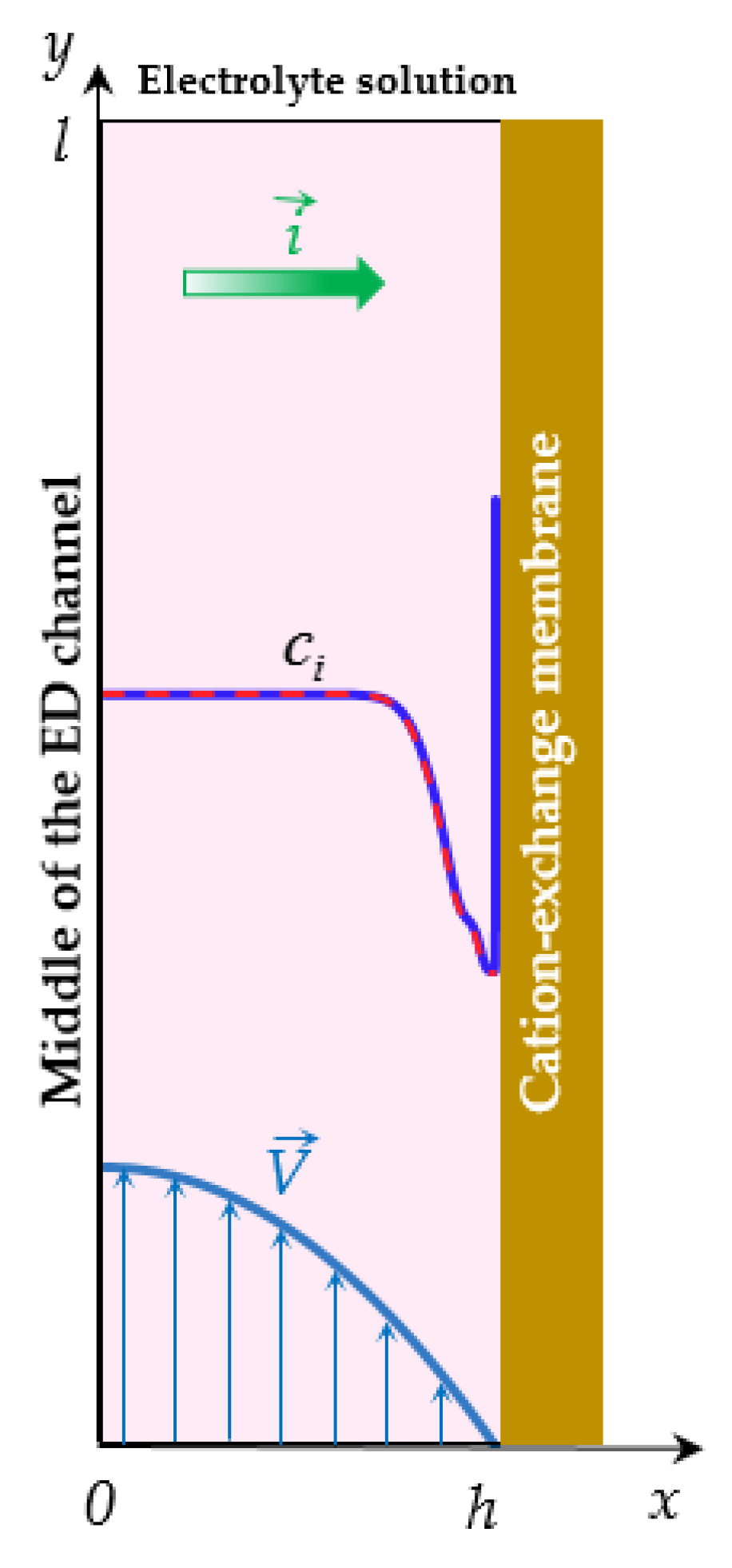
2.1. Formulation for the PD Regime
2.2. Formulation for the GD Regime
2.3. Numerucal Implementation
3. Results
3.1. Parameters Used in Computations
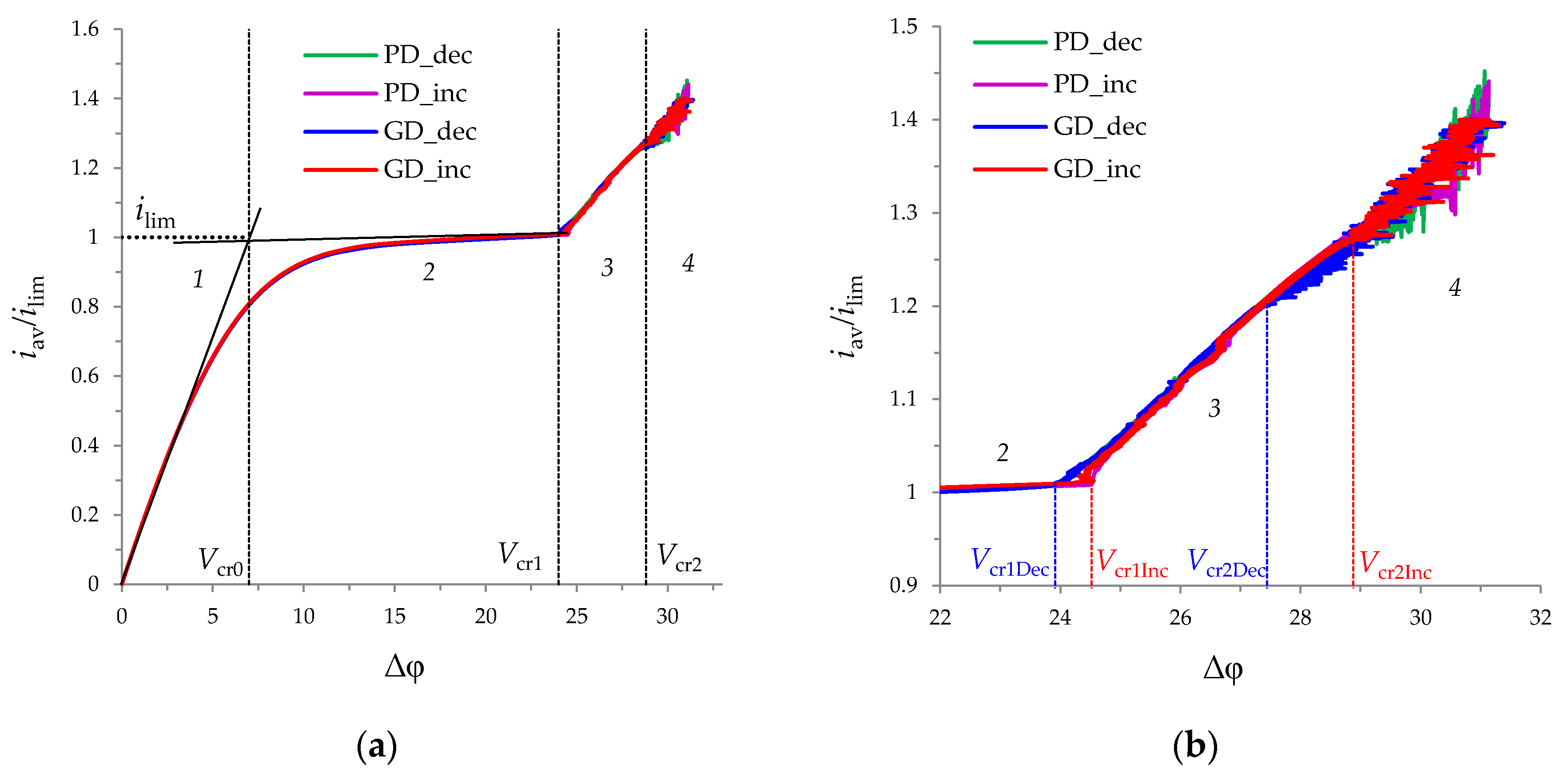
3.2. Current-Voltage Curves
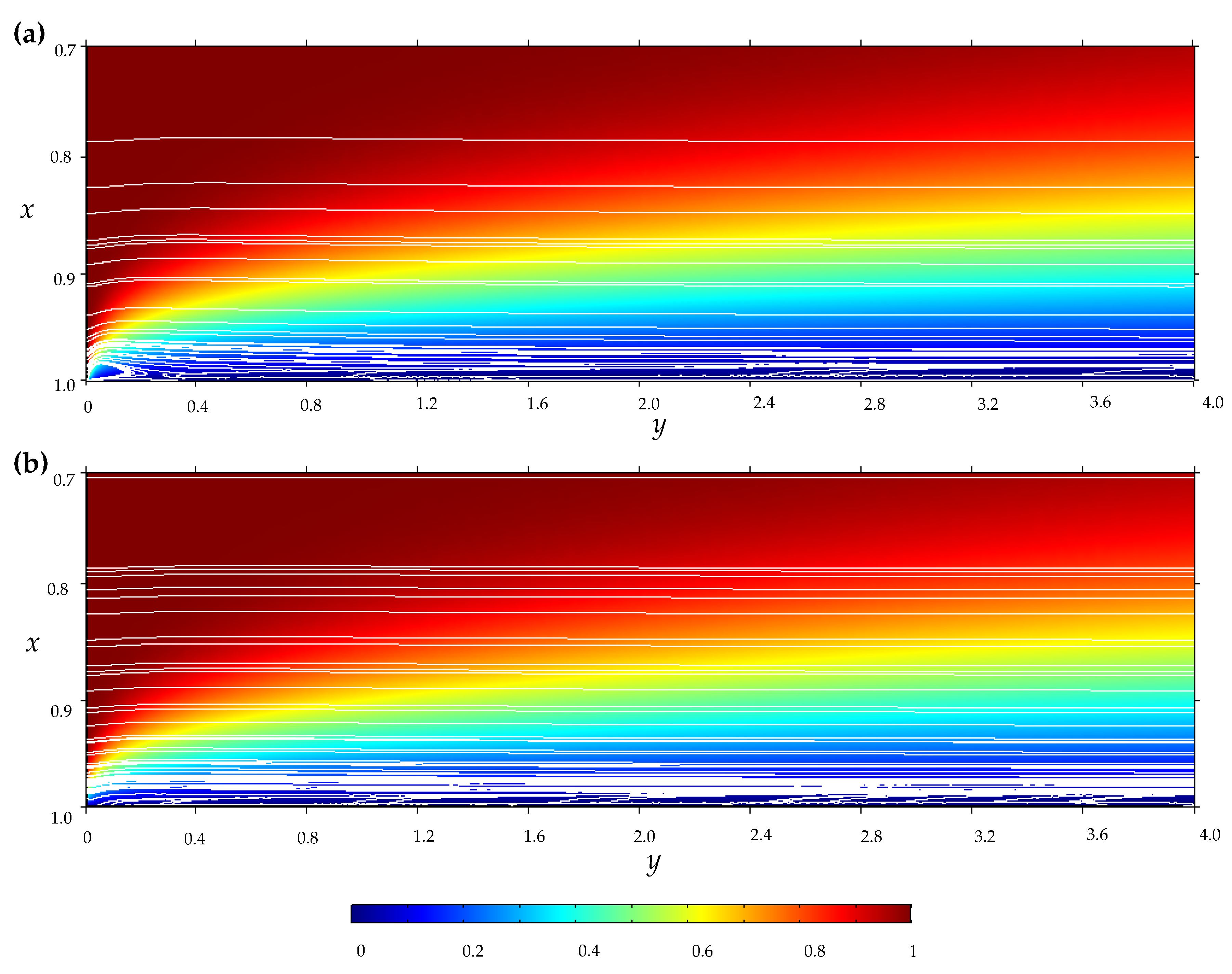
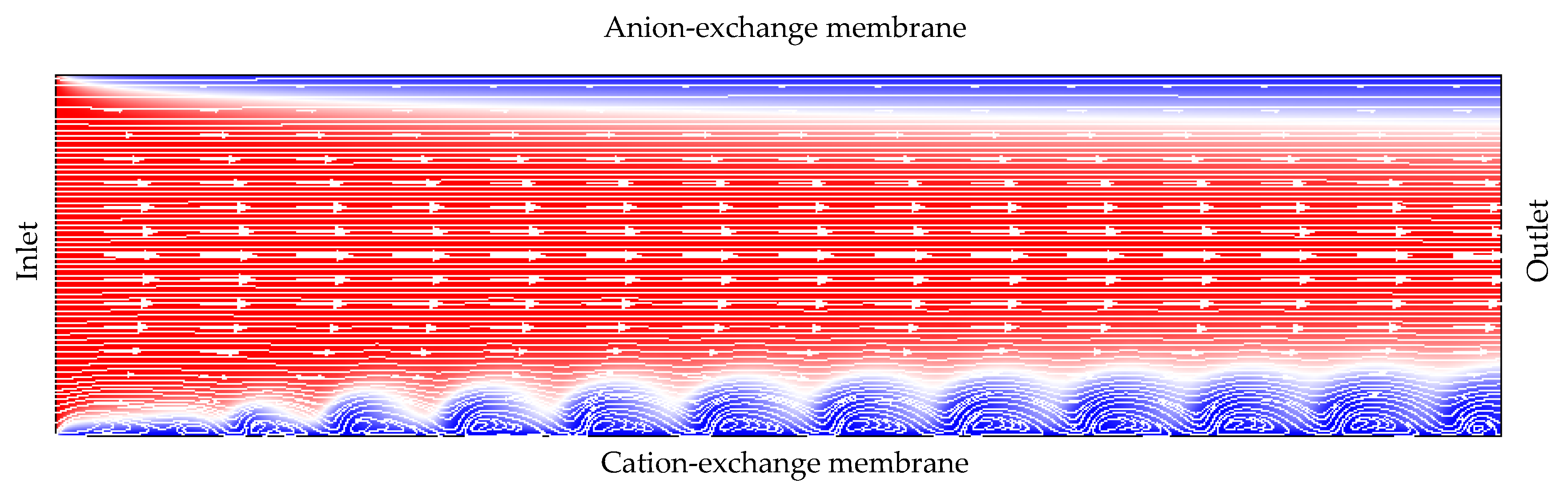
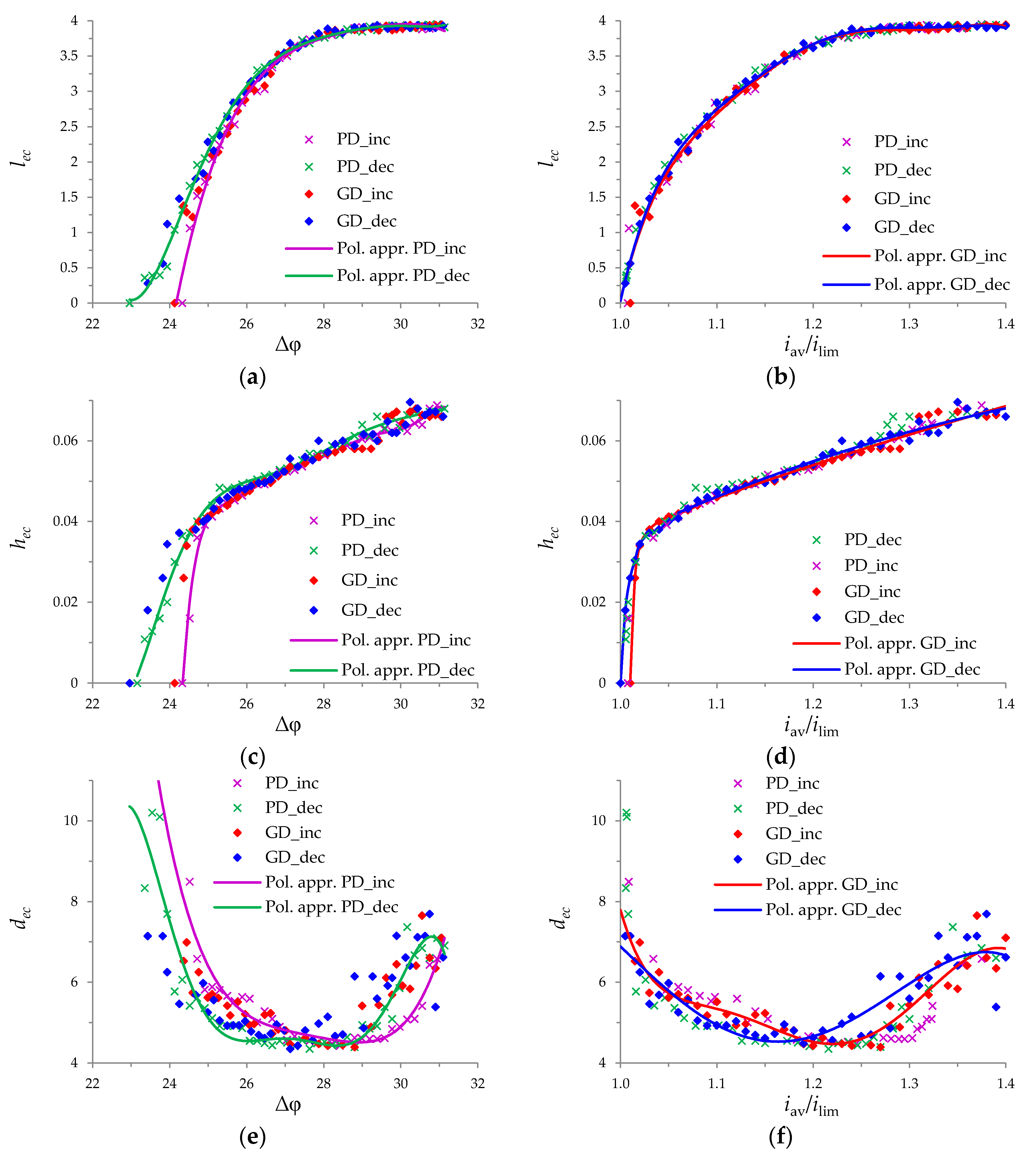
3.3. Electroconvective Vortex Layer
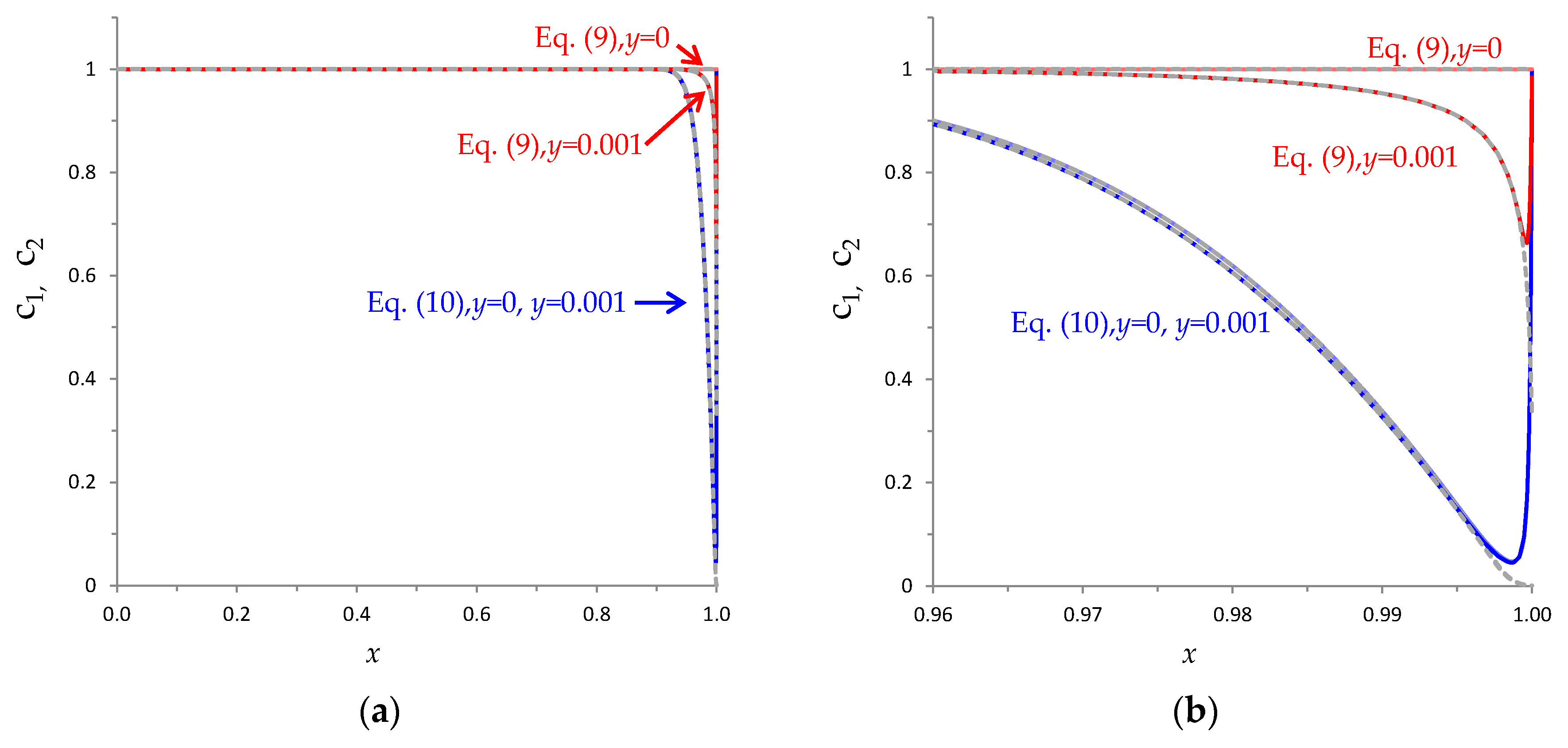
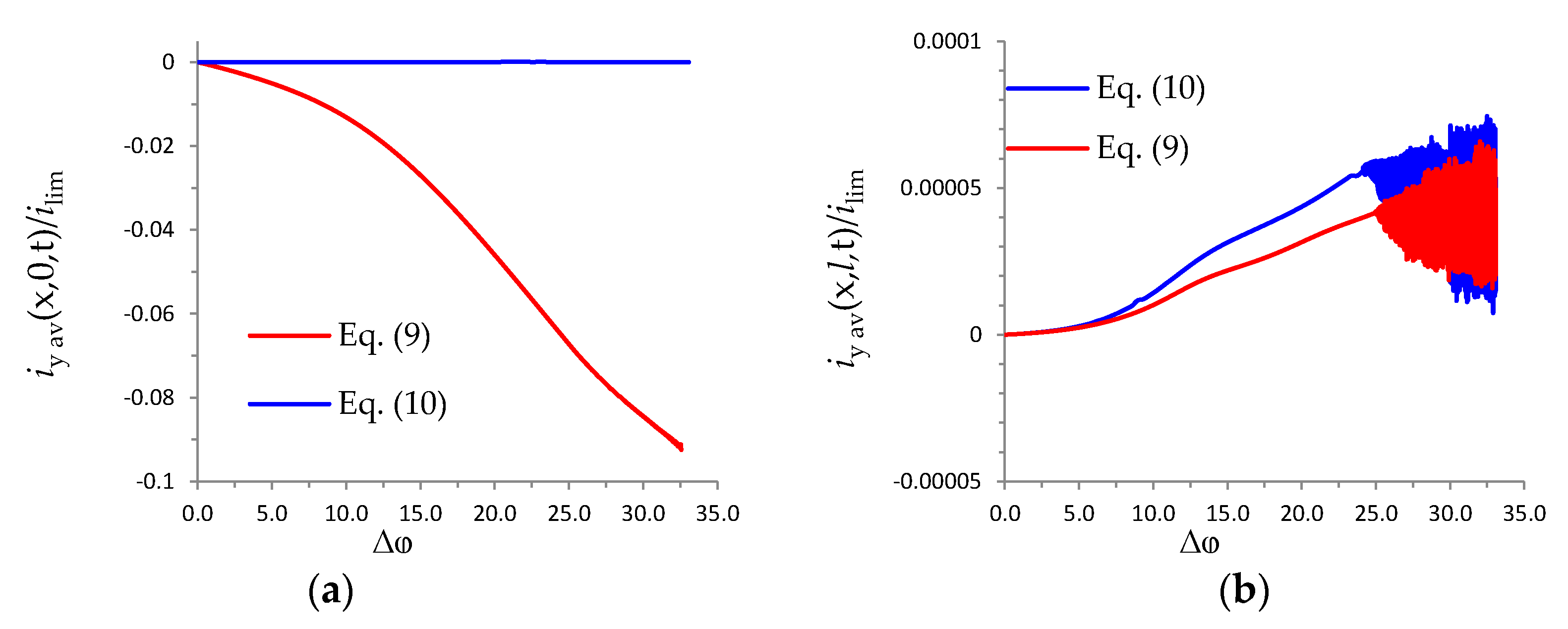
3.4. Comparison of Increasing and Decreasing Regimes (Hysteretic Behavior)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Shannon, M.A.; Bohn, P.W.; Elimelech, M.; Georgiadis, J.G.; Mariñas, B.J.; Mayes, A.M. Science and technology for water purification in the coming decades. Nature 2008, 452, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-J.; Ko, S.-H.; Kang, K.H.; Han, J. Direct seawater desalination by ion concentration polarization. Nature Nanotechnol. 2010, 5, 297–301. [Google Scholar] [CrossRef] [PubMed]
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268. [Google Scholar] [CrossRef]
- Elimelech, M.; Phillip, W.A. The Future of Seawater Desalination: Energy, Technology, and the Environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef] [PubMed]
- Belova, E.I.; Lopatkova, G.Y.u.; Pismenskaya, N.D.; Nikonenko, V.V.; Larchet, C.; Pourcelly, G. The effect of anion-exchange membrane surface properties on mechanisms of overlimiting mass transfer. J. Phys. Chem. B 2006, 110, 13458. [Google Scholar] [CrossRef] [PubMed]
- Nikonenko, V.V.; Kovalenko, A.V.; Urtenov, M.K.; Pismenskaya, N.D.; Han, J.; Sistat, P.; Pourcelly, G. Desalination at overlimiting currents: State-of-the-art and perspectives. Desalination 2014, 342, 85–106. [Google Scholar] [CrossRef]
- Maletzki, F.; Rosler, H.W.; Staude, E. Ion transfer across electrodialysis membranes in the overlimiting current range: Stationary voltage current characteristics and current noise power spectra under different conditions of free convection. J. Membr. Sci. 1992, 71, 105–116. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V.; Pismenskaya, N.D.; Laktionov, E.V.; Urtenov, M.K.; Strathmann, H.; Wessling, M.; Koops, G.H. Coupled transport phenomena in overlimiting current electrodialysis. Sep. Purif. Technol. 1988, 14, 255–267. [Google Scholar] [CrossRef]
- Rubinshtein, I.; Zaltzman, B.; Pretz, J.; Linder, C. Experimental Verification of the Electroosmotic Mechanism of Overlimiting Conductance Through a Cation Exchange Electrodialysis Membrane. Russ. J. Electrochem. 2002, 38, 853–863. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Nikonenko, V.V.; Belova, E.I.; Lopatkova, G.Y.; Sistat, P.; Pourcelly, G.; Larchet, C. Coupled convection of solution near the surface of ion-exchange membranes in intensive current regimes. Russ. J. Electrochem. 2007, 43, 307. [Google Scholar] [CrossRef]
- Rubinstein, S.M.; Manukyan, G.; Staicu, A.; Rubinstein, I.; Zaltzman, B.; Lammertink, R.G.H. Direct Observation of a Nonequilibrium Electro-Osmotic Instability. Phys. Rev. Lett. 2008, 101, 236101. [Google Scholar] [CrossRef] [PubMed]
- Kwak, R.; Guan, G.; Peng, W.K.; Han, J. Microscale electrodialysis: Concentration profiling and vortex visualization. Desalination 2013, 308, 138–146. [Google Scholar] [CrossRef]
- Bellon, T.; Polezhaev, P.; Vobecká, L.; Svoboda, M.; Slouka, S. Experimental observation of phenomena developing on ion-exchange systems during current-voltage curve measurement. J. Membr. Sci. 2019, 572, 607–618. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electro-osmotically induced convection at a permselective membrane. Phys. Rev. E 2000, 62, 2238–2251. [Google Scholar] [CrossRef]
- Demekhin, E.A.; Shelistov, V.S.; Polyanskikh, S.V. Linear and nonlinear evolution and diffusion layer selection in electrokinetic instability. Phys. Rev. E 2011, 84, 036318. [Google Scholar] [CrossRef]
- Pham, S.V.; Li, Z.; Lim, K.M.; White, J.K.; Han, J. Direct numerical simulation of electroconvective instability and hysteretic current-voltage response of a permselective membrane. Phys. Rev. E 2012, 86, 046310. [Google Scholar] [CrossRef]
- Kwak, R.; Pham, V.S.; Lim, K.M.; Han, J. Shear Flow of an Electrically Charged Fluid by Ion Concentration Polarization: Scaling Laws for Electroconvective Vortices. Phys. Rev. Lett. 2013, 110, 114501. [Google Scholar] [CrossRef]
- Druzgalski, C.L.; Andersen, M.B.; Mani, A. Direct numerical simulation of electroconvective instability and hydrodynamic chaos near an ion-selective surface. Phys. Fluids 2013, 25, 110804. [Google Scholar] [CrossRef]
- Urtenov, M.K.; Uzdenova, A.M.; Kovalenko, A.V.; Nikonenko, V.V.; Pismenskaya, N.D.; Vasil’eva, V.I.; Sistat, P.; Pourcelly, G. Basic mathematical model of overlimiting transfer enhanced by electroconvection in flow-through electrodialysis membrane cells. J. Membr. Sci. 2013, 447, 190–202. [Google Scholar] [CrossRef]
- Shaposhnik, V.A.; Vasileva, V.I.; Praslov, D.B. Concentration Fields of Solutions under Electrodialysis with Ion-Exchange Membranes. J. Membr. Sci. 1995, 101, 23–30. [Google Scholar] [CrossRef]
- Shaposhnik, V.A.; Vasil’eva, V.I.; Grigorchuk, O.V. The interferometric investigations of electromembrane processes. Adv. Colloid Interface Sci. 2008, 139, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Frilette, V.J. Electrogravitational Transport at Synthetic Ion Exchange Membrane Surfaces. J. Phys. Chem. 1957, 61, 168–174. [Google Scholar] [CrossRef]
- Balster, J.; Yildirim, M.H.; Stamatialis, D.F.; Ibanez, R.; Lammertink, R.G.H.; Jordan, V.; Wessling, M. Morphology and microtopology of cation-exchange polymers and the origin of the overlimiting current. J. Phys. Chem. B 2007, 111, 2152–2165. [Google Scholar] [CrossRef] [PubMed]
- Nikonenko, V.V.; Mareev, S.A.; Pis’menskaya, N.D.; Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Pourcelly, G. Effect of Electroconvection and Its Use in Intensifying the Mass Transfer in Electrodialysis (Review). Russ. J. Electrochem. 2017, 53, 1122–1144. [Google Scholar] [CrossRef]
- Rubinstein, I.; Shtilman, L. Voltage against current curves of cation exchange membranes. J. Chem. Soc. Faraday Trans. 1979, 75, 231–246. [Google Scholar] [CrossRef]
- Dydek, E.V.; Zaltzman, B.; Rubinstein, I.; Deng, D.S.; Mani, A.; Bazant, M.Z. Overlimiting current in a microchannel. Phys. Rev. Lett. 2011, 107, 118301. [Google Scholar] [CrossRef]
- Abu-Rjal, R.; Prigozhin, L.; Rubinstein, I.; Zaltzman, B. Equilibrium Electro-Convective Instability in Concentration Polarization: The Effect of Non-Equal Ionic Diffusivities and Longitudinal Flow. Russ. J. Electrochem. 2017, 53, 903–918. [Google Scholar] [CrossRef]
- Demekhin, E.A.; Nikitin, N.V.; Shelistov, V.S. Direct numerical simulation of electrokinetic instability and transition to chaotic motion. Phys. Fluids 2013, 25, 122001. [Google Scholar] [CrossRef]
- Demekhin, E.A.; Ganchenko, G.S.; Kalaydin, E.N. Transition to Electrokinetic Instability near Imperfect Charge-Selective Membranes. Phys. Fluids 2018, 30, 082006. [Google Scholar] [CrossRef]
- Pham, S.V.; Kwon, H.; Kim, B.; White, J.K.; Lim, G.; Han, J. Helical vortex formation in three-dimensional electrochemical systems with ion-selective membranes. Phys. Rev. E 2016, 93, 033114. [Google Scholar] [CrossRef]
- Karatay, E.; Druzgalski, C.L.; Mani, A. Simulation of Chaotic Electrokinetic Transport: Performance of Commercial Software versus Custom-built Direct Numerical Simulation Codes. J. Colloid Interface Sci. 2015, 446, 67–76. [Google Scholar] [CrossRef] [PubMed]
- Magnico, P. Spatial distribution of mechanical forces and ionic flux in electro-kinetic instability near a permselective membrane. Phys. Fluids 2018, 30, 014101. [Google Scholar] [CrossRef]
- Magnico, P. Electro-Kinetic Instability in a Laminar Boundary Layer Next to an Ion Exchange Membrane. Int. J. Mol. Sci. 2019, 20, 2393. [Google Scholar] [CrossRef] [PubMed]
- Davidson, S.M.; Wessling, M.; Mani, A. On the Dynamical Regimes of Pattern-Accelerated Electroconvection. Sci. Rep. 2016, 6, 22505. [Google Scholar] [CrossRef] [PubMed]
- Andersen, M.; Wang, K.; Schiffbauer, J.; Mani, A. Confinement effects on electroconvective instability. Electrophoresis 2017, 38, 702–711. [Google Scholar] [CrossRef] [PubMed]
- Kirii, V.A.; Shelistov, V.S.; Demekhin, E.A. Hydrodynamics of spatially inhomogeneous real membranes. J. Appl. Mech. Tech. Phy. 2017, 58, 635–640. [Google Scholar] [CrossRef]
- Dukhin, S.S.; Mishchuk, N.A. Unlimited current growth through the ion exchanger granule. Colloid J. 1988, 49, 1047. [Google Scholar]
- Dukhin, S.S. Electrokinetic phenomena of the 2nd kind and their applications. Adv. Colloid Interface Sci. 1991, 35, 173–196. [Google Scholar] [CrossRef]
- Mishchuk, N.A. Concentration polarization of interface and non-linear electrokinetic phenomena. Adv. Colloid Interface Sci. 2010, 160, 16–39. [Google Scholar] [CrossRef]
- Chang, H.-C.; Demekhin, E.A.; Shelistov, V.S. Competition Between Dukhin’s and Rubinstein’s Electrokinetic Modes. Phys. Rev. E 2012, 86, 046319. [Google Scholar] [CrossRef]
- Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K. Mathematical Models of Electroconvection in Electromembrane Systems; KCHGU: Karachaevsk, Russia, 2011. [Google Scholar]
- Kwak, R.; Pham, V.S.; Han, J. Sheltering the perturbed vortical layer of electroconvection under shear flow. J. Fluid Mech. 2017, 813, 799–823. [Google Scholar] [CrossRef]
- Mareev, S.; Kozmai, A.; Nikonenko, V.; Belashova, E.; Pourcelly, G.; Sistat, P. Chronopotentiometry and impedancemetry of homogeneous and heterogeneous ion-exchange membranes. Desalin. Water Treat. 2014, 56, 1–4. [Google Scholar] [CrossRef]
- Mareev, S.A.; Nichka, V.S.; Butylskii, D.Y.; Urtenov, M.K.; Pismenskaya, N.D.; Apel, P.Y.; Nikonenko, V.V. Chronopotentiometric Response of Electrically Heterogeneous Permselective Surface: 3D Modeling of Transition Time and Experiment. J. Phys. Chem. C 2016, 120, 13113–13119. [Google Scholar] [CrossRef]
- Mareev, S.A.; Nebavskiy, A.V.; Nichka, V.S.; Urtenov, M.K.; Nikonenko, V.V. The nature of two transition times on chronopotentiograms of heterogeneous ion exchange membranes: 2D modelling. J. Membr. Sci. 2019, 575, 179–190. [Google Scholar] [CrossRef]
- Uzdenova, A. 2D mathematical modelling of overlimiting transfer enhanced by electroconvection in flow-through electrodialysis membrane cells in galvanodynamic mode. Membranes 2019, 9, 39. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Vasil’eva, V.I.; Akberova, E.M.; Uzdenova, A.M.; Urtenov, M.K.; Kovalenko, A.V.; Pismenskaya, N.D.; Mareev, S.A.; Pourcelly, G. Competition between diffusion and electroconvection at an ion-selective surface in intensive current regimes. Adv. Colloid Interface Sci. 2016, 235, 233–246. [Google Scholar] [CrossRef]
- Danckwerts, P.V. Continuous flow systems. Distribution of residence times. Chem. Eng. Sci. 1953, 2, 1–13. [Google Scholar] [CrossRef]
- Uzdenova, A.; Kovalenko, A.; Urtenov, M.; Nikonenko, V. 1D Mathematical Modelling of Non-Stationary Ion Transfer in the Diffusion Layer Adjacent to an Ion-Exchange Membrane in Galvanostatic Mode. Membranes 2018, 8, 84. [Google Scholar] [CrossRef]
- Comsol Multiphysics Reference Manual. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.comsol/COMSOL_ReferenceManual.pdf (accessed on 10 March 2020).
- Urtenov, M.A.K.; Kirillova, E.V.; Seidova, N.M.; Nikonenko, V.V. Decoupling of the Nernst-Planck and Poisson equations, Application to a membrane system at overlimiting currents. J. Phys. Chem. B 2007, 11151, 14208–14222. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzdenova, A.; Urtenov, M. Potentiodynamic and Galvanodynamic Regimes of Mass Transfer in Flow-Through Electrodialysis Membrane Systems: Numerical Simulation of Electroconvection and Current-Voltage Curve. Membranes 2020, 10, 49. https://doi.org/10.3390/membranes10030049
Uzdenova A, Urtenov M. Potentiodynamic and Galvanodynamic Regimes of Mass Transfer in Flow-Through Electrodialysis Membrane Systems: Numerical Simulation of Electroconvection and Current-Voltage Curve. Membranes. 2020; 10(3):49. https://doi.org/10.3390/membranes10030049
Chicago/Turabian StyleUzdenova, Aminat, and Makhamet Urtenov. 2020. "Potentiodynamic and Galvanodynamic Regimes of Mass Transfer in Flow-Through Electrodialysis Membrane Systems: Numerical Simulation of Electroconvection and Current-Voltage Curve" Membranes 10, no. 3: 49. https://doi.org/10.3390/membranes10030049
APA StyleUzdenova, A., & Urtenov, M. (2020). Potentiodynamic and Galvanodynamic Regimes of Mass Transfer in Flow-Through Electrodialysis Membrane Systems: Numerical Simulation of Electroconvection and Current-Voltage Curve. Membranes, 10(3), 49. https://doi.org/10.3390/membranes10030049