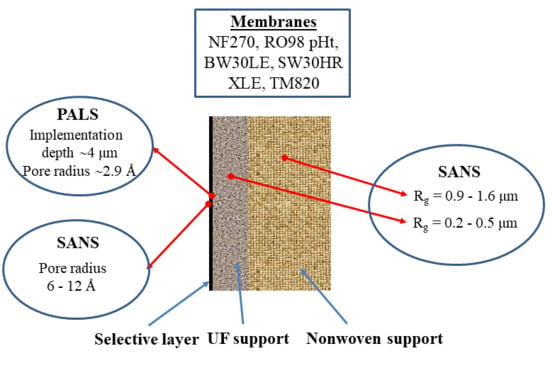
Morphology of Thin Film Composite Membranes Explored by Small-Angle Neutron Scattering and Positron-Annihilation Lifetime Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Thin Film Composite Membranes
2.2. Small-Angle Neutron Scattering (SANS) Instruments
2.3. Positron-Annihilation Lifetime Spectroscopy (PALS)
3. Results and Discussion
3.1. Identification of the Scattering Centers from SANS Contrast Variation
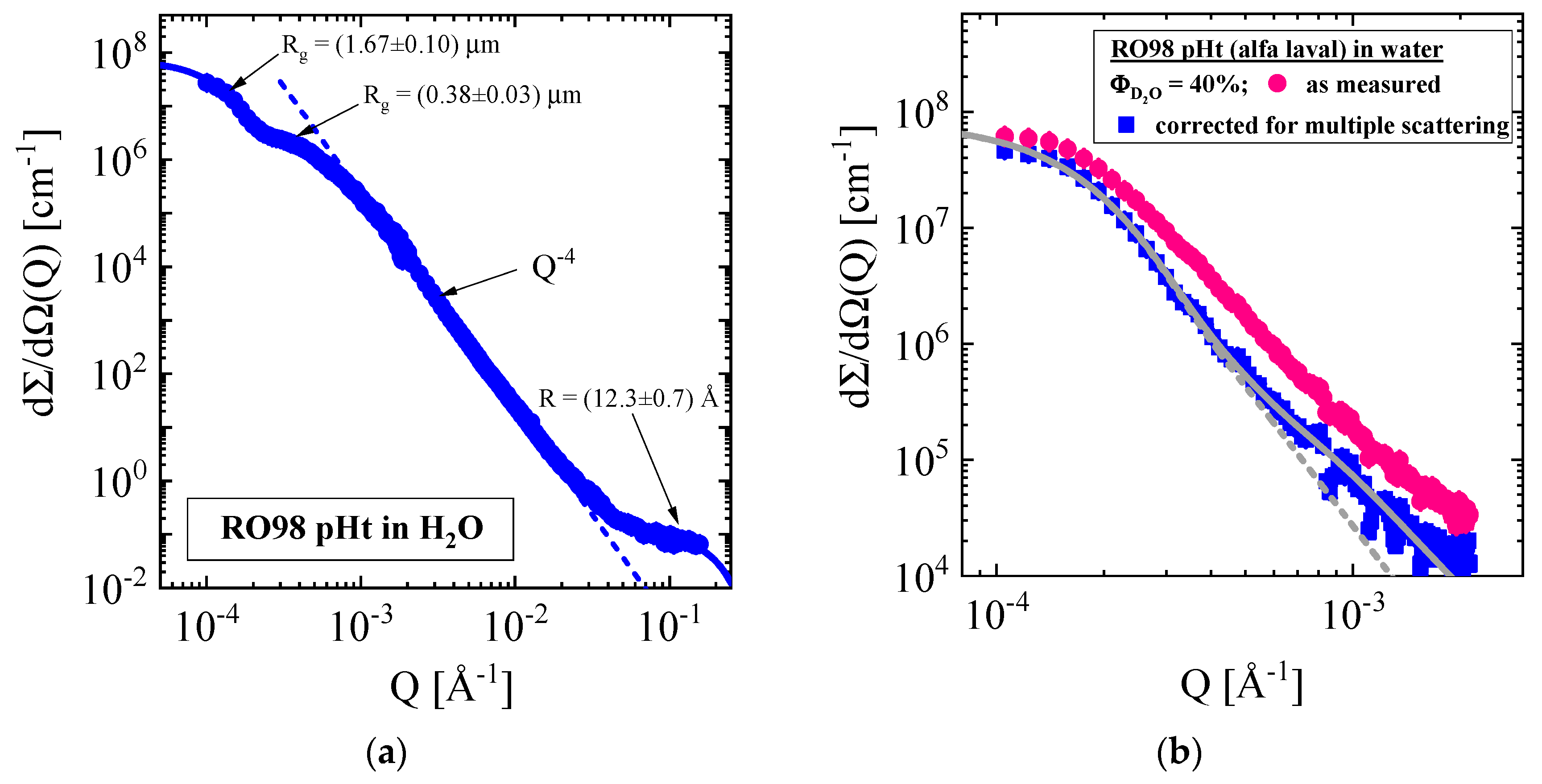
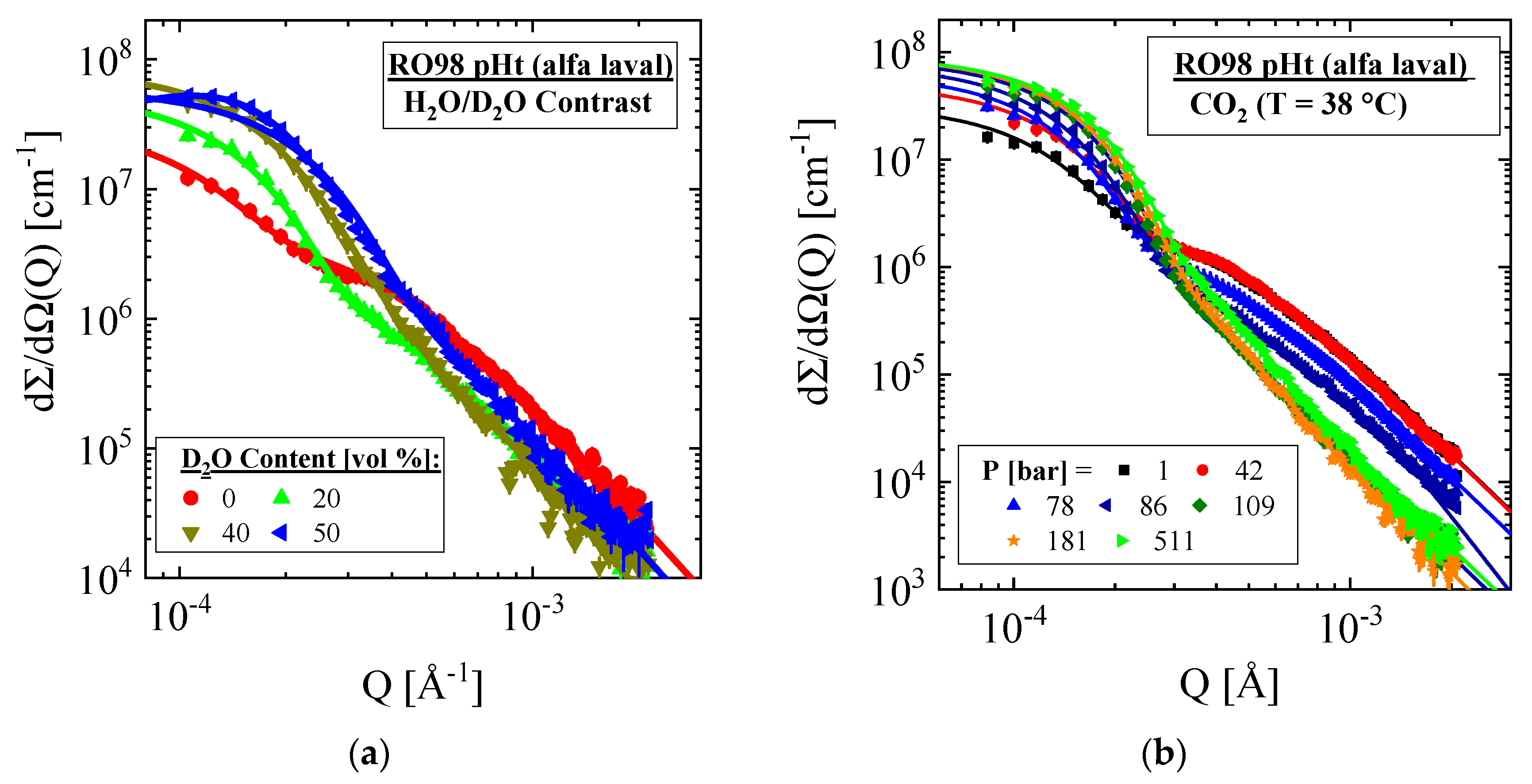
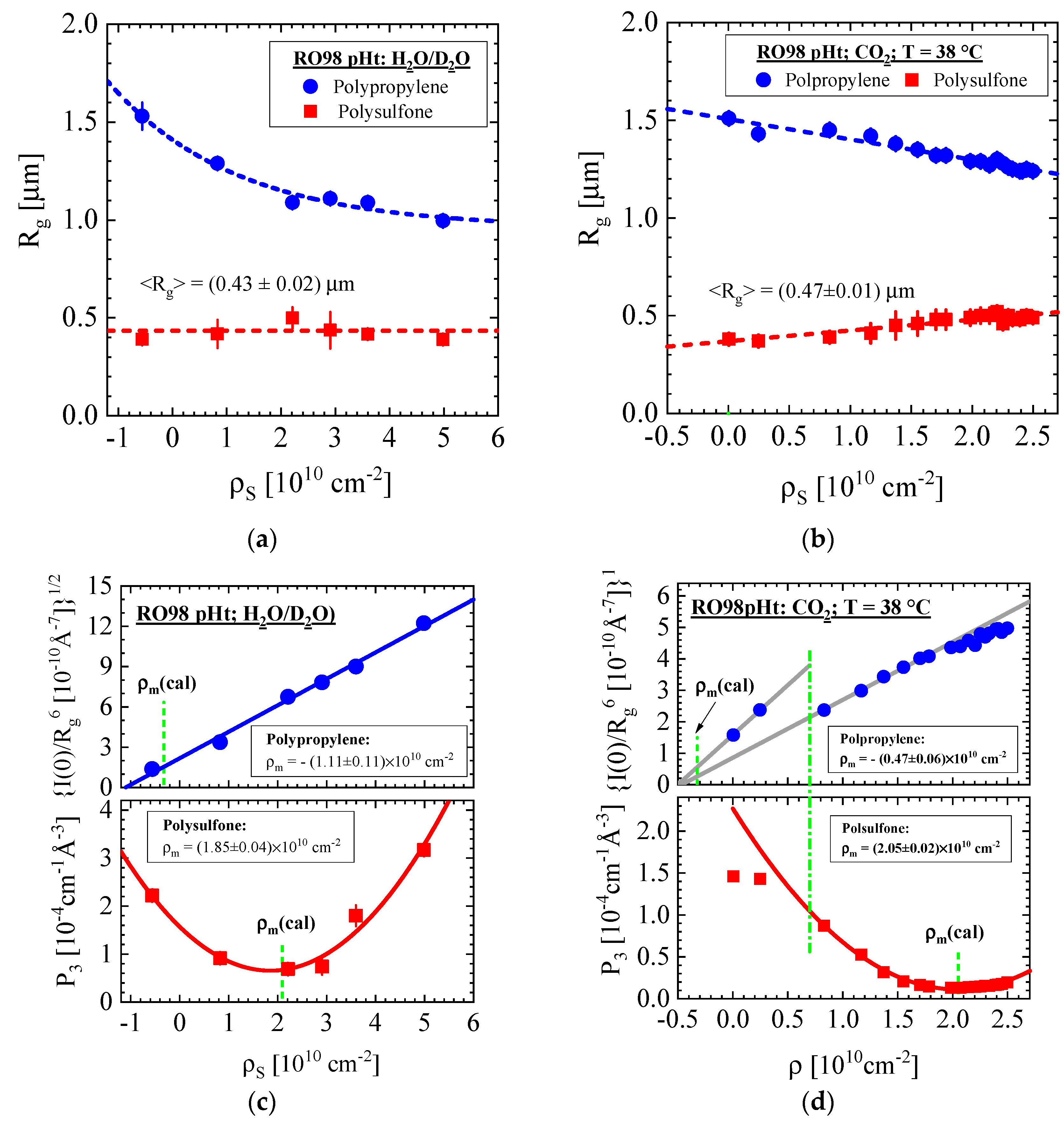
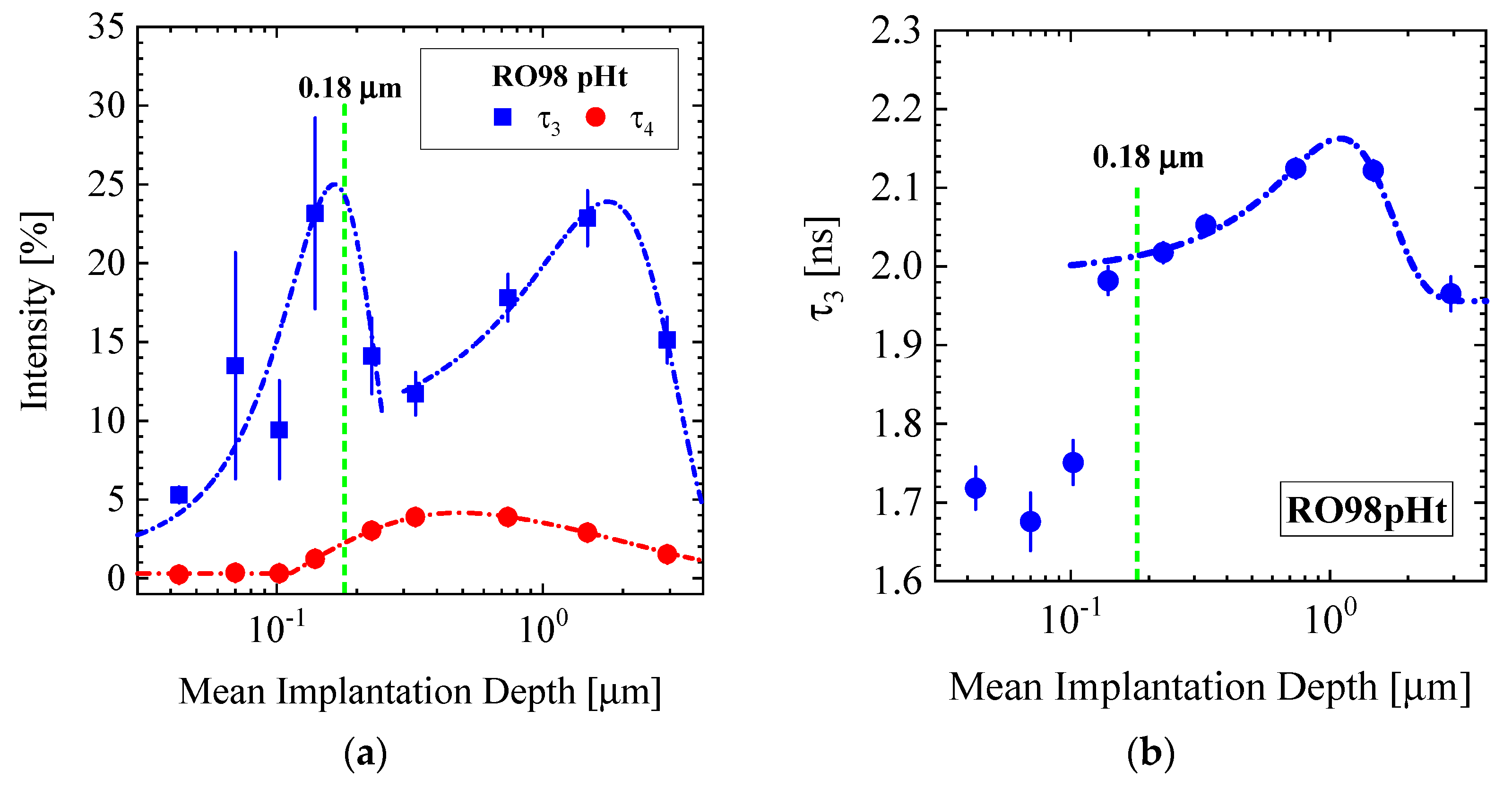
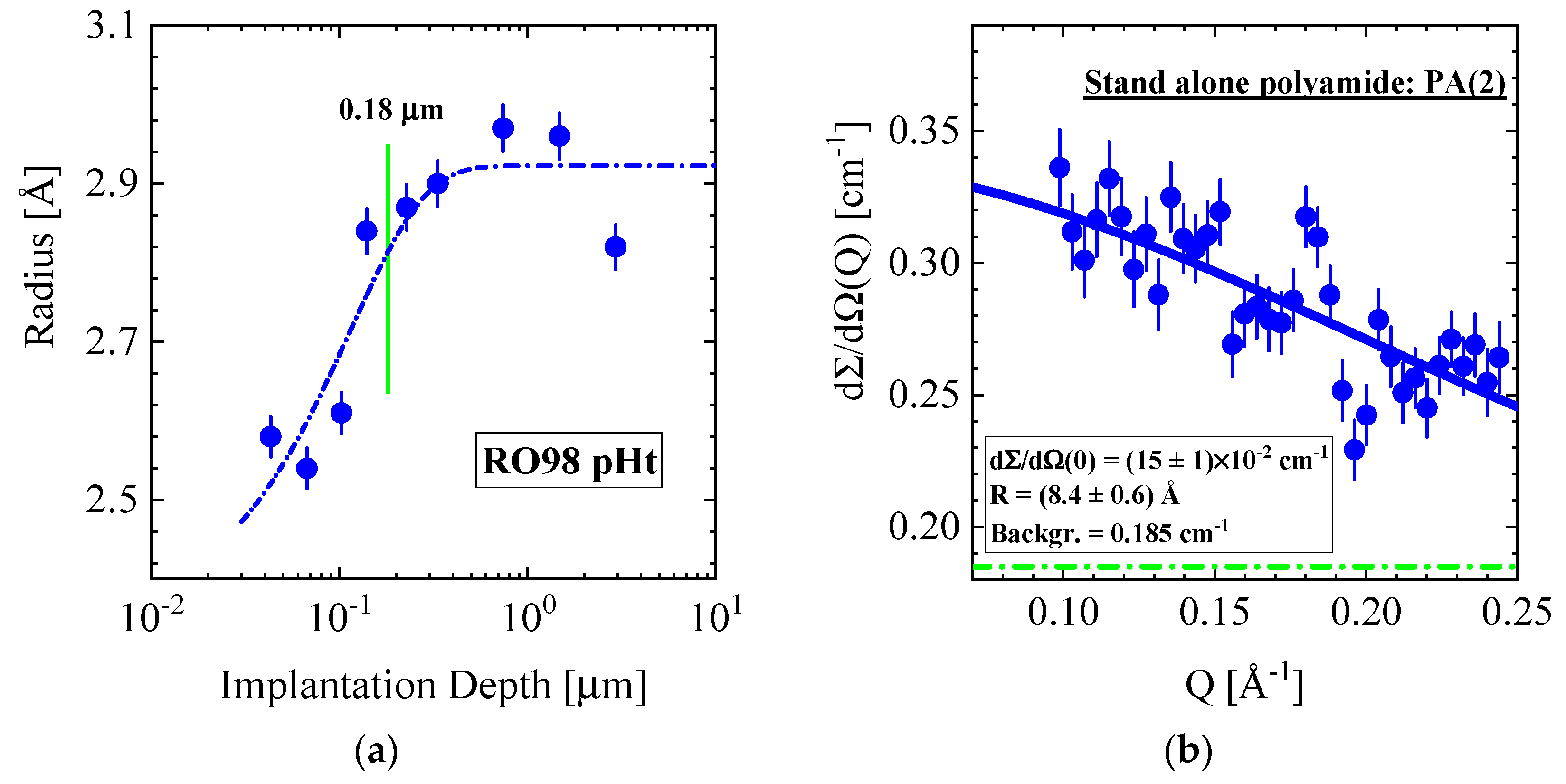
3.1.1. RO98 pHt Membrane with Polypropylene Nonwoven Support
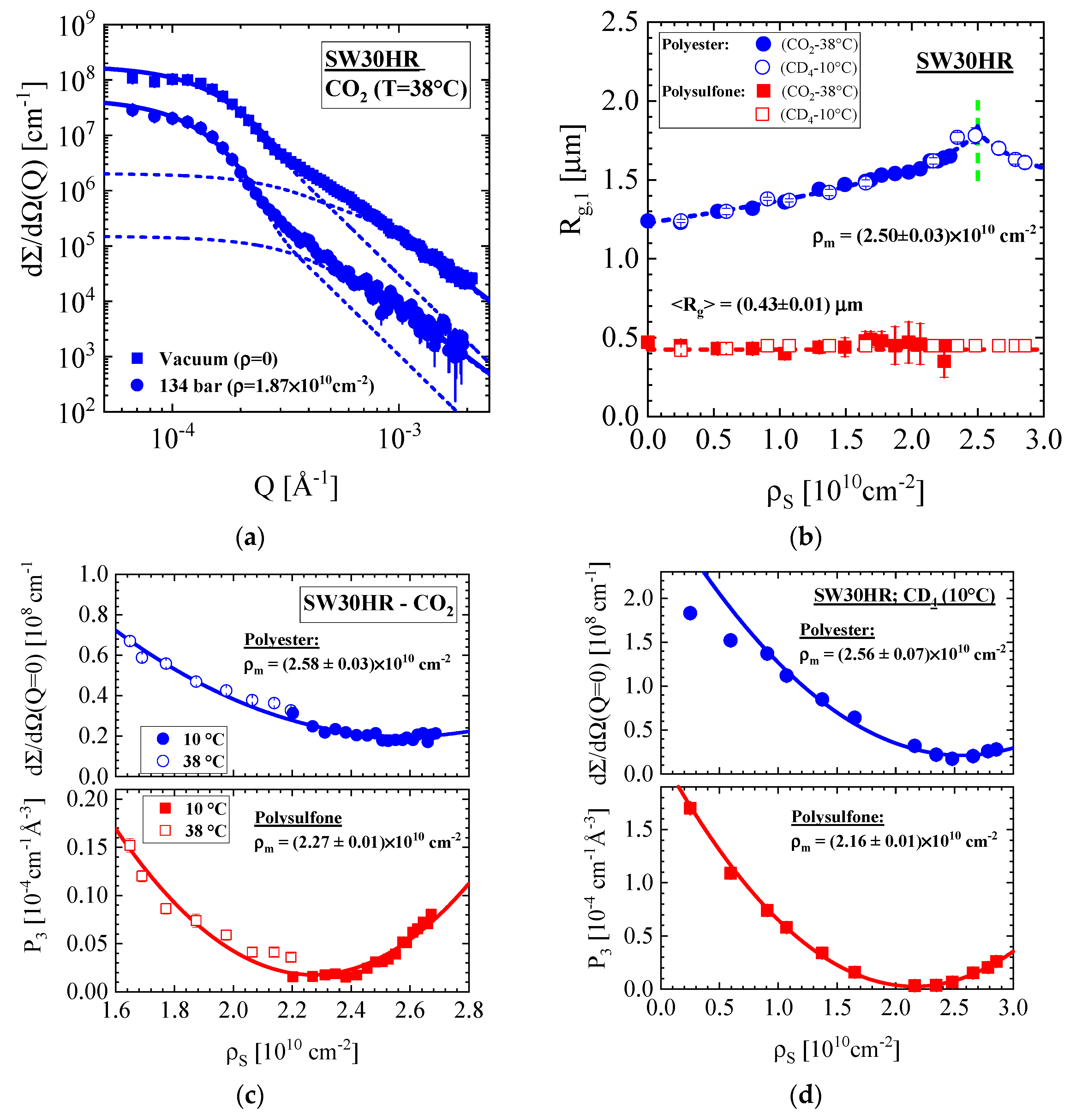
3.1.2. SW30HR Sea Water RO Membrane with Polyester Nonwoven Support Layer
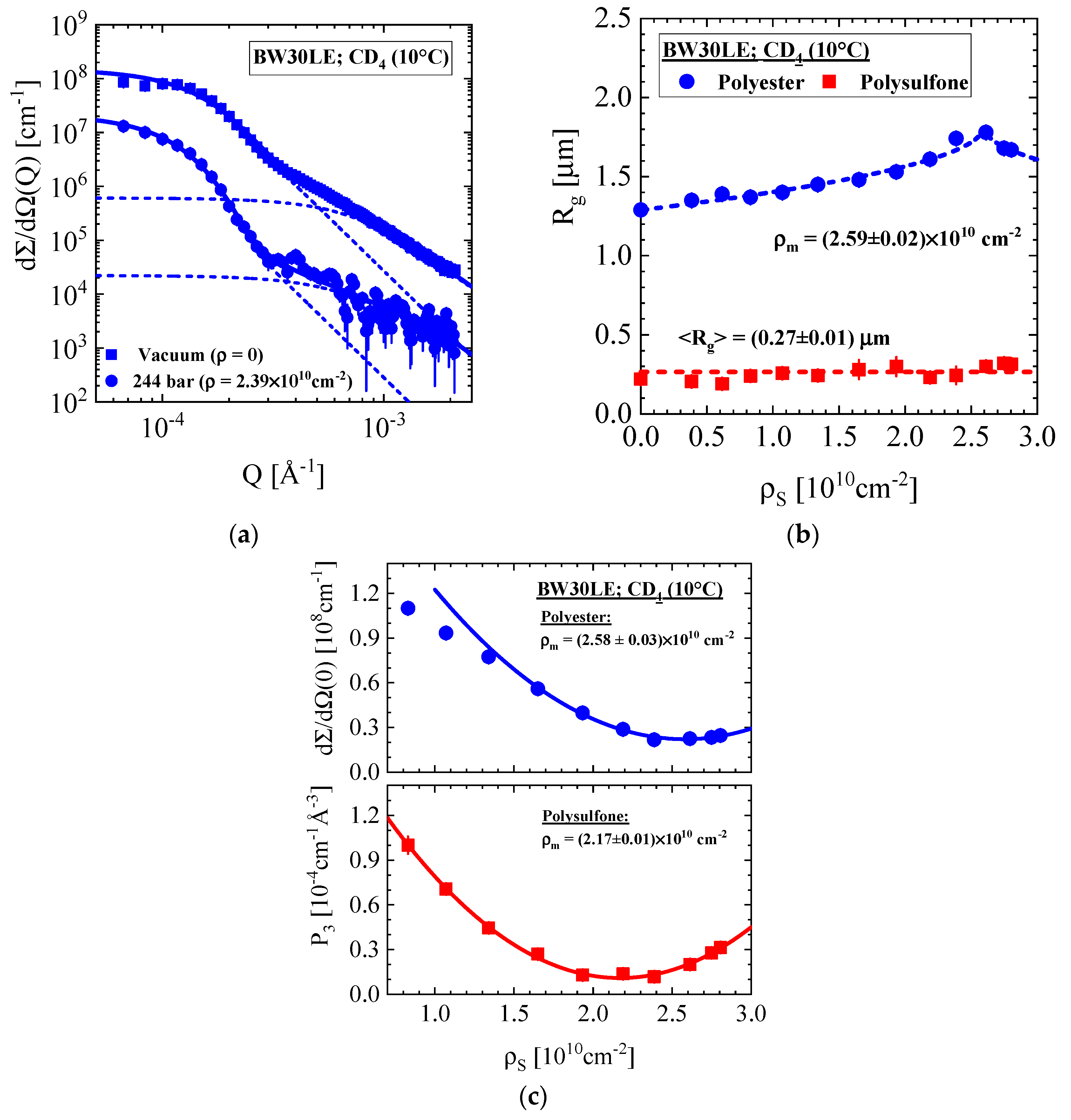
3.1.3. BW30LE Low Energy Brackish Water RO Membrane
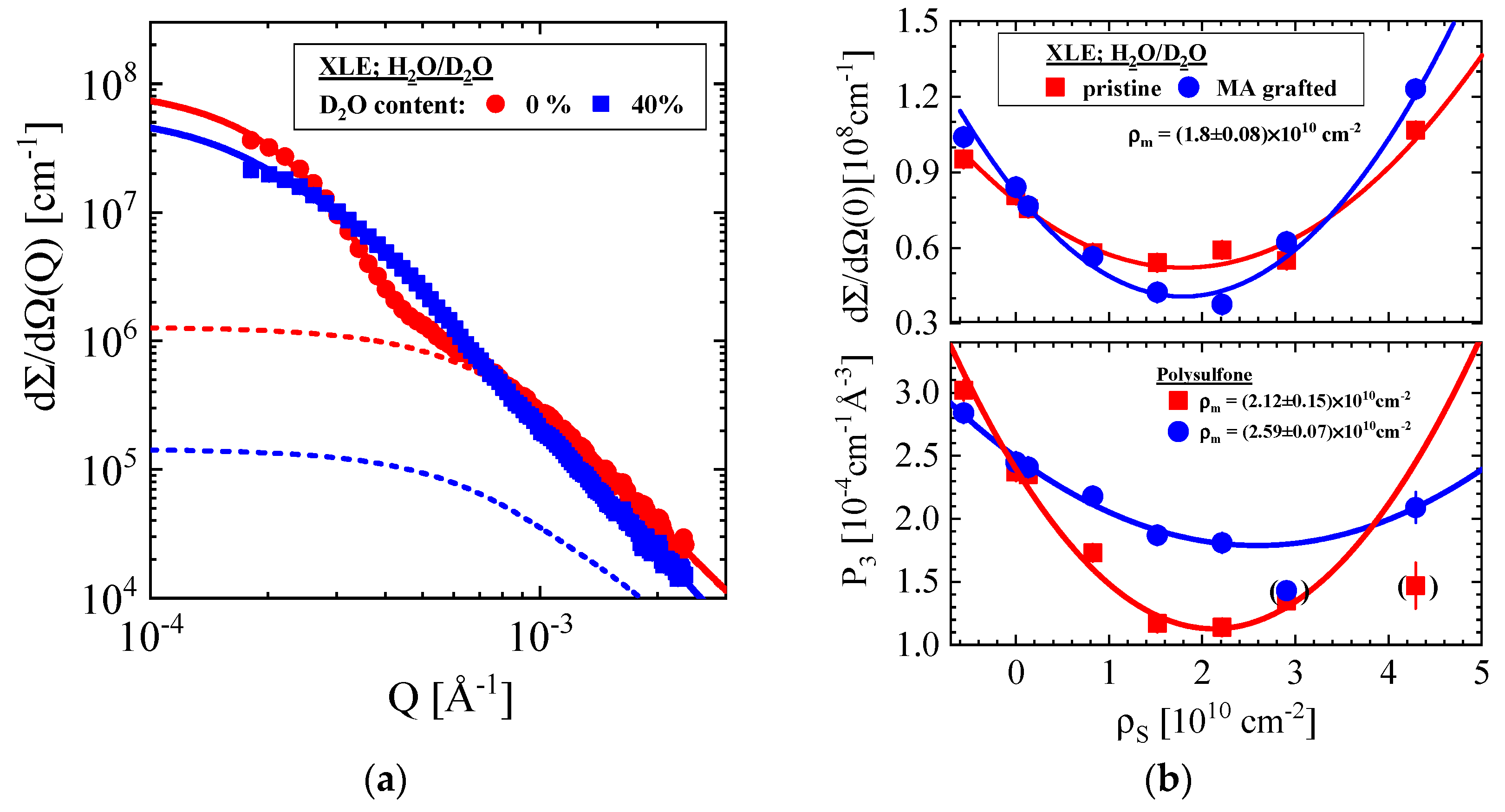
3.1.4. Pristine and Grafted XLE BWRO Membrane
3.2. Discussion of the SANS Data from the Supporting Layers
3.2.1. Nonwoven Fabric Support
3.2.2. Porous Support Layer
3.3. PALS Data
3.4. Pores of Nanoscale Dimension Determined from PALS and SANS
3.4.1. RO98 pHt Membrane
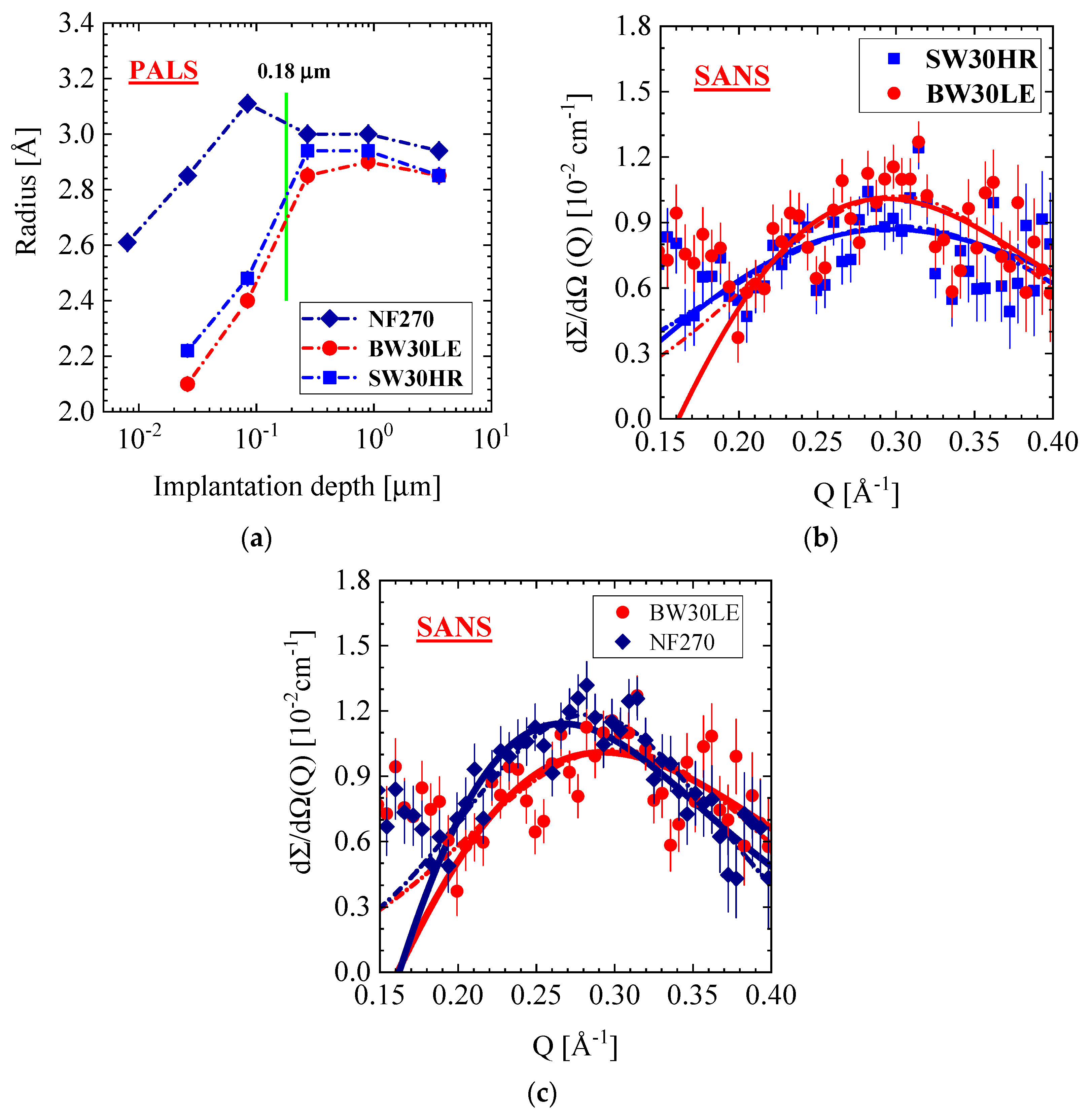
3.4.2. SW30HR, BW30LE, and NF270 Membranes
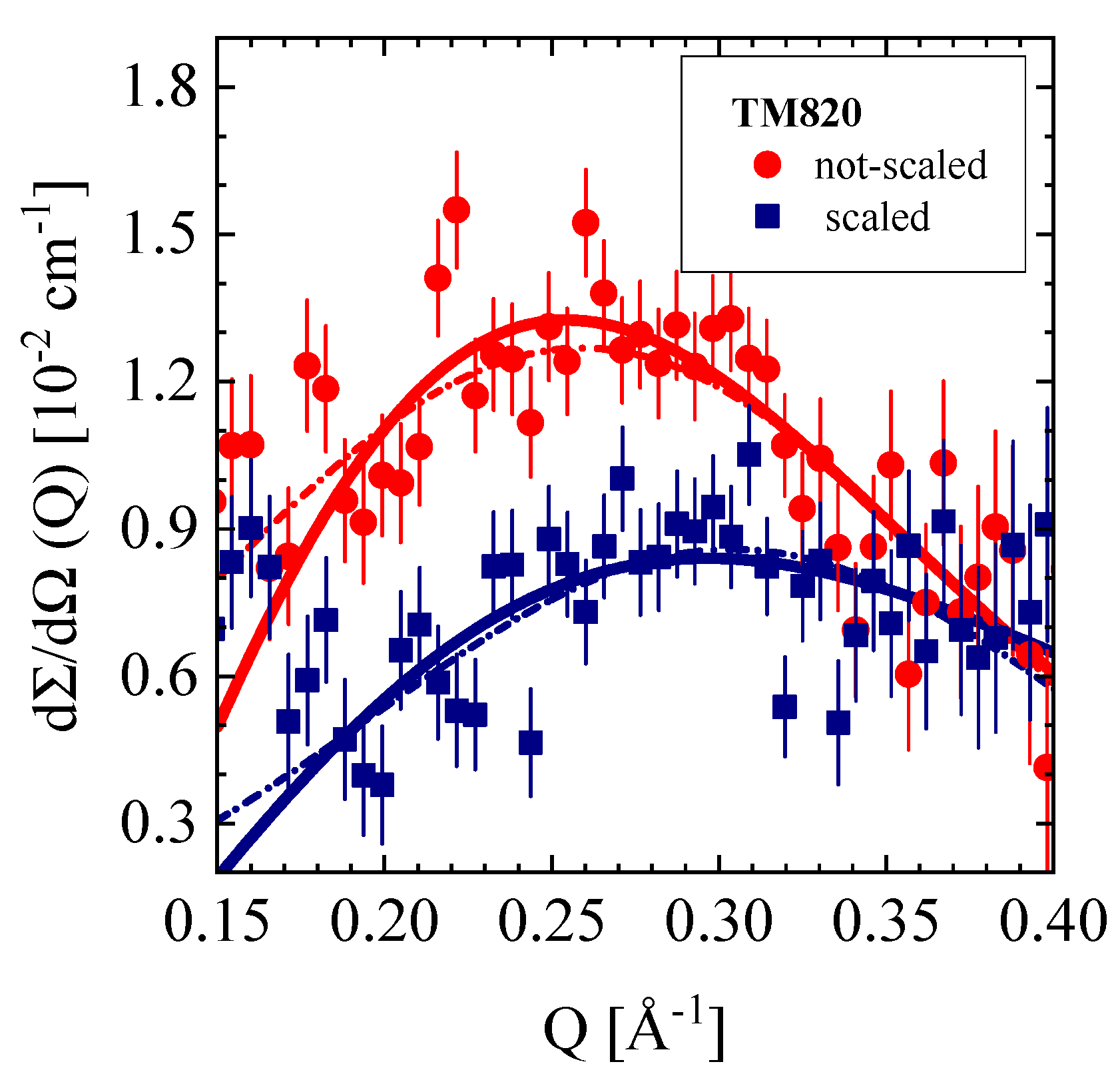
3.4.3. TM820 Seawater RO Membrane, Pristine and Scaled
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A1. SANS Scattering Laws
Appendix A2. Correction for Multiple Scattering
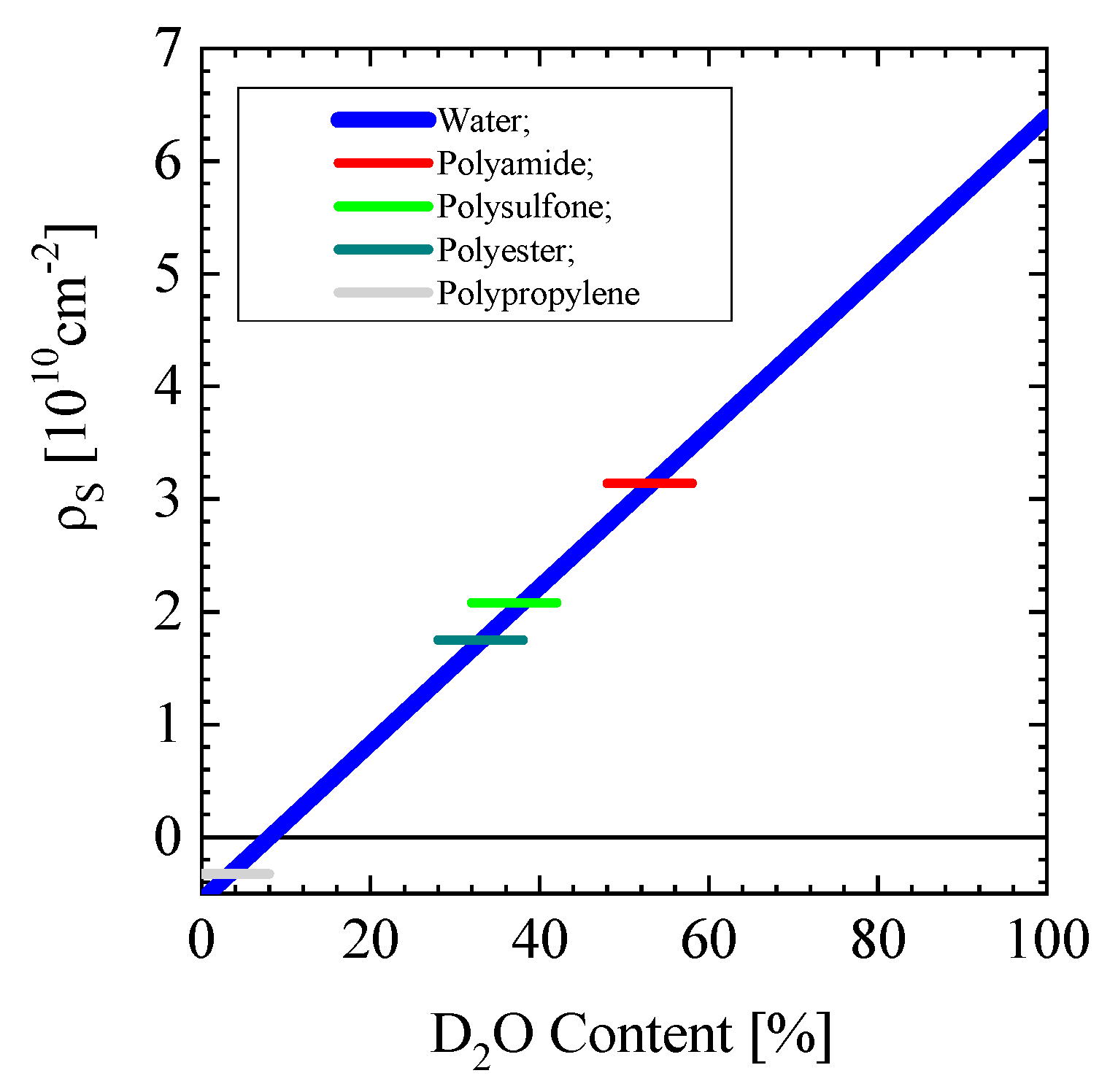
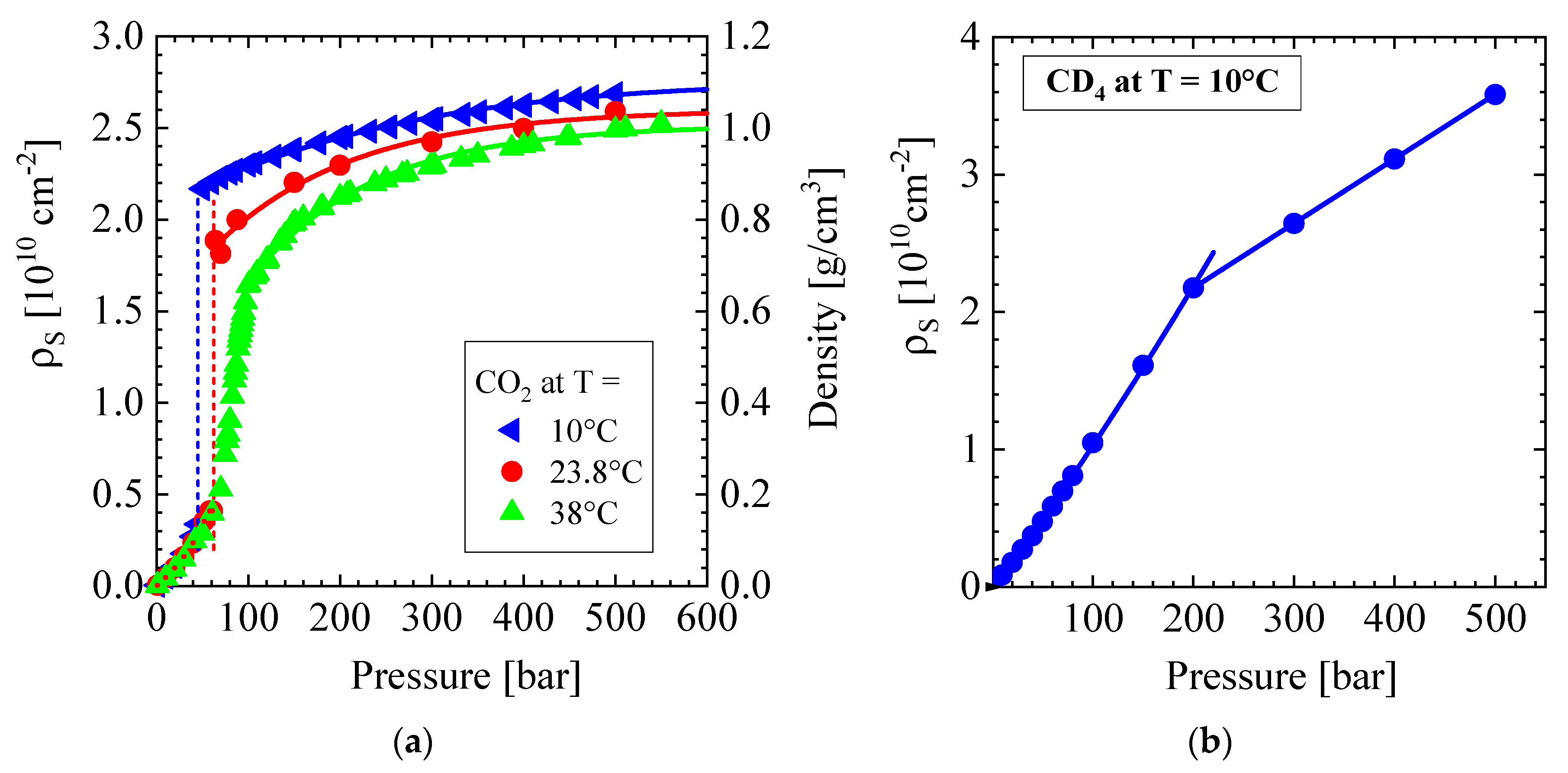
Appendix A3. The Importance of the Contrast Media for SANS Evaluation of TFC Membranes
Appendix A4. PALS in Polymers

Abbreviations
| SANS | small-angle neutron scattering |
| PALS | positron-annihilation lifetime spectroscopy |
| dΣ/dΩ(Q) | differential macroscopic cross-section |
| dΣ/dΩinc | incoherent scattering cross-section. |
| δ | scattering angle |
| λ | wavelength of neutron |
| k | wavenumber of neutron (2π/λ) |
| Q | momentum transfer defined as |
| Q2 | second moment with meaning of the invariant of scattering, |
| bi | coherent scattering length of atom “i” |
| ΩM | volume of molecule “M” |
| ρM | coherent scattering length density of molecule “M” (ρM = Σ bi / ΩM ) |
| Φmatch | concentration of D2O in mixture of H2O/D2O showing the same ρ of the sample |
| Rg | radius of gyration |
| P4 | Porod constant |
| α | exponent of power law of dΣ/dΩ at Q > 1/Rg |
| Vp, Sp, Np, Φp | volume, surface, number density, and volume fraction of domains exposed to scattering. |
| DS | thickness of sample |
| RO | reverse osmosis |
| NF | nanofiltration |
| TFC | thin film composite |
| TMP | trans membrane pressure |
| SSE | simulated secondary effluent |
| SCF | supercritical fluid |
| MA | methacrylic acid |
References
- Qasim, M.; Badrelzaman, M.; Darwish, N.N.; Darwish, N.A.; Hilal, N. Reverse osmosis desalination: A state-of-the-art review. Desalination 2019, 459, 59–104. [Google Scholar] [CrossRef]
- Rodríguez-Calvo, A.; Silva-Castro, G.A.; Osorio, F.; González-López, J.; Calvo, C. Reverse osmosis seawater desalination: Current status of membrane systems. Desalin. Water Treat. 2015, 56, 849–861. [Google Scholar] [CrossRef]
- Lee, K.P.; Arnot, T.C.; Mattia, D. A review of reverse osmosis membrane materials for desalination—Development to date and future potential. J. Membr. Sci. 2011, 370, 1–22. [Google Scholar] [CrossRef]
- Pipich, V.; Schlenstedt, K.; Dickmann, M.; Kasher, R.; Meier-Haack, J.; Hugenschmidt, C.; Petry, W.; Oren, Y.; Schwahn, D. Morphology and porous structure of standalone aromatic polyamide films as used in RO membranes—An exploration with SANS, PALS, and SEM. J. Membr. Sci. 2019, 573, 167–176. [Google Scholar] [CrossRef]
- Steiner, Z.; Rapaport, H.; Oren, Y.; Kasher, R. Effect of surface-exposed chemical groups on calcium-phosphate mineralization in water-treatment systems. Environ. Sci. Technol. 2010, 44, 7937–7943. [Google Scholar] [CrossRef]
- Pipich, V.; Dahdal, Y.N.; Rapaport, H.; Kasher, R.; Oren, Y.; Schwahn, D. Effects of Biological Molecules on Calcium Mineral Formation Associated with Wastewater Desalination as Assessed using Small-Angle Neutron Scattering. Langmuir 2013, 29, 7607–7617. [Google Scholar] [CrossRef]
- Dahdal, Y.N.; Pipich, V.; Rapaport, H.; Oren, Y.; Kasher, R.; Schwahn, D. Small-Angle Neutron Scattering Studies of Mineralization on BSA coated Citrate capped Gold Nano-Particles used as a Model Surface for Membrane Scaling in RO Wastewater Desalination. Langmuir 2014, 30, 15072–15082. [Google Scholar] [CrossRef]
- Schwahn, D.; Feilbach, H.; Starc, T.; Pipich, V.; Kasher, R.; Oren, Y. Design and Test of Reverse Osmosis Pressure Cell for in-situ Small-Angle Neutron Scattering Studies. Desalination 2017, 405, 40–50. [Google Scholar] [CrossRef][Green Version]
- Shtreimer, K.N.; Avisdris, T.; Arnusch, C.J.; Kasher, R. Grafted Polymer Coatings Enhance Fouling Inhibition by an Antimicrobial Peptide on Reverse Osmosis Membranes. Langmuir 2018, 35, 1935–1943. [Google Scholar] [CrossRef]
- Werber, J.R.; Osuji, C.O.; Elimelech, M. Materials for next-generation desalination and water purification membranes. Nat. Rev. Mater. 2016, 1, 16018. [Google Scholar] [CrossRef]
- Jiang, S.X.; Li, Y.N.; Ladewig, B.P. A review of reverse osmosis membrane fouling and control strategies. Sci. Total Environ. 2017, 595, 567–583. [Google Scholar] [CrossRef] [PubMed]
- Heinz Maier-Leibnitz Zentrum. Available online: http://www.mlz-garching.de/instrumente-und-labore/nanostrukturen/kws-3.html (accessed on 2 March 2020).
- Alefeld, B.; Schwahn, D.; Springer, T. New Developments of Small-Angle Neutron Scattering Instruments with Focussing. Nucl. Instrum. Methods Phys. Res. 1989, A274, 210–216. [Google Scholar] [CrossRef]
- Goerigk, G.; Varga, Z. Comprehensive Upgrade of the High-Resolution Small-Angle Neutron Scattering Instrument KWS-3 at FRM II. J. Appl. Crystallogr. 2011, 44, 337–342. [Google Scholar] [CrossRef]
- Sears, V.F. Neutron scattering lengths and cross sections. Neutron News 1992, 3, 26–37. [Google Scholar] [CrossRef]
- Gupta, V.B. Some developments of poly(ethylene terephthalate) fiber production and structure-property relationships. Indian J. Fibre Text. Res. 1995, 20, 43–59. [Google Scholar]
- Fakirov, S.; Fischer, E.W.; Schmidt, G.F. Unit cell dimensions of poly (ethylene terephthalate. Makromol. Chem. 1975, 176, 2459–2465. [Google Scholar] [CrossRef]
- Swift, G.; Bailey, J.; Kroschwitz, J.I. (Eds.) Acrylic (and methacrylic) acid polymers. In Encyclopedia of Polymer Science and Technology; Wiley: Hoboken, NJ, USA, 2003; Volume 1, pp. 79–96. [Google Scholar]
- Jean, Y.C.; van Horn, J.D.; Hung, W.-S.; Lee, K.-R. Perspective of positron annihilation spectroscopy in polymers. Macromolecules 2013, 46, 7133–7145. [Google Scholar] [CrossRef]
- Algers, J.; Sperr, P.; Egger, W.; Kögel, G.; Maurer, F. Median implantation depth implantation profile of 3–18 keV positrons in amorphous polymers. Phys. Rev. B 2003, 67, 12–14. [Google Scholar] [CrossRef]
- Egger, W. Pulsed low energy positron system (PLEPS) at the Munich Research Reactor FRM II.pdf. Phys. Status Solidi 2007, 4, 3969–3972. [Google Scholar]
- Sperr, P.; Egger, W.; Kögel, G.; Dollinger, G.; Hugenschmidt, C.; Repper, R.; Piochacz, C. Status of the pulsed low energy positron beam system (PLEPS) at the Munich Research Reactor FRM-II. Appl. Surf. Sci. 2008, 255, 35–38. [Google Scholar] [CrossRef]
- Hugenschmidt, C.; Piochacz, C.; Reiner, M.; Schreckenbach, K. The NEPOMUC up-grade and advanced positron beam experiments. New J. Phys. 2012, 14, 055027. [Google Scholar] [CrossRef]
- Lemmon, E.W.; McLinden, M.O.; Friend, D.G. Thermophysical Properties of Fluid Systems. In NIST Chemistry WebBook; Linstrom, P.J., Mallard, W.G., Eds.; NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD, USA; p. 20899. [CrossRef]
- Kalebek, N.A.; Babaarslan, O. Fiber Selection for the Production of Nonwovens; IntechOpen: London, UK, 2016; Volume 1, pp. 1–32. [Google Scholar] [CrossRef]
- Roe, R.J. Methods of X-ray and Neutron Scattering in Polymer Science; University Press: Oxford, UK, 2000. [Google Scholar]
- de Gennes, P.-G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Dubrovski, P.D.; Brezocnik, M. Porosity and nonwoven fabric vertical wicking rate. Fibers Polym. 2016, 17, 801–808. [Google Scholar] [CrossRef]
- Yoon, D.Y.; Flory, P.J. Small-angle neutron scattering by semicrystalline polyethylene. Polymer 1977, 18, 509–513. [Google Scholar] [CrossRef]
- Ballard, D.G.H.; Cheshire, P.; Janke, E.; Nevin, N.; Schelten, J. Conformation of the molecules in drawn polypropylene revealed by neutron scattering. Polymer 1982, 23, 1875–1883. [Google Scholar] [CrossRef]
- Hahn, K.; Kerth, J.; Zolk, R.; Schwahn, D.; Springer, T.; Kugler, J. Determination of the chain conformation in fast-spun polypropylene fibers by small-angle neutron scattering. Macromolecules 1988, 21, 1541–1543. [Google Scholar] [CrossRef]
- Song, X.; Gan, B.; Qi, S.; Guo, H.; Tang, C.Y.; Zhou, Y.; Gao, C. Intrinsic Nanoscale Structure of Thin Film Composite Polyamide Membranes: Connectivity, Defects, and Structure–Property Correlation. Environ. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Eldrup, M.; Lightbody, D.; Sherwood, J.N. The temperature dependence of positron lifetimes in solid pxvalic acid. Chem. Phys. 1981, 63, 51–58. [Google Scholar] [CrossRef]
- Olsen, J.V.; Kirkegaard, P.; Pedersen, N.J.; Eldrup, M. PALSfit: A new program for the evaluation of positron lifetime spectra. Phys. Status Solidi 2007, 4, 4004–4006. [Google Scholar] [CrossRef]
- Gidley, D.W.; Peng, H.-G.; Vallery, R.S. Positron annihilation as a method to characterize porous materials. Annu. Rev. Mater. Res. 2006, 36, 49–79. [Google Scholar] [CrossRef]
- Kłosowski, M.M.; McGilvery, C.M.; Li, Y.; Abellan, P.; Ramasse, Q.; Cabral, J.T.; Livingston, A.G.; Porter, A.E. Micro-to nano-scale characterisation of polyamide structures of the SW30HR RO membrane using advanced electron microscopy and stain tracers. J. Membr. Sci. 2016, 520, 465–476. [Google Scholar] [CrossRef]
- Guinier, A. X-ray Diffraction; W.H. Freeman and Company: San Francisco, CA, USA, 1963. [Google Scholar]
- Fujioka, T.; Oshima, N.; Suzuki, R.; Price, W.E.; Nghiem, L.D. Probing the internal structure of reverse osmosis membranes by positron annihilation spectroscopy: Gaining more insight into the transport of water and small solutes. J. Membr. Sci. 2015, 486, 106–118. [Google Scholar] [CrossRef]
- Kim, S.H.; Kwak, S.Y.; Susuki, T. Positron annihilation spectroscopic evidence to demonstrate the flux-enhancement mechanism in morphology-controlled thin-film-composite (TFC) membrane. Environ. Sci. Technol. 2005, 39, 1764–1770. [Google Scholar] [CrossRef] [PubMed]
- Fujioka, T.; Oshima, N.; Suzuki, R.; Khan, S.J.; Roux, A.; Poussade, Y.; Drewes, J.E.; Nghiem, L.D. Rejection of small and uncharged chemicals of emerging concern by reverse osmosis membranes: The role of free volume space within the active skin layer. Sep. Purif. Technol. 2013, 116, 426–432. [Google Scholar] [CrossRef]
- Priestley, R.D.; Ellison, C.J.; Broadbelt, L.J.; Torkelson, J.M. Structuaral relaxation of polymer glasses at surfaces, interfaces, and in between. Science 2005, 309, 456–459. [Google Scholar] [CrossRef]
- Freger, V. Nanoscale Heterogeneity of Polyamide Membranes Formed by Interfacial Polymerization. Langmuir 2003, 19, 4791–4797. [Google Scholar] [CrossRef]
- Beaucage, G. Approximations leading to a unified exponential power-law approach to small-angle scattering. J. Appl. Crystallogr. 1995, 28, 717–728. [Google Scholar] [CrossRef]
- Frielinghaus, H. Strategies for removing multiple scattering effects revisited. Nucl. Instrum. Methods Phys. A 2018, 904, 9–14. [Google Scholar] [CrossRef]
- Schelten, J.; Schmatz, W. Multiple Scattering Treatment for Small-Angle Scattering Problems. J. Appl. Cryst. 1980, 13, 385–390. [Google Scholar] [CrossRef]
- Vestergaard Jensen, G.; Barker, J.G. Effects of multiple scattering encountered for various small-angle scattering model functions. J. Appl. Cryst. 2018, 51, 1455–1466. [Google Scholar] [CrossRef]
- Program. Available online: https://jugit.fz-juelich.de/sans/muscatt (accessed on 2 March 2020).
- Pipich, V.; Schwahn, D. Densification of supercritical carbon cioxide (CO2) accompanied by droplet formation when passing the Widom line. Phys. Rev. Lett. 2018, 120, 145701. [Google Scholar] [CrossRef]
- Hugenschmidt, C.; Ceeh, H. The free volume in dried and H2O-loaded biopolymers studied by positron lifetime measurements. J. Phys. Chem. B 2014, 118, 9356–9360. [Google Scholar] [CrossRef] [PubMed]
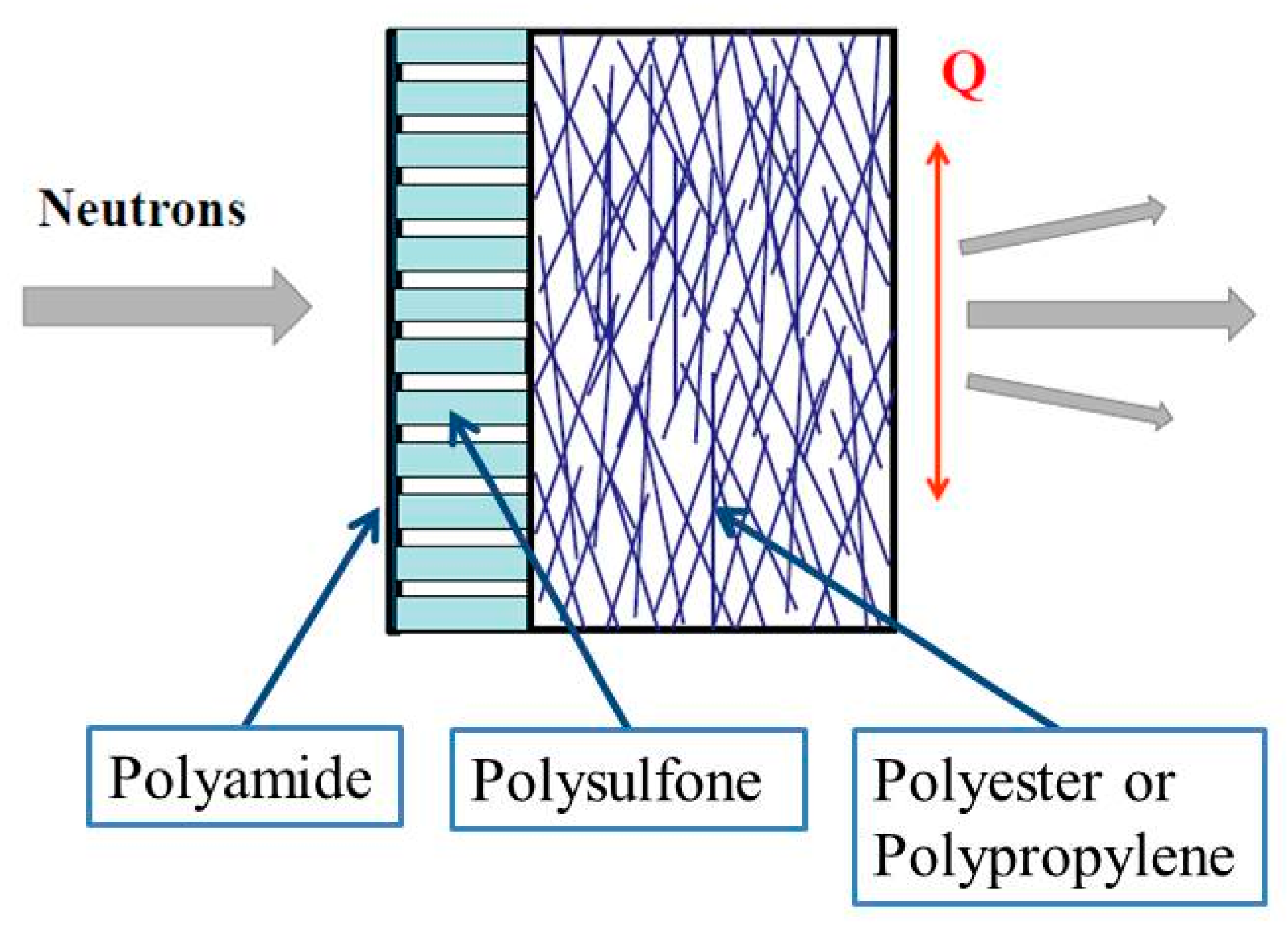

| Producer | Membrane | Type | Composition | Membrane Thickness [μm] | Experimental Technique |
|---|---|---|---|---|---|
| Alfa Laval 1 | RO98 pHt | RO membrane | polyamide polysulfone-polypropylene | 300 | SANS/PALS |
| Dow 2 Filmtec | SW30HR | seawater high rejection | polyamide-polysulfone-polyester | 140 | SANS/PALS |
| BW30LE | brackish water low energy | 150 | SANS/PALS | ||
| XLE [8] | low pressure RO membrane | 140 | SANS | ||
| NF270 | nanofiltration membrane (NF) | SANS/PALS | |||
| Toray 3 (Japan) | TM820 | sea water RO membrane | SANS |
| Molecule | Chemical Formula | Mass Density [g/cm3] | Molar Weight [g/mol] | Glass Transition Temp. TG [°C] | Scattering Cross-Section dΣ/dΩinc. [cm−1] | Scattering Length Density ρ [1010 cm−2] | Φmatch (D2O) |
|---|---|---|---|---|---|---|---|
| Aromatic Polyamide (PA) (Kevlar) | N2C14H10O2 | 1.44 | 238 | 60–75 | 0.233 | 3.10 ± 0.07 | 0.53 |
| Polysulfone (PSU) | C27H22O4S | 1.24 | 442.54 | ~220 | 0.237 | 2.08 | 0.38 |
| Polyethersulfone (PES) | C12H10O4S | 1.3–1.4 | 250.27 | 0.225 | 2.22 | 0.40 | |
| Polypropylene | C3H6 | 0.91 | 42.08 | −10 | 0.50 | −0.325 | 0.034 |
| Polyethylenterephthalate (PET¸ Polyester) | C10H8O4 | 1.38 [16,17] | 192.17 | ~79 | 0.37 | 2.58 | 0.45 |
| PET (amorphous) | 1.33 [16] | 0.36 | 2.49 | 0.44 | |||
| PET (crystalline) | 1.52 [17] | 0.41 | 2.84 | 0.49 | |||
| Low density Polyethylene (PE) | C2H4 | 0.88 | 28.05 | −125 | 0.48 | −0.31 | 0.036 |
| Methacrylic acid (MA) [18] | C4H6O2 | 1.015 | 84.83; (R = 3.23 Å) | - | 0.27 | 1.12 | 0.24 |
| Membrane | Polymer | Medium | ρm [1010 cm−2] | dΣ/dΩ(0) [107 cm−1] | Rg [μm] | Ratio γ (Equation (A8)) | Q2 [10−4 cm−1Å−3] | Φfil [vol %] | Φint [vol %] |
|---|---|---|---|---|---|---|---|---|---|
| RO98 pHt | PP | 40 vol % D2O (Δρ = 2.68 × 1010 cm−2) | −(1.11 ± 0.11) | 8.27 ± 0.22 | 1.10 ± 0.01 | - | 2.35 | 1.66 | - |
| PP | CO2 38 °C, 181 bars (Δρ = 2.07 × 1010 cm−2) | −(0.47 ± 0.06) | 9.14 ± 0.2 | 1.30 ± 0.01 | - | 1.09 | 1.29 | - | |
| SW30HR | PET | Vacuum | 2.59 ± 0.03 | 18.1 ± 0.6 | 1.25 ± 0.01 | 0.12 | 3.2 | 2.9 | 0.4 |
| BW30LE | PET | 2.58 ± 0.03 | 14.6 ± 0.5 | 1.26 ± 0.02 | 0.15 | 2.64 | 1.7 | 0.3 | |
| XLE | PET0.73/PE0.27 | 1.80 ± 0.08 | 8.08 ± 0.05 | 0.91 ± 0.04 | 0.65 | 2.89 | 1.6 | 2.9 | |
| Grafted XLE | 1.79 ± 0.08 | 8.40 ± 0.06 | 0.94 ± 0.01 | 0.48 | 2.18 | 1.8 | 1.6 |
| Polymer | Medium | ρm [1010 cm−2] | dΣ/dΩ(0) [106 cm−1] | Rg * [μm] | γ | Q2 [10−4 cm−1Å−3] | Φpore [vol %] | Φint [vol %] | |
|---|---|---|---|---|---|---|---|---|---|
| RO98 pHt | PSU | H2O (Δρ = 2.36×1010cm−2) | 1.85 ± 0.04 | 3.89 ± 0.05 | 0.43 ± 0.02 | 0.44 | 4.32 | 2.2 | 1.7 |
| Vacuum | 2.05 ± 0.02 | 2.27 ± 0.01 | 0.47 ± 0.01 | 0.05 | 4.01 | 4.6 | 0.2 | ||
| SW30HR | PES | (2.16 to 2.27) ± 0.01 | 2.04 ± 0.27 | 0.43 ± 0.01 | 0.02 | 4.06 | 4.3 | 0.1 | |
| BW30LE | PES | 2.17 ± 0.01 | 0.70 ± 0.03 | 0.22 ± 0.02 | 0.05 | 4.62 | 4.7 | 0.3 | |
| XLE | PSU | 2.12 ± 0.15 | 1.08 ± 0.02 | 0.23 ± 0.02 | 0.48 | 6.25 | 3.6 | 3.4 | |
| MA grafted XLE | 2.59 ± 0.07 | 1.77 ± 0.05 | 0.28 ± 0.01 | 0.73 | 6.50 | 1.3 | 3.6 |
| Parameter | RO98 pHt | SW30HR | BW30LE | NF270 |
|---|---|---|---|---|
| PALS | ||||
| R [Å] (at penetration depth > 0.18 μm) | 2.88 ± 0.02 | 2.91 ± 0.05 | 2.87 ± 0.03 | 2.98 ± 0.04 |
| SANS—Gaussian Distribution | ||||
| QC [Å−1] | - | 0.30 ± 0.01 | 0.30 ± 0.01 | 0.28 ± 0.002 |
| Q2 [10−4 cm−1 Å−3] | - | 2.37 | 2.28 | 2.02 |
| ΦQ2 [vol %] | - | 1.72 | 1.66 | 1.47 |
| Model of Spheres | Model of Hard-Spheres (Equation (A5)) | |||
| dΣ/dΩ(0) [10,[10−2 cm−1] | 12 ± 1 | 2.08 ± 0.10 | 2.64 ± 0.15 | 3.1 ± 0.1 |
| R [Å] | 12.3 ± 0.7 | 6.1 ± 0.5 | 6.8 ± 0.4 | 6.1 ± 0.2 |
| Φ0 [%] | - | 14 ± 2 | 21 ± 4 | 26 ± 2 |
| Q2 [10−4 cm−1 Å−3] | 2.33 | 2.6 | 2.53 | 2.3 |
| ΦQ2 [vol %] | 0.9–1.1 | 1.9 | 1.84 | 1.66 |
| deff [μm] | - | 19 | 12 | 9 |
| Parameter | Pristine Membrane | Scaled Membrane |
|---|---|---|
| PALS | ||
| R [Å] | 1.82 ± 0.41 | 0.93 ± 0.84 |
| SANS—Gaussian Distribution | ||
| QC [Å−1] | 0.26 ± 0.01 | 0.30 ± 0.01 |
| Q2 [10−4 cm−1 Å−3] | 2.69 | 2.16 |
| SANS—Model of hard-spheres | ||
| dΣ/dΩ(0) [10,[10−2 cm−1] | 3.3 ± 0.2 | 2.0 ± 0.6 |
| R [Å] | 7.6 ± 0.8 | 6.8 ± 2.6 |
| Φ0 [vol %] | 18 ± 4 | 17 ± 7 |
| Q2 [10−4 cm−1 Å−3] | 2.78 | 2.50 |
| ΦQ2 [vol %] | 2.02 | 1.82 |
| deff [μm] | ~16 | ~14 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pipich, V.; Dickmann, M.; Frielinghaus, H.; Kasher, R.; Hugenschmidt, C.; Petry, W.; Oren, Y.; Schwahn, D. Morphology of Thin Film Composite Membranes Explored by Small-Angle Neutron Scattering and Positron-Annihilation Lifetime Spectroscopy. Membranes 2020, 10, 48. https://doi.org/10.3390/membranes10030048
Pipich V, Dickmann M, Frielinghaus H, Kasher R, Hugenschmidt C, Petry W, Oren Y, Schwahn D. Morphology of Thin Film Composite Membranes Explored by Small-Angle Neutron Scattering and Positron-Annihilation Lifetime Spectroscopy. Membranes. 2020; 10(3):48. https://doi.org/10.3390/membranes10030048
Chicago/Turabian StylePipich, Vitaliy, Marcel Dickmann, Henrich Frielinghaus, Roni Kasher, Christoph Hugenschmidt, Winfried Petry, Yoram Oren, and Dietmar Schwahn. 2020. "Morphology of Thin Film Composite Membranes Explored by Small-Angle Neutron Scattering and Positron-Annihilation Lifetime Spectroscopy" Membranes 10, no. 3: 48. https://doi.org/10.3390/membranes10030048
APA StylePipich, V., Dickmann, M., Frielinghaus, H., Kasher, R., Hugenschmidt, C., Petry, W., Oren, Y., & Schwahn, D. (2020). Morphology of Thin Film Composite Membranes Explored by Small-Angle Neutron Scattering and Positron-Annihilation Lifetime Spectroscopy. Membranes, 10(3), 48. https://doi.org/10.3390/membranes10030048