Curvature-Dependent Electrostatic Field as a Principle for Modelling Membrane-Based MEMS Devices. A Review
Abstract
1. Introduction
2. Some Theoretical Backgrounds
The Cassani-d’O-Ghoussoub Model and Some Theoretical Backgrounds
3. The Physical-Mathematical Approach: Proportional to the Curvature of the Membrane
Electrostatic and Mechanical Pressures
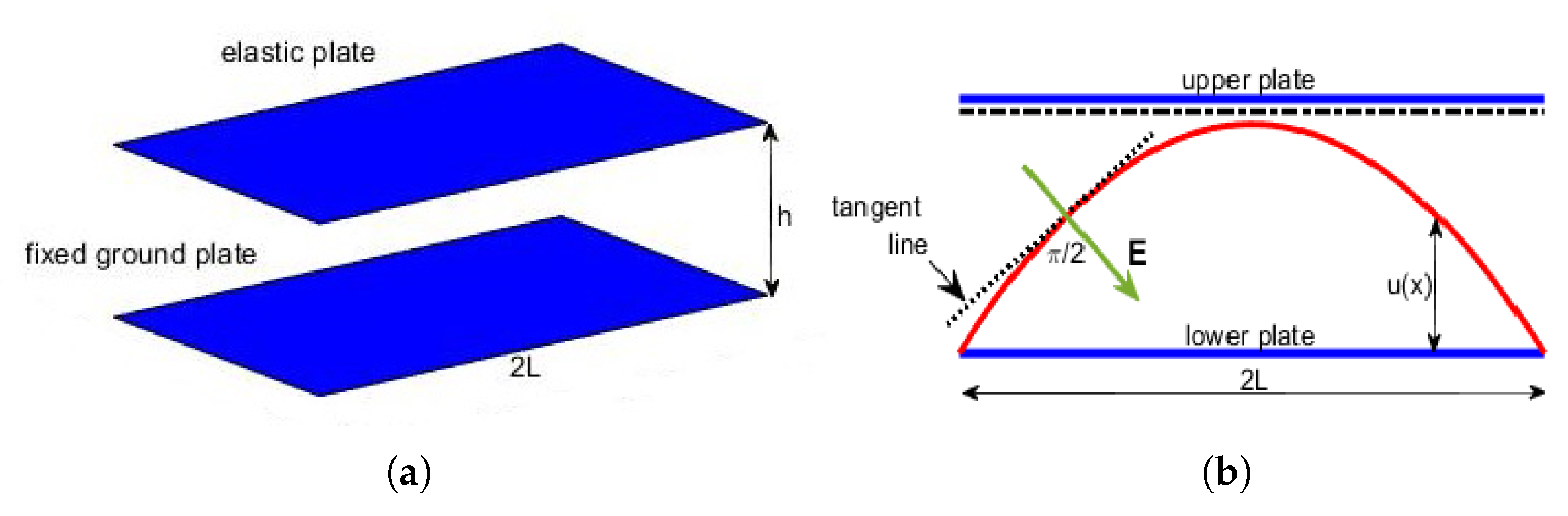
4. 1D Membrane MEMS Device: The Differential Model
- 1.
- , thus . Here being linear, from it follows that . Thus, there exists also when , so that this condition must be discarted.
- 2.
- Therefore
General Formulation of the 1D Model
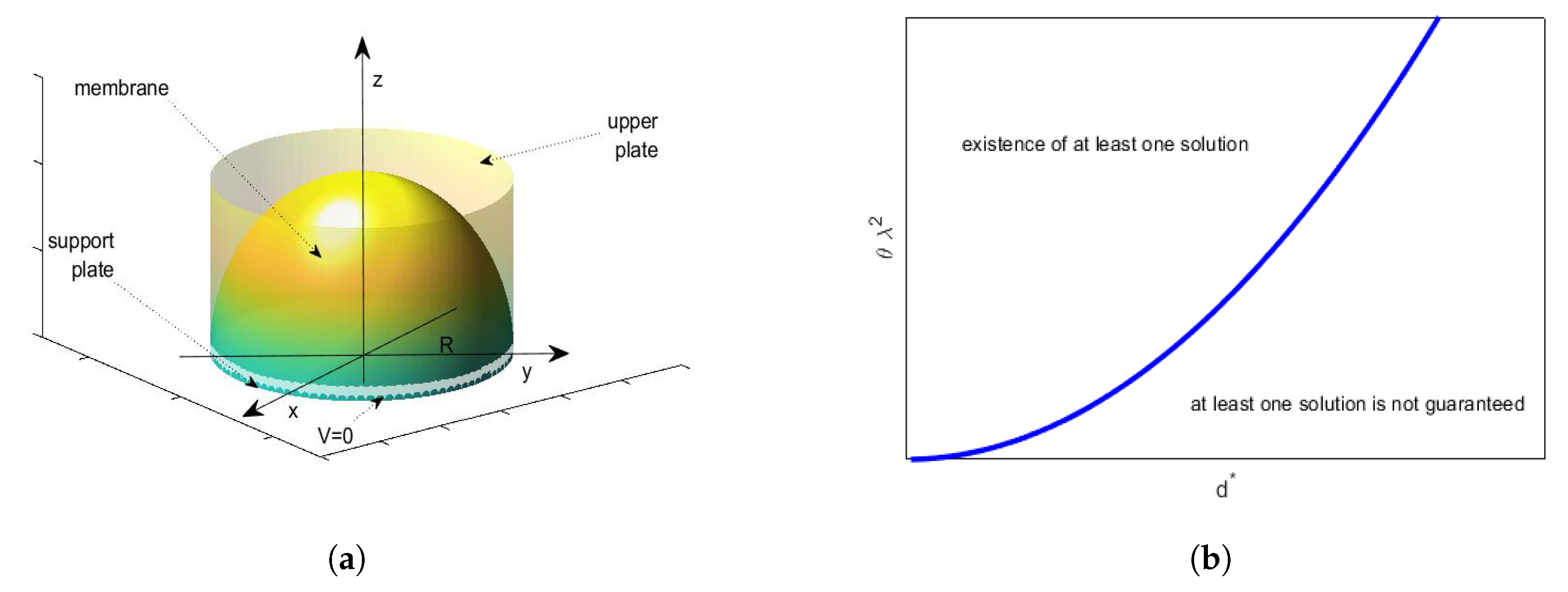
5. 2D Circular Membrane MEMS Device: The Differential Model
General Formulation of the 2D Model
6. A Comparison of the Algebraic Conditions Ensuring the Existence of at Least One Solution for both 1D and 2D Models
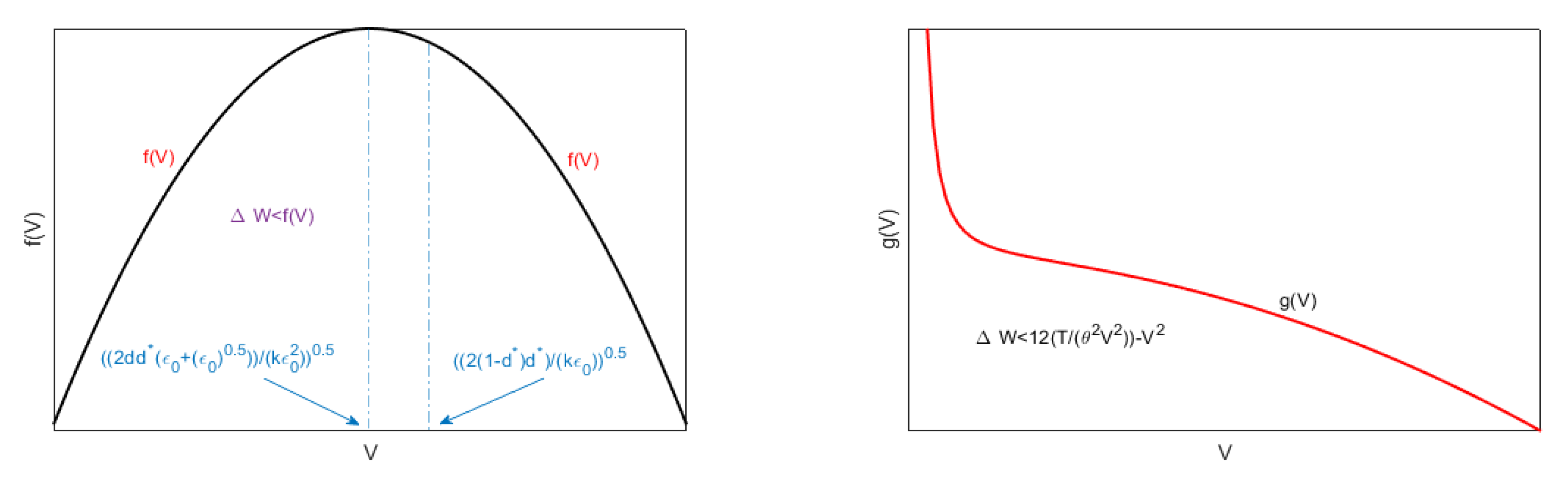
6.1. On the Existence of at Least One Solution for the 1D Model
6.2. On the Existence of at Least One Solution for the 2D Model
6.3. Conditions Ensuring the Existence of at Least one Solutions for 1D and 2D Geometries: A Comparison
7. On the Uniqueness of the Solution for both 1D and 2D Models
7.1. On the Uniqueness of the Solution for the Model (17)
- (1)
- , ;
- (2)
- is symmetric with respect to the origin;
- (3)
- ;
- (4)
- is analytical.
7.2. On the Uniqueness of the Solution for the Model (24)
8. Conditions Ensuring both Existence and Uniqueness
8.1. 1D Geometry
8.2. 2D Geometry
8.3. 1D and 2D Geometries: A Comparison
9. Stability and Optimal Control Problems in 1D Geometry
9.1. Stability and Optimal Control in 1D Geometry
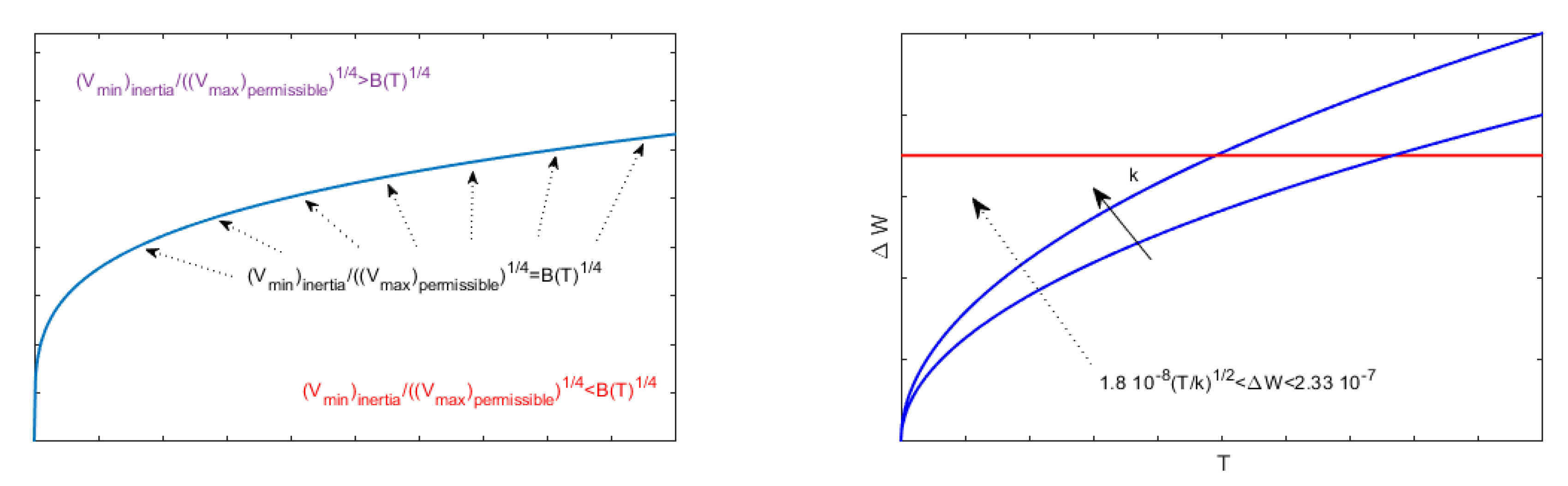
9.2. to Overcome the Inertia of the Membrane in 1D Geometry
9.3. in Order That the Membrane Does Not Reach the Upper Plate in 1D Geometry
9.4. Relationship between and in 1D Geometry
9.5. Some Remarks about the Potential Energy in the Device in 1D Geometry
9.6. A Limitation for Obtained Starting from in 1D Geometry
10. Stability and Optimal Control in 2D Geometry
10.1. Critical Points and Stability
10.2. On the Stability of the Critical Point
10.3. Admissible Values for V in 2D Geometry
and the Problem to Win the Mechanical Inertia of the Membrane
10.4. in 2D Configuration
10.5. Relationship between and in 2D Geometry
10.6. Some Optimal Control Conditions in 2D Geometry
10.7. On the Values of V that Maximize
10.8. From A to a Useful Limitation for
11. Numerical Approaches for Recovering of the Membrane Profile in 1D Geometry
11.1. Shooting Procedure and Ordinary Differential Equation Solvers
11.1.1. Zeros of : The Dekker–Brent Approach
11.1.2. Obtaining the Solution
11.2. Relaxation Procedure and Keller–Box Scheme
11.3. Collocation Procedure and III/IV-Stage Lobatto IIIa Formulas
11.3.1. The Collocation Procedure
11.3.2. Implicit Runge–Kutta Procedures
11.3.3. The Three-Stage Lobatto IIIa Formula
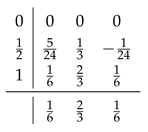
11.3.4. Four-Stage Lobatto IIIa Formula
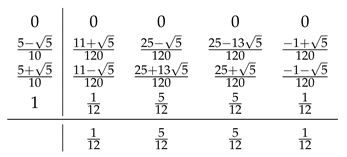
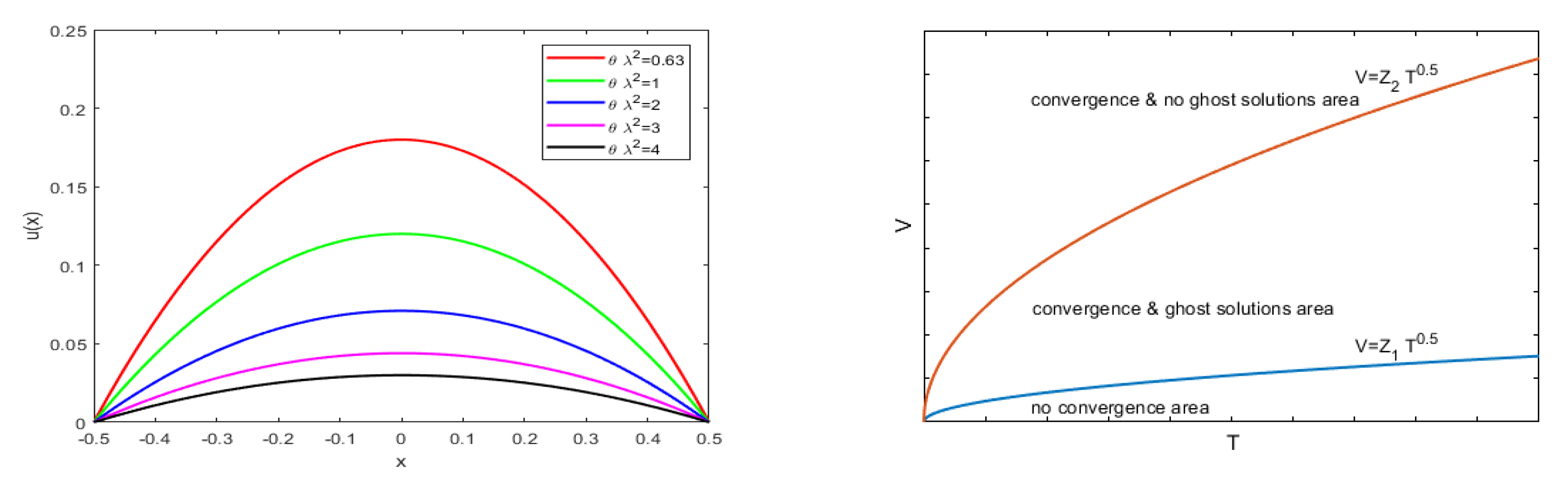
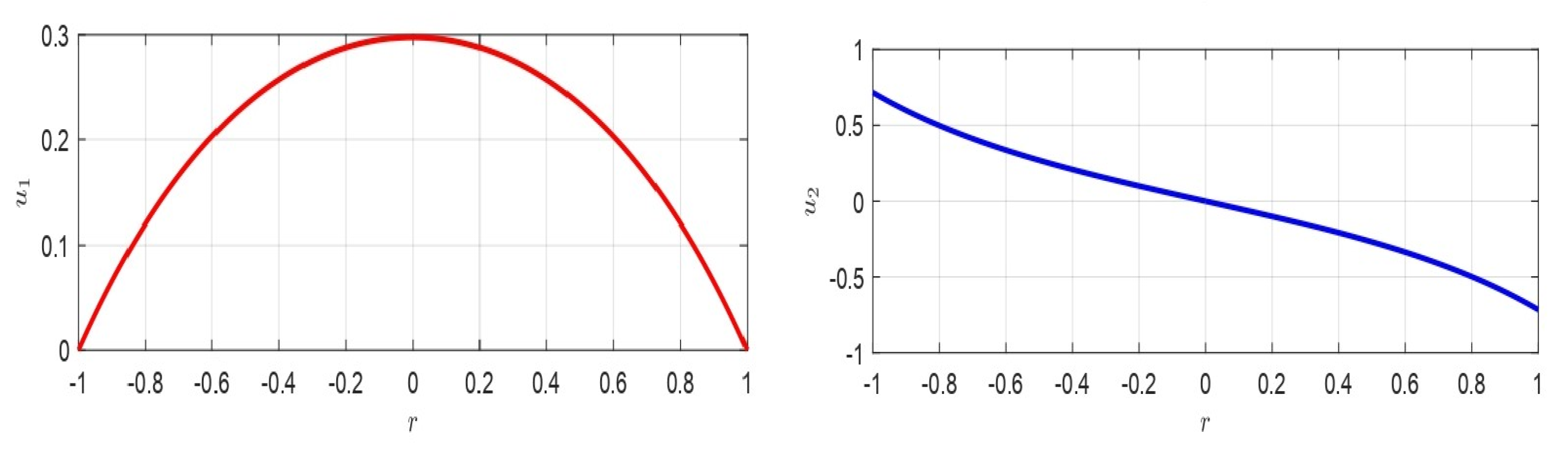
11.4. Numerical Results
11.5. Convergence of the Numerical Approaches
11.6. Convergence and Ghost Solutions
11.7. Range of Parameters for the Correct Use of the Device
12. Numerical Approaches for Recovering of the Membrane Profile in 2D Geometry
12.1. On the Applicability of the Numerical Procedure
12.2. Numerical Procedure and Convergence: Interesting Ranges of and
12.2.1. and Its Characteristics Ranges
- Case 1
- Case 2
- Case 3
12.2.2. and Analytical Condition of Uniqueness of the Solution
12.3. An Overview on the Ghost Solutions Areas
12.4. Electromechanical Properties of the Membrane, V and Ghost Solutions: Exploitation of the Device
13. Electromechanical Properties of the Membrane and Exploitation of the Device: A Useful Comparison between the 1D and 2D Formulations in Convergence Conditions
14. Conclusion and Perspectives
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MEMS | Micro-Electro-Mechanical-System |
| V | applied voltage |
| u | deflection of the membrane |
| electrostatic field | |
| amplitude of the electrostatic field | |
| K | curvature of the membrane |
| boundary region | |
| , , | parameters related to the electric and mechanic properties of the membrane |
| Coulombian exponent | |
| electrostatic potential | |
| D | flexural stiffness |
| T | mechanical tension of the membrane |
| permittivity of the free space | |
| distance between the two parallel plates | |
| rigidity of the plate | |
| aspect ratio of the system | |
| critical security distance | |
| electrostatic pressure | |
| p | mechanical pressure |
| k | coefficient of proportionality between and p |
| parameter of proportionality for | |
| function of proportionality between K and | |
| dielectric strength of the material constituting the membrane | |
| R | radius of the disks in 2D geometry |
| r | radial coordinate |
| electrostatic capacintance | |
| mean curvature | |
| G | Green function |
| H | |
| BVP | boundary value problem |
| IVP | initial value problem |
| RK | Runge–Kutta approach |
Appendix A. Mean Curvature and 2D Modellization
Appendix B
Appendix C. Proof of Theorem 1
Appendix D. Proof of Theorem 2
Appendix E. Proof of Theorem 3
Appendix F. Proof of Theorem 4
Appendix G. Proof of Theorem 5
Appendix H. Proof of Theorem 6
Appendix I. Proof of Theorem 7
Appendix J. Proof of Proposition 3
Appendix J.1. Linearization of the Non-Linear First-Order Differential Equations System around the Equilibrium Configuration
Appendix J.1.1. A Suitable Change of Variables
Appendix J.1.2. On the Use of the Taylor Series up to the First-Order
Appendix J.2. Stability of the Equilibrium Configuration
Appendix J.2.1. Eigenvalues of the Coefficient Matrix and Algebraic Multiplicity
Appendix J.2.2. Point of Equilibrium: Evaluation of Its stability
Appendix K. Proof of Proposition 42
Appendix L. Proof of Proposition 6
Appendix M. Proof of Proposition 8
Appendix N. Proof of Proposition 9
Appendix O. Proof of Proposition 10
References
- Khalaf, O.I.; Sabbar, B.M. An Overview on Wireless Sensor Networks and Finding Optimal Location of Nodes. Period. Eng. Nat. Sci. 2019, 7, 1096–1101. [Google Scholar] [CrossRef]
- Shetti, N.P.; Bukkitgar, D.; Reddy, R.R.; Reddy, C.V.; Aminabhavi, T.M. ZnO-based nanostructured electrodes for electrochemical sensors and biosensors in biomedical applications. Biosens. Bioelectron. 2019, 141, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Gao, Q.; Zhang, J.; Xie, Z.; Omisore, O.; Zhang, J.; Wang, L.; Li, H. Highly Stretchable Sensors for Wearable Biomedical Applications. J. Mater. Sci. 2019, 54, 5187–5223. [Google Scholar] [CrossRef]
- Di Barba, P.; Wiak, S. MEMS: Field Models and Optimal Design. In Lecture Notes in Electrical Engineering; Springer International Publishing, Springer Nature Switzerland AG: Cham, Switzerland, 2020. [Google Scholar]
- Pelesko, J.A.; Bernestein, D.H. Modeling MEMS and NEMS; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Di Barba, P.; Mognaschi, E.; Sieni, E. Many Objectiove Optimization of a Magnetic Micro-Electro-Mechanical (MEMS) Micromirror with Bounded MP-NSGA Algorithm. Mathematics 2020, 8, 1509. [Google Scholar] [CrossRef]
- Khoshnoud, F.; De Silva, F. Recent Advances in MEMS Sensor Technology—Biomedical Applications. IEEE Instrum. Meas. Mag. 2012. [Google Scholar] [CrossRef]
- Kimura, M. Temperature Sensors and Their Applications to MEMS Thermal Sensors. In Recent Advances in Sensing Technology. Lecture Notes in Electrical Engineering; Mukhopadhya, S.C., Gupta, G.S., Huangy, R.Y., Eds.; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Q.; Sun, Y.; Zhang, X.; Chen, J.; Yang, Z.; Ding, G. Ultrathin Radiation Coating Enabling High Accuracy and High Resolution Real-Time Infrared Imaging of Thermal MEMS Devices. In Proceedings of the 2019 IEEE 32nd International Conference on Micro Electro Mechanical Systems (MEMS), Seoul, Korea, 27–31 January 2019; pp. 1049–1052. [Google Scholar]
- Magrab, E.B. Vibrations of Elastic Systems with Applications to MEMS and NEMS; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Pelesko, J.A. Electrostatic in MEMS and NEMS. In Micromechanics and Nanoscale Effects; Springer: Dordrecht, The Netherlands, 2004; Volume 10. [Google Scholar]
- Plander, I.; Stepanovsky, M. MEMS Technology in Optical Switching. In Proceedings of the IEEE 10th International Scientific Conference on Informatics, Poprad, Slovakia, 14–16 November 2017. [Google Scholar]
- Brace, E. Opto-Mechanical Analysis of a Harsh Environment MEMS Fabry-Perot Pressure Sensor; University of Waterloo Library: Wasterloo, ON, Canada, 2019. [Google Scholar]
- Esposito, P.; Ghoussoub, N.; Guo, Y. Mathematical Analysis of Partial Differential Equations Modeling Electrostatic MEMS; American Mathematical Society: New York, NY, USA, 2010. [Google Scholar]
- Cassami, D.; d’O, M.; Ghoussoub, N. On a Fourth Order Elliptic Problem with a Singular Nonlinearity. Nonlinear Stud. 2009, 9, 189–209. [Google Scholar]
- Di Barba, P.; Fattorusso, L.; Versaci, M. Electrostatic field in terms of geometric curvature in membrane MEMS devices. Commun. Appl. Ind. Math. 2017, 8, 165–184. [Google Scholar] [CrossRef]
- Angiulli, G.; Jannelli, A.; Morabito, F.C.; Versaci, M. Reconstructing the membrane detection of a 1D electrostatic-driven MEMS device by the shooting method: Convergence analysis and ghost solutions identification. Comput. Appl. Math. 2018, 37, 4484–4498. [Google Scholar] [CrossRef]
- Fattorusso, L.; Versaci, M. A New One-Dimensionale Electrostatic Model for Membrane MEMS Devices, Engineering and Computer Science. In Proceedings of the World Congress on Engineering, London, UK, 4–6 July 2018; Volume 1, pp. 50–55. [Google Scholar]
- Versaci, M.; Angiulli, G.; Fattorusso, L.; Jannelli, A. On the uniqueness of the solution for a semi-linear elliptic boundary value problem of the membrane MEMS device for reconstructing the membrane profile in absence of ghost solution. Int. J. Non-Linear Mech. 2019, 109, 24–31. [Google Scholar] [CrossRef]
- Di Barba, P.; Fattorusso, L.; Versaci, M. A 2D Non-Linear Second-Order Differential Model for Electrostatic Circular Membrane MEMS Devices: A Result of Existence and Uniqueness. Mathematics 2019, 7, 1193. [Google Scholar] [CrossRef]
- Versaci, M.; Morabito, F.C. Membrane Micro Electro-Mechanical Systems for Industrial Applications. In Handbook of Research on Advanced Mechatronic Systems and Intelligent Robotics; IGI Global: Hershey, PA, USA, 2020; pp. 139–175. [Google Scholar]
- Versaci, M.; Jannelli, A.; Angiulli, G. Electrostatic Micro-Electro-Mechanical-Systems (MEMS) Devices: A Comparison Among Numerical Techniques for Recovering the Membrane Profile. IEEE Access 2020, 8, 125874–125886. [Google Scholar] [CrossRef]
- Versaci, M.; Angiulli, G.; Jannelli, A. Recovering of the Membrane Profile of an Electrostatic Circular MEMS by a Three-Stage Lobatto Procedure: A Convergence Analysis in the Absence of Ghost Solutions. Mathematics 2020, 8, 487. [Google Scholar] [CrossRef]
- Fattorusso, L.; Versaci, M. A New Mathematical Model for a Membrane MEMS Device. In Transactions on Engineering Technologies; Ao, S.-I., Gelman, L., Kim, H.K., Eds.; Springer: Singapore, 2020; pp. 1–18. [Google Scholar]
- Do Carmo, M.P. Differential Geometry of Curves and Surfaces; Prentice Hall, Inc.: Englewood, NJ, USA, 2016. [Google Scholar]
- DiBarba, P.; Fattorusso, L.; Versaci, M. Curvature Dependent Electrostatic Field in the Deformable MEMS Device: Stability and Optimal Control. Commun. Appl. Ind. Math. 2020, 11, 35–54. [Google Scholar]
- Ida, N. Engineering Electromagnetics; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Kline, M. Calculus—An Intuitive and Physical Approach. In Dover Books on Mathematics; Dover Publications: New York, NY, USA, 2009. [Google Scholar]
- Tu Lorin, W. Differential Geometry—Connections, Curvature, and Characteristic Classes; Springer International Publishing: Dallas, TX, USA, 2018. [Google Scholar]
- Iserles, A. A First Course in the Numerical Analysis of Differential Equations; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical M1thematics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Ghosh, P. Numerical, Symbolic and Statistical Computing for Chemical Engineers Using MatLab®; PHI: Delhi, India, 2018. [Google Scholar]
- Russell, R.D.; Shampine, L.F. Numerical Methods for Singular Boundary Value Problems. SIAM J. Num. Anal. 1975, 12, 13–36. [Google Scholar] [CrossRef]
- Bailey, P.B.; Shampine, L.F.; Waltman, P.E. Nonlinear Two Point Boundary Value Problems; Academic Press: New York, NY, USA; London, UK, 1968. [Google Scholar]
- Boyce, W.E.; DiPrima, R.C. Elementary Differential Equations and Boundary Value Problems; John Wiley & Sons, Inc.: London, UK, 2005. [Google Scholar]
- Bowman, F. Introduction to Bessel Functions; Dover Publications: Denver, CO, USA, 2013. [Google Scholar]



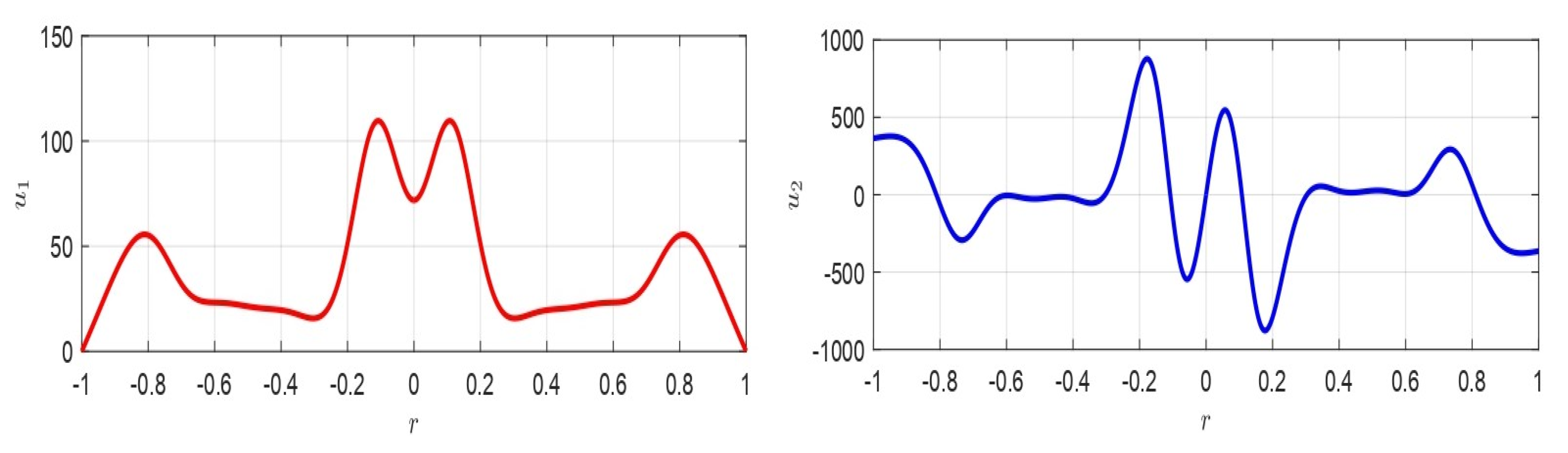
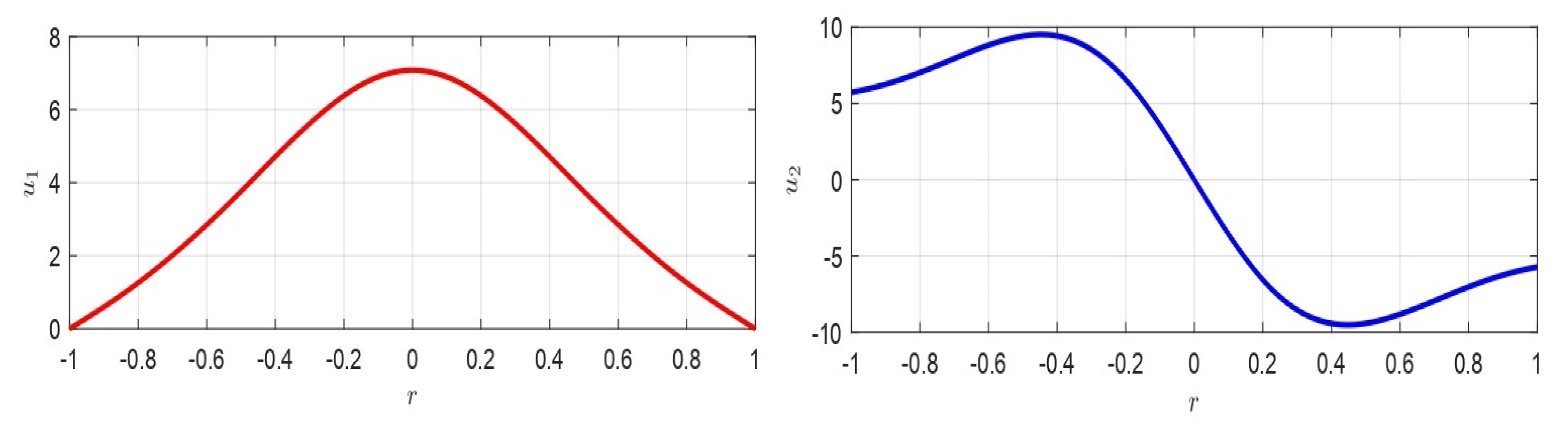
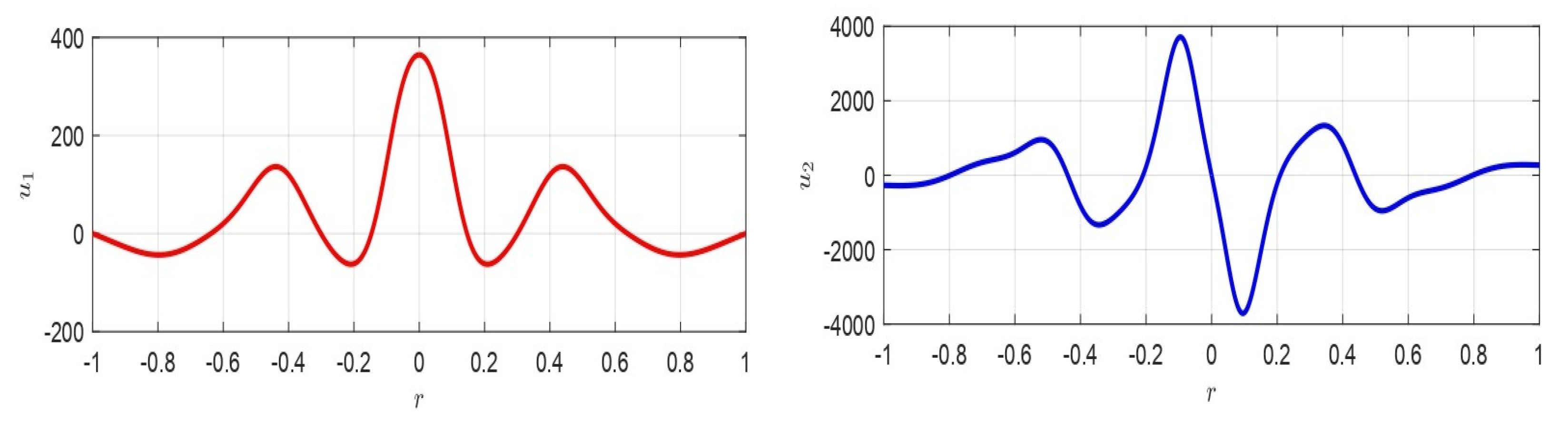


| 1D Geometry | 2D Geometry | |
|---|---|---|
| Existence | ||
| Uniqueness | not ensured | |
| Existence and Uniqueness |
| Methods | ||||
| Shoot&23 | 64 | 20 | ||
| Shoot&45 | 364 | 56 | ||
| Rel&Box | 4000 | 4000 | ||
| Col&III | 44 | 12 | ||
| Col&IV | 40 | 10 | ||
| Methods | ||||
| Shoot&23 | 14 | 14 | ||
| Shoot&45 | 52 | 52 | ||
| Rel&Box | 4000 | 4000 | ||
| Col&III | 4 | 4 | ||
| Col&IV | 6 | 4 | ||
| Shooting | ||
| ode23 | convergence | no convergence |
| Shooting | ||
| ode45 | convergence | no convergence |
| Keller-Box | ||
| convergence | no convergence | |
| Three Stage | ||
| Lobatto IIIa(bvp4c) | convergence | no convergence |
| Four Stage | ||
| Lobatto IIIa(bvp5c) | convergence | no convergence |
| No Convergence | Convergence and Instability | Convergence and Stability |
|---|---|---|
| No Ghost Solutions if | No Ghost Solutions | No Ghost Solutions |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Versaci, M.; di Barba, P.; Morabito, F.C. Curvature-Dependent Electrostatic Field as a Principle for Modelling Membrane-Based MEMS Devices. A Review. Membranes 2020, 10, 361. https://doi.org/10.3390/membranes10110361
Versaci M, di Barba P, Morabito FC. Curvature-Dependent Electrostatic Field as a Principle for Modelling Membrane-Based MEMS Devices. A Review. Membranes. 2020; 10(11):361. https://doi.org/10.3390/membranes10110361
Chicago/Turabian StyleVersaci, Mario, Paolo di Barba, and Francesco Carlo Morabito. 2020. "Curvature-Dependent Electrostatic Field as a Principle for Modelling Membrane-Based MEMS Devices. A Review" Membranes 10, no. 11: 361. https://doi.org/10.3390/membranes10110361
APA StyleVersaci, M., di Barba, P., & Morabito, F. C. (2020). Curvature-Dependent Electrostatic Field as a Principle for Modelling Membrane-Based MEMS Devices. A Review. Membranes, 10(11), 361. https://doi.org/10.3390/membranes10110361







