Short-Term Load Forecasting for Electric Vehicle Charging Stations Based on Deep Learning Approaches
Abstract
:1. Introduction
2. Deep Learning Models
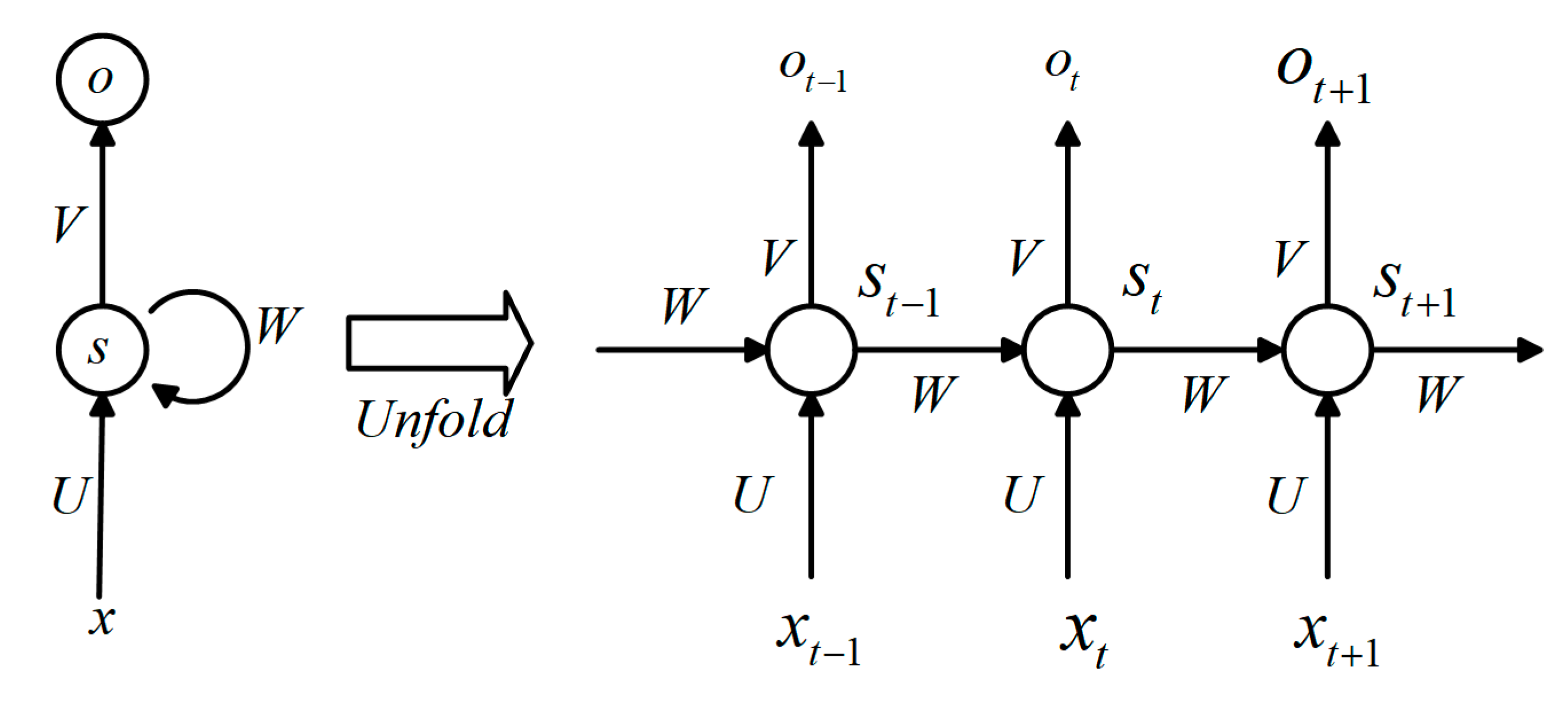
2.1. Recurrent Neural Networks
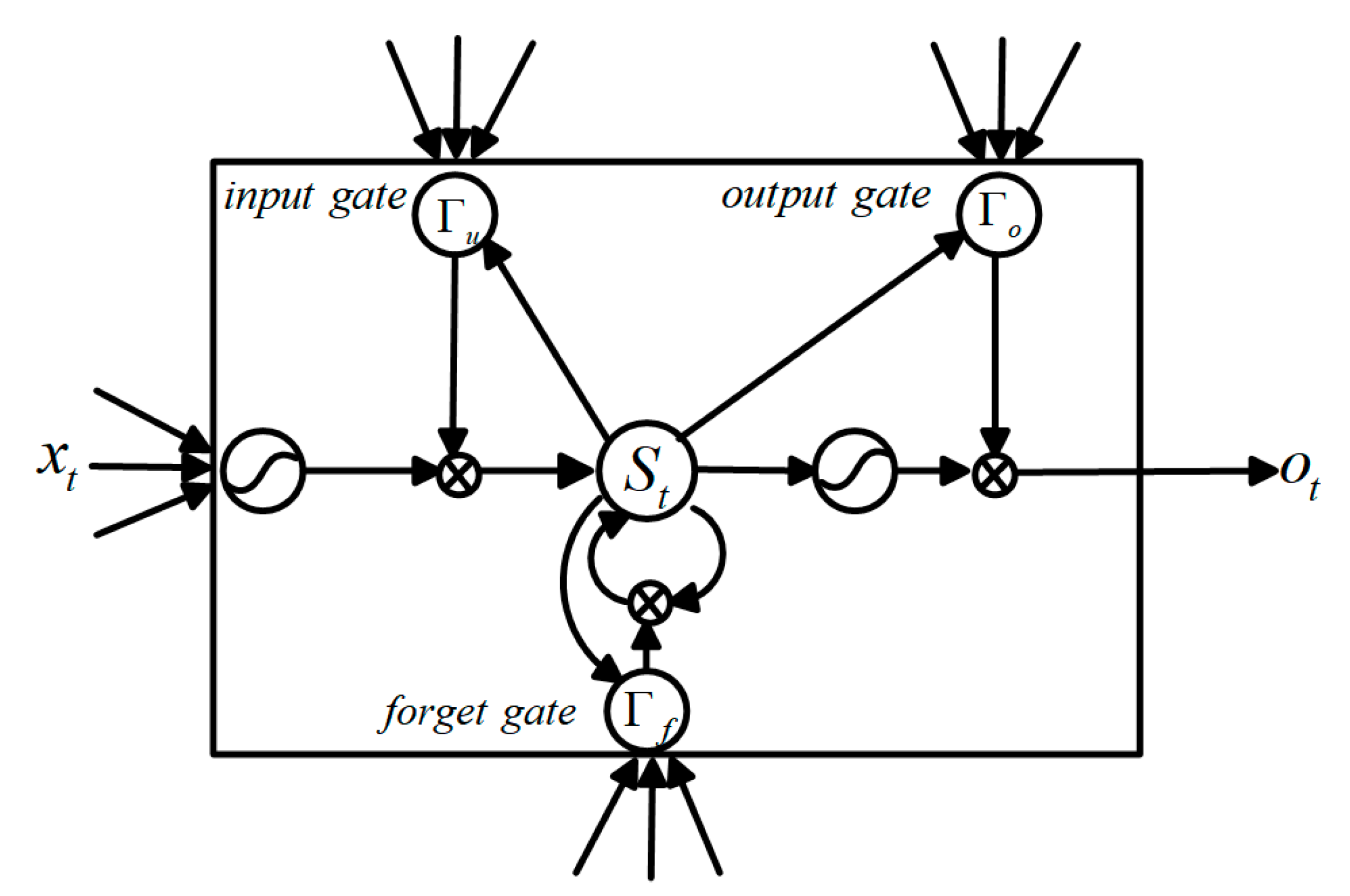
2.2. Long-Short Term Memory
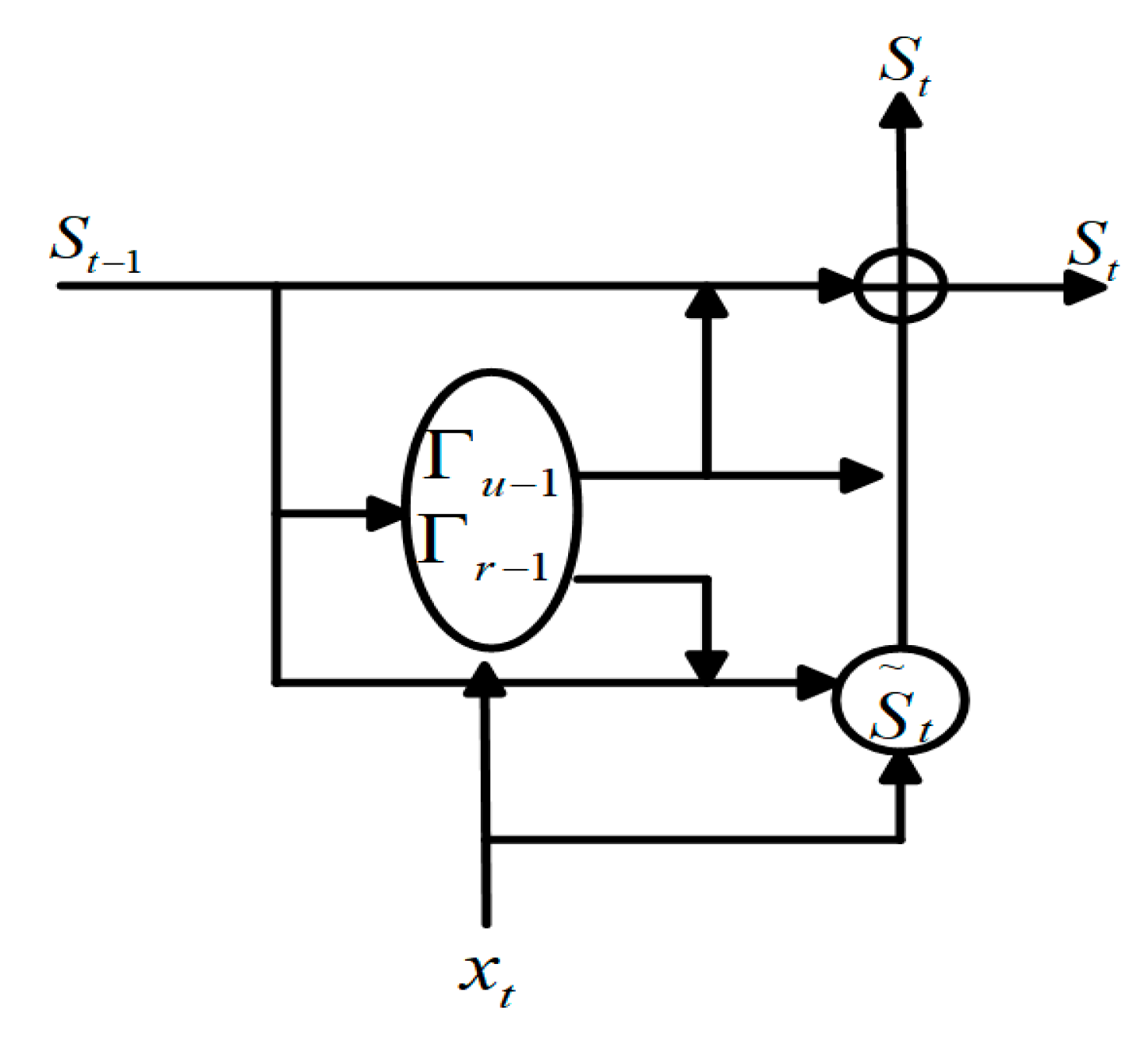
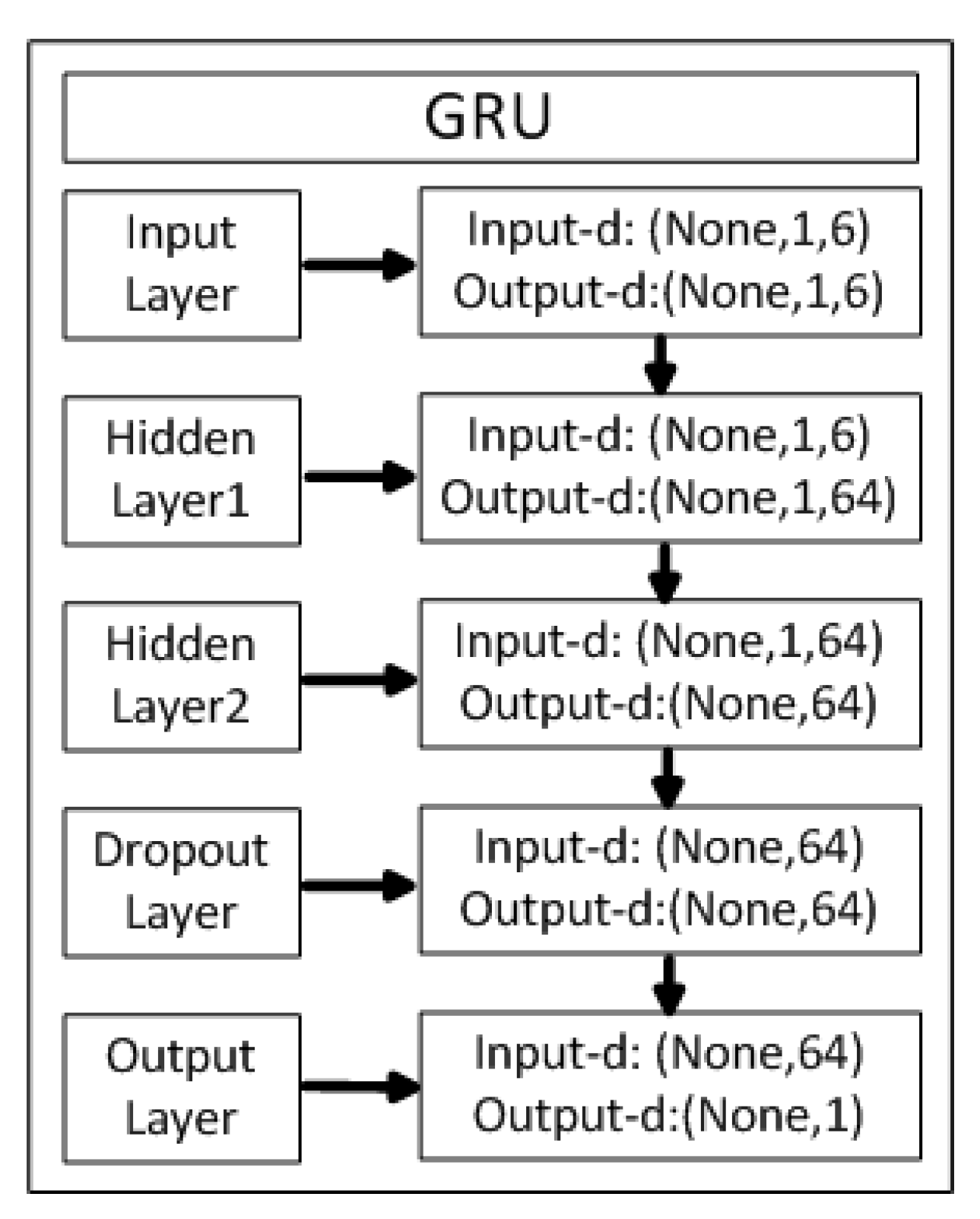
2.3. Gated Recurrent Units
3. Data Analysis and Forecasting Process
3.1. Introduction of the Dataset
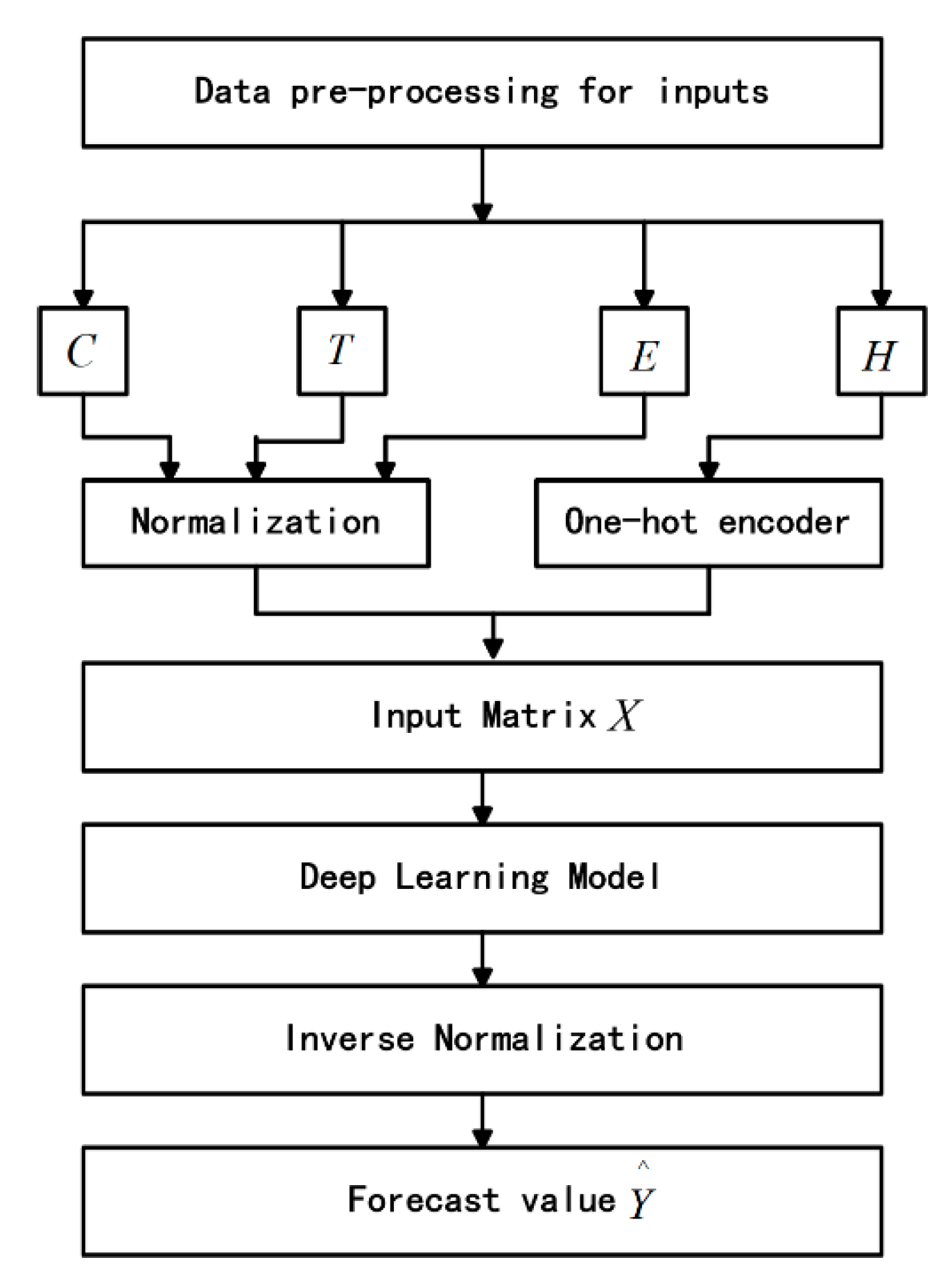
3.2. Data Pre-Processing
3.2.1. Outlier Processing
3.2.2. Time Interval Processing
3.2.3. Normalized Processing
3.3. Load Forecasting Based on Models
- The charging load sequence of 24 points per day from April 2017 to June 2018 is denoted as C.
- The charging time sequence of 24 points per day from April 2017 to June 2018 is represented as T.
- The sequence of real-time electricity prices for peak and valley periods is denoted as E. The real-time electricity price has a greater impact on the charging load. Most electric vehicles will choose to charge during the valley price period (23:00–7:00), and the charging load will reach the peak within one day. The charging load is usually at a minimum during the peak price (9:00–12:00, 14:00–17:00, 19:00–21:00).
- The corresponding binary holiday marks H involving the weekday and the weekend are 1 and 2 respectively, and a special holiday is 3.
4. Experimental Results and Discussion
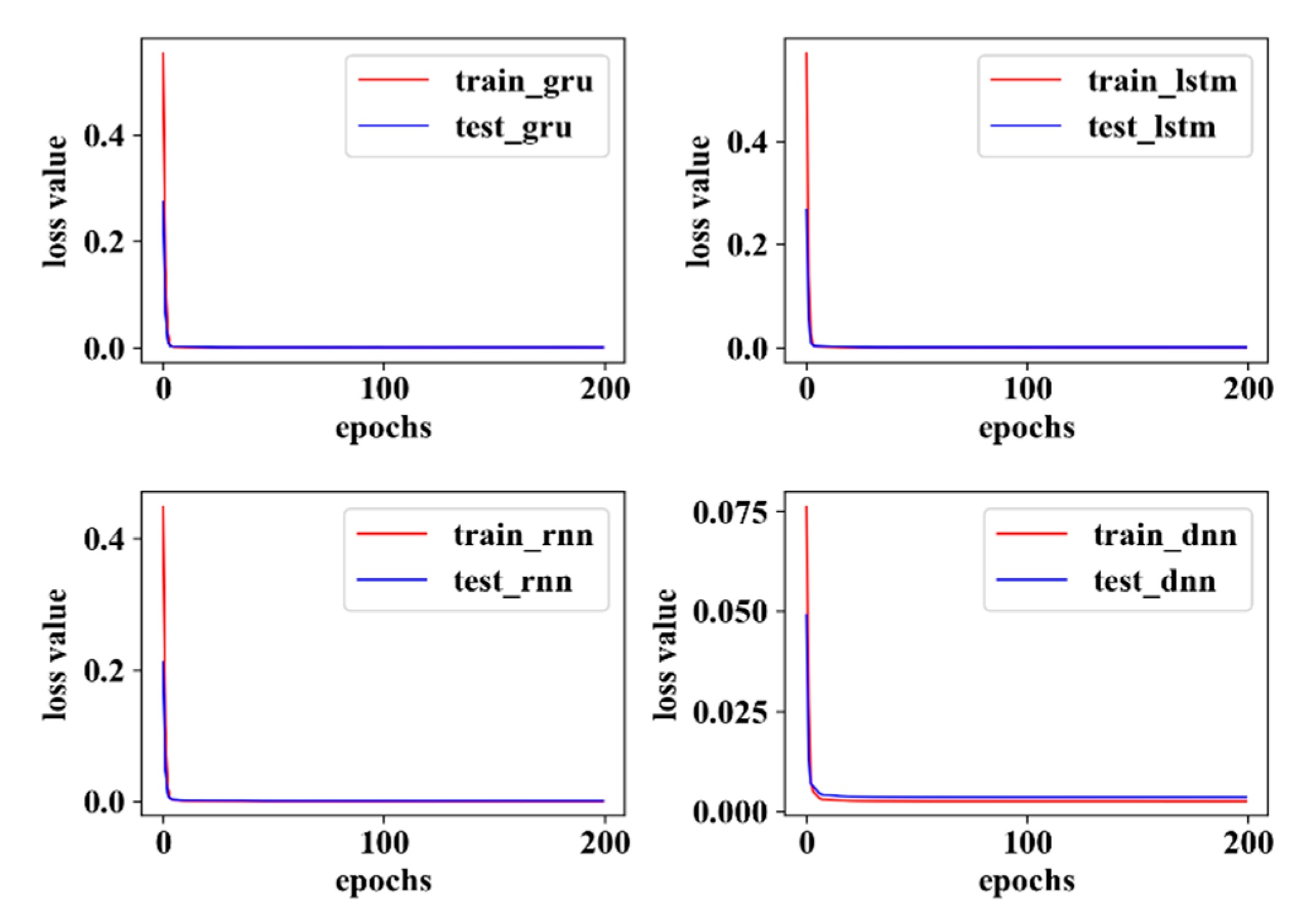
4.1. Model Evaluation
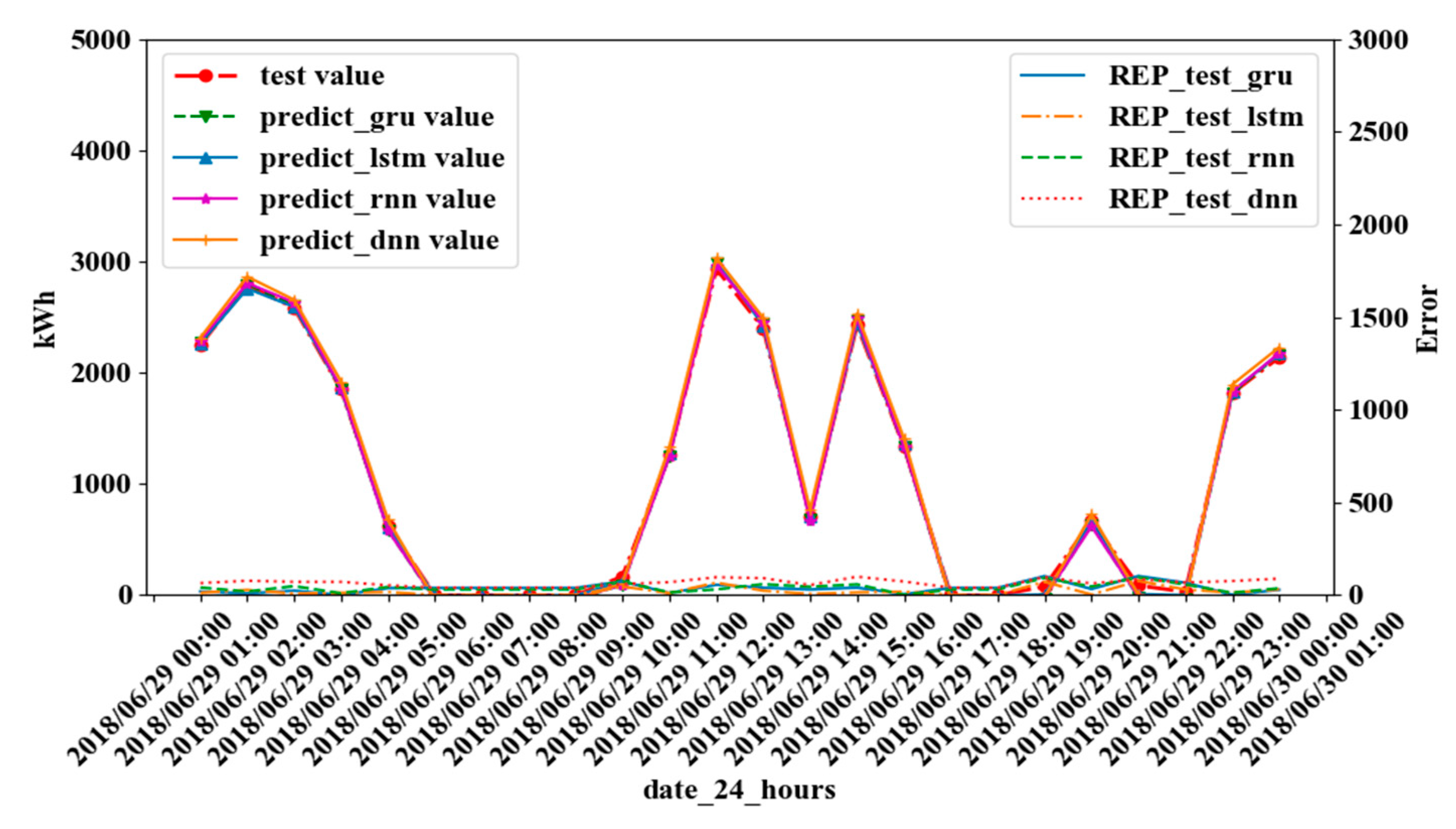
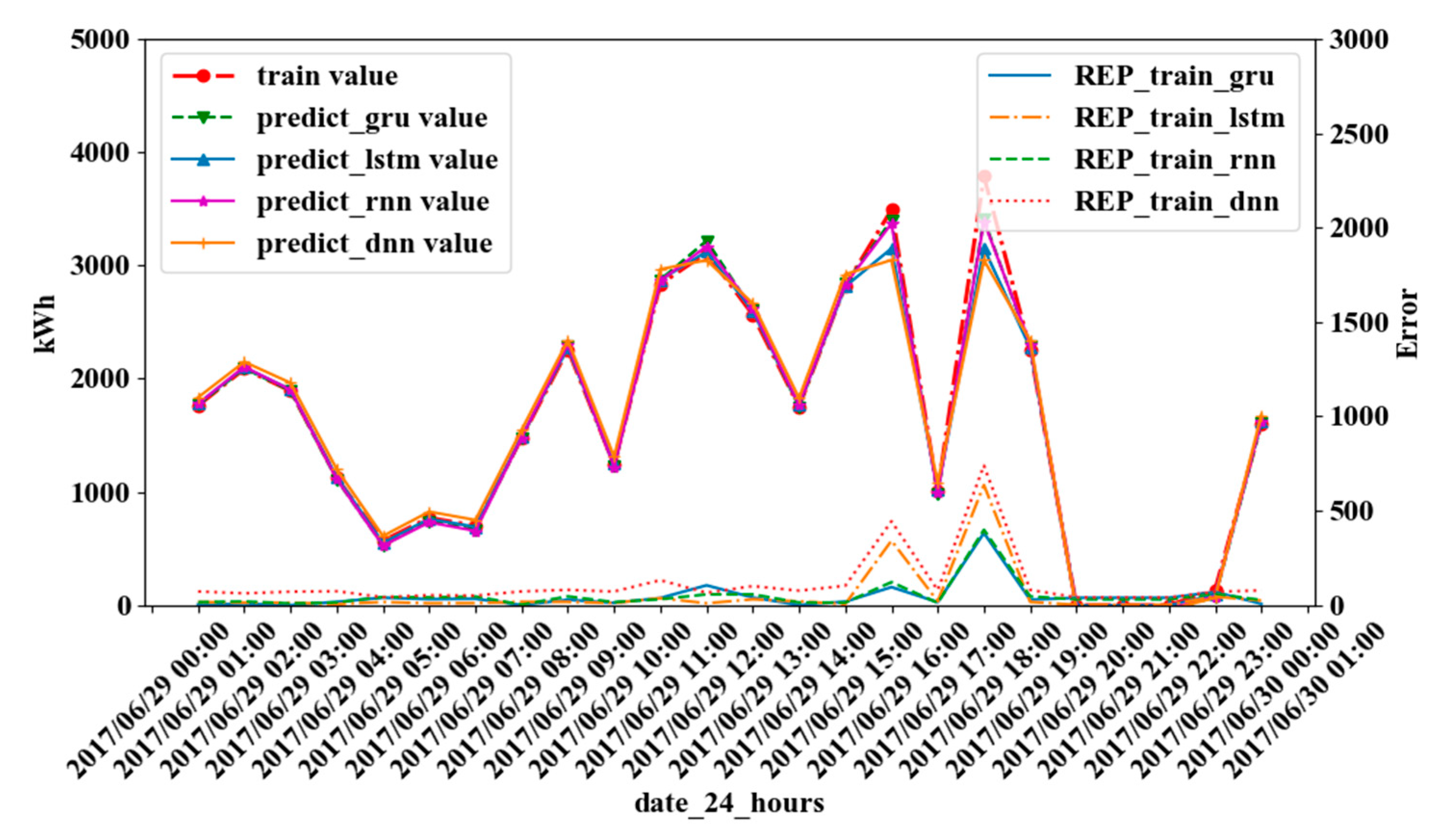
4.2. Experimental Results
5. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Lai, C.S.; Jia, Y.; Xu, Z.; Lai, L.L.; Li, X.; Cao, J.; McCulloch, M.D. Levelized cost of electricity for photovoltaic/biogas power plant hybrid system with electrical energy storage degradation costs. Energy Convers. Manag. 2017, 153, 34–47. [Google Scholar] [CrossRef]
- Lai, C.S.; Jia, Y.; Lai, L.L.; Xu, Z.; McCulloch, M.D.; Wong, K.P. A comprehensive review on large-scale photovoltaic system with applications of electrical energy storage. Renew. Sustain. Energy Rev. 2017, 78, 439–451. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Li, W.; Zhang, Z.-G. Based on time sequence of ARIMA model in the application of short-term electricity load forecasting. In Proceedings of the 2009 International Conference on Research Challenges in Computer Science, 28–29 December 2009; pp. 11–14. [Google Scholar]
- Haida, T.; Muto, S. Regression based peak load forecasting using a transformation technique. IEEE Trans. Power Syst. 1994, 9, 1788–1794. [Google Scholar] [CrossRef]
- Shankar, R.; Chatterjee, K.; Chatterjee, T.K. A Very Short-Term Load forecasting using Kalman filter for Load Frequency Control with Economic Load Dispatch. J. Eng. Sci. Technol. Rev. 2012, 5, 97–103. [Google Scholar] [CrossRef]
- Park, D.C.; El-Sharkawi, M.A.; Marks, R.J.; Atlas, L.E.; Damborg, M.J. Electric load forecasting using an artificial neural network. IEEE Trans. Power Syst. 1991, 6, 442–449. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.J.; Chang, M.W. Load forecasting using support vector machines: A study on EUNITE competition 2001. IEEE Trans. Power Syst. 2004, 19, 1821–1830. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 24–27 June 2014; pp. 580–587. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural network. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Vermaak, J.; Botha, E.C. Recurrent neural networks for short-term load forecasting. IEEE Trans. Power Syst. 1998, 13, 126–132. [Google Scholar] [CrossRef]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building energy load forecasting using deep neural networks. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; pp. 7046–7051. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M. Optimal deep learning lstm model for electric load forecasting using feature selection and genetic algorithm: Comparison with machine learning approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for solar power forecasting—An approach using AutoEncoder and LSTM Neural Networks. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 002858–002865. [Google Scholar]
- Kumar, J.; Goomer, R.; Singh, A.K. Long short term memory recurrent neural network (lstm-rnn) based workload forecasting model for cloud datacenters. Procedia Comput. Sci. 2018, 125, 676–682. [Google Scholar] [CrossRef]
- Kuan, L.; Yan, Z.; Xin, W.; Yan, C.; Xiangkun, P.; Wenxue, S.; Zhe, J.; Yong, Z.; Nan, X.; Xin, Z. Short-term electricity load forecasting method based on multilayered self-normalizing GRU network. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–5. [Google Scholar]
- Yunyan, L.; Yuansheng, H.; Meimei, Z. Short-Term Load Forecasting for Electric Vehicle Charging Station Based on Niche Immunity Lion Algorithm and Convolutional Neural Network. Energies 2018, 11, 1253. [Google Scholar] [Green Version]
- Cho, K.; Van Merriënboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Zeiler, M.D. ADADELTA: An adaptive learning rate method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Tieleman, T.; Hinton, G. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; Kudlur, M. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI’16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Oceans 1985, 90, 8995–9005. [Google Scholar] [CrossRef]
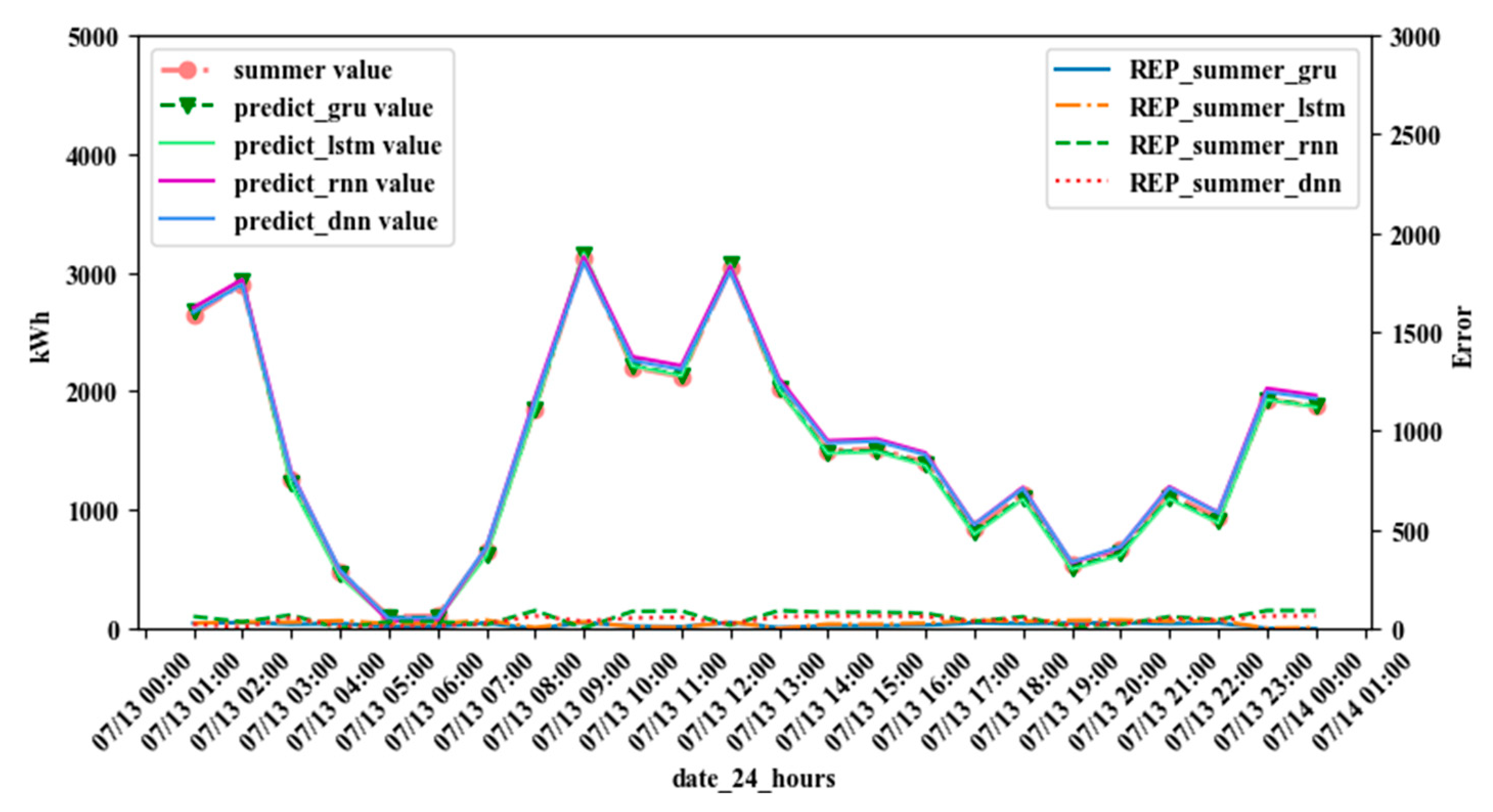
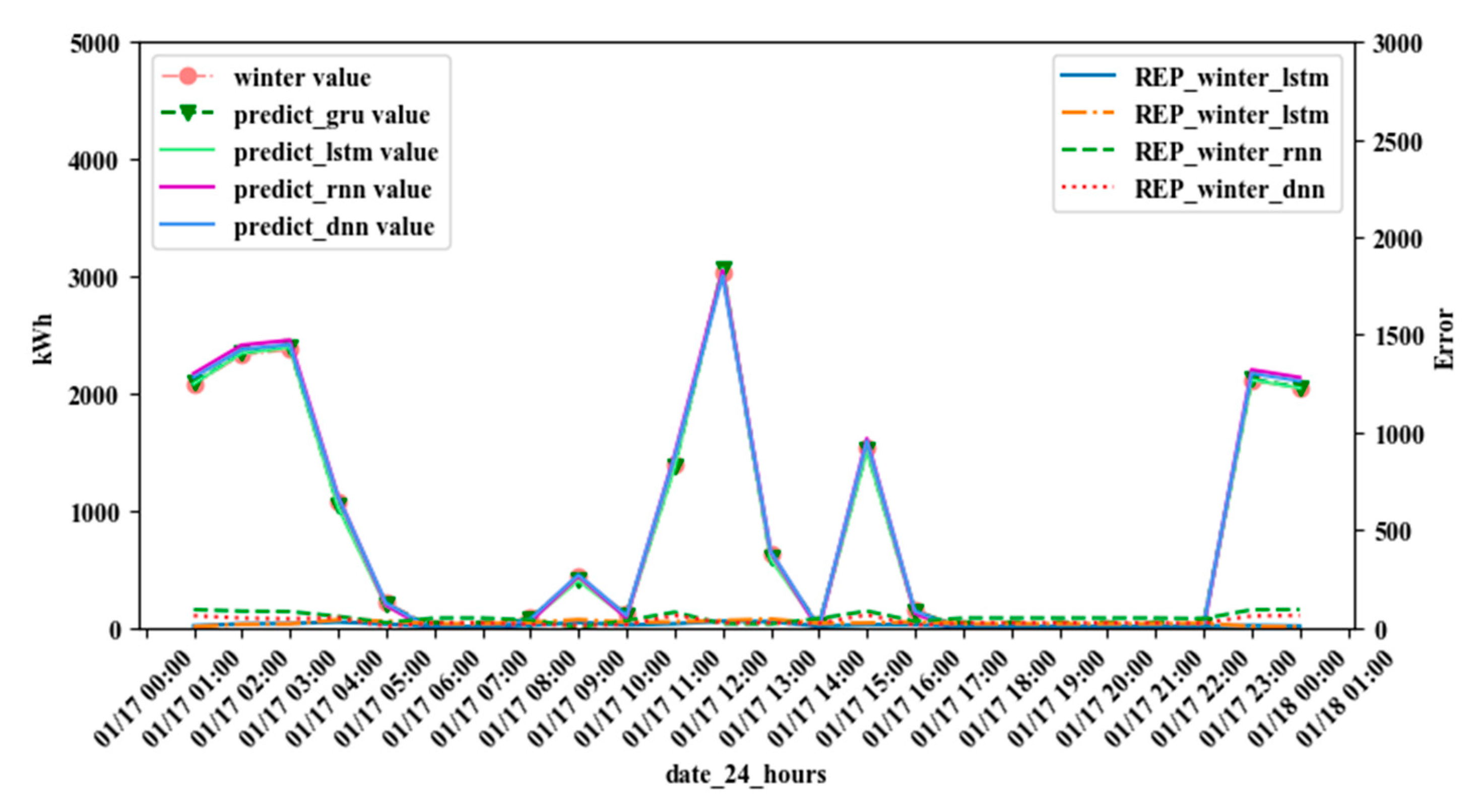
| Model | Hidden Layers | Train-NRMSE (%) | Test-NRMSE (%) | Train-NMAE (%) | Test-NMAE (%) |
|---|---|---|---|---|---|
| DNN | 2 3 4 | 2.05 1.97 1.98 | 3.69 3.79 3.81 | 1.06 0.50 0.46 | 1.32 0.94 0.92 |
| RNN | 1 2 3 | 1.50 1.52 1.61 | 2.91 2.91 2.96 | 0.62 0.70 0.84 | 0.91 1.01 1.19 |
| LSTM | 1 2 3 | 1.71 1.71 1.74 | 3.36 3.36 3.39 | 0.59 0.79 0.68 | 0.90 1.11 1.01 |
| GRU | 1 2 3 | 1.48 1.56 1.52 | 2.89 2.92 2.91 | 0.47 0.48 0.51 | 0.77 0.78 0.84 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Yang, Z.; Guo, Y.; Zhang, J.; Yang, H. Short-Term Load Forecasting for Electric Vehicle Charging Stations Based on Deep Learning Approaches. Appl. Sci. 2019, 9, 1723. https://doi.org/10.3390/app9091723
Zhu J, Yang Z, Guo Y, Zhang J, Yang H. Short-Term Load Forecasting for Electric Vehicle Charging Stations Based on Deep Learning Approaches. Applied Sciences. 2019; 9(9):1723. https://doi.org/10.3390/app9091723
Chicago/Turabian StyleZhu, Juncheng, Zhile Yang, Yuanjun Guo, Jiankang Zhang, and Huikun Yang. 2019. "Short-Term Load Forecasting for Electric Vehicle Charging Stations Based on Deep Learning Approaches" Applied Sciences 9, no. 9: 1723. https://doi.org/10.3390/app9091723
APA StyleZhu, J., Yang, Z., Guo, Y., Zhang, J., & Yang, H. (2019). Short-Term Load Forecasting for Electric Vehicle Charging Stations Based on Deep Learning Approaches. Applied Sciences, 9(9), 1723. https://doi.org/10.3390/app9091723





