Generalization of an Optical ASA Switch
Abstract
1. Introduction
2. Preliminaries
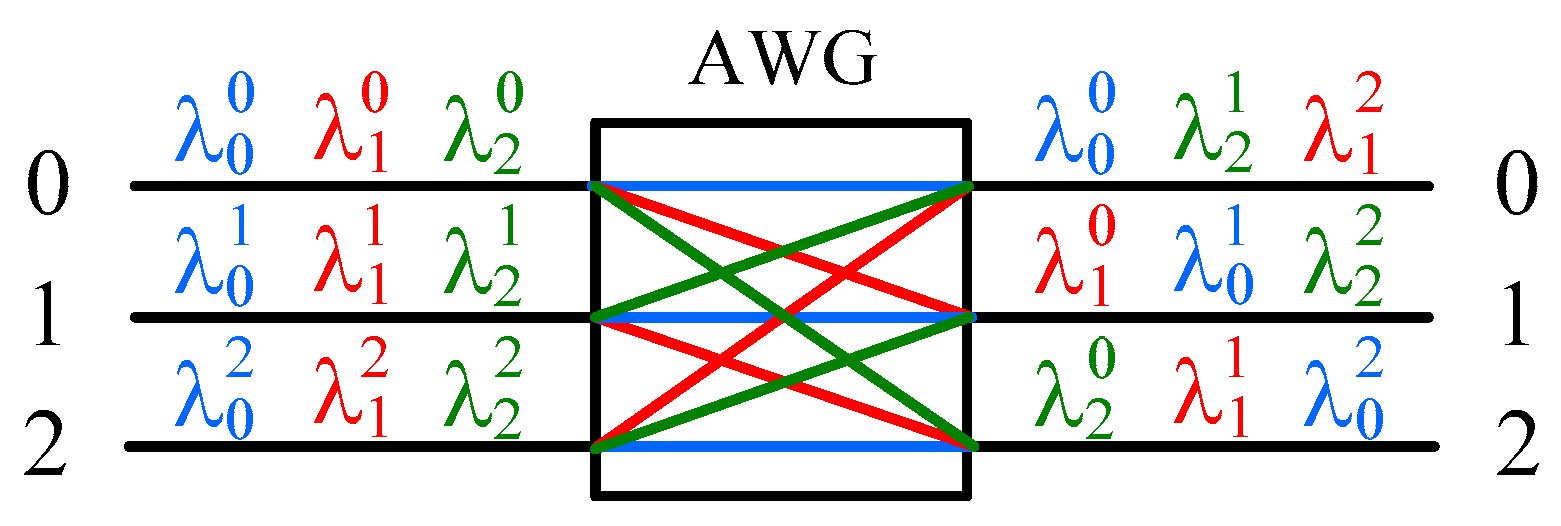
2.1. AWG
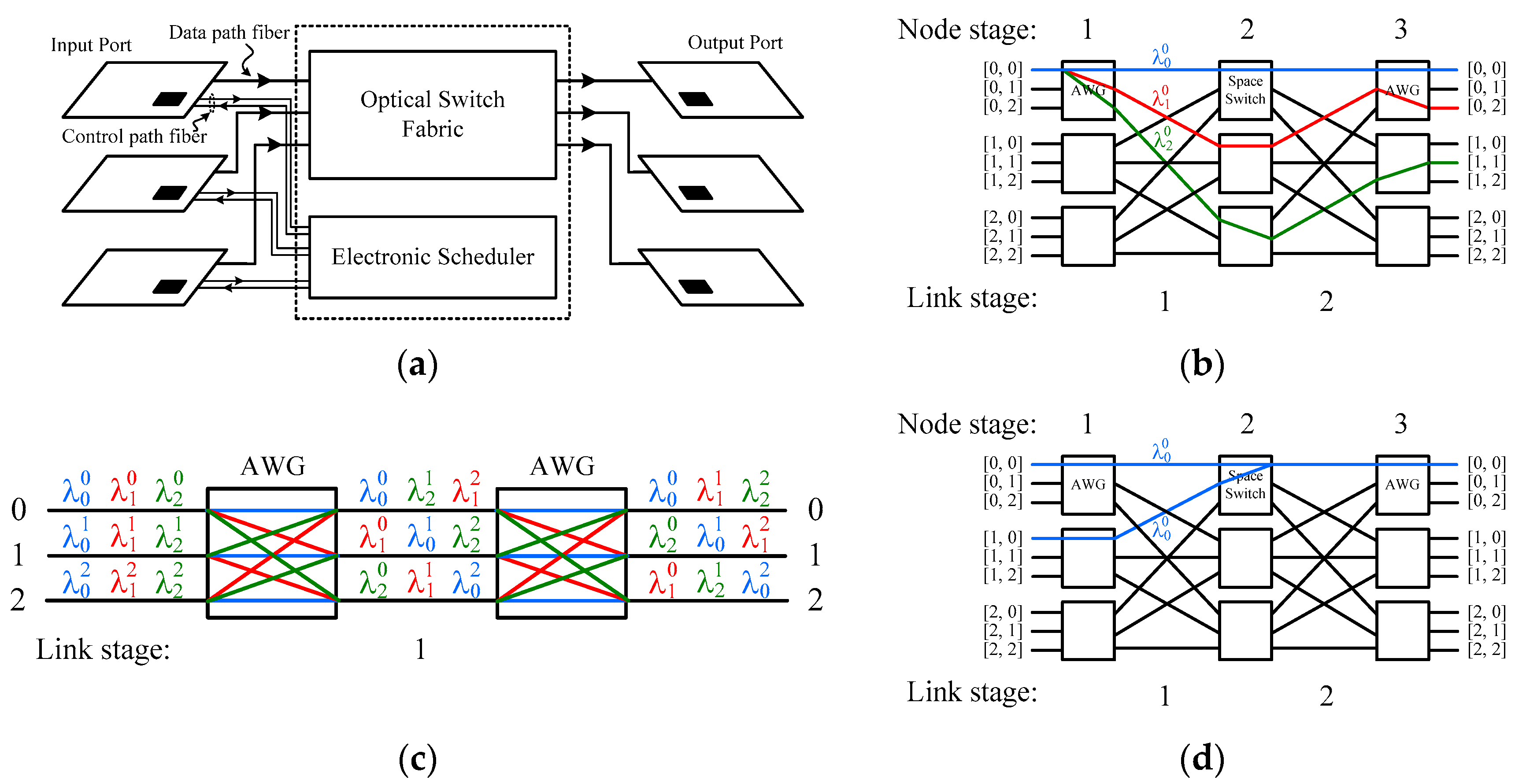
2.2. 3-Stage ASA Switch Architecture
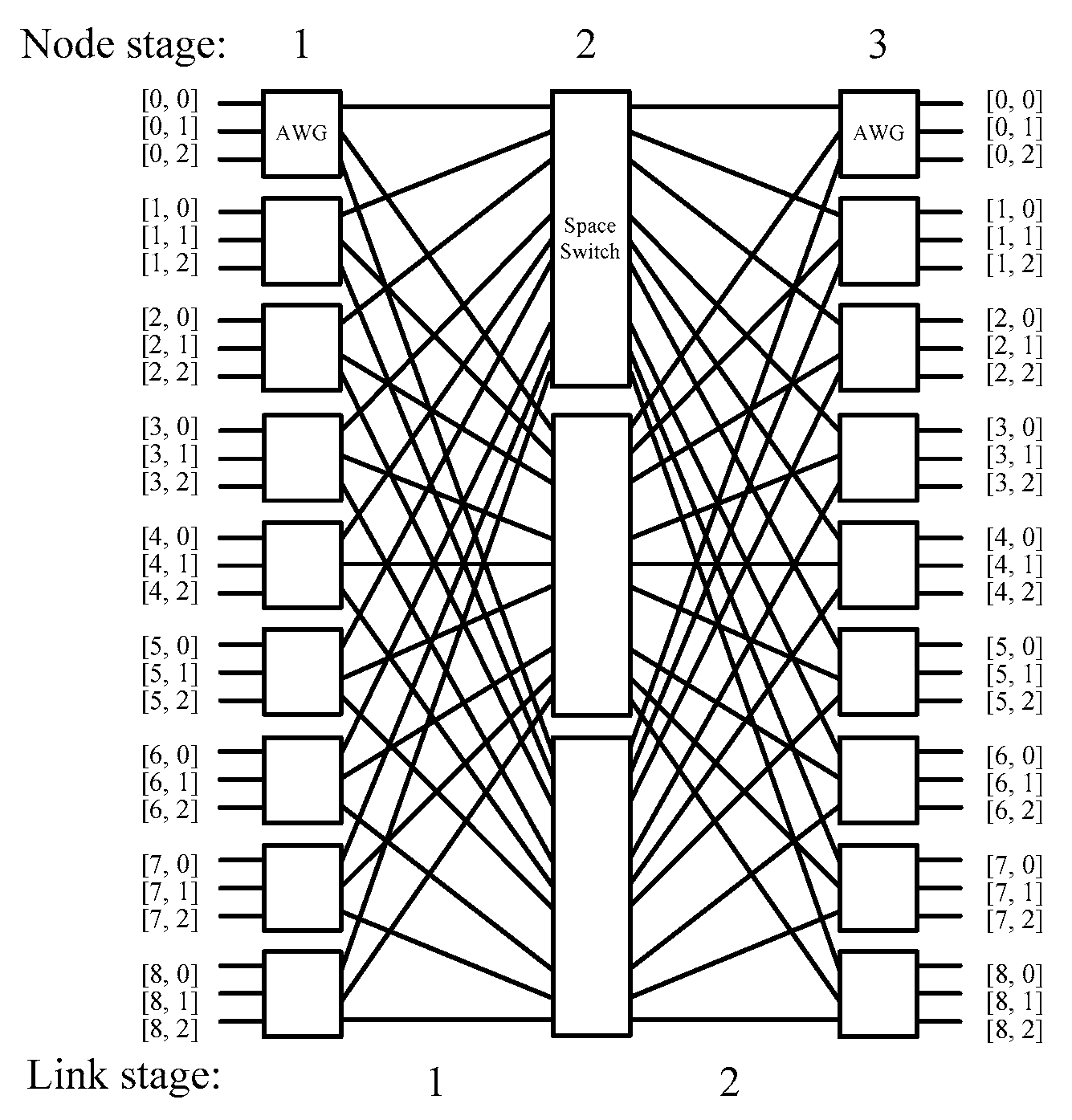
3. General 3-Stage ASA Switch Architecture
- (i)
- Equation (3) guarantees that each input [gs, ms] of an AWG in the first stage using N different wavelengths w can reach all outputs [gd, md] of an AWG in the last stage, if N is odd and the kth output of the AWG in the first stage connects the kth input of the AWG in the last stage [24]. Given an A(N, N, Nt−1) switch, since the kth space switch in the middle stage connects the kth output (or input) of each AWG in the first (or last) stage, it is implied that the kth output of each AWG in the first stage connects the kth input of all AWGs in the last stage through the kth space switch in the middle stage. Thus, each input can reach all outputs if it uses N different wavelengths.
- (ii)
- Given an A(N, N, Nt−1) switch, each link in stage 1 carries only signals from the same N × N AWG in the first stage. Recall that all the N2 signals of an N × N AWG can traverse the device simultaneously without blocking each other (Equation (1)). This implies that two different signals using the same wavelength will not pass through the same link in stage 1.
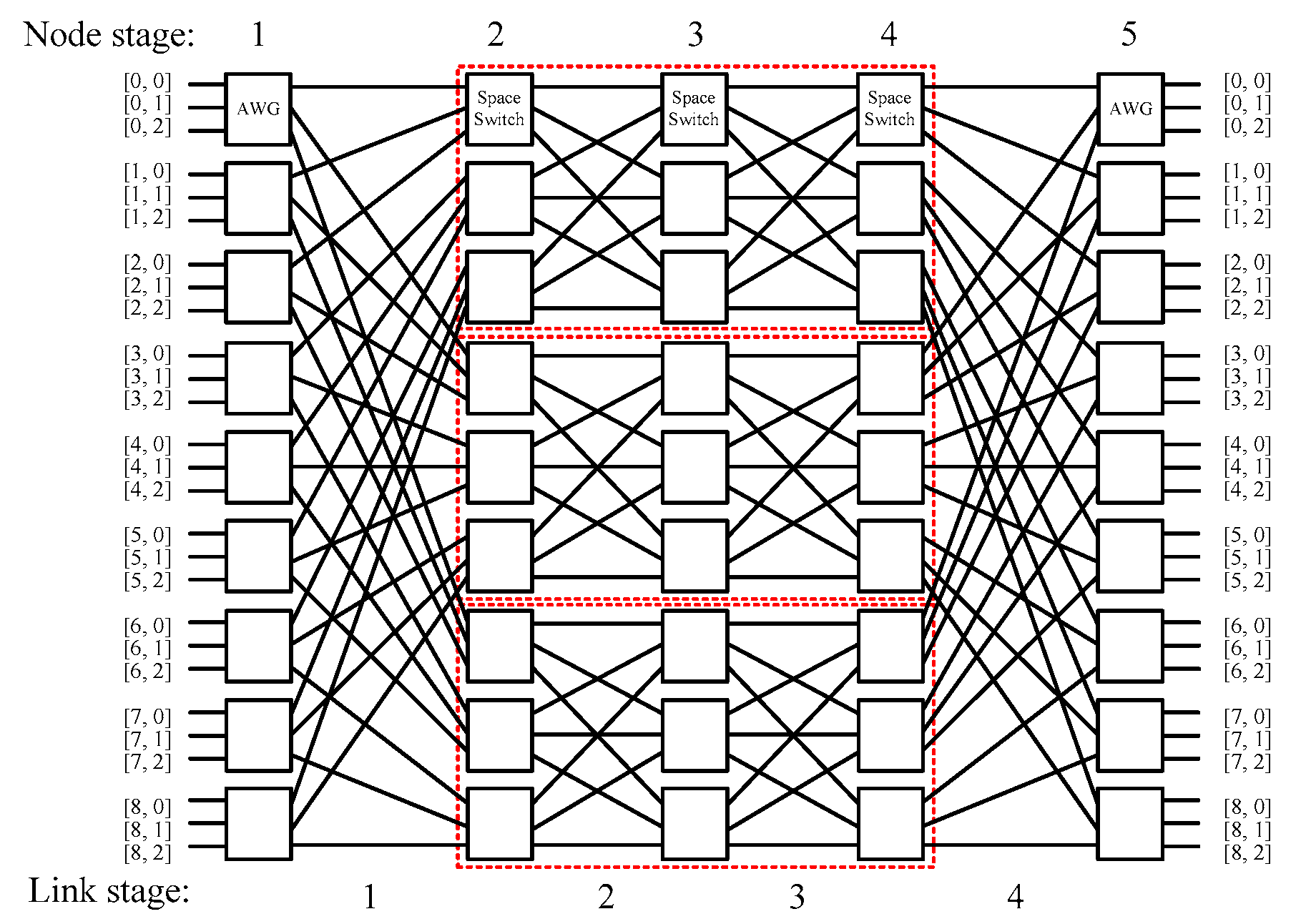
4. General Multi-Stage ASA Switch Architecture
4.1. Construction of a General Multi-Stage ASA Switch
4.2. Evaluation Results
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Salsi, M.; Koebele, C.; Tran, P.; Mardoyan, H.; Dutisseuil, E.; Renaudier, J.; Bigot-Astruc, M.; Provost, L.; Richard, S.; Sillard, P.; et al. Transmission of 96 × 100 Gb/s with 23% super-FEC overhead over 11,680km, using optical spectral engineering. In Proceedings of the 2011 Optical Fiber Communication Conference, Los Angeles, CA, USA, 6–10 March 2011. [Google Scholar]
- Okamoto, S.; Watanabe, A.; Sato, K.-I. Optical path cross-connect node architectures for photonic transport network. J. Lightw. Technol. 1996, 14, 1410–1422. [Google Scholar] [CrossRef]
- Iannone, E.; Sabella, R. Optical path technologies: A comparison among different cross-connect architectures. J. Lightw. Technol. 1996, 14, 2184–2196. [Google Scholar] [CrossRef]
- Marom, D.M.; Blau, M. Switching Solutions for WDM-SDM Optical Networks. IEEE Commun. Mag. 2015, 53, 60–68. [Google Scholar] [CrossRef]
- Cheyns, J.; Develder, C.; Breusegem, E.V.; Colle, D.; Turck, F.D.; Lagasse, P.; Pickavet, M.; Demeester, P. Clos lives on in optical packet switching. IEEE Commun. Mag. 2004, 42, 114–120. [Google Scholar] [CrossRef]
- Pattavina, A.; Zanzottera, R. Non-blocking WDM switches based on arrayed waveguide grating and shared wavelength conversion. In Proceedings of the IEEE INFOCOM 2006. 25th IEEE International Conference on Computer Communications, Barcelona, Spain, 23–29 April 2006. [Google Scholar]
- Ngo, H.Q.; Pan, D.; Qiao, C. Constructions and analyses of nonblocking WDM switches based on arrayed waveguide grating and limited wavelength conversion. IEEE Trans. Netw. 2006, 14, 205–217. [Google Scholar] [CrossRef]
- Ye, T.; Lee, T.T.; Hu, W. AWG-Based Non-Blocking Clos Networks. IEEE Trans. Netw. 2015, 23, 491–504. [Google Scholar] [CrossRef]
- Ye, T.; Lee, T.T.; Hu, W. A study of modular AWGs for large-scale optical switching systems. J. Lightw. Technol. 2012, 30, 2125–2133. [Google Scholar] [CrossRef]
- Eramo, V.; Listanti, M. Power Consumption in Bufferless Optical Packet Switches in SOA Technology. J. Commun. Netw. 2009, 1, B15–B29. [Google Scholar] [CrossRef]
- Yin, Y.; Proietti, R.; Ye, X.; Nitta, C.; Akella, V.; Yoo, S.J.B. LIONS: An AWGR-based low latency optical switch for high-performance computing and data centers. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 3600409. [Google Scholar] [CrossRef]
- Proietti, R.; Cao, Z.; Nitta, C.; Li, Y.; Yoo, S.J.B. A scalable, low-latency, high throughput, optical interconnect architecture based on arrayed waveguide grating routers. J. Lightw. Technol. 2015, 33, 911–920. [Google Scholar] [CrossRef]
- Grani, P.; Proietti, R.; Cheung, S.; Yoo, S.J.B. Flat-topology high-throughput compute node with AWGR-based optical-interconnects. J. Lightw. Technol. 2016, 34, 2959–2968. [Google Scholar] [CrossRef]
- Lin, B.C.; Lea, C.T. Construction of nonblocking wavelength/space switches with AWGs and WSSes. Appl. Sci. 2017, 7, 555–570. [Google Scholar] [CrossRef]
- Xiao, X.; Proietti, R.; Zhang, K.; Yoo, S.J.B. Experimental demonstration of flex-LIONS for reconfigurable all-to-all optical interconnects. In Proceedings of the 2018 European Conference on Optical Communication, Roma, Italy, 23–27 September 2018. [Google Scholar]
- Takahashi, H.; Oda, K.; Toba, H. Impact of crosstalk in an arrayed waveguide multiplexer on N × N optical interconnection. J. Lightw. Technol. 1996, 14, 1097–1105. [Google Scholar] [CrossRef]
- Bianco, A.; Hay, D.; Neri, F. Crosstalk-preventing scheduling in single-and two-stage AWG-based cell switches. IEEE/ACM Trans. Netw. 2010, 19, 142–155. [Google Scholar] [CrossRef]
- Kamei, S.; Ishii, M.; Kaneko, A.; Itoh, M. N × N cyclic frequency router with improved performance based on arrayed waveguide grating. J. Lightw. Technol. 2009, 27, 4097–4104. [Google Scholar] [CrossRef]
- Monnard, P.; Doerr, C.R.; Dragone, C.; Cappuzzo, M.; Laskowski, E.; Paunescu, A. Large N × N waveguide grating routers. J. Lightw. Technol. 2000, 18, 985–991. [Google Scholar]
- Niwa, T.; Hasegawa, H.; Sato, K.; Watanabe, T.; Takahashi, H. Large port count wavelength routing optical switch consisting of cascaded small size cyclic arrayed waveguide gratings. IEEE Photon. Technol. Lett. 2012, 24, 2027–2030. [Google Scholar] [CrossRef]
- N × N AWG Multiplexers and Demultiplexers Router Module (APRTE). Available online: http://www.enablence.com/media/pdfs/Datasheet_OCSD_AWG_Other_NxN_APRTE_0.pdf (accessed on 1 January 2019).
- Xi, K.; Kao, Y.H.; Yang, M.; Chao, H.J. Petabit Optical Switch for Data Center Networks; Technical Report; Polytechnic Institute of New York University: Brooklyn, NY, USA, September 2010. [Google Scholar]
- Sato, K.; Hasegawa, H.; Niwa, T.; Watanabe, T. A large scale wavelength routing optical switch for high-performance computing and data centers. IEEE Commun. Mag. 2013, 51, 46–52. [Google Scholar] [CrossRef]
- Lea, C.T. Scalable AWGR-based optical switch. J. Lightw. Technol. 2015, 33, 4612–4621. [Google Scholar]
- Chen, S.; Lea, C.T. On scalability of AWGR-based optical switches. In Proceedings of the 2016 Photonics North (PN), Quebec City, QC, Canada, 24–26 May 2016. [Google Scholar]
- Hwang, F. The Mathematical Theory of Nonblocking Switching Networks; World Scientific: Singapore, 2004. [Google Scholar]
- Ramamirtham, J.; Turner, J.; Friedman, J. Design of wavelength converting switches for optical burst switching. IEEE J. Sel. Areas Commun. 2003, 21, 1122–1132. [Google Scholar] [CrossRef]
- Maier, G.; Valzasina, P.; Pattavina, A. AWG-based shuffle-exchange optical-interconnection architectures. In Proceedings of the 2011 Proceedings of 20th International Conference on Computer Communications and Networks (ICCCN), Maui, HI, USA, 31 July–4 August 2011. [Google Scholar]
- Benes, V.E. Mathematical Theory of Connecting Networks and Telephone Traffic; Academic: New York, NY, USA, 1965. [Google Scholar]
- McKeown, N. iSLIP: A scheduling algorithm for input-queued switches. IEEE Trans. Netw. 1999, 7, 188–201. [Google Scholar] [CrossRef]
- Web Portal of Apollo Inc. APSS Apollo Application Note on Array Waveguide Grating (AWG). 2003. Available online: https://zh.scribd.com/document/329520304/APN-APSS-AWG-pdf (accessed on 1 January 2019).
- High Performance RF/Microwave GaAs MMIC Switches for SPST, SPDT, SP3T, SP4T, and SP5T Switching Requirements. Available online: https://www.custommmic.com/mmic-switches/ (accessed on 1 January 2019).
| t = 2 | t = 3 | t = 4 | t = 5 | t = 6 | |
|---|---|---|---|---|---|
| Size of multi-stage ASA | 312 × 312 | 313 × 313 | 314 × 314 | 315 × 315 | 316 × 316 |
| Power loss | 16 dB | 20 dB | 24 dB | 28 dB | 32 dB |
| Maximum number of space switches | 31 | 2883 | 148,955 | 6,464,647 | 257,662,359 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, B.-C. Generalization of an Optical ASA Switch. Appl. Sci. 2019, 9, 1096. https://doi.org/10.3390/app9061096
Lin B-C. Generalization of an Optical ASA Switch. Applied Sciences. 2019; 9(6):1096. https://doi.org/10.3390/app9061096
Chicago/Turabian StyleLin, Bey-Chi. 2019. "Generalization of an Optical ASA Switch" Applied Sciences 9, no. 6: 1096. https://doi.org/10.3390/app9061096
APA StyleLin, B.-C. (2019). Generalization of an Optical ASA Switch. Applied Sciences, 9(6), 1096. https://doi.org/10.3390/app9061096





