The Exoskeleton Balance Assistance Control Strategy Based on Single Step Balance Assessment
Abstract
1. Introduction
2. Single Step Balance Assessment Method
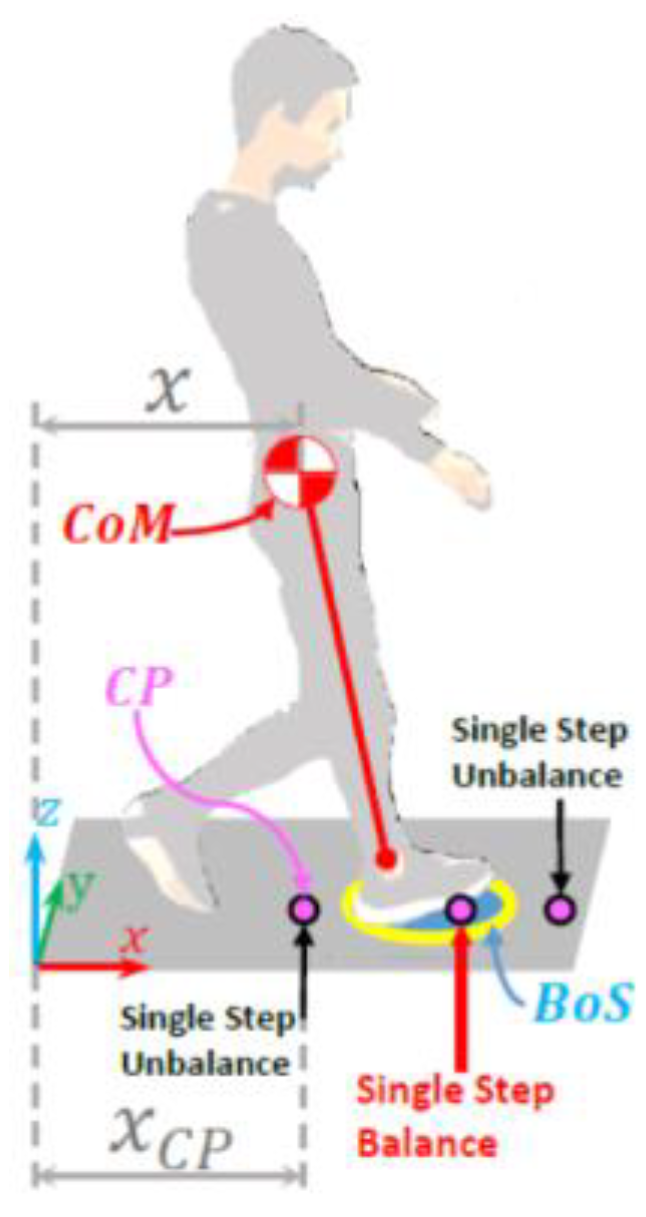
2.1. The Concept of Single Step Balance
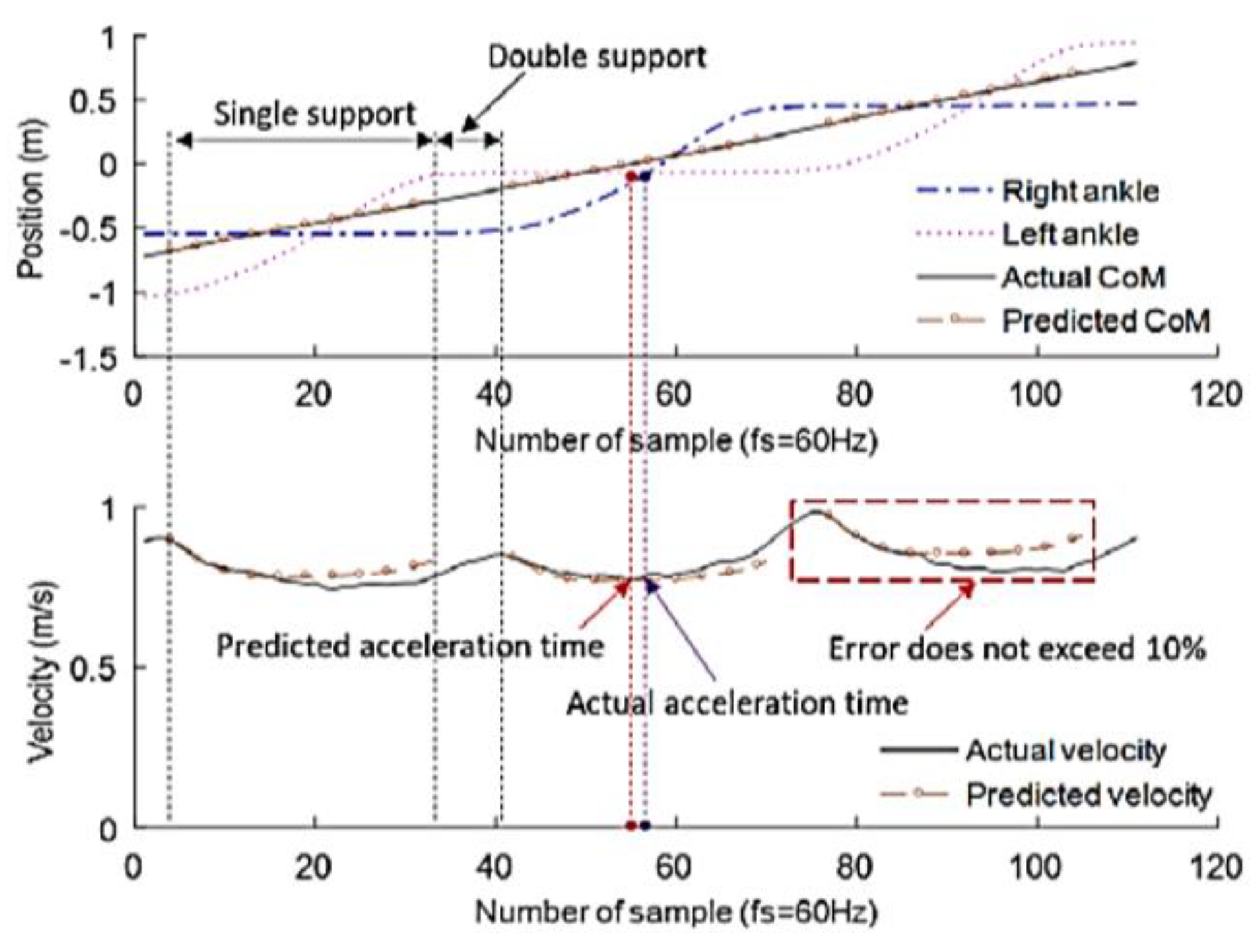
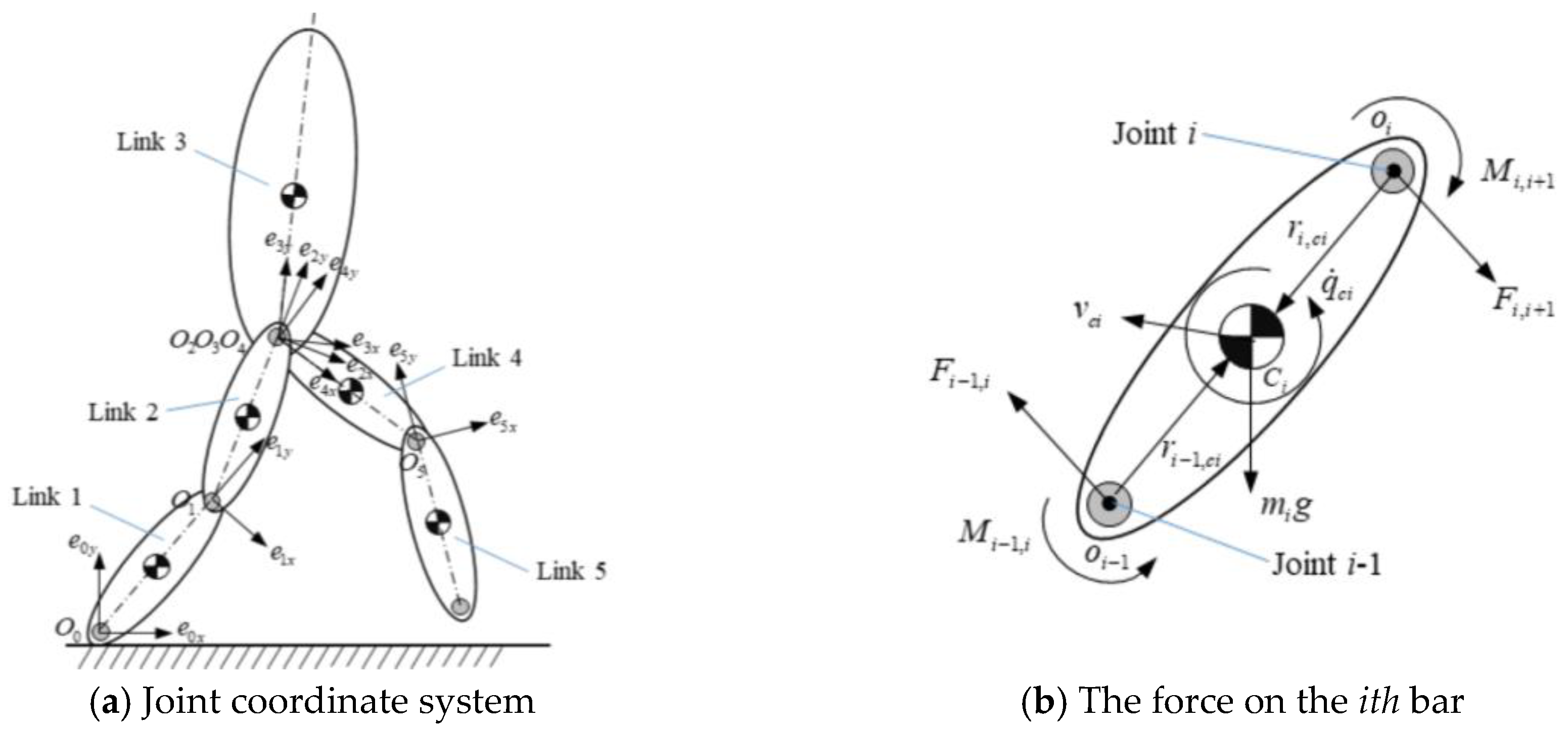
2.2. Method for Single Step Balance Assessment
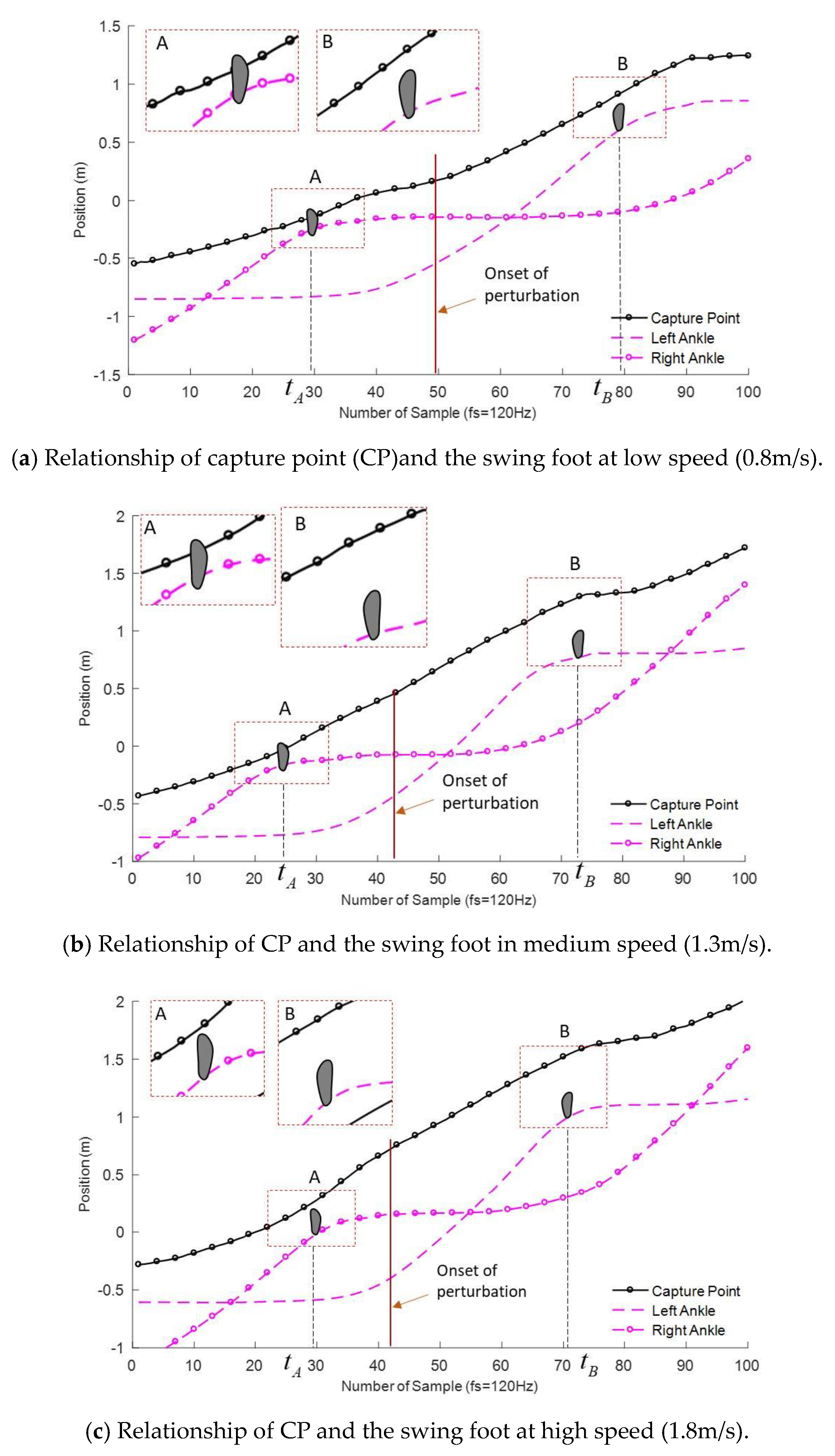
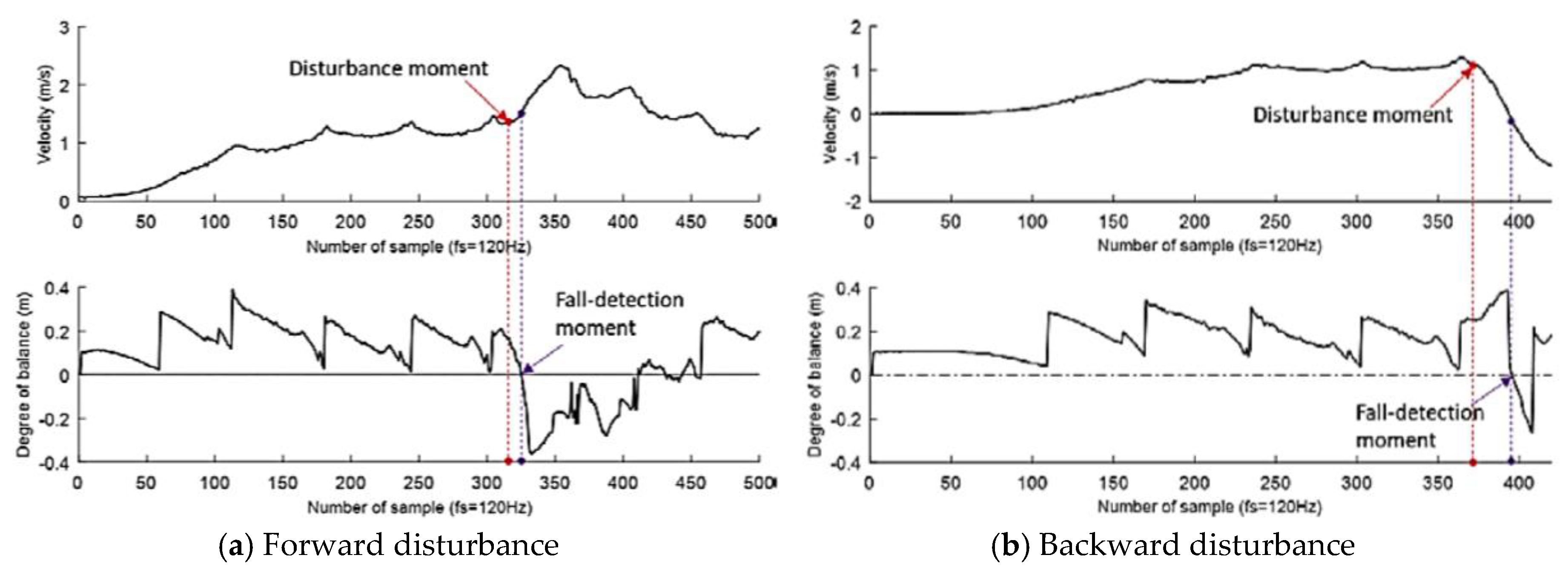
2.3. Single Step Balance Assesment Experiment
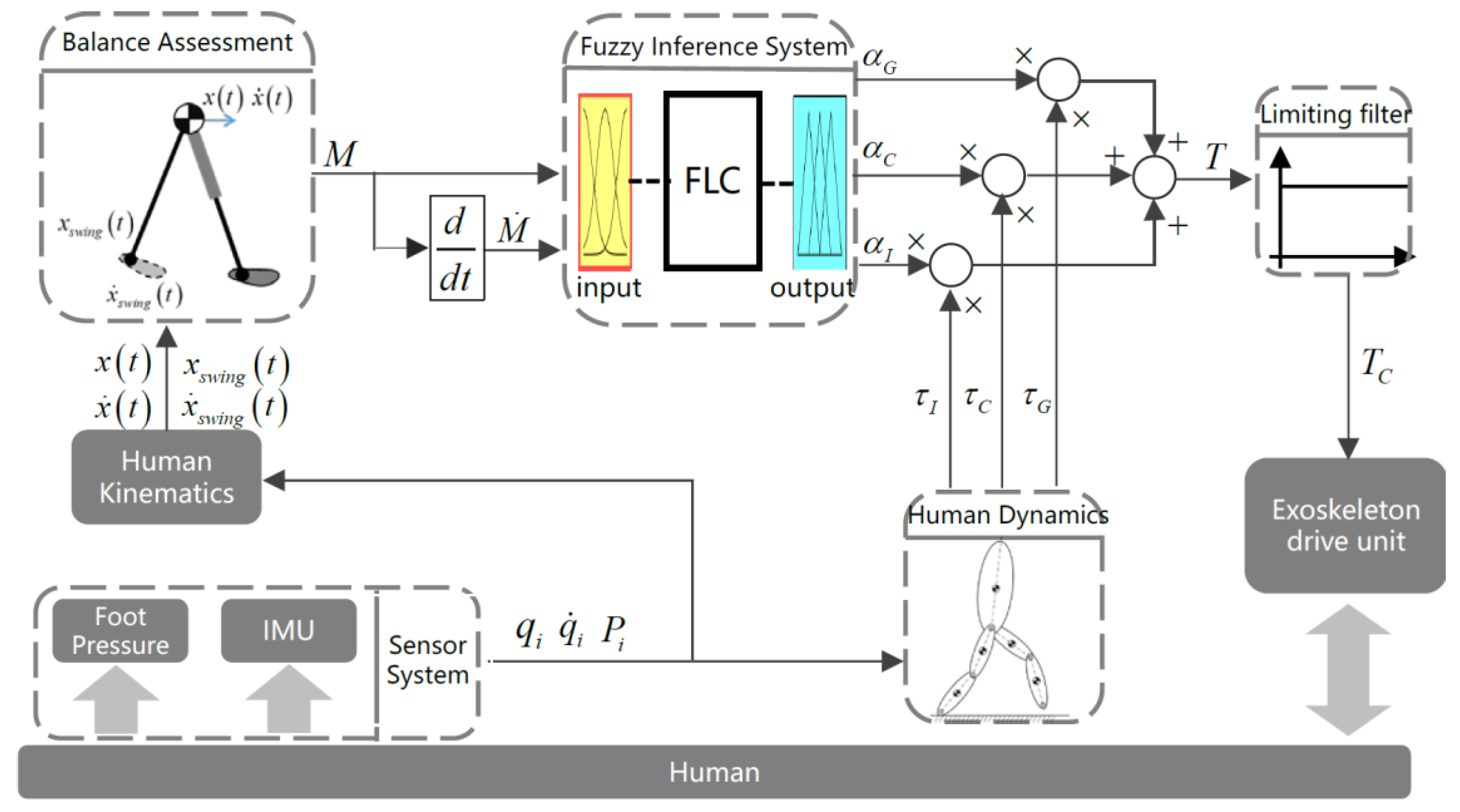
3. Exoskeleton Balance Assistance Control Strategy
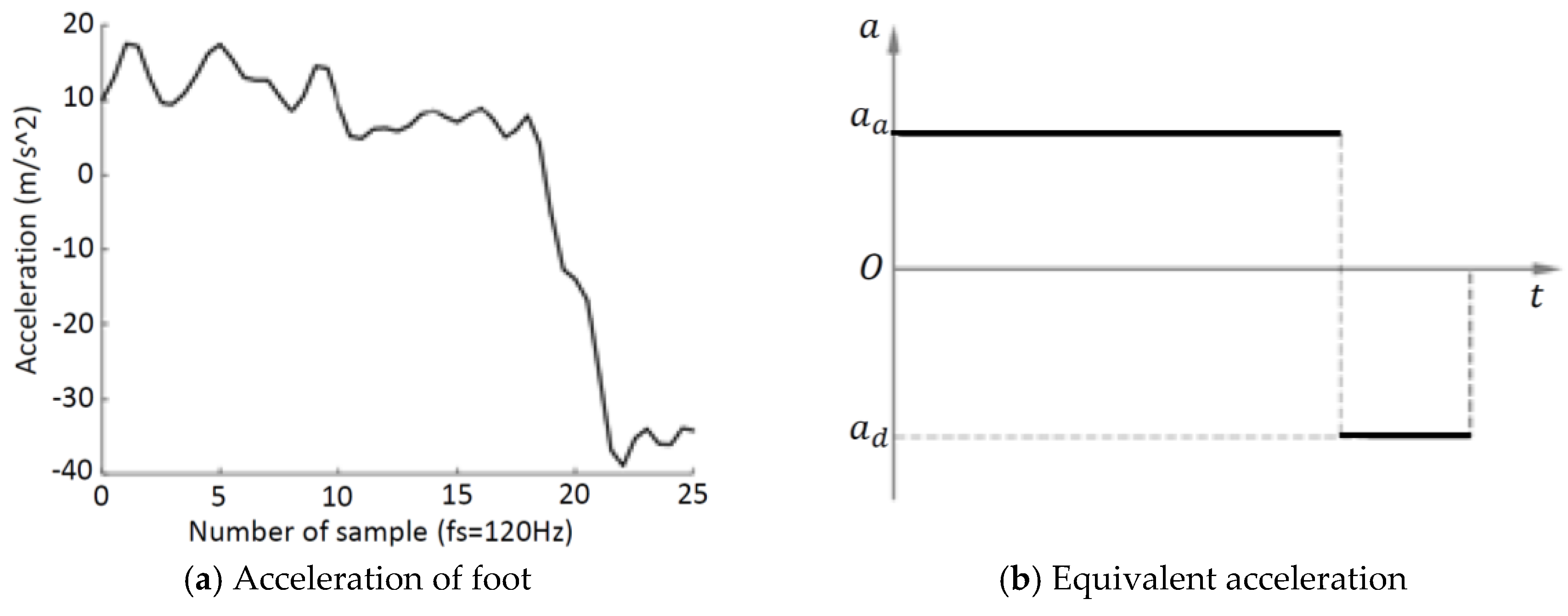
3.1. Assistant Torque
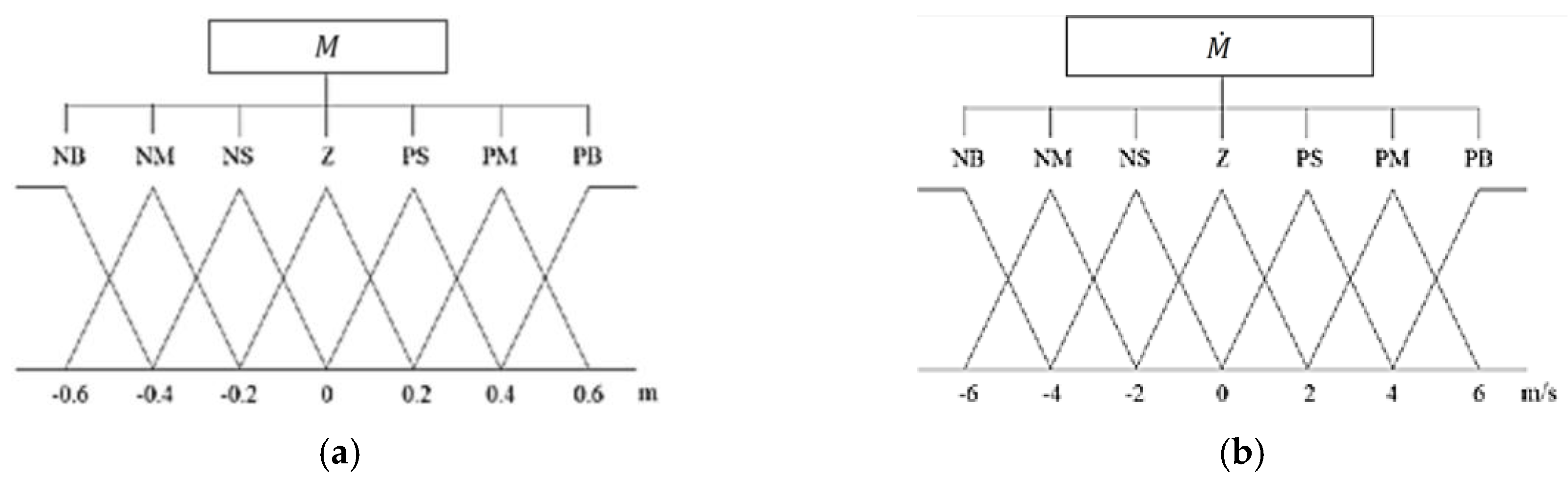
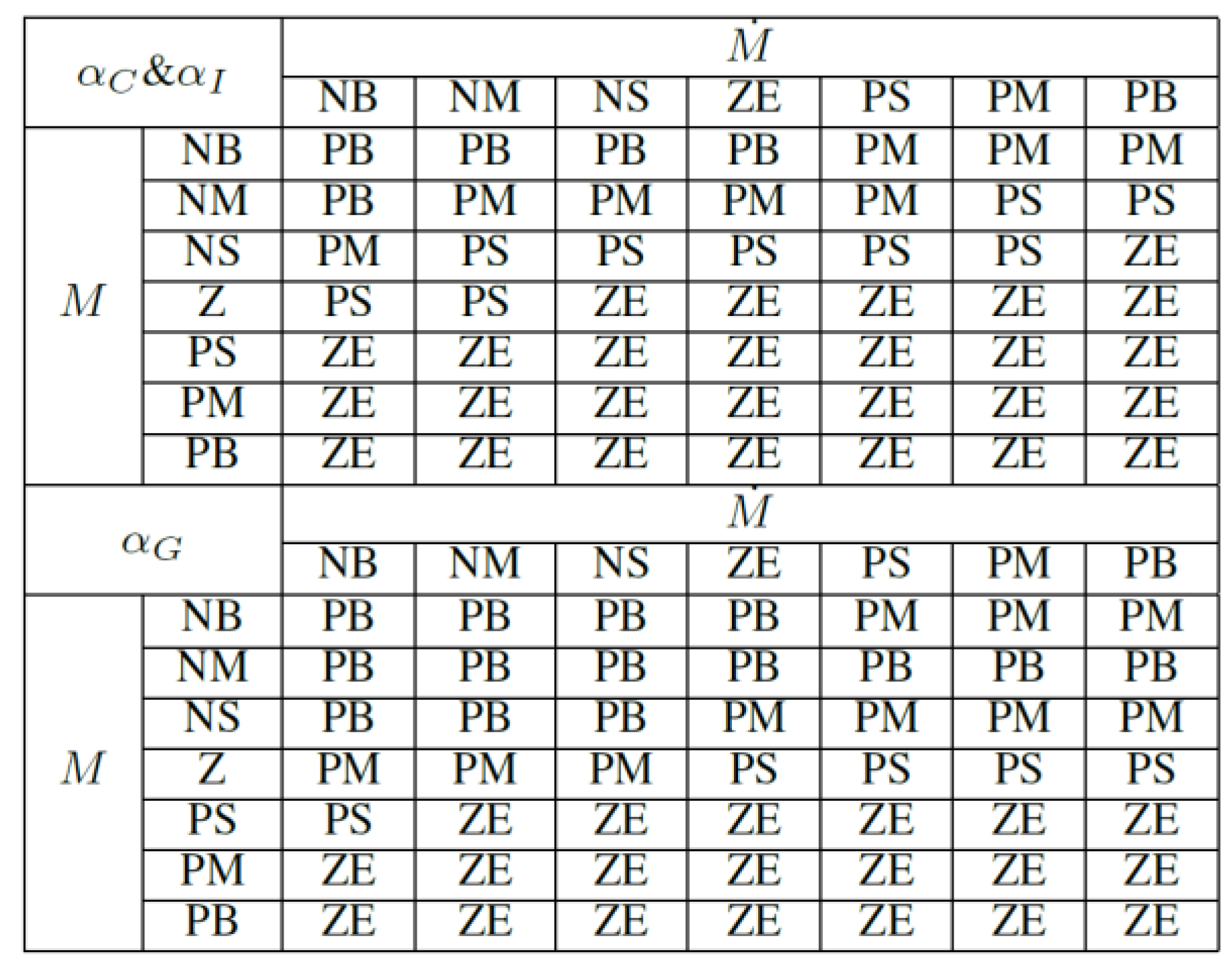
3.2. Assistant Coefficient Generated by FLC
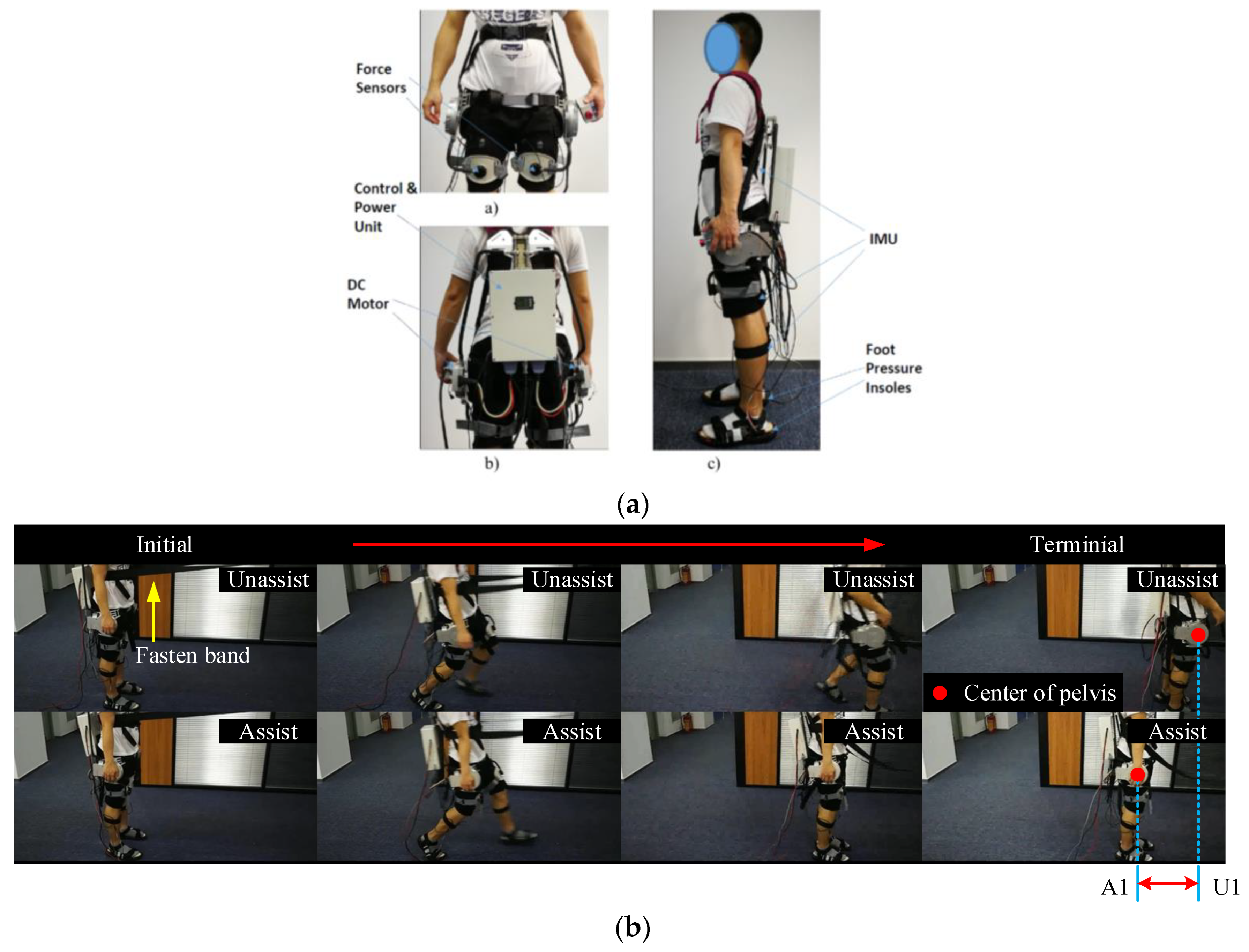
4. Exoskeleton Balance Assistance Control Experiment
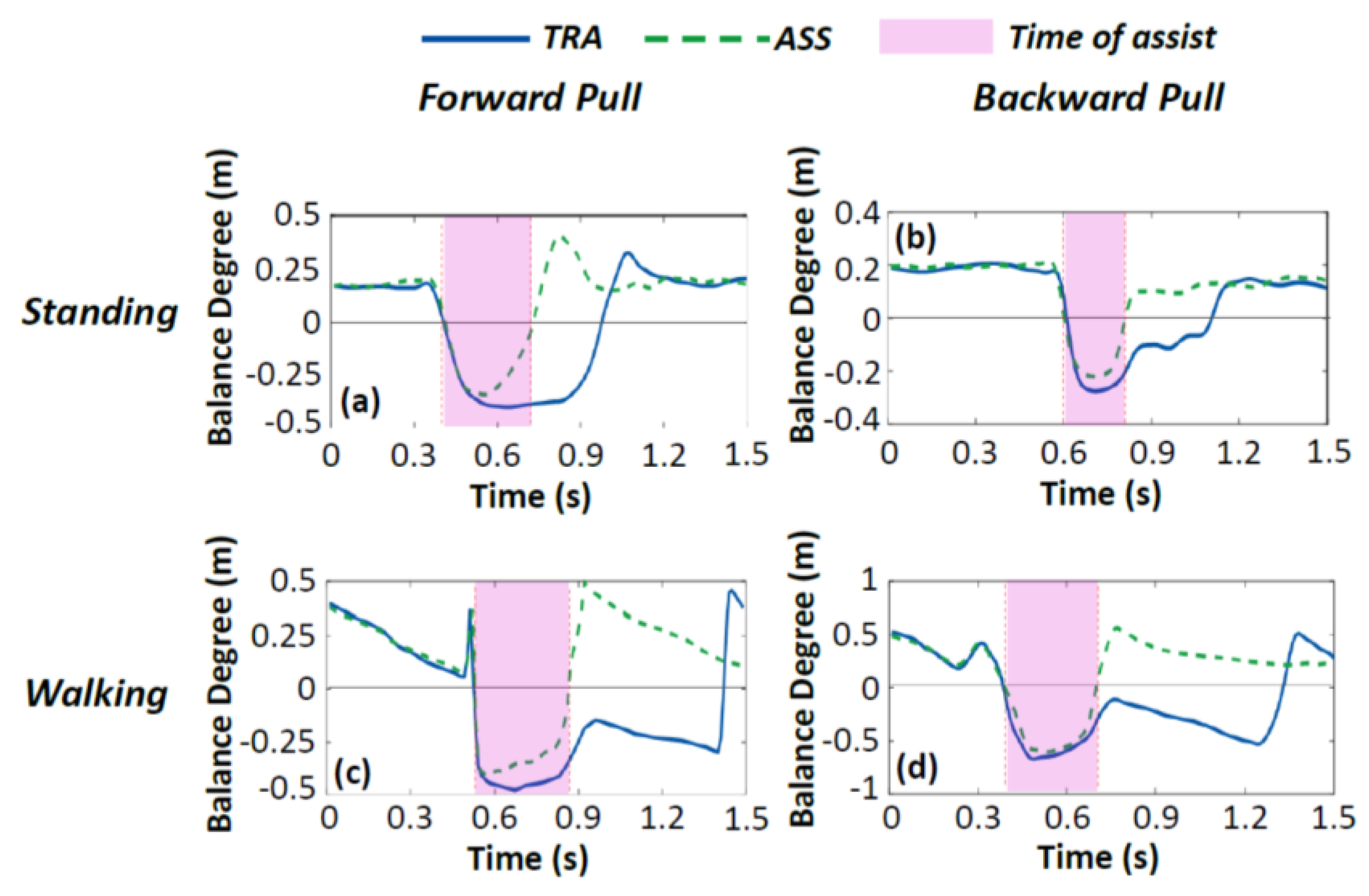
4.1. Analysis of the Degree of Single Balance
4.2. Analysis of the Hip Joint Angle
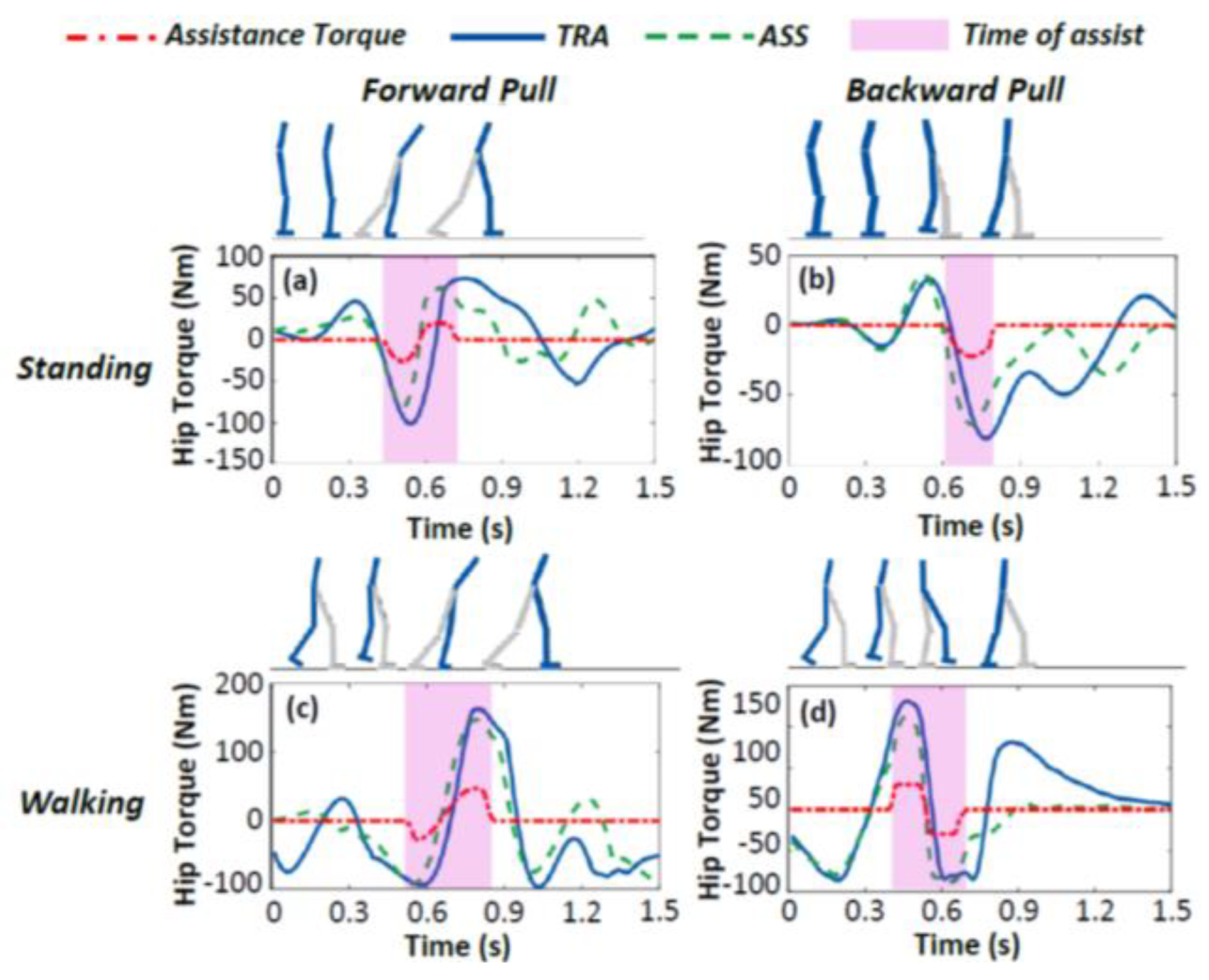
4.3. Analysis of the Hip Joint Torque
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Monaco, V.; Tropea, P.; Aprigliano, F.; Martelli, D.; Parri, A.; Cortese, M.; Molino-Lova, R.; Vitiello, N.; Micera, S. An ecologically-controlled exoskeleton can improve balance recovery after slippage. Sci. Rep. 2017, 7, 46721. [Google Scholar] [CrossRef] [PubMed]
- Pavol, M.J.; Owings, T.M.; Foley, K.T.; Grabiner, M.D. Influence of Lower Extremity Strength of Healthy Older Adults on the Outcome of an Induced Trip. J. Am. Geriatr. Soc. 2002, 50, 256–262. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, Y.; Carey, J.P.; Della Santina, C.C.; Schubert, M.C.; Minor, L.B. Diabetes, vestibular dysfunction, and falls: Analyses from the National Health and Nutrition Examination Survey. Otol. Neurotol. Off. Publ. Am. Otol. Soc. Am. Neurotol. Soc. Eur. Acad. Otol. Neurotol. 2010, 31, 1445–1450. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, K.; Mito, G.; Kawamoto, H.; Hasegawa, Y.; Sankai, Y. Intention-based walking support for paraplegia patients with Robot Suit HAL. Adv. Robot. 2007, 21, 1441–1469. [Google Scholar]
- Kazerooni, H.; Steger, R.; Huang, L. Hybrid Control of the Berkeley Lower Extremity Exoskeleton (BLEEX). IEEE/ASME Trans. Mechatron. 2006, 11, 128–138. [Google Scholar] [CrossRef]
- Raab, K.; Krakow, K.; Tripp, F.; Jung, M. Effects of training with the ReWalk exoskeleton on quality of life in incomplete spinal cord injury: A single case study. Spinal Cord 2016, 2, 15025. [Google Scholar] [CrossRef] [PubMed]
- Buesing, C.; Fisch, G.; O’Donnell, M.; Shahidi, I.; Thomas, L.; Mummidisetty, C.K.; Williams, K.J.; Takahashi, H.; Rymer, W.Z.; Jayaraman, A. Effects of a wearable exoskeleton stride management assist system (SMA?) on spatiotemporal gait characteristics in individuals after stroke: A randomized controlled trial. J. Neuroeng. Rehabil. 2015, 12, 69. [Google Scholar] [CrossRef] [PubMed]
- Parri, A.; Yan, T.; Giovacchini, F.; Cortese, M.; Muscolo, M.; Fantozzi, M.; Lova, R.M.; Vitiello, N. A Portable Active Pelvis Orthosis for Ambulatory Movement Assistance. In Proceedings of the Wearable Robotics: Challenges and Trends; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Wang, S.; Wang, L.; Meijneke, C.; Van Asseldonk, E.; Hoellinger, T.; Cheron, G.; Ivanenko, Y.; La Scaleia, V.; Sylos-Labini, F.; Molinari, M.; et al. Design and control of the MINDWALKER exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Tran, M.; Huang, H. Design and Experimental Verification of Hip Exoskeleton with Balance Capacities for Walking Assistance. IEEE/ASME Trans. Mechatron. 2018, 23, 274–285. [Google Scholar] [CrossRef]
- Giovacchini, F.; Vannetti, F.; Fantozzi, M.; Cempini, M.; Cortese, M.; Parri, A.; Yan, T.; Lefeber, D.; Vitiello, N. A light-weight active orthosis for hip movement assistance. Robot. Auton. Syst. 2015, 73, 123–134. [Google Scholar] [CrossRef]
- Li, D.; Vallery, H. Gyroscopic assistance for human balance. In Proceedings of the 2012 12th IEEE International Workshop on Advanced Motion Control (AMC), Sarajevo, Bosnia-Herzegovina, 25–27 March 2012; pp. 1–6. [Google Scholar]
- El-Bendary, N.; Tan, Q.; Pivot, F.C.; Lam, A. Fall detection and prevention for the elderly: A review of trends and challenges. Int. J. Smart Sens. Intell. Syst. 2013, 6, 1230–1266. [Google Scholar] [CrossRef]
- Aphiratsakun, N.; Parnichkun, M. Balancing Control of AIT Leg Exoskeleton Using ZMP based FLC. Int. J. Adv. Robot. Syst. 2010, 6, 319–328. [Google Scholar] [CrossRef]
- Pratt, J.; Carff, J.; Drakunov, S.; Goswami, A. Capture Point: A Step toward Humanoid Push Recovery. In Proceedings of the 2006 6th IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006; pp. 200–207. [Google Scholar]
- Tropea, P.; Vitiello, N.; Martelli, D.; Aprigliano, F.; Micera, S.; Monaco, V. Detecting Slipping-Like Perturbations by Using Adaptive Oscillators. Ann. Biomed. Eng. 2014, 43, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Rajasekaran, V.; Aranda, J.; Casals, A.; Pons, J.L. An adaptive control strategy for postural stability using a wearable robot. Robot. Auton. Syst. 2015, 73, 16–23. [Google Scholar] [CrossRef]
- Ugurlu, B.; Doppmann, C.; Hamaya, M.; Forni, P.; Teramae, T.; Noda, T.; Morimoto, J. Variable Ankle Stiffness Improves Balance Control: Experiments on a Bipedal Exoskeleton. IEEE/ASME Trans. Mechatron. 2016, 21, 79–87. [Google Scholar] [CrossRef]
- Huynh, V.; Bidard, C.; Chevallereau, C. Balance Control for an Active Leg Exoske-leton based on Human Balance Strategies. In International Workshop on Medical & Service Robots; Springer: Cham, Switzerland, 2016; pp. 197–211. [Google Scholar]
- Sergey, J.; Sergei, S.; Andrey, Y. Comparative analysis of global optimization-based controller tuning methods for an exoskeleton performing push recovery. In Proceedings of the 2016 20th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 13–15 October 2016; pp. 107–112. [Google Scholar]
- Song, K.T.; Chien, Y.L. Development of an assistive torque generation system for a lower limb exoskeleton. In Proceedings of the 2016 International Conference on System Science and Engineering (ICSSE), Puli, Taiwan, 7–9 July 2016; pp. 1–4. [Google Scholar]
- Hof, A.L.; Gazendam, M.G.J.; Sinke, W.E. The condition for dynamic stability. J. Biomech. 2005, 38, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Krishnaswamy, P.; Brown, E.N.; Herr, H.M. Human leg model predicts ankle muscle-tendon morphology, state, roles and energetics in walking. PLoS Comput. Biol. 2011, 7, e1001107. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.H.; Mansour, J.M. Linear approximations for swing leg motion during gait. J. Biomech. Eng. 1984, 106, 137. [Google Scholar] [CrossRef] [PubMed]
- Aguirre-Ollinger, G.; Colgate, J.E.; Peshkin, M.A.; Goswami, A. Design of an active one-degree-of-freedom lower-limb exoskeleton with inertia compensation. Int. J. Robot. Res. 2011, 30, 486–499. [Google Scholar] [CrossRef]





| Walking Speed | Average Groups | |||
|---|---|---|---|---|
| Success | Fail | |||
| Low (0.8 m/s) | 30 | 0 | 0.115 | 0.307 |
| Medium (1.3 m/s) | 29.7 | 0.3 | 0.124 | 0.401 |
| High (1.8 m/s) | 0.8 | 29.2 | 0.293 | 0.538 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zha, F.; Sheng, W.; Guo, W.; Qiu, S.; Wang, X.; Chen, F. The Exoskeleton Balance Assistance Control Strategy Based on Single Step Balance Assessment. Appl. Sci. 2019, 9, 884. https://doi.org/10.3390/app9050884
Zha F, Sheng W, Guo W, Qiu S, Wang X, Chen F. The Exoskeleton Balance Assistance Control Strategy Based on Single Step Balance Assessment. Applied Sciences. 2019; 9(5):884. https://doi.org/10.3390/app9050884
Chicago/Turabian StyleZha, Fusheng, Wentao Sheng, Wei Guo, Shiyin Qiu, Xin Wang, and Fei Chen. 2019. "The Exoskeleton Balance Assistance Control Strategy Based on Single Step Balance Assessment" Applied Sciences 9, no. 5: 884. https://doi.org/10.3390/app9050884
APA StyleZha, F., Sheng, W., Guo, W., Qiu, S., Wang, X., & Chen, F. (2019). The Exoskeleton Balance Assistance Control Strategy Based on Single Step Balance Assessment. Applied Sciences, 9(5), 884. https://doi.org/10.3390/app9050884





