1. Introduction
With the development of Advanced Metering Infrastructure (AMI), Smart Metering as an important research subject in Smart Grid (SG) plays an increasingly important role and is closely associated with people’s daily life [
1,
2]. Aggregating fine-grained metering data attracts householders and power suppliers. Power suppliers can calculate, forecast, and regulate accurately power distribution/price of the next period in real time while detecting fraud reports. Based on billing details and current power price, householders can adjust its appliance consumption module to reduce the power billing at the peak time; however, accessing householder’s information on metering may cause security and privacy concerns, such as daily routines, the type of applications, etc. [
1,
2]. For this, in SG systems, one of the challenges faced by power big data is how to design one aggregation mechanism to balance the use of power data and individual privacy protection [
2].
Protecting such sensitive private data from individual privacy threats needs to limit the authority of the utility company employee [
2]. Namely, Supplier Billing System (SBS, sub-suppliers) will know only the total amount of the consumption for each customer, while the Energy Management System (EMS, demand prediction division) should know only the total consumption of customers in a certain region for each time period. To achieving the goals, smart metering systems often introduce the Meter Data Management System (MDMS), which stores the measured values of smart meters (SMs), and aggregates it before sending the aggregation to the SBS and EMS [
2].
With the appearance of MDMS, another concern is upgrading, namely the malicious action of householders and regional MDMS employees. Unfortunately, a malicious householder may collude with the regional MDMS employee to report a false consumption to the SBS department; attackers may steal or forge power usage and consumption information. In addition, a regional MDMS employee may submit a fraudulent aggregation in a neighborhood. A World Bank report finds that each year over 6 billion dollars cannot post due to the energy theft and fraud report in the United States, in 2009, the FBI reported a wide and organized attempt that may have cost up to
$400 million loss annually and power supplier suffered a great monetary loss [
3]. To fend off this type of attack, it is desirable that suppliers or the public should detect the fraud profile from malicious aggregators or dishonest householders [
4].
Privacy-preserving metering protocols have been discussed in lots of literatures [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24]. They mainly focused on the studies of homomorphic aggregation [
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
20,
23,
24], by which, aggregators can only obtain the fine-grained aggregation data within a certain region or householders’ billing in a serial period while protecting individual privacy. However, most of them can only resist against single external or semi-trustable attack [
11,
13,
14,
19], and how to fend off internal attackers (e.g. aggregators or householders) is an open problem. Internal attackers can legally collect and store power consumption information of users; therefore, they pose a higher threat than external attackers [
18].
Most of existing works [
5,
6,
7,
8,
9,
10,
18,
20,
21,
23,
24] about additively homomorphic, multiplicative homomorphic, and their combination with other cryptography endeavored to address the problem. Most of them improved Paillier encryption [
6,
7,
8,
9] by their combination with other cryptography, such as stream ciphers [
5,
19,
23] and modular addition [
7,
24], to prevent power suppliers/operators from intercepting individual user data, and to detect fraudulent from dishonest users. To ensure the integrity of transmitted messages and fend off attacks such as man-in the middle attack and denial-of-service attack against SG, signature and authentication methods are proposed in References [
8,
15,
16,
17].
Lu et al. [
6] proposed a privacy-preserving, multi-dimensional metering aggregation scheme in a neighborhood-wide grid with piallier encryption, bilinear pairing and computational Diffie-Hellman (DH) methods. For resisting against internal attackers possessing private keys, Xiao [
8] introduced a spatial and temporal aggregation and authentication scheme by randomizing Paillier encryption with Lagrange interpolation. Their protocol requires
O(
n2) bytes of inter-action between the individual meters as well as relatively expensive cryptography on the meters (public key encryption). Chen [
9] also improved Paillier encryption and proposed a privacy-preserving aggregation scheme resisting at most
t compromised servers in a control center with threshold protocol.
Dimitriou et al. [
20] provided a verifiable publicly aggregation scheme against dishonest users that attempt to provide fraudulent data. Any user node in the community can prove its computation accuracy by zero-knowledge proof that the two encrypted message with different public keys corresponding to the same plaintext message. While we can prove our scheme costs lower overhead to resist fraudulent report from internal nodes.
Erkin et al. [
23] adopted a stream cipher (e.g. RC4) to generate pseudo-random keys as masking keys between nodes to prevent internal nodes from possessing private keys. During the aggregation within a neighborhood, all masking random keys cancelled out and the aggregation value is revealed without compromising individual privacy based on the security properties of the Paillier encryption and stream cipher. We follow its Pseudo-Random Function and combine it with modular addition. The main difference from ours is they impose the random keys from PRF on the plaintext before encrypting it with Paillier cryptography, and send the encrypted message to all nodes. We set a security parameter
k to represent the number of communicate nodes in a neighborhood and improve the encryption method by replacing the costly Paillier encryption with the simple and lightweight combination. More significantly, we supplement a publicly verifiable property to detect the fraudulent profile from malicious aggregators or dishonest user nodes.
Castelluccia et al. [
19] protected individual data by imposing masking keys from RC4 on the plaintext data under the multi-level wireless sensors network model, However, the protection protocol cannot resist malicious aggregators, as the session keys are generated by the sink as the aggregator. We extend its PRF method into the peer-to-peer system model and propose a privacy-preserving scheme against maliciously internal attack.
In addition, traditional modular addition was adopted in [
7,
24] by partitioning individual plaintext data into
n shares and exchanging them between nodes (
n is the number size of users in a neighborhood). Flavio et al. [
7] adopted Paillier encryption and modular addition, in which every user node partitions its meter reading into
n shares and transmits the encrypted shares with different public keys to the aggregator, which aggregates the data with the same public key before sending the aggregation to the users. Finally, the aggregator collects the plaintext sums to obtain the final aggregation. The method is privacy-preserving; however, during each spatial aggregation, three message exchanges are required between every user and the aggregator. Thus, the number of homomorphic encryption per user increases linearly with
n increases, and the communication overhead is
O(
n2) messages [
20]. Jia et al. [
24] also generated partitioned data with modular addition and imposed them on a high-order polynomial coefficient. The values of the polynomial at different points are transmitted to the aggregator which finds the coefficients of the polynomial with the private key and gains the aggregation, so the scheme is under the semi-trusted model and the aggregator is trustable. In addition, the computation overhead is relatively higher when
k is increasing. As every node does the
xk polynomial operation before the matrix multiplication operation, the scheme increases greatly the computation overhead.
Ohara K et al. [
4] summarized the function requirements during smart metering against internal attackers: calculating billing and obtaining statistics for energy management. We follow the statistic function requirements and the spatial and temporal scenarios in References [
8,
23] against malicious MDMS/aggregators or dishonest users:
- (1)
Spatial aggregation. A neighborhood-wide grid corresponds to a group of householders each equipped with a SG. They submit their encrypted meterings to the MDMS at a timestamp (e.g., 15 min). The latter aggregates homomorphically them before sending the aggregation to the EMS. During this aggregation, the individual data are confidential to the MDMS or the EMS.
- (2)
Temporal aggregation. A single SM submits its power consumption in a series of timestamps to the MDMS for the billing purpose. In this scenario, SBS charges the householders in serial timestamps.
Throughout this paper, we refer to the building area network (BAN) region as a neighborhood, and the regional MDMS as the regional gateway (GW), and the regional SBS as the control center (CC), respectively.
The main contribution can be summarized as follows:
- (1)
We design and implement a distributive, temporal and spatial aggregation scheme in the SG, in which every node sends and receives k encrypted message from k pairwise nodes distributively. The scheme provides spatial aggregation in a neighborhood at a fine-grained time scale (e.g. 15 min) and an individual temporal aggregation (e.g. monthly) in a series of timestamps for the billing purpose.
- (2)
The proposed encryption scheme minimizes the computation and communication overhead by replacing the costly public key cryptography adopted in most literatures with a combination of modular addition and PRF.
- (3)
The novel feature is that the masking keys are imposed on the partitioned data, and the latter are implemented by traditional modular addition. As the process of modular addition is processed by the node itself, other nodes cannot gain the true partitioned data, the masking key is only known to the pairwise nodes, and the combination ensures the confidentiality of individual data to any node including CC, aggregators, and n-2 nodes at most in a neighborhood.
- (4)
To detect malicious aggregators or dishonest users, we propose innovatively a publicly verifiable aggregation method. By this way, any user node in a neighborhood can receive the communication flow, and verify the accuracy of local aggregation from other nodes or total aggregation from the aggregator without compromising individual fine-grained data.
- (5)
The publicly available property for the aggregation also facilities householders regulating in time its current consumption module and consumption demand in the next time period, as by comparing their own consumptions with those of other nodes and checking if there is redundant power, householders can decide to store more energy or to sell excess power to the power supplier or other nodes. The scenarios are especially very important for self-sufficient, remote places, particularly, in developing countries, which can only afford renewable energy, such as wind turbines, solar panels, and carbon-based fuels [
23].
The paper is organized as follows: in
Section 2, we provide related preliminaries and formalize the system and attack models. In
Section 3, we introduce our proposed aggregation scheme and correctness analysis. Security notions and proof are given in
Section 4, followed by performance evaluation and comparison in
Section 5. The conclusion is drawn in
Section 6.
2. Preliminaries and Models
For ease of reading, we summarize the main notations in the paper in
Table 1.
2.1. Additively Homomorphic Encryption Based on The Keystream
Our security property partly comes from the stream cipher. The keystream generated from the pseudo-random function satisfies the security properties of the additively homomorphic encryption in the stream cipher. The basic idea [
19] is denoted as follows:
Encryption is written as: where K is randomly generated keystream, m is the plaintext and .
Decryption is described as: .
Additively homomorphic property of ciphertext are described as: ; then, the aggregated ciphertext is expressed as: , where .
2.2. Pseudo-Random Keystream Generator—RC4
As a popular PRF generator, with secret keys between communication nodes, RC4 can generate a keystream. This secret key is pre-computed during the system initialization. As any stream cipher, the generated keystream can be used for encryption by combining it with the plaintext using bit-wise Exclusive-Or [
19]. However our scheme is to replace the XOR (Exclusive-OR) operation typically found in stream ciphers with modular addition operation (+). To generate the keystream, RC4 needs two algorithms, i.e. Key-scheduling algorithm (KSA) and Pseudo-random generation algorithm (PRGA) [
5,
14].
KSA: KSA is to initialize a permutation with a variable length key between 40 and 2048 bits for PRGA.
PRGA: once the permutation initialization of KSA has been completed, the stream of bits is generated using the PRGA.
| Algorithm 1: Key-scheduling algorithm (KSA) |
Input: i = 0;
j = 0 //Two 8-bit index-pointers
S //The initial key keyed with a secret key
Output: S //A permutation of all 256 possible bytes
1. for (i = 0; i <= 255; ++ i)
2. S[i] = i;
3. end
4. k = 0;
5. for (i = 0; i <= 255; ++ i)
6. j = (j + s[i] + key[i mod keylength]) mod 256;
7. k = S[i];
8. S[i] = S[j];
9. S[j] = k;
10. end |
| Algorithm 2: Pseudo-random generation algorithm (PRGA) |
Input: i = 0;
j = 0 //Two 8-bit index-pointers
Output: Z // Pseudo-random keystream
1. k = 0;
2. for (i = 0; i <= 255; ++ i)
3. i = (I + 1) mod 256;
4. j = (j + S[i]) mod 256;
5. k = S[i];
6. S[i] = S[j];
7. S[j] = k;
8. Z = S[(S[i] + S[j]) mod 256];
9. end |
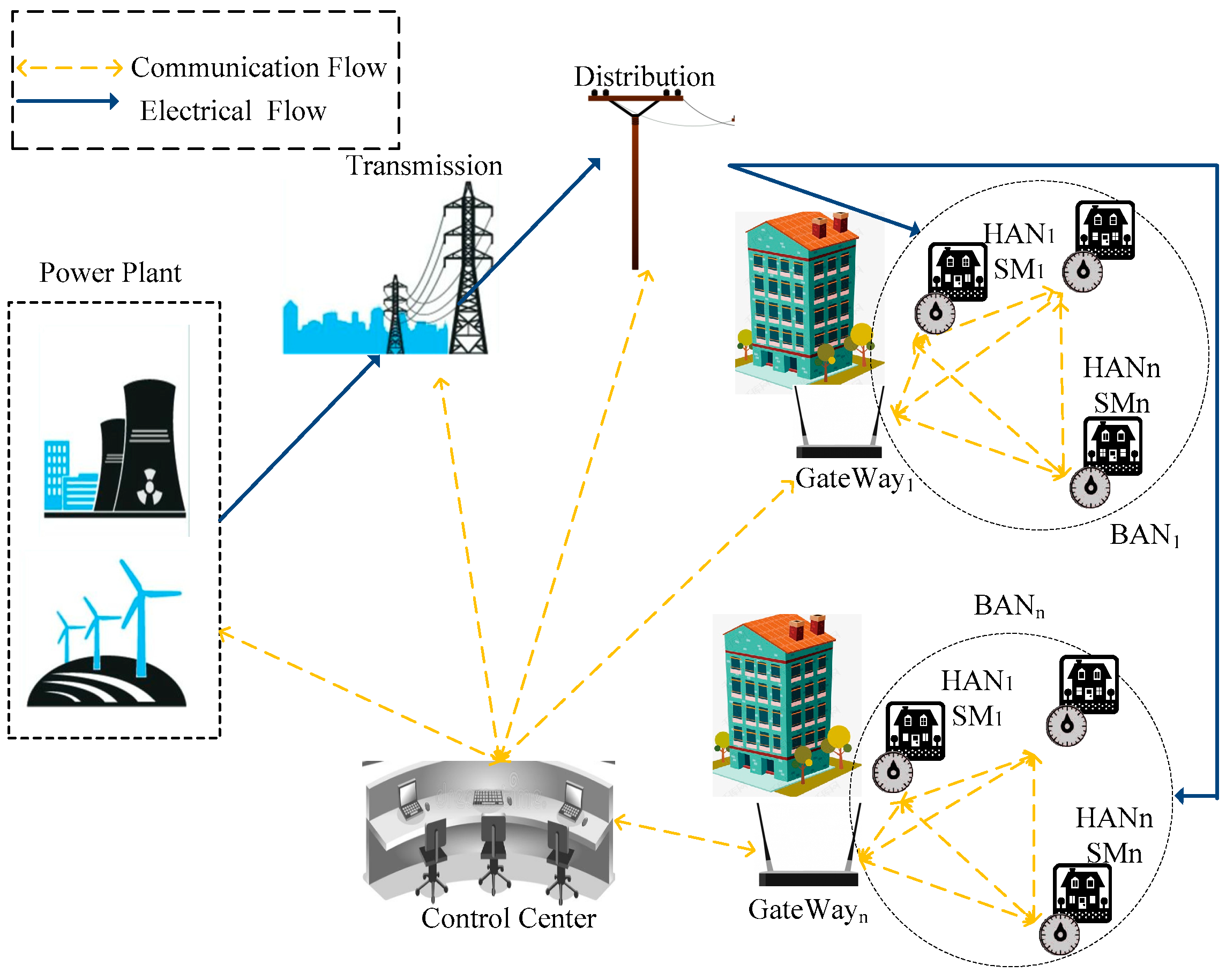
2.3. System Model
In our system model, we consider a typical SG communication architecture [
8,
9,
11,
15,
16,
17], as shown in
Figure 1. It is based on the SG network model presented from the National Institute of Standards and Technology (NIST) and consists of six domains, i.e., the power plant, the transmission domain, the distribution domain and a CC, a residential GW, and the user domain. We mainly focus on how to report and aggregate the users’ privacy-preserving data into the CC. Hence, the system model divides especially the BAN into numbers of Household area network (HAN) equipped with a SG and every BAN includes a GW and numbers of users.
CC: It acts as the SBS and EMS in reality. It needs to monitor the actual data on how much power is consumed at which timestamp in one BAN (neighborhood), how much power should be reserved for the next time period, and cumulative consumption for individual billing on a monthly basis, and how much power is being distributed to a specified neighborhood. In the paper, it is curious about the individual fine-grained data and may attempt to it as far as possible by all available resources, so it is assumed a semi-trusted entity.
GW: A powerful entity, acting as the local MDMS, represents a locality (e.g., a region within a building) is responsible for aggregating real-time spatial data in a neighborhood and individual temporal data in a series of timestamps, and then transmitting the aggregation to the CC. The employment of GW relieves CC of aggregation and reducing largely the communication latency. However, the cost that potentially malicious attacks done to users or power suppliers is unignorable, as discussed earlier. We assume it is a malicious entity here. A BAN GW represents a locality (e.g., a region within a neighborhood). For facilitating the communication between BAN GW and CC, WiMax and other broadband wireless technologies can be adopted. We consider a scenario that one BAN neighborhood covers a hundred or more HANs, so the longest distance from the BAN GW to a HAN is more than a hundred miles, so WiMax maybe more suitable for this kind of distance communication. Household Smart Meter (HSM): A bidirectional communication entity deployed at householders’ premises. The modern SM is given a certain level of autonomy via trusted elements and the ability to collect, store, aggregate, and encrypt the usage data. Hence it has two interfaces—one interface is for reading power of householders and the other one acts as a communication GW. Even if we assume SM is tamper-resistant, it is not powerful as a GW, so it may be vulnerable to be compromised by the GW to infer the object users’ data.
2.4. Communication Model
As can be seen in the
Figure 1, all SMs connect each other in a neighborhood by WiFi technique, which constructs public verifiable foundation. Each user would select randomly
k pairwise nodes in one round and can ensure that if
chooses
, then
chooses
and the keys between them are opposite mutually. The value
k as a security parameter can take any value from 2 to
n, and depend on the specific application circumstance. The higher the value of
k is, the higher the complexity is, and vice versa, and the scheme is more vulnerable to be attacked.
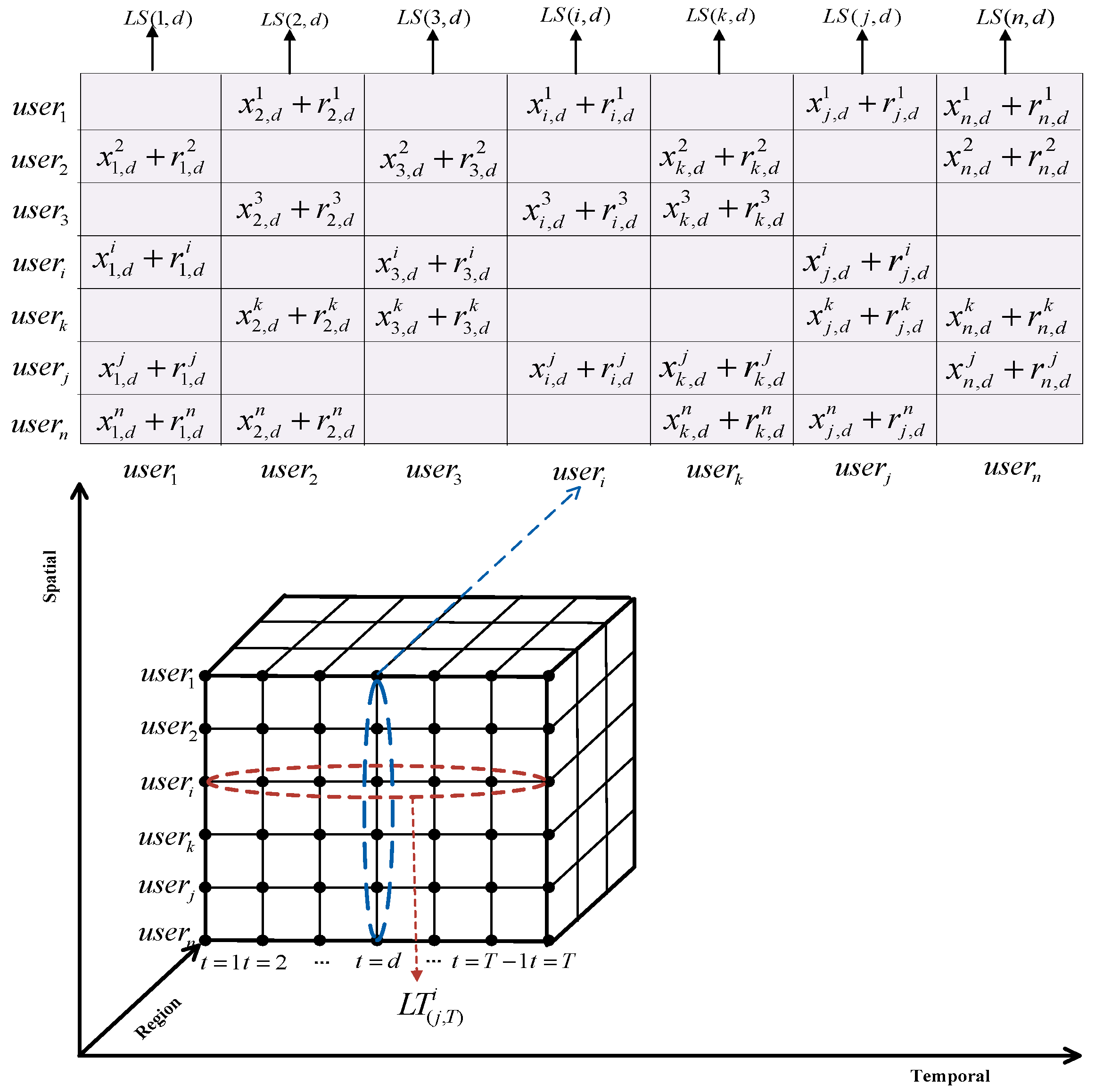
2.5. Data Model
Let
be the meter reading of the
ith (1 ≤
i ≤
N) user node at the
dth (1 ≤
d ≤
T) fine-grained timestamp, where
N is the number of user in a BAN (a neighborhood-wide grid), and
T is a billing period. At each fine-grained time index
d, a neighborhood grid (over the entire BAN) spatially aggregated utility usage can be expressed as:
At the end of a billing period (
d =
T), a temporally aggregated utility usage data for the
ith user is expressed as:
2.6. Security Requirement and Attack Model
Within the system model, there are four types of actors involved in the meter data reporting process: the ith user (self), other users in the same neighborhood (BAN), the GW, and the CC. The CC requires the spatially aggregated fine-grained neighborhood usage data to optimize power delivery efficiency and the temporally aggregated user-specific utility usage data for the billing purpose. Hence, we stipulate the following security/privacy requirements:
Requirement R1. Fine-grained, individual utility data are private and should not be disclosed to CC, GW, or other users.
Requirement R2. Temporal aggregation for an individual user and spatial aggregation in one neighborhood cannot be tampered by the malicious aggregator or other internal nodes. For this, we envision a secure and reliable communication model comprising a verifiable publically method, which is customized to the correctness verification of the aggregation value of SG.
For this, our attack model is based on the malicious aggregator who attempts to tamper the aggregation value in a neighborhood and the billing value for individual users, or infers fine-grained meterings of the individual user by colluding with other n-2 compromised nodes at most. Following the above security requirements, different compositions of the attackers and actions may be grouped into the following attack types:
(1). External attack
External attackers may compromise the meterings of the object users by eavesdropping the communication flow between communication nodes through various eavesdropping malware.
(2). Malicious attack
False aggregation report. The aggregator may alter or drop maliciously any individual data, or tamper the aggregation data to the CC; any malicious user node may provide false local aggregation to the GW.
Collusion with compromised nodes. The aggregator may collude with compromised users to attempt to infer the uncompromised users’ data.
(3). Semi-trustable internal attack
The curious CC or any user node can also acquire data through the public communication flow, such as the message from the user node to the GW or from the GW to the CC. They may infer the object user’s fine-grained data by the public communication flow.
An attack is an arrangement that enables unauthorized parties to gain access to private data or to tamper secured data (even by the user itself) without being detected. In this work, we assume the SMs are tamper-resistant [
7,
20,
23], and can perform the measurement and reporting operations normally, but do not exclude the possibility of tampering with local aggregation values by itself.
4. Security Notions
4.1. Security Proof
In this section, we mainly elaborate the security properties of our scheme. In particular, based on the security requirement and attack model discussed in
Section 2.6, we prove our scheme can ensure the confidentiality of fine-grained meterings for an individual user and the aggregation integrity that the local aggregation, and total aggregation cannot tampered by malicious individual user nodes or the aggregator.
We firstly construct the Individual Metering Indistinguishable (IMI) security game to represent the adversary’s actions.
Definition 1. (IMI security game).
Setup: the challenger runs the initialization algorithm and first initializes a group of size n, then generates the system parameter k to the adversary.
Queries: the adversary can not only capture meters’ encrypted report but also acquire the encryption and compromise queries until meeting the constraints.
Encrypt: The adversary A choosesand specifiesto ask for the ciphertext. The challenger returns it the ciphertext.
Compromise: The adversary A specifies an integer . If q = 0, the challenger returns the adversary the aggregator’ capability, else returns ’s message.
Challenge. We denote withthe set of the uncompromised users. The adversary selects randomly two meteringsandat the timestamp d. The challenger flips a random bituniformly and returns the adversary.
Guess: The adversary outputs a guess , and A wins if b = b’ with unignorable advantage.
Definition 2. (IMI security)
The proposed temporal and spatial aggregation scheme is IMI if no probabilistic polynomial-time adversaries A have more than an ignorable advantage in the IMI security game. The ignorable function for A is as follows: Theorem 1. The proposed encryption scheme is IMI.
The intuition behind the theorem is any adversary cannot distinguish the encrypted individual metering and the scheme cannot leak any individual user consumption at the dth timestamp.
Proof:
Setup: The challenger initiates the whole system. The challenger generates a group of scale n and pairs number k, and then gives the parameters (n, k) to the adversary.
Queries:
(1). Spatial aggregation
Encrypt: A issues the encryption query with to the challenger. The challenger generates the pairwise key between the pairwise nodes, and imposes it on the randomly partitioned data to generate the encrypted measure formed as .
Compromise: A may compromise the aggregator or up to n-1 users in any pairwise set in order to acquire more messages for object users. However, the compromise will encounter restriction when meeting with uncompromised users.
Challenge. For simplifying the proof process and not losing the generalization, we consider the extreme circumstance that
. If the theorem holds for this circumstance, then it holds for
. We assume the user j is the only uncompromised user in
. The adversary selects the two meterings and gives
to the challenger, the challenger flips a random bit
uniformly and returns the adversary
when
b = 0, and returns
when
b = 1, and then
In the Equations (14) and (15), the adversary A cannot solve the two equations at the dth timestamp and gain the exact and even if he knows , as the two equations have three unknown variables, so it is more impossible for A to acquire and which ensures the scheme’s security.
(2). Temporal aggregation
□
In the Equations (16) and (17), the two equations with four unknown variables make the adversary A impossible to acquire or .
Hence, the encrypted aggregation method can ensure the individual, fine-grained meterings indistinguishable security as long as there is at least one uncompromised user in its pairwise set. Our security properties are based on the randomness of modular addition and stream cipher which is used to blind the individual meterings.
4.2. Security Analysis
We can prove that our proposed solution will withstand the other attacks discussed in
Section 2.6 and ensure the integrity of the aggregated data, whether total aggregation or local aggregation.
(1). Eavesdropping resistance
Our proposed scheme supports the openness of communication flow. Whether it is the internal node with access to the communication flow in a community or the external eavesdropper, they can only get the encrypted individual data , local aggregation value or total aggregation value sent by GW to CC. However, all of them can not obtain the fine-grained data. We have proved that even if all but one node is compromised, object metering still cannot be leaked. Hence, the proposed encryption method satisfies the security requirement R1.
(2). False command from the GW
The GW attempts to obtain object user’s meterings by issuing false billing commands in the name of CC, even if he cannot compromise its pairwise nodes. He tries to obtain valuable information from them at any timestamp. However, even so, he can only get the indistinguishable, individual meterings, due to the Equations (14)–(17).
We cannot exclude the possibility that all pairwise keys of at a timestamp are all compromised nodes by the malicious aggregator or external attackers. In this case, the object ’s privacy is exposed. That is the does not select any one honest node, then the probability is . Obviously, the larger the value of |c| is, the smaller the value of k is, and the bigger the probability is. We improve the probability as much as possible and assume n = 1000, k = 30, and |c| = 500 (50% nodes are compromised), and then the probability is 2.47 × 10−7, so much small probability implies it is almost impossible that one user does not select any one honest node in one timestamp. Even if we fix a bigger pairs period T = 1 month, then we would have to cost 38.51 years to acquire individual data.
4.3. Publicly Verifiable Property
The security requirement R2 given earlier needs to be satisfied with the publicly verifiable property. We provide the public communication flow between nodes in a neighborhood is to ensure the integrity of aggregation data. Any internal node in the community can verify publicly the accuracy of the local aggregation from other nodes and the total aggregation from the GW without compromising the individual fine-grained data. The special public verification process comprises two parties:
4.3.1. Spatial Verification
Based on the public communication flow, any node in the neighborhood can gain the encrypted message formed as from the pairwise nodes, and compute its local aggregation formed as LS(i,d) and , and thus the total aggregation and for the neighborhood can be computed and compared with the reported result from the GW. If the result is questionable, the user can report directly to the CC. With such a supervision, the CC can detect the fraudulent profile of the malicious GW.
4.3.2. Temporal Verification
The public verification method to the spatial aggregation is equally effective to the temporal verification. For any node, one of its pairwise nodes in the neighborhood gain its encrypted message formed as in a billing period before computing its local temporal aggregation, and thus its total temporal aggregation is computed and verified by summing up local temporal aggregations from all its pairwise nodes.
Thus, the billing user itself or any user node can verify the accuracy of the billing from the GW without revealing individual fine-grained data. Hence, they can detect if there is a malicious and fraudulent profile of the malicious GW and reports it to the CC in time.
5. Performance Evaluation
We evaluate the performance of the proposed aggregation scheme to assess the overheads. The performance metrics used in our empirical evaluation are defined as follows:
- (1)
Computation overhead: node’s runtime of the proposed scheme in terms of spatial and temporal aggregation.
- (2)
Communication overhead: the size of a message transmitted between the nodes and GW (number of bits).
- (3)
Security parameter k: we analyze the impact of the different value of k on the two overheads.
We compare these results against several existing works [
23,
24] using performance metrics based on Friendly ARM [
25] and the library in [
17]. By comparison with them, we intend to illustrate our computing and communication advantages in terms of the combination of PRF and modular addition methods adopted, respectively, in the scheme [
23] and [
24]. Each experiment consists of 50 independent trials and the averaged results of these trials are reported. The computation time required for these tasks is listed in
Table 2.
We fix the number of users at 1 million; the number of C is 10; the number of GW ranges from 1 to 20. Let n denotes a possible number of users in a group, and it ranges from 1 to 5000. We present the impact of a different number of users in the GW and a different value of k (ranging from 1 to 100) on the performance. We also assume, for simplicity, that all SMs can be functioning normally.
5.1. Computation Overhead
(1). Spatial aggregation
Let Cma and Cprf denote respectively the cost of Modular addition operation and keys generation operation with PRF, respectively let Cadd and Cmul denote the cost of addition and multiplication operation respectively, and Cenc and Cdec denote the cost of homomorphic encryption and decryption operation respectively.
In our spatial aggregation scheme, for every node, partitioning individual data into k partitions costs one Cma; generating k pairwise keys costs k·Cprf; receiving k encrypted messages and adding them up cost , then the computation overhead per node is Cma + k·Cprf + k·Cadd and the total computation overhead per aggregator is (n-1)·Cadd for aggregating data from n nodes.
In Erkin et al.’s scheme [
23], at the
dth time step, every hash function cost is
Chash,
k masking random keys cost is
and computing total masking keys cost is
, and then encrypting individual data cost is
, so the total computation overhead is
.
In Jia et al.’s scheme [
24], at the
dth time step, the additive secret sharing cost is
Css,
k hash functions cost is
, and then
k-order polynomial operation is x
k and
k matrix multiplication operations cost is
, so the total computation overhead is:
.
We provide the individual spatial computation overhead comparison in
Table 3.
As described in the related work, the scheme in Reference [
23] sets all nodes as communication nodes instead of selecting a limited number of communication nodes as in ours and [
22]; however, for convenient comparison, we assume that
k communication nodes are selected, which is on the same experiment platform as ours and the scheme in [
23]. Even under such relaxation, we can still prove ours is superior in terms of computation and communication cost through the following performance evaluation.
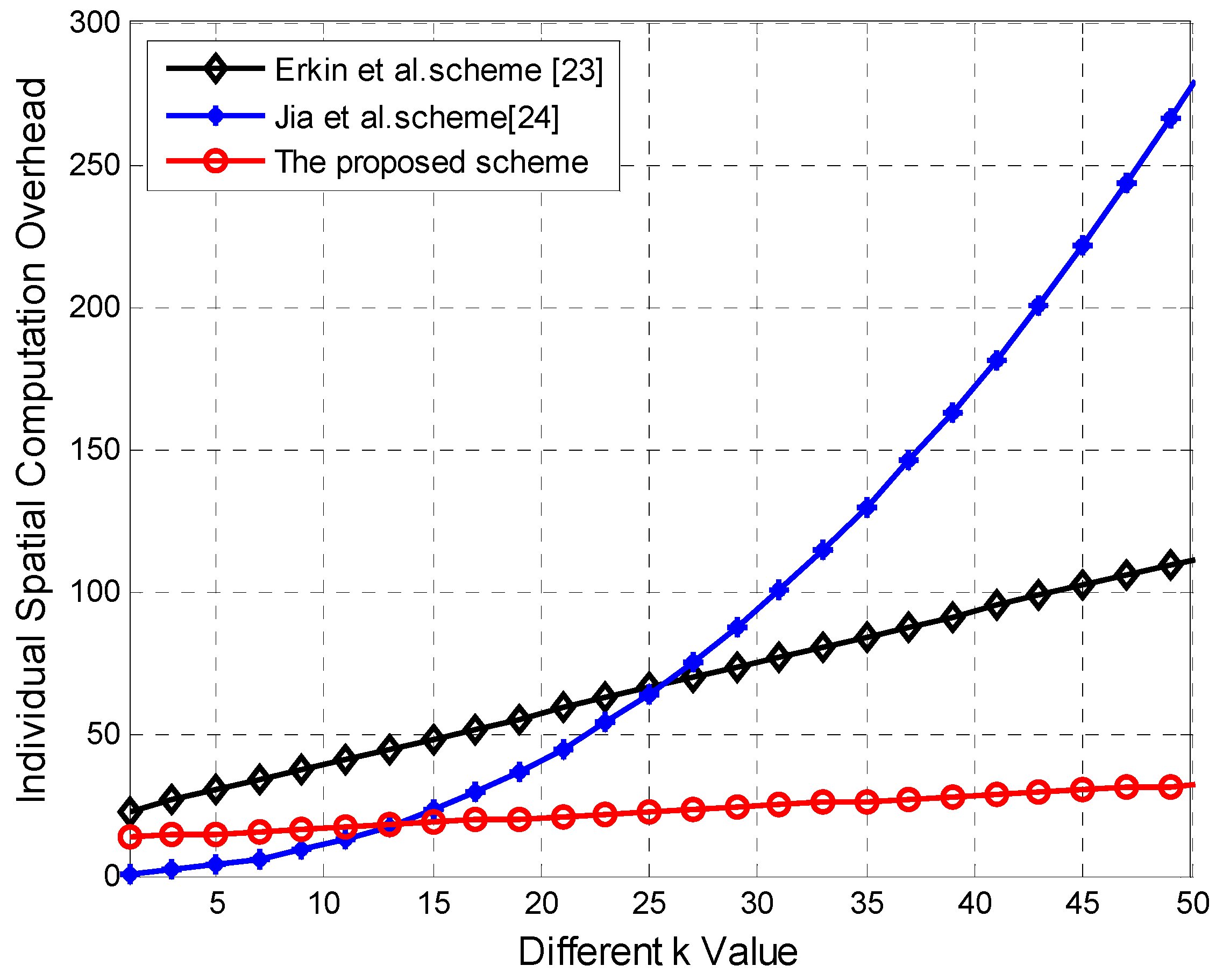
The
Figure 4 plots the comparison of spatial computation overhead between our scheme and the schemes in References [
23,
24] with the value of
k increasing. The
Figure 4 shows that the three schemes’ computation overheads all increase with the value of
k increasing, the computation overhead in Reference [
23] and ours are lower compared with the scheme in References [
24], in which polynomial operation
and
k matrix multiplication operations generate too much computation overhead with
k growing, it has more cost significantly than ours and Erkin et al.’s scheme [
23], ours is lower slightly than the scheme in [
23], and both of them are close to
.
(2). Temporal aggregation
In the proposed scheme, each node chooses the same nodes every billing period to satisfy with the Equation (5), so total temporal computation overhead in T serial time slots for every node is .
In Erkin et al.’s scheme [
23], each node sends
T fine-grained utility readings in each of the
T time steps, so the overhead per node is
. In fact, the temporal aggregation overhead of the scheme in Reference [
23] is higher than it, as with the modification of Paillier encryption, spatial and temporal aggregations are not being synchronized. To compensate the lack, every user must add an additional random key
at
Tth timestamp, which costs much overhead. However, our scheme has no extra cost and the third party’s involvement.
We set the fine-grained reporting interval to be 15 minutes, and billing period
T = 2880 (roughly one month).
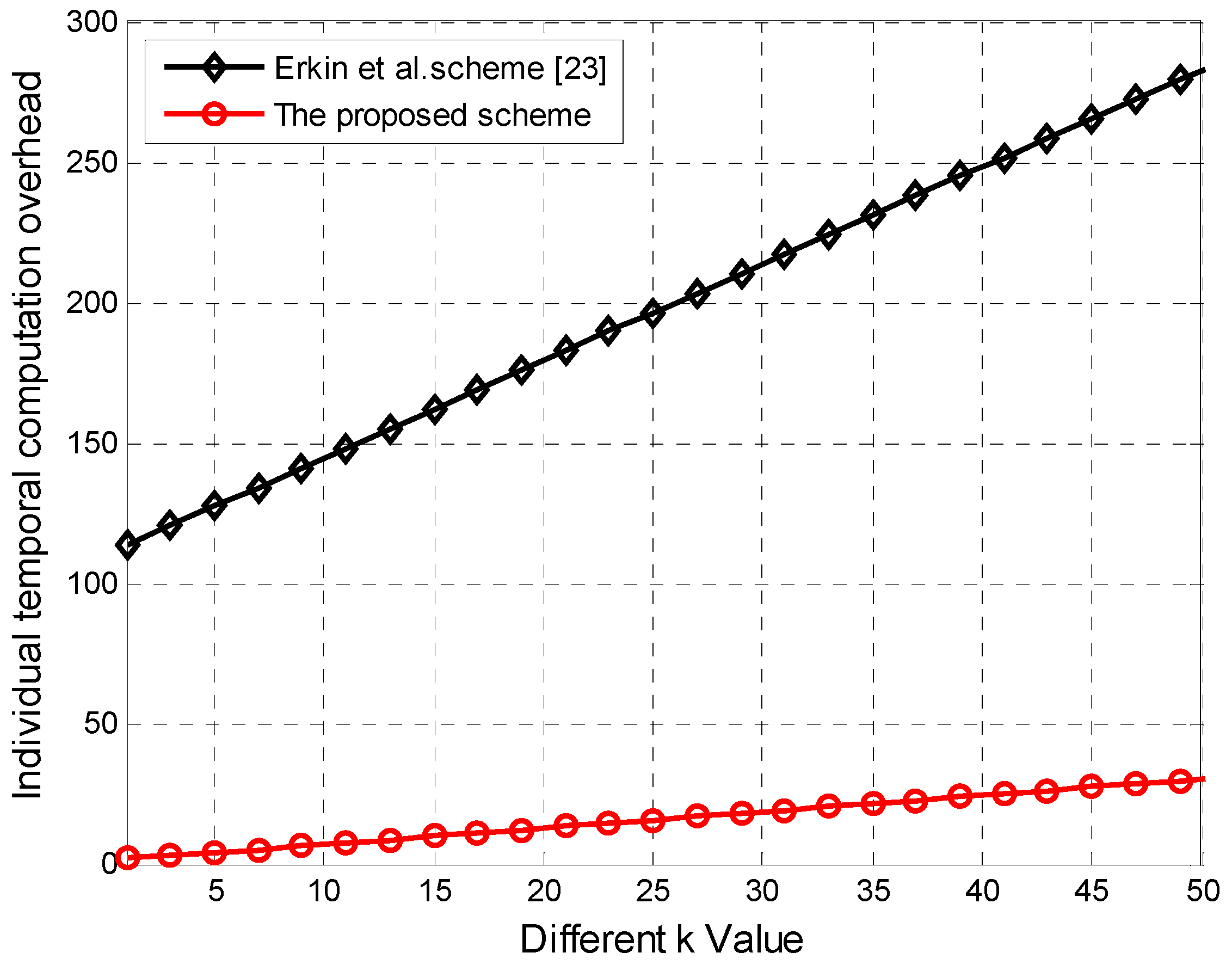
Figure 5 plots the comparison of two schemes in terms of temporal computation overhead in every billing period for
k ranging from 0 to 50. From
Figure 5, we can see the temporal computation overhead per node grows with the increasing of
k value in two schemes; however, our proposed scheme increases slightly compared with the scheme in References [
23], as the latter costs much overhead on Paillier encryption, while our scheme achieves the same privacy protection effect as the asymmetric encryption with simple and low-cost modular addition.
5.2. Communication Overhead
We assume the format of a packet is the same as that in TinyOS [
26]. The timestamp occupies 128 bits. The sizes of prime numbers
p, and
q needed in the Paillier encryption are 512 bits each. The size of elements in
is 1024 bits. We further assume the plaintext data occupies 32 bits, then random from stream cipher occupies the same byte width with the plaintext data, and Paillier encryption occupies 4096 bits, while the hash function with timestamp occupies 256 bits.
For simplicity, we denote as the plaintext data size, masking random key (noise) size, Paillier encryption size, and the size of hash function random.
5.2.1. Spatial Communication Overhead Per Node
To generate the spatial aggregation, every node sends the local aggregation to the GW after adding up the encrypted message from all k pairs. The data sent per node can be denoted as , the size is bits (a partitioned part size is bits, k partitions take bits; a noise key takes bits, and then k noise keys take bits), so the total packet size is bits.
For the scheme in Reference [
23], the spatial aggregation packet per node is in the form as
, its size is
bits.
Every user node in Reference [
24] generates
k results, the data is in the form of
, in which
involves the computation of data sharing and hash random value, so its size is
bits.
We provide the individual spatial communication overhead comparison in
Table 4.
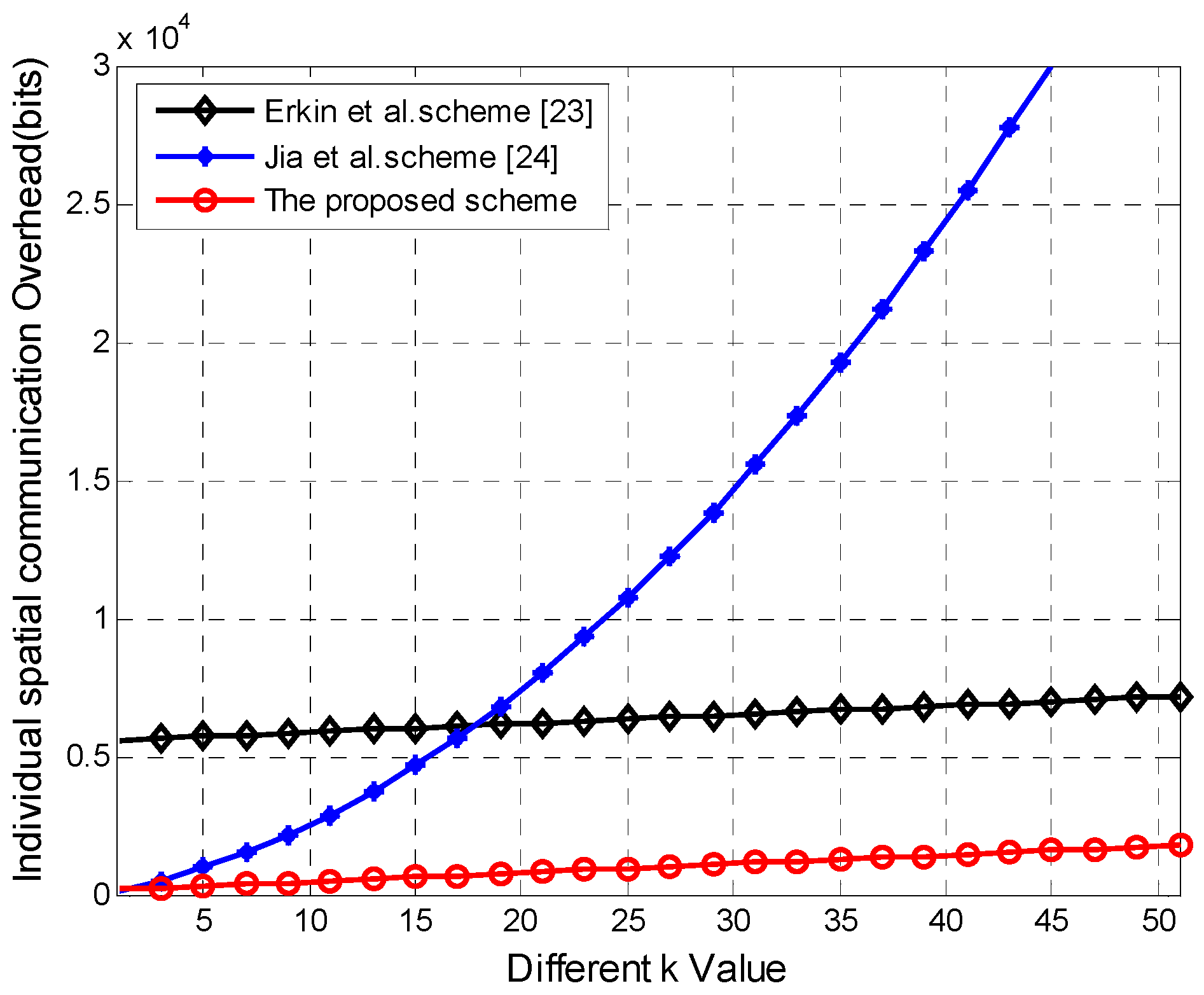
We plot the individual communication overhead comparison between our scheme and the other two schemes [
23,
24] during spatial aggregation in the
Figure 6. We can see clearly the three schemes’ individual overhead all grow with the increasing of
k value. The packet width per node in the scheme in Reference [
24] grows significantly than the other two schemes, especially when
k value is relatively higher, and communication overhead closes to O(
k2), due to the x
k polynomial operation per node before the matrix multiplication operation. Our scheme’s growth rate is close to the scheme in Reference [
23], which is higher always slightly higher than ours, due to the relatively higher public key encryption width.
5.2.2. Temporal Communication Overhead Per Node
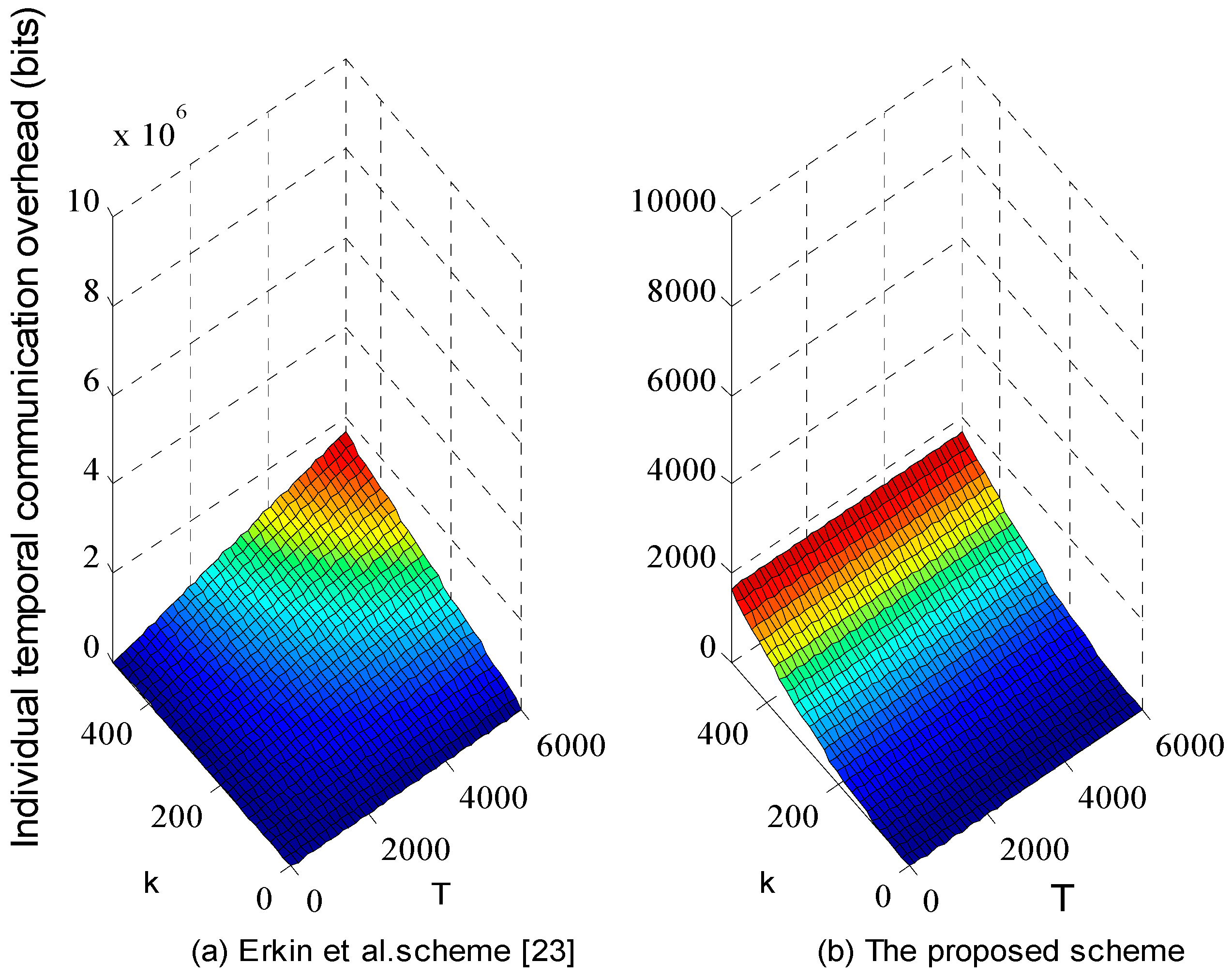
Figure 7 shows the comparison result of ours and the scheme [
23] in terms of temporal communication overhead per node when
k ranges from 0 to 600, and
T ranges from 0 to 6000 mins.
In
Figure 7, our scheme reduces significantly the packet size sent per node to almost three orders of magnitude than the scheme [
23], due to the high overhead of public key encryption. During temporal aggregation, if the process of exchanging random between communication nodes is ignorable, then every node sends its serial encrypted packet formed as
to the aggregator, so the packet size is
bits, while in our scheme, one node’s temporal aggregation is computed synchronously before being reported to the aggregator by
k communication nodes, and they sends the local temporal aggregation packet size of
bits to the aggregator every
T timeslot, so aggregating one node’s temporal consumption in
T serial time slots costs
bits. Hence, when
, ours overhead is always lower significantly lower than the scheme in Reference [
23]. Just as the description above, we shorten the number of the communication nodes in Reference [
23] into
k, and the performance evaluation shows the proposed collection of modular addition and masking keys from PRF saves much computation and communication overhead compared with traditional public key encryption without compromising individual privacy.