Seismic Behavior of Steel Plate-Concrete Shear Walls with Holes
Abstract
1. Introduction
2. Experiment
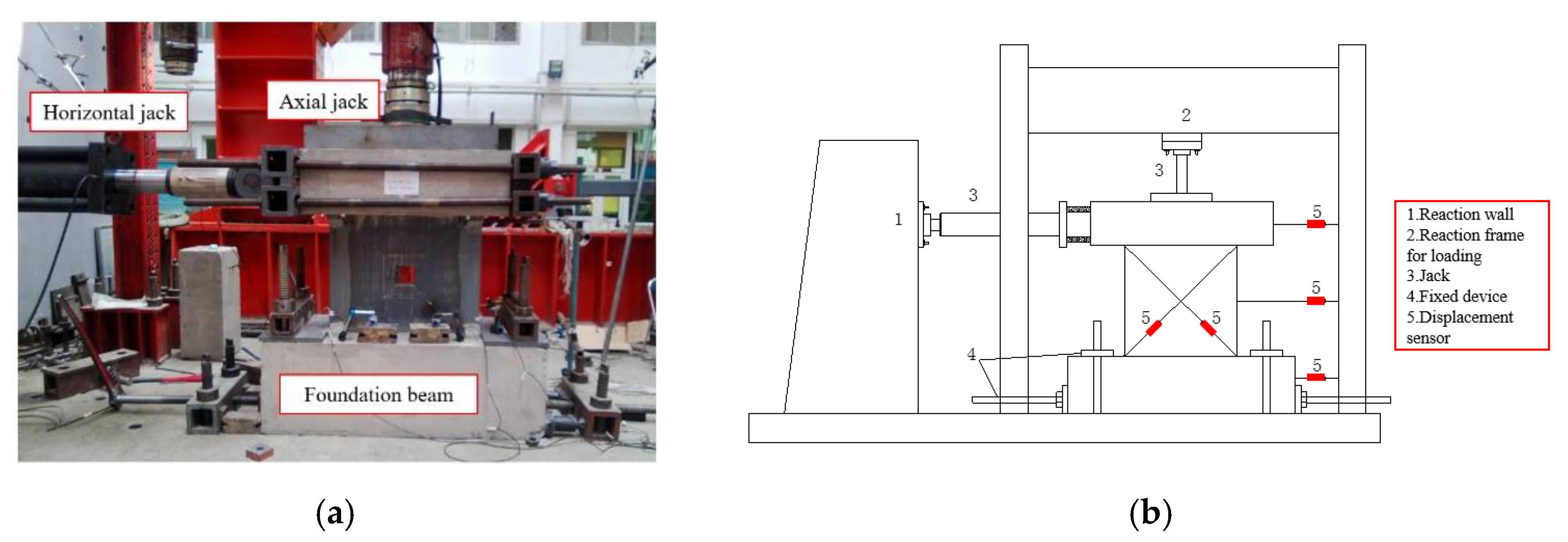
2.1. Experimental Apparatus
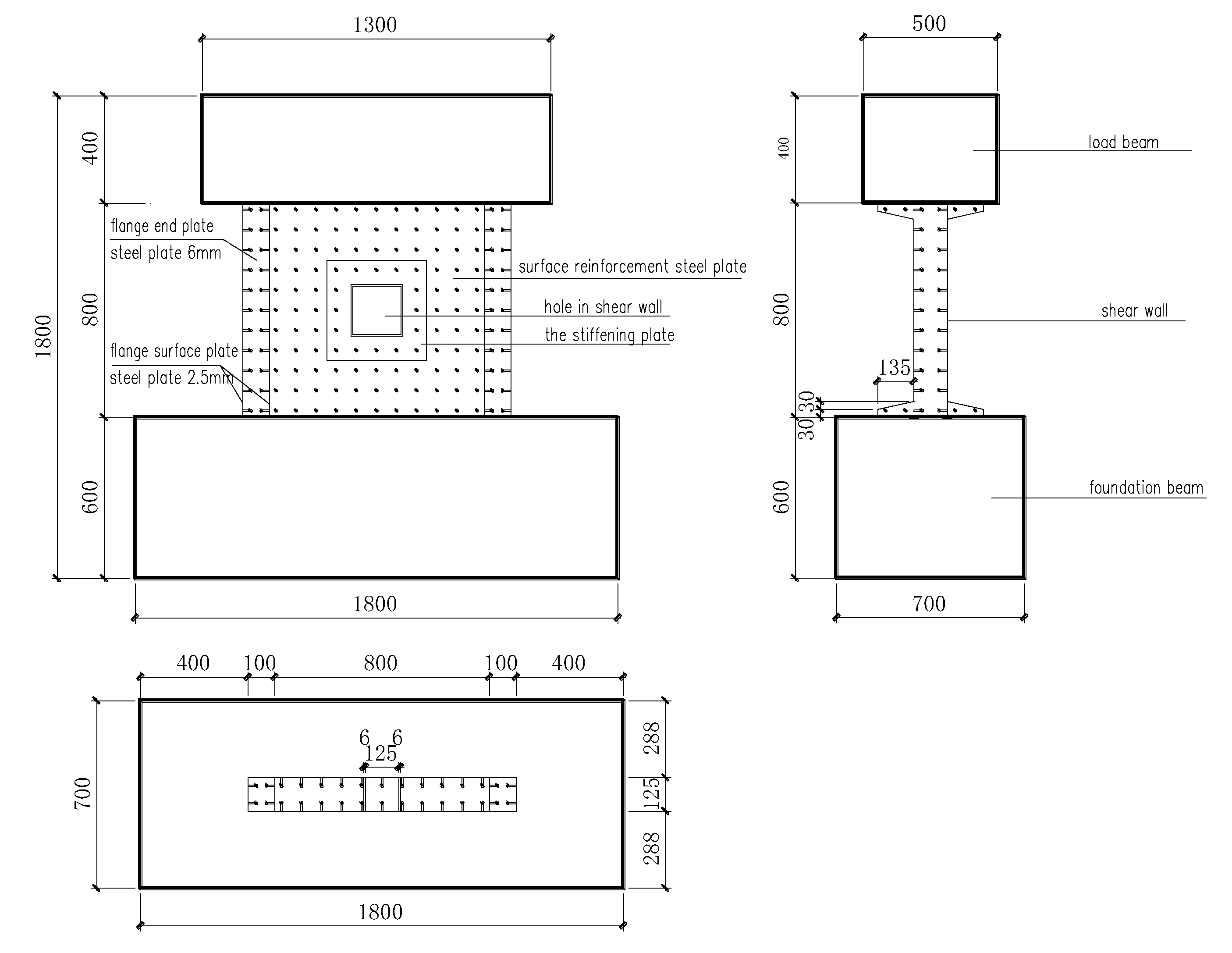
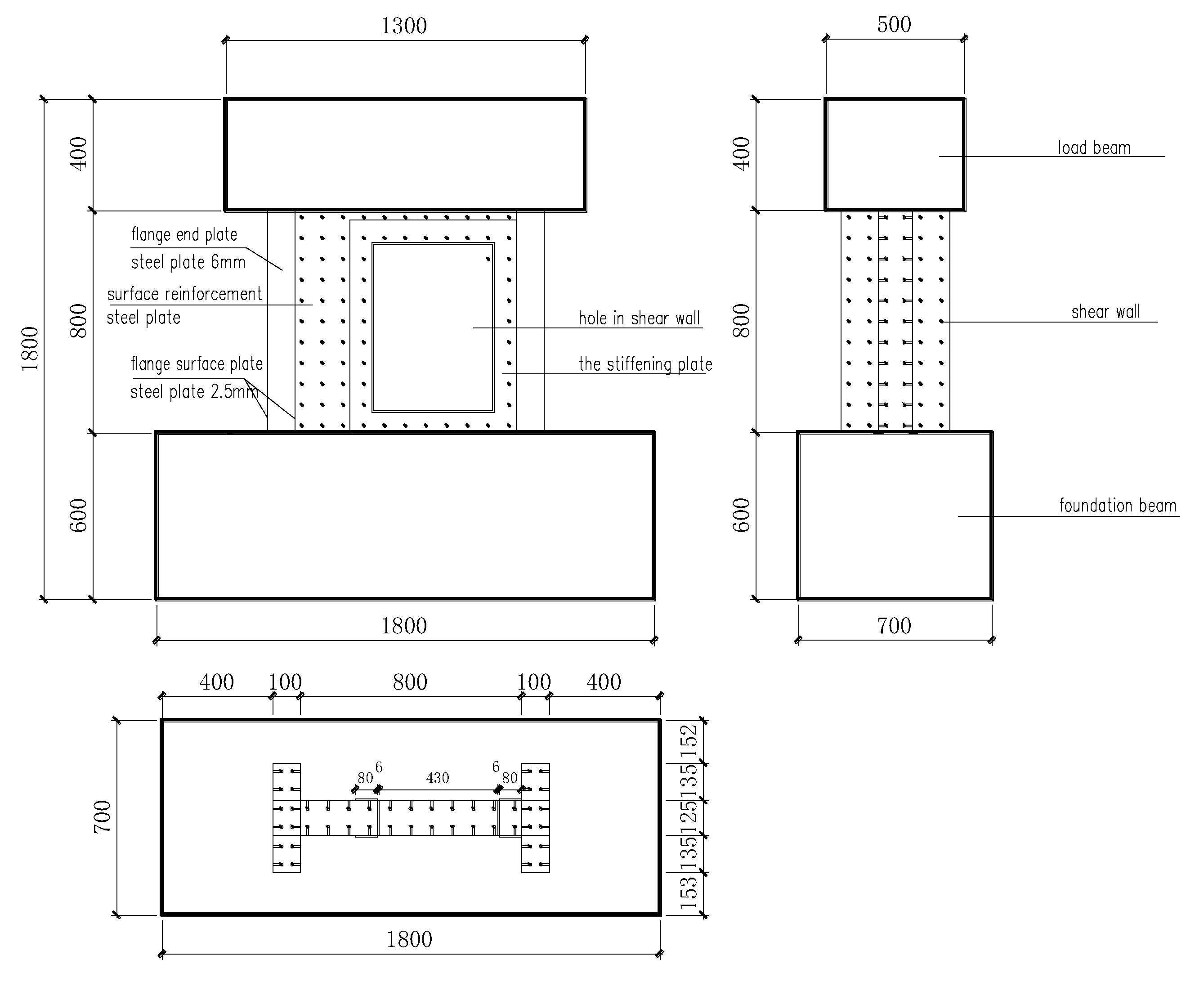
2.2. Design of Specimens and Instrumentation
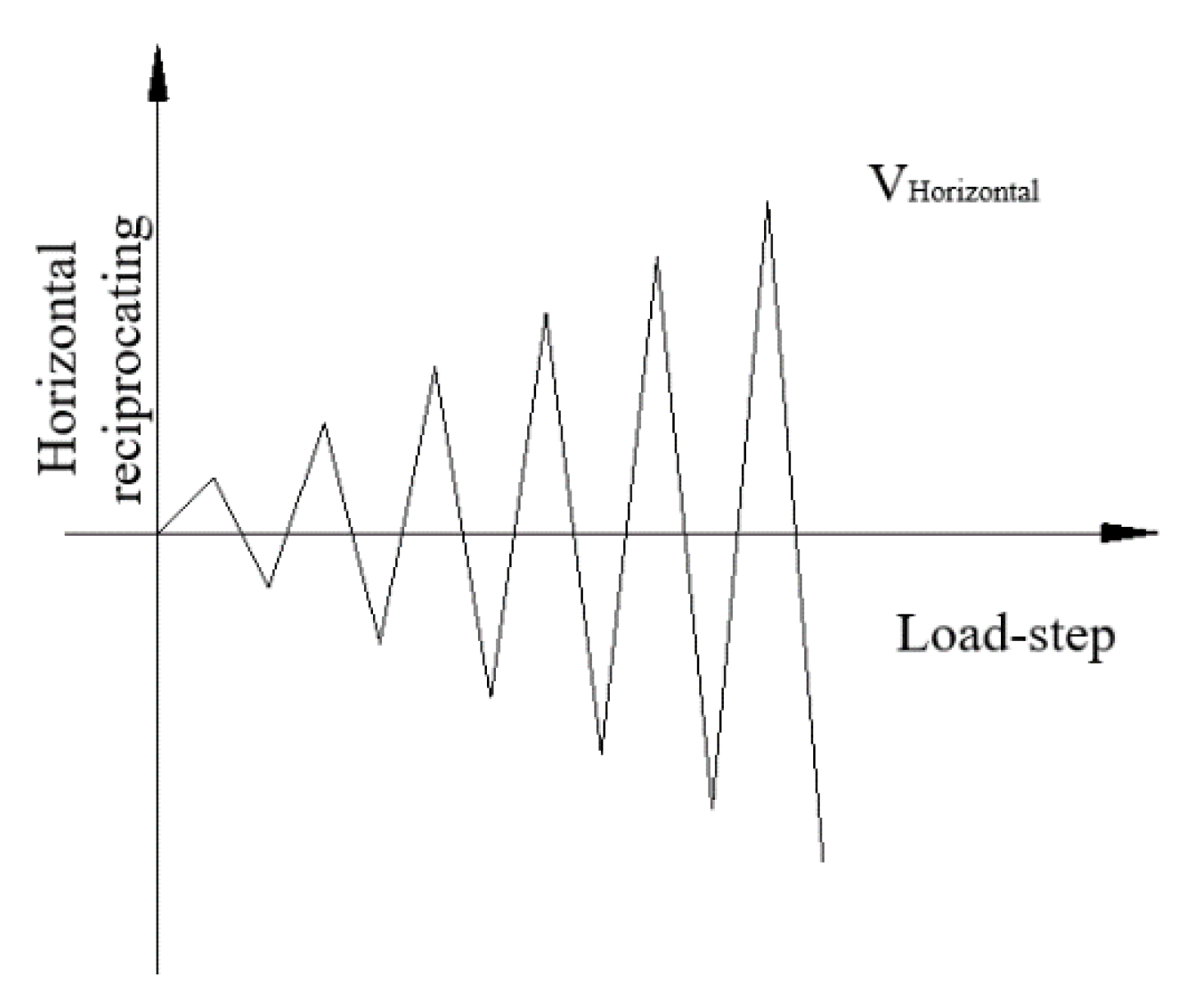
2.3. Loading Mode
- (1)
- The bearing capacity of specimens decreased to lower than 85%.
- (2)
- Serious failure occurred in specimens, such as heaving of steel plates or crushing of concrete, thereby resulting in a difficult loading.
3. Experimental Analysis
3.1. Failure Mode
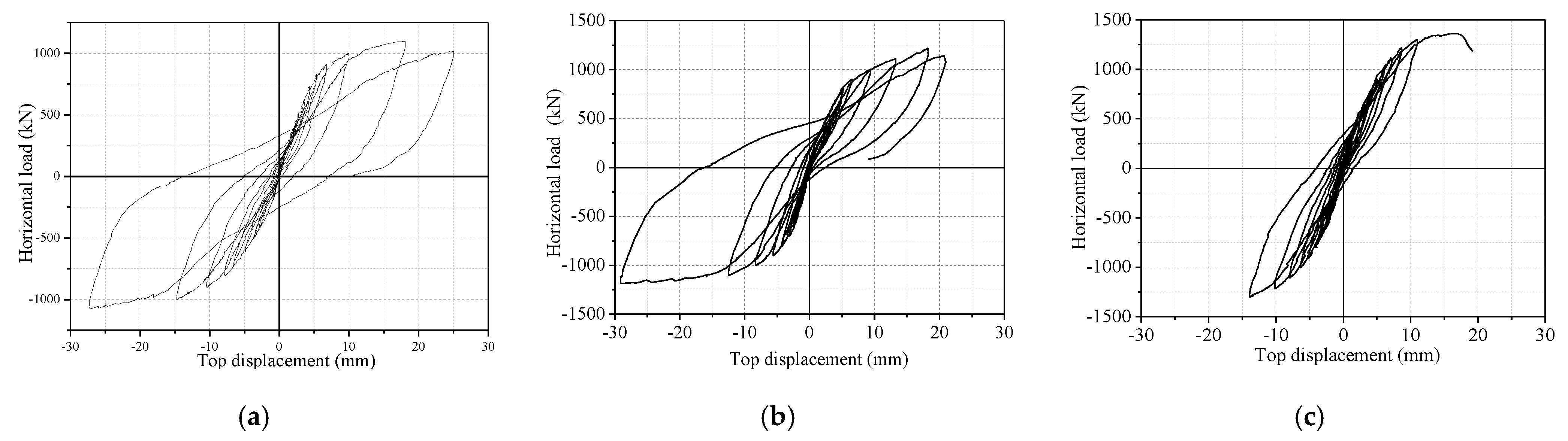
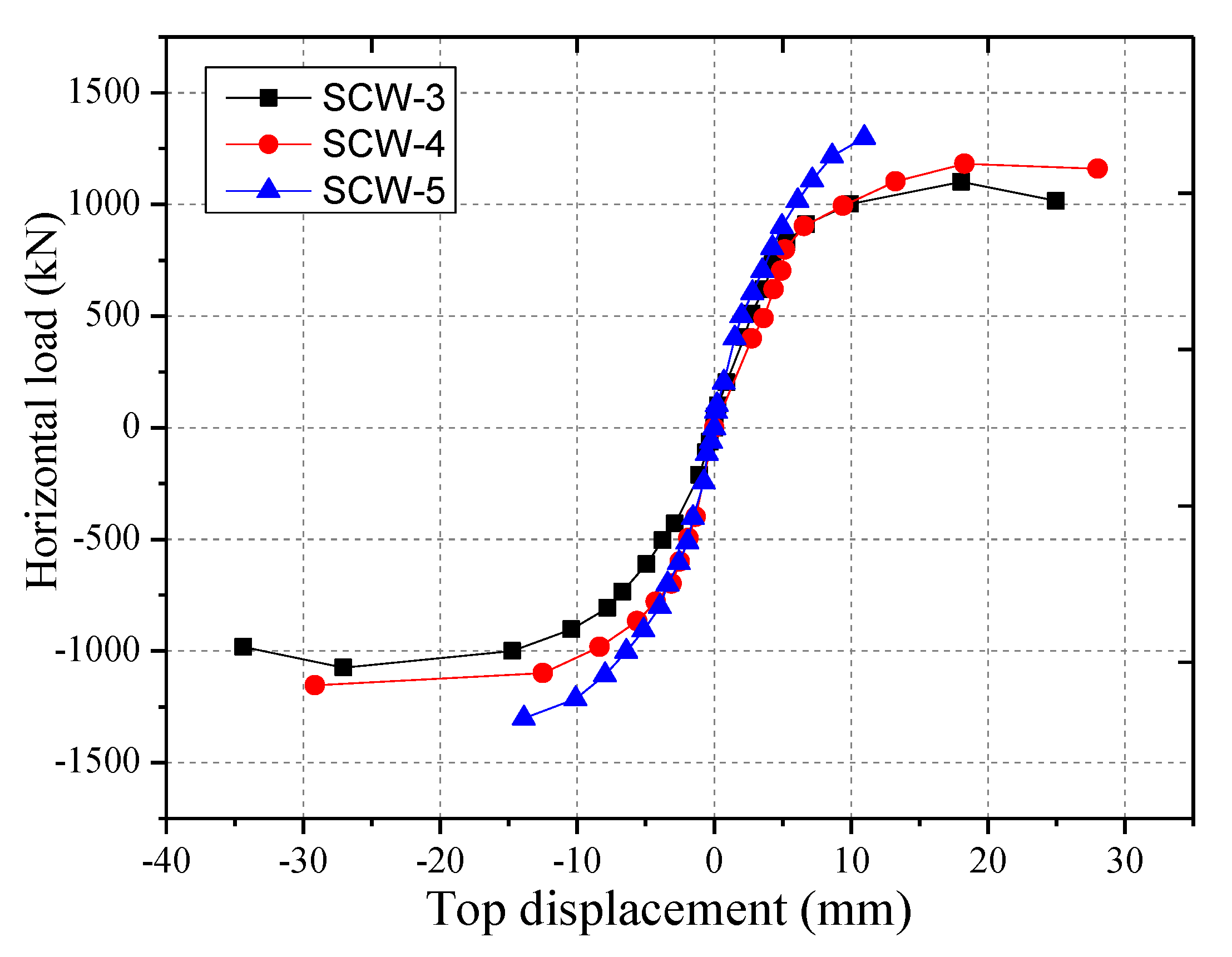
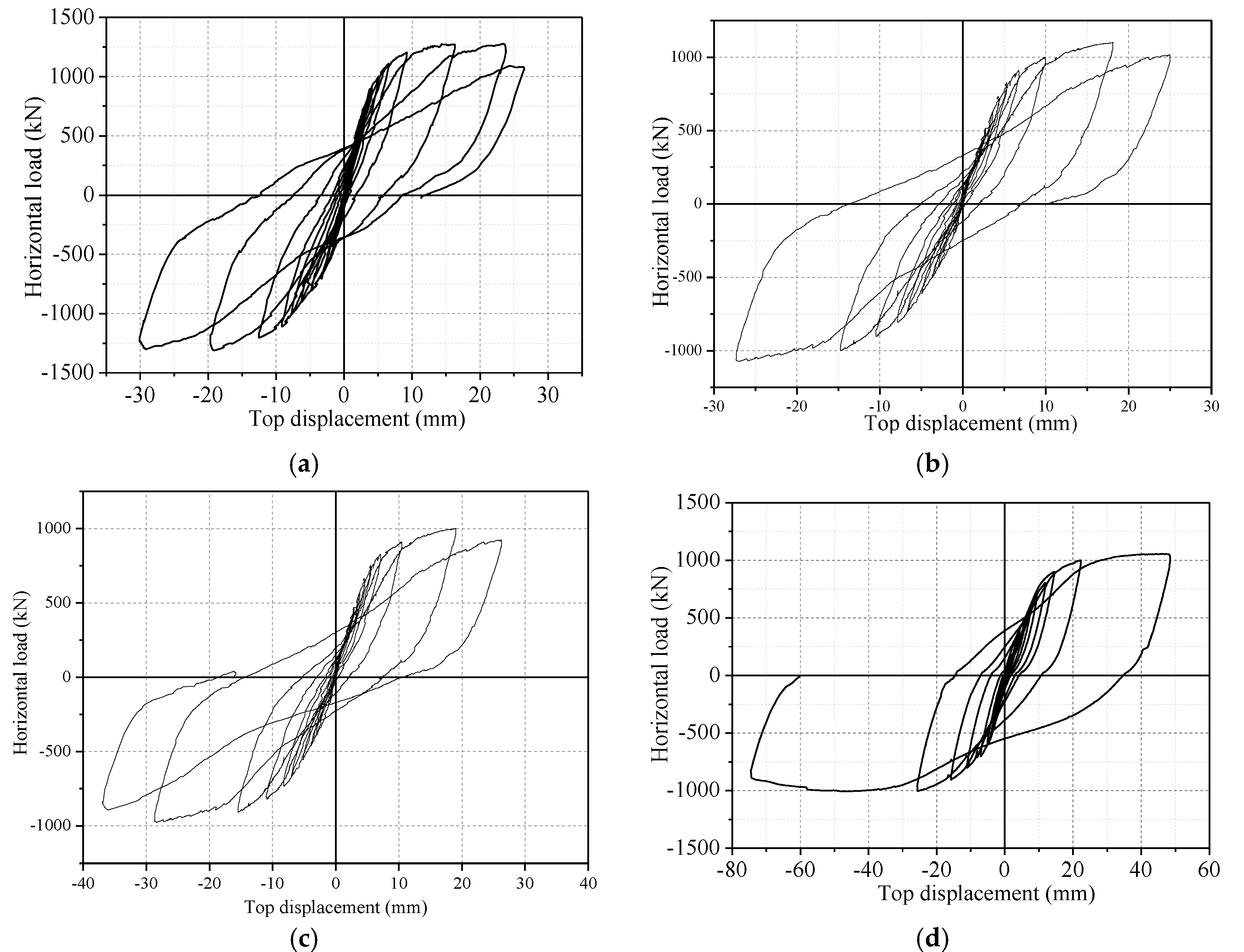
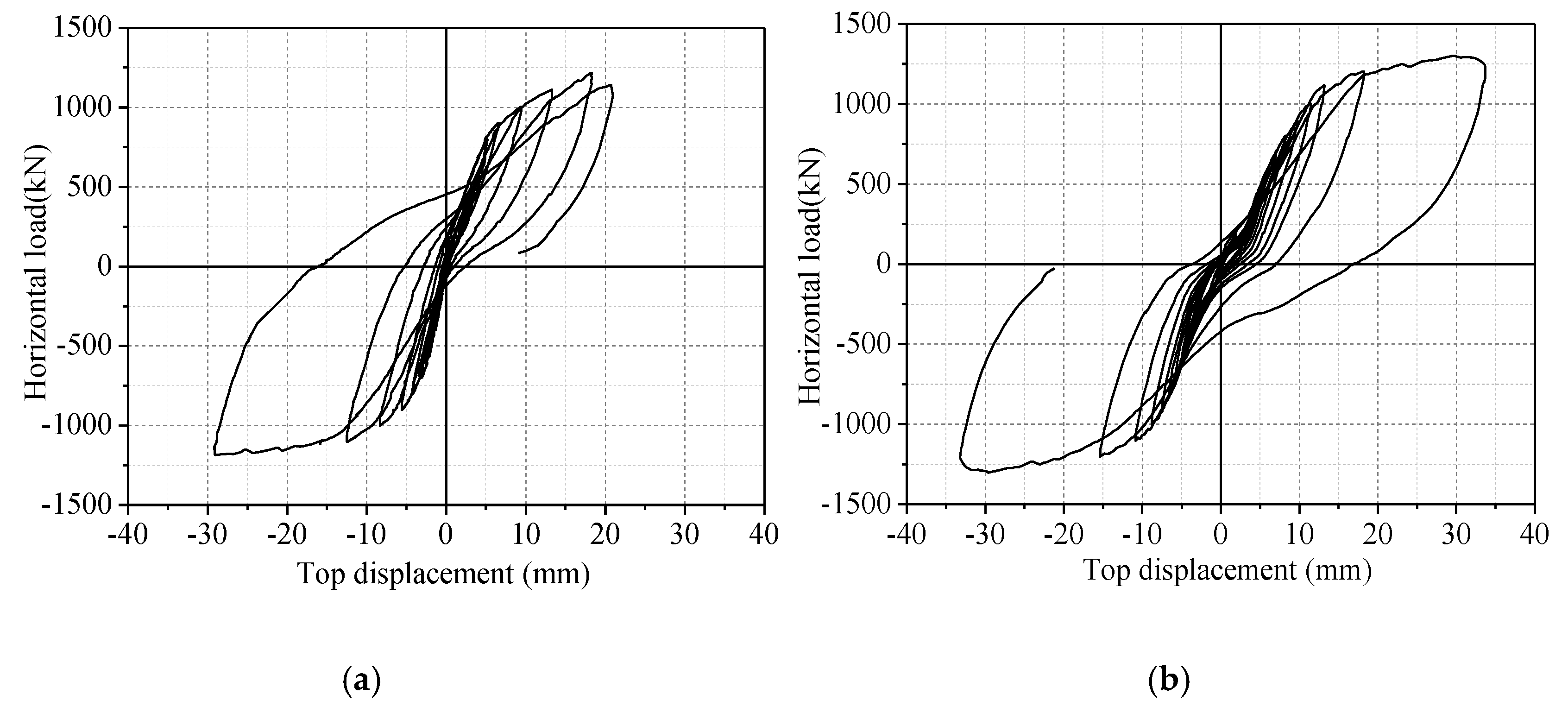
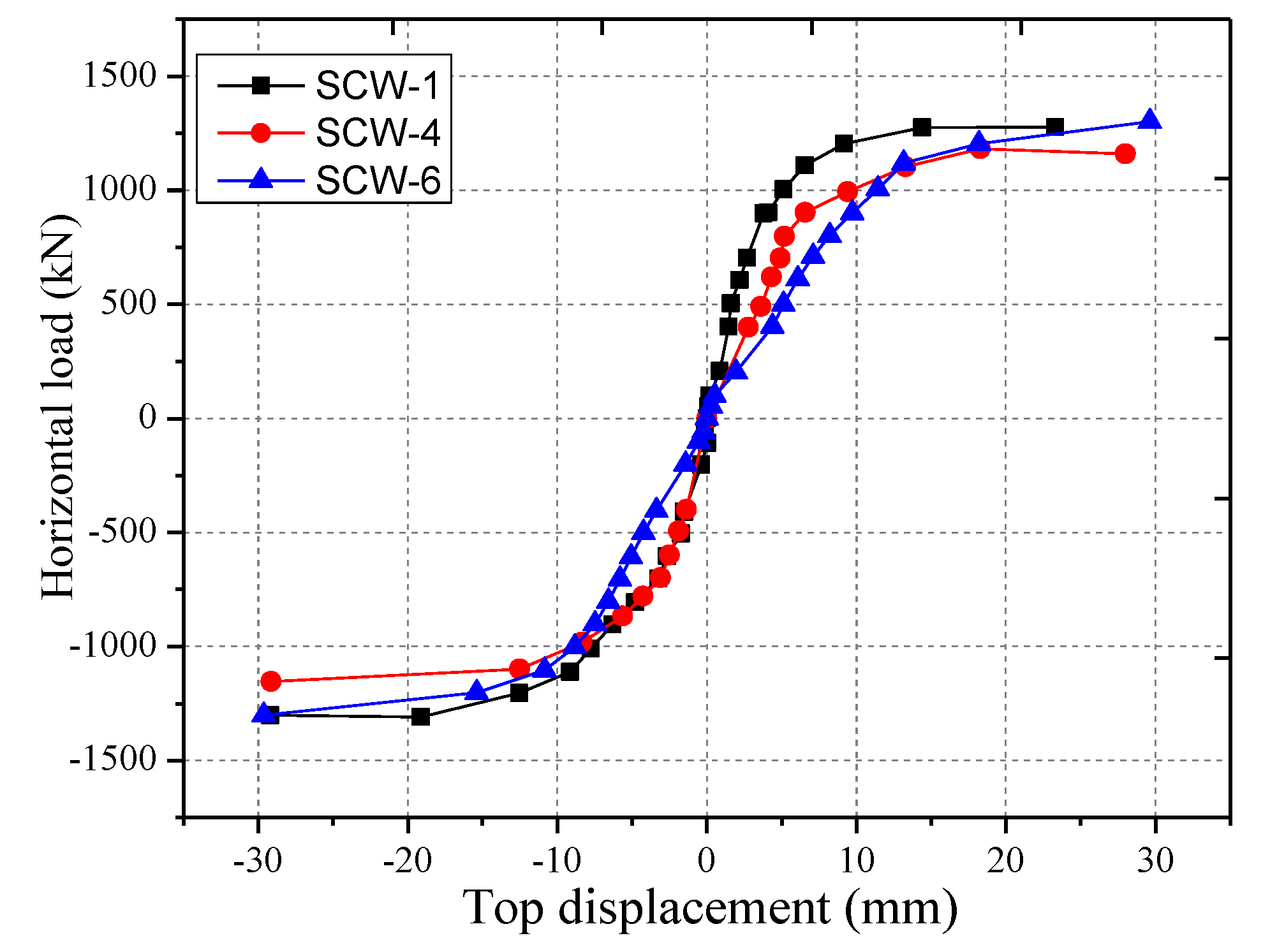
3.2. Effects of Axial Compression Ratio on the Hysteretic Performance of SPSW Specimens
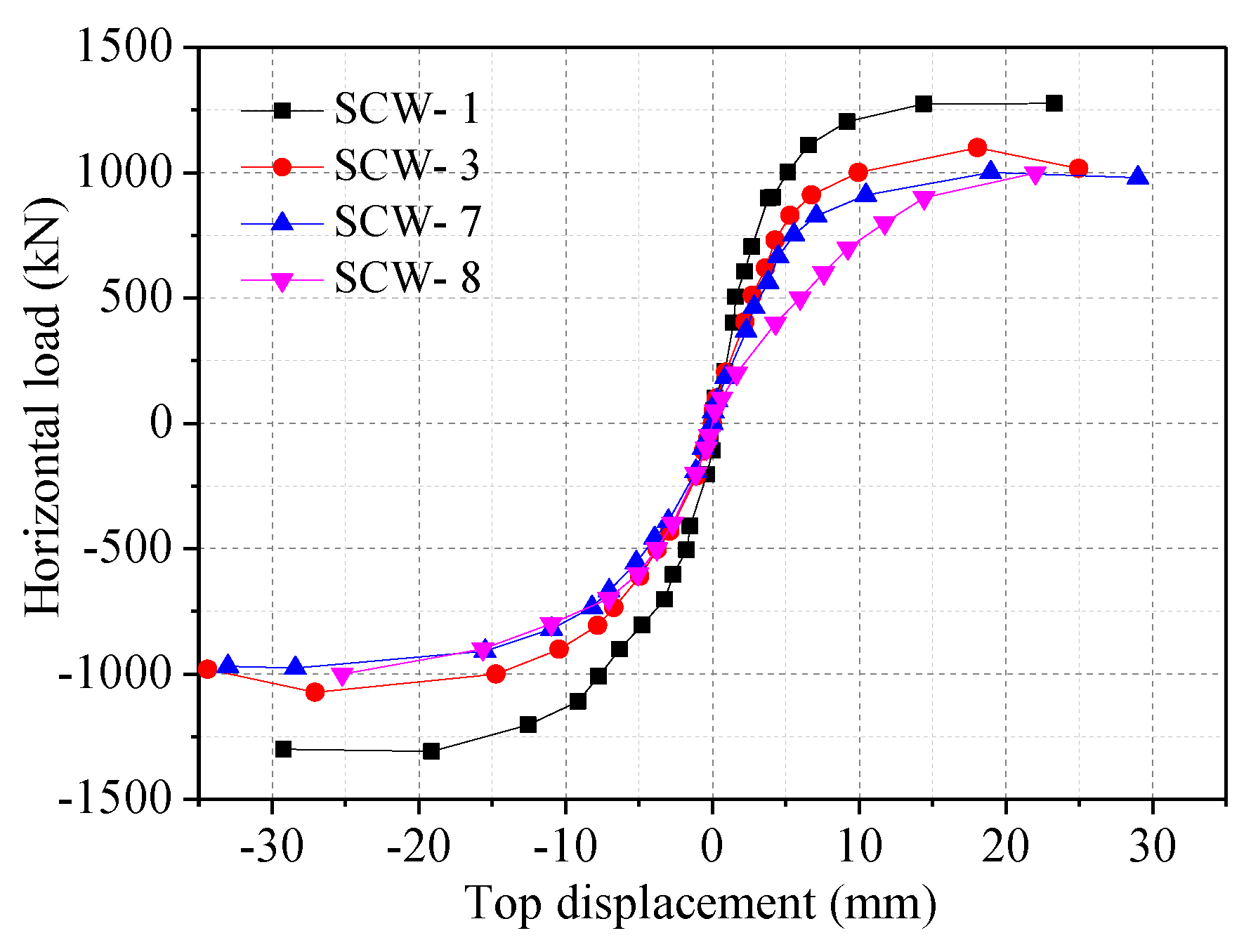
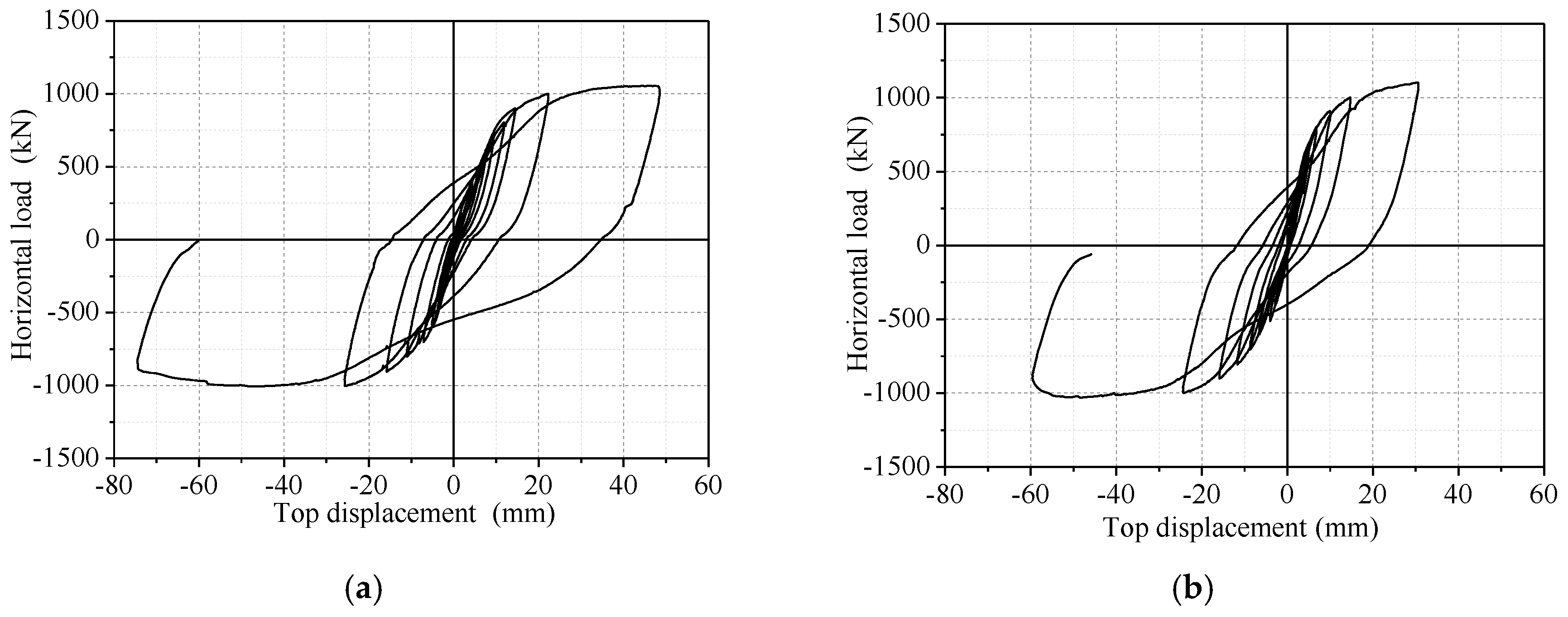
3.3. Effects of Hole Area on the Hysteretic Performance of SPSW Specimens
3.4. Effects of the Thickness of the Stiffening Plate on the Seismic Behavior of SPSW Specimens
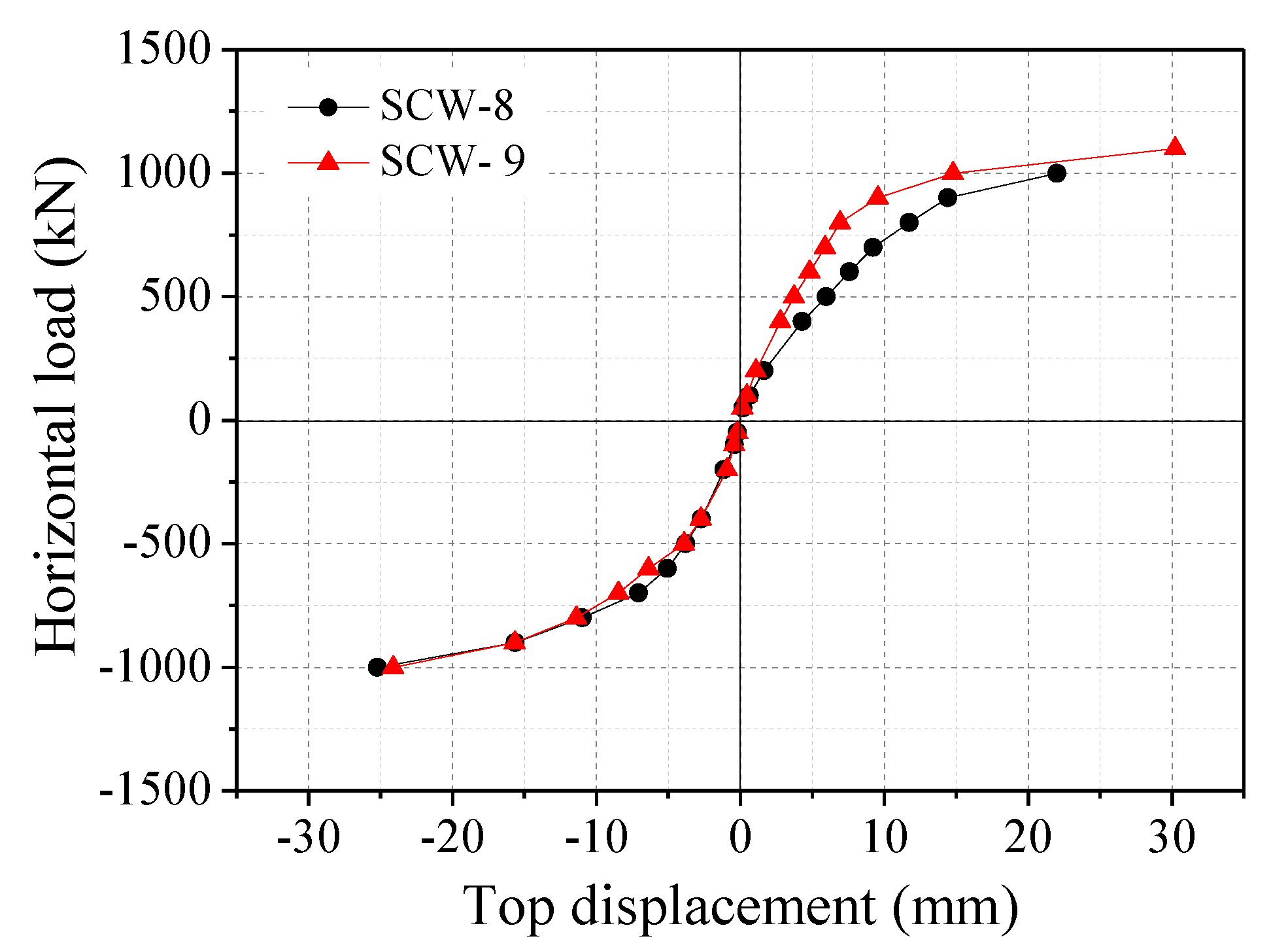
3.5. Effects of Hole Position on the Seismic Behavior of SPSW Specimens
4. Theoretical Calculation
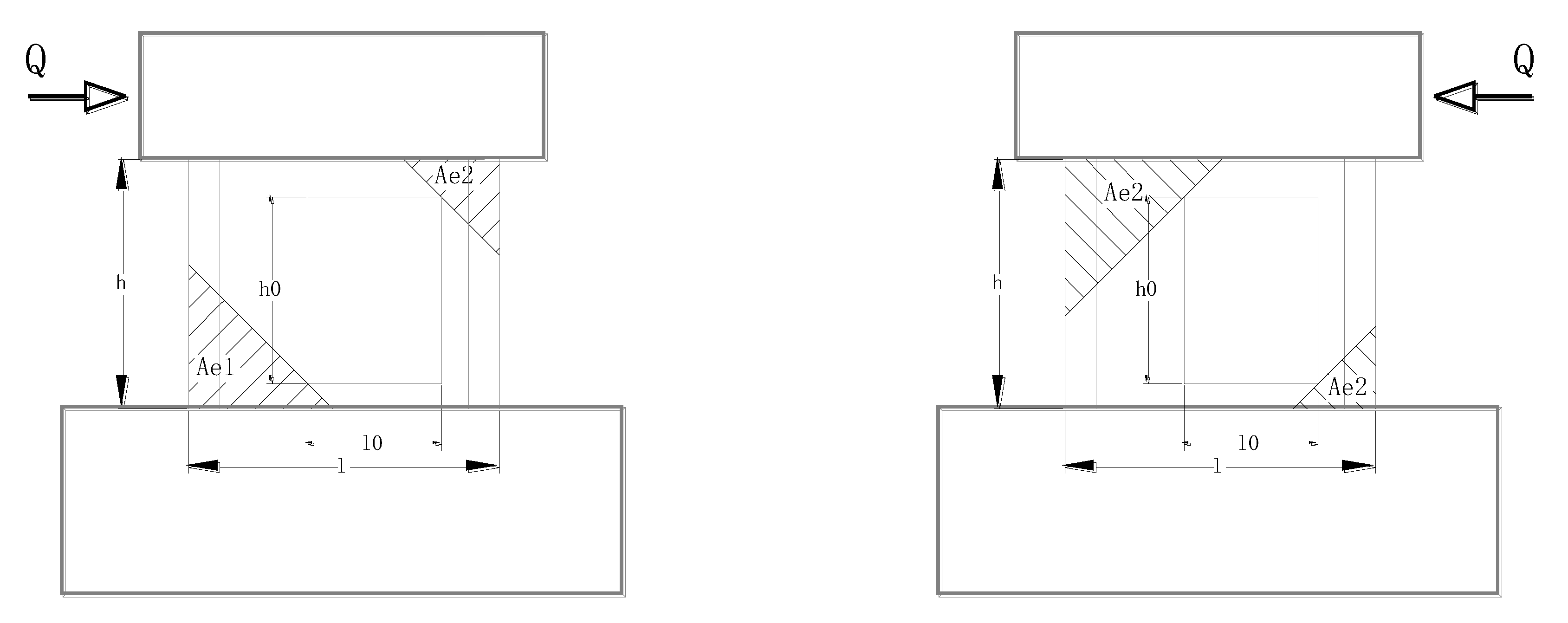
4.1. ReductionRate Calculation Method of AIJ
4.2. Ono Reduction Rate Calculation
5. Conclusions
- (1)
- SPSW structures without holes mainly develop failures at the roots of shear walls, accompanied with the concrete and bending failures of steel plates. SPSW structures with small holes also develop failures at the roots, but several steel plates crack along the corners of the holes. The failure mode is brittle to a certain extent. SPSW structures with large holes develop significant deformation and better ductility than SPSW structures with small holes but low ultimate loads.
- (2)
- Concrete cracks early under high axial compression ratio. The ultimate strength of SPSW structures increases, but the deformation capacity and ductility decrease to a certain extent. Deformation capacity is enhanced, but the ultimate bearing capacity decreases as hole size increases. With an increase in the thickness of stiffening plates, the ultimate bearing capacity of SPSW specimens increases. Eccentric holes decrease the earthquake-resistant energy-dissipation capacity of SPSW structures, and such a reduction is disadvantageous to seismic design. Therefore, eccentric holes on SPSW structures should be avoided.
- (3)
- The calculated results of AIJ codes are safe, but those of the Ono formula have high accuracy because it considers the influences of loading directions. In summary, both calculation formulas are feasible to calculate the ultimate shear capacity of SPSW structures with holes.
Author Contributions
Funding
Conflicts of Interest
References
- Akiyama, H.; Sekimoto, H.; Tanaka, M.; Inoue, K.; Fukihara, M.; Okuda, Y. 1/10th scale model test of inner concrete structure composed of concrete filled steel bearing wall. In Proceedings of the 10th SMi RT Conference H73, SMiRT 10, Anaheim, CA, USA, 22–27 August 1989; pp. 73–78. [Google Scholar]
- Lubell, A.S.; Prion, H.G.; Ventura, C.E.; Rezai, M. Unstiffened steel plate shear wall performance under cyclic loading. J. Struct. Eng. 2000, 124, 453–460. [Google Scholar] [CrossRef]
- USNRC Regulatory Guide 1.142 Revision 2. In Safety-Related Concrete Structures for Nuclear Power Plants (Other than Reactor Vessels and Containments); NRC: Washington, DC, USA, 2001.
- Japanese Association of Architectural Technicians. 100 Typical Examples of Japanese Structural Technology; Architecture and Building Press: Beijing, China, 2005. [Google Scholar]
- Berman, J.W.; Celik, O.C.; Bruneau, M. Comparing hysteretic behavior of light-gauge steel plate shear walls and braced frames. Eng. Struct. 2005, 27, 475–485. [Google Scholar] [CrossRef]
- Gan, C.; Lu, X.; Wang, W. Experimental study on the steel plate reinforced concrete shear walls. In Proceedings of the International Conference on Advances in Experimental Structural Engineering, Tongji University, Shanghai, China, 4–6 December 2007; pp. 176–188. [Google Scholar]
- Zhao, W.Y.; Guo, Q.Q.; Huang, Z.Y.; Tan, L.; Chen, J.; Ye, Y. Hysteretic model for steel–concrete composite shear walls subjected to in-plane cyclic loading. Eng. Struct. 2016, 106, 461–470. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Y.; Lu, Z. Experimental study on seismic behavior of steel plate reinforced concrete composite shear wall. Eng. Struct. 2018, 160, 281–292. [Google Scholar] [CrossRef]
- Li, X.H.; Li, X.J. Steel plates and concrete filled composite shear walls related nuclear structural engineering: Experimental study for out-of-plane cyclic loading. Nucl. Eng. Des. 2017, 315, 144–154. [Google Scholar] [CrossRef]
- Huang, S.T.; Huang, Y.S.; He, A.; Tang, X.; Chen, Q.; Liu, X.; Cai, J. Experimental study on seismic behavior of an innovative composite shear wall. J. Construct. Steel Res. 2018, 148, 165–179. [Google Scholar] [CrossRef]
- Rafiei, S.; Hossain, K.M.A.; Lachemi, M.; Behdinan, K.; Anwar, M.S. Finite element modeling of double skin profiled composite shear wall system under in-plane loadings. Eng. Struct. 2013, 56, 46–57. [Google Scholar] [CrossRef]
- Hu, H.S.; Nie, J.G.; Eatherton, M.R. Deformation capacity of concrete-filled steel plate composite shear walls. J. Constr. Steel Res. 2014, 103, 148–158. [Google Scholar] [CrossRef]
- Booth, P.N.; Varma, A.H.; Sener, K.C.; Mori, K. Seismic behavior and design of a primary shield structure consisting of steel-plate composite (SC) walls. Nucl. Eng. Des. 2015, 295, 829–843. [Google Scholar] [CrossRef]
- Nguyen, N.H.; Whittaker, A.S. Numerical modelling of steel-plate concrete composite shear walls. Eng. Struct. 2017, 150, 1–11. [Google Scholar] [CrossRef]
- Wang, B.; Jiang, H.; Lu, X. Seismic performance of steel plate reinforced concrete shear wall and its application in China Mainland. J. Construct. Steel Res. 2017, 131, 132–143. [Google Scholar] [CrossRef]
- Sato, K. Kitano Masato Experimental Study on Steel Plate Reinforced Concrete Structure Part 23 Bending Shear Tests (Test Results for SC Wall with Opening). In Summary of Academic Speeches; Japanese Architectural Society: Toyko, Japan, 1999; pp. 1227–1228. [Google Scholar]
- Satou, K. Experimental Study on Steel Plate Reinforced Concrete Structure Part 24 Bending Shear Tests (Analysis of SC wall with Opening). In Summary of Academic Speeches; Japanese Architectural Society: Toyko, Japan, 1999; pp. 1229–1230. [Google Scholar]
- Ishida, M. Experimental Study on Steel Plate Reinforced Concrete Structure Part 25 Bending Shear Tests (Evaluation Method for SC wall with Opening). In Summary of Academic Speeches; Japanese Architectural Society: Toyko, Japan, 1999; pp. 1231–1232. [Google Scholar]
- Fujita, T. Experimental Study on Steel Plate Reinforced Concrete Structure Part 26 Shear Tests (Outline of the Experimental Study on SC Panels having Opening). In Summary of Academic Speeches; Japanese Architectural Society: Toyko, Japan, 1999; pp. 123–1234. [Google Scholar]
- Osuka. Experimental Study on Steel Plate Reinforced Concrete Structure Part 27 Shear Tests (Discussion of Analytical Results and Experimental ones on SC Panels having Opening). In Summary of Academic Speeches; Japanese Architectural Society: Toyko, Japan, 1999; pp. 1235–1236. [Google Scholar]
- Khatir, S.; Wahab, M.A. A computational approach for crack identification in plate structures using XFEM, XIGA, PSO and Jaya algorithm. Theor. Appl. Fract. Mech. 2019, 103, 102240. [Google Scholar] [CrossRef]
- Liang, Y.C.; Sun, Y.P. Hole/Crack Identification in Circular Piezoelectric Plates. Procedia Eng. 2014, 79, 194–203. [Google Scholar] [CrossRef]
- Khatira, S.; Wahabb, M.A. Fast simulations for solving fracture mechanics inverse problems using POD-RBF XIGA and Jaya algorithm. Eng. Fract. Mech. 2019, 205, 285–300. [Google Scholar] [CrossRef]
- Japanese Code (JEAC 4618-2009). Technical Specification for Seismic Design of Steel Plate Concrete Structures; Japan Electric Association: Toyko, Japan, 1999.
- Industrial Standard of the People’s Republic of China. Specification for Seismic Test of Building: JGJ/T 101-2015; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2015.
- Japanese Architectural Society (AIJ). The Calculation Standards and Specification for Reinforced Concrete Structure; Japan Electric Association: Toyko, Japan, 1999. [Google Scholar]
- Ono, M. NISIYAMA taku. Experimental Study on Reinforced Concrete Opening Wall above Opening Periphery Ratio 0.4: Part 2. Area Expansion, Ultimate Strength. In Summary of Academic Speeches; Japanese Architectural Society: Japan, Tokyo, 1995; pp. 147–150. [Google Scholar]



| Specimen | Flange Size (mm) | Thickness of Steel Plate (mm) | Hole Size (mm) | Hole Position | Thickness of Stiffening Plate | Axial Compression Ratio | Wall Type | |
|---|---|---|---|---|---|---|---|---|
| Width | Thickness | |||||||
| SCW-1 | − | − | 2.5 | − | − | − | 0.3 | Flat |
| SCW-2 | − | − | 2.5 | 125 × 125 | Center | − | 0.15 | Flat |
| SCW-3 | − | − | 2.5 | 125 × 125 | Center | 2.5 | 0.15 | Flat |
| SCW-4 | − | − | 2.5 | 125 × 125 | Center | 2.5 | 0.3 | Flat |
| SCW-5 | − | − | 2.5 | 125 × 125 | Center | 2.5 | 0.5 | Flat |
| SCW-6 | − | − | 2.5 | 125 × 125 | Center | 3.5 | 0.3 | Flat |
| SCW-7 | − | − | 2.5 | 180 × 180 | Center | 2.5 | 0.15 | Flat |
| SCW-8 | 395 | 110 | 2.5 | 430 × 600 | Center | 2.5 | 0.15 | I-shaped |
| SCW-9 | 395 | 110 | 2.5 | 430 × 600 | Eccentricity | 2.5 | 0.15 | I-shaped |
| Thickness of Steel Plate (mm) | Yield Strength (MPa) | Tensile Strength (MPa) | Elasticity Modulus (MPa) | Maximum Elongation (%) |
|---|---|---|---|---|
| 2.5 | 369 | 486 | 2.02 × 105 | 28.5 |
| Material Number | Axial Compressive Strength (MPa) | Axial Tension Strength (MPa) | Elasticity Modulus (MPa) |
|---|---|---|---|
| C35 | 25.98 | 2.33 | 3.25 × 104 |
| Specimens | Ultimate Loads (kN) | Ultimate Displacements (mm) | ||
|---|---|---|---|---|
| Positive | Negative | Positive | Negative | |
| SCW-3 | 1100 | −1074 | 18.09 | −27.05 |
| SCW-4 | 1217 | −1185 | 18.46 | −28.60 |
| SCW-5 | 1362 | −1301 | 16.56 | −13.88 |
| Specimens | Hole Size (mm) | Ultimate Loads (kN) | Ultimate Displacements (mm) | ||
|---|---|---|---|---|---|
| Positive | Negative | Positive | Negative | ||
| SCW-1 | − | 1277 | −1310 | 23.15 | −19.27 |
| SCW-3 | 125 × 125 | 1100 | −1074 | 18.09 | −27.05 |
| SCW-7 | 180 × 180 | 1190 | −1105 | 37.43 | −27.45 |
| SCW-8 | 430 × 600 | 1055 | −1007 | 51.94 | −43.49 |
| Specimens | Ultimate Loads (kN) | Ultimate Displacements (mm) | ||
|---|---|---|---|---|
| Positive | Negative | Positive | Negative | |
| SCW-1 | 1277 | −1310 | 23.15 | −19.27 |
| SCW-4 | 1217 | −1185 | 18.46 | −28.60 |
| SCW-6 | 1260 | −1302 | 21.41 | −28.11 |
| Specimens | Ultimate Loads (kN) | Ultimate Displacements (mm) | ||
|---|---|---|---|---|
| Positive | Negative | Positive | Negative | |
| SCW-8 | 1055 | −1007 | 51.94 | −43.49 |
| SCW-9 | 1103 | −1031 | 34.14 | −44.41 |
| Specimen | Stress State | Axial Compression/kN | Type of Walls | |||||
|---|---|---|---|---|---|---|---|---|
| SCW-4 | Stressed | 1185 | 1127 | 0.95 | 1135 | 0.96 | 950 | Flat |
| Tensioned | 1217 | 1098 | 0.90 | 1106 | 0.91 | Flat | ||
| SCW-6 | Stressed | 1302 | 1127 | 0.87 | 1269 | 0.98 | 950 | Flat |
| Tensioned | 1260 | 1098 | 0.87 | 1237 | 0.98 | Flat | ||
| SCW-8 | Stressed | 1007 | 734 | 0.73 | 820 | 0.81 | 320 | I-shaped |
| Tensioned | 1055 | 734 | 0.70 | 857 | 0.81 | I-shaped | ||
| SCW-9 | Stressed | 1031 | 734 | 0.71 | 836 | 0.81 | 320 | I-shaped |
| Tensioned | 1103 | 734 | 0.67 | 836 | 0.76 | I-shaped | ||
| Average ratio | 0.80 | 0.88 |
| Specimens | Axial Compression/kN | ||||||
|---|---|---|---|---|---|---|---|
| SCW-4 | Negative | 41.43 | 56.11 | 1.35 | 67.64 | 1.63 | 950 |
| Positive | 65.90 | 45.51 | 0.69 | 54.87 | 0.83 | ||
| SCW-6 | Negative | 46.31 | 56.11 | 1.21 | 67.64 | 1.46 | 950 |
| Positive | 58.86 | 45.51 | 0.77 | 54.87 | 0.93 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Wu, J.; Liu, H. Seismic Behavior of Steel Plate-Concrete Shear Walls with Holes. Appl. Sci. 2019, 9, 5255. https://doi.org/10.3390/app9235255
Chen Z, Wu J, Liu H. Seismic Behavior of Steel Plate-Concrete Shear Walls with Holes. Applied Sciences. 2019; 9(23):5255. https://doi.org/10.3390/app9235255
Chicago/Turabian StyleChen, Zhihua, Jingshu Wu, and Hongbo Liu. 2019. "Seismic Behavior of Steel Plate-Concrete Shear Walls with Holes" Applied Sciences 9, no. 23: 5255. https://doi.org/10.3390/app9235255
APA StyleChen, Z., Wu, J., & Liu, H. (2019). Seismic Behavior of Steel Plate-Concrete Shear Walls with Holes. Applied Sciences, 9(23), 5255. https://doi.org/10.3390/app9235255





