Supplier Selection and Performance Evaluation for High-Voltage Power Film Capacitors in a Fuzzy Environment
Abstract
1. Introduction
2. Literature Review
2.1. Supplier Selection
- Cost/Price: the procurement costs, labor costs, material costs, and transportation costs of a company;
- Quality: the quality of supplier products;
- Delivery period: the time to delivery of the suppliers;
- Technology: the implementation of modern technology;
- Relations: the duration of collaboration and the closeness of relationships with the suppliers;
- Service: the ability of the suppliers to support and coordinate with products or technologies;
- Communication: the ability of the suppliers to respond regarding products or services and communicate with internal and external partners;
- Green: whether the products or packaging of the suppliers have green marks and follow the 3 Rs (reduce, reuse and recycle);
- Sustainability: the impact of the suppliers (or their products) on society, the economy, and the environment.
2.2. Fuzzy Theory in Supplier Selection
3. Material and Methods
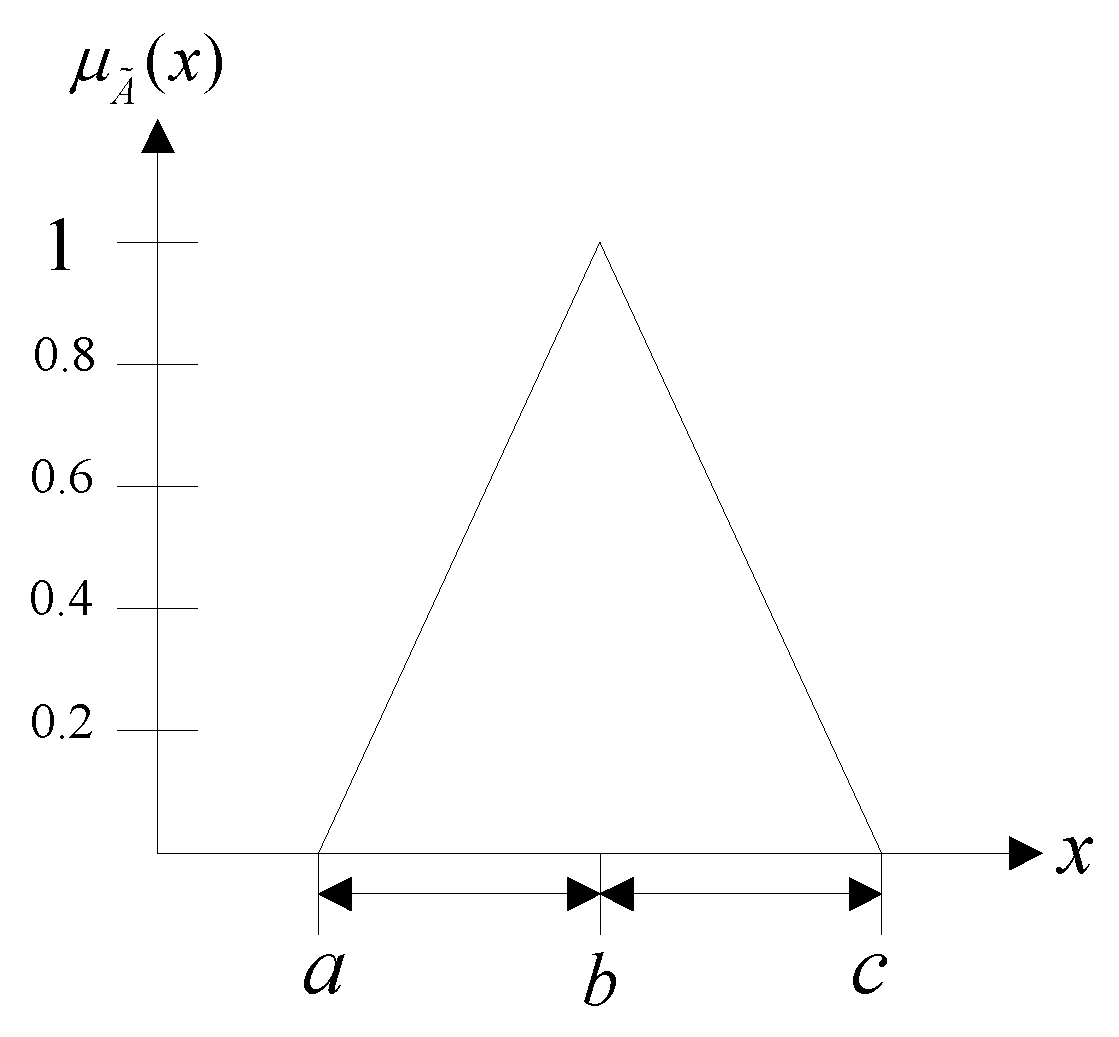
3.1. Fuzzy Operations for Supplier Evaluation and Selection
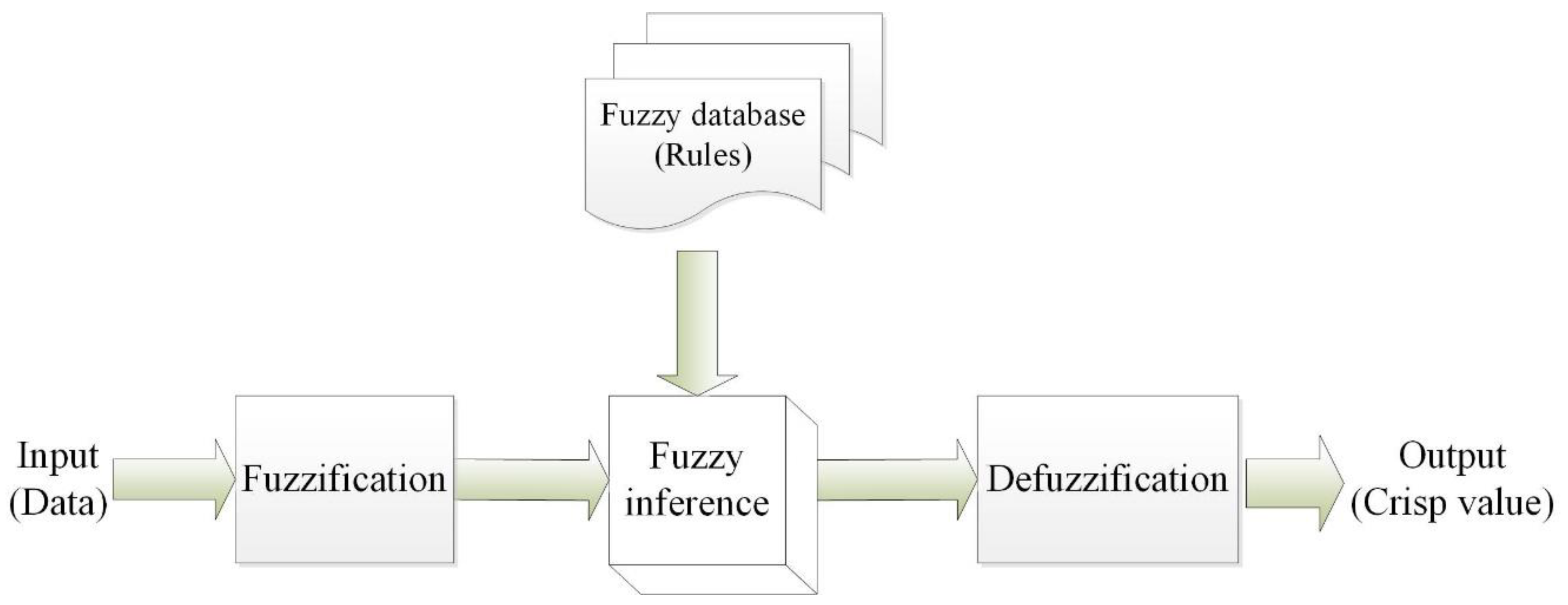
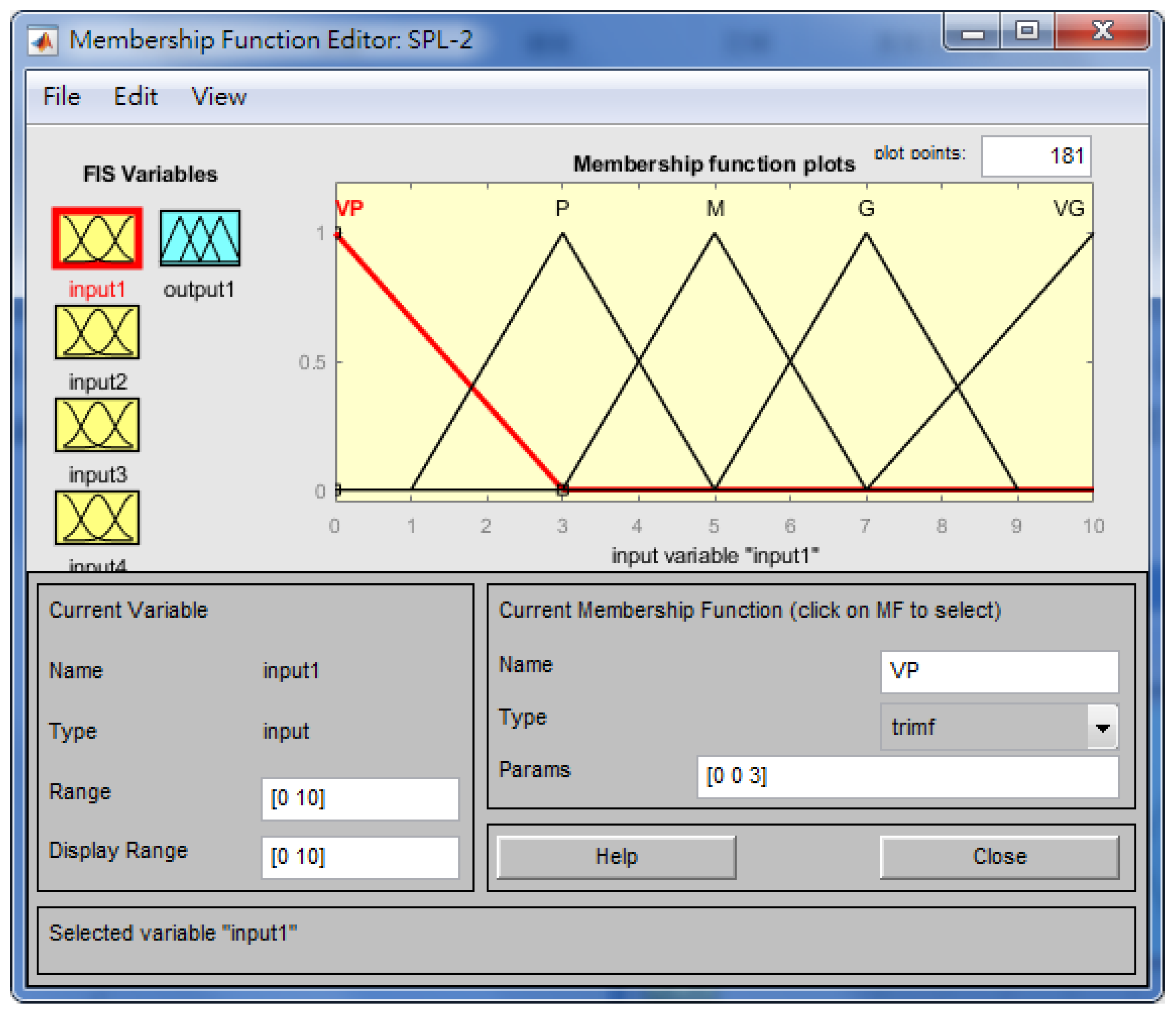
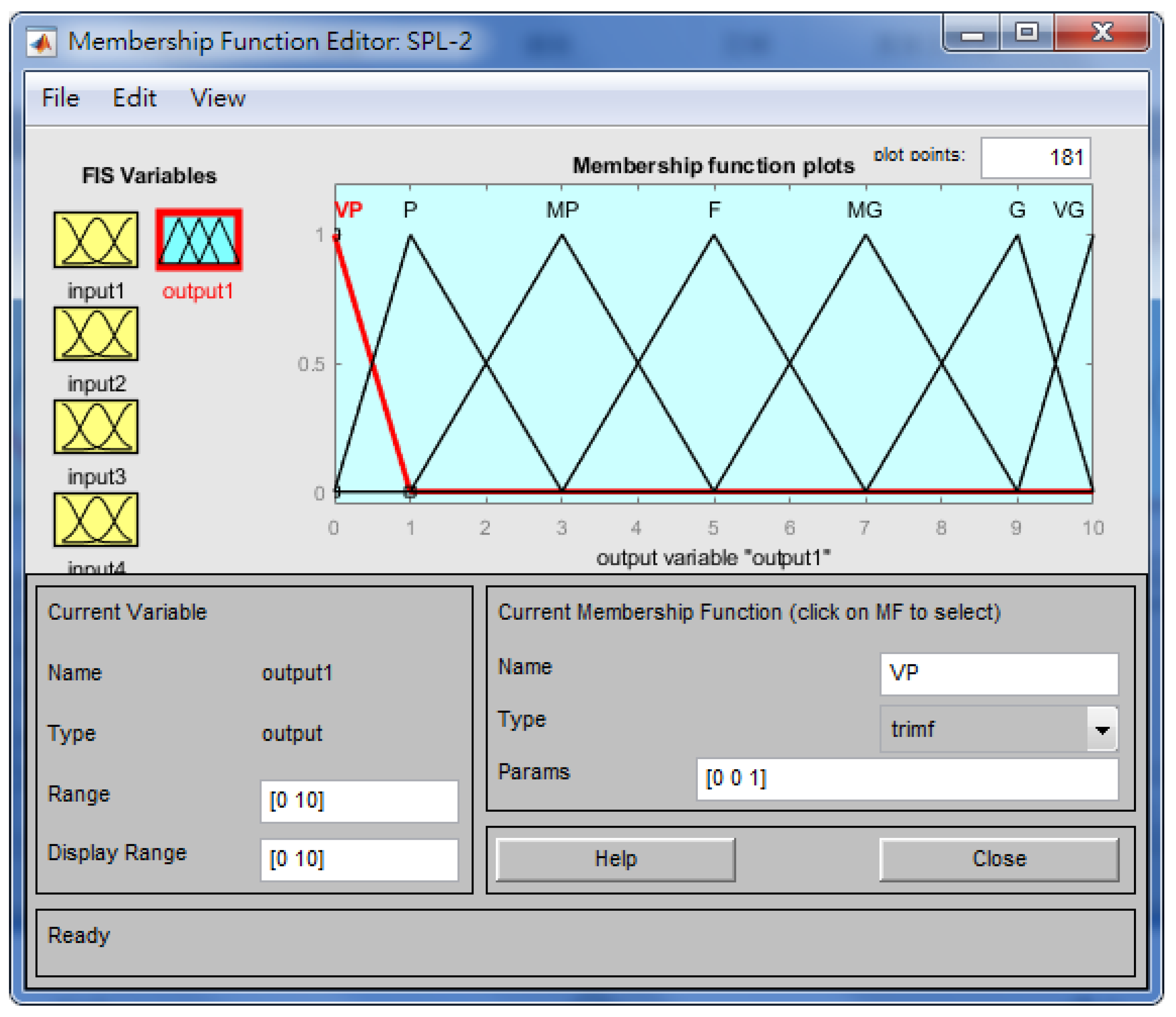
3.2. Fuzzy-Rule-Based System for Supplier Evaluation and Selection
3.3. Supplier Performance Index
4. Case Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dyer, J.H. Effective interfirm collaboration: How firms minimize transaction costs and maximize transaction value. Strategic Manage. J. 1997, 18, 535–556. [Google Scholar] [CrossRef]
- Chen, K.L.; Chen, K.S.; Li, R.K. Suppliers capability and price analysis chart. Int. J. Prod. Econ. 2005, 98, 315–327. [Google Scholar] [CrossRef]
- Fallahpour, A.; Olugu, E.U.; Musa, S.N.; Wong, K.Y.; Noori, S. A decision support model for sustainable supplier selection in sustainable supply chain management. Comput. Ind. Eng. 2017, 105, 391–410. [Google Scholar] [CrossRef]
- Govindan, K.; Shankar, M.; Kanna, D. Supplier selection based on corporate social responsibility practices. Int. J. Prod. Econ. 2018, 200, 353–379. [Google Scholar] [CrossRef]
- Benítez, J.M.; Martín, J.C.; Román, C. Using fuzzy number for measuring quality of service in the hotel industry. Tour. Manage. 2007, 28, 544–555. [Google Scholar] [CrossRef]
- Juan, Y.K.; Perng, Y.H.; Castro-Lacouture, D.; Lu, K.S. Housing refurbishment contractors selection based on a hybrid fuzzy-QFD approach. Automat. Constr. 2009, 18, 139–144. [Google Scholar] [CrossRef]
- Chou, C.C.; Liu, L.J.; Huang, S.F.; Yih, J.M.; Han, T.C. An evaluation of airline service quality using the fuzzy weighted SERVQUAL method. Appl. Soft Comput. 2011, 11, 2117–2128. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Mohanta, J.C.; Keshari, A. A knowledge based fuzzy-probabilistic roadmap method for mobile robot navigation. Appl. Soft Comput. 2019, 79, 391–409. [Google Scholar] [CrossRef]
- Lin, P.H.; Jin, Y.M. Applying fuzzy theory in selecting the image quality factors of 3D televisions. Int. J. Ind. Ergonom. 2019, 74, 102841. [Google Scholar] [CrossRef]
- Plewa, C.; Ho, J.; Conduit, J.; Karpen, I.O. Reputation in higher education: A fuzzy set analysis of resource configurations. J. Bus. Res. 2016, 69, 3087–3095. [Google Scholar] [CrossRef]
- Akman, G. Evaluating suppliers to include green supplier development programs via fuzzy c-means and VIKOR methods. Comput. Ind. Eng. 2015, 86, 69–82. [Google Scholar] [CrossRef]
- Cid-López, A.; Hornos, M.J.; Carrasco, R.A.; Herrera-Viedma, E. Applying a linguistic multi-criteria decision-making model to the analysis of ICT suppliers’ offers. Expert Syst. Appl. 2016, 57, 127–138. [Google Scholar] [CrossRef]
- Garcia, N.; Puente, J.; Fernandez, I.; Priore, P. Suitability of a consensual fuzzy inference system to evaluate suppliers of strategic products. Symmetry 2018, 10, 22. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, K.; Zeng, B.; Xu, H.; Yang, Y. Supplier selection in nuclear power industry with extended VIKOR method under linguistic information. Appl. Soft Comput. 2016, 48, 444–457. [Google Scholar] [CrossRef]
- Wang, Y.J.; Lee, H.S. Generalizing TOPSIS for fuzzy multiple-criteria group decision-making. Comput. Math Appl. 2007, 53, 1762–1772. [Google Scholar] [CrossRef]
- Kuo, R.J.; Lee, L.Y.; Hu, T.L. Developing a supplier selection system through integrating fuzzy AHP and fuzzy DEA: a case study on an auto lighting system company in Taiwan. Prod. Plan. Control Manage. Oper. 2010, 21, 468–484. [Google Scholar] [CrossRef]
- Junior, F.R.L.; Osiro, L.; Carpinetti, L.C.R. A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection. Appl. Soft Comput. 2014, 21, 194–209. [Google Scholar] [CrossRef]
- Chen, W.; Zou, Y. An integrated method for supplier selection from the perspective of risk aversion. Appl. Soft Comput. 2017, 54, 449–455. [Google Scholar] [CrossRef]
- Junior, F.R.L.; Carpinetti, L.C.R. A multicriteria approach based on fuzzy QFD for choosing criteria for supplier selection. Comput. Ind. Eng. 2016, 101, 269–285. [Google Scholar] [CrossRef]
- Jeang, A.; Chung, C.P. Process capability analysis based on minimum production cost and quality loss. Int. J. Adv. Manuf. Tech. 2009, 43, 710–719. [Google Scholar] [CrossRef]
- Kuo, R.J.; Wang, Y.C.; Tien, F.C. Integration of artificial neural network and MADA methods for green supplier selection. J. Clean. Prod. 2010, 18, 1161–1170. [Google Scholar] [CrossRef]
- Schramm, F.; Morais, D.C. Decision support model for selecting and evaluating suppliers in the construction industry. Pesqui. Oper. 2012, 32, 643–662. [Google Scholar]
- Tseng, M.L.; Chiu, A.S. Evaluating firm’s green supply chain management in linguistic preferences. J. Clean. Prod. 2013, 40, 22–31. [Google Scholar] [CrossRef]
- Nair, A.; Jayaram, J.; Das, A. Strategic purchasing participation, supplier selection, supplier evaluation and purchasing performance. Int. J. Prod. Res. 2015, 53, 6263–6278. [Google Scholar] [CrossRef]
- Plebankiewicz, E.; Kubek, D. Multicriteria selection of the building material supplier using AHP and Fuzzy AHP. J. Constr. Eng. Manage. 2016, 142, 04015057. [Google Scholar] [CrossRef]
- Pramanik, D.; Haldar, A.; Mondal, S.C.; Naskar, S.K.; Ray, A. Resilient supplier selection using AHP-TOPSIS-QFD under a fuzzy environment. Int. J. Manage. Sci. Eng. Manage. 2016, 12, 45–54. [Google Scholar] [CrossRef]
- Asadabadi, M.R. A customer based supplier selection process that combines quality function deployment, the analytic network process and a Markov chain. Eur. J. Oper. Res. 2017, 263, 1049–1062. [Google Scholar] [CrossRef]
- Luthra, S.; Govindan, K.; Kannan, D.; Mangla, S.K.; Garg, C.P. An integrated framework for sustainable supplier selection and evaluation in supply chains. J. Clean. Prod. 2017, 140, 1686–1698. [Google Scholar] [CrossRef]
- Babbar, C.; Amin, S.H. A multi-objective mathematical model integrating environmental concerns for supplier selection and order allocation based on fuzzy QFD in beverages industry. Expert Syst. Appl. 2016, 92, 27–38. [Google Scholar] [CrossRef]
- Kannan, D.; Govindan, K.; Rajendran, S. Fuzzy Axiomatic Design approach based green supplier selection: A case study from Singapore. J. Clean. Prod. 2015, 96, 194–208. [Google Scholar] [CrossRef]
- Osiro, L.; Lima-Junior, F.R.; Carpinetti, L.C.R. A group decision model based on quality function deployment and hesitant fuzzy for selecting supply chain sustainability metrics. J. Clean. Prod. 2018, 183, 964–978. [Google Scholar] [CrossRef]
- Hsu, C.H.; Chang, A.Y.; Luo, W. Identifying key performance factors for sustainability development of SMEs—Integrating QFD and fuzzy MADM methods. J. Clean. Prod. 2017, 161, 629–645. [Google Scholar] [CrossRef]
- Li, J.; Fang, H.; Song, W. Sustainability evaluation via variable precision rough set approach: A photovoltaic module supplier case study. J. Clean. Prod. 2018, 192, 751–765. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Karsak, E.E.; Dursun, M. An integrated fuzzy MCDM approach for supplier evaluation and selection. Comput. Ind. Eng. 2015, 82, 82–93. [Google Scholar] [CrossRef]
- Parkouhi, S.V.; Ghadikolaei, A.S. A resilience approach for supplier selection: Using Fuzzy Analytic Network Process and grey VIKOR techniques. J. Clean. Prod. 2017, 161, 431–451. [Google Scholar] [CrossRef]
- Banaeian, N.; Mobli, H.; Fahimnia, B.; Nielsen, I.E.; Omid, M. Green supplier selection using fuzzy group decision making methods: A case study from the agri-food industry. Comput. Oper. Res. 2018, 89, 337–347. [Google Scholar] [CrossRef]
- Chen, K.S.; Wang, C.H.; Tan, K.H. Developing a fuzzy green supplier selection model using six sigma quality indices. Int. J. Prod. Econ. 2019, 212, 1–7. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Z.; Tian, G.; Fathollahi-Fard, A.M.; Hao, N.; Li, Z.; Wang, W.; Tan, J. A novel hybrid fuzzy grey TOPSIS method: Supplier evaluation of a collaborative manufacturing enterprise. Appl. Sci. 2019, 9, 3770. [Google Scholar] [CrossRef]
- Gupta, S.; Soni, U.; Kumar, G. Green supplier selection using multi-criterion decision making under fuzzy environment: A case study in automotive industry. Comput. Ind. Eng. 2019, 136, 663–680. [Google Scholar] [CrossRef]
- Chen, C.T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Set Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Bakeshlou, E.A.; Khamseh, A.A.; Asl, M.A.G.; Sadeghi, J.; Abbaszadeh, M. Evaluating a green supplier selection problem using a hybrid MODM algorithm. J. Intell. Manuf. 2014, 28, 913–927. [Google Scholar] [CrossRef]
- Hu, H.Y.; Chiu, S.I.; Yen, T.M.; Cheng, C.C. Assessment of supplier quality performance of computer manufacturing industry by using ANP and DEMATEL. TQM J. 2015, 27, 122–134. [Google Scholar] [CrossRef]
- Krishankumar, R.; Ravichandran, K.S.; Saeid, A.B. A new extension to PROMETHEE under intuitionistic fuzzy environment for solving supplier selection problem with linguistic preferences. Appl. Soft Comput. 2017, 60, 564–576. [Google Scholar]
- Kuo, T.C.; Wu, H.H.; Shieh, J.I. Integration of environmental considerations in quality function deployment by using fuzzy logic. Expert Syst. Appl. 2009, 36, 7148–7156. [Google Scholar] [CrossRef]
- Kwong, C.K.; Chen, Y.; Bai, H.; Chan, D.S.K. A methodology of determining aggregated importance of engineering characteristics in QFD. Comput. Ind. Eng. 2007, 53, 667–679. [Google Scholar] [CrossRef]
- Hsieh, K.L.; Tong, L.I.; Wang, M.C. The application of control chart for defects and defect clustering in IC manufacturing based on fuzzy theory. Expert Syst. Appl. 2007, 32, 765–776. [Google Scholar] [CrossRef]
- Kaya, I.; Kahraman, C. Development of fuzzy process accuracy index for decision making problems. Inf. Sci. 2010, 180, 861–872. [Google Scholar] [CrossRef]
- Yang, C.M.; Lin, K.P.; Chen, K.S. Confidence interval based fuzzy evaluation model for an integrated-circuit packaging molding process. Appl. Sci. 2019, 9, 2623. [Google Scholar] [CrossRef]
- Ouyang, L.Y.; Hsu, C.H.; Yang, C.M. A new process capability analysis chart approach on the chip resistor quality management. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 227, 1075–1082. [Google Scholar] [CrossRef]
- Ouyang, L.Y.; Chen, K.S.; Yang, C.M.; Hsu, C.H. Using a QCAC–Entropy–TOPSIS approach to measure quality characteristics and rank improvement priorities for all substandard quality characteristics. Int. J. Prod. Res. 2014, 52, 3110–3124. [Google Scholar] [CrossRef]
- Hsu, C.H.; Chen, K.S.; Yang, C.M. Construction of closed interval for process capability indices Cpu, Cpl, and Spk based on Boole’s inequality and de Morgan’s laws. J. Stat. Comput. Sim. 2016, 86, 3701–3714. [Google Scholar] [CrossRef]
- Chen, K.S.; Hsu, C.H.; Ouyang, L.Y.; Yang, C.M. Applying MQCAC and fuzzy TOPSIS to improve the unleaded gasoline quality. J. Test. Eval. 2017, 45, 1045–1057. [Google Scholar] [CrossRef]
- Chen, K.S.; Yang, C.M. Developing a performance index with a Poisson process and an exponential distribution for operations management and continuous improvement. J. Comput. Appl. Math. 2018, 343, 737–747. [Google Scholar] [CrossRef]
- Kane, V.E. Process capability indices. J. Qual. Technol. 1986, 18, 41–52. [Google Scholar] [CrossRef]
- Chen, K.S.; Chen, H.T.; Tong, L.I. Performance assessment of processing and delivery times for very large scale integration using process capability indices. Int. J. Adv. Manuf. Tech. 2002, 20, 526–531. [Google Scholar] [CrossRef]
- Chen, T.W.; Chen, K.S.; Lin, J.Y. Fuzzy evaluation of process capability for bigger-the-best type products. Int. J. Adv. Manuf. Tech. 2003, 21, 820–826. [Google Scholar] [CrossRef]
- Yang, C.M.; Chen, K.S. Two-phase selection framework that considers production costs of suppliers and quality requirements of buyers. Int. J. Prod. Res. 2019, 57, 6351–6368. [Google Scholar] [CrossRef]

| Reference | Criterion | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Cost/Price | Quality | Delivery | Technology | Relations | Service | Communication | Green | Sustainability | |
| Reference [20] | √ | √ | √ | √ | |||||
| Reference [21] | √ | √ | |||||||
| Reference [22] | √ | √ | √ | √ | √ | ||||
| Reference [23] | √ | √ | √ | √ | √ | ||||
| Reference [24] | √ | √ | √ | √ | √ | ||||
| Reference [25] | √ | √ | √ | ||||||
| Reference [26] | √ | √ | √ | √ | √ | ||||
| Reference [27] | √ | √ | √ | ||||||
| Reference [28] | √ | √ | |||||||
| Reference [29] | √ | √ | √ | √ | √ | √ | |||
| Reference [30] | √ | √ | √ | √ | |||||
| Reference [31] | √ | √ | √ | √ | √ | ||||
| Reference [32] | √ | √ | √ | √ | √ | √ | √ | √ | |
| Reference [33] | √ | √ | √ | √ | |||||
| Reference [34] | √ | √ | √ | ||||||
| Linguistic Label | Fuzzy Numbers |
|---|---|
| Very Poor (VP)/Very High (VH) | (0, 0, 3) |
| Poor (P)/High (H) | (1, 3, 5) |
| Normal (N) | (3, 5, 7) |
| Good (G)/Low (L) | (5, 7, 9) |
| Very Good (VG)/Very Low (VL) | (7, 10, 10) |
| Reference | Fuzzy Linguistics | Cognitive Differences | Reasonable Evaluation Criteria | Empirical Research |
|---|---|---|---|---|
| Reference [19] | ✓ | |||
| Reference [43] | ✓ | ✓ | ||
| Reference [44] | ✓ | ✓ | ||
| Reference [45] | ✓ | ✓ | ||
| Reference [46] | ✓ | ✓ | ✓ | |
| Proposed method | ✓ | ✓ | ✓ | ✓ |
| n | bn | n | bn | n | bn | n | bn |
|---|---|---|---|---|---|---|---|
| 3 | 0.580 | 10 | 0.914 | 17 | 0.952 | 24 | 0.967 |
| 4 | 0.725 | 11 | 0.923 | 18 | 0.955 | 25 | 0.968 |
| 5 | 0.798 | 12 | 0.930 | 19 | 0.958 | 26 | 0.970 |
| 6 | 0.841 | 13 | 0.936 | 20 | 0.960 | 27 | 0.971 |
| 7 | 0.869 | 14 | 0.941 | 21 | 0.962 | 28 | 0.972 |
| 8 | 0.888 | 15 | 0.945 | 22 | 0.964 | 29 | 0.973 |
| 9 | 0.903 | 16 | 0.949 | 23 | 0.965 | 30 | 0.974 |
| Score | Performance | Result |
|---|---|---|
| Crisp value > 75 | Excellent | Buyers will order again, and suppliers will not change their model. |
| 60 ≤ Crisp value ≤ 75 | Good | Buyers will order again, but suppliers should prevent their product quality from falling. |
| 30 < Crisp value < 60 | Fair | Buyers will decline to order again unless the buyer is willing to reduce the level of demand. |
| Crisp value ≤ 30 | Poor | Buyers will decline to order, and suppliers should improve product quality. |
| Manager | Position | Experience (Year) |
|---|---|---|
| Manager 1 | General manager | 15 |
| Manager 2 | Quality manager | 12 |
| Manager 3 | Merchandising manager | 10 |
| Manager 4 | Production manager | 17 |
| Manager 5 | Sales manager | 12 |
| Manager 6 | Operations manager | 13 |
| Criterion | C1 (Cost) | C2 (Cost) | C3 (Benefit) | C4 (Benefit) | Crisp Value | |
|---|---|---|---|---|---|---|
| Manager | ||||||
| Manager 1 | N (5) | G (7) | VG (9) | VG (9) | 86.4 | |
| Manager 2 | L (7) | L (7) | VG (9) | N (5) | 70 | |
| Manager 3 | L (7) | L (7) | G (7) | G (7) | 86.7 | |
| Manager 4 | VL (9) | N (5) | VG (9) | N (5) | 70 | |
| Manager 5 | N (5) | L (7) | G (7) | VG (9) | 70 | |
| Manager 6 | VL (9) | VL (9) | VG (9) | VG (9) | 96.7 | |
| = 80.0 | ||||||
| s = 11.5 | ||||||
| Criterion | C1 (Cost) | C2 (Cost) | C3 (Benefit) | C4 (Benefit) | Crisp Value | |
|---|---|---|---|---|---|---|
| Manager | ||||||
| Manager 1 | N (5) | VL (9) | G (7) | VG (9) | 86.4 | |
| Manager 2 | L (7) | VL (9) | N (5) | G (7) | 70 | |
| Manager 3 | VL (9) | N (5) | G (7) | N (5) | 70 | |
| Manager 4 | L (7) | N (5) | VG (9) | G (7) | 70 | |
| Manager 5 | L (7) | L (7) | G (7) | G (7) | 86.7 | |
| Manager 6 | VL (9) | N (5) | N (5) | VG (9) | 70 | |
| = 75.5 | ||||||
| s = 8.5 | ||||||
| Criterion | C1 (Cost) | C2 (Cost) | C3 (Benefit) | C4 (Benefit) | Crisp Value | |
|---|---|---|---|---|---|---|
| Manager | ||||||
| Manager 1 | VL (9) | VL (9) | G (9) | VG (9) | 96.7 | |
| Manager 2 | N (5) | L (7) | N (5) | N (5) | 50 | |
| Manager 3 | L (7) | L (7) | N (5) | VG (9) | 70 | |
| Manager 4 | VL (9) | VL (9) | G (9) | VG (9) | 96.7 | |
| Manager 5 | L (7) | N (5) | N (5) | VG (9) | 70 | |
| Manager 6 | VL (9) | VL (9) | N (5) | N (5) | 70 | |
| = 75.5 | ||||||
| s = 18.11 | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.-M.; Chen, K.-S.; Hsu, T.-H.; Hsu, C.-H. Supplier Selection and Performance Evaluation for High-Voltage Power Film Capacitors in a Fuzzy Environment. Appl. Sci. 2019, 9, 5253. https://doi.org/10.3390/app9235253
Yang C-M, Chen K-S, Hsu T-H, Hsu C-H. Supplier Selection and Performance Evaluation for High-Voltage Power Film Capacitors in a Fuzzy Environment. Applied Sciences. 2019; 9(23):5253. https://doi.org/10.3390/app9235253
Chicago/Turabian StyleYang, Chun-Ming, Kuen-Suan Chen, Ting-Hsin Hsu, and Chang-Hsien Hsu. 2019. "Supplier Selection and Performance Evaluation for High-Voltage Power Film Capacitors in a Fuzzy Environment" Applied Sciences 9, no. 23: 5253. https://doi.org/10.3390/app9235253
APA StyleYang, C.-M., Chen, K.-S., Hsu, T.-H., & Hsu, C.-H. (2019). Supplier Selection and Performance Evaluation for High-Voltage Power Film Capacitors in a Fuzzy Environment. Applied Sciences, 9(23), 5253. https://doi.org/10.3390/app9235253






