A Shearlets-Based Method for Rain Removal from Single Images
Abstract
Featured Application
Abstract
1. Introduction
2. Motivations of the Proposed Method
- -
- The directional multilevel transform, Shearlets transform, is utilized to describe the sparse structure of rain streaks and the background layer. Different from the rotation UTV method, the Shearlets-based method can obtain the gradient variation in different directions and different scales efficiently, thus the recovery keeps more directional singularities details.
- -
- For different directions of rain streaks, the Shearlets transform can capture the rain streak layer details due to its multi-direction property. Moreover, the fast algorithm for solving the proposed model can be obtained as the discrete Shearlets transform and inverse are available.
- -
- The split Bregman algorithm is utilized to solve the proposed convex optimization model, which guarantees that the solver is global optimal. The computation of algorithm includes three soft-thresholding processes and two Shearlets transforms, and the total computing complexity is , where N is the total number of pixels.
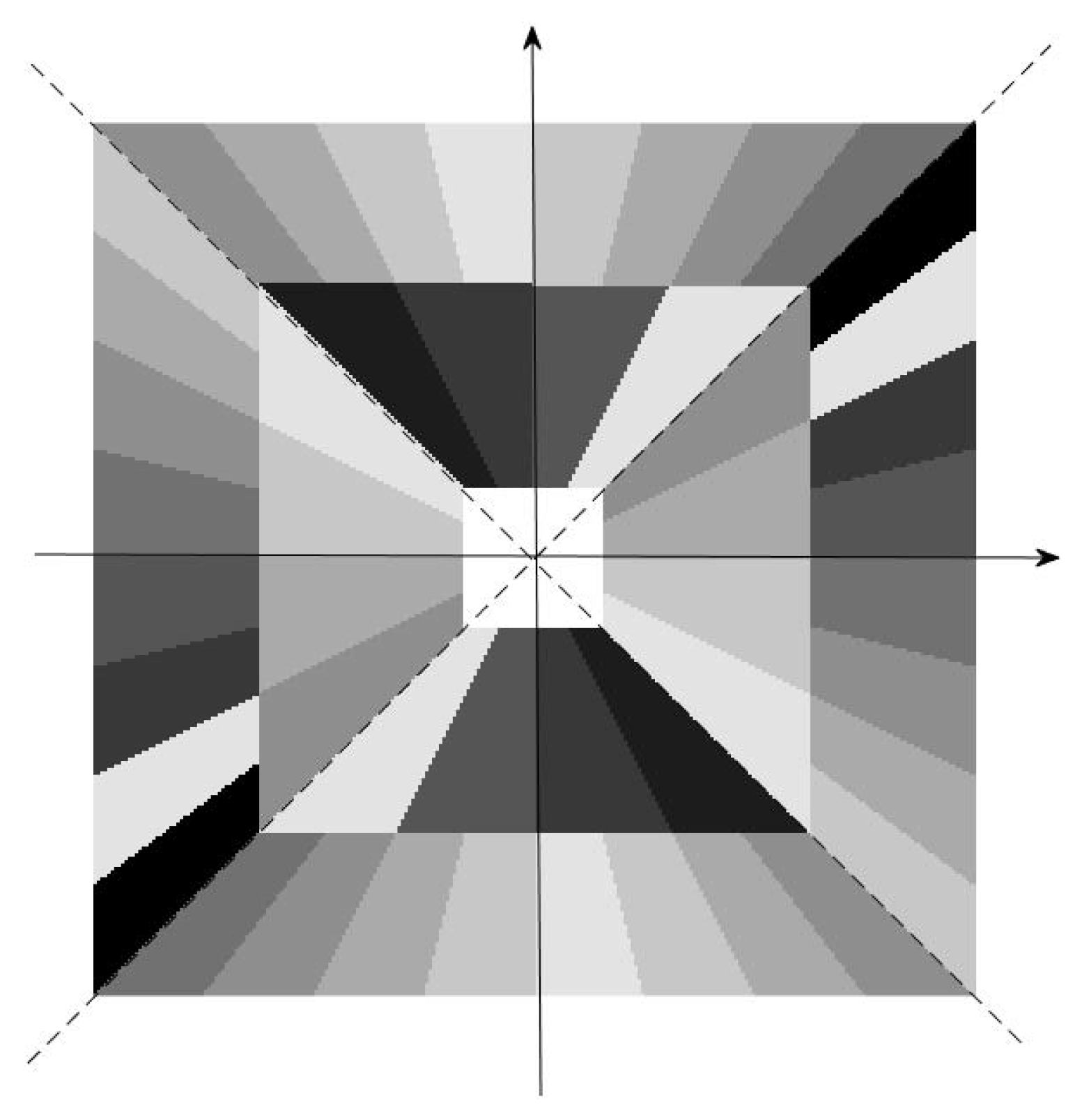
3. Shearlets
4. The Proposed Method
4.1. The Proposed Optimization Model
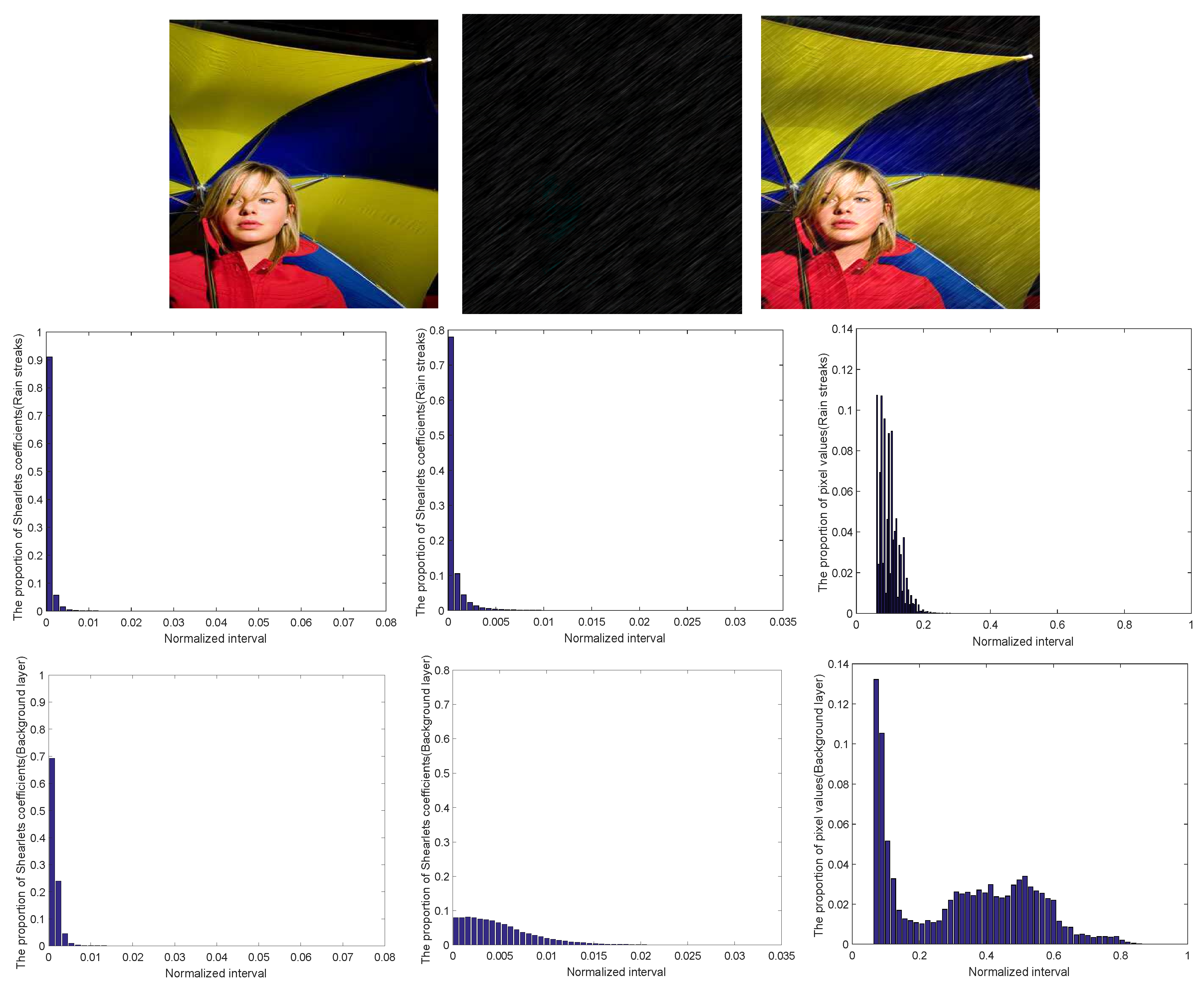
- The sparse constraint of the Shearets coefficients of the background layer in the rain drops’ direction. In fact, the Shearlets decomposition coefficients of the background layer in high frequency can be approximately considered (in the rain drops’ direction) as sparse (see Figure 1) due to the intensity distribution for multilevel coefficients. In order to describe this sparse regularizer, the norm of multilevel coefficients in different scales, along the direction of the rain-free layer is used, which also reflects the discontinuity of rain streaks, specificallywhere is the Shearlets transform of the rain-free layer in the rain drops’ direction.
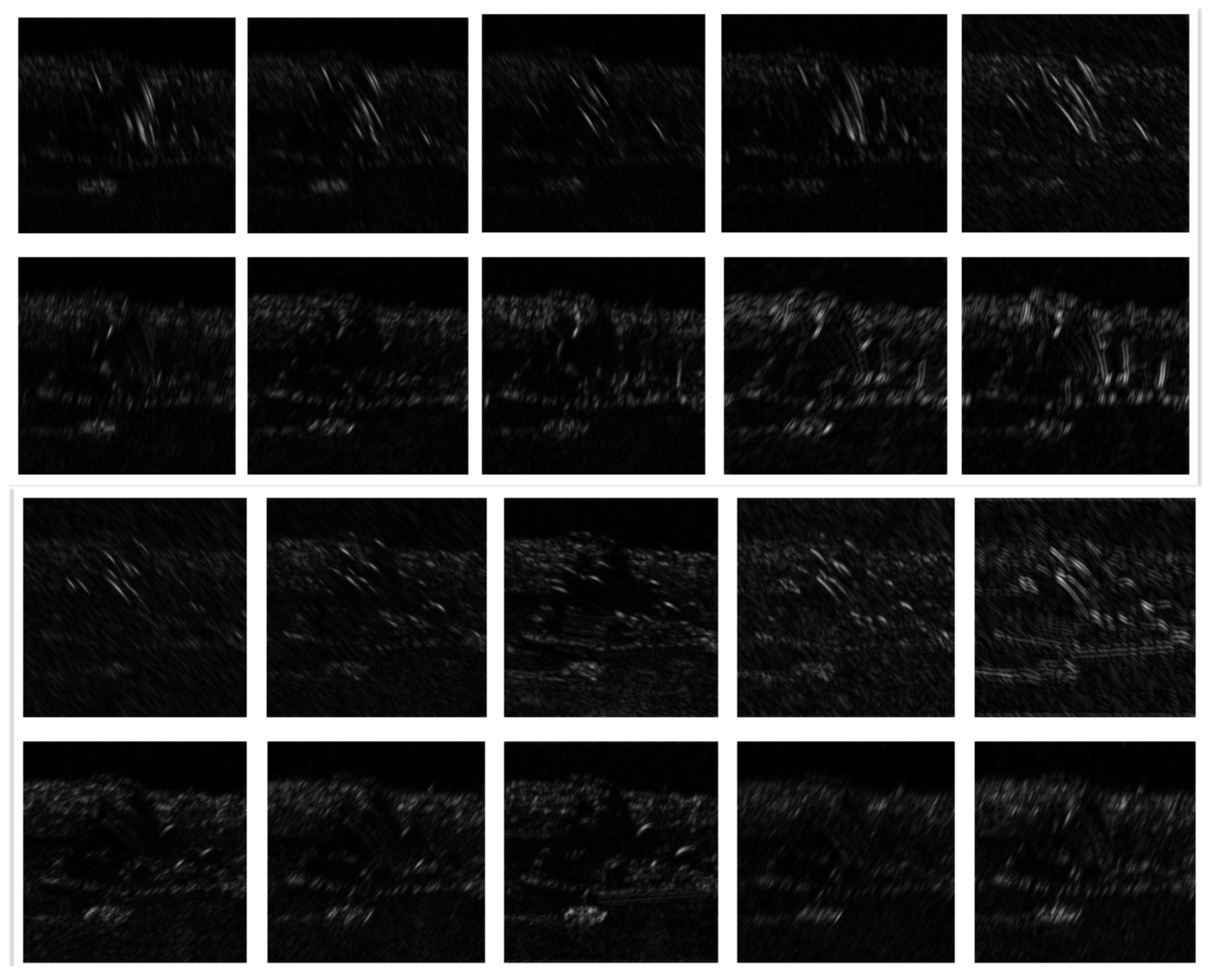
- The sparse constraint of the Shearlets coefficients of the rain streaks across the rain drops’ direction. In the real scenes of rainfall, the shape of rain streaks is a stretched ellipse in a specific direction reflected in pixels, therefore the directional multilevel transform is more sensitive than UTV in detecting the directional singularities in images. From Figure 2, it shows that the Shearlets coefficient in scale 2 across the rain drops’ direction of the rain streak has sparse structure. Similarly,where is the Shearlets transform of the rain streak across the rain drops’ direction.
- The sparse constraint of rain streaks (see Figure 1). In general, the rain streak is sparse when the rain is not heavy, therefore its sparsity can be described by norm, which represents the number of nonzero elements. Here, the is utilized to replace the norm due to its non-convexity, thus we have the following sparse regularizer of rain streaks
- Some non-negative constraints of r and b. For the rain streaks removal problem, the pixel of the rain streaks layer r and the background layer b are non-negative, therefore the following constraints hold
4.2. Solving the Proposed Model
| Algorithm 1: The split Bregman algorithm for proposed model (13) |
 |
5. Numerical Experiments
- The relative error (RelErr) is defined aswhere u and are the original signal and the recovered signal, and represents the Frobenius norm.
- The peak signal–noise ration (PSNR) is defined aswhere is the maximum value of u, andwhere M, N are the size of the signal u.
- The structural similarity (SSIM) is defined aswhere and represent the average of u and , , and represent the standard deviation of u and , is the covariance of u, and , .
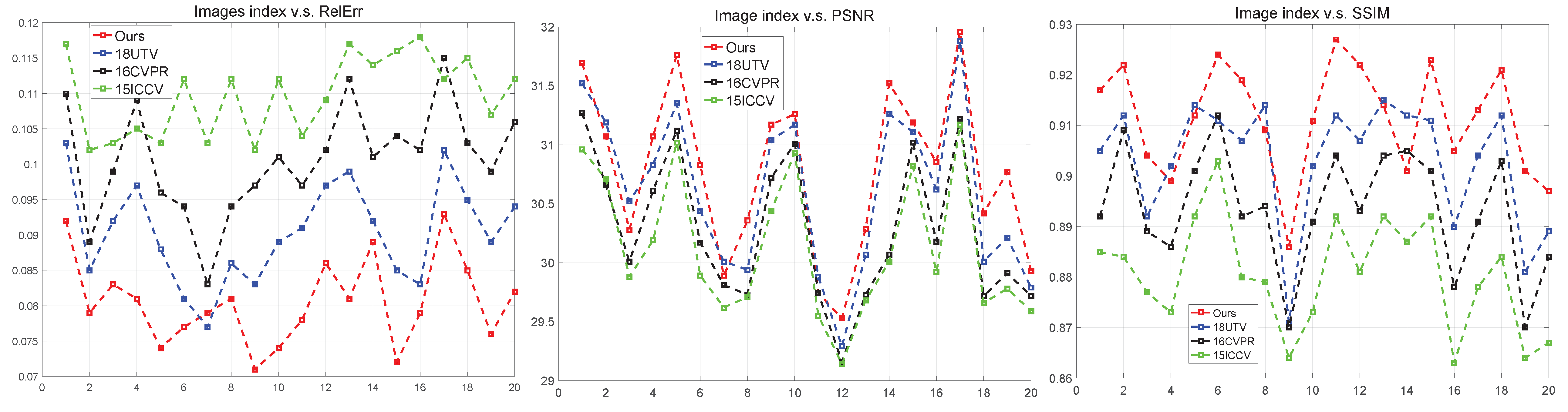
5.1. Comparison Tests of the Synthetic Data
- the method 15ICCV cannot remove rain streaks completely, especially with heavy rain;
- the method 16CVPR does remove rain streaks completely, but the resulted background seems to be over-smooth;
- the method 18UTV can remove rain streaks completely, but rain streaks are detected by TV, which leads to a non-smooth background, especially in the heavy rain case;
- the proposed method using multilevel system performs better both in rain streaks removal and details preservation in heavy and light rain cases.
5.2. Results and Discussion for the Real Data
6. Some Discussion for the Proposed Method
6.1. Computation Complexity
6.2. Description for Parameters
6.3. Simple Discussion of Regularization Terms
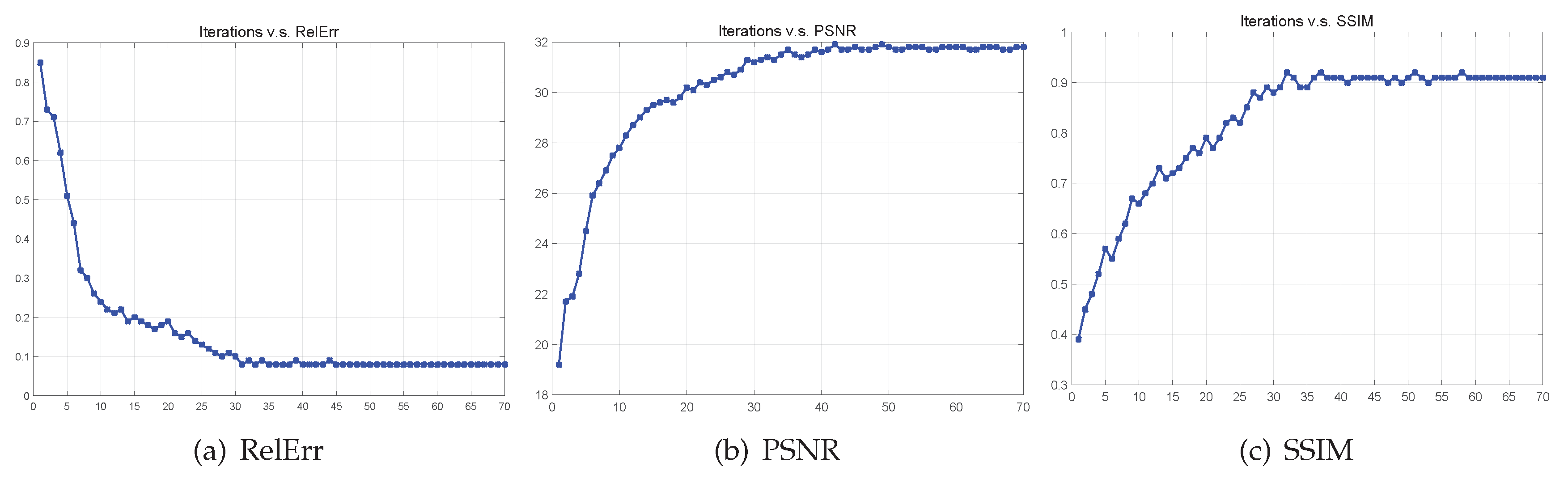
6.4. Convergency of the Proposed Algorithm
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| RelRrr | The relative error |
| PSNR | The peak signal to noise ratio |
| SSIM | The structural similarity index |
References
- Garg, K.; Nayar, S.K. Detection and removal of rain from videos. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004. [Google Scholar]
- Zhang, X.; Li, H.; Qi, Y.; Leow, W.K.; Ng, T.K. Rain Removal in Video by Combining Temporal and Chromatic Properties. In Proceedings of the IEEE International Conference on Multimedia and Expo, Toronto, ON, Canada, 9–12 July 2006. [Google Scholar]
- Barnum, P.C.; Narasimhan, S.; Kanade, T. Analysis of Rain and Snow in Frequency Space. Int. J. Comput. Vis. 2010, 86, 256. [Google Scholar] [CrossRef]
- Garg, K.; Nayar, S.K. When does a camera see rain? In Proceedings of the Tenth IEEE International Conference on Computer Vision, Beijing, China, 17–20 October 2005.
- Chen, Y.L.; Hsu, C.T. A Generalized Low-Rank Appearance Model for Spatio-temporally Correlated Rain Streaks. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Santhaseelan, V.; Asari, V.K. Utilizing Local Phase Information to Remove Rain from Video. Int. J. Comput. Vis. 2015, 112, 71–89. [Google Scholar] [CrossRef]
- Abdel-Hakim, A.E. A Novel Approach for Rain Removal from Videos Using Low-Rank Recovery. In Proceedings of the International Conference on Intelligent Systems, Warsaw, Poland, 24–26 September 2014. [Google Scholar]
- Tripathi, A.K.; Mukhopadhyay, S. Removal of rain from videos: a review. Signal Image Video Process. 2014, 8, 1421–1430. [Google Scholar] [CrossRef]
- Jin-Hwan, K.; Jae-Young, S.; Chang-Su, K. Video deraining and desnowing using temporal correlation and low-rank matrix completion. IEEE Trans. Image Process. 2015, 24, 2658–2670. [Google Scholar]
- Jiang, T.X.; Huang, T.Z.; Zhao, X.L.; Deng, L.J.; Wang, Y. A Novel Tensor-based Video Rain Streaks Removal Approach via Utilizing Discriminatively Intrinsic Priors. In Proceedings of the Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Yu, L.; Yong, X.; Hui, J. Removing Rain from a Single Image via Discriminative Sparse Coding. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- He, K.; Jian, S.; Tang, X. Single Image Haze Removal Using Dark Channel Prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Li, Y. Rain Streak Removal Using Layer Priors. In Proceedings of the Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Kang, L.W.; Lin, C.W.; Fu, Y.H. Automatic single-image-based rain streaks removal via image decomposition. IEEE Trans. Image Process. 2012, 21, 1742–1755. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Lee, C.; Sim, J.Y.; Kim, C.S. Single-image deraining using an adaptive nonlocal means filter. In Proceedings of the IEEE International Conference on Image Processing, Melbourne, Australia, 15–18 September 2013. [Google Scholar]
- Sun, S.H.; Fan, S.P.; Wang, Y.C.F. Exploiting image structural similarity for single image rain removal. In Proceedings of the IEEE International Conference on Image Processing, Québec City, QC, Canada, 27–30 September 2015. [Google Scholar]
- Pei, S.C.; Tsai, Y.T.; Lee, C.Y. Removing rain and snow in a single image using saturation and visibility features. In Proceedings of the IEEE International Conference on Multimedia and Expo Workshops, Chengdu, China, 14–18 July 2014. [Google Scholar]
- Son, C.H.; Zhang, X.P. Rain Removal via Shrinkage of Sparse Codes and Learned Rain Dictionary. In Proceedings of the IEEE International Conference on Multimedia and Expo Workshops, Seattle, WA, USA, 11–15 July 2016. [Google Scholar]
- Wang, Y.; Liu, S.; Chen, C.; Zeng, B. A Hierarchical Approach for Rain or Snow Removing in A Single Color Image. IEEE Trans. Image Process. 2017, 26, 3936–3950. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Fu, C.W.; Lischinski, D.; Heng, P.A. Joint Bi-Layer Optimization for Single-Image Rain Streak Removal. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Deng, L.J.; Huang, T.Z.; Zhao, X.L.; Jiang, T.X. A directional global sparse model for single image rain removal. Appl. Math. Model. 2018, 59, 179–192. [Google Scholar] [CrossRef]
- Bouali, M.; Ladjal, S. Toward Optimal Destriping of MODIS Data Using a Unidirectional Variational Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2924–2935. [Google Scholar] [CrossRef]
- Yang, W.; Tan, R.T.; Feng, J.; Liu, J.; Guo, Z.; Yan, S. Deep Joint Rain Detection and Removal from a Single Image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Fu, X.; Huang, J.; Zeng, D.; Yue, H.; Ding, X.; Paisley, J. Removing Rain from Single Images via a Deep Detail Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Fu, X.; Huang, J.; Ding, X.; Liao, Y.; Paisley, J. Clearing the Skies: A Deep Network Architecture for Single-Image Rain Removal. IEEE Trans. Image Process. 2017, 26, 2944–2956. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Sindagi, V.; Patel, V.M. Image De-raining Using a Conditional Generative Adversarial Network. IEEE Trans. Circuits Syst. Video Technol. 2017. [Google Scholar] [CrossRef]
- Yin, W.; Osher, S.; Goldfarb, D.; Darbon, J. Bregman Iterative Algorithms for ℓ1-Minimization with Applications to Compressed Sensing. Siam J. Imaging Sci. 2008, 1, 143–168. [Google Scholar] [CrossRef]
- Kutyniok, G.; Lim, W.Q.; Steidl, G. Shearlets: Theory and Applications. GAMM-Mitteilungen 2014, 37, 259–280. [Google Scholar] [CrossRef]
- Kutyniok, G. Shearlets. Appl. Numer. Harmon. Anal. 2012, 117, 14–49. [Google Scholar]
- Kutyniok, G.; Shahram, M.; Zhuang, X. ShearLab: A Rational Design of a Digital Parabolic Scaling Algorithm. Siam J. Imaging Sci. 2011, 5, 1291–1332. [Google Scholar] [CrossRef]
- Kutyniok, G.; Labate, D. Introduction to Shearlets. Appl. Numer. Harmonic Anal. 2012, 24, 1–38. [Google Scholar]
- Kutyniok, G.; Lim, W.Q. Image separation using shearlets. Preprint 2011, 1, 1–37. [Google Scholar]
- Zhou, W.; Alan Conrad, B.; Hamid Rahim, S.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar]







| Parameters | |||
|---|---|---|---|
| 1 | [0.02, 0.04, 0.06, 0.08] | 10 | 30 |
| 2 | 0.04 | [10, 20, 30, 40] | 15 |
| 3 | 0.04 | 10 | [−15, −5, 0, 5, 15] |
| Rainy Type | Heavy | Light | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Background | Rainy Streaks | Times(s) | Background | Rainy Streaks | Times(s) | ||||||||||
| Image | Methods | PSNR | SSIM | RelErr | PSNR | SSIM | RelErr | PSNR | SSIM | RelErr | PSNR | SSIM | RelErr | ||
| Pic1 | 15ICCV | 28.79 | 0.8673 | 11.832 | 27.51 | 0.4831 | 15.642 | 71.54 | 29.84 | 0.9002 | 10.273 | 27.16 | 0.495 | 11.416 | 78.32 |
| 16CVPR | 30.49 | 0.8892 | 7.682 | 30.67 | 0.6417 | 7.394 | 948.27 | 30.76 | 0.9123 | 10.791 | 30.52 | 0.533 | 10.376 | 941.96 | |
| 18UTV | 30.83 | 0.9027 | 7.591 | 30.91 | 0.6793 | 7.427 | 0.87 | 32.87 | 0.9345 | 5.964 | 32.79 | 0.6497 | 5.873 | 0.68 | |
| Ours | 31.62 | 0.9115 | 8.244 | 30.76 | 0.6954 | 7.082 | 2.39 | 33.28 | 0.9452 | 5.417 | 33.19 | 0.6719 | 5.314 | 2.26 | |
| Pic2 | 15ICCV | 27.12 | 0.8117 | 12.027 | 27.01 | 0.4193 | 12.314 | 73.94 | 28.96 | 0.8936 | 10.217 | 28.74 | 0.4019 | 10.127 | 82.37 |
| 16CVPR | 28.54 | 0.8629 | 9.264 | 28.31 | 0.5763 | 10.028 | 926.85 | 29.94 | 0.9187 | 9.026 | 29.78 | 0.4693 | 10.201 | 931.57 | |
| 18UTV | 30.17 | 0.9056 | 8.3146 | 30.09 | 0.6493 | 8.217 | 0.94 | 32.69 | 0.9221 | 7.424 | 31.79 | 0.6019 | 7.619 | 0.79 | |
| Ours | 31.68 | 0.9195 | 8.027 | 30.59 | 0.6952 | 8.335 | 4.08 | 32.94 | 0.9207 | 7.506 | 32.84 | 0.6394 | 6.701 | 3.15 | |
| Pic3 | 15ICCV | 27.64 | 0.8327 | 10.837 | 27.28 | 0.4237 | 10.316 | 98.69 | 30.96 | 0.9017 | 7.462 | 29.85 | 0.5173 | 7.438 | 96.54 |
| 16CVPR | 28.94 | 0.8725 | 8.497 | 29.03 | 0.4887 | 9.287 | 837.29 | 32.15 | 0.9102 | 7.4179 | 32.36 | 0.5782 | 7.419 | 864.61 | |
| 18UTV | 30.42 | 0.9013 | 7.694 | 30.25 | 0.5473 | 7.415 | 1.29 | 32.83 | 0.9274 | 7.018 | 32.59 | 0.5995 | 6.131 | 1.25 | |
| Ours | 31.52 | 0.9113 | 8.917 | 30.83 | 0.591 | 7.4953 | 4.76 | 33.65 | 0.9431 | 6.294 | 33.46 | 0.6554 | 5.831 | 4.93 | |
| Pic4 | 15ICCV | 26.84 | 0.7916 | 13.94 | 26.95 | 0.4017 | 14.92 | 80.64 | 29.07 | 0.8114 | 9.148 | 28.96 | 0.4771 | 10.167 | 82.17 |
| 16CVPR | 28.41 | 0.8792 | 11.64 | 28.44 | 0.4657 | 10.13 | 1147.09 | 32.18 | 0.9104 | 8.365 | 32.06 | 0.4993 | 9.725 | 1129.68 | |
| 18UTV | 32.17 | 0.9208 | 8.61 | 32.07 | 0.6129 | 8.486 | 1.17 | 32.36 | 0.9502 | 7.628 | 31.59 | 0.6107 | 8.847 | 1.89 | |
| Ours | 31.88 | 0.9159 | 8.05 | 32.16 | 0.6283 | 7.971 | 3.87 | 32.87 | 0.9221 | 7.391 | 32.72 | 0.6194 | 7.872 | 3.84 | |
| Pic5 | 15ICCV | 29.76 | 0.8339 | 10.017 | 30.01 | 0.4996 | 9.172 | 44.93 | 32.69 | 0.9017 | 7.286 | 32.54 | 0.5162 | 7.836 | 31.26 |
| 16CVPR | 31.94 | 0.8992 | 8.274 | 31.79 | 0.5194 | 7.139 | 428.16 | 33.94 | 0.9317 | 6.264 | 33.72 | 0.5997 | 6.938 | 441.27 | |
| 18UTV | 33.26 | 0.9331 | 6.192 | 33.86 | 0.5917 | 6.985 | 0.61 | 34.92 | 0.9427 | 5.947 | 34.94 | 0.627 | 5.846 | 0.57 | |
| Ours | 31.86 | 0.9141 | 7.214 | 30.94 | 0.5711 | 8.718 | 2.95 | 32.09 | 0.9197 | 7.172 | 30.52 | 0.6844 | 9.873 | 3.17 | |
| Rain Type | Methods | Background | Rainy Streaks | Time(s) | ||||
|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | RMSE | PSNR | SSIM | RMSE | |||
| 15ICCV | 28.74 ± 2.49 | 0.8293 ± 0.0513 | 11.57 6 ± 2.895 | 26.19 ± 3.42 | 0.4702 ± 0.0527 | 13.042 ± 3.521 | 144.27 | |
| 16CVPR | 29.64 ± 2.01 | 0.8846 ± 0.0312 | 9.142 ± 1.259 | 27.41 ± 1.39 | 0.5327 ± 0.0932 | 9.741 ± 1.692 | 1152.64 | |
| 18UTV | 30.74 ± 0.63 | 0.8811 ± 0.0737 | 9.747 ± 0.994 | 27.94 ± 0.53 | 0.6017 ± 0.0574 | 9.226 ± 1.726 | 1.59 | |
| Ours | 31.02 ± 1.722 | 0.8842 ± 0.0397 | 8.117 ± 0.692 | 28.52 ± 0.63 | 0.6064 ± 0.0827 | 8.017 ± 0.923 | 3.94 | |
| 15ICCV | 26.39 ± 1.64 | 0.7923 ± 0.6249 | 12.971 ± 2.063 | 27.73 ± 1.36 | 0.4713 ± 0.0539 | 12.973 ± 2.918 | 119.57 | |
| 16CVPR | 28.94 ± 1.92 | 0.8709 ± 0.0319 | 10.559 ± 1.947 | 28.59 ± 2.74 | 0.5904 ± 0.1752 | 9.172 ± 2.072 | 1397.46 | |
| 18UTV | 29.59 ± 2.17 | 0.8906 ± 0.0216 | 9.311 ± 1.509 | 28.74 ± 1.915 | 0.6607 ± 0.0793 | 10.703 ± 1.448 | 1.97 | |
| Ours | 30.16 ± 1.43 | 0.9042 ± 0.0161 | 9.942 ± 1.772 | 28.94 ± 2.73 | 0.692 ± 0.1154 | 9.954 ± 2.142 | 4.57 | |
| 15ICCV | 28.74 ± 1.89 | 0.8841 ± 0.0719 | 11.409 ± 1.173 | 28.97 ± 1.83 | 0.5516 ± 0.0967 | 12.712 ± 1.837 | 86.53 | |
| 16CVPR | 30.55 ± 1.93 | 0.892 ± 0.0517 | 10.929 ± 1.846 | 30.59 ± 1.73 | 0.6012 ± 0.0953 | 10.397 ± 2.066 | 1493.27 | |
| 18UTV | 31.27 ± 1.53 | 0.9004 ± 0.0439 | 7.492 ± 0.793 | 31.37 ± 1.74 | 0.6112 ± 0.0571 | 10.973 ± 0.722 | 1.38 | |
| Ours | 31.42 ± 1.71 | 0.9087 ± 0.0164 | 7.928 ± 0.271 | 32.17 ± 0.54 | 0.6292 ± 0.0803 | 9.364 ± 0.574 | 4.61 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, G.; Leng, J.; Cattani, C. A Shearlets-Based Method for Rain Removal from Single Images. Appl. Sci. 2019, 9, 5137. https://doi.org/10.3390/app9235137
Sun G, Leng J, Cattani C. A Shearlets-Based Method for Rain Removal from Single Images. Applied Sciences. 2019; 9(23):5137. https://doi.org/10.3390/app9235137
Chicago/Turabian StyleSun, Guomin, Jinsong Leng, and Carlo Cattani. 2019. "A Shearlets-Based Method for Rain Removal from Single Images" Applied Sciences 9, no. 23: 5137. https://doi.org/10.3390/app9235137
APA StyleSun, G., Leng, J., & Cattani, C. (2019). A Shearlets-Based Method for Rain Removal from Single Images. Applied Sciences, 9(23), 5137. https://doi.org/10.3390/app9235137






