Abstract
Gas insulated substations (GISs) are broadly used for transmission and distribution in electric power networks. Very fast transient overvoltage (VFTO) caused by SF6 discharge during switching operations in a GIS may threaten the insulation of electrical equipment. In this paper, a novel VFTO suppression method with great prospects in engineering, called the spiral tube damping busbar, is proposed. The suppressing mechanism of the new method is analyzed. The structure and the design characteristics of the damping busbar are introduced as well. Moreover, a calculation method for the self-inductance of the damping busbar at high frequency is presented. According to the structural characteristics of the damping busbar, the inductance effect on suppressing VFTO is analyzed. A further improvement in damping VFTO is investigated by designing a spiral litz coil connected in series with the busbar, which increases the damping effect. The simulation results show that the improved damping busbar has a significant suppressing effect on the amplitude and the frequency of VFTO.
1. Introduction
Power system demands are increasing due to the increase in economic activities and national developments. With the increase in demand, power systems operators have upgraded their transmission systems to higher voltage levels in order to achieve economical and reliable power transfer between the generation side and the demand side [1]. Therefore, high voltage and extra-high-voltage substations are widely deployed in modern systems, and their number will be greatly increased in the near future [2]. Thus, gas insulated substations (GISs) have been widely used over the last three decades in power systems and other fields such as intelligent transportation systems, high-speed trains, and underground, because of their high reliability, easy maintenance, and small ground space requirements. The higher personal and operational safety level and easy installation and commissioning make high-voltage GISs in significant demand, particularly in heavily industrial areas, in comparison with conventional air insulated substations (AIS) [3,4,5,6,7]. Although GISs have been involved in power systems for a long time, with the development of GISs and the voltage level of transmission lines, many new problems are occurring, such as very fast transient overvoltage (VFTO) caused by SF6 discharge during switching operations in GISs. VFTO could cause damage to power devices. A reduction of the insulating capability of the dielectric gas in GISs is caused mainly by the peak magnitude and high-frequency oscillations of VFTO. The internal VFTO causes stress on the main insulation in the GIS, while the external VFTO poses a threat mainly to the main transformer and the secondary equipment within the substation [8]. These transients have extremely short rise time, in the nanoseconds range.
Several methods have been considered to mitigate such overvoltages [9,10]. VFT suppression has been proposed by many researchers using a disconnector equipped with a damping resistor [11], a disconnector with reduced voltage during the opening operation (the so-called trapped charge voltage (TCV)) [12], surge arresters [13,14], high-frequency resonators [15,16], magnetic rings of different types [17,18,19,20], and VFTO mitigation by controlling the voltage conditions preceding voltage breakdown in SF6 gas [21,22]. It could be well observed from the literature that an accurate design using the specific parameters of the GIS DS (Disconnector) contact system is required for VFTO mitigation by controlling the voltage conditions preceding voltage breakdowns in the disconnector contact system. As a consequence, additional costs will increase for new combinations.
Most of the suppression methods may require a change in GIS design and construction, which makes them complicated and expensive with low reliability. Disconnecting switches fitted with damping resistors and grounding switches were developed by Yamagata, Y. et al. [23]. The amplitude of the VFTO was reduced by up to 25% after applying the damping resistor. However, the damping resistor method showed limitations because any increment of the resistance leads the VFTO to be decreased and the dimension of the disconnector to be increased. In addition, the dissipated power requirements for the resistor are increasingly high. Furthermore, the slow operating speed of the GIS DS (2–3 m/s) leads to nonability for arc extinction. As a result, the lifetime of the contactor is reduced because of these nanosecond arcs.
TCV has been noticed on the load side of the disconnector after the occurrence of the last re-strike when the disconnector opening operation is completed. Charge leakage across the insulators leads to decay of the trapped charge, which is a prolonged operation, taking hours or days. During the next closing operation of the disconnector, due to the slow contact speed, the first pre-strike occurs when the source side and the load side have the same voltage with different polarity, where the load-side voltage is TCV resulting from the previous operation. The main challenge in the TCV approach is the optimum design of the disconnector which should be considered to achieve significant VFTO reduction with an acceptable sparking time, as explained clearly by Chen, W. et al. [24].
Moreover, surge arresters can suppress the amplitude of the VFTO, but they have no effect on the steepness. The difficulty in using surge arresters is implementing the optimum number of arrester discs for a noticeable damping effect and at a convenient location. The appropriate location of surge arresters in order to eliminate VFTO was investigated by Yadav, D.N. [25].
It could be well seen from the literature [15,16] that the main disadvantage of the cavity resonator method is the absorption of VFTO energy in only a narrow band of its broad frequency spectrum. Consequently, there is no observed damping effect when the resonant frequency of the resonator does not fit the dominant harmonic component of the VFTO. However, compared with the ferrite ring method, the magnetic rings become saturated in high current under high frequency and lose their suppressing effect, as confirmed by Rama Rao, J. V. G. et al. [26]. Furthermore, ferrite magnetic rings are still in the experimental stage, and they may have no obvious suppressing effect on VFTO.
As a consequence, in order to ensure the reliability of substations, it is essential to carry out research on suppressing VFTO. This paper presents a design of a damping busbar to suppress VFTO. We hollow out the conventional busbar to a spiral tube, and then the busbar conductor is changed into a series circuit with a multiturn hollow inductance coil and multiturn gap; based on this, paralleling the damping resistance with the newly designed spiral tube inductance circuit, the spiral tube damping busbar is formed. The mechanism of VFTO suppression by the proposed damping busbar is analyzed, and the distributed equivalent circuit is established. Furthermore, an illustrative structure of the damping busbar is introduced. VFTO with the proposed damping busbar is simulated, and the suppression effects before and after installing the damping busbar are compared. An improved design of the damping busbar is proposed, and a higher damping effect is verified.
The remainder of this paper is structured as follows. In Section 2, the suppressing mechanism of the new method is analyzed. The simulation results and the damping effect of the damping busbar are discussed in Section 3. In Section 4, the influence of the inductance value of the damping busbar on suppressing VFTO is investigated. An improved design of the damping busbar in order to increase the suppression effect is proposed in Section 5. This section presents an investigation on a spiral coil made of litz wire, used to damp VFTO. Such winding meets the requirement of sufficient resistance to damp VFTO. Section 6 summarizes the damping effects of the damping busbar and the improved design. Finally, conclusions are drawn in Section 7.
2. The Suppression Mechanism of the New Method
Several studies have shown that VFTO is generated as a superposition of multiple different reflected electromagnetic waves with complex nonharmonic time dependence and covers a wide frequency range from 100 kHz to 100 MHz [27]. The wavefront steepness, amplitude, and high-frequency components of VFTO can be suppressed by inductance and resistance. Based on this, this research proposes a VFTO suppression method—the spiral tube damping busbar—located before the disconnector switch (DS), as shown in Figure 1b. At the rated frequency, the damping busbar transmits current and voltage waves like a normal busbar, but when VFTO passes through the damping busbar, it will be suppressed. Also, the energy of the travelling waves is consumed by the resistance. When the resistance and inductance of the damping busbar match each other, the biggest wave energy consumption can be obtained and the best VFT damping can be achieved.

Figure 1.
The new damping busbar installed in a gas insulated substations (GIS): (a) general view of the damping busbar with its components; (b) the placement of the damping busbar.
2.1. The Structure of the Damping Busbar
The conventional GIS busbar was hollowed out into a spiral tube, and the busbar conductor was changed into a series circuit with a multiturn hollow inductance coil and a multiturn gap; then, we paralleled the damping resistance with the spiral tube inductance circuit. This method increases the active losses of the busbar by changing the wave impedance of the busbar. As a result, the transient energy is consumed, and the amplitude of the VFTO is reduced. Thus, the main components of the spiral tube damping busbar are (a) a spiral tube damping busbar made by screwing out the conventional busbar to a spiral slotted solenoid busbar; (b) solid metal oxide resistors with an antipulse voltage function as the noninductive damping resistors, as shown in Figure 2; and (c) electrical connection tools.
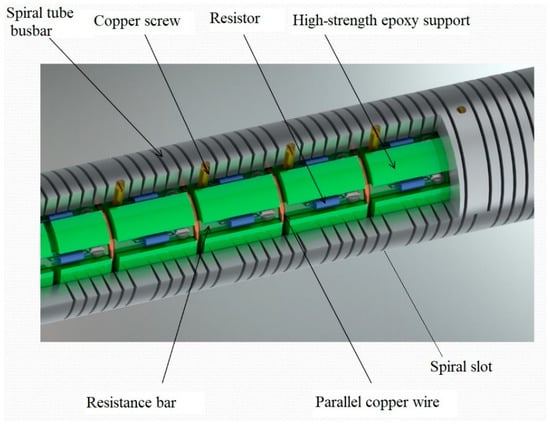
Figure 2.
The structure of the damping busbar.
2.2. The Equivalent Circuit of the Damping Busbar
The equivalent circuit of the damping busbar is resistance and inductance connected in series with the GIS bus, as shown in Figure 3. Li(i = 0,1,2,…) represents the inductance of each unit coil of the metal spiral tube conductor. Ri and LRi(i = 0,1,2,…) represent the noninductive resistance and its residual inductance of the parallel connection of each turn, respectively, and the value of the resistance can be adjusted to achieve the best damping effect. gi(i = 0,1,2,…) is the hollowing gap of the damping busbar and ri(i = 0,1,2,…) is the arcing resistance of the gap, which represents the losses formed by the discharge channel.

Figure 3.
The distributed parameters of the equivalent circuit of the damping busbar.
Inductance Calculation of the Damping Busbar at High Frequency-Damping Busbar Parameters
The purpose of this section is to calculate a fairly precise value of the inductance. Determining the inductance was carried out by studying the effect of high-frequency fields with all the geometrical parameters of the busbar [28]. To this end, a calculation method for the self-inductance of the damping busbar at high frequency was developed and analyzed by the finite element method (FEM). In order to design the damping busbar, we needed to use a simulation method to obtain the VFTO waveform and then calculate the VFTO distributions. Thus, the mathematical expression of the VFTO waveform was theoretically calculated using the curve fitting method to get the fitting data of the VFTO waveform [29]. Then, the curve fitting method was applied to get the fitting data of the associated very fast transient current (VFTC) waveform for a single SF6 gas discharge. Due to VFTC being assigned as current excitation for the simulation procedures, the VFTC equation was obtained for Fourier 8, with goodness of fit parameters R-square = 0.9768 and adjusted R-square = 0.9759.
Table 1 illustrates the coefficients of the VFTC equation.

Table 1.
Coefficients of the very fast transient current (VFTC) equation.
The aim of the simulation study was to calculate the equivalent inductance of the damping busbar at high frequency, so some assumptions were proposed for ease of simulation. In this paper, the simple geometry model was imported into ANSYS Maxwell, and the eddy current solution type was chosen. However, this design depends on many variables according to ANSYS analysis: material properties (aluminum); the geometry of the busbar (busbar body); and operating frequency and input current (the VFTC frequency is 2 MHz and the VFTC peak value is 8256 A—see Equation (1)—for singular switching opening operation, as shown in Figure 4). All of these can be included in design sweeps to study how the impedance matrix—and, therefore, the inductance—is affected by changes in these properties (frequency sweep setup: set the frequency field from 1 to 2 MHz with 0.1 MHz step size).
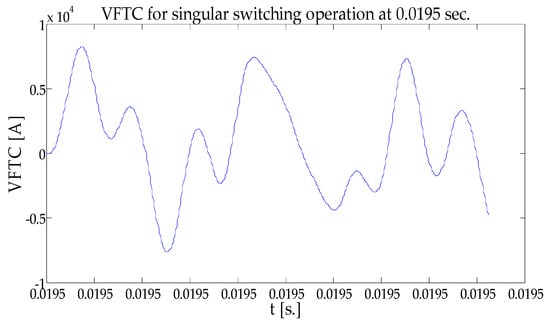
Figure 4.
VFTC for a single breakdown at 0.0195 s.
The simulation results show a decrease in the inductance value of the damping busbar taking place for different frequencies, as illustrated in Figure 5. Notably, however, Figure 5 shows that the inductance value of the damping busbar is 0.33656 at 2 MHz. As a consequence, the damping busbar parameters are illustrated in Table 2.
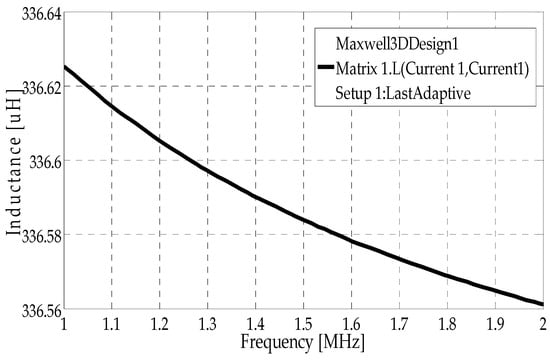
Figure 5.
Inductance calculation of the damping busbar at high frequency.

Table 2.
Damping busbar parameters.
3. Simulation Results
3.1. Modelling of a 1000 kV GIS
The equivalent circuit diagram of a 1000 kV GIS was simulated by using EMTP (Electromagnetic Transients Program) simulation in order to study the VFTO with and without installing the damping busbar [30]. However, the high-frequency characteristics of VFTO led to simulating GIS components as capacitances dominating the other parameters. In order to model the GIS bus duct, distributed parameters and lumped elements can be utilized. Surge impedance and wave velocity could be calculated for a GIS section of any length by using the physical dimensions of the bus duct [31,32]. In the following equations, C and L are self-capacitance and inductance, Z is surge impedance, and V is wave velocity in the GIS [33,34]:
Figure 6 shows the equivalent circuit of a 1000 kV GIS using EMTP simulation after installing the equivalent circuit of the damping busbar, as illustrated in Table 2.
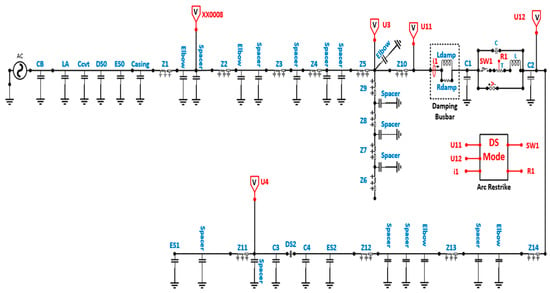
Figure 6.
The equivalent circuit of a 1000 kV GIS after installing the damping busbar.
Let r be the inner radius of the GIS shell and R be the inner radius of the GIS bus. In addition, ε0 = 8.85418782 × 10−12 F/m, εr = 1.0024 and μ0 = 4π × 10−7 H/m. According to the dimensions of the GIS busbar, the calculations showed that the propagation velocity is and the surge impedance is about .
3.2. Discussion
As shown in Figure 7a, when the disconnector is opened, the VFTO for the whole process at the power supply side appears as a superposition of high-frequency transients and a sine wave. After SF6 gas discharges, the disconnector gap restores the insulation state; then, the current disappears, the high-frequency transient components gradually decay, and, finally, the voltage wave continues as a sinusoidal wave with the supply voltage.
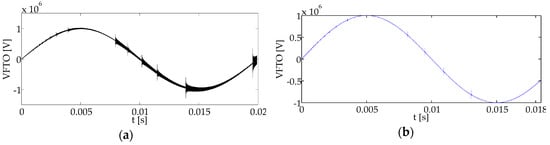
Figure 7.
Very fast transient overvoltage (VFTO) and VFTC waveforms: VFTO at the source side (a) before installing the damping busbar and (b) after installing it; VFTO at the load side (c) before installing the damping busbar and (d) after installing it; VFTC (e) before installing the damping busbar and (f) after installing it.
In addition, the VFTO for the full process at the load side has an approximate step shape, which is a superposition of high-frequency transients and a stepped wave. Each step of the ladder wave corresponds to SF6 gas breakdown, the step magnitude is the breakdown voltage, and the narrow pulse at the ladder edge is the highest frequency of the VFTO, as shown in Figure 7c.
Moreover, the VFTC for the whole process is the superposition of high-frequency transients with zero current amplitude. When the critical breakdown voltage (BV) of the SF6 gas is equal to the transient recovery voltage of the gap, the SF6 gas collapses and the gap transfers from the insulation state into a conductive state; then, the circuit produces a high-frequency transient current, as shown in Figure 7e. Additionally, when the critical breakdown voltage of SF6 gas exceeds the transient recovery voltage of the gap, the current disappears during discharge of the SF6 gas.
The simulation results show that the maximum amplitude of the VFTO decreased from 1.554 to 1.13 p.u., which means that the damping busbar functioned as a VFTO suppressor. The damping effect of the new design is evident from the simulation results, and the mitigation effect was about 27%. Table 3 illustrates the transient characteristics of the VFTO waveform under opening operation before and after installing the damping busbar. A singular switching operation (opening) of the disconnector was simulated in EMTP-ATP (Alternative Transients Program) software.

Table 3.
The transient characteristics of VFTO under an opening operation at the load side before and after installing the damping busbar.
4. Inductance Effect on Suppressing VFTO
When VFTO passes through the inductance, the wavefront is smoothed, its steepness is reduced, and the amplitude is decreased. The inductance Li increases the round-trip time of the travelling wave, which in turn leads to a reduction in the high-frequency components of the VFTO. The travelling wave leads to a higher voltage on the inductance of the small circuit, which causes the parallel resistance to absorb the travelling wave energy, increase the consumption of active power, and reduce the amplitude of the VFTO.
The inductance value of the damping busbar is an important factor for an obvious VFTO suppression effect. The limitation on the steepness of the transients is a result of the inductance effect of the damping busbar. Figure 8 describes the influence of the inductance value on VFTO suppression at the load side during transient phenomena.
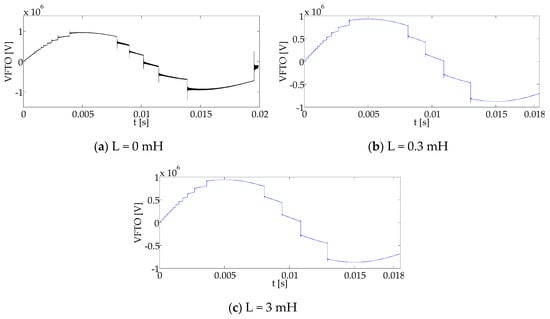
Figure 8.
Influence of the inductance value on VFTO suppression at the load side of a 1000 kV GIS: at inductance values (a) L = 0 mH, (b) L = 0.3 mH, (c) L = 3 mH.
The more considerable value of the equivalent inductance of the damping busbar leads to an obvious suppression effect. Table 4 illustrates the transient characteristics of the VFTO waveform under an opening operation for different values of equivalent inductance of the damping busbar.

Table 4.
Influence of the equivalent inductance of the damping busbar on VFTO suppression.
It can be observed that a higher damping effect was achieved by increasing the equivalent inductance of the damping busbar. Furthermore, increasing the inductance value can damp the VFT waveform’s front. It is also helpful for absorbing the sharp spikes of the VFT since surge arresters do not act quickly enough to prevent steep-fronted switching transients. Therefore, installing an additional spiral coil with the damping busbar is highly valuable to attenuating the effects of VFTs. For this reason, a spiral coil of resistive litz wire was designed to be installed in the helical groove and connected in series with the damping busbar.
5. The Improved Design of the Damping Busbar
A further enhancement of the suppression effect was investigated by designing a spiral litz coil connected in series with the busbar, which increases the total inductance value. In order to design the spiral coil, an algorithm based on air-gap calculation was developed. This algorithm designs a spiral coil for a specific inductance value, which was determined as an input value. Other parameters, such as VFTC characteristics and the number of turns of the damping busbar, were also inserted in the input data.
Furthermore, litz wire was chosen for the improved design because it is mostly used for the frequency range 10 kHz to 2 MHz. The main advantage of this configuration is to minimize the power losses due to “skin and proximity effect”, and it is desirable in high-frequency applications as well. Sullivan, C.R. and Zhang, R.Y applied a simple method for a suitable litz wire design [35]. The flowchart of the procedure used to calculate the spiral coil design parameters is shown in Figure 9. By determining the inductance value and the number of turns, then magnetic flux density could be calculated. After that, the eddy power losses in the litz coil were calculated for the optimal design. However, we can divide the strand-level proximity effect into the internal proximity effect (the effect of other currents within the bundle) and the external proximity effect, but the total proximity effect may be considered a result of the total field at any given strand [36,37,38]:
where is the angular frequency, is the length of the bundle, is the resistivity of copper, is the pitch of the twisting, is the number of strands in a bundle, is the diameter of each strand, is the peak magnetic flux density, and is the strand packing factor. Thus, the AC resistance factor, , for a litz-wire winding for arbitrary waveforms and 2-D or 3-D field geometries can be expressed as follows:
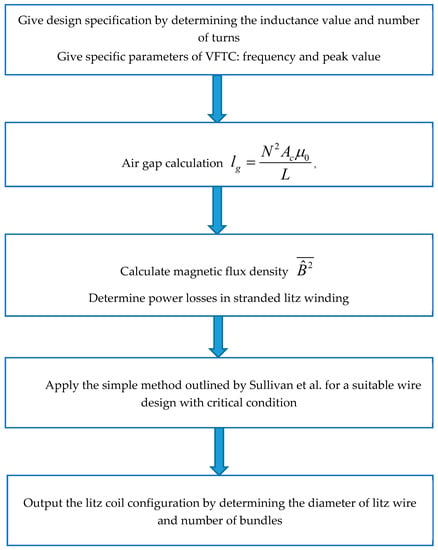
Figure 9.
The flowchart of the procedure to calculate the litz coil design.
The power loss in a stranded-wire winding is derived from , where As is the cross-sectional area of a strand. Consequently, by inserting the operating frequency, the AWG (American wire gauge) can be chosen (i.e., when frequency range is from 1.4 MHz to 2.8 MHz, then the best choice is AWG = 48), which means that about 70% loss reduction is achieved. Eddy power losses were calculated, and the final design was determined according to the critical factor (diameter of litz wire no more than the width of the spiral slot on the damping busbar surface).
The aim of calculating the air gap was to determine the magnetic flux density in order to calculate the power losses in the litz wire for the optimal design of the coil. Thus, for a typical design, we completed the following:
- Determine Ac of the core, which was an aluminum cylinder (busbar body) in our study.
- Determine the number of turns which was commensurate with the design.
- Determine the inductance value which achieves an effective design to avoid saturation.
- Calculate the air gap length as a first step to calculate the magnetic flux density in order to calculate the power loss in the litz wire for the optimal design of the coil. Thus, the length of the air gap was calculated by using Ampere’s law, as shown below:
Many different combinations of strand diameter and number of strands could be designed and manufactured for any given cost. Thus, the number of bundles and, finally, the litz coil diameter could be obtained using a critical condition (diameter of the litz wire no greater than the width of the spiral slot on the damping busbar surface). The previously described technique was used to calculate the litz coil design. Simulations were performed using MATLAB software by keeping the length of the coil, number of turns, and transient current parameters constant. The results are listed in Table 5.

Table 5.
Simulation results for the litz coil design.
It is worth noting that the inductance value of both the damping busbar and the spiral litz coil was calculated at 2 MHz. An accurate choice of construction type of the litz design leads to a higher capability for greater current carrying capacities. The larger Type 2 and 3 litz designs have this essential feature for high-frequency power supply, inverter, and grounding applications. A Type 2 litz construction is distinguished by bundles of twisted wires together, while Type 3 features individually insulated bundles of Type 2 litz wire [39]. As a consequence, in this study we aimed to add a spiral litz coil located in the sweeping spiral on the surface of the damping busbar in order to improve its performance in VFTO mitigation. EMTP simulation was carried out to study the VFTO with and without installing the improved damping busbar. mH is the equivalent inductance of the spiral litz coil and mH is the equivalent inductance of the damping busbar. Thus, mH is the equivalent inductance of the improved damping busbar. The simulation was set up based on mH, as presented in Figure 6. Thus, Figure 10b shows the higher damping effect of the improved damping busbar. In order to clarify the damping effect, Figure 10d illustrates the damping effect of the improved damping busbar for a singular switching operation at approximately the same moment (0.013 s.). In order to clarify the higher damping effect shown in Figure 10b, further details about the damping effect of the improved design are discussed in the next section.
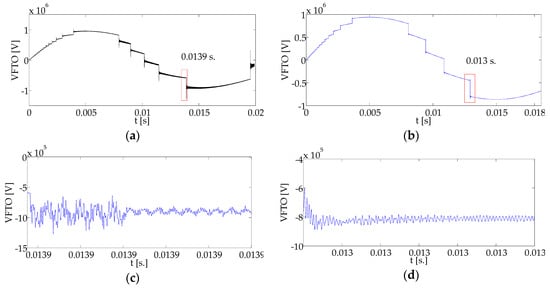
Figure 10.
VFTO waveform at the load side: (a) before installing the damping busbar, (b) after installing the improved design of the damping busbar; VFTO at the load side for one breakdown at 0.013 s: (c) before installing the damping busbar, (d) after installing the improved design of the damping busbar.
6. Summary
In this work, a higher damping effect was investigated by designing a spiral litz coil connected in series to the damping busbar, which increased the total inductance value. The simulation results show that there was a considerable increase in the damping effect, as shown in Figure 10. Furthermore, improving the design and material type could be useful to achieving an optimal suppressing effect. The main advantages of this improved design are the higher damping effect, accuracy, simplicity, and ability to be used in any existing GIS without any change in the GIS design or construction. The transient characteristics of the VFTO after adding a 0.1 mH litz coil are illustrated in Table 6.

Table 6.
The transient characteristics of VFTO under an opening operation at load side with and without installing the spiral litz coil (0.1 mH).
Another obvious advantage of this improved design is no magnetic saturation problem and mitigation of the overvoltage magnitude due to dissipation of the transient energy in the damping resistance. On the other hand, litz wire has been classified as a cost-effective choice to reduce eddy current loss in high-frequency transformer and inductor windings. Some solutions could be successful in increasing the dielectric strength for a high voltage level or for safety requirements, like adding thermoplastic insulation such as PTFE, which could be used for bundle insulation on litz wire in some applications [36].
The proposed improved damping busbar has limitations when thermoplastic insulation is added due to the extra cost. So, in future work, it will be fundamental to develop the design to improve the estimation quality to meet the industry’s requirements for low costs. However, compared with other existing expensive VFTO suppression methods that require changes in GIS design and construction, the proposed method can be easily implemented in any existing GIS without any change in its structure, making it very cost-effective. Therefore, it is necessary to use simulation calculations to optimize the insulation reliability of the uniform electric field and increase the insulation of the busbar. Table 7 shows the mitigation effect of different damping methods, including the new method.

Table 7.
Comparison of different mitigation methods with the new damping busbar.
7. Conclusions
A new method to suppress VFTO was proposed, called a damping busbar. The mechanism of this new method was analyzed. A calculation method for the self-inductance of the damping busbar at high frequency was presented. Moreover, the inductance effect of the damping busbar on VFTO suppression was studied as well. As a result, the amplitude of the VFTO was reduced by approximately 27% after applying the damping busbar. A further enhancement of the suppression effect was investigated by designing a spiral litz coil connected in series with the busbar, which increased the total inductance value. Consequently, a good damping effect was achieved by utilizing the inductive and resistance arrangement which was formed by the improved design of the spiral tube damping busbar. The conclusions are as follows.
- We proposed a new design which has a significantly better damping effect when compared with other existing suppression methods. The proposed damping busbar can be easily implemented in any existing GIS without any change in its structure and is therefore very cost-effective.
- We investigated a calculation method for the self-inductance at high frequency.
- We improved the performance of the damping busbar by adding a spiral litz coil connected in series with the busbar in order to enhance the suppression effect, and we developed an algorithm based on air gap calculation to design the litz coil.
- We compared the damping effect with and without the damping busbar and the improved design.
However, research on improving the proposed design to increase the equivalent inductance value by increasing the length of the busbar and the number of turns has to be considered. Many different adaptations, tests, and experiments should be investigated in future work (i.e., experimental study of a 1000 kV GIS station VFTO after installing the improved damping busbar).
Author Contributions
Conceptualization, R.A.A., Y.-X.S., and W.X.; formal analysis, R.A.A.; investigation, R.A.A., Y.-X.S., and W.X.; writing—original draft preparation, R.A.A. and W.X.; supervision, Y.-X.S., and W.X.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Povh, D.; Pyc, I.; Retzmann, D.; Weinhold, M.G. Future Developments in Power Industry. In Proceedings of the 14th IERE General Meeting and IERE Central and Eastern Europe Forum, Krakow, Poland, 17–21 October 2004; pp. 1–12. [Google Scholar]
- Riechert, U.; Holaus, W. Ultra High-Voltage Gas-Insulated Switchgear—A technology milestone. Eur. Trans. Electr. Power 2012, 22, 60–82. [Google Scholar] [CrossRef]
- Chauhan, M.; Joshi, U.; Asija, U.D. Features and Design Concepts of Gas Insulated Switch Gear. Int. J. Adv. Res. Sci. Eng. 2014, 8354, 60–67. [Google Scholar]
- Mikes, E.; Ponchon, P.; Doumer, P. GIS Substation Extensions and Upgrades. In Proceedings of the CEPSI Paper T1-068 Conference, Manila, Philippines, 23–27 October 2000; pp. 1–8. [Google Scholar]
- Nagarsheth, R.; Sushant, S. Study of Gas Insulated Substation and its Comparison with Air Insulated Substation. Int. J. Electr. Power Energy Syst. 2014, 55, 481–485. [Google Scholar] [CrossRef]
- Singha, J.T.M.; Thomas, J.; Naidu, M.S. Study of Fast Transients Generated in a GIS Bus Duct in Compressed SF6-N2 Gas Mixtures Containing Lower Percentages of SF6. In Proceedings of the Dielectric Materials, Measurements and Applications Conference Publication, Bengaluru, India, 17–21 September 2000; pp. 118–122. [Google Scholar]
- Ullah, R.; Ullah, Z.; Haider, A.; Amin, S.; Khan, F. Dielectric Properties of Tetrafluoroethane (R134) Gas and its Mixtures with N2 and Air as a Sustainable Alternative to SF6 in High Voltage Applications. Electr. Power Syst. Res. 2018, 163, 532–537. [Google Scholar] [CrossRef]
- Carsimamovic, S.; Bajramovic, Z.; Ljevak, M.; Veledar, M. Very Fast Electromagnetic Transients in Air Insulated Substations and Gas Insulated Substations due to Disconnector Switching. In Proceedings of the International Symposium on Electromagnetic Compatibility (EMC), Chicago, IL, USA, 8–12 August 2005; pp. 382–387. [Google Scholar]
- Tavakoli, A.; Gholami, A.; Nouri, H.; Negnevitsky, M. Comparison Between Suppressing Approaches of Very Fast Transients in Gas-Insulated Substations (GIS). IEEE Trans. Power Deliv. 2013, 28, 303–310. [Google Scholar] [CrossRef]
- Dhaware, A.M.; Potdar, M.S. Review on Mitigation Methods of Very Fast Transient Overvoltage in Gas-Insulated Switchgear. Resincap Int. J. Sci. Eng. 2017, 1, 20–25. [Google Scholar]
- Yamagata, Y.; Tanaka, K.; Nishiwaki, S.; Takahashi, N.; Kokumai, T.; Miwa, I.; Komukai, T.; Imai, K. Suppression of VFT in 1100kV GIS by Adopting Resistor-Fitted Disconnector. IEEE Trans. Power Deliv. 1996, 11, 872–880. [Google Scholar] [CrossRef]
- Szewczyk, M.; Piasecki, W.; Stosur, M.; Riechert, U.; Kostovic, J. Impact of Disconnector Design on Very Fast Transient Overvoltages in Gas-Insulated UHV Switchgear. In Proceedings of the International Symposium on High Voltage Engineering (ISH), Hannover, Germany, 22–26 August 2011; pp. 35–38. [Google Scholar]
- Burow, S.; Straumann, U.; Kohler, W.; Tenbohlen, S. New Methods of Damping Very Fast Transient Overvoltages in Gas-Insulated Switchgear. IEEE Trans. Power Deliv. 2014, 29, 2332–2339. [Google Scholar] [CrossRef]
- Babaeilaktarashani, M. A New Cost Effective Approach to Suppress Very Fast Transients on Power Transformers Connected to Gas Insulated Substations. Master’s Thesis, Curtin University, Perth, Australia, 2016. [Google Scholar]
- Smajic, J.; Shoory, A.; Burow, S.; Holaus, W.; Riechert, U.; Tenbohlen, S. Simulation Based Design of HF-Resonators for Damping of Very Fast Transients in GIS. IEEE Trans. Power Deliv. 2014, 29, 2528–2533. [Google Scholar] [CrossRef]
- Riechert, U.; Bösch, M.; Smajic, J.; Shoory, A.; Szewczyk, M.; Piasecki, W.; Burow, S.; Tenbohlen, S. Mitigation of Very Fast Transient Overvoltages in Gas Insulated UHV Substations. In Proceedings of the CIGRÉ Report A3-110, 44th CIGRÉ Session 2012, Palais des Congrès de Paris (CIGRÉ), Paris, France, 26–31 August 2012; pp. 26–31. [Google Scholar]
- Szewczyk, M.; Pawłowski, J.; Kutorasiński, K.; Piasecki, W.; Florkowski, M.; Straumann, U. High-Frequency Model of Magnetic Rings for Simulation of VFTO Damping in Gas-Insulated Switchgear with Full-Scale Validation. IEEE Trans. Power Deliv. 2015, 30, 2331–2338. [Google Scholar] [CrossRef]
- He, J.; Guan, Y.; Liu, W.; Chen, W.; Li, Z. Design Optimization of Ferrite Rings for VFTO Mitigation. IEEE Trans. Power Deliv. 2015, 32, 1181–1186. [Google Scholar] [CrossRef]
- Guan, Y.; Yue, G.; Chen, W.; Li, Z.; Liu, W. Experimental Research on Suppressing VFTO in GIS by Magnetic Rings. IEEE Trans. Power Deliv. 2013, 28, 2558–2565. [Google Scholar] [CrossRef]
- Reddy, P.R.; Amarnath, J. Nanocrystalline to Suppress VFTO and VFTC for 245kV Gas Insulated Substations. Int. J. Comput. Appl. 2013, 70, 1–6. [Google Scholar]
- Szewczyk, M.; Kuniewski, M.; Piasecki, W.; Florkowski, M.; Straumann, U. Determination of Breakdown Voltage Characteristics of 1’100 kV Disconnector for Modeling of VFTO in Gas-Insulated Switchgear. IEEE Trans. Power Deliv. 2016, 31, 2151–2158. [Google Scholar] [CrossRef]
- Szewczyk, M.; Kuniewski, M. Controlled Voltage Breakdown in Disconnector Contact System for VFTO Mitigation in Gas-Insulated Switchgear (GIS). IEEE Trans. Power Deliv. 2017, 32, 2360–2366. [Google Scholar] [CrossRef]
- Yamagata, Y.; Nakada, Y.; Nojima, K.; Kosakada, M.; Ozawa, J.; Ishigaki, I. Very Fast Transients in 1000 kV Gas Insulated Switchgear. In Proceedings of the 1999 IEEE Transmission and Distribution Conference (Cat. No. 99CH36333), New Orleans, LA, USA, 11–16 April 1999; pp. 501–508. [Google Scholar]
- Chen, W.J.; Wang, H.; Han, B.; Wang, L.; Ma, G.M.; Yue, G.C.; Li, Z.; Hu, H. Study on the Influence of Disconnector Characteristics on Very Fast Transient Overvoltages in 1100 kV Gas-Insulated Switchgear. IEEE Trans. Power App. Syst. 2015, 30, 2037–2044. [Google Scholar] [CrossRef]
- Yadav, D.N.; Gorayan, R.S. Investigation of VFTO’s in GIS Using EMTP. In Proceedings of the 13th National Power Systems Conference NPSC, Madras, India, 27–30 December 2004; pp. 619–623. [Google Scholar]
- Rao, J.R.; Amarnath, J.; Kamakshaiah, S. Simulation and Measurement of Very Fast Transient Over Voltages in a 245kV GIS and Research on Suppressing Method Using Ferrite Rings. ARPN J. Eng. Appl. Sci. 2010, 5, 88–95. [Google Scholar]
- Li, Y.; Shang, Y.; Zhang, L.; Shi, R.; Shi, W. Analysis of Very Fast Transient Overvoltages (VFTO) from Onsite Measurements on 800 kV GIS. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 2102–2110. [Google Scholar]
- Coffin, J.G. The Influence of Frequency upon the Self-Inductance of Coils. Proc. Am. Acad. Arts Sci. 1906, 41, 275–296. [Google Scholar] [CrossRef]
- Almenweer, R.A.; Yixin, S.; Xixiu, W. Research on the Fitting Method to Describe the Mathematical Expression of VFTO in GIS. IET. J. Eng. 2019, 2019, 2053–2057. [Google Scholar] [CrossRef]
- Rodríguez-Medina, B.; Santiago-Luna, M. Quick Guide ATP/EMTP; Electric Power Engineering Group: Mayagüez, Puerto Rico, 18 June 2002; pp. 1–34. [Google Scholar]
- Ram, A.R.; Kumar, K.S. Analysis of Very Fast Transients in EHV Gas Insulated Substations. Int. J. Eng. Sci. Innov. Technol. 2012, 1, 18–26. [Google Scholar]
- Prakasam, K.; Prabhavathi, D.; Kalavathi, M.S.; Reddy, B.R. Analysis of Very Fast Transient Over Voltages in Gas Insulated Substation. Int. J. Electr. Eng. Technol. 2015, 6, 51–59. [Google Scholar]
- Hu, R.; Cui, X.; Chen, W.; Sun, Z.; Qi, L.; Zhang, W.; Li, Z.; Dai, M. Simulation of Very Fast Transient Overvoltage on UHV 1000kV GIS Test Circuit. In Proceedings of the 6th International Conference on Electromagnetic Field Problems and Applications-ICEF, Dalian, China, 19–21 June 2012; pp. 1–4. [Google Scholar]
- Hosseini, S.M.H.; Bagheri, Z.; Niafenderi, S.D. Modeling of 420 kV GIS Substation and Research on Very Fast Transient Overvoltage (VFTO). Res. J. Appl. Sci. Eng. Technol. 2013, 5, 2656–2660. [Google Scholar] [CrossRef]
- Sullivan, C.R.; Zhang, R.Y. Simplified Design Method for Litz Wire. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition—APEC, Fort Worth, TX, USA, 16–20 March 2014; pp. 2667–2674. [Google Scholar]
- Tang, X.; Sullivan, C.R. Optimization of Stranded-Wire Windings and Comparison with Litz Wire on the Basis of Cost and Loss. In Proceedings of the IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; pp. 854–860. [Google Scholar]
- Murgatroyd, P.N. Calculation of Proximity Losses in Multi-stranded Conductor Bunches. IEE Proc. Sci. Meas. Technol. 1989, 136, 115–120. [Google Scholar]
- Wojda, R.P. Winding Resistance and Winding Power Loss of High-Frequency Power Inductors. Ph.D. Thesis, Wright State University, Dayton, OH, USA, 2012. [Google Scholar]
- Reese, B.A.; Joseph, R.; Sullivan, C.R. Improved Litz-Wire Designs for the MHz Range. In Proceedings of the IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padua, Italy, 25–28 June 2018; pp. 1–8. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).