Emotion, Respiration, and Heart Rate Variability: A Mathematical Model and Simulation Analyses
Abstract
:1. Introduction
2. Methods
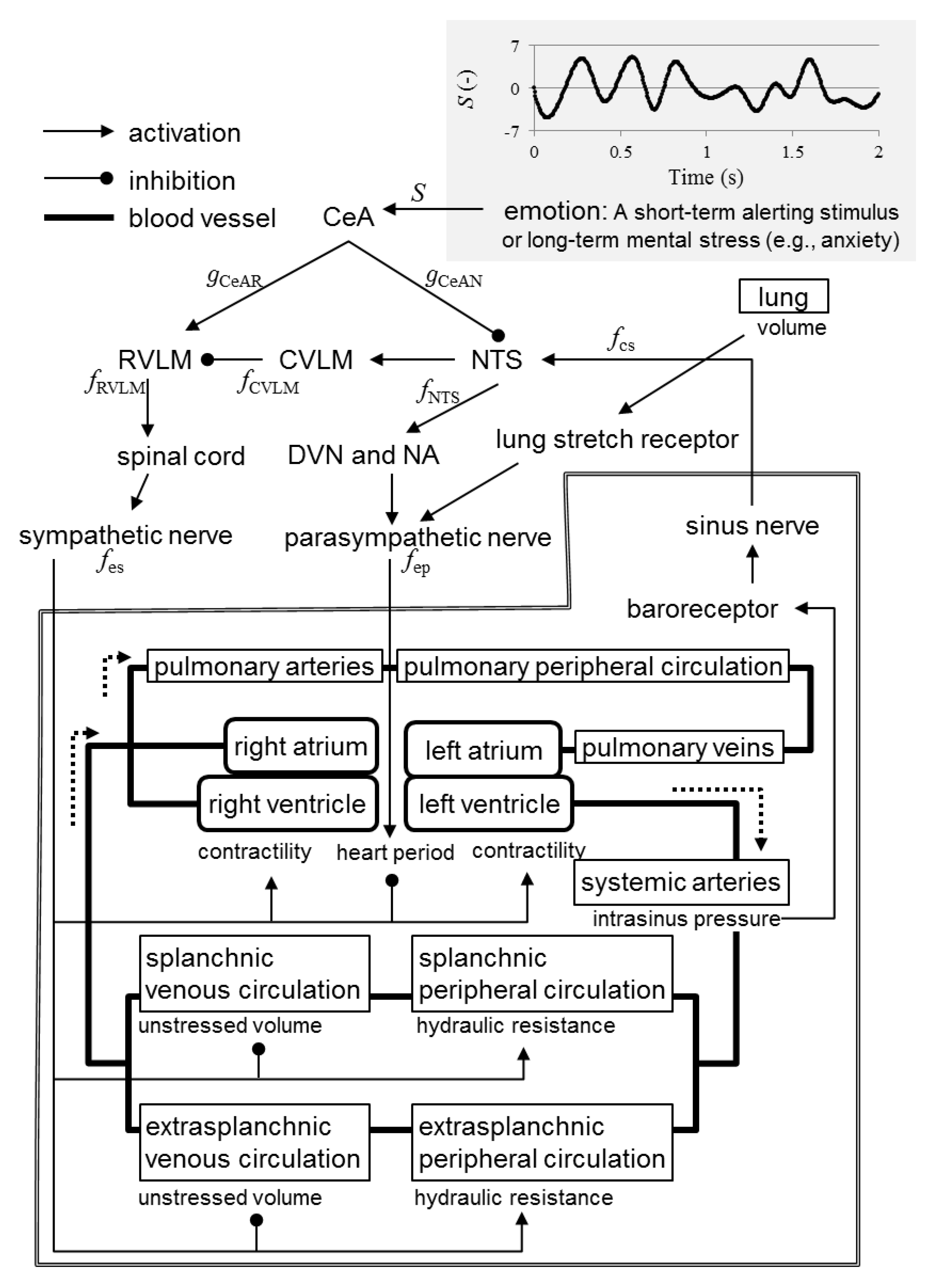
2.1. Mathematical Model
- A short-term alerting stimulus or long-term mental stress (e.g., anxiety) triggers excitatory synaptic projections from the CeA to the rostral ventrolateral medulla (RVLM).
- A short-term alerting stimulus or long-term mental stress (e.g., anxiety) triggers inhibitory synaptic projections from the CeA to the nucleus tractus solitarii (NTS).
- The RVLM activates the sympathetic nervous system via the spinal cord.
- The NTS activates the parasympathetic nervous system via the dorsal vagal motor nucleus (DVN) and nucleus ambiguus.
- The NTS activates the caudal ventrolateral medulla (CVLM).
- The CVLM inhibits the RVLM.
- The sinus nerve activates the NTS.
- Increased spike frequency in the sinus nerve results in exponential decrease in the spike frequency in the sympathetic fibers.
- Increased spike frequency in the sinus nerve results in exponential increase in the spike frequency in the parasympathetic fibers with upper saturation.
2.2. Analysis
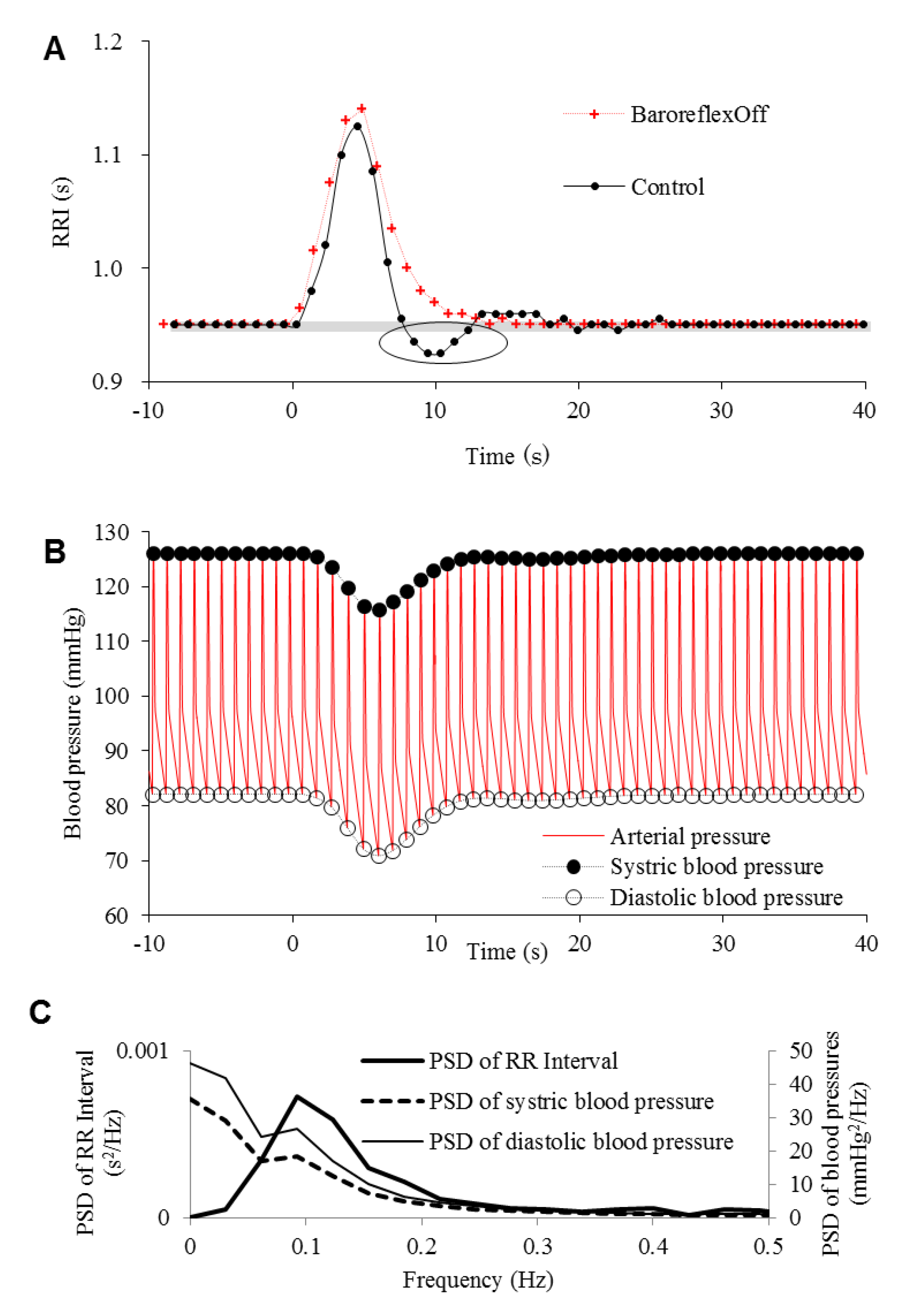
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| (-) | Intensity of emotion triggering the synaptic projection of the CeA |
| (-) | Intensity of the influence of the synaptic projection on the RVLM |
| (-) | Intensity of the influence of the synaptic projection on the NTS |
| (Hz) | Firing frequency of the sinus nerve |
| (Hz) | Firing frequency of the sympathetic nerve |
| (Hz) | Firing frequency of the parasympathetic nerve |
| (Hz) | Firing frequency of the RVLM |
| (Hz) | Firing frequency of the CVLM |
| (Hz) | Firing frequency of the NTS |
| (mmHg) | Intrathoracic pressure |
| (m3) | Lung volume |
| (-) | Inspiration duration (normalized with the respiratory period) |
| (-) | Expiration duration (normalized with the respiratory period) |
| (-) | Time passed since the inspiration starts (normalized with the respiratory period) |
| (-) | Lower saturation of |
| (-) | Upper saturation of |
| (-) | Value of at the center of the sigmoid function representing |
| (-) | Constant related to the shape of the sigmoid function representing |
| (-) | Lower saturation of |
| (-) | Upper saturation of |
| (-) | Value of at the center of the sigmoid function representing |
| (-) | Constant related to the shape of the sigmoid function representing |
| (Hz) | Lower saturation of |
| (Hz) | Upper saturation of |
| (Hz) | Value of at the center of the sigmoid function representing |
| (Hz) | Constant related to the shape of the sigmoid function representing |
| (m3) | Value of at the center of the sigmoid function representing |
| (m3) | Constant related to the shape of the sigmoid function representing |
| (Hz) | Strength of the effect on |
| (-) | Constant representing the relationship between and |
| (Hz) | in the condition with extremely large |
| (Hz) | Strength of the effect on |
| (s) | Constant related to the shape of the exponential function representing |
| (Hz) | Strength of the effect on |
| (-) | Constant representing the relationship between and |
| (-) | Strength of the effect on |
| (-) | Strength of the effect on |
| (s) | Heart period |
| (s) | Heart period change controlled by the sympathetic nerve |
| (s) | Heart period change controlled by the parasympathetic nerve |
| (s) | Time constant of |
| (s) | Time constant of |
| (s/Hz) | Constant gain factors of |
| (s/Hz) | Constant gain factors of |
| (Hz) | 2 s before |
| (Hz) | 0.2 s before |
| (s) | Offset of the heart period |
References
- Albracht-Schulte, K.; Robert-McComb, J. The effects of yoga and quiet rest on subjective levels of anxiety and physiological correlates: A 2-way crossover randomized trial. BMC Complement. Altern. Med. 2018, 18, 280. [Google Scholar] [CrossRef] [PubMed]
- Lang, P.J.; Greenwald, M.K.; Bradley, M.M.; Hamm, A.O. Looking at pictures: Affective, facial, visceral, and behavioral reactions. Psychophysiology 1993, 30, 261–273. [Google Scholar] [CrossRef] [PubMed]
- Shinba, T.; Kariya, N.; Matsui, Y.; Ozawa, N.; Matsuda, Y.; Yamamoto, K. Decrease in heart rate variability response to task is related to anxiety and depressiveness in normal subjects. Psychiatry Clin. Neurosci. 2008, 62, 603–609. [Google Scholar] [CrossRef] [PubMed]
- Baek, H.J.; Lee, H.B.; Kim, J.S.; Choi, J.M.; Kim, K.K.; Park, K.S. Nonintrusive biological signal monitoring in a car to evaluate a driver’s stress and health state. Telemed. J. e-Health 2009, 15, 182–189. [Google Scholar] [CrossRef]
- Critchley, H.D.; Rotshtein, P.; Nagai, Y.; O’Doherty, J.; Mathias, C.J.; Dolan, R.J. Activity in the human brain predicting differential heart rate responses to emotional facial expressions. NeuroImage 2005, 24, 751–762. [Google Scholar] [CrossRef]
- Hamann, S.B.; Ely, T.D.; Grafton, S.T.; Kilts, C.D. Amygdala activity related to enhanced memory for pleasant and aversive stimuli. Nat. Neurosci. 1999, 2, 289–293. [Google Scholar] [CrossRef]
- Wager, T.D.; Waugh, C.E.; Lindquist, M.; Noll, D.C.; Fredrickson, B.L.; Taylor, S.F. Brain mediators of cardiovascular responses to social threat: Part I: Reciprocal dorsal and ventral sub-regions of the medial prefrontal cortex and heart-rate reactivity. NeuroImage 2009, 47, 821–835. [Google Scholar] [CrossRef]
- Kemp, A.H.; Quintana, D.S.; Gray, M.A.; Felmingham, K.L.; Brown, K.; Gatt, J.M. Impact of depression and antidepressant treatment on heart rate variability: A review and meta-analysis. Biol. Psychiatry 2010, 67, 1067–1074. [Google Scholar] [CrossRef]
- Napadow, V.; Dhond, R.; Conti, G.; Makris, N.; Brown, E.N.; Barbieri, R. Brain correlates of autonomic modulation: Combining heart rate variability with fMRI. NeuroImage 2008, 42, 169–177. [Google Scholar] [CrossRef]
- Wallentin, M.; Nielsen, A.H.; Vuust, P.; Dohn, A.; Roepstorff, A.; Lund, T.E. Amygdala and heart rate variability responses from listening to emotionally intense parts of a story. NeuroImage 2011, 58, 963–973. [Google Scholar] [CrossRef]
- Yang, T.T.; Simmons, A.N.; Matthews, S.C.; Tapert, S.F.; Bischoff-Grethe, A.; Frank, G.K.; Arce, E.; Paulus, M.P. Increased amygdala activation is related to heart rate during emotion processing in adolescent subjects. Neurosci. Lett. 2007, 428, 109–114. [Google Scholar] [CrossRef] [PubMed]
- Berntson, G.G.; Cacioppo, J.T.; Quigley, K.S. Respiratory sinus arrhythmia: Autonomic origins, physiological mechanisms, and psychophysiological implications. Psychophysiology 1993, 30, 183–196. [Google Scholar] [CrossRef] [PubMed]
- Berntson, G.G.; Bigger, J.T.; Eckberg, D.L.; Grossman, P.; Kaufmann, P.G.; Malik, M.; Nagaraja, H.N.; Porges, S.W.; Saul, J.P.; Stone, P.H.; et al. Heart rate variability: Origins, methods, and interpretive caveats. Psychophysiology 1997, 34, 623–648. [Google Scholar] [CrossRef] [PubMed]
- Yildiz, M.; Ider, Y.Z. Model based and experimental investigation of respiratory effect on the HRV power spectrum. Physiol. Meas. 2006, 27, 973–988. [Google Scholar] [CrossRef] [PubMed]
- Taelman, J.; Vandeput, S.; Spaepen, A.; Van Huffel, S. Influence of mental stress on heart rate and heart rate variability. In 4th European Conference of the International Federation for Medical and Biological Engineering 23–27 November 2008, Antwerp, Belgium, 1st ed.; van der Sloten, J., Verdonck, P., Nyssen, M., Haueisen, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 22, pp. 1366–1369. [Google Scholar] [CrossRef]
- Malpas, S.C. Neural influences on cardiovascular variability: Possibilities and pitfalls. Am. J. Physiol. 2002, 282, H6–H20. [Google Scholar] [CrossRef] [PubMed]
- Papaioannou, V.E. Heart rate variability, baroreflex function and heart rate turbulence: Possible origin and implications. Hell. J. Cardiol. 2007, 48, 278–289. [Google Scholar]
- Montano, N.; Gnecchi-Ruscone, T.; Porta, A.; Lombardi, F.; Malliani, A.; Barman, S.M. Presence of vasomotor and respiratory rhythms in the discharge of single medullary neurons involved in the regulation of cardiovascular system. J. Auton. Nerv. Syst. 1996, 57, 116–122. [Google Scholar] [CrossRef]
- Ursino, M. Interaction between carotid baroregulation and the pulsating heart: A mathematical model. Am. J. Physiol. 1998, 275, H1733–H1747. [Google Scholar] [CrossRef]
- Ursino, M.; Magosso, E. Acute cardiovascular response to isocapnic hypoxia. I. A mathematical model. Am. J. Physiol. 2000, 279, H149–H165. [Google Scholar] [CrossRef]
- Magosso, E.; Ursino, M. Cardiovascular response to dynamic aerobic exercise: A methematical model. Med. Biol. Eng. Comput. 2002, 40, 660–674. [Google Scholar] [CrossRef]
- Ursino, M.; Magosso, E. Role of short-term cardiovascular regulation in heart period variability: A modeling study. Am. J. Physiol. 2003, 284, H1479–H1493. [Google Scholar] [CrossRef] [PubMed]
- Saha, S. Role of the central nucleus of the amygdala in the control of blood pressure: Descending pathways to medullary cardiovascular nuclei. Clin. Exp. Pharmacol. Physiol. 2005, 32, 450–456. [Google Scholar] [CrossRef] [PubMed]
- Critchley, H.D.; Eccles, J.; Garfinkel, S.N. Interaction between cognition, emotion, and the autonomic nervous system. Handb. Clin. Neurol. 2013, 117, 59–77. [Google Scholar] [CrossRef] [PubMed]
| Equation | Parameters | |||
|---|---|---|---|---|
| Equation (4) | ||||
| Equation (5) | ||||
| Equation (6) | Hz | Hz | Hz | Hz |
| m3 | = 8.0 m3 | |||
| Equation (7) | Hz | |||
| Equation (8) | Hz | Hz | s | |
| Hz | ||||
| Equation (9) | ||||
| Equation (10) | ||||
| Equation (11) | s | s/Hz | ||
| Equation (12) | s | s/Hz | ||
| Equation (13) | s | |||
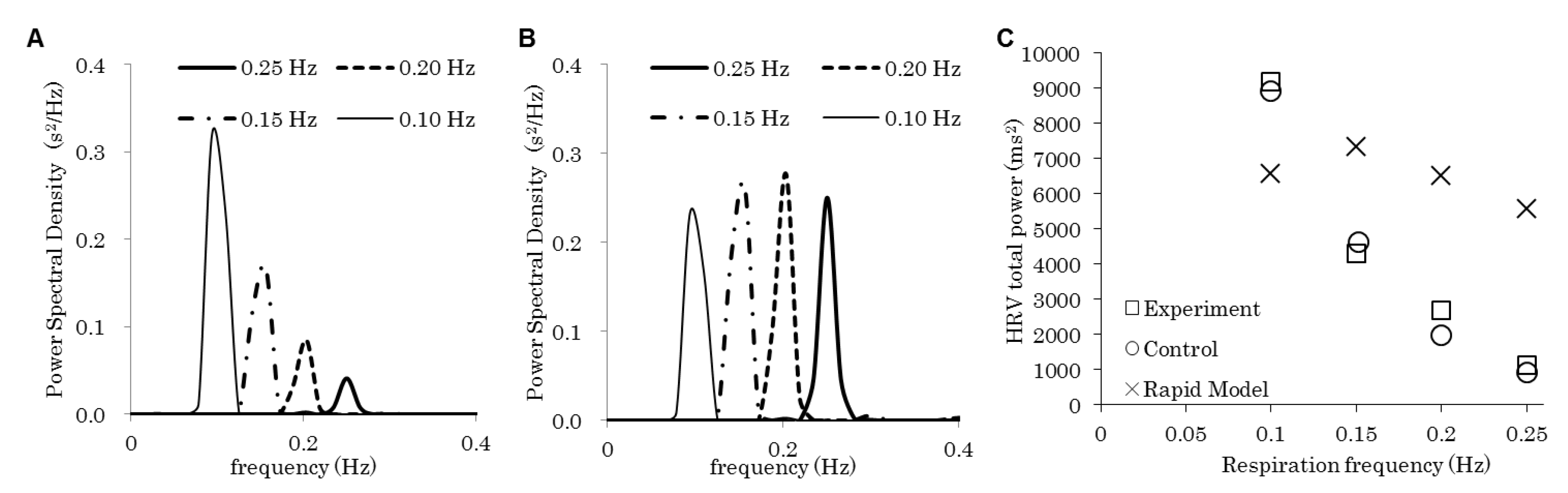
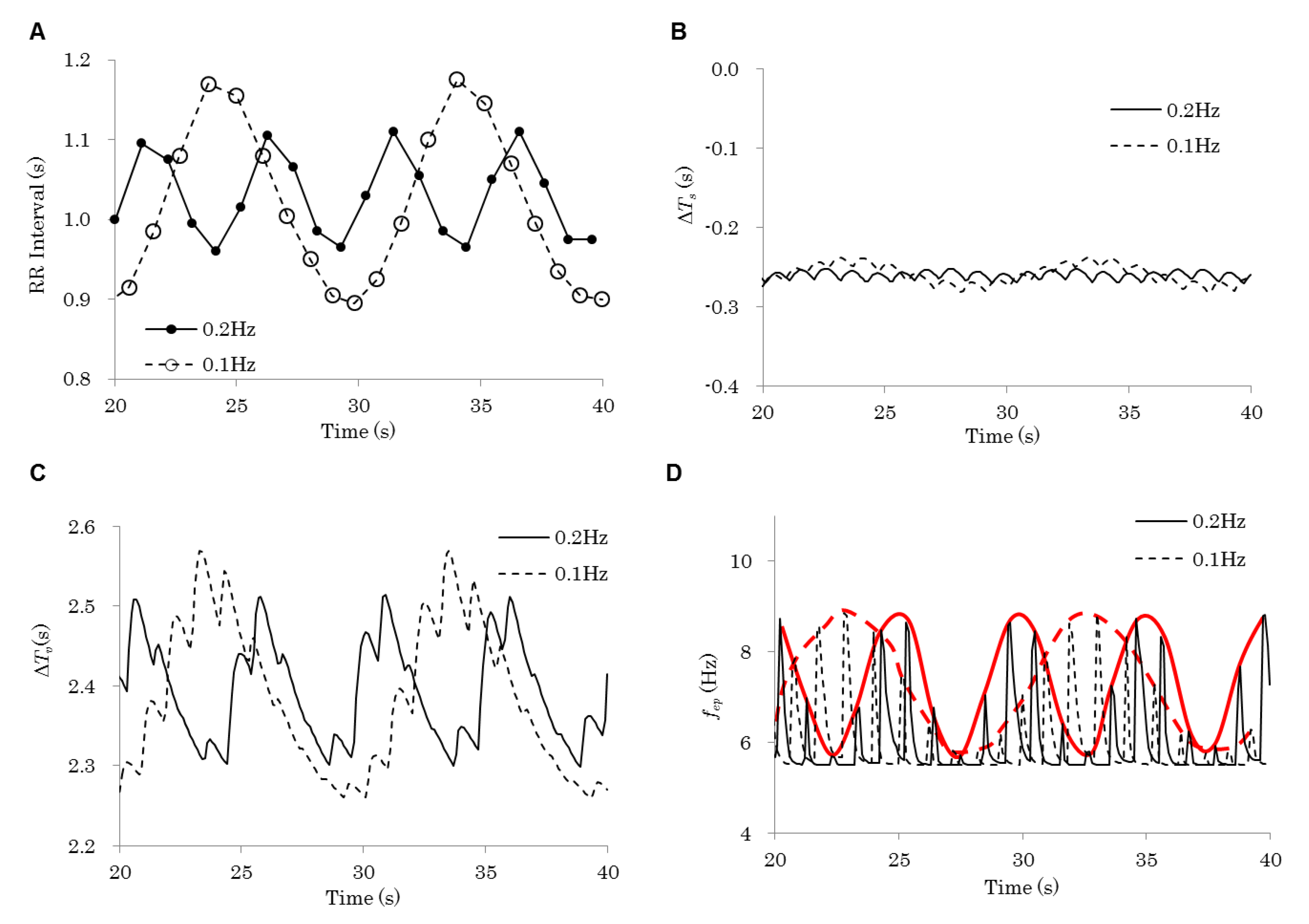
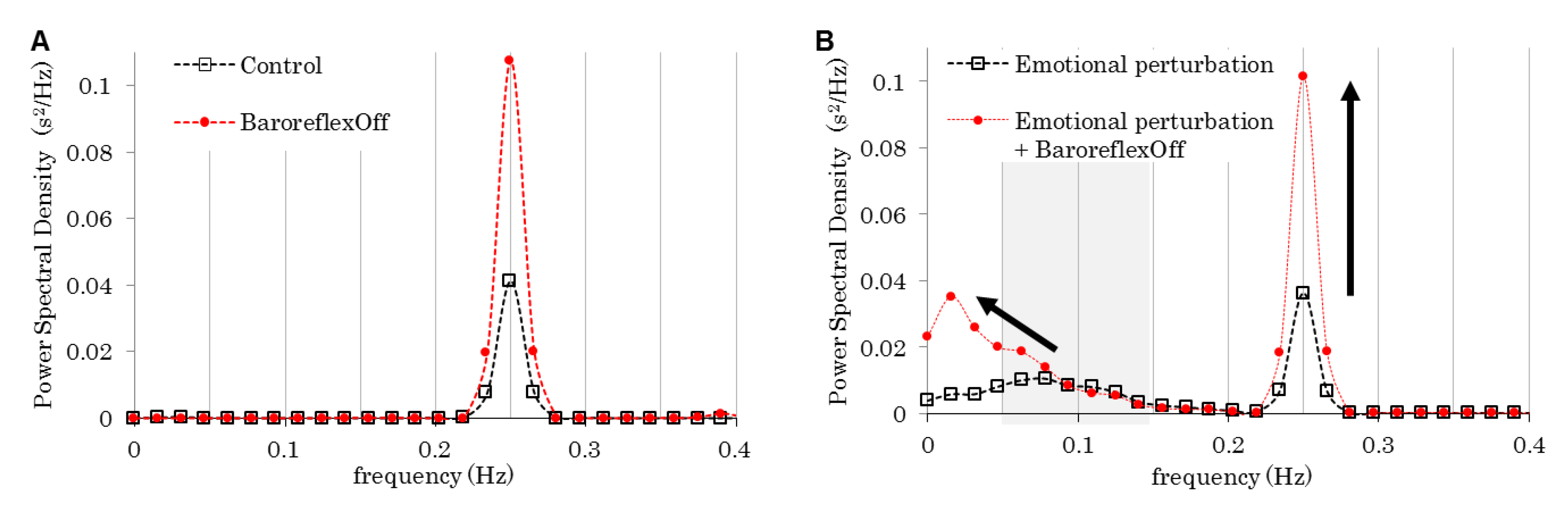
| Figure | Model | Respiration Frequency (Hz) | Baroreflex | Emotion | |
|---|---|---|---|---|---|
| 2 | A and “control” in C | Control | 0.10, 0.15, 0.20, 0.25 | On | Flat |
| B and “rapid model” in C | Rapid | ||||
| 3 | 0.2 Hz | Control | 0.20 | On | Flat |
| 0.1 Hz | 0.10 | ||||
| 4 | Control | Control | 0.25 | On | Flat |
| Emotional perturbation | Perturbed | ||||
| Baroreflex off | Off | Flat | |||
| Emotional perturbation & Baroreflex off | Perturbed | ||||
| 5 | Control | Control | Pulmonary stretch receptor (PSR) is removed | On | Stimulation |
| Baroreflex off | Off | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirabayashi, S.; Iwamoto, M. Emotion, Respiration, and Heart Rate Variability: A Mathematical Model and Simulation Analyses. Appl. Sci. 2019, 9, 5008. https://doi.org/10.3390/app9235008
Hirabayashi S, Iwamoto M. Emotion, Respiration, and Heart Rate Variability: A Mathematical Model and Simulation Analyses. Applied Sciences. 2019; 9(23):5008. https://doi.org/10.3390/app9235008
Chicago/Turabian StyleHirabayashi, Satoko, and Masami Iwamoto. 2019. "Emotion, Respiration, and Heart Rate Variability: A Mathematical Model and Simulation Analyses" Applied Sciences 9, no. 23: 5008. https://doi.org/10.3390/app9235008
APA StyleHirabayashi, S., & Iwamoto, M. (2019). Emotion, Respiration, and Heart Rate Variability: A Mathematical Model and Simulation Analyses. Applied Sciences, 9(23), 5008. https://doi.org/10.3390/app9235008





