Absorption and Remission Characterization of Pure, Dielectric (Nano-)Powders Using Diffuse Reflectance Spectroscopy: An End-To-End Instruction
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
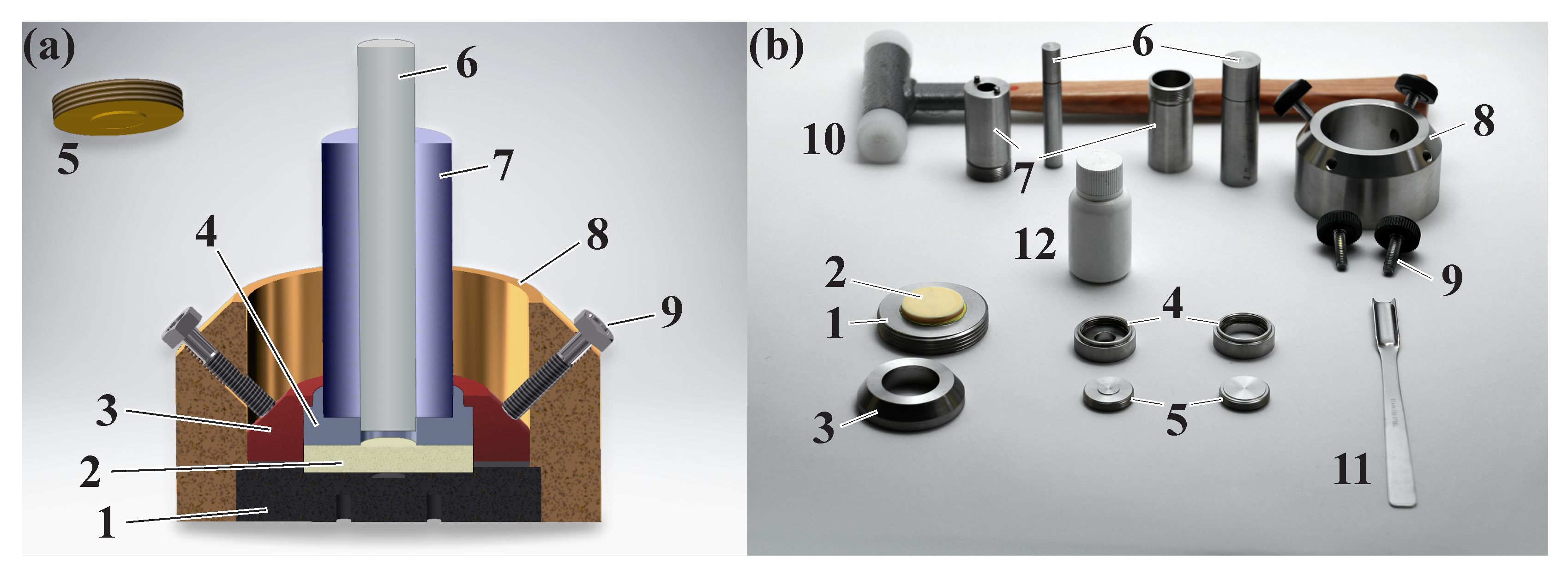
2.1.1. The Manufacturer’s Choice
- Stainless steel bottom plate.
- Ceramic slice (glued on the bottom plate by a two-component adhesive).
- Stainless steel bouncing plate (for fixating other components).
- Stainless steel sample ring (depending on the available amount of powder we suggest a diameter of 10 –20 and depth).
- Stainless steel cover plate (suitable for fitting the sample ring).
- Stainless steel tappet (matching the funnel).
- Stainless steel funnel (for inserting powder and directing the tappet).
- Stainless steel cylinder.
- Aluminum screws (to affix the other components. Aluminum is used in order to reduce wear of the adjacent components).
- Recoil-free hammer.
- Stainless steel spatula (for filling in the powder).
- (Nano/micro) powder sample.
- Let the tappet slide in the funnel on a clean planar surface (e.g., table, but not on the ceramic slice) and mark the position on the tappet at the upper end of the funnel. The ceramic slice itself must never come in contact with the tappet or other components as this would cause contamination of its surface which are relayed onto the sample.
- Affix the clean and dry bottom plate (including the ceramic slice) to the bottom of the cylinder, either by a screw thread or a plug connection.
- Place the sample ring on the ceramic slice and cover it with the bouncing plate.
- Fix the bouncing plate with the screws through the cylinder’s threads.
- Screw the funnel into the sample ring.
- Pour sample powder through the funnel.
- Gently tap the powder with the tappet by hand.
- Fill sufficient powder into the funnel to allow compression by hammer-tapping. Throughout compression, the tappet may not come into contact with the sample ring as further strokes will be directed into the ceramic plate, potentially causing it to shatter while abraded metal could contaminate the sample.
- Stop tapping when the powder cannot be compressed further, so that the marked position on the tappet can be seen at the upper end of the funnel now.
- Unscrew the funnel and adjust the cover plate into the sample ring.
- Carefully unscrew the fixing screws from the cylinder.
- Hold your fingers on the bouncing plate and carefully turn the whole powder press upside down.
- Pull off the cylinder and examine the surface of the sample pellet.
2.1.2. The Poor Man’s/DIY Choice
- Recoil-free hammer.
- Dried paper.
- (Nano/micro) powder.
- Stainless steel spatula (for filling in the powder).
- Tappet (with a planar surface).
- Hollowed stainless steel sample holder (depending on the available amount of sample material, we suggest a bore hole diameter of approx. 10 and at least 3 in depth).
- Razor/doctor blade, or
- Thin glass slide.
- Place the paper (and sample) in an oven at around 60 (if sample allows) for a few hours to remove excess humidity. This way, the amount of powder sticking to the paper during later preparation will be minimized. Furthermore, traces of water in the diffuse reflectance spectrum are strongly reduced.
- Pour or scoop the dry powder sample into a clean sample holder using the spatula.
- When the sample holder is filled with a heap of material, the dried sheet of paper is placed on top. Then the powder is compressed by placing the tappet onto the paper and hitting former with a hammer.
- Repeat adding additional powder into the sample holder until the pellet is no longer compressible.
- If a heap of material remains, carefully stroke it away with a clean razor blade (preferably doctor blade) or a thin glass slide, respectively. Add additional powder if necessary and repeat the above procedure.
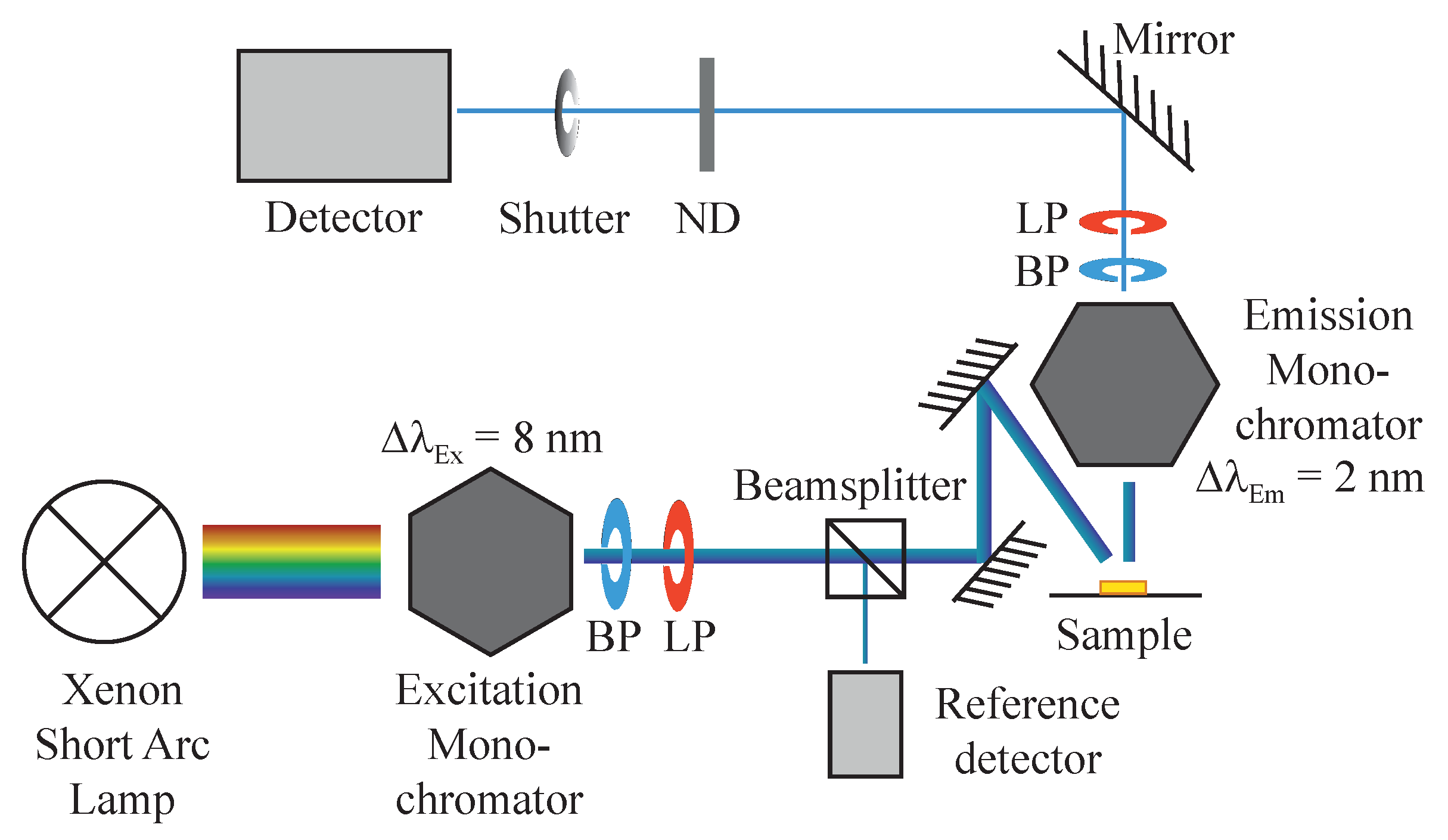
2.2. Measurement Setup: Requirements and Procedures
2.2.1. Experimental Difficulties
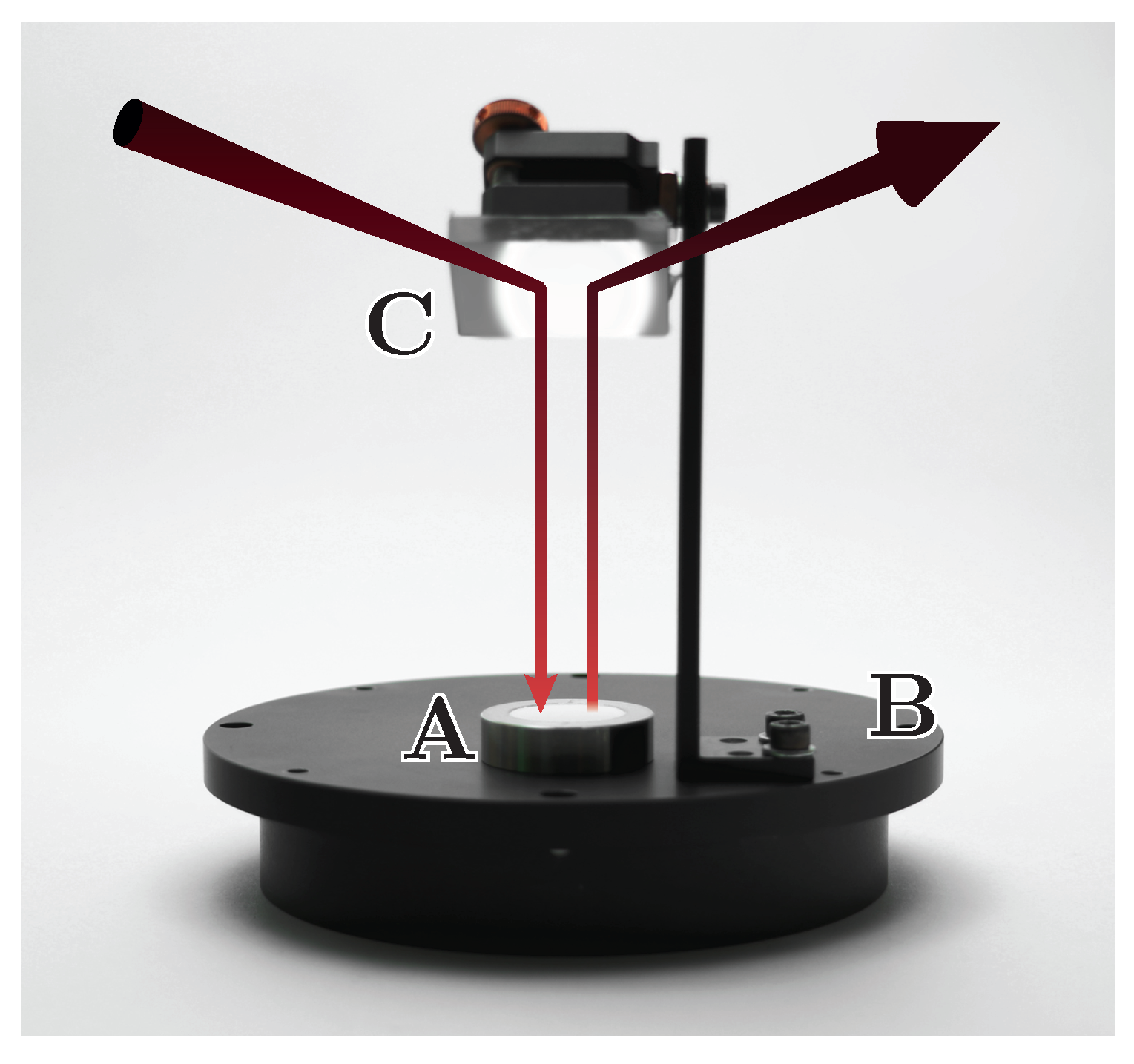
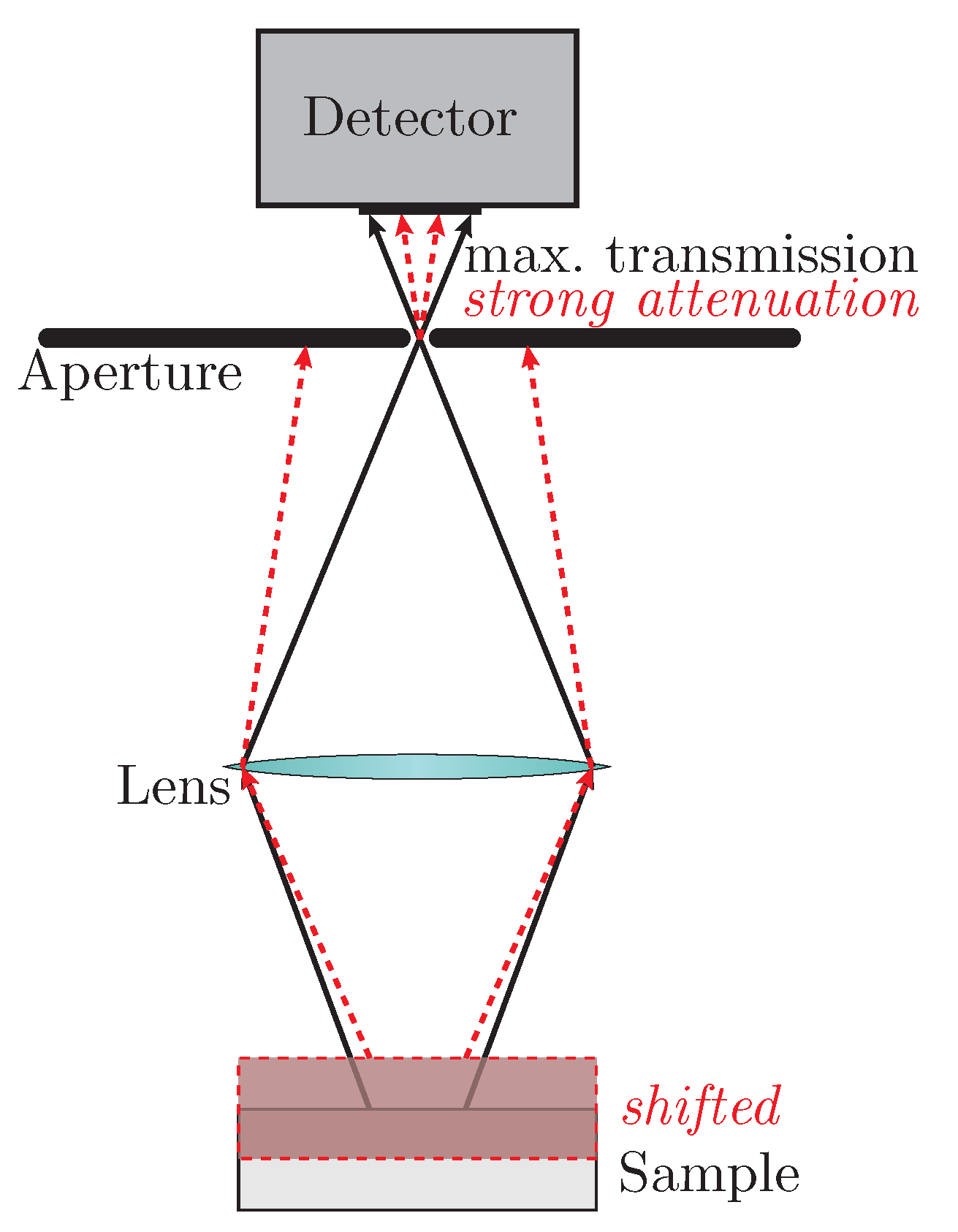
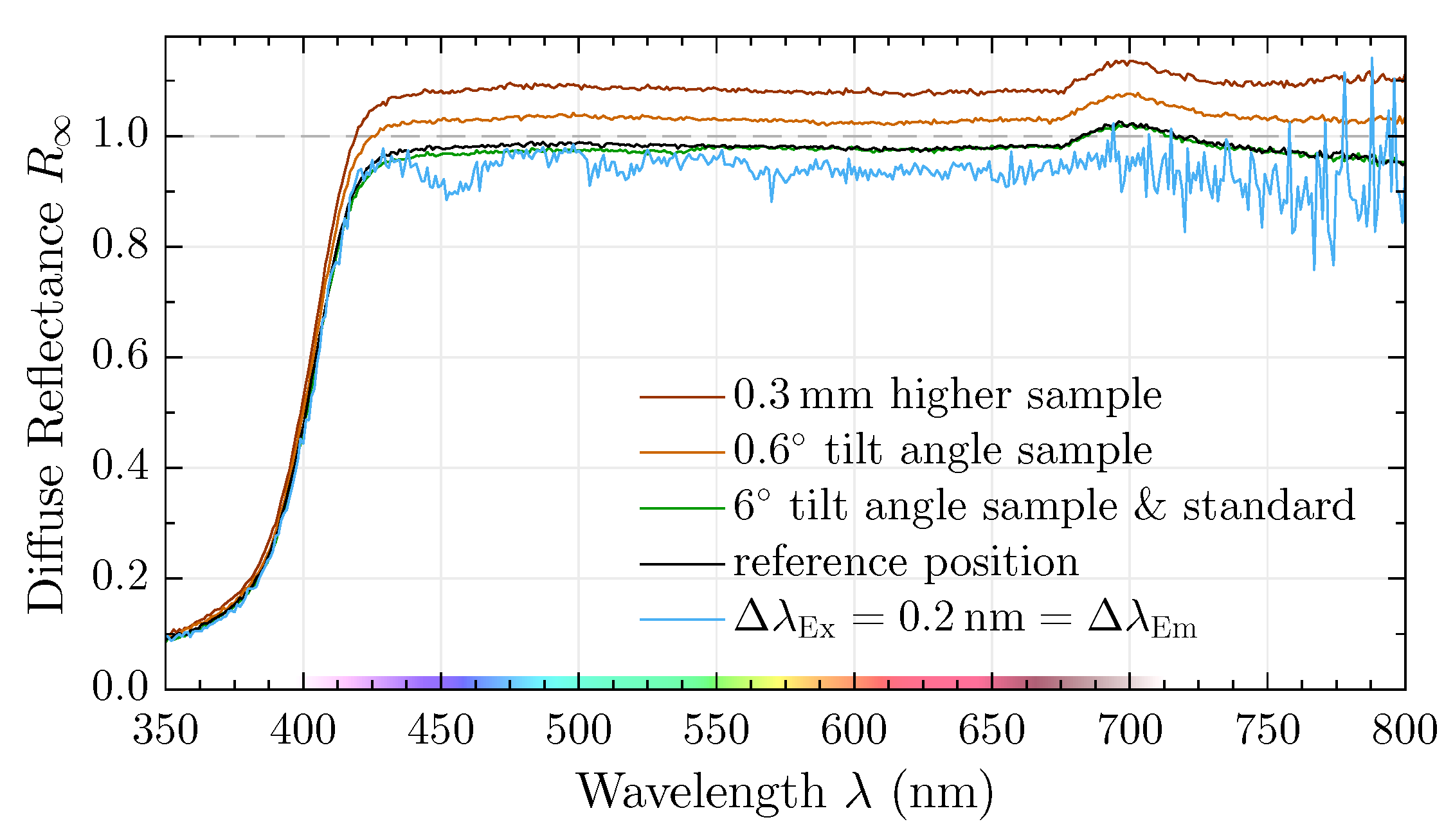
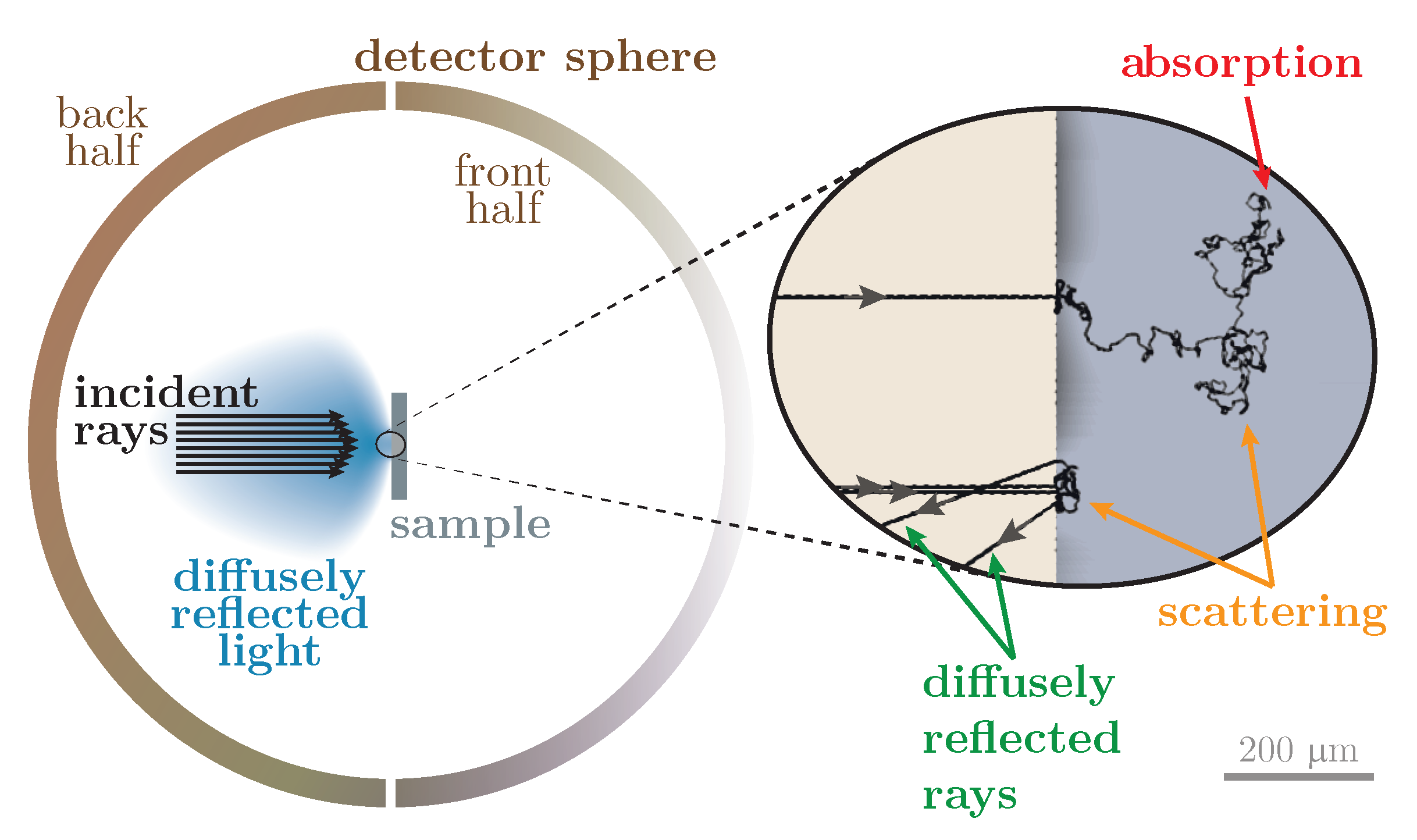
- Different distances between light source and sample surfaces: excitation and/or detected diffuse reflectance intensity changes ( with optical pathlength r for a point light source). Furthermore, focusing optics are frequently used to increase the illumination intensity. When the axial position of the sample is altered, the excitation spot size may also vary, thereby modifying the incident intensity. This effect may be enhanced by possible focusing optics and/or apertures within the beam path. Likewise, since the detection arm collects diffusely reflected light from a defined solid angle, a change in the diffuse reflectance position results in an altered amount of light that is being relayed to the detector (cf. Figure 5. Note that even in the absence of an aperture, the detector will collect a different intensity depending on the sample position).As a result, even minimal deviations in the axial position can cause significant variation in the measured signal intensity yielding large errors in the observed diffuse reflectance, if the positions among the white standard and powder samples differs as will be shown at a later point (cf. Figure 11).
- Thin layers: the sample is partly translucent. Light reaches the sample carrier and (depending on its optical properties) can be reflected or transmitted further, thereby significantly altering the backscattering properties. Depending on the material, we recommend well-pressed pellets with thicknesses of at least 3 to minimize such effects.
- Irregularities of the sample-surface: bumps, gaps or slants. Remitted intensities change considerably under grazed incidence angles as quantified by Lambert’s Cosine law [1,3]. With a severely disturbed matte surface, Lambertian behavior cannot be assumed anymore and diffuse reflectance is affected by geometrical instead of material specific effects. In this case, a re-preparation of the sample becomes necessary.
- Unequal irradiation positions on sample surface: the smaller the irradiation area, the higher the influence of local sample inhomogeneities on the diffuse reflectance. This way, reproducibility is severely hampered and significant signal fluctuations between individual positions can be expected. Improvement is achieved by maximizing the irradiation area to the sample size, thereby averaging out local irregularities. Nevertheless, there must be a significant separation of illumination area and sample border in order to avoid light propagation through the sample onto the sample-holder wall, as only the sample must be illuminated. Exposure of any other component must be avoided.
- Inappropriate monochromator bandwidths: for a synchronous scan, the excitation and emission band need to share a spectrally high overlap. In particular, the transmission bandwidth of one monochromator must be a subset of the other such that a slight discrepancy in central wavelengths of the monochromators do not cause a sudden drop-off of the signal. If, for example, both monochromators transmit a bandwidth of a white light continuum (i.e., the spectral intensity is constant throughout the investigated range) but the central wavelength of the emission monochromator is detuned by in comparison to the excitation monochromator, half of the signal is lost in this specific case. For a different wavelength, the detuning may be either smaller or larger, thereby severely affecting the measured diffuse reflectance. During a wavelength sweep, one monochromator should therefore be set to a broader spectral bandwidth than the other while exceeding the spectral resolutions of each (e.g., vs. ). Naturally, the spectral bandwidth depends on the exact type and resolution of the utilized monochromators and the desired wavelength quantization in the experiment. It has to be optimized for each spectrometer separately. As with position-deviations, this effect is highlighted in more detail in Figure 11.
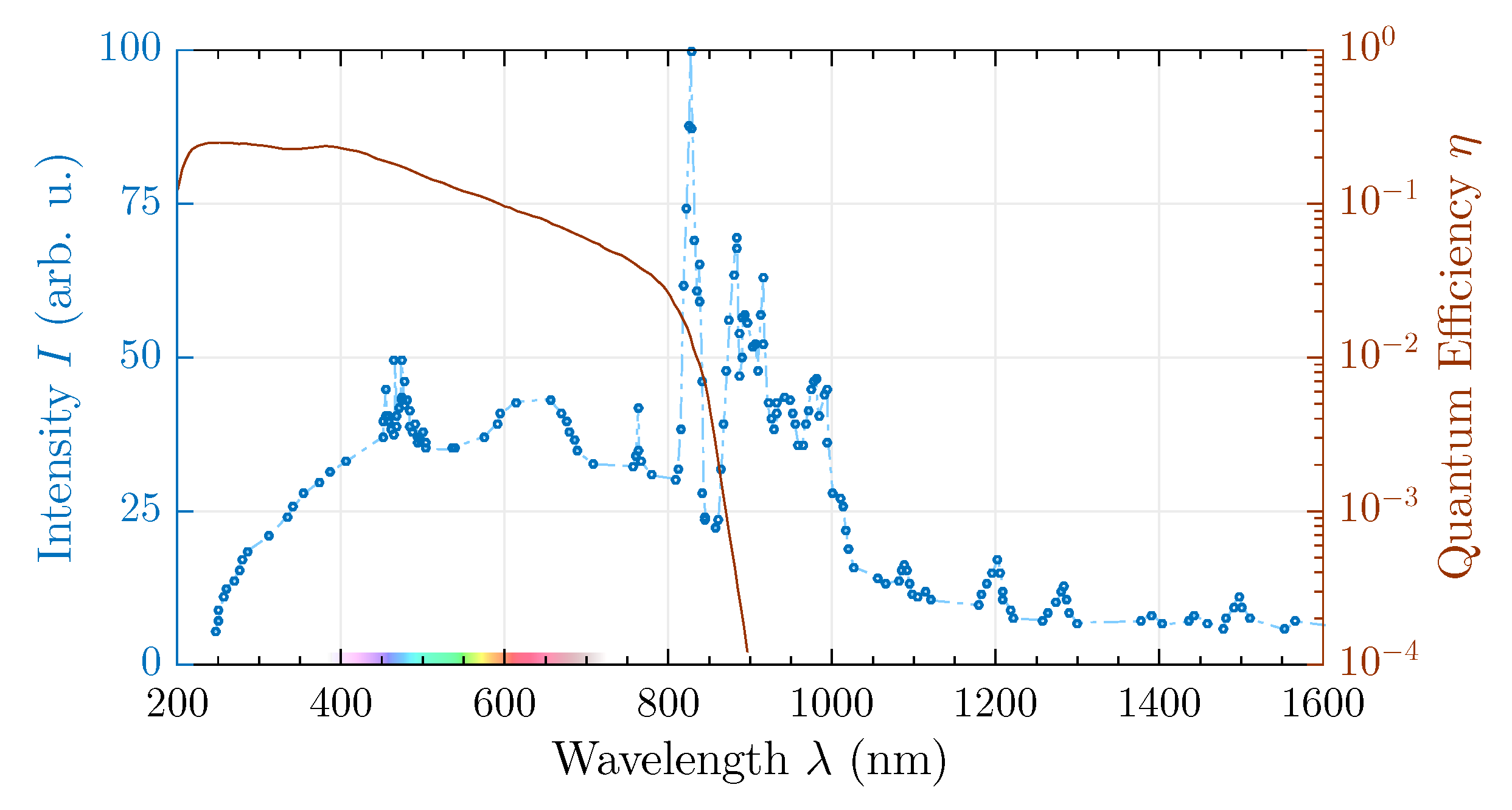
- Low detection signals: Noise becomes a sizable factor in measured signals. Because the diffuse reflectance is defined through a division between sample and white standard intensity, low count levels, especially with the white standard, will lead to potentially diverging diffuse reflectance values. This situation is mostly reinforced by considerable intensity differences of the excitation light source for varying wavelengths as well as by the utilized blazed gratings within the monochromators which are only designed for specific spectral ranges. With the present setup, this becomes apparent for wavelengths above 800 as will be shown in Figure 6 and Figure 7. A remedy consists of splitting the investigated spectral range into subsections, optimizing each for satisfactory signal quality and finally merging all scans into a single diffuse reflectance spectrum.
- Very high detection signals exceeding the detector’s linearity range. For very large irradiances, the detector undergoes saturation, i.e., higher intensities lead to a sublinear increase of the signal, and thereby distort diffuse reflectance spectra (in the worst case, also damage the detector irreversibly). Subdivision of the spectral range and merging these individual scans may prove beneficial here as well.
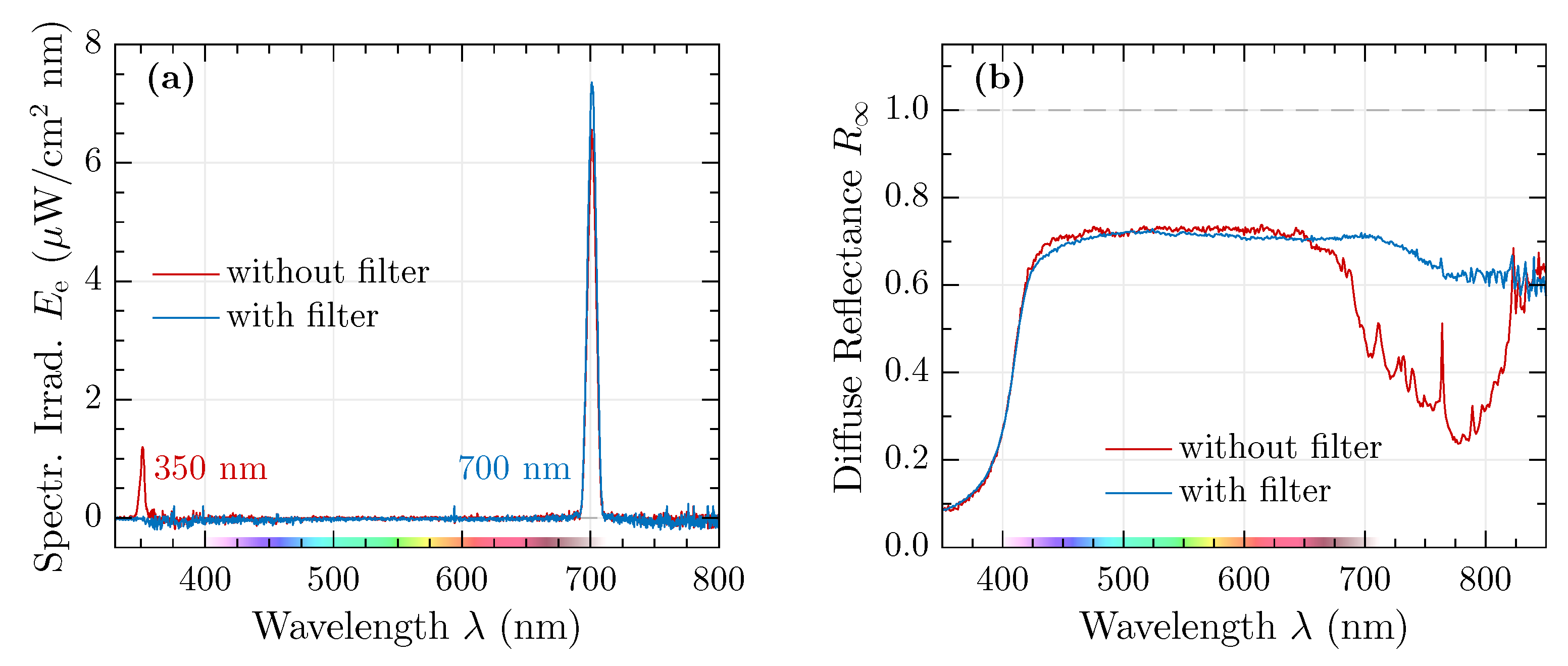
- Higher order diffraction from monochromators: Additional wavelengths unintentionally irradiate the sample and contribute to an artificially increased signal. Hence, additional wavelength discrimination by bandpass or longpass filters becomes mandatory. The resulting diffuse reflectance in the absence of such filtering will be shown in Figure 9b.
- Material luminescence (fluorescence and phosphorescence): Additional light is emitted by the sample at a different wavelength. While spectral filtering of the emission signal provides some control about the wavelengths reaching the detector, a wavelength sweep from UV to VIS means that long-lived states may still luminesce when the emission wavelength is reached [57,58]. Unless the substance to be characterized is known to be an upconversion material [59,60], scanning from longer towards shorter wavelengths or at least limiting the investigated spectral range can help suppressing luminescence.
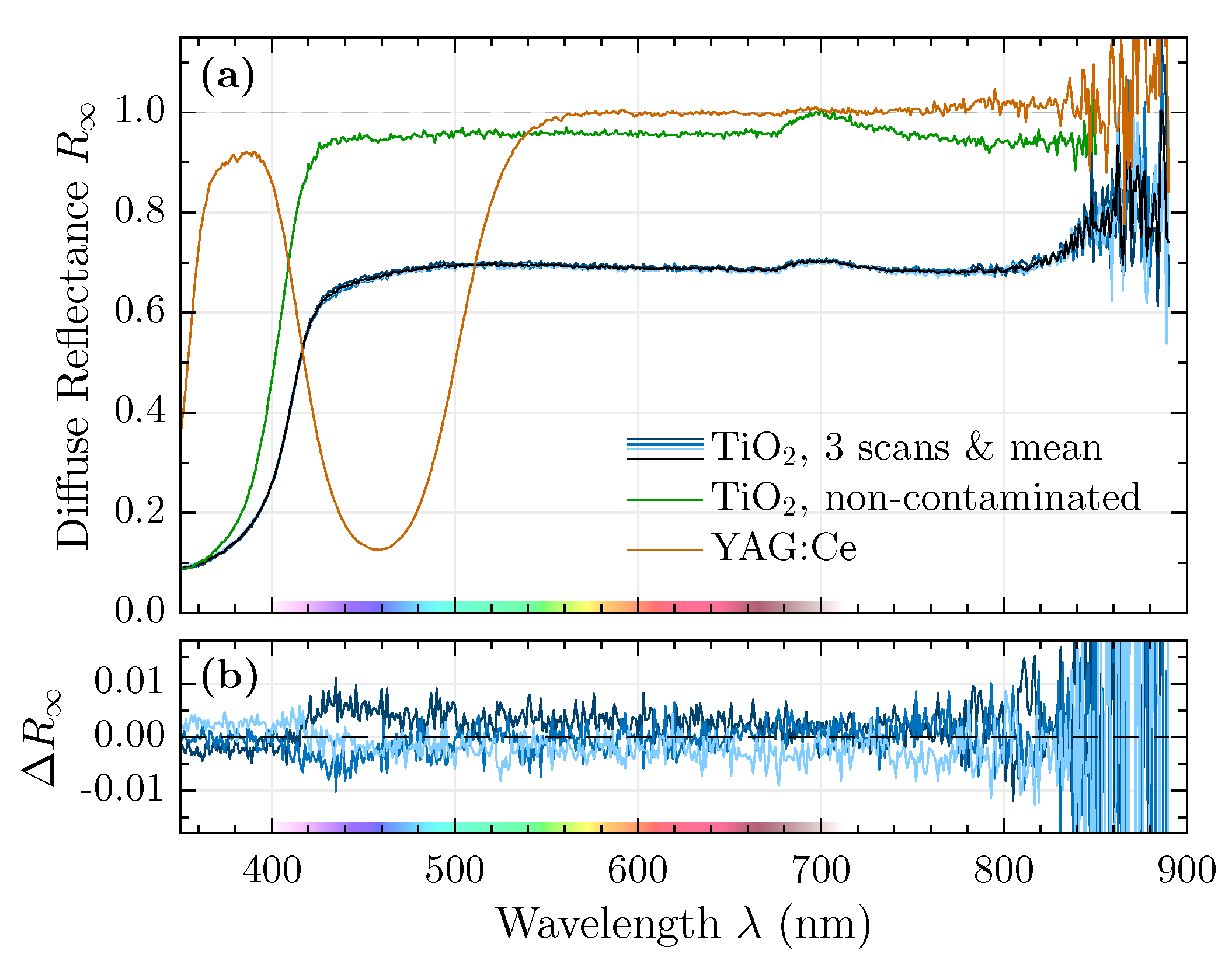
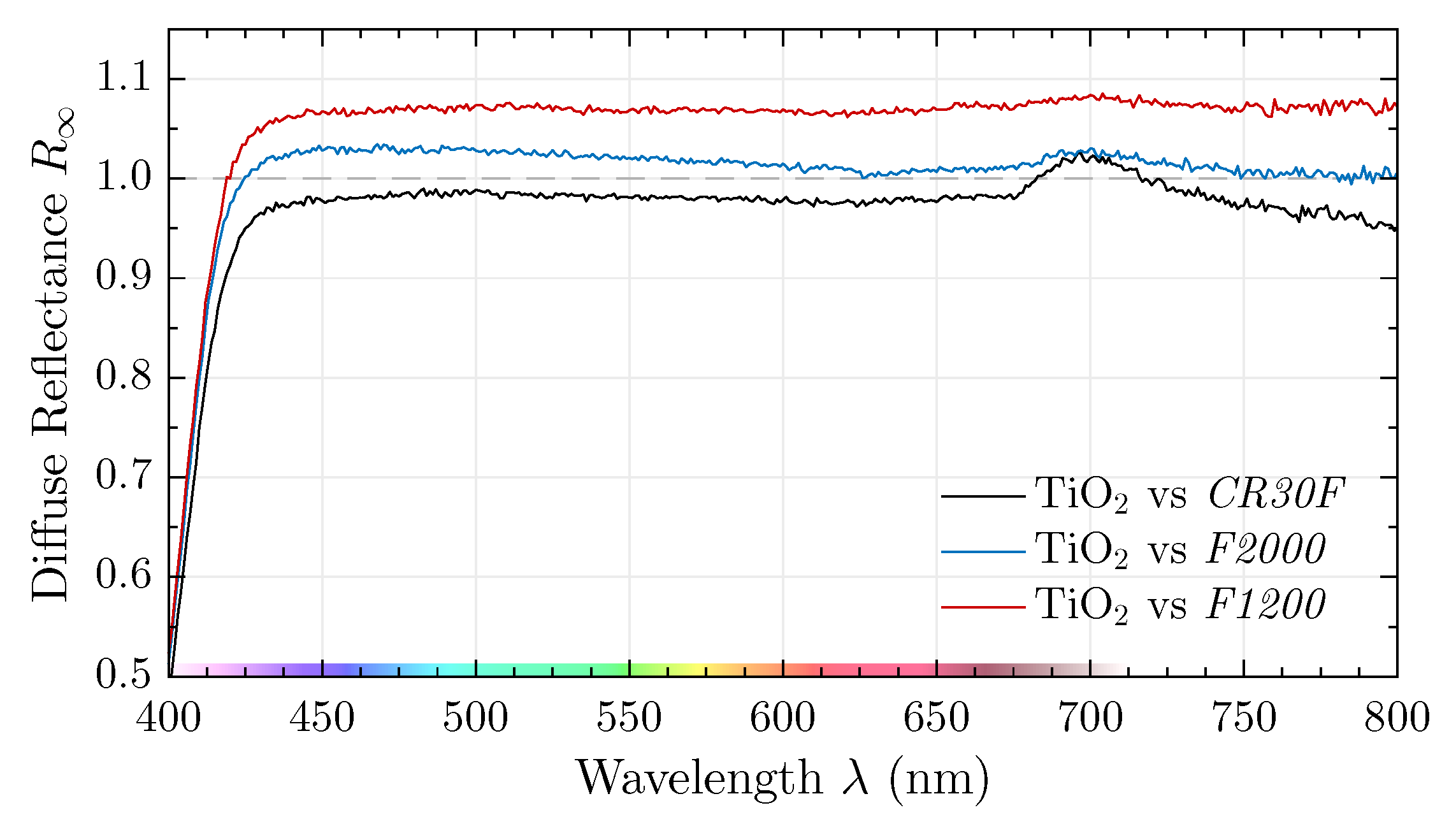
2.2.2. White Standards
2.2.3. Signal-To-Noise Ratio
- Measure white standard.
- Measure sample.
- Measure white standard.
- Measure white standard.
- Measure sample.
- Measure white standard.
- Measure sample.
- Measure white standard.
- ...
3. Diffuse Reflectance Spectroscopy: Analyzing Results
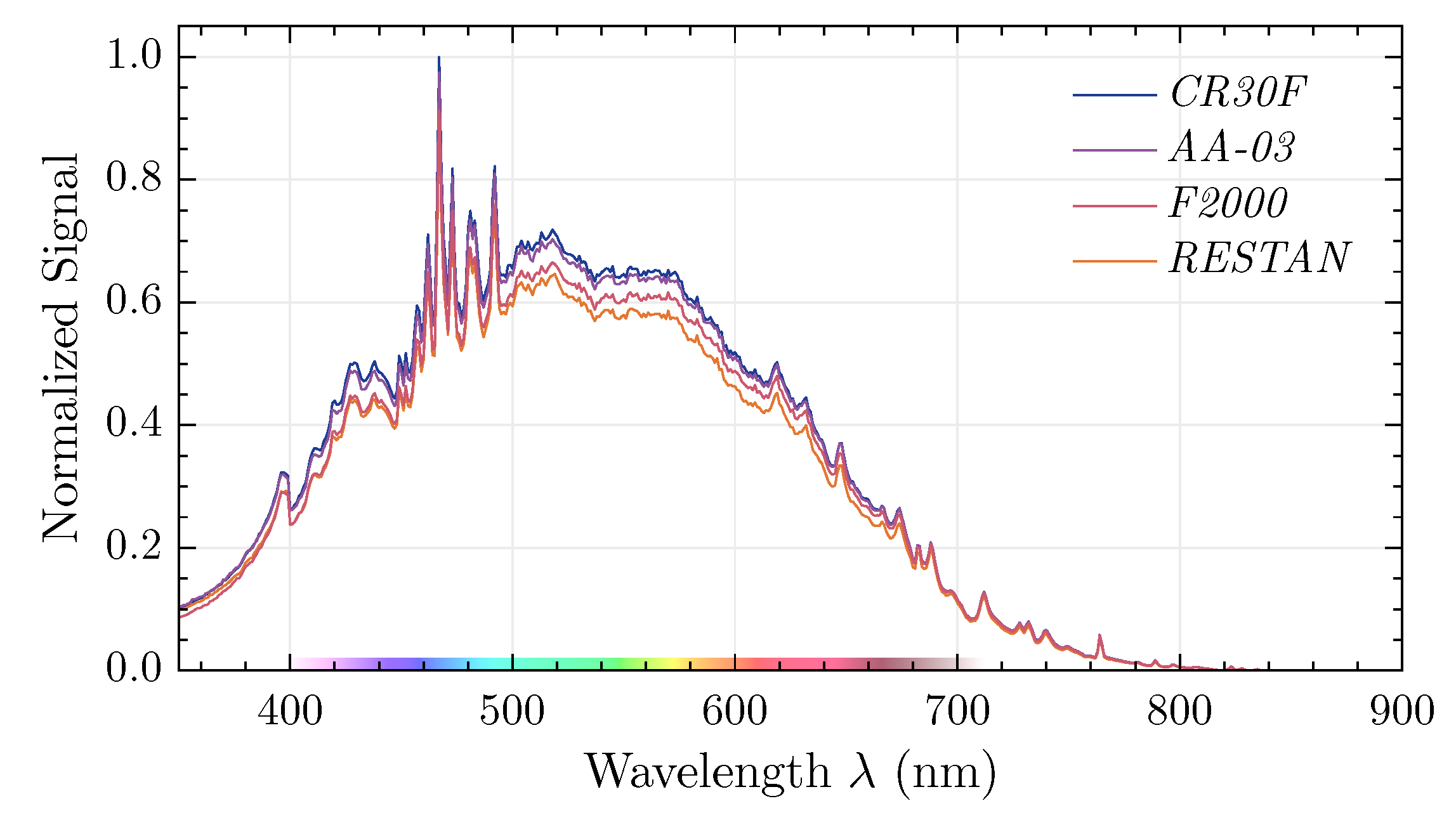
3.1. (White) Standard Comparison
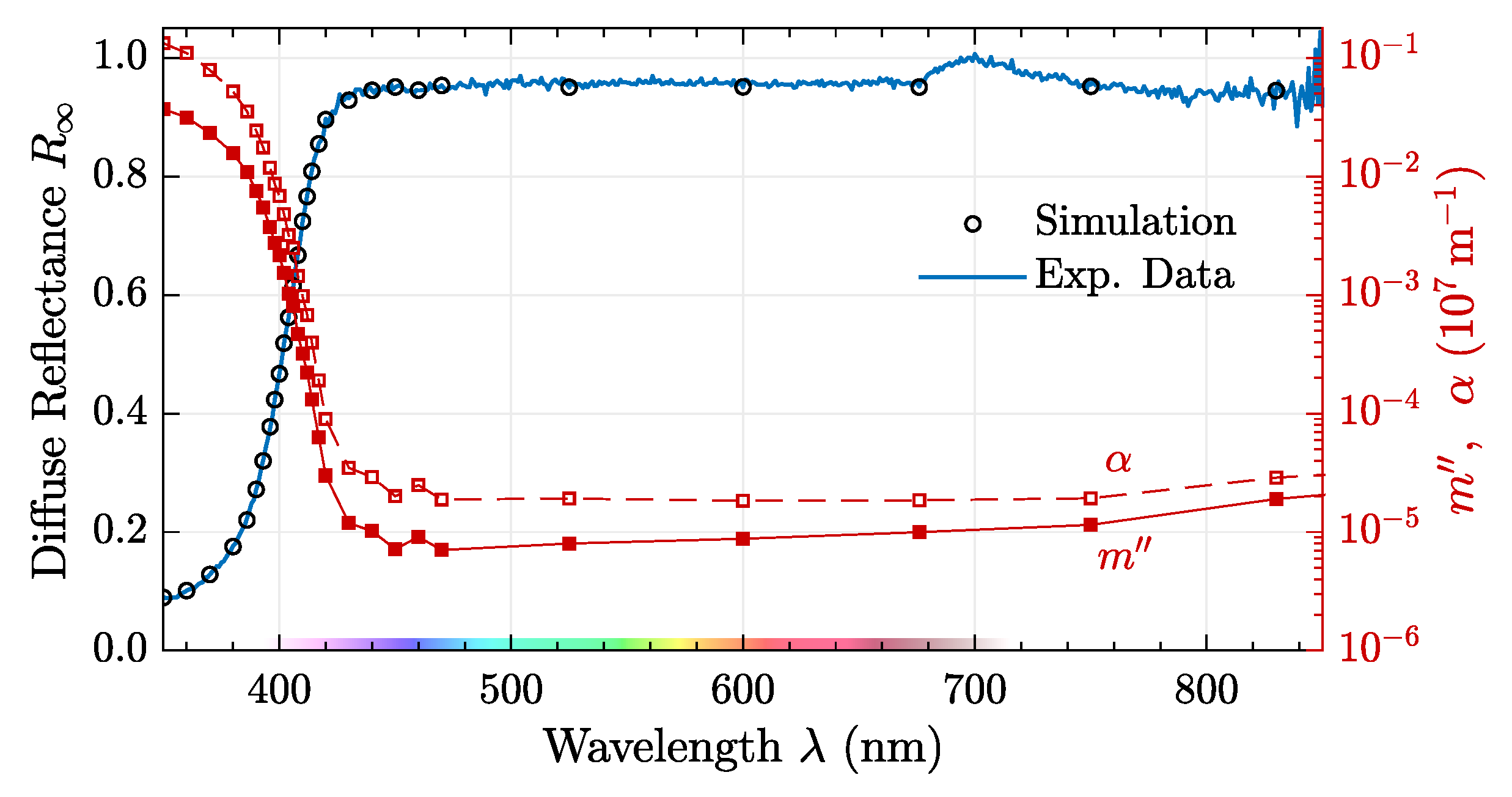
3.2. Example Materials
3.3. Pitfalls and Artifacts
3.3.1. Higher Order Diffraction
3.3.2. Sample Positioning and Monochromator Settings
3.3.3. Luminescence
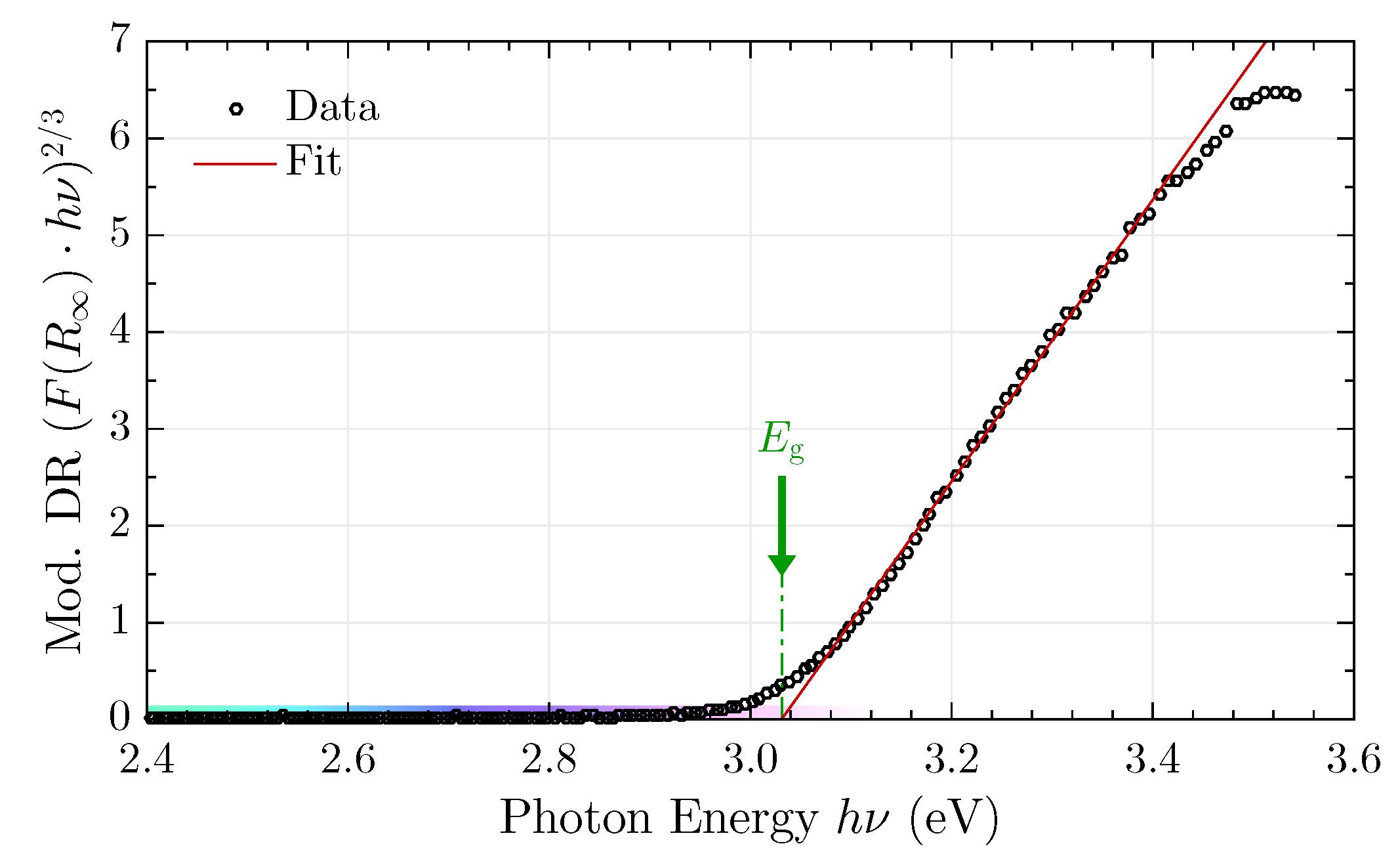
3.4. Tauc Plot
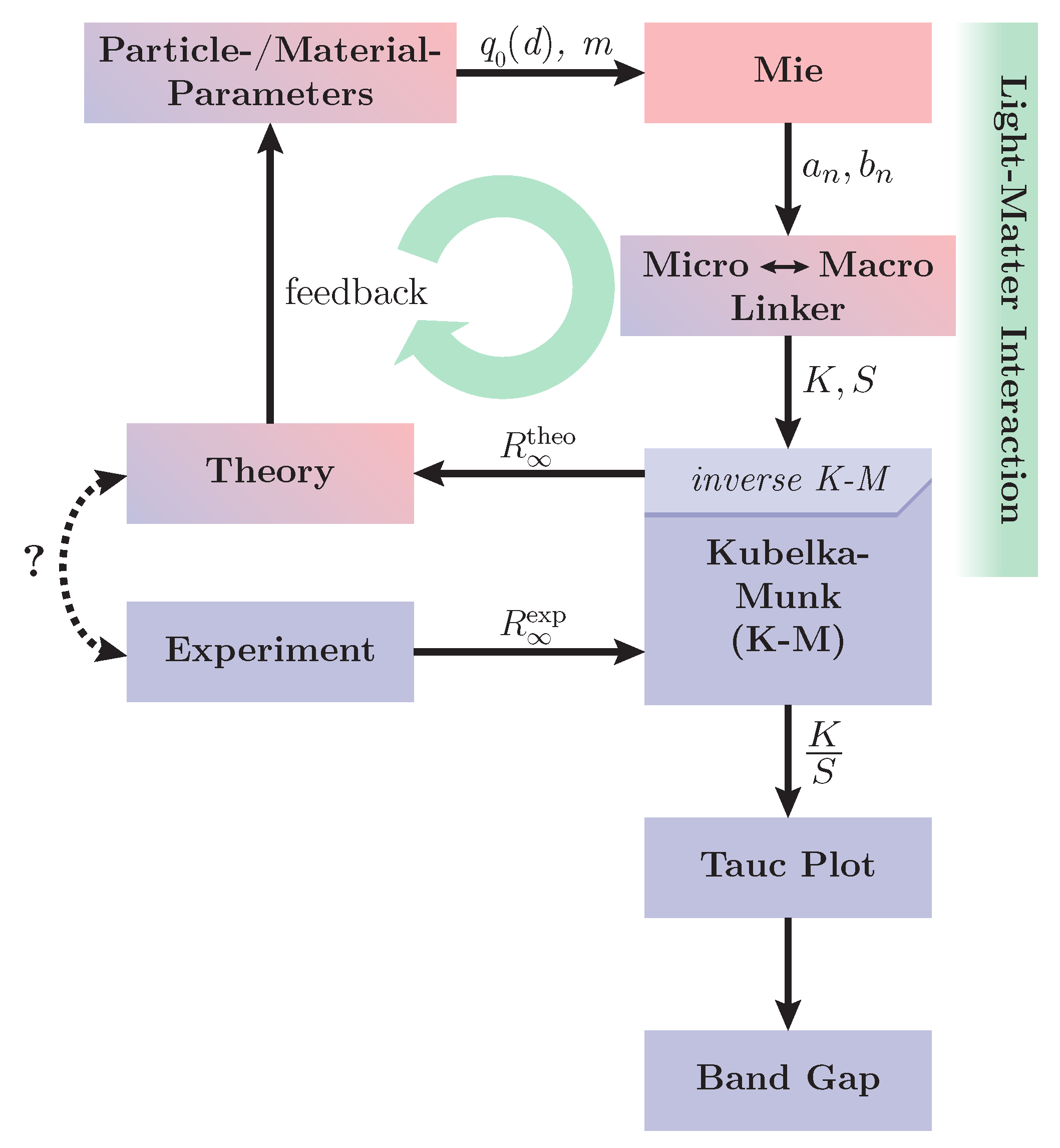
4. Theoretical Background and Simulations
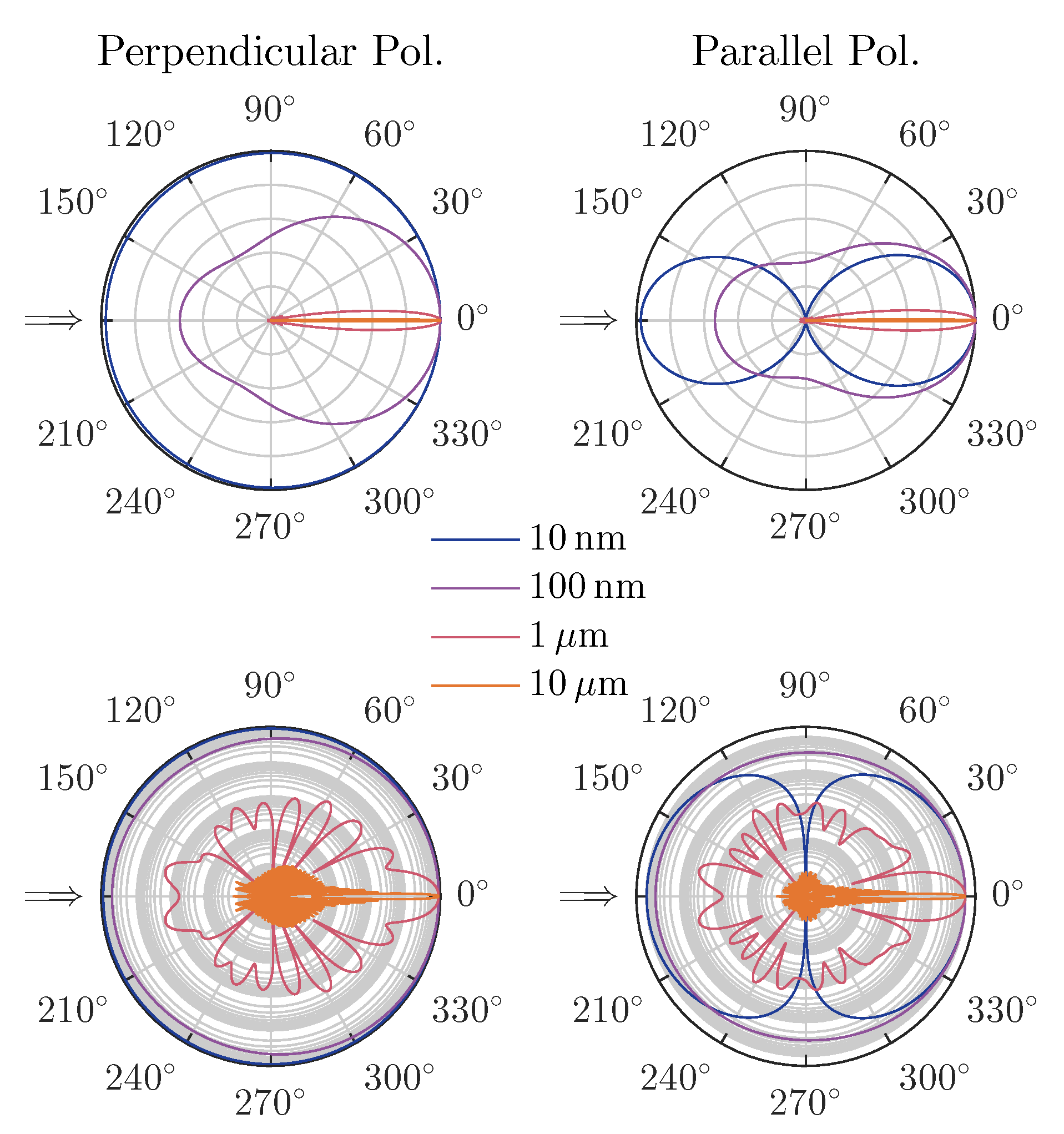
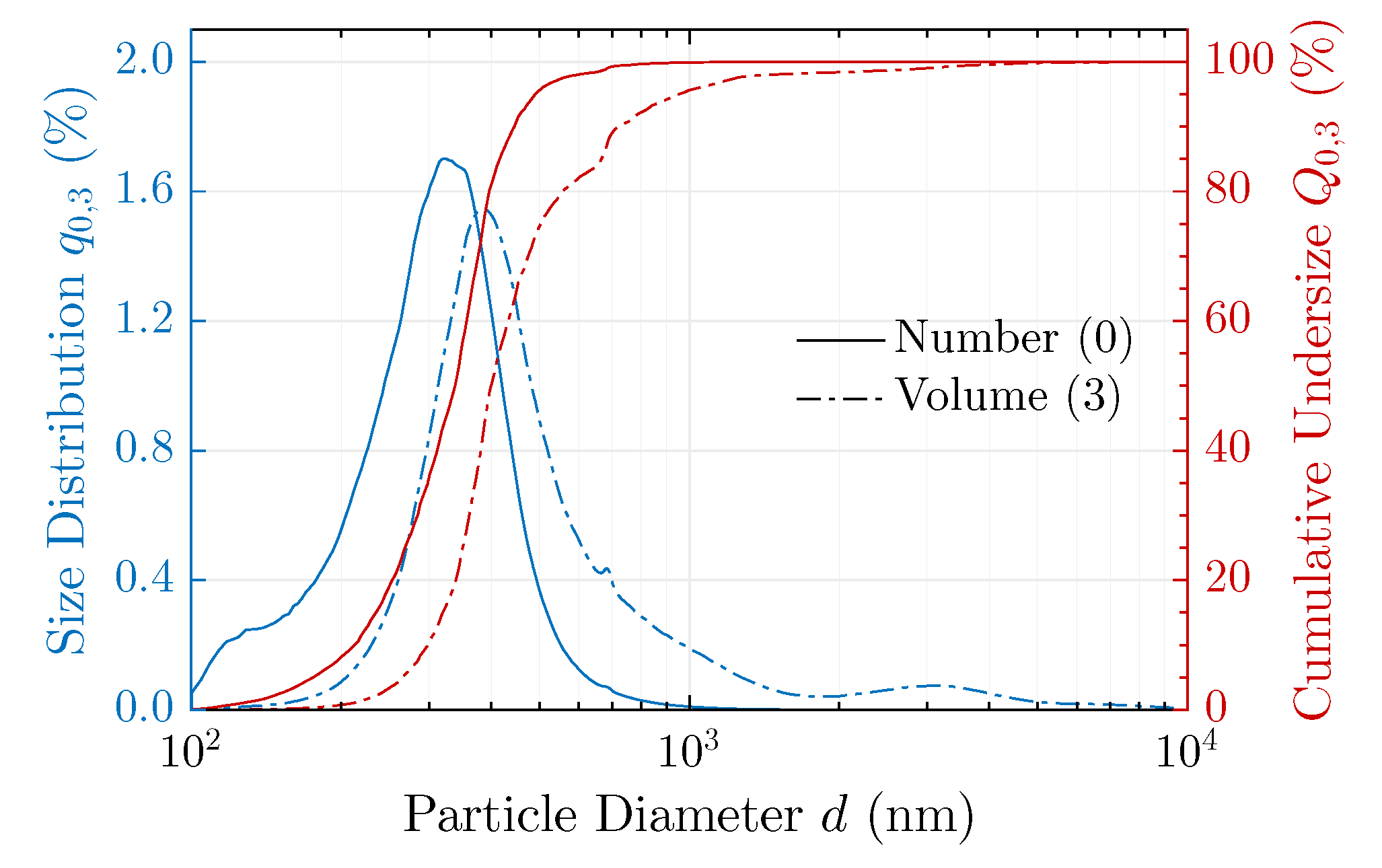
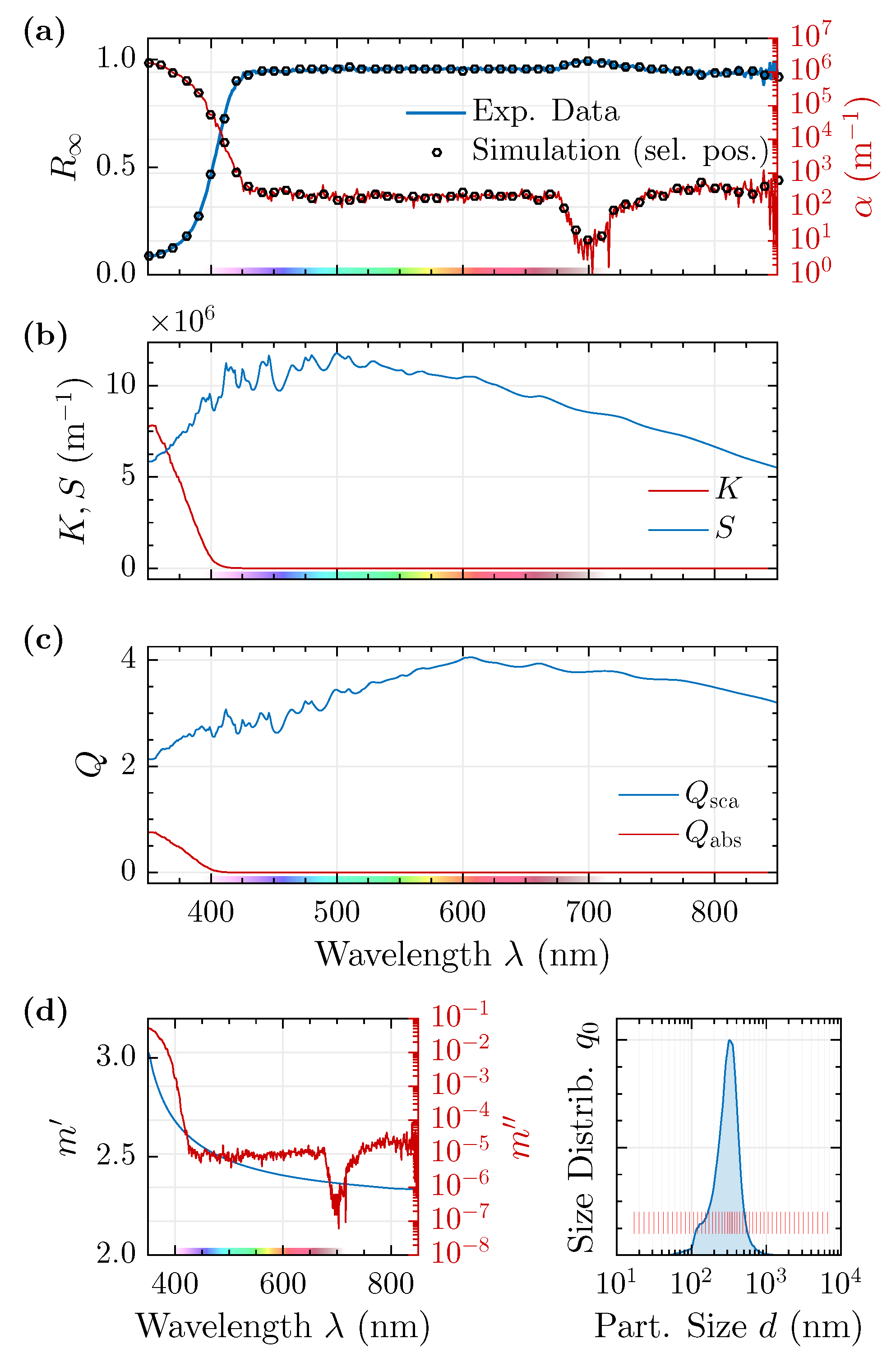
4.1. From Microscopic to Macroscopic Quantities: Ab Initio Calculations
- Use a Mie model to calculate the (microscopic) scattering and absorption efficiencies , as well as the scattering amplitudes , from the Mie coefficients , [1,119,153,154]. This can be based on classic Mie theory of spheres or advanced models such as stratified spheres, anisotropic particles or arbitrary objects. For simplicity, we exclusively consider isotropic spheres henceforth.
- For sufficiently thick samples, Equation (3) can be solved for , yielding:In this case, neither particle size d nor volume filling fraction play any further role as they cancel out in Equation (9). However, for a translucent coating layer, Equation (9) becomes inaccurate and needs to be expanded to expressions including the diffuse reflectance of layers beneath the sample [1,152]. However, since this case is not covered by classic K-M theory, it will be omitted within this context.
4.2. Monte Carlo Simulation
5. Summary
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kortüm, G. Reflectance Spectroscopy: Principles, Methods, Applications; Kortüm, G., Ed.; Springer: Heidelberg/Berlin, Germany, 1969. [Google Scholar]
- Frei, R.W.; Frodyma, M.M.; Lieu, V.T. Diffuse reflectance spectroscopy. In Instrumentation for Spectroscopy. Analytical Atomic Absorption and Fluorescence Spectroscopy. Diffuse Reflectance Spectroscopy; Svehla, G., Ed.; Wilson & Wilson’s Comprehensive Analytical Chemistry; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1975; Volume 4, Chapter 3; pp. 263–345. [Google Scholar]
- Höpe, A. Diffuse Reflectance and Transmittance. In Spectrophotometry: Accurate Measurement of Optical Properties of Materials; Germer, T.A., Zwinkels, J.C., Tsai, B.K., Eds.; Experimental Methods in the Physical Sciences; Academic Press Elsevier Inc.: Amsterdam, The Netherlands, 2014; Volume 46, Chapter 6; pp. 179–219. [Google Scholar]
- Lambert, J.H. Lambert’s Photometrie. Photometria Sive De Mensura Et Gradibus Luminis, Colorum et Umbrae (1760); Anding, E., Ed.; Ostwald’s Klassiker der exakten Wissenschaften; Verlag von Wilhelm Engelmann: Leipzig, Germany, 1892; Volume 31. [Google Scholar]
- Bouguer, P. Traité D’optique sur la Gradation de la Lumiere; I’Abbé de la Caille, M., Ed.; De l’Imprimerie de H.L. Guerin & L.F. Delatour: Paris, France, 1760. [Google Scholar]
- Ångström, K. Ueber die Diffusion der strahlenden Wärme von ebenen Flächen. Ann. Phys. 1885, 262, 253–287. [Google Scholar] [CrossRef]
- Messerschmitt, J.B. Ueber diffuse Reflexion. Ann. Phys. 1888, 270, 867–896. [Google Scholar] [CrossRef]
- Seeliger, H. Zur Photometrie zerstreut reflectirender Substanzen. In Sitzungsberichte der Mathematisch-Physikalischen Classe der k. b. Akademie der Wissenschaften zu München; Franz, G., Ed.; Verlag der K. Akademie: Munich, Germany, 1888; Volume 18, pp. 201–248. [Google Scholar]
- Lommel, E. Die Photometrie der diffusen Zurückwerfung. Ann. Phys. 1889, 272, 473–502. [Google Scholar] [CrossRef]
- Uljanin, W. Ueber das Lambert’sche Gesetz und die Polarisation der schief emittirten Strahlen. Ann. Phys. 1897, 298, 528–542. [Google Scholar] [CrossRef]
- Wright, H. Die diffuse Reflexion des Lichtes an matten Oberflächen. Ann. Phys. 1900, 306, 17–41. [Google Scholar] [CrossRef]
- Pokrowski, G.I. Zur Theorie der diffusen Lichtreflexion. Z. Phys. 1924, 30, 66–72. [Google Scholar] [CrossRef]
- Schulz, H. Untersuchungen über die Reflexion an teilweise lichtzerstreuenden Flächen. Z. Phys. 1925, 31, 496–506. [Google Scholar] [CrossRef]
- Harrison, V.G.W. The light-diffusing properties of magnesium oxide. Proc. Phys. Soc. 1946, 58, 408–419. [Google Scholar] [CrossRef]
- Torrent, J.; Barrón, V. Diffuse Reflectance Spectroscopy. In Methods of Soil Analysis Part 5–Mineralogical Methods; Number 5 in the Soil Science Society of America Book Series; Ulery, A.L., Drees, L.R., Eds.; Soil Science Society of America Inc.: Madison, WI, USA, 2008; Volume 5, Chapter 13; pp. 367–385. [Google Scholar]
- Blake, T.A.; Johnson, T.J.; Tonkyn, R.G.; Forland, B.M.; Myers, T.L.; Brauer, C.S.; Su, Y.F.; Bernacki, B.E.; Hanssen, L.; Gonzalez, G. Methods for quantitative infrared directional-hemispherical and diffuse reflectance measurements using an FTIR and a commercial integrating sphere. Appl. Opt. 2018, 57, 432–446. [Google Scholar] [CrossRef]
- Clarke, F.J.J.; Compton, J.A. Correction Methods for Integrating-Sphere Measurement of Hemispherical Reflectance. Color Res. Appl. 1986, 11, 253–262. [Google Scholar] [CrossRef]
- Kortüm, G.; Braun, W.; Herzog, G. Prinzip und Meßmethodik der diffusen Reflexionsspektroskopie. Angew. Chem. 1963, 75, 653–661. [Google Scholar] [CrossRef]
- Hanssen, L. Integrating-sphere system and method for absolute measurement of transmittance, reflectance, and absorptance of specular samples. Appl. Opt. 2001, 40, 3196–3204. [Google Scholar] [CrossRef] [PubMed]
- Abrams Engineering Services GmbH & Co. KG. Abrams Premium Steel. Available online: http://www.steel-guide.eu/alternatives/440B (accessed on 18 June 2019).
- Boroumand, F.; Moser, J.E.; van den Bergh, H. Quantitative Diffuse Reflectance and Transmittance Infrared Spectroscopy of Nondiluted Powders. Appl. Spectrosc. 1992, 46, 1874–1886. [Google Scholar] [CrossRef]
- Romaco Group. Romaco Kilian—Leading International Supplier of Tablet Press Machines. Available online: https://www.romaco.com/en/exploiting-technologies/kilian (accessed on 18 June 2019).
- Coperion GmbH. Tablet Coating and Press Lubrication. 2019. Available online: https://www.coperion.com/en/industries/pharmaceutical/tablet-coating-and-press-lubrication (accessed on 18 June 2019).
- Verdict Media Limited. Medelpharm Tablet Press Manufacture for Compaction Simulation and Powder Analysis. 2019. Available online: https://www.pharmaceutical-technology.com/contractors/contract/medelpharm-pharma (accessed on 18 June 2019).
- Nyström, C.; Karehill, P.G. The Importance of Intermolecular Bonding Forces and the Concept of Bonding Surface Area. In Pharmaceutical Powder Compaction Technology; Alderborn, G., Nyström, C., Eds.; Drugs and the Pharmaceutical Sciences; Marcel Dekker Inc.: New York, NY, USA, 1996; Volume 71, pp. 17–53. [Google Scholar]
- LFA Machines Oxford LTD. VICE Hand Held Press. 2018. Available online: https://www.lfatabletpresses.com/vice-hand-held-tablet-press (accessed on 18 June 2019).
- LFA Machines Oxford LTD. TDP 0 Desktop Tablet Press. 2018. Available online: https://www.lfatabletpresses.com/desktop-tablet-press-tdp-0 (accessed on 18 June 2019).
- Fritsch GmbH. Operating Manuals for Older Models of the Pellet Press; Operating Manual Pellet Press: Idar-Oberstein, Germany, 2019; Available online: https://www.fritsch-international.com/services/downloads-videos/pellet-press/ (accessed on 18 June 2019).
- Retsch GmbH. Pellet Press PP 25. 2019. Available online: https://www.retsch.com/products/assisting/pellet-presses/pp-25/function-features (accessed on 18 June 2019).
- Specac Limited. Pellet Press Dies | FTIR + XRF Dies. 2019. Available online: https://www.specac.com/en/products/ftir-xrf-sample-preparation-equipment/pellet-dies/evacuable-standard/pellet-press-dies-ftir-xrf-dies (accessed on 18 June 2019).
- Kaplan Scientific. Mini-Pellet Press. Available online: https://kaplanscientific.nl/product/mini-pellet-press/ (accessed on 18 June 2019).
- Weidner, V.R. Gray scale of diffuse reflectance for the 250–2500-nm wavelength range. Appl. Opt. 1986, 25, 1265–1266. [Google Scholar] [CrossRef]
- Fuller, M.P.; Griffiths, P.R. Diffuse Reflectance Measurements by Infrared Fourier Transform Spectrometry. Anal. Chem. 1978, 50, 1906–1910. [Google Scholar] [CrossRef]
- Fuller, M.P.; Hamadeh, I.M.; Griffiths, P.R.; Lowenhaupt, D.E. Diffuse reflectance infrared spectroscopy of powdered coals. Fuel 1982, 61, 529–536. [Google Scholar] [CrossRef]
- Christy, A.A.; Tvedt, J.E.; Karstang, T.V.; Velapoldi, R.A. Low-pressure, automated, sample packing unit for diffuse reflectance infrared spectrometry. Rev. Sci. Instrum. 1988, 59, 423–426. [Google Scholar] [CrossRef]
- Chan, H.K.; Ongpipattanakul, B.; Au-Yeung, J. Aggregation of rhDNase Occurred During the Compression of KBr Pellets Used for FTIR Spectroscopy. Pharm. Res. 1996, 13, 238–242. [Google Scholar] [CrossRef]
- Banas, A.; Banas, K.; Bahou, M.; Moser, H.O.; Wen, L.; Yang, P.; Li, Z.J.; Cholewa, M.; Lim, S.K.; Lim, C.H. Post-blast detection of traces of explosives by means of Fourier transform infrared spectroscopy. Vib. Spectrosc. 2009, 51, 168–176. [Google Scholar] [CrossRef]
- Rani, S.; Sanghi, S.; Agarwal, A.; Seth, V.P. Study of optical band gap and FTIR spectroscopy of Li2O·Bi2O3·P2O5 glasses. Spectrochim. Acta A 2009, 74, 673–677. [Google Scholar] [CrossRef]
- Stelte, W.; Clemons, C.; Holm, J.K.; Ahrenfeldt, J.; Henriksen, U.B.; Sanadi, A.R. Fuel Pellets from Wheat Straw: The Effect of Lignin Glass Transition and Surface Waxes on Pelletizing Properties. Bioenergy Res. 2012, 5, 450–458. [Google Scholar] [CrossRef]
- Xu, L.; Cai, C.B.; Cui, H.F.; Ye, Z.H.; Yu, X.P. Rapid discrimination of pork in Halal and non-Halal Chinese ham sausages by Fourier transform infrared (FTIR) spectroscopy and chemometrics. Meat Sci. 2012, 92, 506–510. [Google Scholar] [CrossRef] [PubMed]
- Kijatkin, C.; Eggert, J.; Bock, S.; Berben, D.; Oláh, L.; Szaller, Z.; Kis, Z.; Imlau, M. Nonlinear Diffuse fs-Pulse Reflectometry of Harmonic Upconversion Nanoparticles. Photonics 2017, 4, 11. [Google Scholar] [CrossRef]
- Edinburgh Instruments Ltd. FLS1000 Photoluminescence Spectrometer. Available online: https://www.edinst.com/products/fls1000-photoluminescence-spectrometer (accessed on 18 June 2019).
- Shimadzu Corporation. RF-6000 Spectrofluorophotometer. 2019. Available online: https://www.shimadzu.com/an/molecular_spectro/fluoresence/rf6000/index.html (accessed on 18 June 2019).
- ISS Inc. K2 Multifrequency Cross-Correlation Phase and Modulation Fluorometer. 2019. Available online: http://www.iss.com/fluorescence/instruments/k2.html (accessed on 18 June 2019).
- Horiba Scientific Ltd. Fluorolog Steady State and Lifetime Modular Spectrofluorometer. Available online: https://www.horiba.com/en_en/products/detail/action/show/Product/fluorolog-1586/ (accessed on 18 June 2019).
- Horiba Scientific Ltd. FluoroMax Steady State and Lifetime Bench-top Spectrofluorometer. Available online: https://www.horiba.com/en_en/products/detail/action/show/Product/fluorescence-steady-state-and-lifetime-benchtop-spectrofluorometer-fluoromax-1576/ (accessed on 19 June 2019).
- Hitachi High-Technologies Corporation. Fluorescence Spectrophotometer F-7000. 2001, 2019. Available online: https://www.hitachi-hightech.com/global/product_detail/?pn=ana-f7000 (accessed on 19 June 2019).
- Lastek Pty. Ltd. Zolix OmniFluo Fluorescence Spectrometer. Available online: https://www.lastek.com.au/2182-zolix-omnifluo-fluorescence-spectrometer (accessed on 19 June 2019).
- PicoQuant GmbH. FluoTime 300 High Performance Fluorescence Lifetime and Steady State Spectrometer. Available online: https://www.picoquant.com/products/category/fluorescence-spectrometers/fluotime-300-high-performance-fluorescence-lifetime-spectrometer (accessed on 19 June 2019).
- JASCO Deutschland GmbH. FP-8000 Series. Available online: https://www.jasco.de/Spectroscopy/Fluoreszenz/FP-8000Serie (accessed on 19 June 2019).
- PerkinElmer Inc. FL 8500 Fluorescence Spectrophotometer with Spectrum FL Software. 1998–2019. Available online: https://www.perkinelmer.de/product/fl-8500-with-spectrum-fl-software-n4200030 (accessed on 19 June 2019).
- Agilent Technologies Inc. Fluorescence Systems Cary Eclipse Fluorescence Spectrophotometer. 2019. Available online: https://www.agilent.com/en/products/fluorescence/fluorescence-systems/cary-eclipse-fluorescence-spectrophotometer (accessed on 19 June 2019).
- PerkinElmer Inc. LAMBDA 950 UV/Vis Spectrophotometer. 1998–2019. Available online: https://www.perkinelmer.de/product/lambda-950-uv-vis-nir-spectrophotometer-l950 (accessed on 19 June 2019).
- Shimadzu Corporation. UV-3600 Plus UV-VIS-NIR Spectrophotometer. 2019. Available online: https://www.shimadzu.com/an/molecular_spectro/uv/uv-3600plus.html (accessed on 19 June 2019).
- Hitachi High-Technologies Corporation. Double Beam Spectrophotometer UH5300. 2001, 2019. Available online: https://www.hitachi-hightech.com/global/product_detail/?pn=ana-uh5300 (accessed on 19 June 2019).
- Agilent Technologies Inc. UV-Vis & UV-Vis-NIR Systems Cary 5000 UV-Vis-NIR. 2019. Available online: https://www.agilent.com/en/products/uv-vis-uv-vis-nir/uv-vis-uv-vis-nir-systems/cary-5000-uv-vis-nir (accessed on 19 June 2019).
- Seo, J.A.; Jeon, S.K.; Lee, J.Y. Acridine derived stable host material for long lifetime blue phosphorescent organic light-emitting diodes. Org. Electron. 2016, 34, 33–37. [Google Scholar] [CrossRef]
- Song, T.; Zhang, M.; Liu, Y.; Yang, J.; Gong, Z.; Yan, H.; Zhu, H.; Yan, D.; Liu, C.; Xu, C. Enhanced near infrared persistent luminescence of Zn2Ga2.98Ge0.75O8:Cr0.023+ nanoparticles by partial substitution of Ge4+ by Sn4+. RSC Adv. 2018, 8, 10954–10963. [Google Scholar] [CrossRef]
- Haase, M.; Schäfer, H. Upconverting Nanoparticles. Angew. Chem. Int. Ed. 2011, 50, 5808–5829. [Google Scholar] [CrossRef]
- Chen, G.; Qiu, H.; Prasad, P.N.; Chen, X. Upconversion Nanoparticles: Design, Nanochemistry, and Applications in Theranostics. Chem. Rev. 2014, 114, 5161–5214. [Google Scholar] [CrossRef]
- Jacquez, J.A.; McKeehan, W.; Huss, J.; Dimitroff, J.M.; Kuppenheim, H.F. An Integrating Sphere for Measuring Diffuse Reflectance in the Near Infrared. J. Opt. Soc. Am. 1955, 45, 781–785. [Google Scholar] [CrossRef]
- Goebel, D.G.; Caldwell, B.P.; Hammond, H.K. Use of an Auxiliary Sphere with a Spectroreflectometer to Obtain Absolute Reflectance. J. Opt. Soc. Am. 1966, 56, 783–788. [Google Scholar] [CrossRef]
- Adams, J.B. Interpretation of Visible and Near-Infrared Diffuse Reflectance Spectra of Pyroxenes and other Rock-Forming Minerals. In Infrared and Raman Spectroscopy of Lunar and Terrestrial Minerals; Karr, C., Ed.; Academic Press Inc.: London, UK, 1975; Chapter 4; pp. 91–115. [Google Scholar]
- Hobbs, P.C.D. (Ed.) Coatings, Filters, and Surface Finishes. In Building Electro-Optical Systems: Making It All Work; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; Chapter 5; pp. 180–207. [Google Scholar]
- Sklensky, A.F.; Anderson, J.H.; Wickersheim, K.A. Method for Obtaining Improved Diffuse Reflectance Spectra in the Near Infrared. Appl. Spectrosc. 1967, 21, 339–342. [Google Scholar] [CrossRef]
- Lindberg, J.D.; Snyder, D.G. Diffuse Reflectance Spectra of Several Clay Minerals. Am. Mineral. 1972, 57, 485–493. [Google Scholar]
- Weidner, V.R.; Hsia, J.J. Reflection properties of pressed polytetrafluoroethylene powder. J. Opt. Soc. Am. 1981, 71, 856–861. [Google Scholar] [CrossRef]
- Konrad, A.; Fries, T.; Gahn, A.; Kummer, F.; Herr, U.; Tidecks, R.; Samwer, K. Nanocrystalline Cubic Yttria: Synthesis and Optical Properties. Chem. Vap. Depos. 1999, 5, 207–210. [Google Scholar] [CrossRef]
- Herr, U.; Kaps, H.; Konrad, A. Physics of Nanocrystalline Luminescent Ceramics. In Interfacial Effects and Novel Properties of Nanomaterials; Lojkowski, W., Blizzard, J.R., Eds.; Solid State Phenomena; Trans Tech Publications: Stafa-Zurich, Switzerland, 2003; Volume 94, pp. 85–94. [Google Scholar]
- Kuo, T.W.; Liu, W.R.; Chen, T.M. High color rendering white light-emitting-diode illuminator using the red-emitting Eu2+-activated CaZnOS phosphors excited by blue LED. Opt. Express 2010, 18, 8187–8192. [Google Scholar] [CrossRef]
- Schimpke, T.; Mandl, M.; Stoll, I.; Pohl-Klein, B.; Bichler, D.; Zwaschka, F.; Strube-Knyrim, J.; Huckenbeck, B.; Max, B.; Müller, M.; et al. Phosphor-converted white light from blue-emitting InGaN microrod LEDs. Phys. Status Solidi A 2016, 213, 1577–1584. [Google Scholar] [CrossRef]
- Springsteen, A. Standards for the measurement of diffuse reflectance—An overview of available materials and measurement laboratories. Anal. Chim. Acta 1999, 380, 379–390. [Google Scholar] [CrossRef]
- Cáceres, D.; Colera, I.; Vergara, I.; González, R.; Román, E. Characterization of MgO thin films grown by rf-sputtering. Vacuum 2002, 67, 577–581. [Google Scholar] [CrossRef]
- Abazović, N.D.; Čomor, M.I.; Dramićanin, M.D.; Jovanović, D.J.; Ahrenkiel, S.P.; Nedeljković, J.M. Photoluminescence of Anatase and Rutile TiO2 Particles. J. Phys. Chem. B 2006, 110, 25366–25370. [Google Scholar] [CrossRef]
- Bergin, S. Pathlength Calibration of Integrating Sphere Based Gas Cells. Ph.D. Thesis, Cranfield University, Cranfield, UK, 2016. [Google Scholar]
- Image Engineering. RESTAN (Reflection Standard). Data Sheet. Available online: https://www.image-engineering.de/content/products/equipment/accessories/restan/Downloads/RESTAN_datasheet.pdf (accessed on 19 June 2019).
- Reade International Corp. Mohs’ Hardness (Typical) of Abrasives. 2018. Available online: https://www.reade.com/reade-resources/reference-educational/reade-reference-chart-particle-property- briefings/32-mohs-hardness-of-abrasives (accessed on 22 June 2019).
- Krishnan, R.; Dash, S.; Babu Rao, C.; Subba Rao, R.; Tyagi, A.K.; Raj, B. Laser induced structural and microstructural transformations of plasma sprayed Al2O3 coatings. Scr. Mater. 2001, 45, 693–700. [Google Scholar] [CrossRef]
- Miguel, A. Effect of air humidity on the evolution of permeability and performance of a fibrous filter during loading with hygroscopic and non-hygroscopic particles. J. Aerosol Sci. 2003, 34, 783–799. [Google Scholar] [CrossRef]
- Baikowski, S.A.S. Baikalox Regular Product Code CR30F. Data Sheet. Available online: www.baikowski.com/files/pdf/baikowski_cr30f.pdf (accessed on 22 June 2019).
- Sumitomo Chemical. Product Data: Aluminium Hydroxide, Aluminium Oxide (Alumina), High Purity Alumina (HPA), Activated Alumina / Hydralic Alumina. Data sheet. 2014. Available online: http://www.jinsan-corp.co.kr/upload/bbs/Sumitomo%20Chemical%20Alumina%20(ENG).pdf (accessed on 22 June 2019).
- Imerys Fused Minerals. SAND CASTING. 2014. Available online: http://www.imerys-fusedminerals.com/appl-fa-san.html (accessed on 22 June 2019).
- Image Engineering. Restan Plate White Reference Standard for Calibrating and Measuring. 2019. Available online: https://www.image-engineering.de/products/accessories/all/139-3rd-party-accessory/612-restan-plate?highlight=WyJyZXN0YW4iXQ== (accessed on 19 June 2019).
- Eggert, J. Berührungslose optische Sensorik an technischen Oberflächen: Neue Konzepte und die Rolle ultrakurzer Laserpulse. Ph.D. Thesis, Universität Osnabrück, Osnabrück, Germany, 2018. [Google Scholar]
- Valeeva, A.A.; Kozlova, E.A.; Vokhmintsev, A.S.; Kamalov, R.V.; Dorosheva, I.B.; Saraev, A.A.; Weinstein, I.A.; Rempel, A.A. Nonstoichiometric titanium dioxide nanotubes with enhanced catalytical activity under visible light. Sci. Rep. 2018, 8, 9607. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, V.N.; Glazkova, N.I.; Mikhaylov, R.V.; Serpone, N. In situ study of photo- and thermo-induced color centers in photochromic rutile TiO2 in the temperature range 90–270 K. Photochem. Photobiol. Sci. 2016, 15, 1289–1298. [Google Scholar] [CrossRef] [PubMed]
- Pal, M.; Pal, U.; Jiménez, J.M.G.Y.; Pérez-Rodríguez, F. Effects of crystallization and dopant concentration on the emission behavior of TiO2:Eu nanophosphors. Nanoscale Res. Lett. 2012, 7, 1. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, Y.; Sakuma, T.; Hirai, M. UV Emission from the Second Lowest 5d State in Ce3+: YAG. In Defects in Insulating Materials; Materials Science Forum; Matthews, G.E., Williams, R.T., Eds.; Trans Tech Publications: Stafa-Zurich, Switzerland, 1997; Volume 239–241, pp. 219–222. [Google Scholar]
- Gong, M.; Xiang, W.; Huang, J.; Yin, C.; Liang, X. Facile synthesis and optical properties of Ce:YAG polycrystalline ceramics with different SiO2 content. RSC Adv. 2015, 5, 75781–75786. [Google Scholar] [CrossRef]
- Imerys Fused Minerals Laufenburg GmbH, Treibacher Alodur. Technisches Datenblatt WFA/WSK/ZWSK/ZWSK AT Mikrokorn, Data sheet: TDB- LA 063 Rev. 2.
- Dieter Schmid Werkzeuge GmbH. Conversion Chart Abrasives—Grit Sizes. Available online: https://www.fine-tools.com/G10019.html (accessed on 22 June 2019).
- Trinkler, L.; Berzina, B.; Jakimovica, D.; Grabis, J.; Steins, I. UV-light induced luminescence processes in Al2O3 bulk and nanosize powders. Opt. Mater. 2010, 32, 789–795. [Google Scholar] [CrossRef]
- Trinkler, L.; Berzina, B.; Jakimovica, D.; Grabis, J.; Steins, I. Pecularities of photoluminescence of Al2O3 bulk and nanoszize powders at low temperatures. Opt. Mater. 2011, 33, 817–822. [Google Scholar] [CrossRef]
- Edinburgh Instruments Ltd. Spectrometer Components. In FLS980 User Guide; Issue No. 2 for Systems Delivered after October 2013; Edinburgh Instruments Ltd.: Livingston, UK, 2013; Chapter 2; pp. 13–30. [Google Scholar]
- OSRAM GmbH. XBO for Cinema Projection. 2019. Available online: https://www.osram.com/pia/ecat/XBO-XBO-Specialty%20lamps/com/en/GPS01_1028548/PP_EUROPE_Europe_eCat/ZMP_1006152/ (accessed on 23 June 2019).
- Hamamatsu Photonics K.K. Photomultiplier tube R928. Available online: http://www.hamamatsu.com/eu/en/product/category/3100/3001/R928/index.html (accessed on 23 June 2019).
- Randall, J.T.; Wilkins, M.H.F. Phosphorescence and electron traps I. The study of trap distributions. Proc. R. Soc. Lond. A 1945, 184, 365–389. [Google Scholar]
- Randolph, T.T. Phosphorescent Luminous Door Knobs Cover. U.S. Patent 5,008,551, 16 April 1991. [Google Scholar]
- Kato, K.; Tsutai, I.; Kamimura, T.; Kaneko, F.; Shinbo, K.; Ohta, M.; Kawakami, T. Thermoluminescence properties of SrAl2O4:Eu sputtered films with long phosphorescence. J. Lumin. 1999, 82, 213–220. [Google Scholar] [CrossRef]
- Katsumata, T.; Mochida, S.; Kubo, H.; Usui, Y.; Aizawa, H.; Komuro, S.; Morikawa, T. Fluorescence thermometer based on phase angle measurement. Proc. SPIE 2005, 5855, 727–730. [Google Scholar]
- Akmehmet, G.I.; Šturm, S.; Bocher, L.; Kociak, M.; Ambrožič, B.; Ow-Yang, C.W. Structure and Luminescence in Long Persistence Eu, Dy, and B Codoped Strontium Aluminate Phosphors: The Boron Effect. J. Am. Ceram. Soc. 2016, 99, 2175–2180. [Google Scholar] [CrossRef]
- Yen, W.M.; Shionoya, S.; Yamamoto, H. Phosphor Handbook, 2nd ed.; Yen, W.M., Shionoya, S., Yamamoto, H., Eds.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- López, R.; Gómez, R. Band-gap energy estimation from diffuse reflectance measurements on sol-gel and commercial TiO2: A comparative study. J. Sol-Gel Sci. Technol. 2012, 61, 1–7. [Google Scholar] [CrossRef]
- Butler, M.A. Photoelectrolysis and physical properties of the semiconducting electrode WO3. J. Appl. Phys. 1977, 48, 1914–1920. [Google Scholar] [CrossRef]
- Wooten, F. Interband Transitions. In Optical Properties of Solids; Wooten, F., Ed.; Academic Press Inc.: London, UK, 1972; Chapter 5; pp. 108–172. [Google Scholar]
- Shahane, G.; More, B.; Rotti, C.; Deshmukh, L. Studies on chemically deposited CdS1-xSex mixed thin films. Mater. Chem. Phys. 1997, 47, 263–267. [Google Scholar] [CrossRef]
- Li, P.; Ouyang, S.; Xi, G.; Kako, T.; Ye, J. The Effects of Crystal Structure and Electronic Structure on Photocatalytic H2 Evolution and CO2 Reduction over Two Phases of Perovskite-Structured NaNbO3. J. Phys. Chem. C 2012, 116, 7621–7628. [Google Scholar] [CrossRef]
- Li, P.; Ouyang, S.; Zhang, Y.; Kako, T.; Ye, J. Surface-coordination-induced selective synthesis of cubic and orthorhombic NaNbO3 and their photocatalytic properties. J. Mater. Chem. A 2013, 1, 1185–1191. [Google Scholar] [CrossRef]
- Hassanien, A.S.; Akl, A.A. Influence of composition on optical and dispersion parameters of thermally evaporated non-crystalline Cd50S50-xSex thin films. J. Alloys Compd. 2015, 648, 280–290. [Google Scholar] [CrossRef]
- Morales, A.E.; Mora, E.S.; Pal, U. Use of diffuse reflectance spectroscopy for optical characterization of un-supported nanostructures. Rev. Mex. Fis. Suppl. 2007, 53, 18–22. [Google Scholar]
- Tauc, J.; Grigorovici, R.; Vancu, A. Optical Properties and Electronic Structure of Amorphous Germanium. Phys. Status Solidi B 1966, 15, 627–637. [Google Scholar] [CrossRef]
- Tauc, J. Optical properties and electronic structure of amorphous Ge and Si. Mater. Res. Bull. 1968, 3, 37–46. [Google Scholar] [CrossRef]
- Wang, Z.; Kijatkin, C.; Urban, A.; Haase, M.; Imlau, M.; Kömpe, K. Nonlinear Optical Potassium Niobate Nanocrystals as Harmonic Markers: The Role of Precursors and Stoichiometry in Hydrothermal Synthesis. Nanoscale 2018, 10, 10713–10720. [Google Scholar] [CrossRef]
- Klingshirn, C.F. (Ed.) Forbidden Excitation Transitions. In Semiconductor Optics; Graduate Texts in Physics; Springer: Berlin/Heidelberg, Germany, 2012; Chapter 13.2; pp. 346–354. [Google Scholar]
- Glassford, K.M.; Chelikowsky, J.R. Structural and electronic properties of titanium dioxide. Phys. Rev. B 1992, 46, 1284–1298. [Google Scholar] [CrossRef] [PubMed]
- Amtout, A.; Leonelli, R. Optical properties of rutile near its fundamental band gap. Phys. Rev. B 1995, 51, 6842–6851. [Google Scholar] [CrossRef] [PubMed]
- Scanlon, D.O.; Dunnill, C.W.; Buckeridge, J.; Shevlin, S.A.; Logsdail, A.J.; Woodley, S.M.; Catlow, C.R.A.; Powell, M.J.; Palgrave, R.G.; Parkin, I.P.; et al. Band alignment of rutile and anatase TiO2. Nat. Mater. 2013, 12, 798–801. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kollodialer Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. (Eds.) Absorption and Scattering of Light by Small Particles; John Wiley & Sons Inc.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 1983/2004.
- Rayleigh, F.R.S. On the Electromagnetic Theory of Light. Philos. Mag. 1881, 12, 81–101. [Google Scholar] [CrossRef]
- Rayleigh, F.R.S. On the Transmission of Light through an Atmosphere containing Small Particles in Suspension, and on the Origin of the Blue of the Sky. Philos. Mag. 1899, 47, 375–384. [Google Scholar] [CrossRef]
- Roke, S.; Gonella, G. Nonlinear Light Scattering and Spectroscopy of Particles and Droplets in Liquids. Annu. Rev. Phys. Chem. 2012, 63, 353–378. [Google Scholar] [CrossRef]
- Geng, Y.L.; Wu, X.B.; Li, L.W.; Guan, B.R. Mie scattering by a uniaxial anisotropic sphere. Phys. Rev. E 2004, 70, 056609-1–056609-8. [Google Scholar] [CrossRef]
- Qiu, C.; Gao, L.; Joannopoulos, J.D.; Soljačić, M. Light scattering from anisotropic particles: Propagation, localization, and nonlinearity. Laser Photon. Rev. 2009, 4, 268–282. [Google Scholar] [CrossRef]
- Toon, O.B.; Ackerman, T.P. Algorithms for the calculation of scattering by stratified spheres. Appl. Opt. 1981, 20, 3657–3660. [Google Scholar] [CrossRef]
- Mackowski, D.W.; Altenkirch, R.A.; Menguc, M.P. Internal absorption cross sections in a stratified sphere. Appl. Opt. 1990, 29, 1551–1559. [Google Scholar] [CrossRef] [PubMed]
- Yang, W. Improved recursive algorithm for light scattering by a multilayered sphere. Appl. Opt. 2003, 42, 1710–1720. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Wang, H.; Yu, B.; Xu, Y.; Shen, J. Improved algorithm of light scattering by a coated sphere. China Part. 2007, 5, 230–236. [Google Scholar] [CrossRef]
- Waterman, P. Matrix Formulation of Electromagnetic Scattering. Proc. IEEE 1965, 53, 805–812. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Mackowski, D.W. T-matrix computations of light scattering by nonspherical particles: A review. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 535–575. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Hovenier, J.W.; Travis, L.D. (Eds.) Light Scattering by Nonspherical Particles: Theory, Measurements, and Applications; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Xu, Y.L.; Gustafson, B.Å.S. A generalized multiparticle Mie-solution: Further experimental verification. J. Quant. Spectrosc. Radiat. Transf. 2001, 70, 395–419. [Google Scholar] [CrossRef]
- Pellegrini, G.; Mattei, G.; Bello, V.; Mazzoldi, P. Interacting metal nanoparticles: Optical properties from nanoparticle dimers to core-satellite systems. Mater. Sci. Eng. C 2007, 27, 1347–1350. [Google Scholar] [CrossRef]
- Mackowski, D.W.; Mishchenko, M.I. Direct simulation of multiple scattering by discrete random media illuminated by Gaussian beams. Phys. Rev. A 2011, 83, 013804-1–013804-9. [Google Scholar] [CrossRef]
- Egel, A.; Pattelli, L.; Mazzamuto, G.; Wiersma, D.S.; Lemmer, U. CELES: CUDA-accelerated simulation of electromagnetic scattering by large ensembles of spheres. J. Quant. Spectrosc. Radiat. Transf. 2017, 199, 103–110. [Google Scholar] [CrossRef]
- Drolen, B.L.; Tien, C.L. Independent and dependent scattering in packed-sphere systems. J. Thermophys. Heat Transf. 1987, 1, 63–68. [Google Scholar] [CrossRef]
- Hottel, H.C.; Sarofim, A.F.; Dalzell, W.H.; Vasalos, I.A. Optical Properties of Coatings. Effect of Pigment Concentration. AIAA J. 1971, 9, 1895–1898. [Google Scholar] [CrossRef]
- Wang, B.X.; Zhao, C.Y. Effect of dependent scattering on light absorption in highly scattering random media. Int. J. Heat Mass Transf. 2018, 125, 1069–1078. [Google Scholar] [CrossRef]
- Simon, J.C. Dependent scattering and radiative transfer in dense inhomogeneous media. Phys. A 1997, 241, 77–81. [Google Scholar] [CrossRef]
- Yamada, Y.; Cartigny, J.D.; Tien, C.L. Radiative Transfer With Dependent Scattering by Particles: Part 2—Experimental Investigation. J. Heat Transf. 1986, 108, 614–618. [Google Scholar] [CrossRef]
- Vargas, W.E. Diffuse radiation intensity propagating through a particulate slab. J. Opt. Soc. Am. A 1999, 16, 1362–1372. [Google Scholar] [CrossRef]
- Kubelka, P.; Munk, F. Ein Beitrag zur Optik der Farbanstriche. Z. Tech. Phys. 1931, 12, 593–601. [Google Scholar]
- Gunde, M.K.; Logar, J.K.; Orel, Z.C.; Orel, B. Application of the Kubelka–Munk Theory to Thickness-Dependent Diffuse Reflectance of Black Paints in the Mid-IR. Appl. Spectrosc. 1995, 49, 623–629. [Google Scholar] [CrossRef]
- Vargas, W.E.; Niklasson, G.A. Applicability conditions of the Kubelka–Munk theory. Appl. Opt. 1997, 36, 5580–5586. [Google Scholar] [CrossRef]
- Murphy, A.B. Band-gap determination from diffuse reflectance measurements of semiconductor films, and application to photoelectrochemical water-splitting. Sol. Energy Mater. Sol. Cells 2007, 91, 1326–1337. [Google Scholar] [CrossRef]
- Shi, Z.; Anderson, C.A. Application of Monte Carlo Simulation-Based Photon Migration for Enhanced Understanding of Near-Infrared (NIR) Diffuse Reflectance. Part I: Depth of Penetration in Pharmaceutical Materials. J. Pharm. Sci. 2010, 99, 2399–2412. [Google Scholar] [CrossRef]
- Yang, L.; Kruse, B. Revised Kubelka-Munk theory. I. Theory and application. J. Opt. Soc. Am. A 2004, 21, 1933–1941. [Google Scholar] [CrossRef] [PubMed]
- International Organization for Standardization. Representation of Results of Particle Size Analysis—Part 2: Calculation of Average Particle Size/Diameters and Moments from Particle Size Distributions; ISO 9276-2; International Standard: Geneva, Switzerland, 2014. [Google Scholar]
- Maheu, B.; Letoulouzan, J.N.; Gouesbet, G. Four-flux models to solve the scattering transfer equation in terms of Lorenz-Mie parameters. Appl. Opt. 1984, 23, 3353–3362. [Google Scholar] [CrossRef] [PubMed]
- Vargas, W.E.; Niklasson, G.A. Forward average path-length parameter in four-flux radiative transfer models. Appl. Opt. 1997, 36, 3735–3738. [Google Scholar] [CrossRef] [PubMed]
- Vargas, W.E.; Niklasson, G.A. Intensity of diffuse radiation in particulate media. J. Opt. Soc. Am. A 1997, 14, 2253–2262. [Google Scholar] [CrossRef]
- Liu, L.; Gong, R.; Huang, D.; Nie, Y.; Liu, C. Calculation of emittance of a coating layer with the Kubelka-Munk theory and the Mie-scattering model. J. Opt. Soc. Am. A 2005, 22, 2424–2429. [Google Scholar] [CrossRef]
- Kerker, M. The Scattering of Light and Other Electromagnetic Radiation; Physical Chemistry; Loebl, E.M., Ed.; Academic Press Inc.: New York, NY, USA, 1969; Volume 16. [Google Scholar]
- Schäfer, J.P. Implementierung und Anwendung analytischer und numerischer Verfahren zur Lösung der Maxwellgleichungen für die Untersuchung der Lichtausbreitung in biologischem Gewebe. Ph.D. Thesis, Universität Ulm, Ulm, Germany, 2011. [Google Scholar]
- Hoo, C.M.; Starostin, N.; West, P.; Mecartney, M.L. A comparison of atomic force microscopy (AFM) and dynamic light scattering (DLS) methods to characterize nanoparticle size distributions. J. Nanopart. Res. 2008, 10, 89–96. [Google Scholar] [CrossRef]
- Stöber, W.; Fink, A. Controlled Growth of Monodisperse Silica Spheres in the Micron Size Range. J. Colloid Interface Sci. 1968, 26, 62–69. [Google Scholar] [CrossRef]
- Hunt, J.R. Prediction of Oceanic Particle Size Distributions from Coagulation and Sedimentation Mechanisms. In Particulates in Water; Kavanaugh, M.C., Leckie, J.O., Eds.; Advances in Chemistry; American Chemical Society: Washington, DC, USA, 1980; Volume 189, Chapter 11; pp. 243–257. [Google Scholar]
- Lawler, D.F. Particle size distributions in treatment processes: Theory and practice. Water. Sci. Technol. 1997, 36, 15–23. [Google Scholar] [CrossRef]
- CPS Instruments Europe. Disc Centrifuge. 2001–2013. Available online: http://www.cpsinstruments.eu/centrifuge.html (accessed on 25 June 2019).
- Brookhaven Instruments Corporation. BI-XDC Particle Size Analyzer X-ray Disc Centrifuge. 2019. Available online: https://brookhaveninstruments.com/bi-xdc (accessed on 25 June 2019).
- Siefke, T.; Kroker, S.; Pfeiffer, K.; Puffky, O.; Dietrich, K.; Franta, D.; Ohlídal, I.; Szeghalmi, A.; Kley, E.B.; Tünnermann, A. Materials Pushing the Application Limits of Wire Grid Polarizers further into the Deep Ultraviolet Spectral Range. Adv. Opt. Mater. 2016, 4, 1780–1786. [Google Scholar] [CrossRef]
- Srikant, V.; Clarke, D.R. On the optical band gap of zinc oxide. J. Appl. Phys. 1998, 83, 5447–5451. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, S.; Wang, K.; Luo, X. Measurement and numerical studies of optical properties of YAG:Ce phosphor for white light-emitting diode packaging. Appl. Opt. 2010, 49, 247–257. [Google Scholar] [CrossRef] [PubMed]
- Kijatkin, C. Ultrafast Photon Management: The Power of Harmonic Nanocrystalys in Nonlinear Spectroscopy and Beyond. Ph.D. Thesis, Universität Osnabrück, Osnabrück, Germany, 2019. [Google Scholar]
- Marbach, R.; Heise, H.M. Optical diffuse reflectance accessory for measurements of skin tissue by near-Infrared spectroscopy. Appl. Opt. 1995, 34, 610–621. [Google Scholar] [CrossRef] [PubMed]
- Synopsys Inc. LightTools Illumination Design Software. 2019. Available online: https://www.synopsys.com/optical-solutions/lighttools.html (accessed on 25 June 2019).
- Wu, H.; Jenkins, D.R. Phosphor modeling and characterization. Opt. Eng. 2014, 53, 114107-1–114107-5. [Google Scholar] [CrossRef]
- Flock, S.T.; Wilson, B.C.; Patterson, M.S. Monte Carlo Modeling of Light Propagation in Highly Scattering Tissues–II: Comparison with Measurements in Phantoms. IEEE Trans. Biomed. Eng. 1989, 36, 1169–1173. [Google Scholar] [CrossRef]
- Peters, V.G.; Wyman, D.R.; Patterson, M.S.; Frank, G.L. Optical properties of normal and diseased human breast tissues in the visible and near infrared. Phys. Med. Biol. 1990, 35, 1317–1334. [Google Scholar] [CrossRef] [PubMed]
- Hanrahan, P.; Krueger, W. Reflection from Layered Surfaces due to Subsurface Scattering. In Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’93, Anaheim, CA, USA, 2–6 August 1993; ACM: New York, NY, USA, 1993; pp. 165–174. [Google Scholar]
- Hammer, M.; Roggan, A.; Schweitzer, D.; Müller, G. Optical properties of ocular fundus tissues—An in vitro study using the double-integrating-sphere technique and inverse Monte Carlo simulation. Phys. Med. Biol. 1995, 40, 963–978. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML – Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Prog. Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Yaroslavsky, A.N.; Yaroslavsky, I.V.; Goldbach, T.; Schwarzmaier, H.J. Influence of the scattering phase function approximation on the optical properties of blood determined from the integrating sphere measurements. J. Biomed. Opt. 1999, 4, 47–53. [Google Scholar] [CrossRef]
- Karppinen, M.; Kataja, K.; Mäkinen, J.T.; Juuso, S.; Rajaniemi, H.J.; Pääkkönen, P.; Turunen, J.; Rantala, J.T.; Karioja, P. Wireless infrared data links: Ray-trace simulations of diffuse channels and demonstration of diffractive element for multibeam transmitters. Opt. Eng. 2002, 41, 899–910. [Google Scholar] [CrossRef]
- Ma, X.; Lu, J.Q.; Brock, R.S.; Jacobs, K.M.; Yang, P.; Hu, X.H. Determination of complex refractive index of polystyrene microspheres from 370 to 1610 nm. Phys. Med. Biol. 2003, 48, 4165–4172. [Google Scholar] [CrossRef]
- Péry, E.; Blondel, W.C.P.M.; Thomas, C.; Guillemin, F. Monte Carlo modeling of multilayer phantoms with multiple fluorophores: Simulation algorithm and experimental validation. J. Biomed. Opt. 2009, 14, 024048-1–024048-11. [Google Scholar]
- Rievers, B.; Lämmerzahl, C.; Dittus, H. Modeling of Thermal Perturbations Using Raytracing Method with Preliminary Results for a Test Case Model of the Pioneer 10/11 Radioisotopic Thermal Generators. Space Sci. Rev. 2010, 151, 123–133. [Google Scholar] [CrossRef]
- Bish, S.F.; Sharma, M.; Wang, Y.; Triesault, N.J.; Reichenberg, J.S.; Zhang, J.X.; Tunnell, J.W. Handheld Diffuse Reflectance Spectral Imaging (DRSi) for in-vivo characterization of skin. Biomed. Opt. Express 2014, 5, 573–586. [Google Scholar] [CrossRef] [PubMed]
- Solodovnyk, A.; Riedel, D.; Lipovšek, B.; Osvet, A.; Gast, J.; Stern, E.; Forberich, K.; Batentschuk, M.; Krč, J.; Topič, M.; et al. Determination of the complex refractive index of powder phosphors. Opt. Mater. Express 2017, 7, 2943–2954. [Google Scholar] [CrossRef]
- Xie, B.; Cheng, Y.; Hao, J.; Shu, W.; Wang, K.; Luo, X. Precise optical modeling of quantum dots for white light-emitting diodes. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef]
- Meretska, M.L.; Uppu, R.; Vissenberg, G.; Lagendijk, A.; Ijzerman, W.L.; Vos, W.L. Analytical modeling of light transport in scattering materials with strong absorption. Opt. Express 2017, 25, A906–A921. [Google Scholar] [CrossRef]
- Nesse, W.D. (Ed.) Refractometry. In Introduction to Optical Mineralogy, 2nd ed.; Oxford University Press, Inc.: New York, NY, USA, 1991; Chapter 3; pp. 25–33. [Google Scholar]
- Cargille-Sacher Laboratories Inc. About Reference Standards. 2003–2018. Available online: https://cargille.com/about-reference-standards/ (accessed on 25 June 2019).
- Van Hilten, D. Refractive indices of minerals through the microscope: A simpler method by oblique observation. Am. Mineral. 1981, 66, 1089–1091. [Google Scholar]
- Schmidt, W.; Baier, E. (Eds.) C: Bestimmung der Brechzahl. In Lehrbuch der Mineralogie; Lehrbücher und Monographien aus dem Gebiet der exakten Wissenschaften—Minealogisch-geotechnische Reihe; Springer: Basel, Switzerland, 1955; Volume 6, Chapter 3; pp. 90–93. [Google Scholar]
- Klockmann, F. (Ed.) Capitel III: § 4. Methoden zur Bestimmung der Brechungsindices. In Lehrbuch der Mineralogie; Reprint of the Original from 1903; TP Verone Publishing House Ltd.: Nikosia, Cyprus, 2017; pp. 152–161. [Google Scholar]
- Synopsys Inc. Illumination in LightTools; Introduction to LightTools Training. 2012. Available online: https://nanoptics.files.wordpress.com/2012/08/illumination-in-lighttools.pdf (accessed on 23 July 2019).
- Luo, J.L.; Wang, S.F.; Liu, W.; Tian, C.X.; Wu, J.W.; Zu, X.T.; Zhou, W.L.; Yuan, X.D.; Xiang, X. Influence of different aluminum salts on the photocatalytic properties of Al doped TiO2 nanoparticles towards the degradation of AO7 dye. Sci. Rep. 2017, 7, 1–16. [Google Scholar] [CrossRef]
- Zhao, Z.; Kou, T.; Zhang, L.; Zhai, S.; Wang, W.; Wang, Y. Dealloying induced N-doping in spindle-like porous rutile TiO2 for enhanced visible light photocatalytic activity. Corros. Sci. 2018, 137, 204–211. [Google Scholar] [CrossRef]

| Fluorescence Spectrometer | Ref. |
| FLS1000, Edinburgh Instruments, Ltd. | [42] |
| RF-6000, Shimadzu Corp. | [43] |
| K2 Fluorometer, ISS, Inc. | [44] |
| Fluorolog, HORIBA Scientific, Ltd. | [45] |
| FluoroMax, HORIBA Scientific, Ltd. | [46] |
| F-7000, Hitachi High-Technologies Corp. | [47] |
| OmniFluo, Zolix Instruments Co., Ltd. | [48] |
| FluoTime 300, PicoQuant GmbH | [49] |
| FP-8000 Series, JASCO Deutschland GmbH | [50] |
| FL 8500, PerkinElmer, Inc. | [51] |
| Cary Eclipse, Agilent Technologies, Inc. | [52] |
| Double-Beam Spectrometer | Ref. |
| LAMBDA 950 UV/VIS, PerkinElmer, Inc. | [53] |
| UV-3600 Plus UV-VIS-NIR, Shimadzu Corp. | [54] |
| UH5300, Hitachi High-Technologies Corp. | [55] |
| Cary 5000 UV-Vis-NIR, Agilent Technologies, Inc. | [56] |
| ws | Limits |
|---|---|
| MgO | |
| TiO | |
| BaSO | |
| Sintered PTFE | |
| -AlO |
|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bock, S.; Kijatkin, C.; Berben, D.; Imlau, M. Absorption and Remission Characterization of Pure, Dielectric (Nano-)Powders Using Diffuse Reflectance Spectroscopy: An End-To-End Instruction. Appl. Sci. 2019, 9, 4933. https://doi.org/10.3390/app9224933
Bock S, Kijatkin C, Berben D, Imlau M. Absorption and Remission Characterization of Pure, Dielectric (Nano-)Powders Using Diffuse Reflectance Spectroscopy: An End-To-End Instruction. Applied Sciences. 2019; 9(22):4933. https://doi.org/10.3390/app9224933
Chicago/Turabian StyleBock, Sergej, Christian Kijatkin, Dirk Berben, and Mirco Imlau. 2019. "Absorption and Remission Characterization of Pure, Dielectric (Nano-)Powders Using Diffuse Reflectance Spectroscopy: An End-To-End Instruction" Applied Sciences 9, no. 22: 4933. https://doi.org/10.3390/app9224933
APA StyleBock, S., Kijatkin, C., Berben, D., & Imlau, M. (2019). Absorption and Remission Characterization of Pure, Dielectric (Nano-)Powders Using Diffuse Reflectance Spectroscopy: An End-To-End Instruction. Applied Sciences, 9(22), 4933. https://doi.org/10.3390/app9224933




