Diffuse Correlation Spectroscopy at Short Source-Detector Separations: Simulations, Experiments and Theoretical Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiments
2.1.1. Instrumentation
2.1.2. Liquid Phantoms
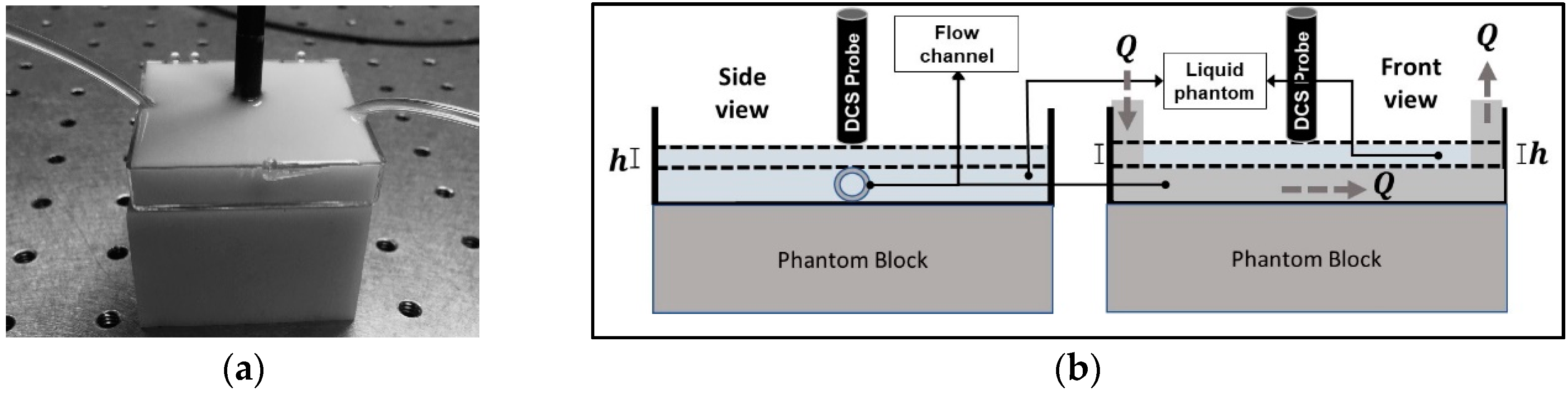
2.1.3. Flow-Chamber Description
2.1.4. Phantom Preparation and Measurement Protocol
2.1.5. Data Acquisition
2.2. Monte Carlo Simulations of Correlation Transport
2.3. Tissue Models Simulated
2.3.1. Semi-Infinite Models
2.3.2. Three-Layer Models
2.4. Theoretical Analyses
2.5. Goodness-of-Fits: Fit Residuals
3. Results
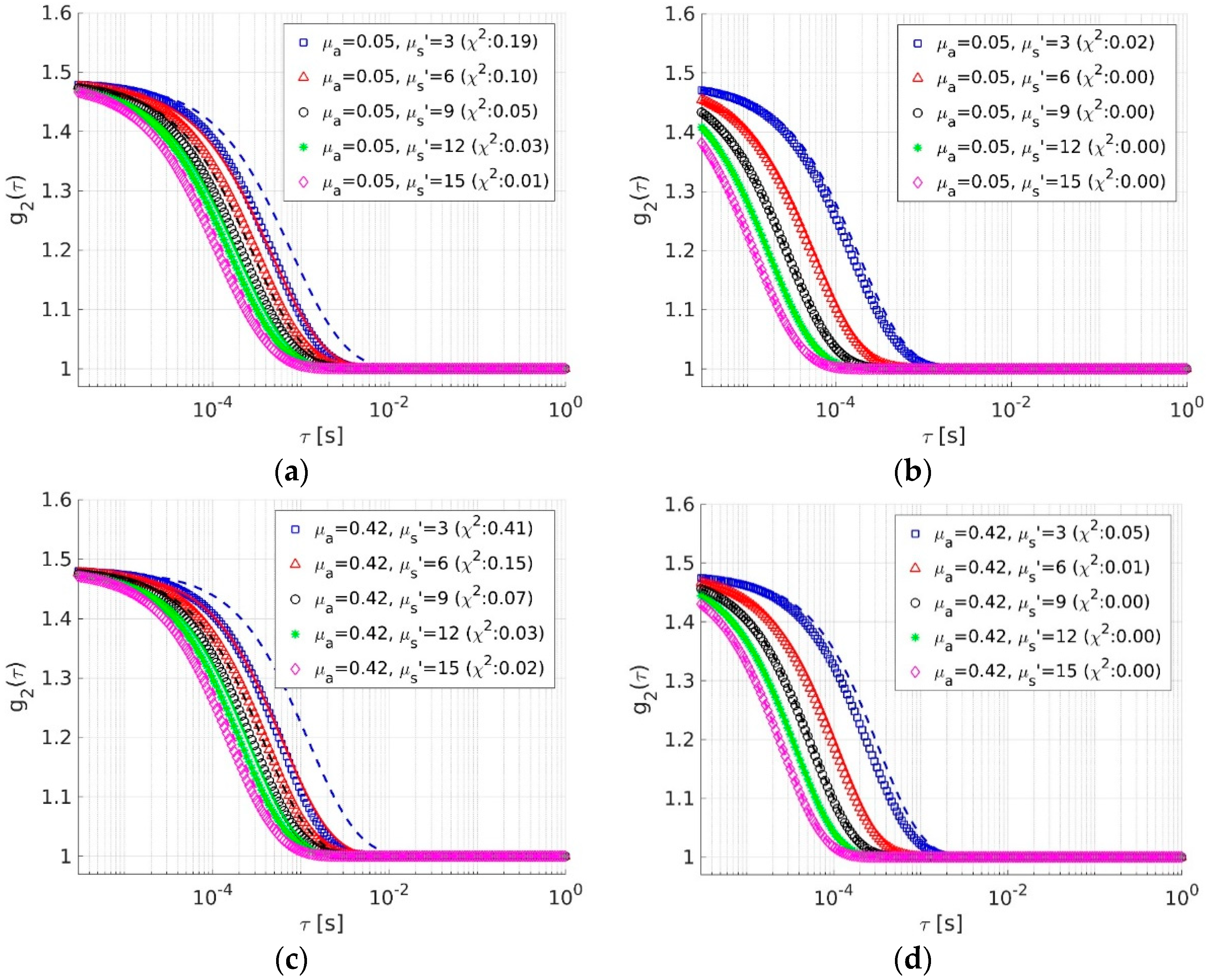
3.1. Simulations in Semi-Infinite Phantoms
3.1.1. Forward Theoretical Calculations vs. Simulations
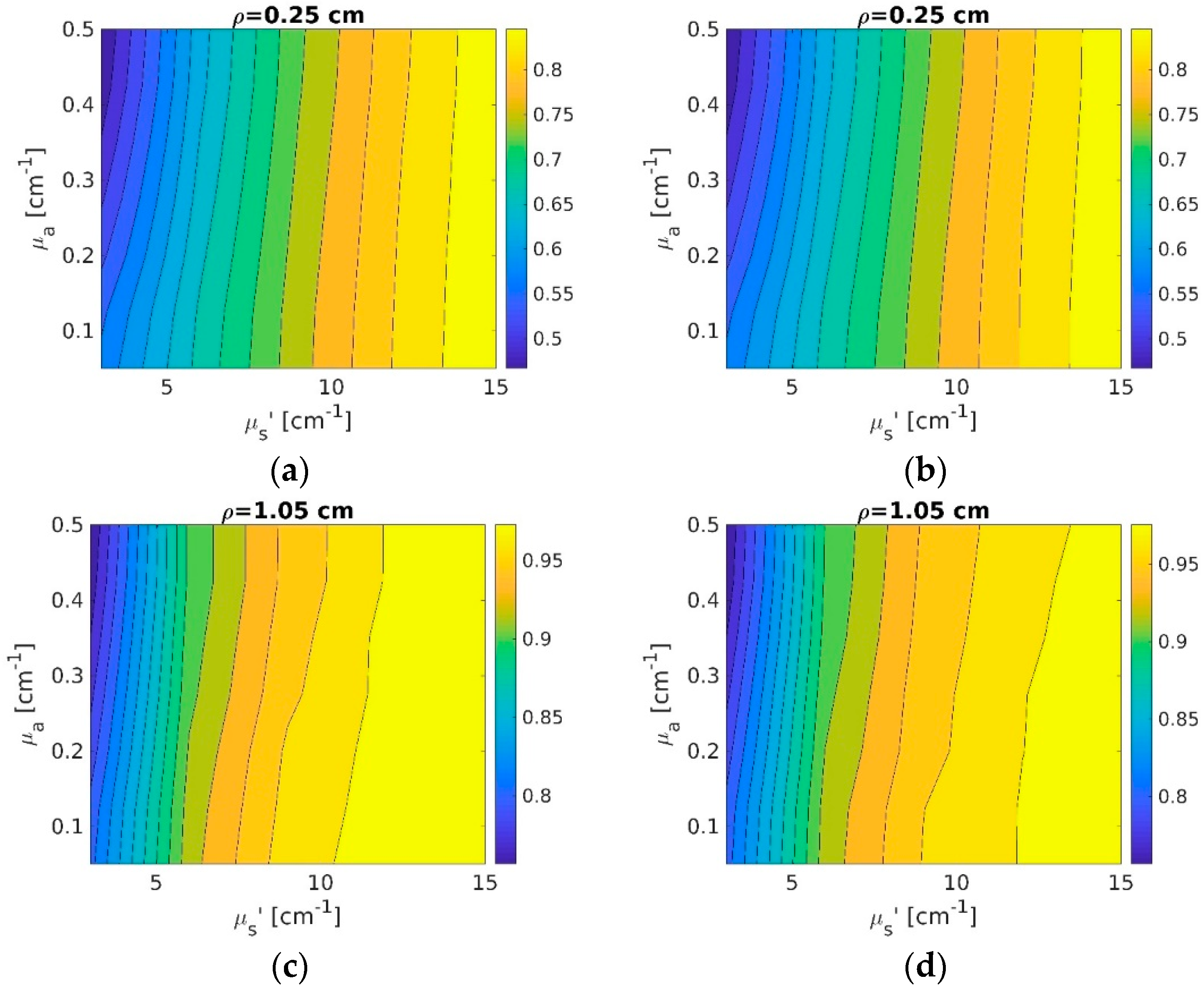
3.1.2. Fitting Simulations Using Theory
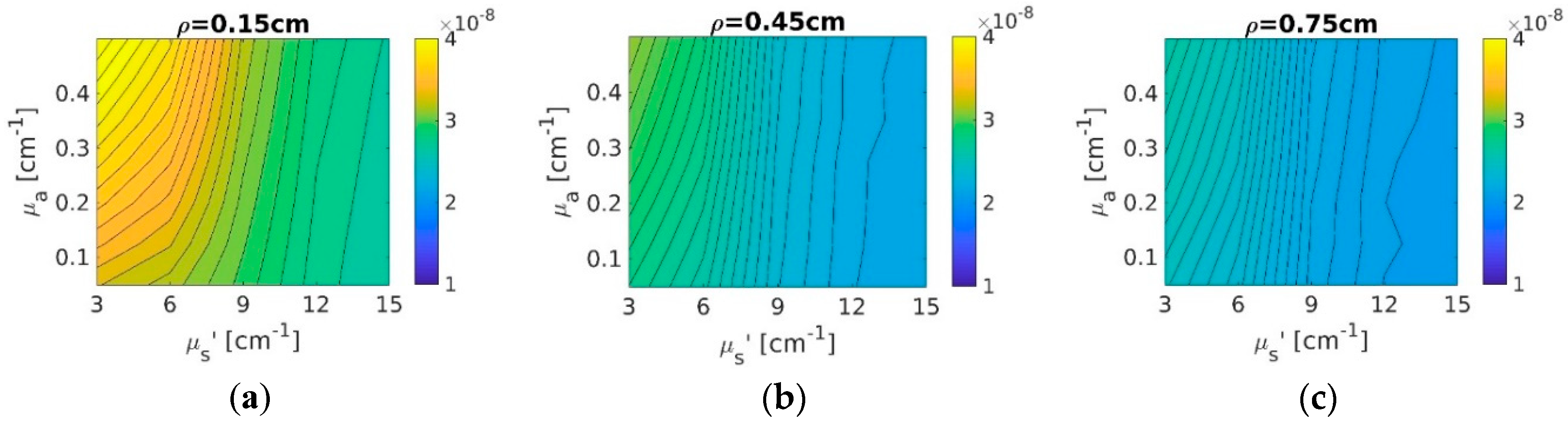
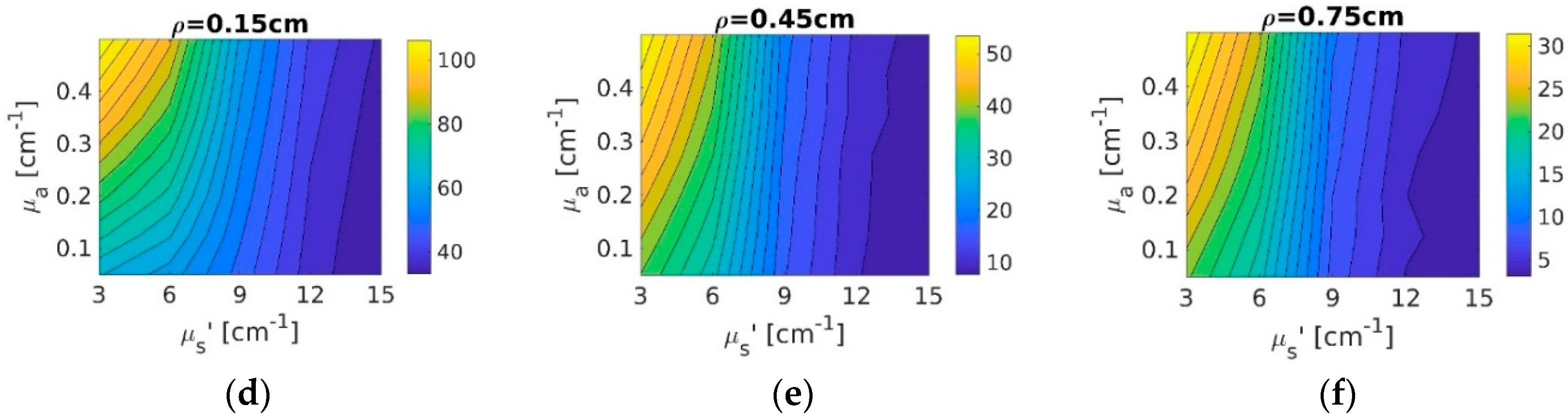
3.1.3. Errors from Theoretical Fits
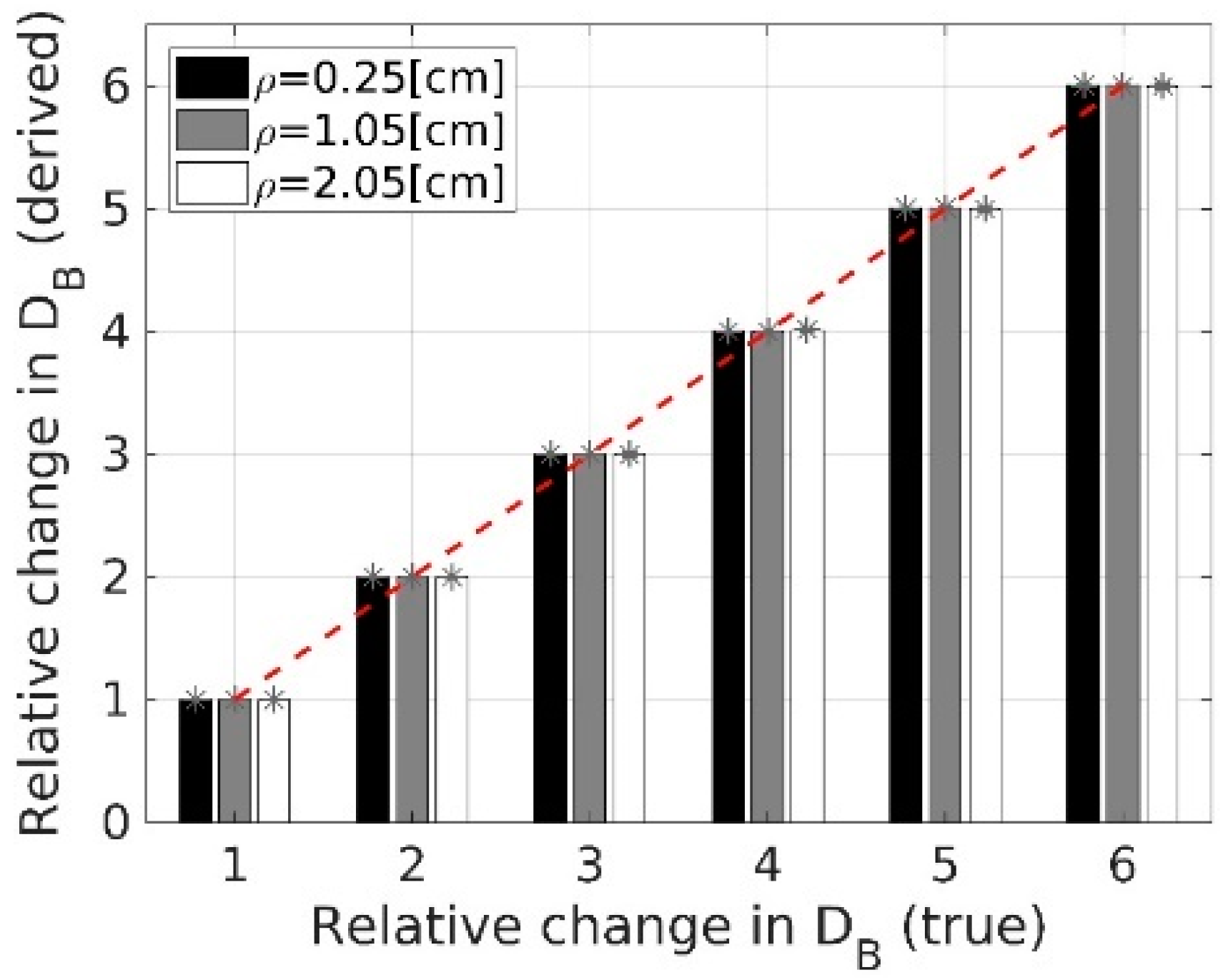
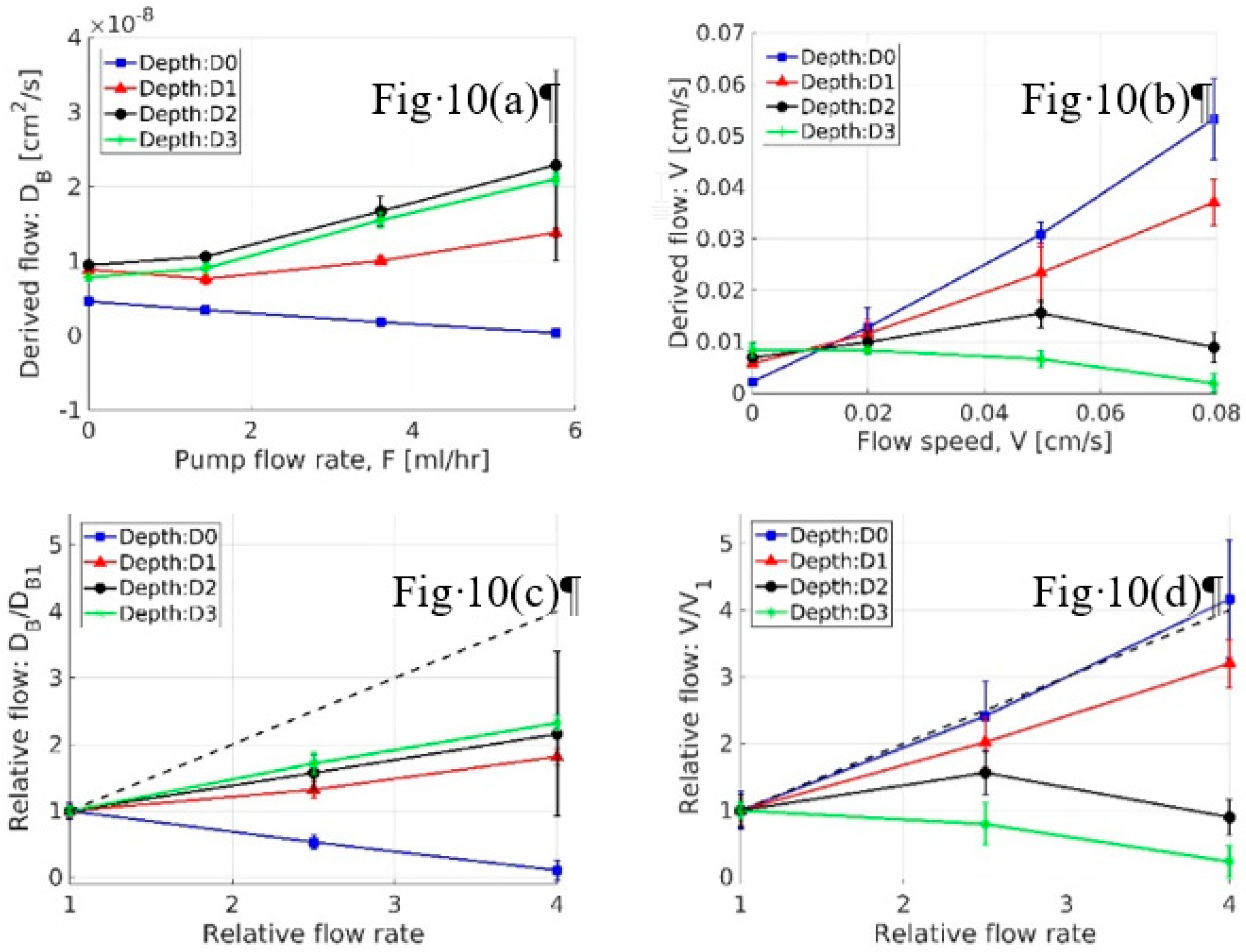
3.1.4. Relative Changes in Flow Coefficients: Simulations vs. Theory
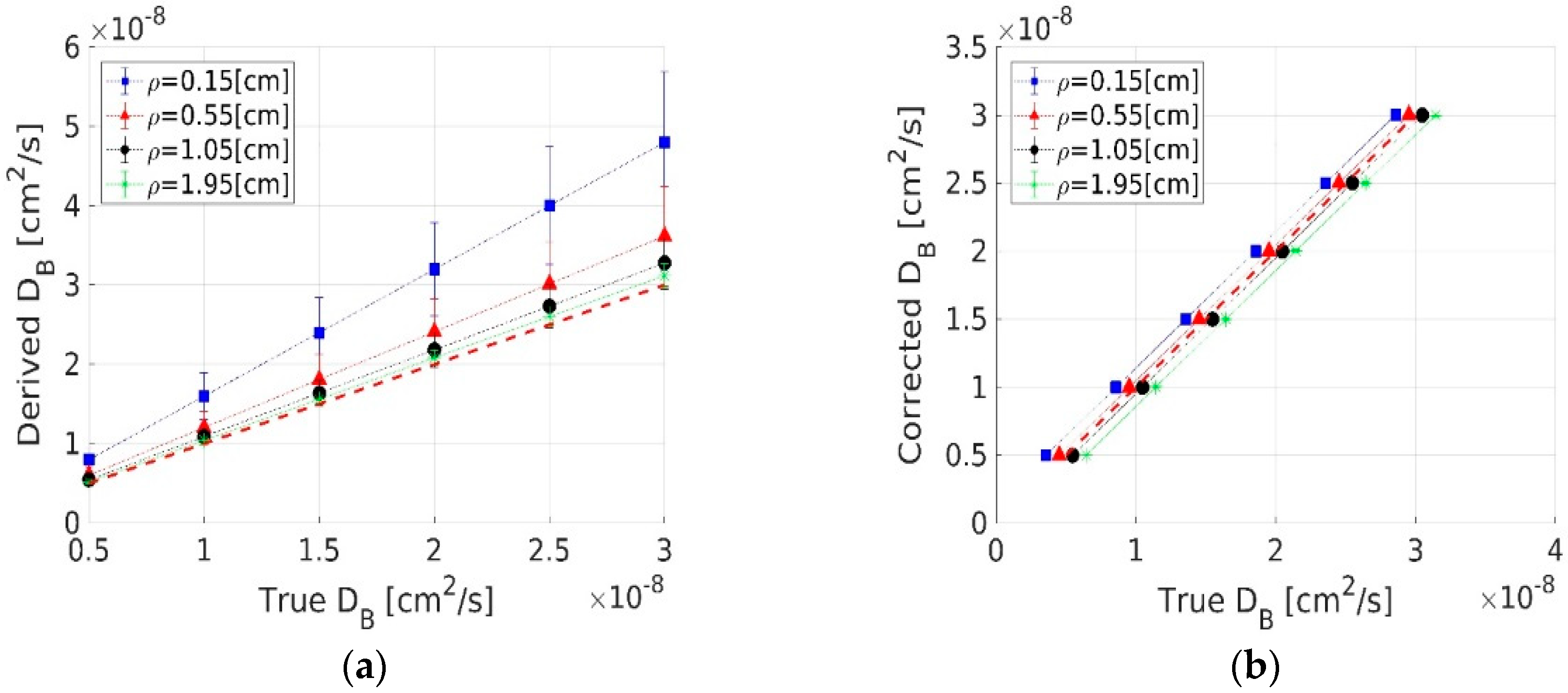
3.1.5. Scaling Factors: Linearly Correcting Retrieved Coefficients
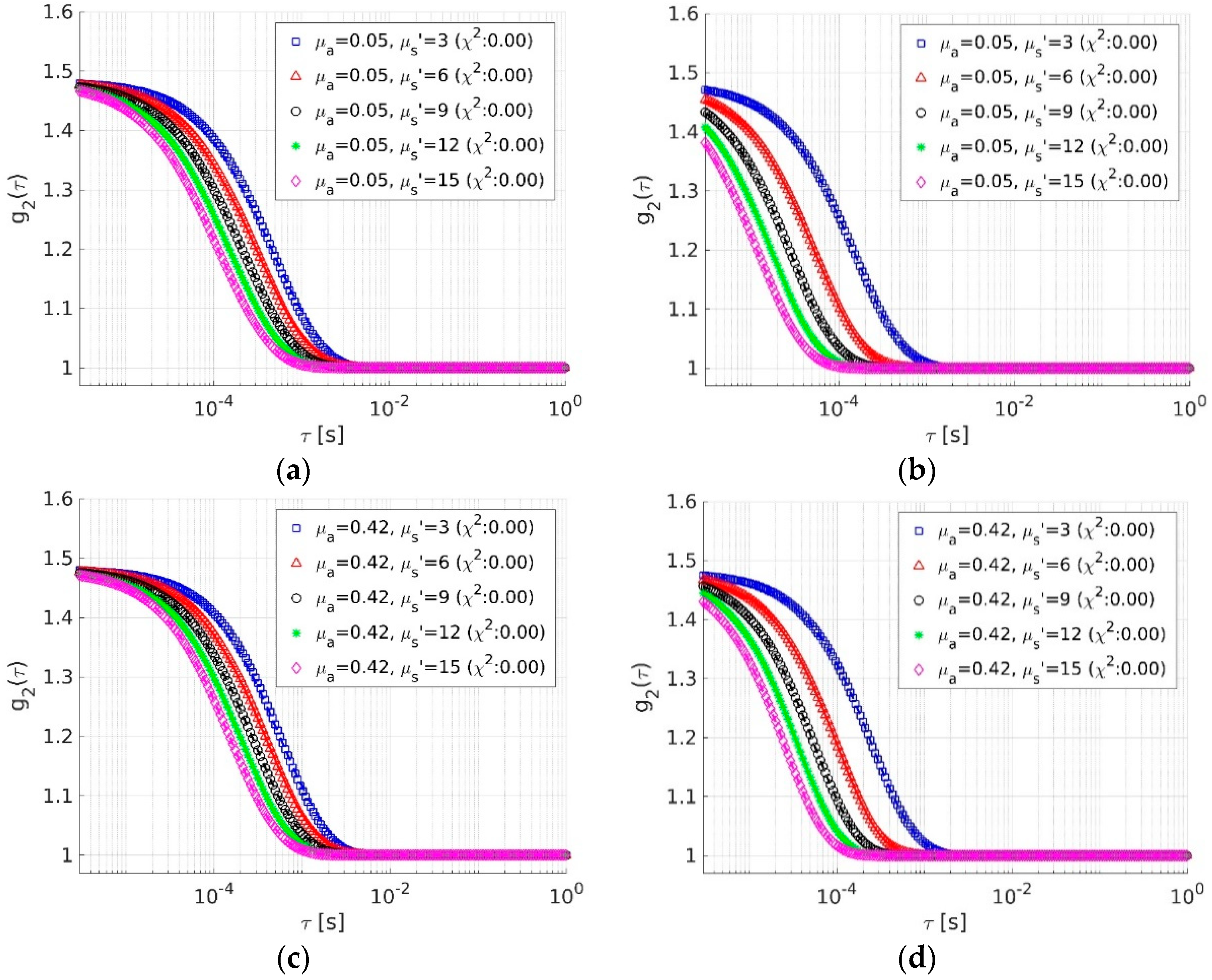
3.2. Diffusion-Theory Based Analysis of Experiments
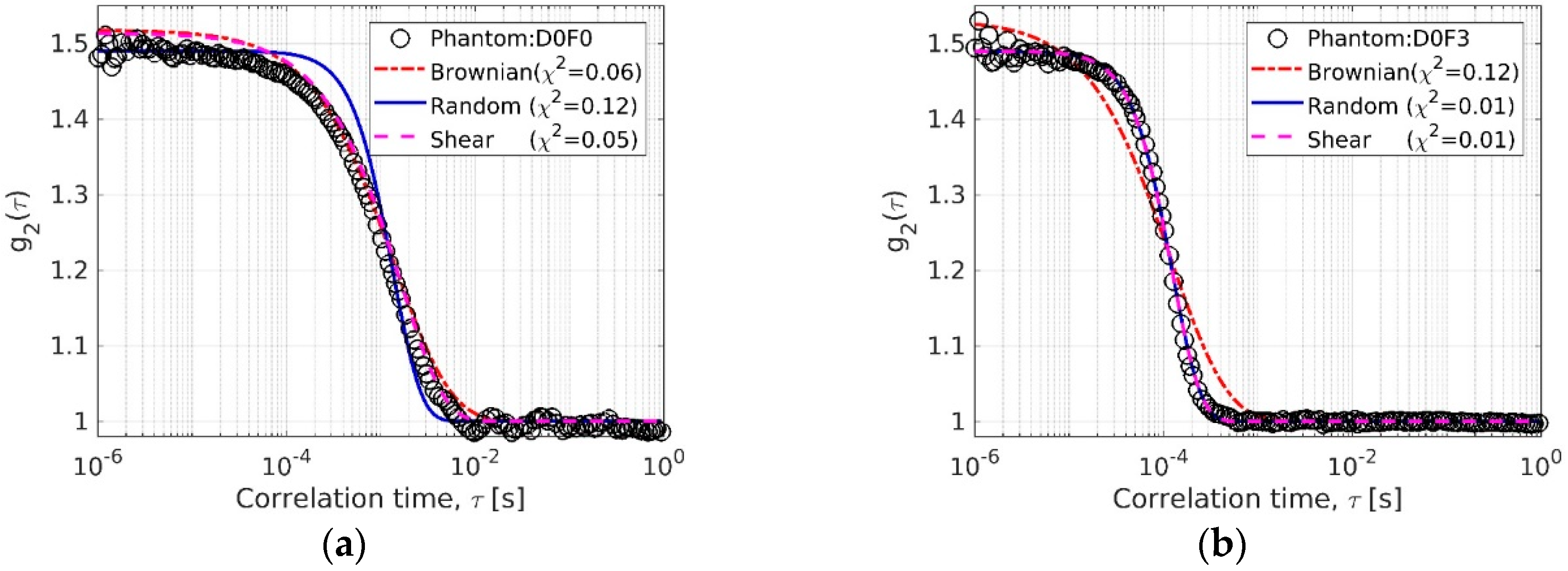
3.2.1. Flow Models for Fitting Experimental Data
3.2.2. Absolute vs. Relative Flow-Coefficients in Phantoms
3.3. Simulating Experimental Data Using MC
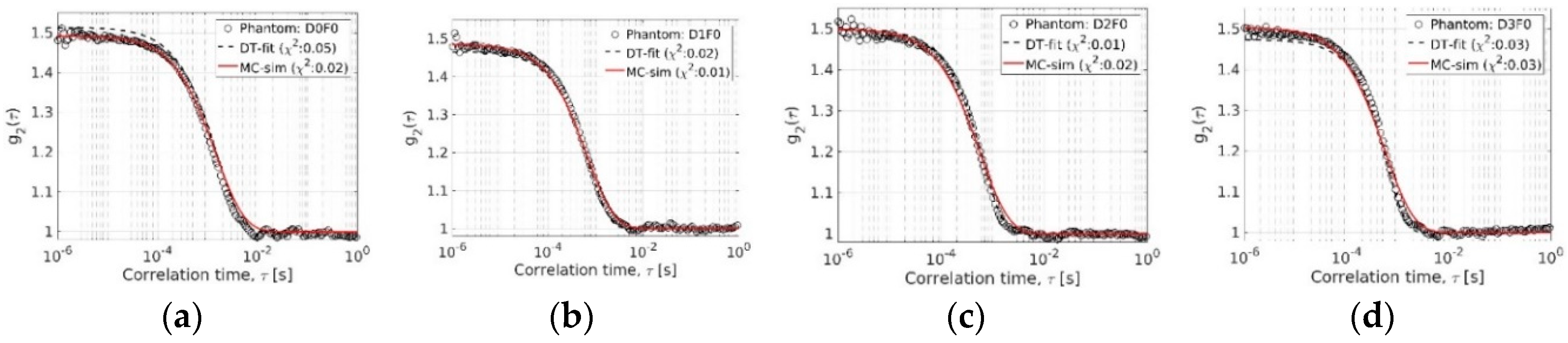
3.3.1. Modeling Phantoms with Inactive Flow
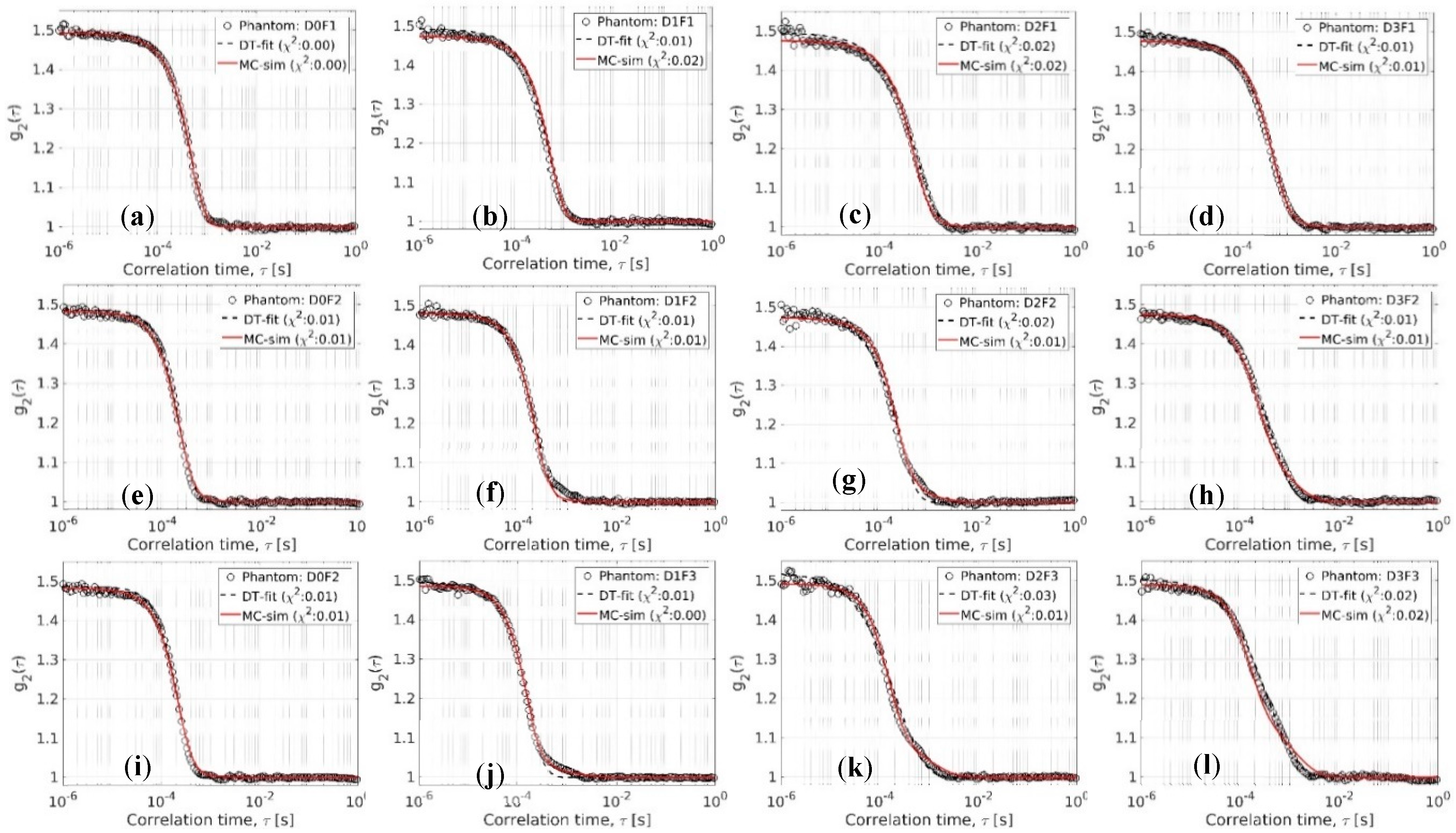
3.3.2. Modeling Phantoms with Actively Pumped Flow
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agochukwu, N.B.; Huang, C.; Zhao, M.; Bahrani, A.A.; Chen, L.; McGrath, P.; Yu, G.; Wong, L. A Novel Noncontact Diffuse Correlation Spectroscopy Device for Assessing Blood Flow in Mastectomy Skin Flaps: A Prospective Study in Patients Undergoing Prosthesis-Based Reconstruction. Plast. Reconstr. Surg. 2017, 140, 26–31. [Google Scholar] [CrossRef]
- Buckley, E.M.; Cook, N.M.; Durduran, T.; Kim, M.N.; Zhou, C.; Choe, R.; Yu, G.; Schultz, S.; Sehgal, C.M.; Licht, D.J.; et al. Cerebral hemodynamics in preterm infants during positional intervention measured with diffuse correlation spectroscopy and transcranial Doppler ultrasound. Opt. Express 2009, 17, 12571. [Google Scholar] [CrossRef]
- Carp, S.A.; Dai, G.P.; Boas, D.A.; Franceschini, M.A.; Kim, Y.R. Validation of diffuse correlation spectroscopy measurements of rodent cerebral blood flow with simultaneous arterial spin labeling MRI; towards MRI-optical continuous cerebral metabolic monitoring. Biomed. Opt. Express 2010, 1, 553–565. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Hoffman, M.D.; Proctor, A.R.; Vella, J.B.; Mannoh, E.A.; Barber, N.E.; Kim, H.J.; Jung, K.W.; Benoit, D.S.W.; Choe, R. Non-Invasive Monitoring of Temporal and Spatial Blood Flow during Bone Graft Healing Using Diffuse Correlation Spectroscopy. PLoS ONE 2015, 10, e0143891. [Google Scholar] [CrossRef]
- Durduran, T.; Yu, G.; Burnett, M.G.; Detre, J.A.; Greenberg, J.H.; Wang, J.; Zhou, C.; Yodh, A.G. Diffuse optical measurement of blood flow, blood oxygenation, and metabolism in a human brain during sensorimotor cortex activation. Opt. Lett. 2004, 29, 1766–1768. [Google Scholar] [CrossRef] [PubMed]
- Varma, H.M.; Valdés, C.P.; Kristoffersen, A.K.; Culver, J.P.; Durduran, T. Speckle contrast optical tomography: A new method for deep tissue three-dimensional tomography of blood flow. Biomed. Opt. Express 2014, 5, 1275–1289. [Google Scholar] [CrossRef]
- Ramirez, G.; Proctor, A.R.; Jung, K.W.; Wu, T.T.; Han, S.; Adams, R.R.; Ren, J.; Byun, D.K.; Madden, K.S.; Brown, E.B.; et al. Chemotherapeutic drug-specific alteration of microvascular blood flow in murine breast cancer as measured by diffuse correlation spectroscopy. Biomed. Opt. Express 2016, 7, 3610–3630. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y.; Symons, T.B.; Durduran, T.; Yodh, A.G.; Yu, G. Effects of muscle fiber motion on diffuse correlation spectroscopy blood flow measurements during exercise. Biomed. Opt. Express 2010, 1, 500–511. [Google Scholar] [CrossRef]
- Weingarten, M.S.; Papazoglou, E.S.; Zubkov, L.; Zhu, L.; Neidrauer, M.; Savir, G.; Peace, K.; Newby, J.G.; Pourrezaei, K. Correlation of near infrared absorption and diffuse reflectance spectroscopy scattering with tissue neovascularization and collagen concentration in a diabetic rat wound healing model. Wound Repair Regen. 2008, 16, 234–242. [Google Scholar] [CrossRef]
- Yazdi, H.S.; O’Sullivan, T.D.; Leproux, A.; Hill, B.; Durkin, A.; Telep, S.; Lam, J.; Yazdi, S.S.; Police, A.M.; Carroll, R.M.; et al. Mapping breast cancer blood flow index, composition, and metabolism in a human subject using combined diffuse optical spectroscopic imaging and diffuse correlation spectroscopy. J. Biomed. Opt. 2017, 22, 045003. [Google Scholar] [CrossRef]
- Yu, G. Near-infrared diffuse correlation spectroscopy in cancer diagnosis and therapy monitoring. J. Biomed. Opt. 2012, 17, 10901. [Google Scholar] [CrossRef]
- Thong, P.; Lee, K.; Toh, H.J.; Dong, J.; Tee, C.S.; Low, K.P.; Chang, P.H.; Bhuvaneswari, R.; Tan, N.C.; Soo, K.C. Early assessment of tumor response to photodynamic therapy using combined diffuse optical and diffuse correlation spectroscopy to predict treatment outcome. Oncotarget 2017, 8, 19902–19913. [Google Scholar] [CrossRef]
- Shang, Y.; Li, T.; Yu, G. Clinical Applications of Near-infrared Diffuse Correlation Spectroscopy and Tomography for Tissue Blood Flow Monitoring and Imaging. Physiol. Meas. 2017, 38, R1–R26. [Google Scholar] [CrossRef]
- Boas, D.A.; Campbell, L.E.; Yodh, A.G. Scattering and Imaging with Diffusing Temporal Field Correlations. Phys. Rev. Lett. 1995, 75, 1855–1858. [Google Scholar] [CrossRef]
- Boas, D.A.; Yodh, A.G. Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation. J. Opt. Soc. Am. A 1997, 14, 192. [Google Scholar] [CrossRef]
- Durduran, T.; Choe, R.; Baker, W.B.; Yodh, A.G. Diffuse Optics for Tissue Monitoring and Tomography. Rep. Prog. Phys. 2010, 73, 76701. [Google Scholar] [CrossRef]
- Durduran, T.; Yodh, A.G. Diffuse correlation spectroscopy for non-invasive, micro-vascular cerebral blood flow measurement. Neuroimage 2014, 85, 51–63. [Google Scholar] [CrossRef]
- Cheung, C.; Culver, J.P.; Takahashi, K.; Greenberg, J.H.; Yodh, A.G. In vivo cerebrovascular measurement combining diffuse near-infrared absorption and correlation spectroscopies. Phys. Med. Biol. 2001, 46, 2053–2065. [Google Scholar] [CrossRef]
- Carp, S.A.; Roche-Labarbe, N.; Franceschini, M.A.; Srinivasan, V.J.; Sakadžić, S.; Boas, D.A. Due to intravascular multiple sequential scattering, Diffuse Correlation Spectroscopy of tissue primarily measures relative red blood cell motion within vessels. Biomed. Opt. Express 2011, 2, 2047–2054. [Google Scholar] [CrossRef]
- Chandran, R.S.; Devaraj, G.; Kanhirodan, R.; Roy, D.; Vasu, R.M. Detection and estimation of liquid flow through a pipe in a tissue-like object with ultrasound-assisted diffuse correlation spectroscopy. J. Opt. Soc. Am. A 2015, 32, 1888–1897. [Google Scholar] [CrossRef]
- Farrell, T.J.; Patterson, M.S.; Wilson, B.C. A diffusion theory model of spatially resolved, steady-state diffuse reflectance for the noninvasive determination of the tissue optical properties in vivo. Med. Phys. 1992, 19, 879–888. [Google Scholar] [CrossRef]
- Kaplan, P.D.; Kao, M.H.; Yodh, A.G.; Pine, D.J. Geometric constraints for the design of diffusing-wave spectroscopy experiments. Appl. Opt. 1993, 32, 3828. [Google Scholar] [CrossRef]
- Durian, D.; Rudnick, J. Photon migration at short times and distances and in cases of strong absorption. J. Opt. Soc. Am. A 1997, 14, 235. [Google Scholar] [CrossRef]
- Venugopalan, V.; You, J.S.; Tromberg, B.J. Radiative transport in the diffusion approximation: An extension for highly absorbing media and small source-detector separations. Phys. Rev. E 1998, 58, 2395–2407. [Google Scholar] [CrossRef]
- Yoon, G.; Prahl, S.A.; Welch, A.J. Accuracies in the diffusion approximation and its similarity relations for laser irradiated biological media. Appl. Opt. 1989, 28, 2250–2255. [Google Scholar] [CrossRef]
- Kienle, A.; Patterson, M.S. Improved solutions of the steady-state and the time-resolved diffusion equations for reflectance from a semi-infinite turbid medium. J. Opt. Soc. Am. A 1997, 14, 246. [Google Scholar] [CrossRef]
- Buckley, E.M.; Miller, B.F.; Golinski, J.M.; Sadeghian, H.; McAllister, L.M.; Vangel, M.; Ayata, C.; Meehan, W.P., 3rd; Franceschini, M.A.; Whalen, M.J. Decreased microvascular cerebral blood flow assessed by diffuse correlation spectroscopy after repetitive concussions in mice. J. Cereb. Blood Flow Metab. 2015, 35, 1995–2000. [Google Scholar] [CrossRef]
- Farzam, P.; Durduran, T. Multidistance diffuse correlation spectroscopy for simultaneous estimation of blood flow index and optical properties. J. Biomed. Opt. 2015, 20, 55001. [Google Scholar] [CrossRef]
- Johansson, J.D.; Mireles, M.; Morales-Dalmau, J.; Farzam, P.; Martínez-Lozano, M.; Casanovas, O.; Durduran, T. Scanning, non-contact, hybrid broadband diffuse optical spectroscopy and diffuse correlation spectroscopy system. Biomed. Opt. Express 2016, 7, 481–498. [Google Scholar] [CrossRef]
- Vishwanath, K.; Gurjar, R.; Wolf, D.; Riccardi, S.; Duggan, M.; King, D. Diffuse optical monitoring of peripheral tissues during uncontrolled internal hemorrhage in a porcine model. Biomed. Opt. Express 2018, 9, 569–580. [Google Scholar] [CrossRef]
- Sathialingam, E.; Lee, S.Y.; Sanders, B.; Park, J.; McCracken, C.E.; Bryan, L.; Buckley, E.M. Small separation diffuse correlation spectroscopy for measurement of cerebral blood flow in rodents. Biomed. Opt. Express 2018, 9, 5719–5734. [Google Scholar] [CrossRef]
- Zhu, C.; Liu, Q. Review of Monte Carlo modeling of light transport in tissues. J. Biomed. Opt. 2013, 18, 50902. [Google Scholar] [CrossRef]
- Bender, J.E.; Vishwanath, K.; Moore, L.K.; Brown, J.Q.; Chang, V.; Palmer, G.M.; Ramanujam, N. A Robust Monte Carlo Model for the Extraction of Biological Absorption and Scattering in Vivo. IEEE Trans. Biomed. Eng. 2009, 56, 960–968. [Google Scholar] [CrossRef]
- Zhu, C.; Palmer, G.M.; Breslin, T.M.; Harter, J.; Ramanujam, N. Diagnosis of breast cancer using diffuse reflectance spectroscopy: Comparison of a Monte Carlo versus partial least squares analysis based feature extraction technique. Lasers Surg. Med. 2006, 38, 714–724. [Google Scholar] [CrossRef]
- Palmer, G.M.; Ramanujam, N. Monte Carlo-based inverse model for calculating tissue optical properties Part I: Theory and validation on synthetic phantoms. Appl. Opt. 2006, 45, 1062. [Google Scholar] [CrossRef]
- Swartling, J.; Dam, J.S.; Andersson-Engels, S. Comparison of spatially and temporally resolved diffuse-reflectance measurement systems for determination of biomedical optical properties. Appl. Opt. 2003, 42, 4612. [Google Scholar] [CrossRef]
- Boas, D.A.; Culver, J.P.; Stott, J.J.; Dunn, A.K. Three dimensional Monte Carlo code for photon migration through complex hetrogeneous media including the adult human head. Opt. Express 2002, 10, 159–170. [Google Scholar] [CrossRef]
- Binzoni, T.; Martelli, F. Assessing the reliability of diffuse correlation spectroscopy models on noise-free analytical Monte Carlo data. Appl. Opt. 2015, 54, 5320–5326. [Google Scholar] [CrossRef]
- Boas, D.A.; Sakadžić, S.; Selb, J.; Farzam, P.; Franceschini, M.A.; Carp, S.A. Establishing the diffuse correlation spectroscopy signal relationship with blood flow. Neurophotonics 2016, 3, 31412. [Google Scholar] [CrossRef]
- Gagnon, L.; Desjardins, M.; Jehanne-Lacasse, J.; Bherer, L.; Lesage, F. Investigation of diffuse correlation spectroscopy in multi-layered media including the human head. Opt. Express 2008, 16, 15514. [Google Scholar] [CrossRef]
- Selb, J.; Boas, D.A.; Chan, S.T.; Evans, K.C.; Buckley, E.M.; Carp, S.A. Sensitivity of near-infrared spectroscopy and diffuse correlation spectroscopy to brain hemodynamics: Simulations and experimental findings during hypercapnia. Neurophotonics 2014, 1, 15005. [Google Scholar] [CrossRef]
- Binzoni, T.; Liemert, A.; Kienle, A.; Martelli, F. Analytical solution of the correlation transport equation with static background: Beyond diffuse correlation spectroscopy. Appl. Opt. 2016, 55, 8500. [Google Scholar] [CrossRef]
- Vishwanath, K.; Chang, K.; Klein, D.; Deng, Y.F.; Chang, V.; Phelps, J.E.; Ramanujam, N. Portable, Fiber-Based, Diffuse Reflection Spectroscopy (DRS) Systems for Estimating Tissue Optical Properties. Appl. Spectrosc. 2011, 65, 206–215. [Google Scholar] [CrossRef]
- Wu, H.I.; Wang, L.V. Raleigh theory and Mie theory for single scatterer. In Biomedical Opticsl Priniciples and Imaging; John Wiley & Sons: Hobken, NJ, USA, 2007. [Google Scholar]
- Taroni, P.; Pifferi, A.; Torricelli, A.; Comelli, D.; Cubeddu, R. In vivo absorption and scattering spectroscopy of biological tissues. Photochem. Photobiol. Sci. 2003, 2, 124–129. [Google Scholar] [CrossRef]
- Barman, I.; Dingari, N.C.; Rajaram, N.; Tunnell, J.W.; Dasari, R.R.; Feld, M.S. Rapid and accurate determination of tissue optical properties using least-squares support vector machines. Biomed. Opt. Express 2011, 2, 592–599. [Google Scholar] [CrossRef]
- Honda, N.; Ishii, K.; Terada, T.; Nanjo, T.; Awazu, K. Determination of the tumor tissue optical properties during and after photodynamic therapy using inverse Monte Carlo method and double integrating sphere between 350 and 1000 nm. J. Biomed. Opt. 2011, 16, 58003. [Google Scholar] [CrossRef]
- Ivanov, K.; Kalinina, M.; Levkovich, Y. Blood flow velocity in capillaries of brain and muscles and its physiological significance. Microvasc. Res. 1981, 22, 143–155. [Google Scholar] [CrossRef]
- Vishwanath, K.; Mycek, M.A. Time-resolved photon migration in bi-layered tissue models. Opt. Express 2005, 13, 7466. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML–Monte Carlo modeling of photon transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Vishwanath, K.; Pogue, B.; Mycek, M.-A. Quantitative fluorescence lifetime spectroscopy in turbid media: Comparison of theoretical, experimental and computational methods. Phys. Med. Biol. 2002, 47, 3387–3405. [Google Scholar] [CrossRef]
- Wu, X.L.; Pine, D.J.; Chaikin, P.M.; Huang, J.S.; Weitz, D.A. Diffusing-wave spectroscopy in a shear flow. J. Opt. Soc. Am. B 1990, 7, 15–20. [Google Scholar] [CrossRef]
- Shang, Y.; Gurley, K.; Yu, G. Diffuse Correlation Spectroscopy (DCS) for Assessment of Tissue Blood Flow in Skeletal Muscle: Recent Progress. Anat. Physiol. 2013, 3, 128. [Google Scholar]
- Binzoni, T.; Liemert, A.; Kienle, A.; Martelli, F. Derivation of the correlation diffusion equation with static background and analytical solutions. Appl. Opt. 2017, 56, 795. [Google Scholar] [CrossRef]
- Binzoni, T.; Sanguinetti, B.; Van De Ville, D.; Zbinden, H.; Martelli, F. Probability density function of the electric field in diffuse correlation spectroscopy of human bone in vivo. Appl. Opt. 2016, 55, 757–762. [Google Scholar] [CrossRef]

| Layer # | ||||||
|---|---|---|---|---|---|---|
| Layer 1 | 0.075 | 120 | 0.9 | 1.35 | ||
| Layer 2 | 0.15 | or | ||||
| Layer 3 | 5 |
| Phantom | ||||
|---|---|---|---|---|
| D0F0 | 0.02 | 3.6 × 10−9 | 3.6 × 10−9 | - |
| D0F1 | - | 5.7 × 10−3 | ||
| D0F2 | - | 1.42 × 10−2 | ||
| D0F3 | - | 2.28 × 10−2 | ||
| D1F0 | 0.05 | 7.9 × 10−9 | 7.9 × 10−9 | - |
| D1F1 | - | 5.7 × 10−3 | ||
| D1F2 | - | 1.42 × 10−2 | ||
| D1F3 | - | 2.28 × 10−2 | ||
| D2F0 | 0.08 | 8.9 × 10−9 | 8.9 × 10−9 | - |
| D2F1 | - | 5.7 × 10−3 | ||
| D2F2 | - | 1.42 × 10−2 | ||
| D2F3 | - | 2.28 × 10−2 | ||
| D3F0 | 0.11 | 9.3 × 10−9 | 9.3 × 10−9 | - |
| D3F1 | - | 5.7 × 10−3 | ||
| D3F2 | - | 1.42 × 10−2 | ||
| D3F3 | - | 2.28 × 10−2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vishwanath, K.; Zanfardino, S. Diffuse Correlation Spectroscopy at Short Source-Detector Separations: Simulations, Experiments and Theoretical Modeling. Appl. Sci. 2019, 9, 3047. https://doi.org/10.3390/app9153047
Vishwanath K, Zanfardino S. Diffuse Correlation Spectroscopy at Short Source-Detector Separations: Simulations, Experiments and Theoretical Modeling. Applied Sciences. 2019; 9(15):3047. https://doi.org/10.3390/app9153047
Chicago/Turabian StyleVishwanath, Karthik, and Sara Zanfardino. 2019. "Diffuse Correlation Spectroscopy at Short Source-Detector Separations: Simulations, Experiments and Theoretical Modeling" Applied Sciences 9, no. 15: 3047. https://doi.org/10.3390/app9153047
APA StyleVishwanath, K., & Zanfardino, S. (2019). Diffuse Correlation Spectroscopy at Short Source-Detector Separations: Simulations, Experiments and Theoretical Modeling. Applied Sciences, 9(15), 3047. https://doi.org/10.3390/app9153047





