Temperature Distributions inside Concrete Sections of Renewable Energy Storage Pile Foundations
Abstract
Featured Application
Abstract
1. Introduction
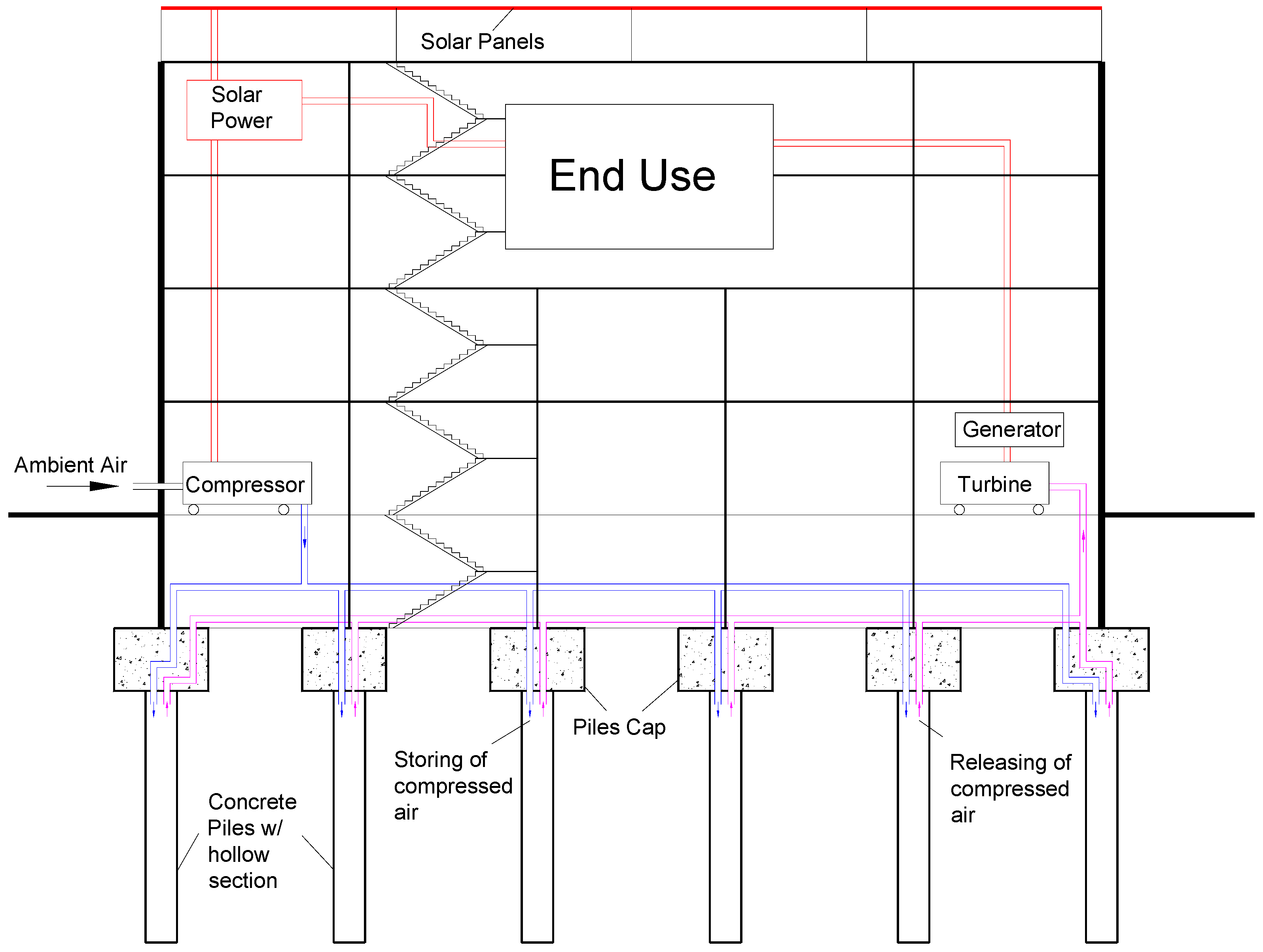
2. Background
2.1. Thermodynamic Processes of CAES
2.2. Thermal Properties
3. Parametric Study
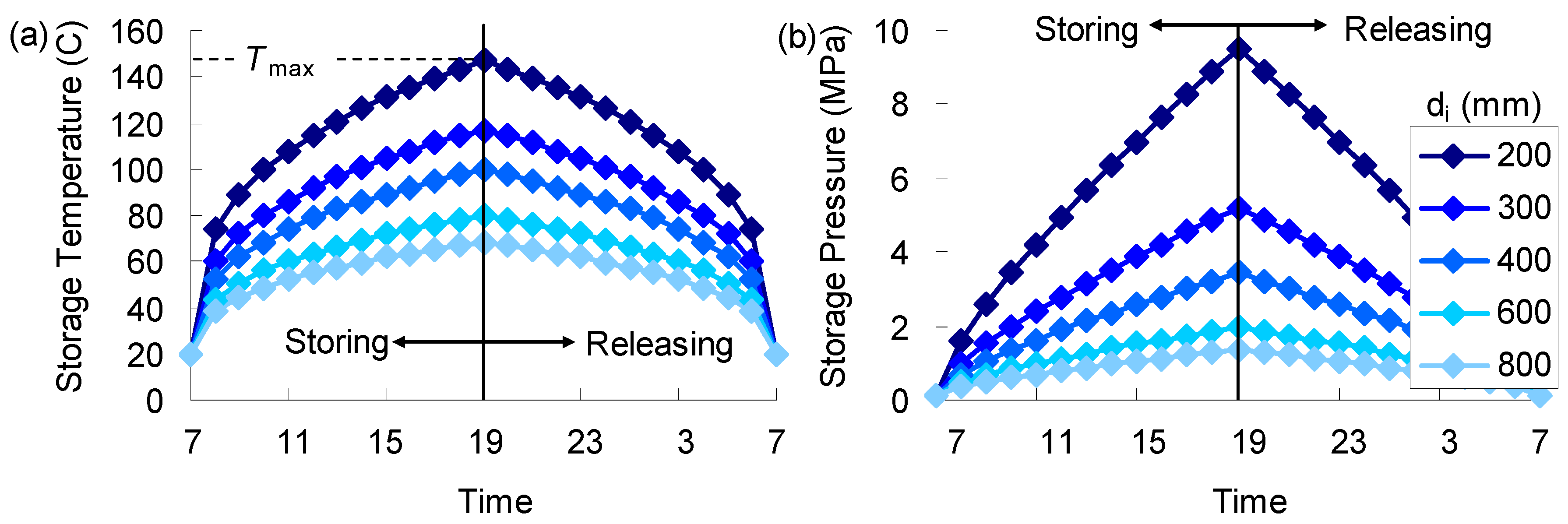
3.1. Pressure and Temperature in the Stored Compressed Air
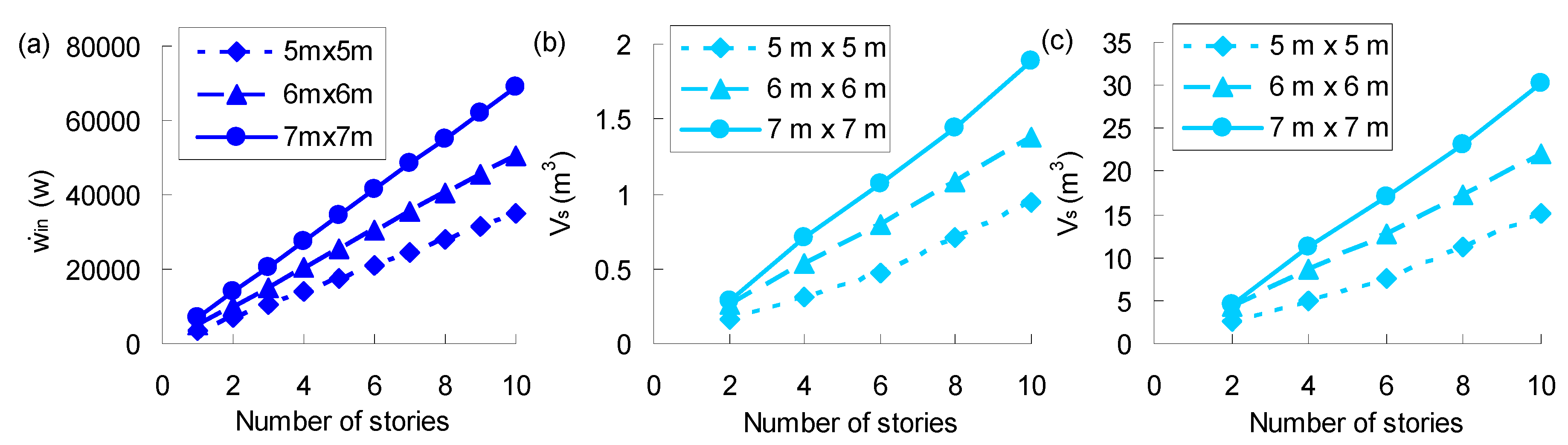
3.2. Study Parameters
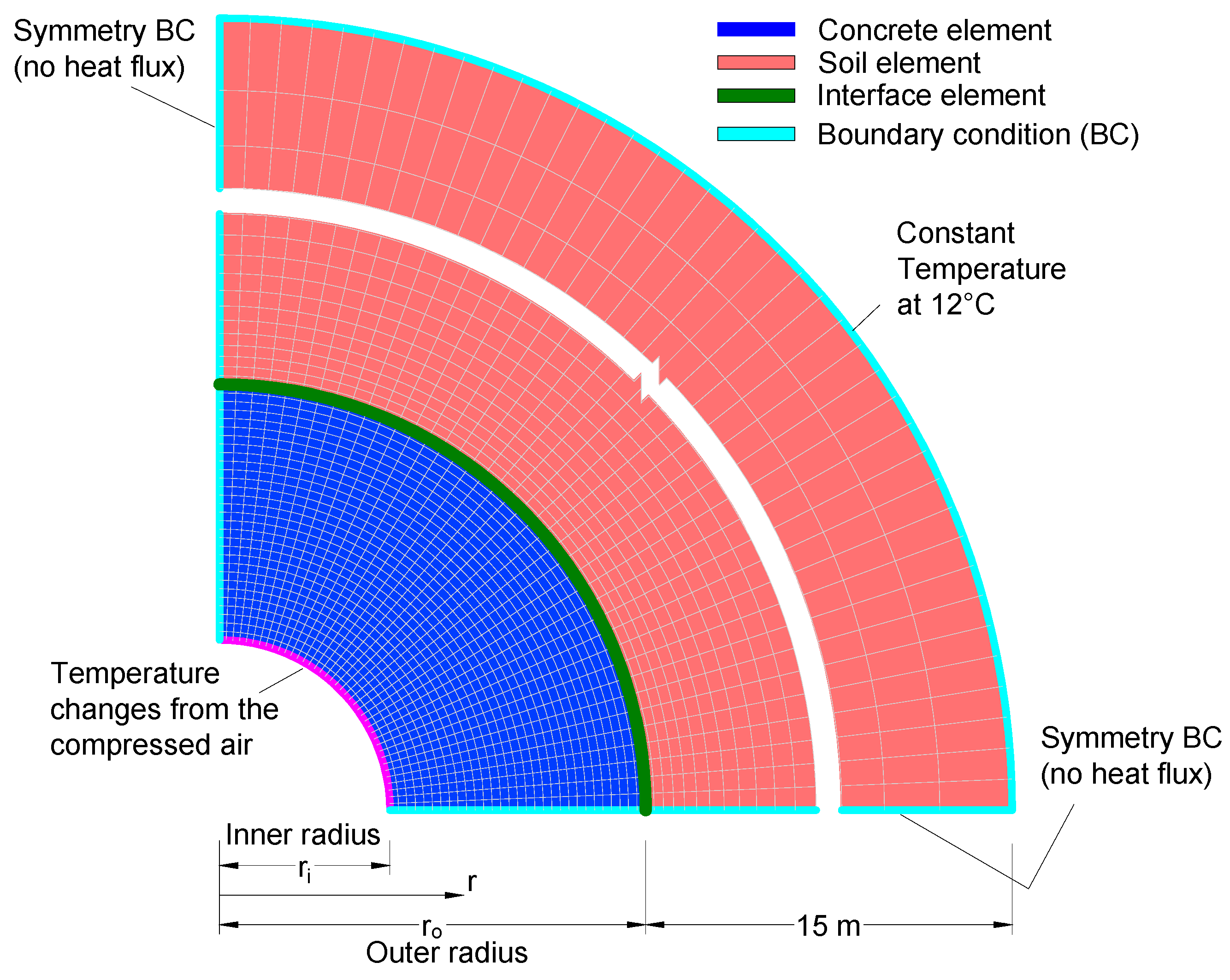
3.3. Numerical Models
4. Numerical Results and Discussion
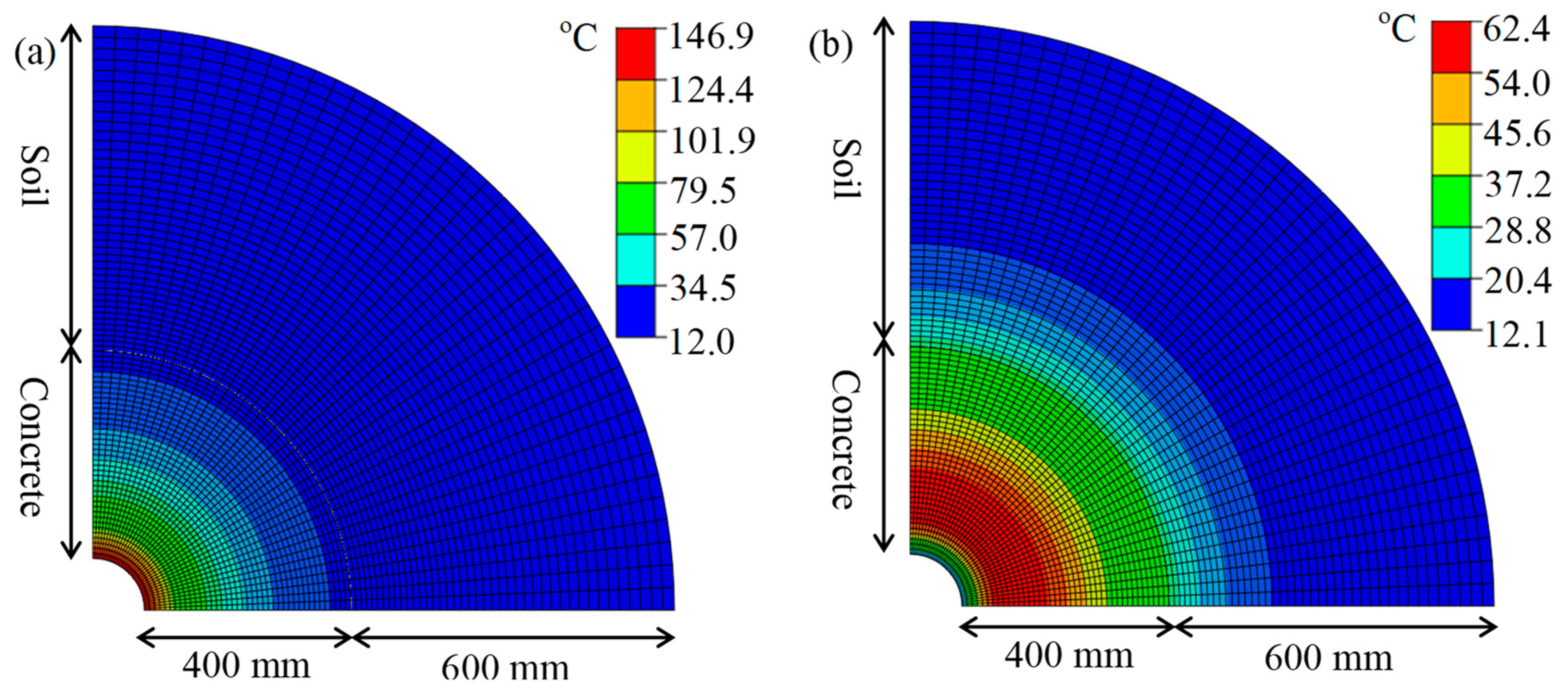
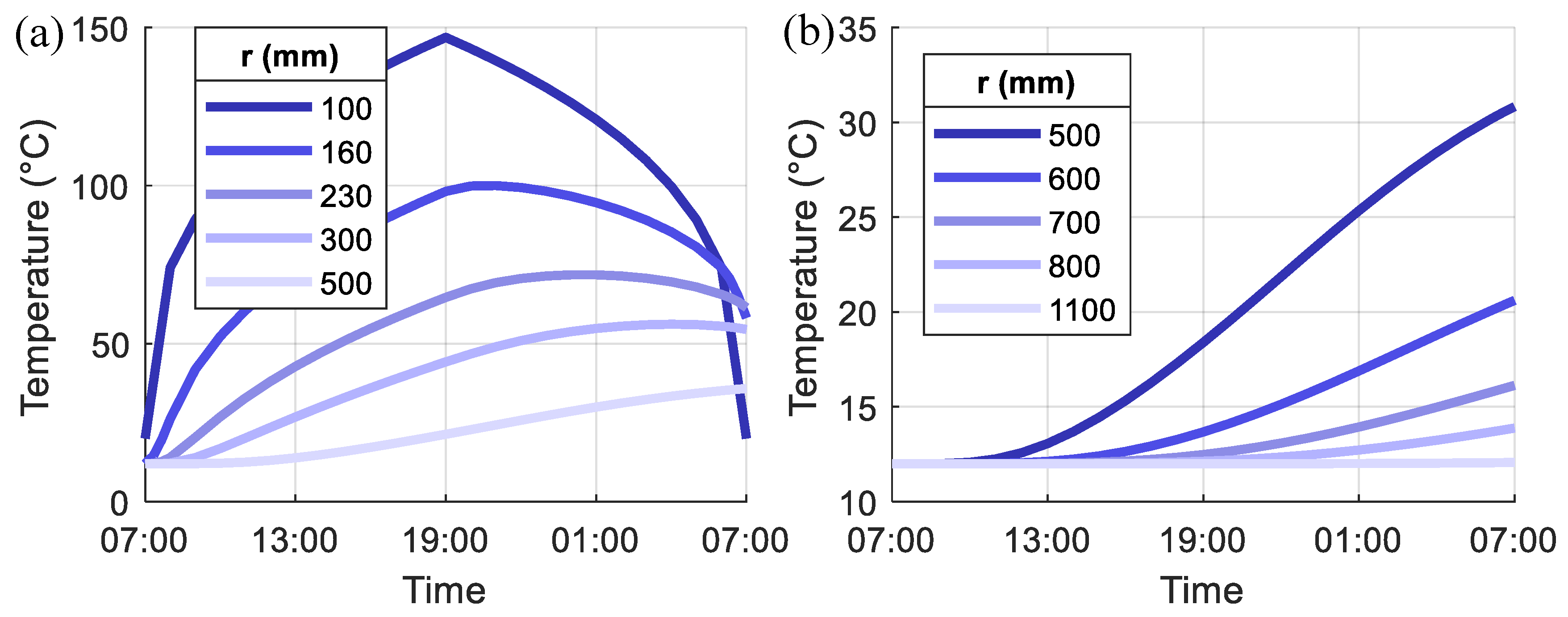
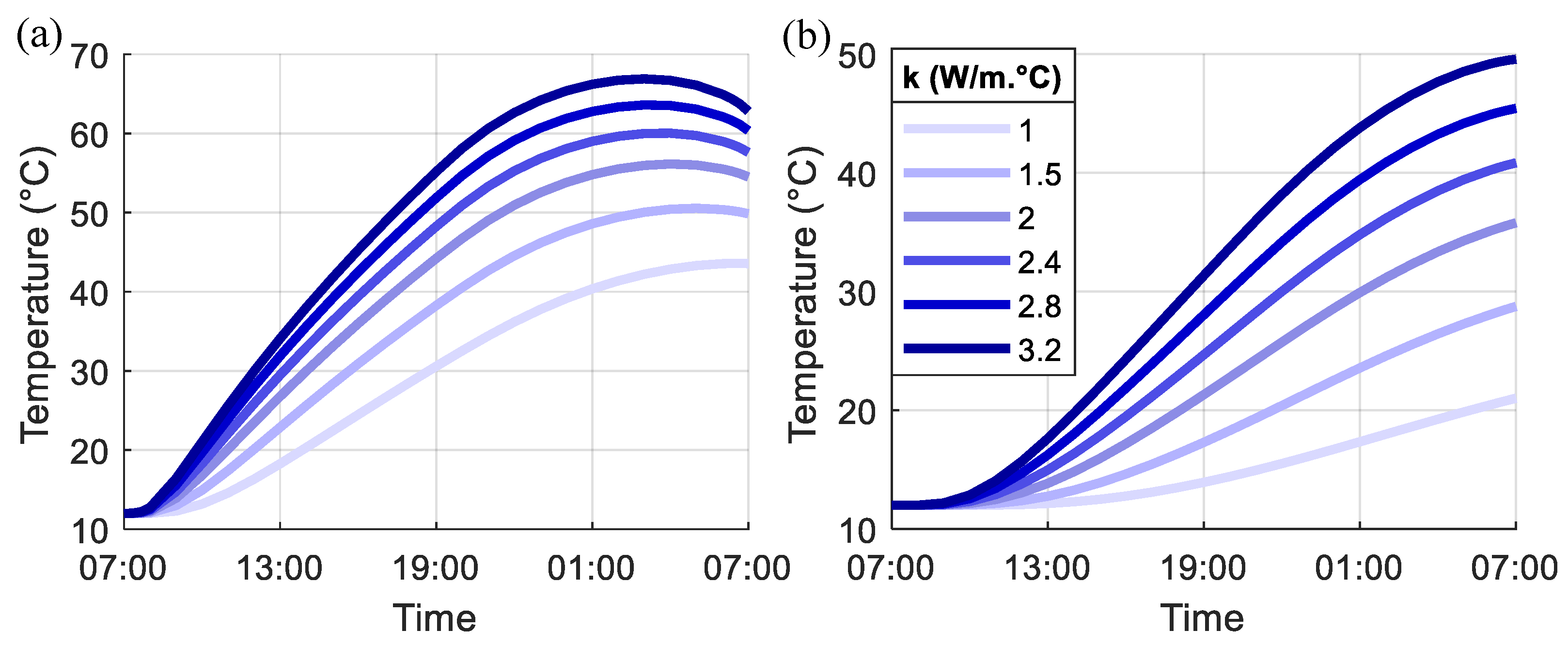
4.1. General Response
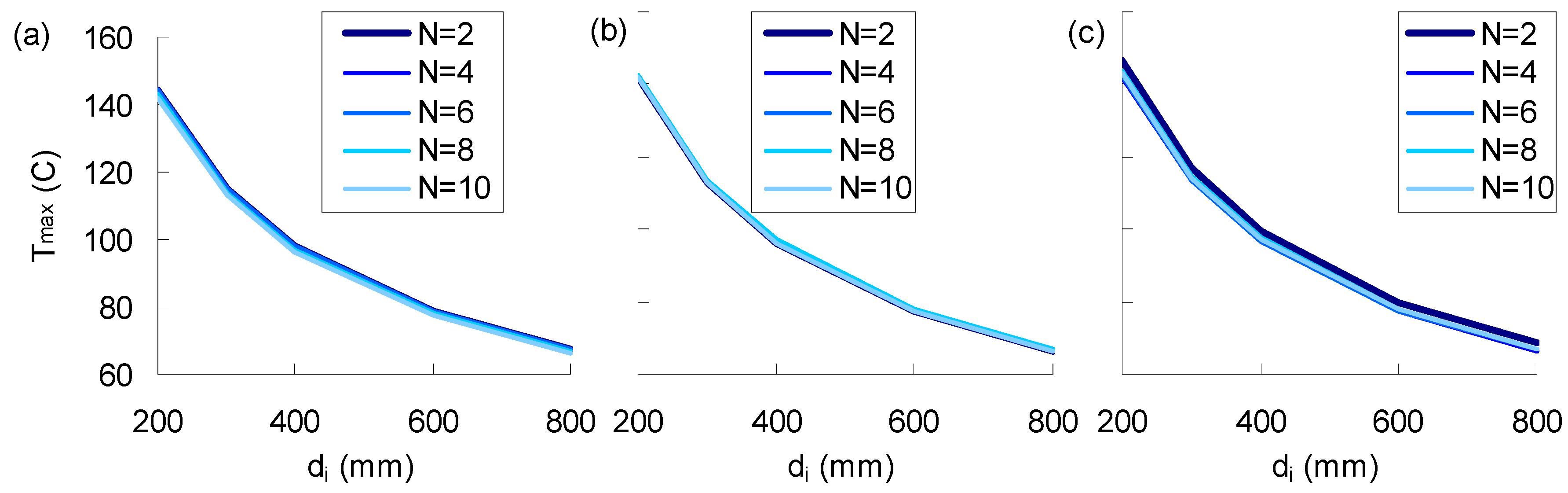
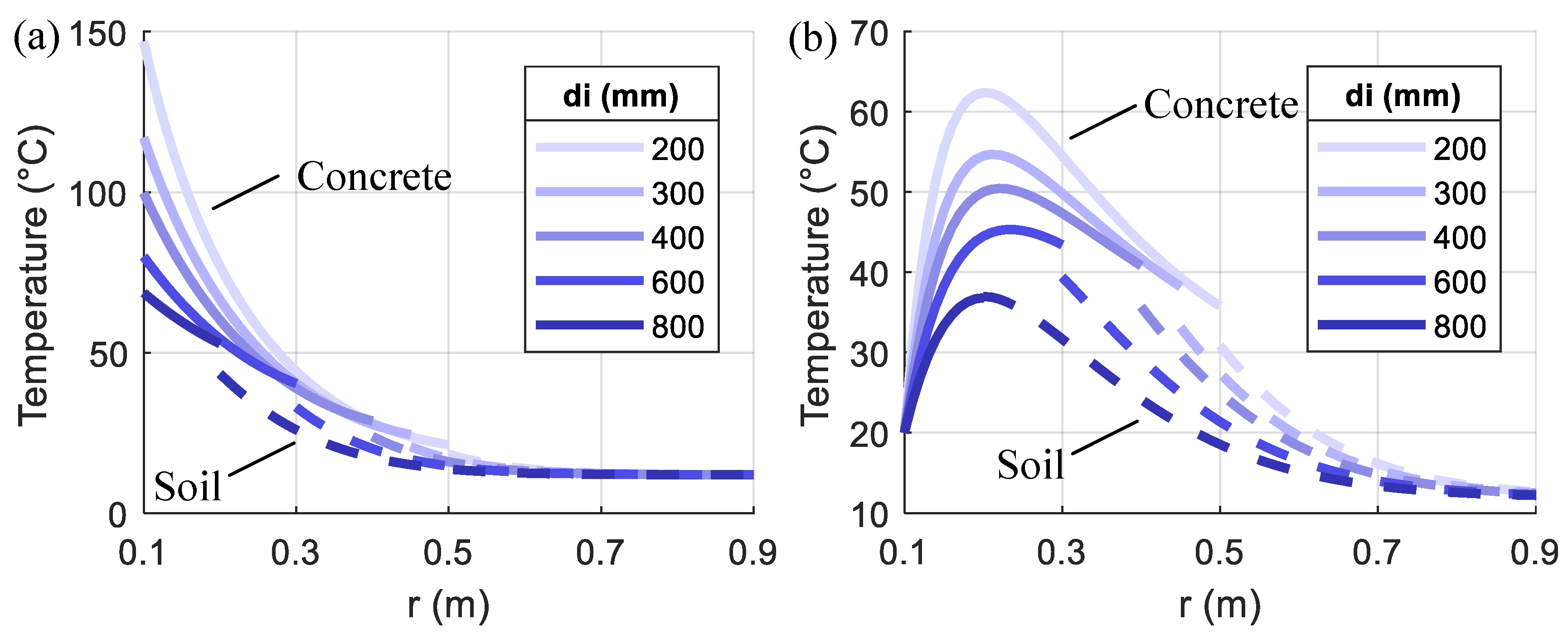
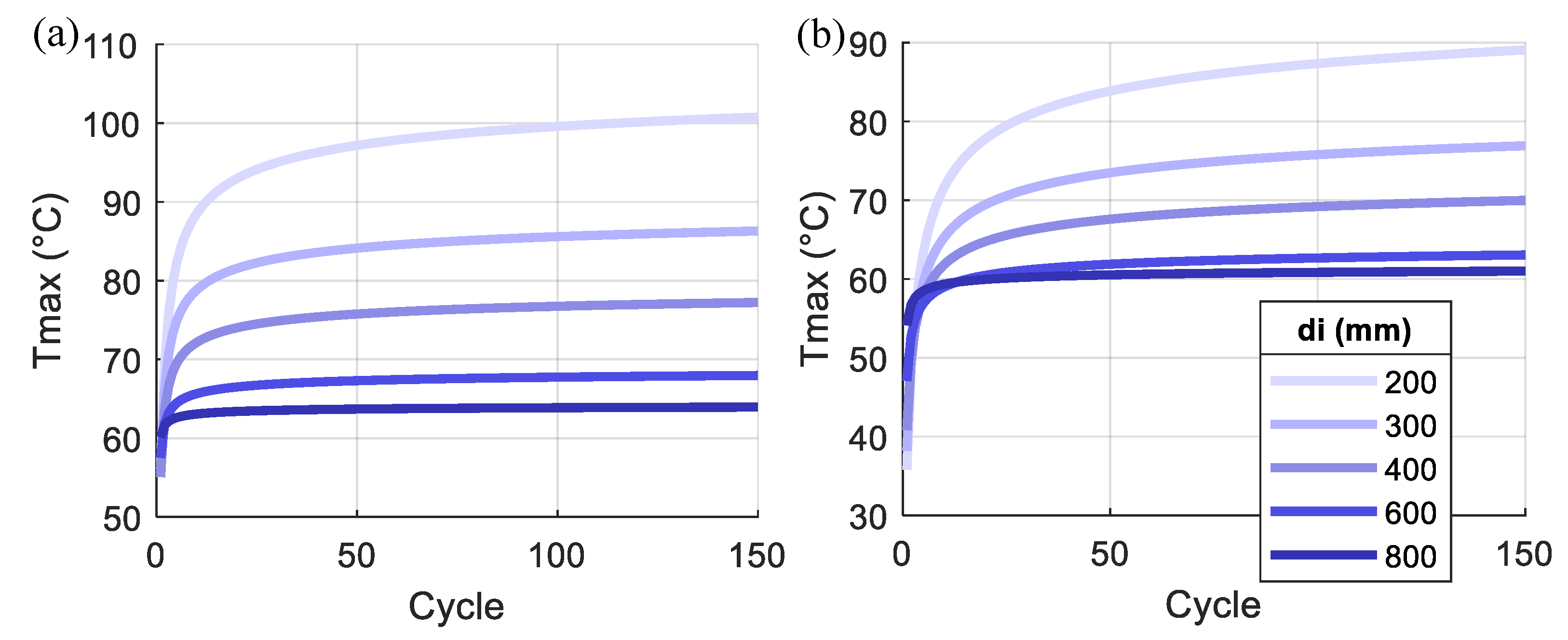
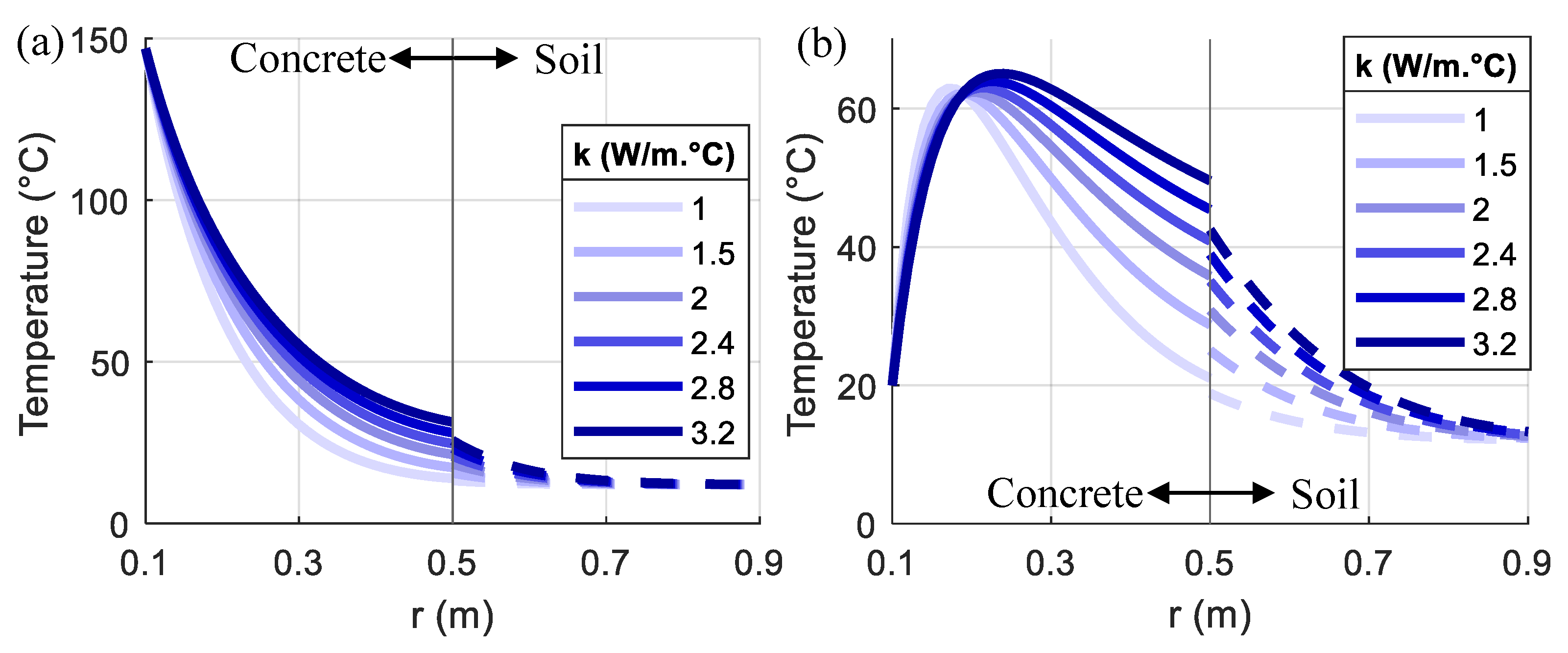
4.2. Parametric Results
5. Conclusions
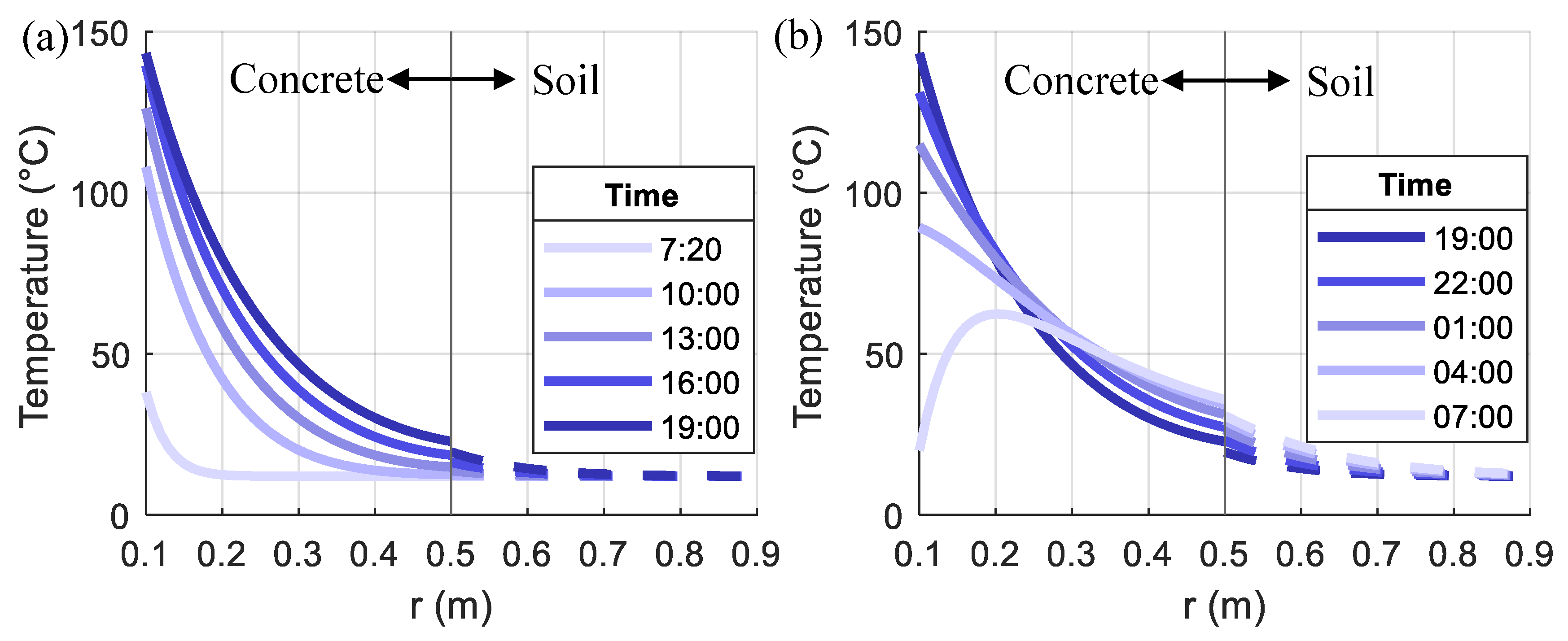
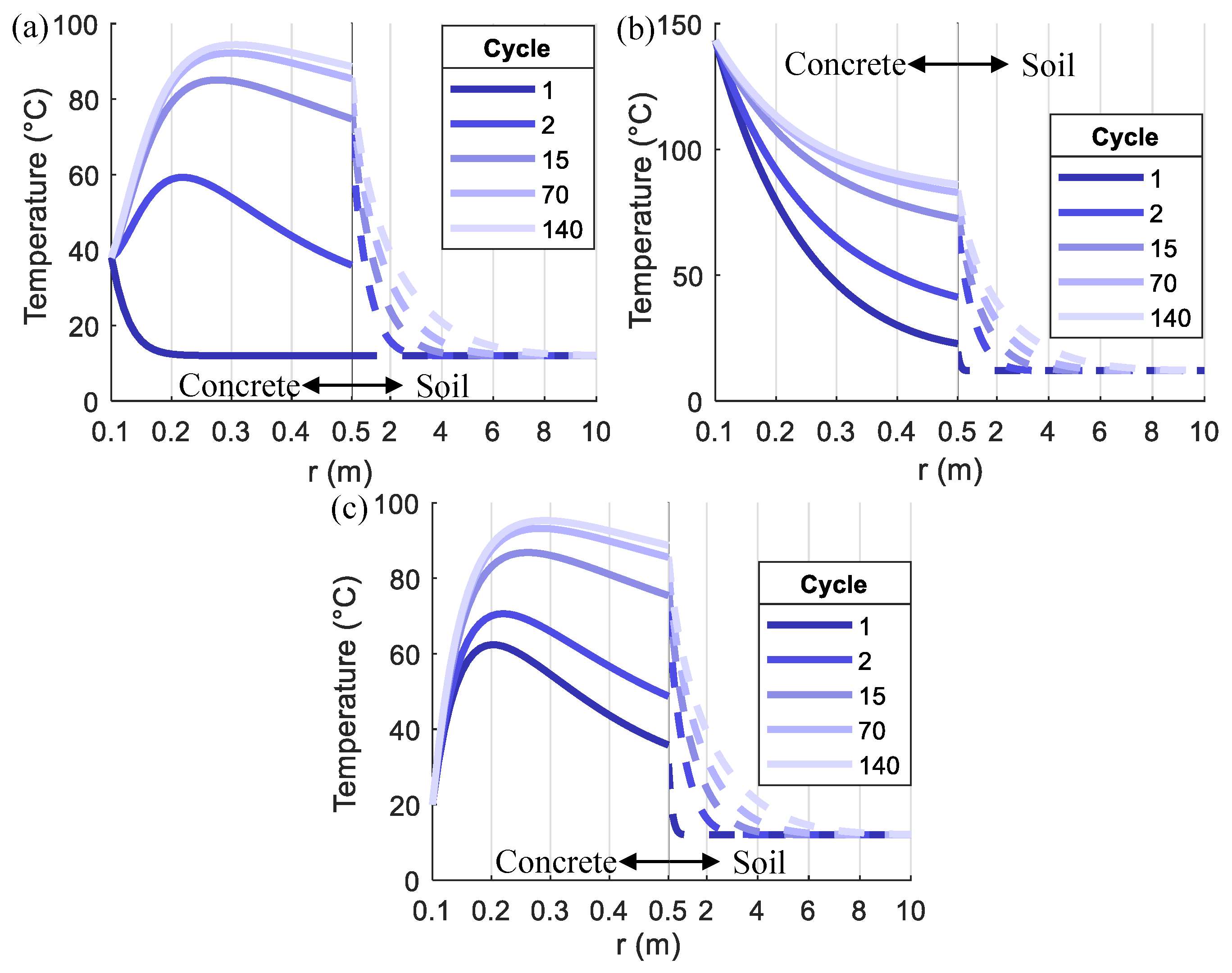
- The heat generated from the compressed air is gradually transferred from the inner to the outer surface of the pile section and causes temperature changes, which become smaller and slower when moving from the inner to the outer surface.
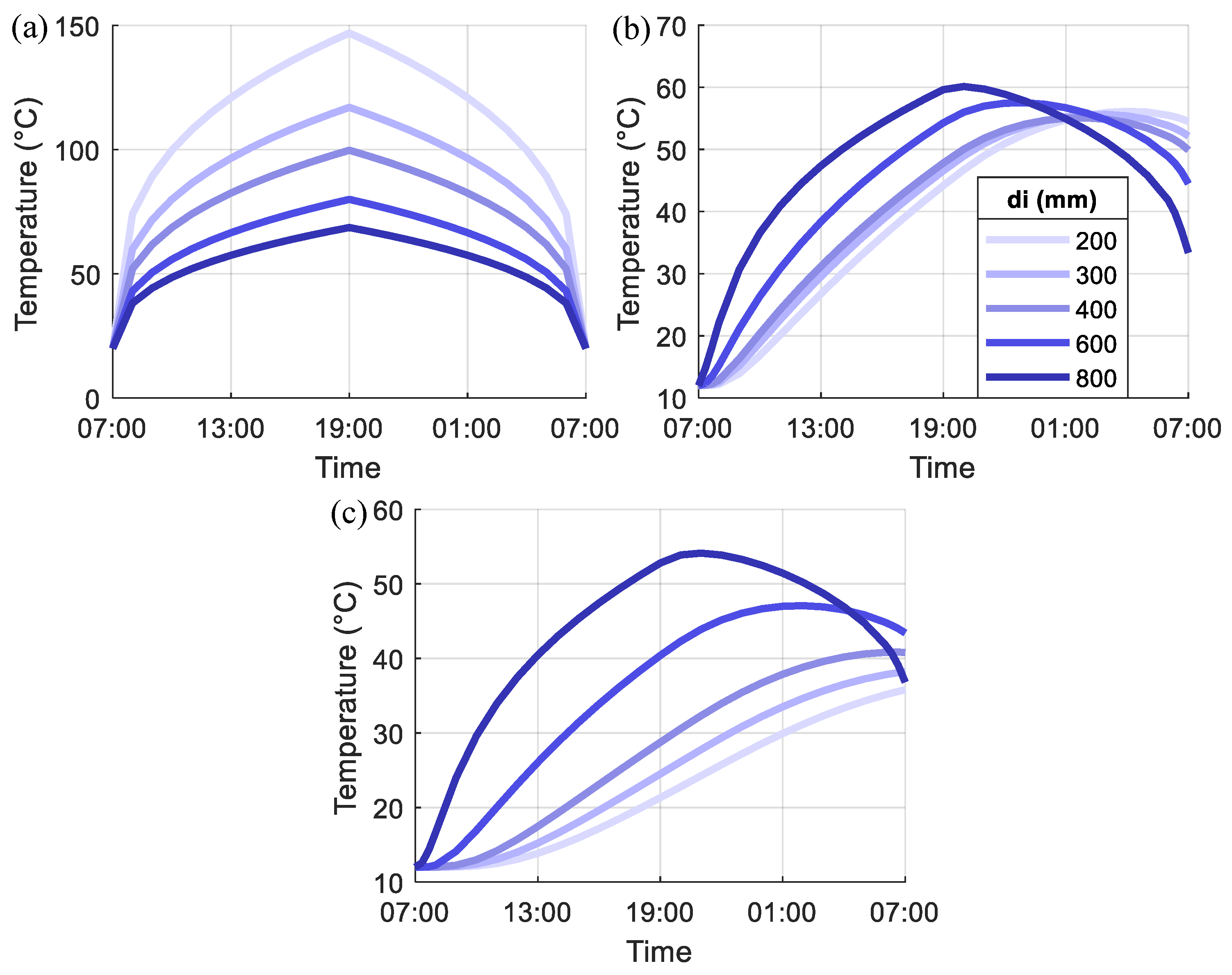
- The temperature distribution along the radius direction in a loading cycle varies with time, especially when the temperature loading starts to drop. Residual temperatures in the pile section are observed at the end of the loading cycle.
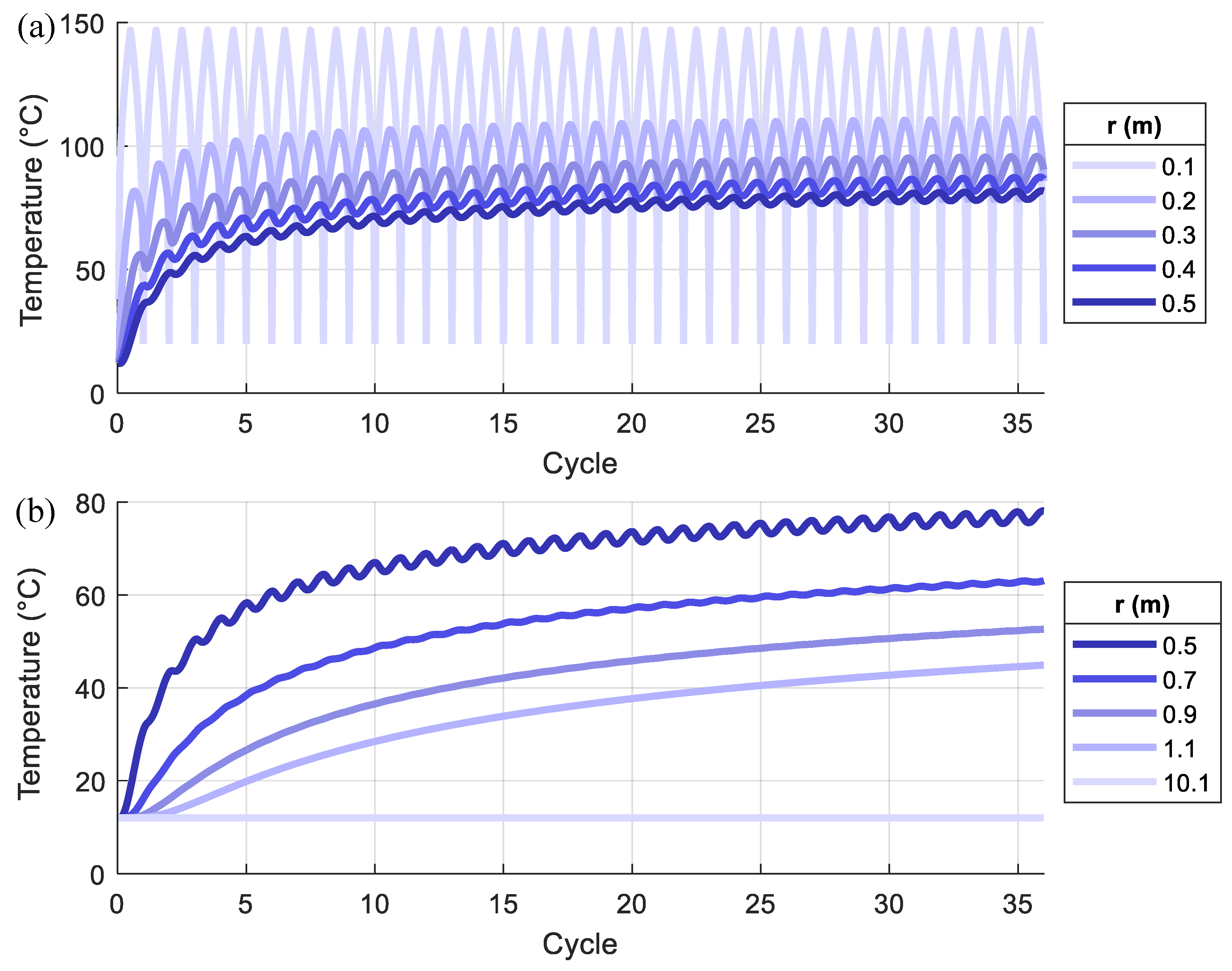
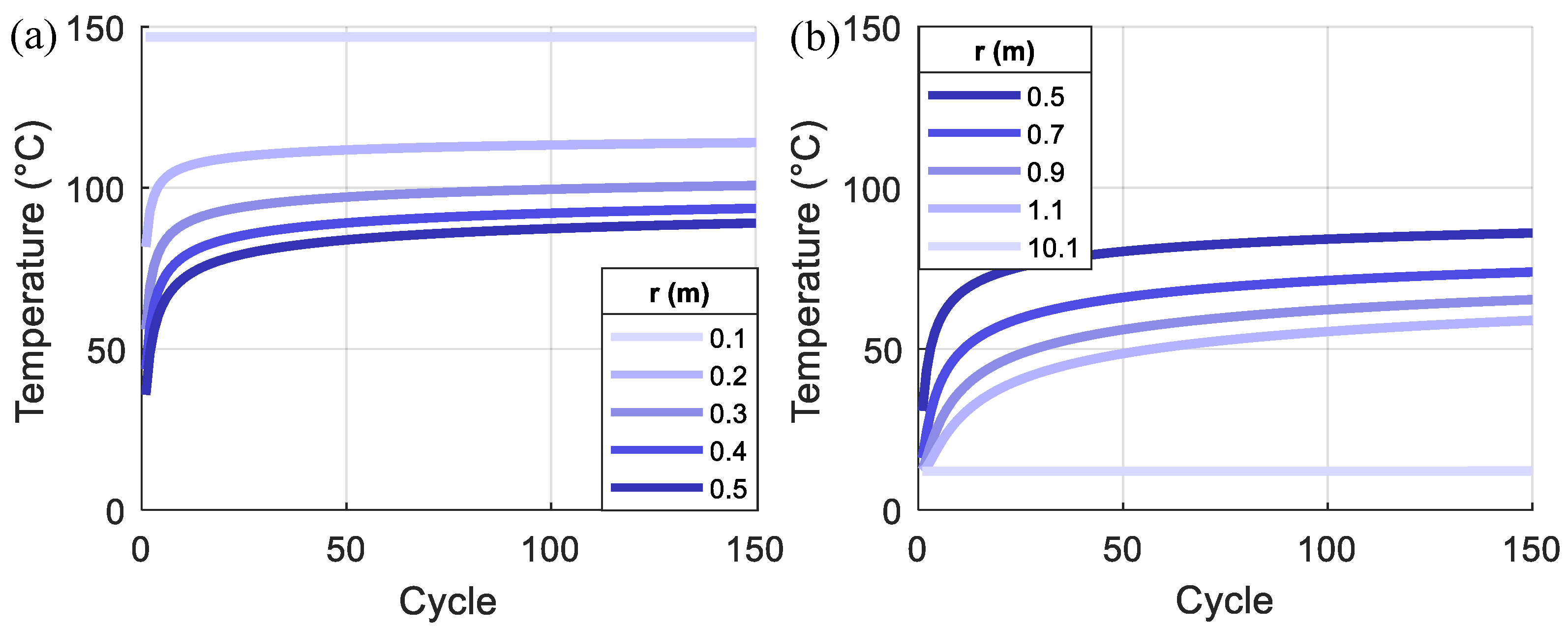
- The temperature in the pile foundation and nearby soil gradually increases with cycles because of the cumulative effect of the residual temperature. As moving from the inner surface to the outer, the increase of temperature with cycles and the temperature variation within each cycle become smaller.
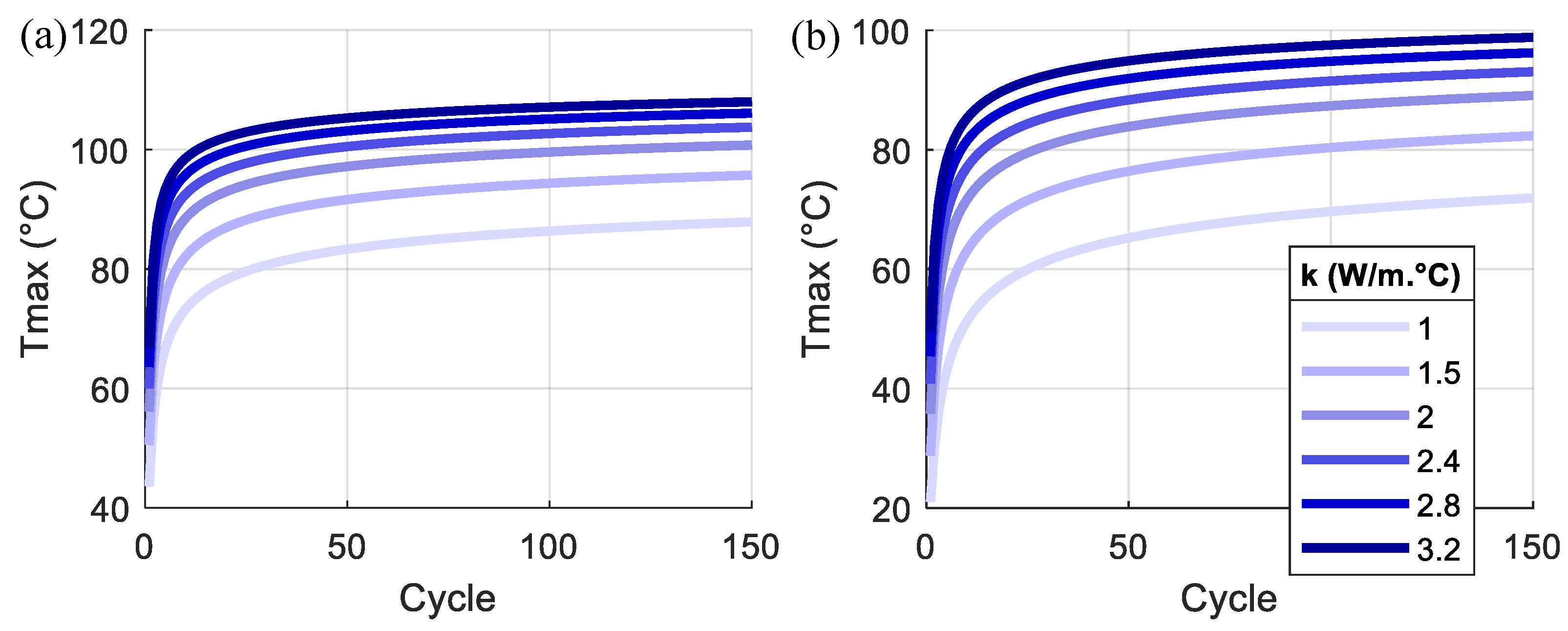
- The maximum temperature in each loading cycle increases with the loading cycles but starts to be converged at a stable value after a sufficient amount of cycles. As moving from the center of the pile foundation, more cycles are needed for the maximum temperature to be converged.
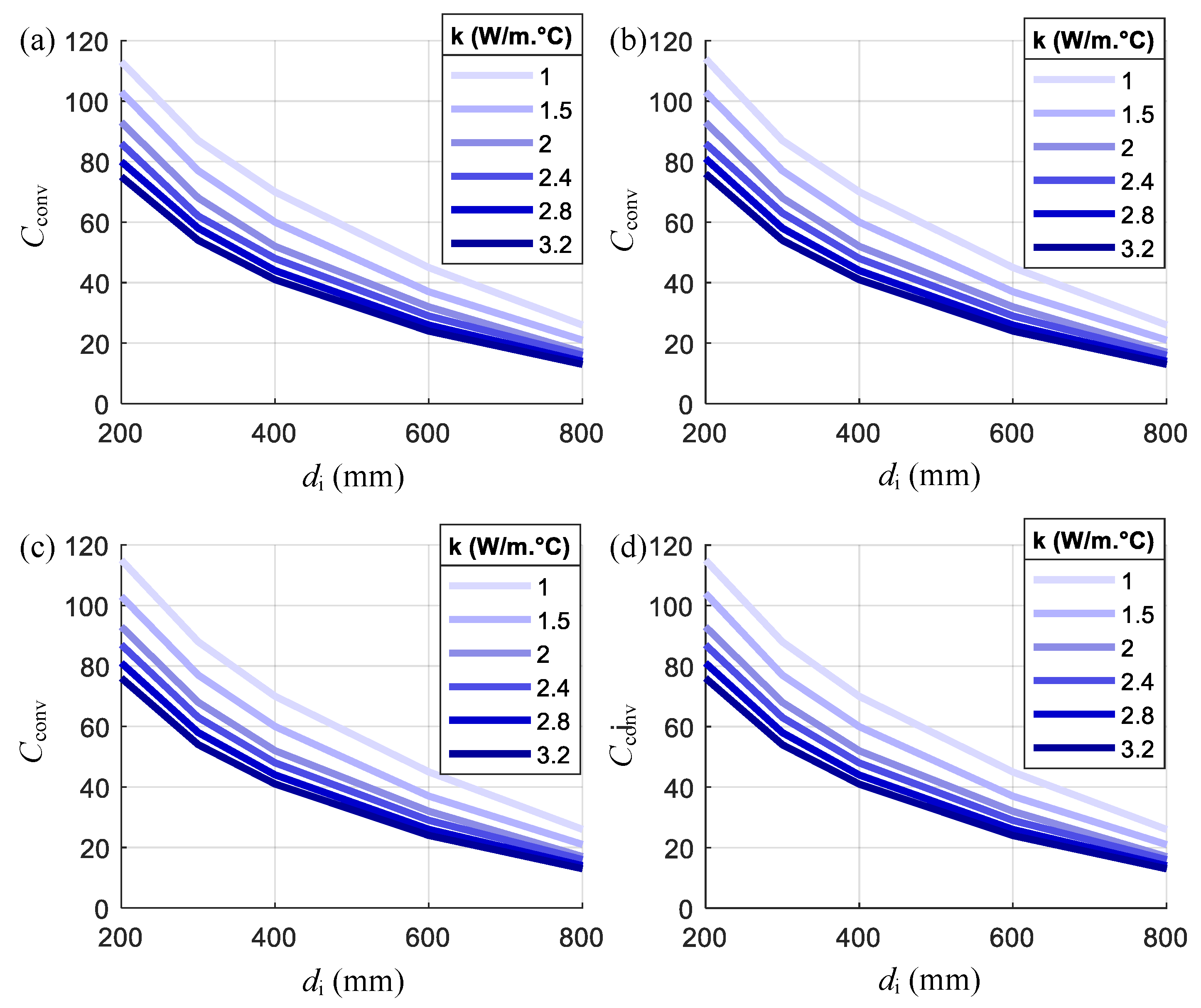
- As the di increases, the section thickness of the pile foundation reduces, which requires less time for the heat transfer from the inner surface to the outer. Therefore, the temperature change in the larger di cases is more significant, but the temperature distribution along the radius direction is more uniform. The convergence of the temperature variation between cycles in the pile foundation is faster for the larger di cases.
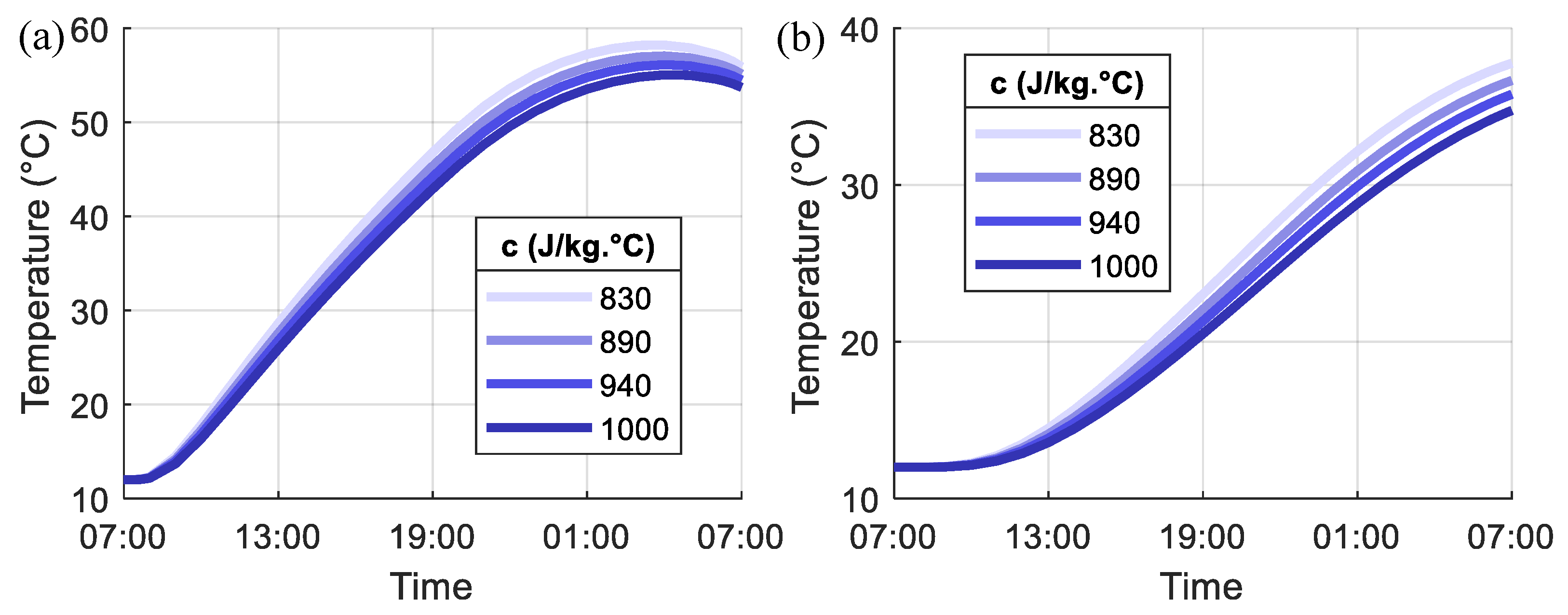
- As the k increases and c reduces, the heat transfer speed increases, which results in larger temperature changes and higher temperatures in the concrete pile foundation. The convergence of the temperature variation between cycles in the pile foundation also becomes faster as k increases and c reduces. The effect of c is much smaller than that of k.
Author Contributions
Funding
Conflicts of Interest
References
- Hayter, S.; Kandt, A. Renewable Energy Applications for Existing Buildings (Technical Report NREL/CP-7A40-52172); National Renewable Energy Lab. (NREL): Golden, CO, USA, 2011. [Google Scholar]
- Rugolo, J.; Aziz, M. Electricity storage for intermittent renewable sources. Energy Environ. Sci. 2012, 5, 7151–7160. [Google Scholar] [CrossRef]
- Zhang, L.; Ahmari, S.; Sternberg, B.; Budhu, M. Feasibility study of compressed air energy storage using steel pipe piles. In GeoCongress; ASCE: Reston, WV, USA, 2012. [Google Scholar]
- Kim, S.; Ko, J.; Kim, S.; Soo, H.; Tummalapudi, M. Investigation of a small-scale compressed air energy storage pile as a foundation system. In Geotechnical Frontiers 2017: Geotechnical Materials, Modeling, and Testing; GSP 280; ASCE: Reston, VA, USA, 2017. [Google Scholar]
- Sabirova, A.; Zhang, D.; Kim, J.; Nguyen, M.; Shon, C. Development of a reinforced concrete foundation system for renewable energy storage. In Proceedings of the 8th Asian Young Geotechnical Engineering Conference, Astana, Kazakhstan, 5–7 August 2016. [Google Scholar]
- Tulebekova, S.; Saliyev, D.; Zhang, D.; Kim, J.; Karabay, A.; Turlybek, A.; Kazybayeva, L. Preliminary analytical study on the feasibility of using reinforced concrete pile foundations for renewable energy storage by compressed air energy storage technology. In IOP Conference Series: Materials Science and Engineering; IOP Publishing Ltd.: London, UK, 2017; p. 012023. [Google Scholar]
- Zhang, D.; Kim, J.; Tulebekova, S.; Saliyev, D.; Lee, D.H. Structural responses of reinforced concrete pile foundations subjected to pressures from compressed air for renewable energy storage. Int. J. Concr. Struct. Mater. 2018, 12, 74. [Google Scholar] [CrossRef]
- Tulebekova, S.; Zhang, D.; Lee, D.; Kim, J.; Barissov, T.; Tsoy, V. Nonlinear responses of energy storage pile foundations with fiber reinforced concrete. Struct. Eng. Mech. 2019, 71, 363–375. [Google Scholar]
- Bektimirova, U.; Shon, C.; Zhang, D.; Sharafutdinov, E.; Kim, J. Proportioning and characterization of reactive powder concrete for an energy storage pile application. Appl. Sci. Switz. 2018, 8, 2507. [Google Scholar] [CrossRef]
- Bektimirova, U.; Tleuken, A.; Satekenova, E.; Shon, C.; Zhang, D.; Kim, J. Preliminary experimental investigation on the strength and air permeability of reactive powder concrete. Mater. Sci. Forum 2017, 917, 321–328. [Google Scholar] [CrossRef]
- Ko, J.; Seo, H.; Kim, S.; Kim, S. Numerical analysis for mechanical behavior of pipe pile utilized for compressed air energy storage. In IFCEE 2018: Installation, Testing, and Analysis of Deep Foundations; GSP 294; ASCE: Reston, VA, USA, 2018. [Google Scholar]
- Agibayeva, A.; Ju, H.; Zhang, D.; Moon, S.W.; Kim, J.; Lee, D.H. Application of CFT pile foundation as an energy storage media. In Proceedings of the 2018 International Conference on Advances in Computational Design, Incheon, South Korea, 28–31 August 2018. [Google Scholar]
- Laloui, L.; Nuth, M.; Vulliet, L. Experimental and numerical investigations of the behaviour of heat exchanger pile. Int. J. Numer. Anal. Methods Geomech. 2016, 30, 763–781. [Google Scholar] [CrossRef]
- Bourne-Webb, P.; Amatya, B.; Soga, K. A framework for understanding energy pile behaviour. Proc. Inst. Civ. Eng. Geotech. Eng. 2013, 166, 170–177. [Google Scholar] [CrossRef]
- Faizal, M.; Bouazza, A.; McCartney, J.S.; Haberfield, C. Effects of cyclic temperature variations on thermal response of an energy pile under a residential building. J. Geotech. Geoenviron. Eng. 2019, 145, 04019066. [Google Scholar] [CrossRef]
- Murphy, K.D.; McCartney, J.S.; Henry, K.S. Evaluation of thermo-mechanical and thermal behavior of full-scale energy foundations. Acta Geotech. 2015, 10, 179–195. [Google Scholar] [CrossRef]
- Di Donna, A.; Loria, A.F.R.; Laloui, L. Numerical study of the response of a group of energy piles under different combinations of thermo-mechanical loads. Comput. Geotech. 2016, 72, 126–142. [Google Scholar] [CrossRef]
- Surayatriyastuti, M.; Mroueh, H.; Burlon, S. Numerical analysis of a thermo-active pile under cyclic thermal loads. In Proceedings of the European Geothermal Conference (EGC 2013), Pisa, Italy, 3–7 June 2013; pp. 1–8. [Google Scholar]
- Assunção, R.M. Thermal and Thermal-Mechanical Analysis of Thermo-Active Pile Foundations. Ph.D. Thesis, Instituto Superior Técnico, University of Lisbon, Lisbon, Portugal, 2014. [Google Scholar]
- Energy Storage Association, Compressed Air Energy Storage, 2019. Available online: http://energystorage.org/compressed-air-energy-storage-caes (accessed on 25 October 2019).
- Kodur, V. Properties of concrete at elevated temperatures. ISRN Civ. Eng. 2014, 1–15. [Google Scholar] [CrossRef]
- Zhu, H.; Wan, K.T.; Satekenova, E.; Zhang, D.; Leung, C.; Kim, J. Development of Lightweight Strain Hardening Cementitious Composite for Structural Retrofit and Energy Efficiency Improvement of Unreinforced Masonry Housings. Constr. Build. Mater. 2018, 167, 791–812. [Google Scholar] [CrossRef]
- Ulykbanov, A.; Sharafutdinov, E.; Chung, C.W.; Zhang, D.; Shon, C.S. Performance-based Model to Predict Thermal Conductivity of Non-Autoclaved Aerated Concrete through Linearization Approach. Constr. Build. Mater. 2019, 196, 555–563. [Google Scholar] [CrossRef]
- Shon, C.S.; Mukashev, T.; Lee, D.H.; Zhang, D.; Kim, J.R. Can Common Reed Become an Effective Construction Material? Physical, Mechanical, and Thermal Properties of Mortar Mixture Containing Common Reed Fiber. Sustainability 2019, 11, 903. [Google Scholar] [CrossRef]
- Eurocode 2: Design of Concrete Structures: British Standard; BSI: London, UK, 2014.
- Shin, K.Y.; Kim, S.B.; Kim, J.H.; Chung, M.; Jung, P.S. Thermo-physical properties and transient heat transfer of concrete at elevated temperatures. Nucl. Eng. Des. 2002, 212, 233–241. [Google Scholar] [CrossRef]
- Lie, T.T.; Kodur, V.K.R. Thermal and mechanical properties of steel-fibre-reinforced concrete at elevated temperatures. Can. J. Civ. Eng. 1996, 23, 511–517. [Google Scholar] [CrossRef]
- Zheng, W.; Luo, B.; Wang, Y. Microstructure and mechanical properties of RPC containing PP fibres at elevated temperatures. Mag. Concr. Res. 2014, 66, 397–408. [Google Scholar] [CrossRef]
- Ju, Y.; Liu, H.B.; Liu, J.H.; Tian, K.P.; Wei, S.; Hao, S. Investigation on thermophysical properties of reactive powder concrete. Sci. China Technol. Sci. 2011, 54, 3382–3403. [Google Scholar] [CrossRef]
- Kodur, V.; Khaliq, W. Effect of temperature on thermal properties of different types of high-strength concrete. J. Mater. Civ. Eng. 2011, 23, 793–801. [Google Scholar] [CrossRef]
- Wan, L.; Wendner, R.; Liang, B.; Cusatis, G. Analysis of the behavior of ultra high performance concrete at early age. Cem. Concr. Compos. 2016, 74, 120–135. [Google Scholar] [CrossRef]
- Kersten, M.S. Thermal Properties of Soils; Bulletin No. 28; University of Minnesota: Minneapolis, MN, USA, 1949. [Google Scholar]
- ASHRAE. ASHRAE Handbook—Fundamentals (SI), American Society of Heating, Refrigerating and Air-Conditioning; ASHRAE: Atlanta, GA, USA, 2009. [Google Scholar]
- Abu-Hamdeh, N.H. Thermal properties of soils as affected by density and water content. Biosyst. Eng. 2003, 86, 97–102. [Google Scholar] [CrossRef]
- Thomas, H.R.; Rees, S.W. Measured and simulated heat transfer to foundation soils. Géotechnique 2009, 59, 365–375. [Google Scholar] [CrossRef]
- Brandl, H. Energy foundations and other thermo active ground structures. Geotechnique 2016, 56, 81–122. [Google Scholar] [CrossRef]

| Thermal Conductivity (k) | Specific Heat Capacity (c) | Inner Diameter (di) |
|---|---|---|
| [W/m·°C] | [J/kg·°C] | [mm] |
| 1.0 | 830 | 200 |
| 1.5 | 890 | 300 |
| 2.0 | 940 | 400 |
| 2.4 | 1000 | 600 |
| 2.8 | - | 800 |
| 3.2 | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Mamesh, Z.; Sailauova, D.; Shon, C.-S.; Lee, D.; Kim, J.R. Temperature Distributions inside Concrete Sections of Renewable Energy Storage Pile Foundations. Appl. Sci. 2019, 9, 4776. https://doi.org/10.3390/app9224776
Zhang D, Mamesh Z, Sailauova D, Shon C-S, Lee D, Kim JR. Temperature Distributions inside Concrete Sections of Renewable Energy Storage Pile Foundations. Applied Sciences. 2019; 9(22):4776. https://doi.org/10.3390/app9224776
Chicago/Turabian StyleZhang, Dichuan, Zhamilya Mamesh, Dilnura Sailauova, Chang-Seon Shon, Deuckhang Lee, and Jong R. Kim. 2019. "Temperature Distributions inside Concrete Sections of Renewable Energy Storage Pile Foundations" Applied Sciences 9, no. 22: 4776. https://doi.org/10.3390/app9224776
APA StyleZhang, D., Mamesh, Z., Sailauova, D., Shon, C.-S., Lee, D., & Kim, J. R. (2019). Temperature Distributions inside Concrete Sections of Renewable Energy Storage Pile Foundations. Applied Sciences, 9(22), 4776. https://doi.org/10.3390/app9224776






