Independent Random Recurrent Neural Networks for Infrared Spatial Point Targets Classification
Abstract
:1. Introduction
2. Infrared Radiation Sequence Model
2.1. Radiation Intensity Analysis
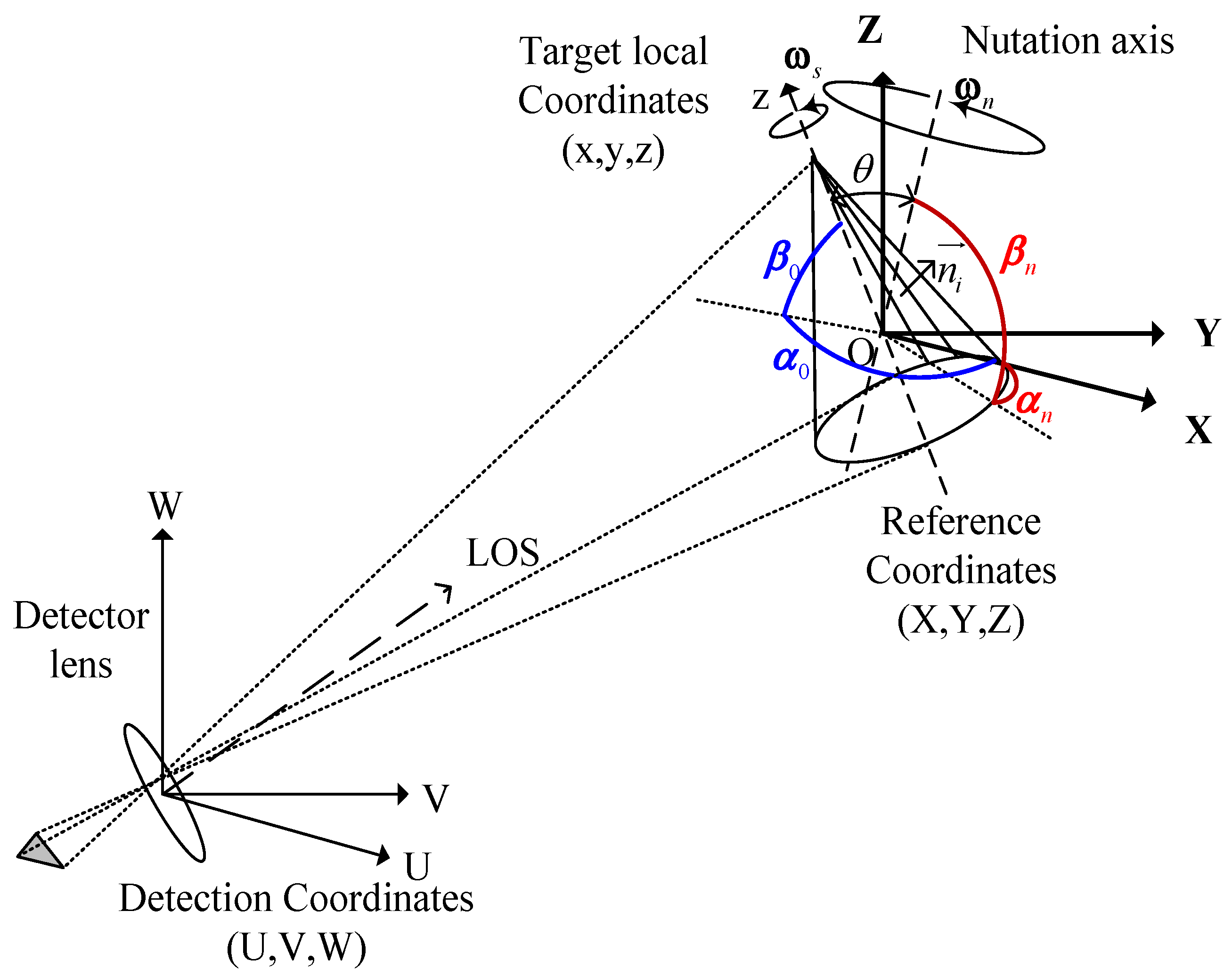
2.2. Attitude Motion Model
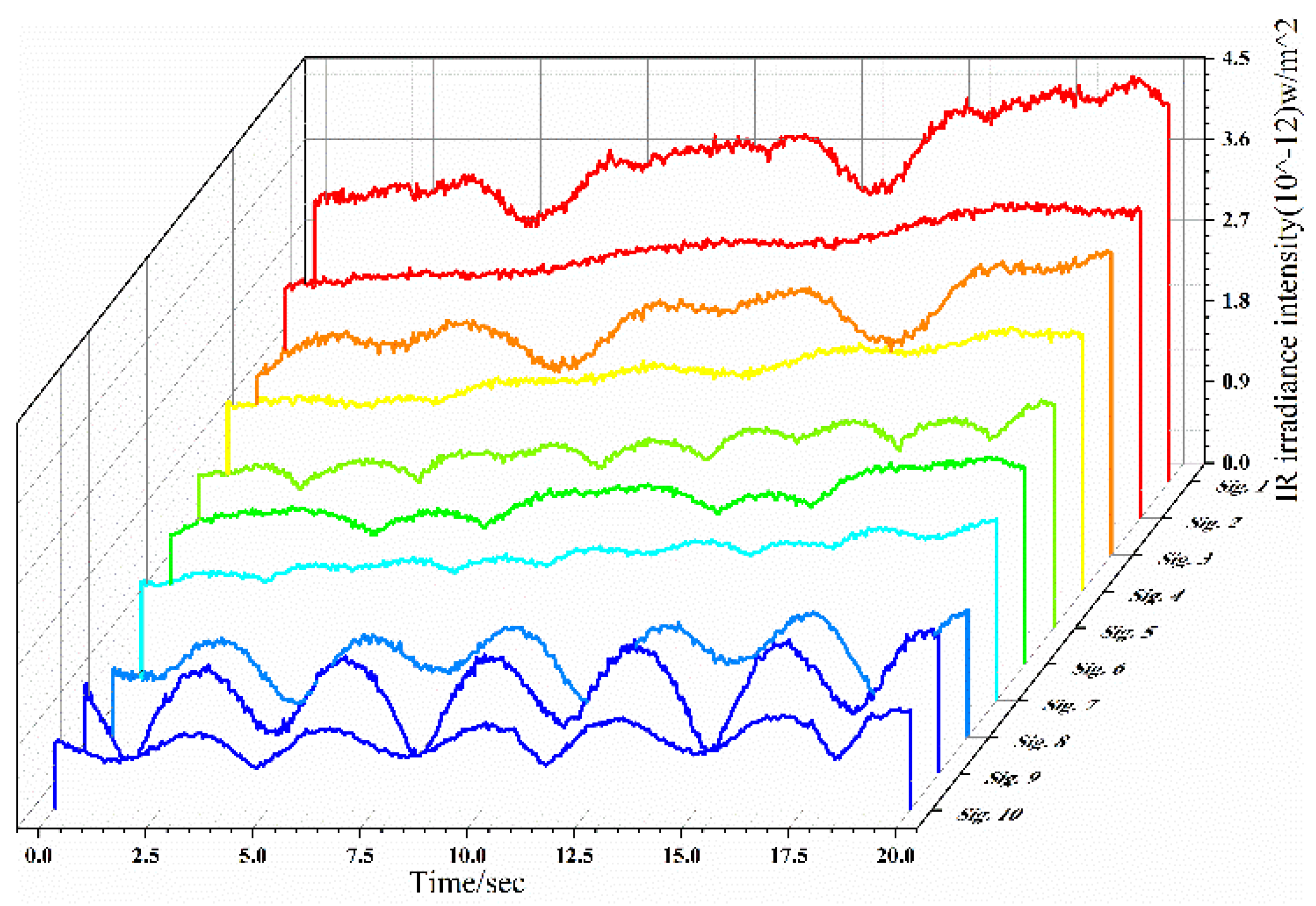
2.3. Infrared Radiation Sequence Simulation
3. Classification of IR Radiation Intensity Sequence Based on IRRNN
3.1. Structure of IndRNN
3.1.1. Analysis of IndRNN Structure
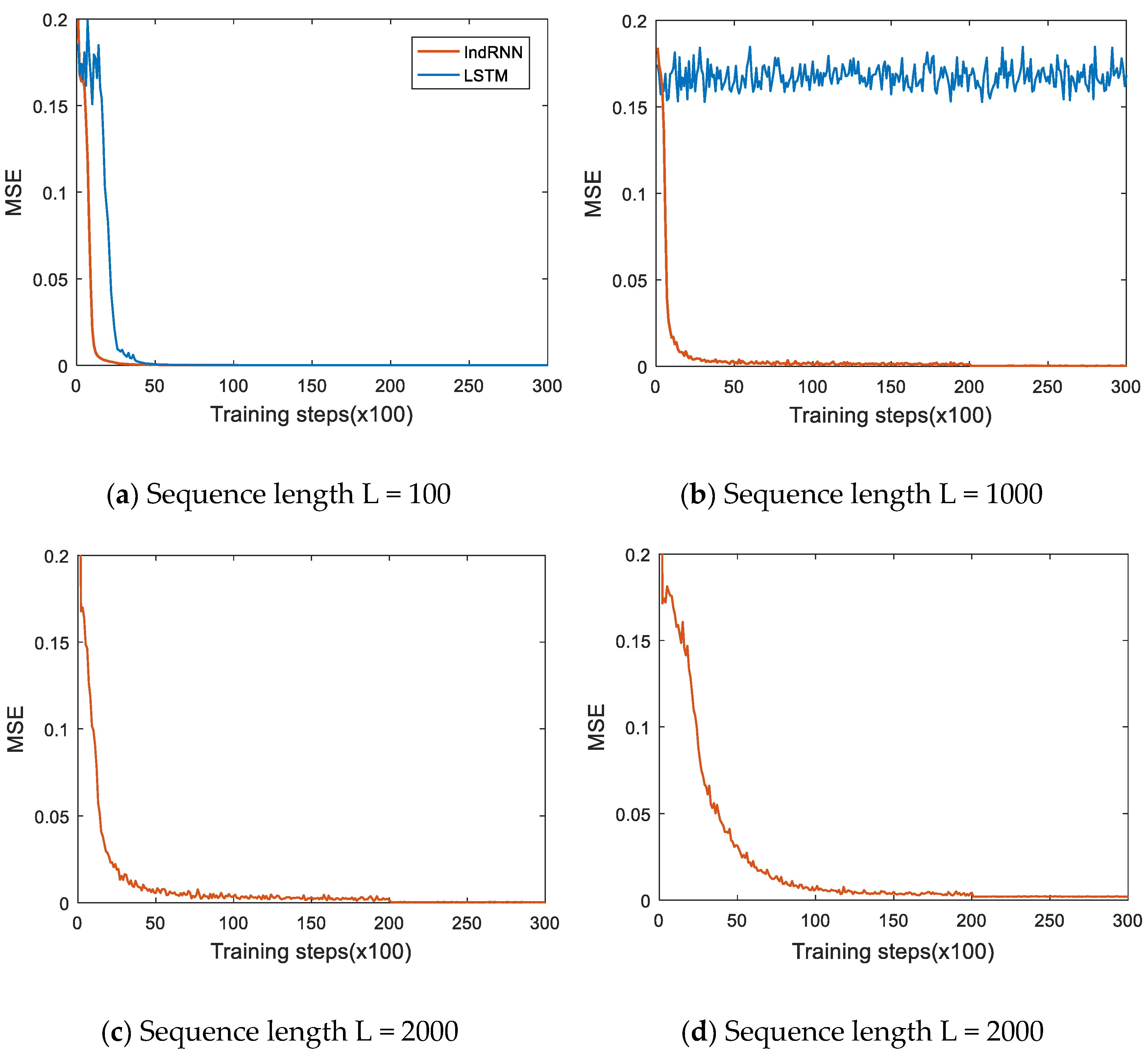
3.1.2. Experiments to Process Long Sequences
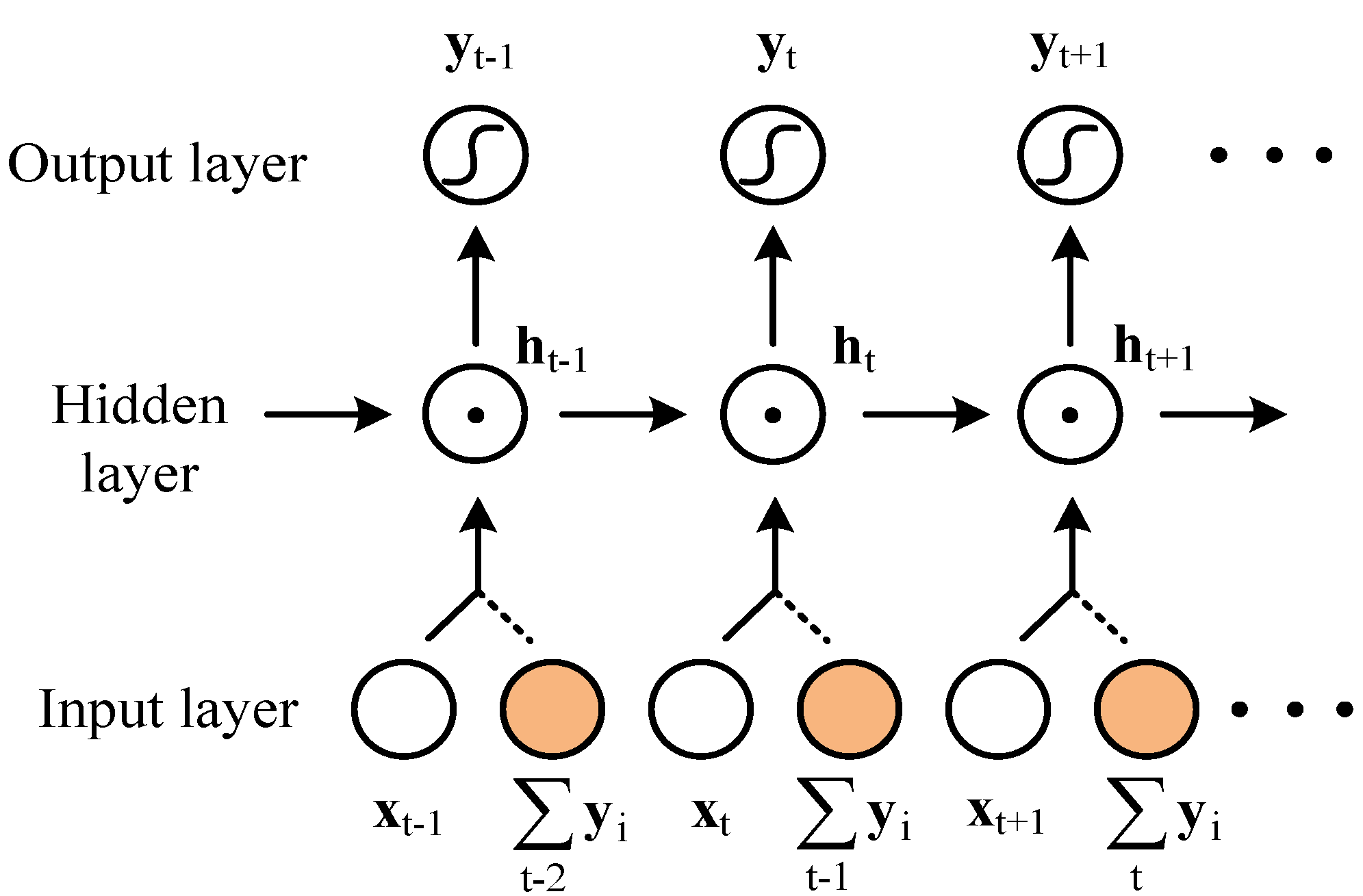
3.2. Structure of RRNN
3.3. Classification Algorithm Based on IRRNN
3.3.1. IRRNN Overall Structure and Algorithm
| Algorithm 1 Training process of time series classification algorithm based on IRRNN. |
1. Determine network parameters:
The training set, validation set, and testing set are divided according to 2:1:1, and generate random weighted matrix W1, W2,…, WT-1. 3. Initialize network weights and offset parameters: Determine the initial value of WHI, w, WHO, BH, BO, etc. 4. Training process: Assume that currently all N sequences in the training sample set for the kth pass, take sequence X(n) = [x1, x2, …, xT] as example (1) For training sample xt at time step t, calculate the value of the network output value and loss function lt, etc. \ (2) Calculate the loss function for all time steps from 1 to T (3) Calculate the gradient of loss function Etrain to parameters , , , etc. (4) Update the network parameters by gradient descent with momentum optimization method, and obtain , , , etc. where m is momentum parameters, m [0, 1]; and λ is the learning rate, α [0, 1]. (5) Enter the next sequence X(n’) in the training sample set and repeat the training process in steps (1) to (4) until all N sample sequences are processed through the network and proceed to the next step. 5. Stop the training, when the training error reaches the threshold. 6. Save the trained network parameters. |
3.3.2. Bi-Direction Extension Structure of IRRNN
4. Experiments and Discussion
4.1. URC Data Set Classification Experiment
4.2. Classification Experiment of Radiation Intensity Sequences
4.2.1. Classification Experiment
4.2.2. Effect of Noise and Sequence Length
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gronlund, L. Countermeasures to the US National Missile Defense. In Proceedings of the Aps April Meeting, Washington, DC, USA, 28 April–1 May 2001. [Google Scholar]
- Resch, C.L. Neural network for exo-atmospheric target discrimination. Proc. SPIE Int. Soc. Opt. Eng. 1998, 3371, 119–128. [Google Scholar]
- Chen, V.C.; Li, F.; Ho, S.S.; Wechsler, H. Micro-Doppler effect in radar: Phenomenon, model, and simulation study. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 2–21. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Chen, S.; Lu, H.; Zhao, B. Micro-motion dynamics analysis of ballistic targets based on infrared detection. J. Syst. Eng. Electron. 2017, 28, 472–480. [Google Scholar]
- Huang, L.; Li, X.; Liu, J. IR radiative properties modeling and feature extraction method on ballistic target. In Proceedings of the Seventh International Conference on Digital Image Processing (ICDIP 2015), Los Angeles, CA, USA, 9–10 April 2015. [Google Scholar]
- Qiu, C.; Zhang, Z.; Lu, H.; Zhang, K. Infrared modeling and imaging simulation of midcourse ballistic targets based on strap-down platform. Syst. Eng. Electron. 2014, 25, 776–785. [Google Scholar] [CrossRef]
- Wang, H.Y.; Zhang, W.; Wang, F.G. Visible characteristics of space-based targets based on bidirectional reflection distribution function. Sci. China Technol. Sci. 2012, 55, 982–989. [Google Scholar] [CrossRef]
- Li, F.; Xu, X. Modeling Time-Evolving Infrared Characteristics for Space Objects with Micromotions. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3567–3577. [Google Scholar] [CrossRef]
- Liu, L.; Du, X.; Ghogho, M.; Hu, W.; McLernon, D. Precession missile feature extraction using the sparse component analysis based on radar measurement. EURASIP J. Adv. Signal Process. 2012, 24. [Google Scholar] [CrossRef]
- Wang, J.; Yang, C. Exo-atmospheric target discrimination using probabilistic neural network. Chin. Opt. Lett. 2011, 9, 070101. [Google Scholar] [CrossRef]
- Bengio, Y. Learning deep architectures for AI. In Foundations Trends Machine Learning; Now Publishers Inc: Hanover, MA, USA, 2009; Volume 2, pp. 1–27. [Google Scholar]
- Graves, A. Supervised Sequence Labeling with Recurrent Neural Networks; Springer: New York, NY, USA, 2012. [Google Scholar]
- Ma, Y.; Chang, Q.; Lu, H.; Liu, J. Reconstruct Recurrent Neural Networks via Flexible Sub-Models for Time Series Classification. Appl. Sci. 2018, 8, 630. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Hammer, B. On the approximation capability of recurrent neural networks. Neurocomputing 2000, 31, 107–123. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Beringer, N.; Schmidhuber, J. Rapid Retraining on Speech Data with LSTM Recurrent Networks; Technical Report No. IDSIA–09–05; Instituto Dalle Molle di studi sull’ intelligenza artificiale: Manno, Switzerland, 2005. [Google Scholar]
- Pierre, B.; Soren, B.; Paolo, F.; Gianluca, P.; Giovanni, S. Bidirectional Dynamics for Protein Secondary Structure Prediction. Seq. Learn. Paradig. Algorithms Appl. 2000, 21, 99–120. [Google Scholar]
- Baldi, P.; Brunak, S.; Frasconi, P.; Pollastri, G.; Soda, G. How to construct deep recurrent neural networks. In Proceedings of the International Conference on Learning Representation, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Li, S.; Li, W.; Cook, C.; Zhu, C.; Gao, Y. Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN. Comput. Vis. and n.a. Recognit. 2018. [Google Scholar] [CrossRef]
- Linares, R.; Jah, M.; Crassidis, J.L.; Christopher, K.N. Space object shape characterization and tracking using light curve and angles data. J. Guid. Control Dyn. 2014, 37, 13–26. [Google Scholar] [CrossRef]
- Wu, Y.; Lu, H.; Zhao, F.; Zhang, Z. Estimating Shape and Micro-Motion Parameter of Rotationally Symmetric Space Objects from the Infrared Signature. Sensors 2016, 16, 1722. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, S.; Lu, H.; Zhao, B. Ballistic targets micro-motion and geometrical shape parameters estimation from sparse decomposition representation of infrared signatures. Appl. Opt. 2017, 56, 1276–1285. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, S.; Lu, H.; Zhao, B. Nutation characteristics analysis and infrared signature simulation of ballistic targets. In Proceedings of the Advanced Information Technology, Electronic and Automation Control Conference, Chongqing, China, 25–26 March 2017; pp. 1001–1005. [Google Scholar]
- Wetterer, C.J.; Jah, M. Attitude estimation from light curves. J. Guid. Control Dyn. 2009, 32, 1648–1651. [Google Scholar] [CrossRef]
- Kaasalainen, M.; Torppa, J. Optimization methods for asteroid light-curve inversion I: Shape determination. Icarus 2001, 153, 24–36. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps; Springer: Berlin, Heidelberg, 2001. [Google Scholar]
- An, G. The effects of adding noise during back-propagation training on a generalization performance. Neural Comput. 1996, 8, 643–674. [Google Scholar] [CrossRef]



| Parameters | Type1 | Type2 | Type3 | Type4 |
|---|---|---|---|---|
| 3Dmodels | 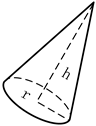 | 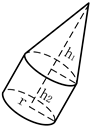 | 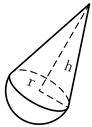 | 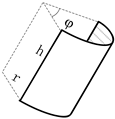 |
| Size parameters | r = 0.3 ± 0.05 m h = 1.0 ± 0.25 m | r = 0.3 ± 0.05 m h1 = 0.4 ± 0.15 m h2 = 0.6 ± 0.10 m | r = 0.3 ± 0.05 m h = 1.0 ± 0.25 m | r = 0.30 ± 0.10 m h = 0.5 ± 0.20 m φ = 0.6 ± 0.1π |
| Micro-motion | Spinning and coning | Spinning and coning | Tumbling | Tumbling |
| Micro-motion parameters | θ = 0.2π ωs = 5.0π rad/s αc = 0.0π βc = 0.35π ωc = 1.0π rad/s | θ = 0.2π ωs = 5.0π rad/s αc = 0.0π βc = 0.35π ωc = 1.0π rad/s | θ = 0.3π αt = 0.0π βt = 0.3π ωt = 1.0π rad/s | θ = 0.3π αt = 0.0π βt = 0.2π ωt = 1.0π rad/s |
| Coating material αV/ε IR | 0.85/0.7 | 0.25/0.50 | 0.25/0.50 | 0.52/0.20 |
| Target weight (g) | 200 | 120 | 85 | 45 |
| Initial temperature (K) | 320 | 320 | 320 | 680 |
| Radiation Intensity Sequence | 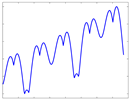 | 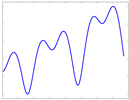 | 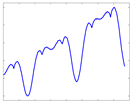 | 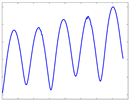 |
| Name | Sequence Length | Accuracy | |||
|---|---|---|---|---|---|
| FNNs | RNNs | LSTM | IRRNN | ||
| ECG200 | 96 | 0.8189 | 0.8433 | 0.8650 | 0.8974 |
| ArrowHead | 251 | 0.7495 | 0.8012 | 0.8166 | 0.8285 |
| SyntheticControl | 60 | 0.7230 | 0.7432 | 0.7843 | 0.7812 |
| OSULeaf | 427 | 0.5823 | 0.6059 | 0.6337 | 0.6828 |
| FaceAll | 131 | 0.5541 | 0.5722 | 0.5870 | 0.6931 |
| SwedishLeaf | 128 | 0.7419 | 0.7692 | 0.7705 | 0.8131 |
| FiftyWords | 270 | 0.3932 | 0.4239 | 0.5152 | 0.6549 |
| Observing Time (s) | Accuracy | ||||
|---|---|---|---|---|---|
| RNNs | IndRNN | RRNN | IRRNN | B-IRRNN | |
| 8 | 0.6375 | 0.8081 | 0.7729 | 0.8856 | 0.9124 |
| 16 | 0.7449 | 0.8424 | 0.8302 | 0.8987 | 0.9176 |
| 24 | 0.7892 | 0.8840 | 0.8743 | 0.9101 | 0.9315 |
| Observing Time (s) | Accuracy | ||||
|---|---|---|---|---|---|
| RNNs | IndRNN | RRNN | IRRNN | B-IRRNN | |
| 8 | 0.6503 | 0.7985 | 0.7946 | 0.8822 | 0.9048 |
| 16 | 0.7455 | 0.8393 | 0.8420 | 0.8995 | 0.9109 |
| 24 | 0.7917 | 0.8867 | 0.8851 | 0.9098 | 0.9272 |
| Observing Time (s) | Accuracy | ||||
|---|---|---|---|---|---|
| RNNs | IndRNN | RRNN | IRRNN | B-IRRNN | |
| 8 | 0.6416 | 0.7953 | 0.7864 | 0.8751 | 0.8939 |
| 16 | 0.7568 | 0.8413 | 0.8395 | 0.8903 | 0.9120 |
| 24 | 0.8059 | 0.8725 | 0.8874 | 0.9026 | 0.9234 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Lu, H.; Hu, M.; Zhao, B. Independent Random Recurrent Neural Networks for Infrared Spatial Point Targets Classification. Appl. Sci. 2019, 9, 4622. https://doi.org/10.3390/app9214622
Wu D, Lu H, Hu M, Zhao B. Independent Random Recurrent Neural Networks for Infrared Spatial Point Targets Classification. Applied Sciences. 2019; 9(21):4622. https://doi.org/10.3390/app9214622
Chicago/Turabian StyleWu, Dongya, Huanzhang Lu, Moufa Hu, and Bendong Zhao. 2019. "Independent Random Recurrent Neural Networks for Infrared Spatial Point Targets Classification" Applied Sciences 9, no. 21: 4622. https://doi.org/10.3390/app9214622
APA StyleWu, D., Lu, H., Hu, M., & Zhao, B. (2019). Independent Random Recurrent Neural Networks for Infrared Spatial Point Targets Classification. Applied Sciences, 9(21), 4622. https://doi.org/10.3390/app9214622




