Multi-Sensor Face Registration Based on Global and Local Structures
Abstract
1. Introduction
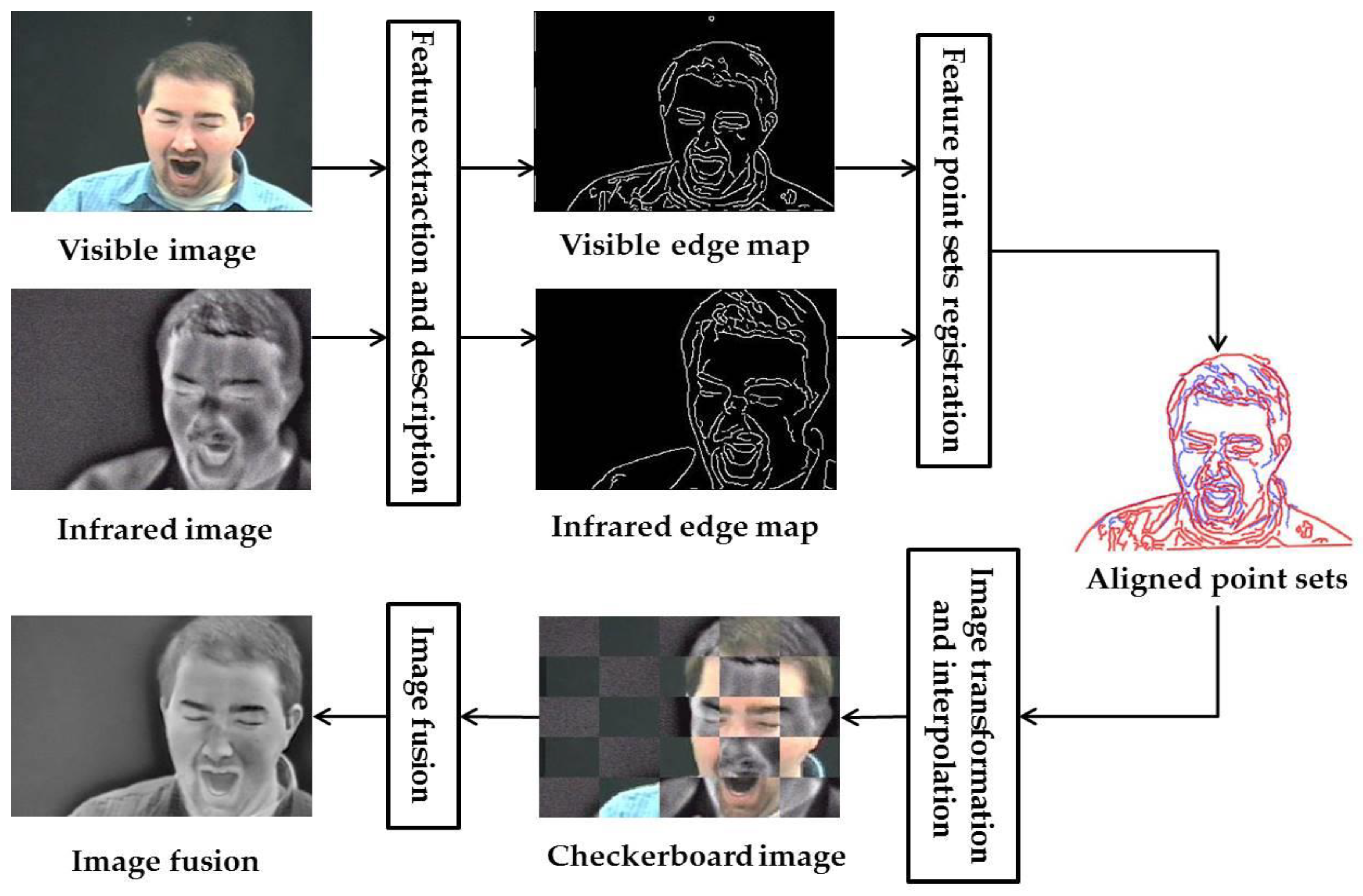
2. The Proposed Registration Method for Visible and Infrared Face Images
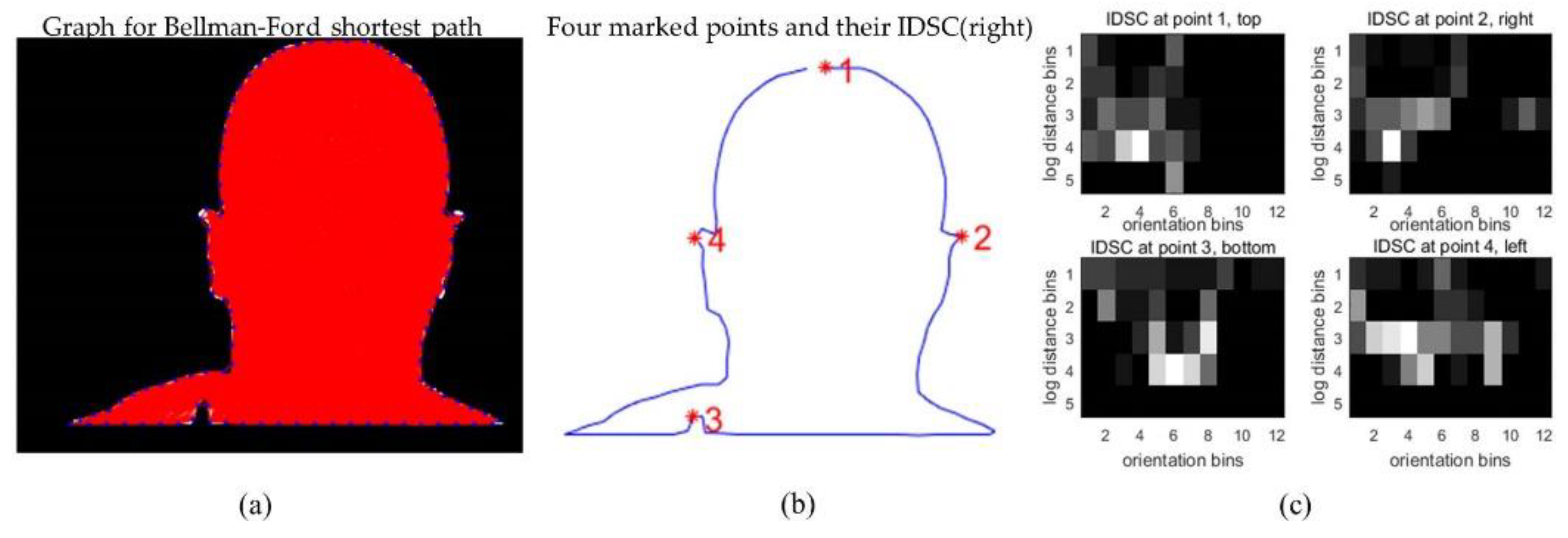
2.1. Inner-Distance Shape Context for 2D Feature Descriptors
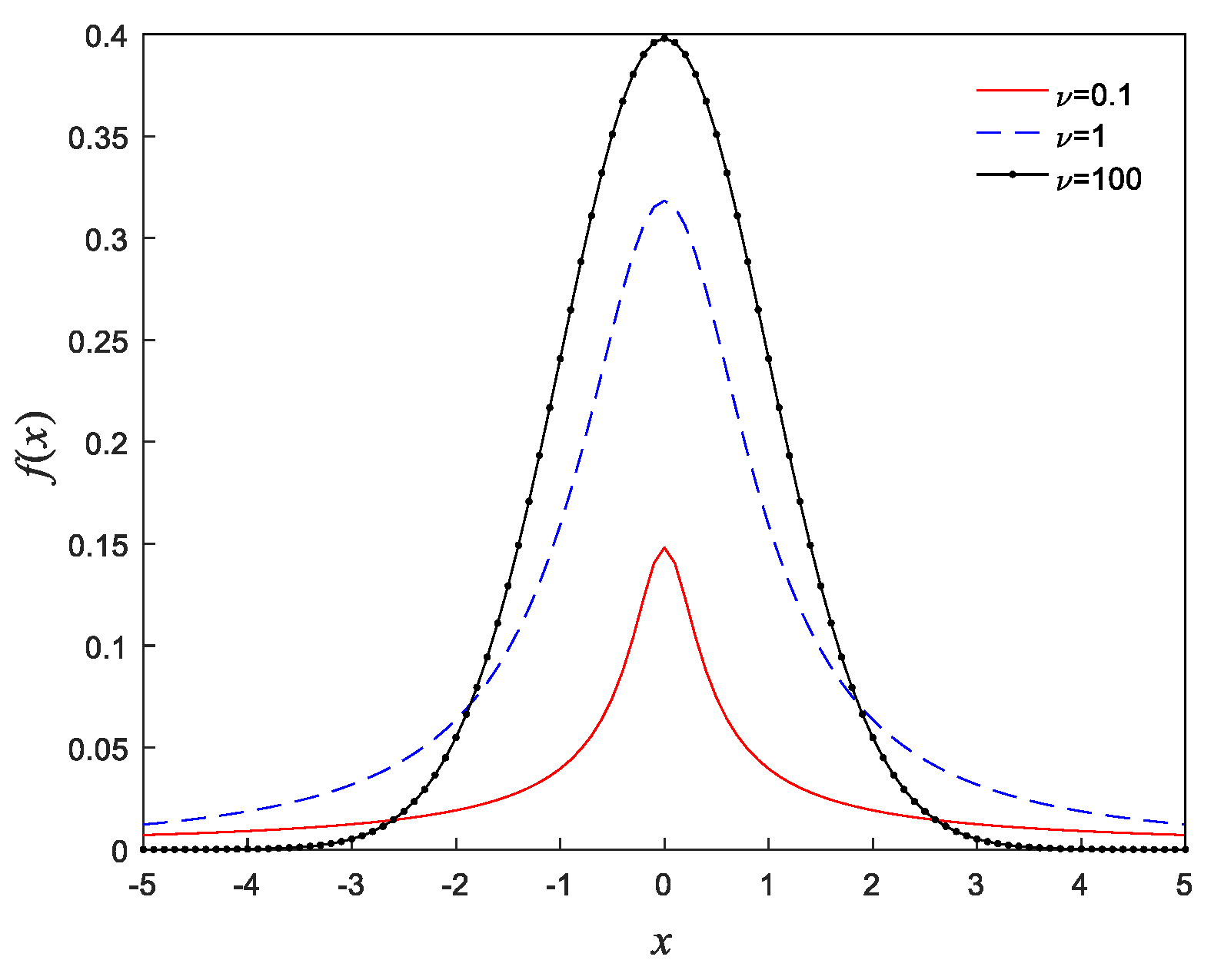
2.2. Student’s t Mixtures for Feature Point Set Registration
2.3. Multi-Spectral Face Registration Using Global and Local Structures
3. The Proposed Fusion Strategies for Visible and Infrared Face Images
4. Experimental Results
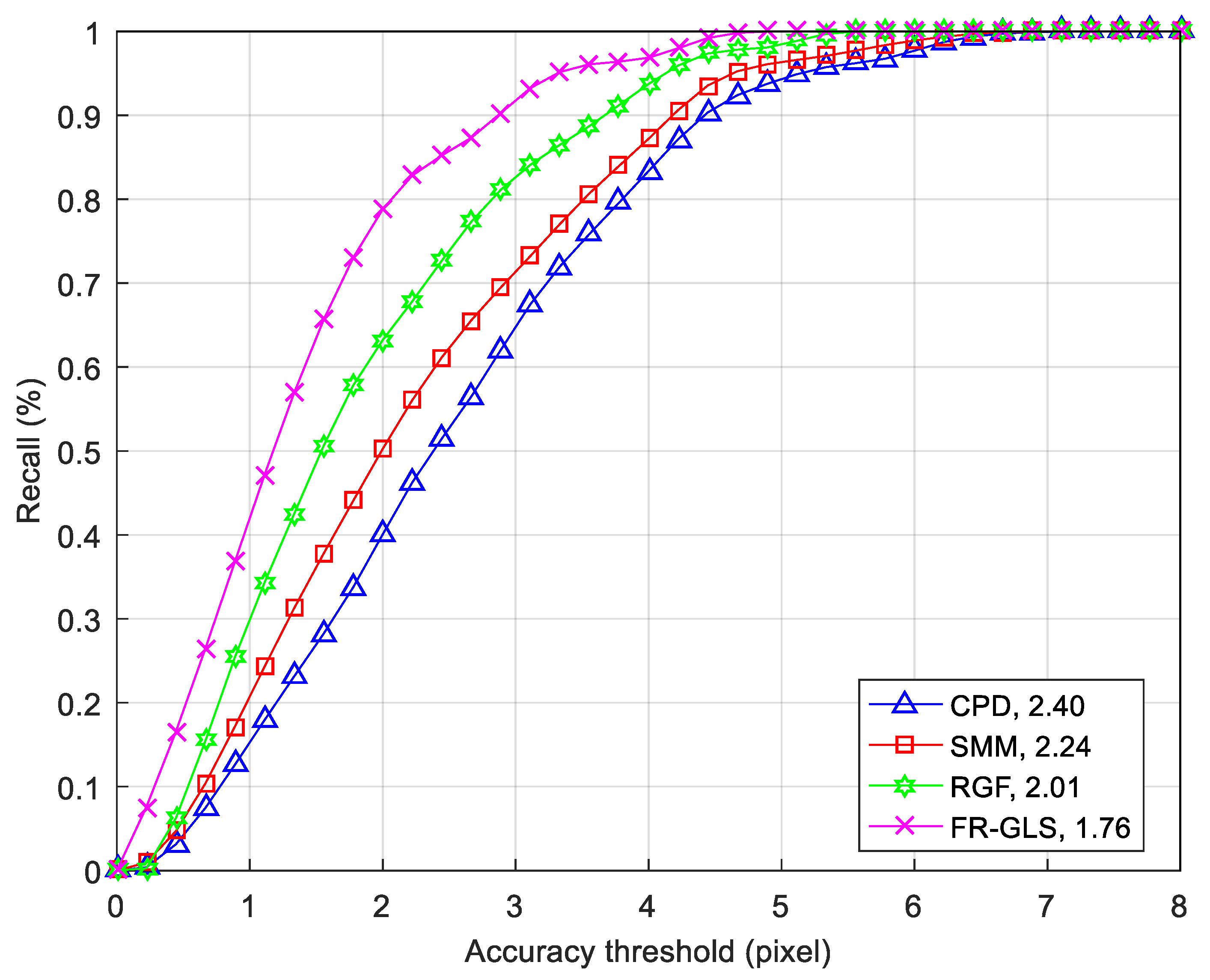
4.1. Registration on Real Face Images with the UTK-IRIS Database
4.1.1. Qualitative Evaluation
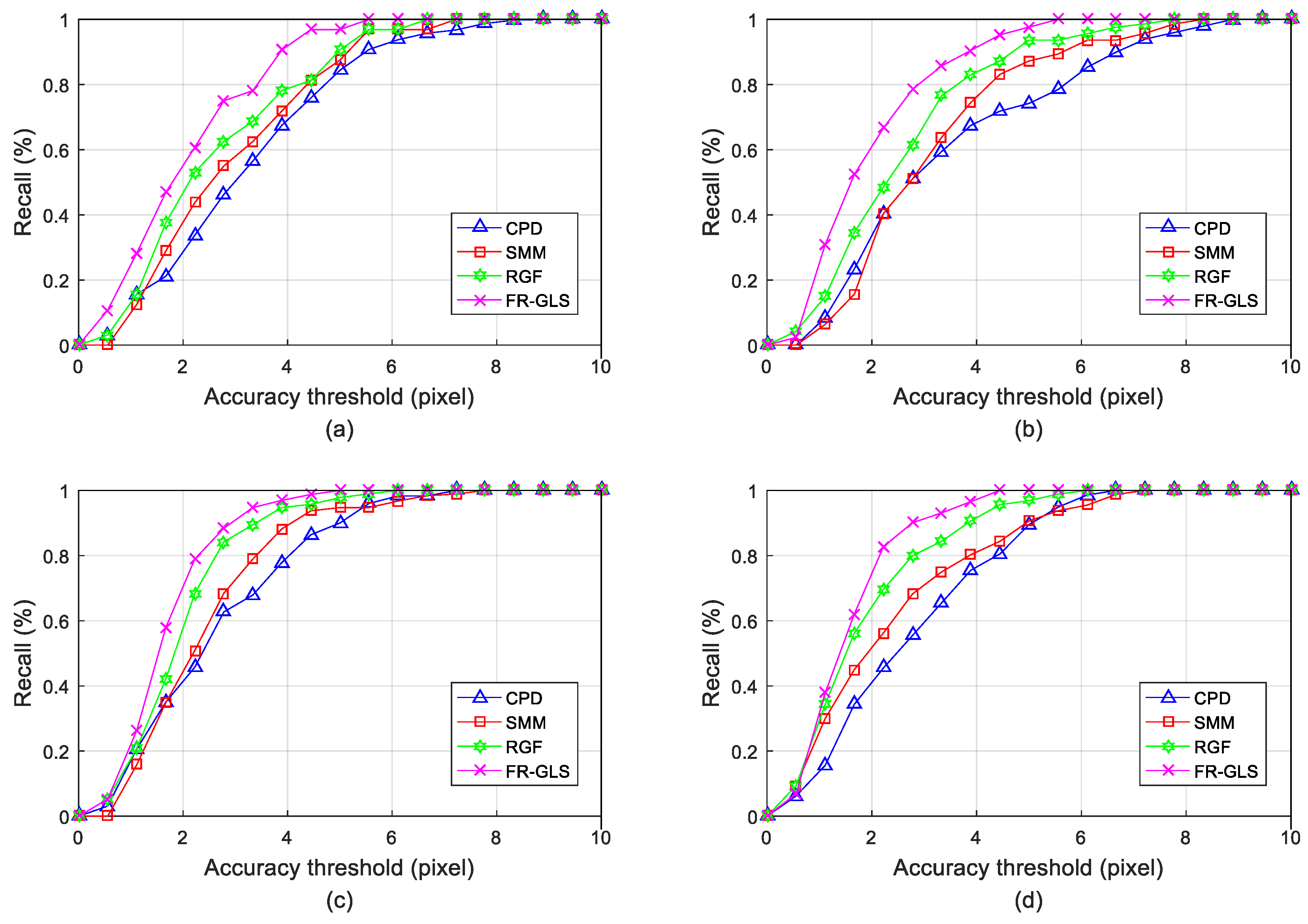
4.1.2. Quantitative Evaluation
4.2. Registration on Real Face Images of Self-Built Multi-Spectral Database
4.2.1. Qualitative Comparison
4.2.2. Quantitative Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ma, J.; Ma, Y.; Li, C. Infrared and visible image fusion methods and applications: A survey. Inf. Fusion 2019, 45, 153–178. [Google Scholar] [CrossRef]
- Ma, J.; Yu, W.; Liang, P. FusionGAN: A generative adversarial network for infrared and visible image fusion. Inf. Fusion 2019, 48, 11–26. [Google Scholar] [CrossRef]
- Huang, Y.; Bi, D.; Wu, D. Infrared and visible image fusion based on different constraints in the non-subsampled shearlet transform domain. Sensors 2018, 18, 1169. [Google Scholar] [CrossRef]
- Ma, J.; Chen, C.; Li, C. Infrared and visible image fusion via gradient transfer and total variation minimization. Inf. Fusion 2016, 31, 100–109. [Google Scholar] [CrossRef]
- Paramanandham, N.; Rajendiran, K. Infrared and visible image fusion using discrete cosine transform and swarm intelligence for surveillance applications. Infrared Phys. Technol. 2018, 88, 13–22. [Google Scholar] [CrossRef]
- Zhu, Z.; Qi, G.; Chai, Y. A geometric dictionary learning based approach for fluorescence spectroscopy image fusion. Appl. Sci. 2017, 7, 161. [Google Scholar] [CrossRef]
- Singh, R.; Vatsa, M.; Noore, A. Integrated multilevel image fusion and match score fusion of visible and infrared face images for robust face recognition. Pattern Recognit. 2008, 41, 880–893. [Google Scholar] [CrossRef]
- Vizgaitis, J.N.; Hastings, A.R. Dual band infrared picture-in-picture systems. Opt. Eng. 2013, 52, 061306. [Google Scholar] [CrossRef]
- Kong, S.G.; Heo, J.; Boughorbel, F. Multiscale fusion of visible and thermal IR images for illumination-invariant face recognition. Int. J. Comput. Vis. 2007, 71, 215–233. [Google Scholar] [CrossRef]
- Oliveira, F.P.M.; Tavares, J.M.R.S. Medical image registration: A review. Comput. Method Biomech. 2014, 17, 73–93. [Google Scholar] [CrossRef]
- Avants, B.B.; Epstein, C.L.; Grossman, M. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 2008, 12, 26–41. [Google Scholar] [CrossRef]
- Pan, W.; Qin, K.; Chen, Y. An adaptable-multilayer fractional fourier transform approach for image registration. IEEE Trans. Pattern Anal. 2008, 31, 400–414. [Google Scholar] [CrossRef]
- Zhuang, Y.; Gao, K.; Miu, X. Infrared and visual image registration based on mutual information with a combined particle swarm optimization—Powell search algorithm. Optik Int. J. Light Electron Opt. 2016, 127, 188–191. [Google Scholar] [CrossRef]
- Sotiras, A.; Davatzikos, C.; Paragios, N. Deformable medical image registration: A survey. IEEE Trans. Med. Imaging 2013, 32, 1153–1190. [Google Scholar] [CrossRef]
- Viergever, M.A.; Maintz, J.B.A.; Klein, S. A survey of medical image registration–under review. Med. Image Anal. 2016, 33, 140–144. [Google Scholar] [CrossRef]
- Moghbel, M.; Mashohor, S.; Mahmud, R. Review of liver segmentation and computer assisted detection/diagnosis methods in computed tomography. Artif. Intell. Rev. 2018, 50, 497–537. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, D.; Sun, J. Adaptive convolutional neural network and its application in face recognition. Neural Process. Lett. 2016, 43, 389–399. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Z.; Li, Z. Joint face detection and alignment using multitask cascaded convolutional networks. IEEE Signal. Proc. Lett. 2016, 23, 1499–1503. [Google Scholar] [CrossRef]
- Myronenko, A.; Song, X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Ma, Y. Non-rigid visible and infrared face registration via regularized Gaussian fields criterion. Pattern Recognit. 2015, 48, 772–784. [Google Scholar] [CrossRef]
- Tian, T.; Mei, X.; Yu, Y. Automatic visible and infrared face registration based on silhouette matching and robust transformation estimation. Infrared Phys. Technol. 2015, 69, 145–154. [Google Scholar] [CrossRef]
- Peel, D.; McLachlan, G.J. Robust mixture modelling using the t distribution. Stat. Comput. 2000, 10, 339–348. [Google Scholar] [CrossRef]
- Gerogiannis, D.; Nikou, C.; Likas, A. Robust Image Registration using Mixtures of t-distributions. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Gerogiannis, D.; Nikou, C.; Likas, A. The mixtures of Student’s t-distributions as a robust framework for rigid registration. Image Vis. Comput. 2009, 27, 1285–1294. [Google Scholar] [CrossRef]
- Zhou, Z.; Zheng, J.; Dai, Y. Robust non-rigid point set registration using student’s-t mixture mode. PloS ONE 2014, 9, e91381. [Google Scholar]
- Zhou, Z.; Tu, J.; Geng, C. Accurate and robust non-rigid point set registration using student’s t mixture model with prior probability modeling. Sci. Rep. UK 2018, 8, 8742. [Google Scholar] [CrossRef]
- Maiseli, B.; Gu, Y.; Gao, H. Recent developments and trends in point set registration methods. J. Vis. Commun. Image Represent. 2017, 46, 95–106. [Google Scholar] [CrossRef]
- Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef]
- Ling, H.; Jacobs, D.W. Shape classification using the inner-distance. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 286–299. [Google Scholar] [CrossRef]
- Li, H.; Wu, X.J. DenseFuse: A Fusion Approach to Infrared and Visible Images. IEEE Trans. Image Process. 2018, 28, 2614–2623. [Google Scholar] [CrossRef]
- Chui, H.; Rangarajan, A. A new point matching algorithm for non-rigid registration. Comput. Vis. Image Underst. 2003, 89, 114–141. [Google Scholar] [CrossRef]
- Riesen, K.; Bunke, H. Approximate graph edit distance computation by means of bipartite graph matching. Image Vis. Comput. 2009, 27, 950–959. [Google Scholar] [CrossRef]
- Li, S.; Kang, X.; Hu, J. Image fusion with guided filtering. IEEE Trans. Image Process. 2013, 22, 2864–2875. [Google Scholar] [PubMed]
- UTK-IRIS Database. Available online: http://www.cse.ohio-state.edu/otcbvs-bench/ (accessed on 10 September 2015).
- Dwith, C.; Ghassemi, P.; Pfefer, T. Free-form deformation approach for registration of visible and infrared facial images in fever screening. Sensors 2018, 18, 125. [Google Scholar] [CrossRef] [PubMed]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Dong, M.; Lu, N.; Lou, X.; Zhou, W. Multi-Sensor Face Registration Based on Global and Local Structures. Appl. Sci. 2019, 9, 4623. https://doi.org/10.3390/app9214623
Li W, Dong M, Lu N, Lou X, Zhou W. Multi-Sensor Face Registration Based on Global and Local Structures. Applied Sciences. 2019; 9(21):4623. https://doi.org/10.3390/app9214623
Chicago/Turabian StyleLi, Wei, Mingli Dong, Naiguang Lu, Xiaoping Lou, and Wanyong Zhou. 2019. "Multi-Sensor Face Registration Based on Global and Local Structures" Applied Sciences 9, no. 21: 4623. https://doi.org/10.3390/app9214623
APA StyleLi, W., Dong, M., Lu, N., Lou, X., & Zhou, W. (2019). Multi-Sensor Face Registration Based on Global and Local Structures. Applied Sciences, 9(21), 4623. https://doi.org/10.3390/app9214623




