Generation of Melodies for the Lost Chant of the Mozarabic Rite
Abstract
1. Introduction
2. Method
2.1. Patterns and Templates
2.2. Statistical Model
2.3. Sampling Compatible Instances of Templates
3. Results
3.1. Corpus
3.2. Template Creation
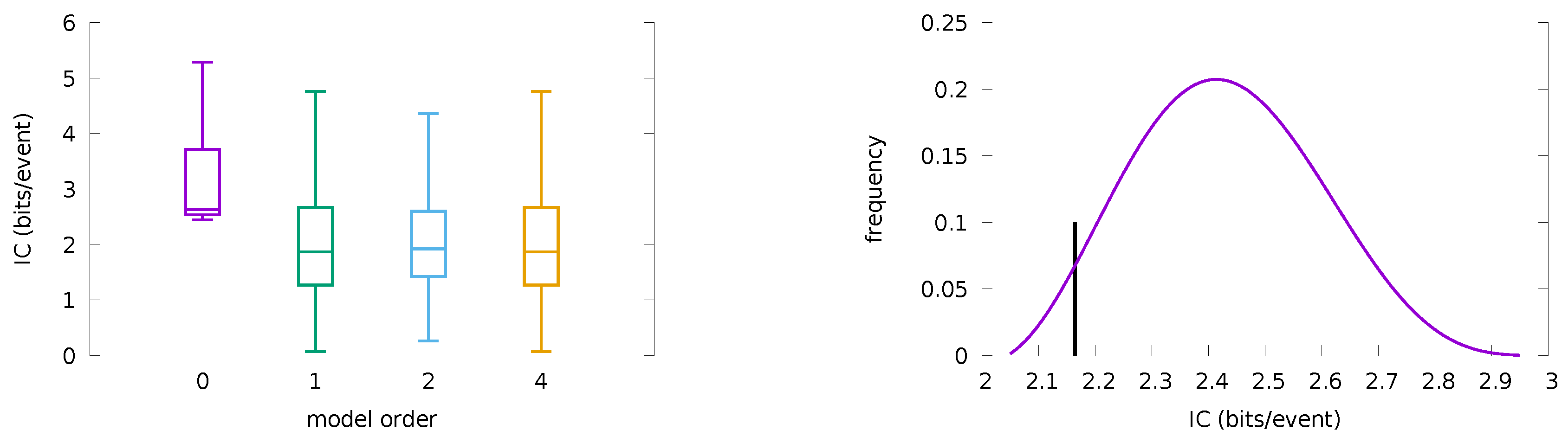
3.3. Statistical Model
3.4. Concert of Generated Chants
3.5. Singer and Audience Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GRE | Gregorian corpus |
| PPM | Prediction by Partial Match |
| LSTM | Long Short-Term Memory |
| IC | Information Content |
Appendix A. Supplementary Information
Appendix A.1. GRE Corpus
Appendix A.2. 22 Templates
Appendix A.3. Scores for Concert Pieces
Appendix A.4. Links to Recordings
Appendix A.5. PPM Backoff Model
References
- Hiley, D. Gregorian Chant; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Randel, D.M.; Nadeau, N. Mozarabic Chant. 2001. Available online: http://www.oxfordmusiconline.com/grovemusic/view/10.1093/gmo/9781561592630.001.0001/omo-9781561592630-e-0000019269 (accessed on 15 April 2019).
- Rojo, C.; Prado, G. El Canto Mozárabe, Estudio Histórico-critico de su Antigüedad y Estado Actual; Diputación Provincial de Barcelona: Barcelona, Spain, 1929. [Google Scholar]
- Maessen, G. Aspects of melody generation for the lost chant of the Mozarabic rite. In Proceedings of the 9th International Workshop on Folk Music Analysis (FMA 2019), Birmingham, UK, 2–4 July 2018; pp. 23–24. [Google Scholar]
- Hornby, E.C.; Maloy, R. Toward a Methodology for Analyzing the Old Hispanic Responsories. In Cantus Planus Study Group of the International Musicological Society; Österreichische Akademie Der Wissenschaften: Vienna, Austria, 2012; pp. 242–249. [Google Scholar]
- Conklin, D. Chord sequence generation with semiotic patterns. J. Math. Music. 2016, 10, 92–106. [Google Scholar] [CrossRef]
- Rivaud, S.; Pachet, F.; Roy, P. Sampling Markov Models under Binary Equality Constraints is Hard. In Journées Francophones sur les Réseaux Bayésiens et les Modéles Graphiques Probabilistes; csl.sony.fr: Clermont-Ferrand, France, June 2016. [Google Scholar]
- Levy, K. Gregorian Chant and the Carolingians; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Maessen, G.; van Kranenburg, P. A Semi-Automatic Method to Produce Singable Melodies for the Lost Chant of the Mozarabic Rite. In Proceedings of the 7th International Workshop on Folk Music Analysis (FMA 2017), Malaga, Spain, 14–16 June 2017; pp. 60–65. [Google Scholar]
- Maessen, G.; Conklin, D. Two methods to compute melodies for the lost chant of the Mozarabic rite. In Proceedings of the 8th International Workshop on Folk Music Analysis (FMA 2018), Thessaloniki, Greece, 26–29 June 2018; pp. 31–34. [Google Scholar]
- Roig, C.; Tardón, L.J.; Barbancho, I.; Barbancho, A.M. Automatic melody composition based on a probabilistic model of music style and harmonic rules. Knowl.-Based Syst. 2014, 71, 419–434. [Google Scholar] [CrossRef]
- Conklin, D. Music generation from statistical models. In Proceedings of the AISB Symposium on Artificial Intelligence and Creativity in the Arts and Sciences, Brighton, UK, 7–11 April 2003; pp. 30–35. [Google Scholar]
- Fernandez, J.D.; Vico, F.J. AI Methods in Algorithmic Composition: A Comprehensive Survey. J. Artif. Intell. Res. 2013, 48, 513–582. [Google Scholar] [CrossRef]
- Brooks, F.P.; Hopkins, A.L., Jr.; Neumann, P.G.; Wright, W.V. An experiment in musical composition. IRE Trans. Electron. Comput. 1956, EC–5, 175–182. [Google Scholar] [CrossRef]
- Pachet, F.; Roy, P.; Barbieri, G. Finite-length Markov processes with constraints. In Proceedings of the 22nd International Joint Conference on Artificial Intelligence (IJCAI 2011), Barcelona, Spain, 16–22 July 2011; pp. 635–642. [Google Scholar]
- Dubnov, S.; Assayag, G.; Lartillot, O.; Bejerano, G. Using Machine-Learning Methods for Musical Style Modeling. IEEE Comput. 2003, 36, 73–80. [Google Scholar] [CrossRef]
- Conklin, D.; Witten, I. Multiple viewpoint systems for music prediction. J. New Music. Res. 1995, 24, 51–73. [Google Scholar] [CrossRef]
- Sturm, B.L.; Santos, J.F.; Ben-Tal, O.; Korshunova, I. Music transcription modelling and composition using deep learning. arXiv 2016, arXiv:1604.08723. [Google Scholar]
- Huang, C.A.; Cooijmans, T.; Roberts, A.; Courville, A.; Eck, D. Counterpoint by convolution. In Proceedings of the 18th International Society for Music Information Retrieval Conference, Suzhou, China, 23–27 October 2017; pp. 211–218. [Google Scholar]
- Walder, C.; Kim, D. Computer assisted composition with Recurrent Neural Networks. JMLR: Workshop Conf. Proc. 2017, 80, 1–16. [Google Scholar]
- Hadjeres, G.; Nielsen, F. Anticipation-RNN: Enforcing unary constraints in sequence generation, with application to interactive music generation. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Medeot, G.; Cherla, S.; Kosta, K.; McVicar, M.; Abdallah, S.; Selvi, M.; Newton-Rex, E.; Webster, K. StructureNet: Inducing Structure in Generated Melodies. In Proceedings of the 19th International Society for Music Information Retrieval Conference (ISMIR 2018), Paris, France, 23–27 September 2018; pp. 725–731. [Google Scholar]
- Cope, D. Virtual Music: Computer Synthesis of Musical Style; The MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Collins, T.; Laney, R.; Willis, A.; Garthwaite, P.H. Developing and evaluating computational models of musical style. Artif. Intell. Eng. Des. Anal. Manuf. 2016, 30, 16–43. [Google Scholar] [CrossRef]
- Cleary, J.G.; Witten, I.H. Data compression using Adaptive coding and Partial String Matching. IEEE Trans. Commun. 1984, 32, 396–402. [Google Scholar] [CrossRef]
- Pearce, M.T.; Wiggins, G.A. Improved methods for statistical modelling of monophonic music. J. New Music. Res. 2004, 33, 367–385. [Google Scholar] [CrossRef]
- Chen, S.F.; Goodman, J. An empirical study of smoothing techniques for language modeling. Comput. Speech Lang. 1999, 13, 359–393. [Google Scholar] [CrossRef]
- Maessen, G.; van Kranenburg, P. A Non-Melodic Characteristic to Compare the Music of Medieval Chant Traditions. In Proceedings of the 8th International Workshop on Folk Music Analysis, Thessaloniki, Greece, 26–29 June 2018; pp. 78–79. [Google Scholar]
- González-Barrionuevo, H. The Simple Neumes of the León Antiphonary. In Calculemus et Cantemus, Towards a Reconstruction of Mozarabic Chant; Maessen, G., Ed.; Gregoriana: Amsterdam, The Netherlands, 2015; pp. 31–52. [Google Scholar]
- Brou, L.; Vives, J. (Eds.) Antifonario visigótico Mozárabe de la Catedral de León (Monumenta Hispaniae Sacra Serie Litúrgica, Vol. V,1); Consejo Superior de Investigaciones Científicas: Madrid, Spain, 1959. [Google Scholar]
- Billecocq, M.C.; Fischer, R. (Eds.) Graduale Triplex; Abbaye Saint-Pierre: Solesmes, France, 1979. [Google Scholar]
- Ott, K.; Fischer, R. (Eds.) Offertoriale Triplex cum Versiculis; Abbaye Saint-Pierre Solesmes: Solesmes, France, 1985. [Google Scholar]
- Randel, D. The Responsorial Psalm Tones for the Mozarabic Office; Princeton University Press: Princeton, NJ, USA, 1969. [Google Scholar]
- Cardine, E. Semiologia Gregoriana; Pontificium Institutum Musicae Sacrae: Rome, Italy, 1968; Reprinted Gregorian Semiology; Abbaye Saint-Pierre de Solesmes: Solesmes, France, 1982. [Google Scholar]
- Conklin, D. Discovery of distinctive patterns in music. Intell. Data Anal. 2010, 14, 547–554. [Google Scholar] [CrossRef]
- Moffat, A. Implementing the PPM data compression scheme. IEEE Trans. Commun. 1990, 38, 1917–1921. [Google Scholar] [CrossRef]


| Viewpoint | Description | Codomain |
|---|---|---|
| set of 15 possible pitches | ||
| position of event in sequence | ||
| contour viewpoints (see text) | Boolean | |
| pitch in range | Boolean |
| number of chants in GRE | 137 |
| mean chant length | 473 notes |
| mean number of words/syllables/neumes | 56/123/318 |
| number of templates | 22 |
| mean template length | 789 notes |
| mean number of defined pitches | 14 |
| mean number of words/syllables/neumes | 107/226/464 |
| mean coverage by intra-opus patterns | 52% |
| mean fraction of events with no specified contours | 34% |
| Audience () | Singers () | |||||||
|---|---|---|---|---|---|---|---|---|
| Genre | Time | Incipit | E-L 8 | IC | Mean | Stdev | Mean | Stdev |
| SNO | 07:03 | Haec dicit Dominus priusquam | 211v10 | 2.03 | 7.5 | 1.8 | 6.2 | 0.8 |
| RS | 04:38 | Zaccarias sacerdos | 212v11 | 2.03 | 7.6 | 1.7 | 6.6 | 0.5 |
| RS | 02:05 | Unde mici adfuit ut veniret | 213v10 | 2.08 | 8.0 | 1.6 | 5.8 | 1.8 |
| RS | 02:31 | Fuit homo missus a Deo | 213v01 | 1.88 | 8.2 | 1.3 | 7.2 | 0.8 |
| RS | 03:47 | Dominus ab utero formabit me | 214r02 | 1.95 | 7.7 | 1.6 | 7.8 | 1.1 |
| RS | 02:14 | Spiritus Domini super me | 213r08 | 1.99 | 8.0 | 1.6 | 8.0 | 0.8 |
| RS | 02:53 | Misit me Dominus sanare | 212v02 | 1.99 | 8.2 | 1.4 | 7.5 | 1.4 |
| RS | 02:16 | Me oportet minui | 214r12 | 1.96 | 8.9 | 1.4 | 6.4 | 0.9 |
| VAR | 07:06 | Benedictus Dominus Deus Israel | 214v12 | 2.08 | 9.4 | 1.0 | 5.9 | 2.5 |
| SCR | 07:22 | Dum complerentur dies | 210r14 | 2.12 | 8.7 | 1.4 | 6.2 | 0.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conklin, D.; Maessen, G. Generation of Melodies for the Lost Chant of the Mozarabic Rite. Appl. Sci. 2019, 9, 4285. https://doi.org/10.3390/app9204285
Conklin D, Maessen G. Generation of Melodies for the Lost Chant of the Mozarabic Rite. Applied Sciences. 2019; 9(20):4285. https://doi.org/10.3390/app9204285
Chicago/Turabian StyleConklin, Darrell, and Geert Maessen. 2019. "Generation of Melodies for the Lost Chant of the Mozarabic Rite" Applied Sciences 9, no. 20: 4285. https://doi.org/10.3390/app9204285
APA StyleConklin, D., & Maessen, G. (2019). Generation of Melodies for the Lost Chant of the Mozarabic Rite. Applied Sciences, 9(20), 4285. https://doi.org/10.3390/app9204285




