State-of-the-Art Model for Music Object Recognition with Deep Learning
Abstract
1. Introduction
2. Related Work
2.1. Object Detection-Based Approaches
2.2. Sequential Recognition-Based Approaches
2.3. Summary
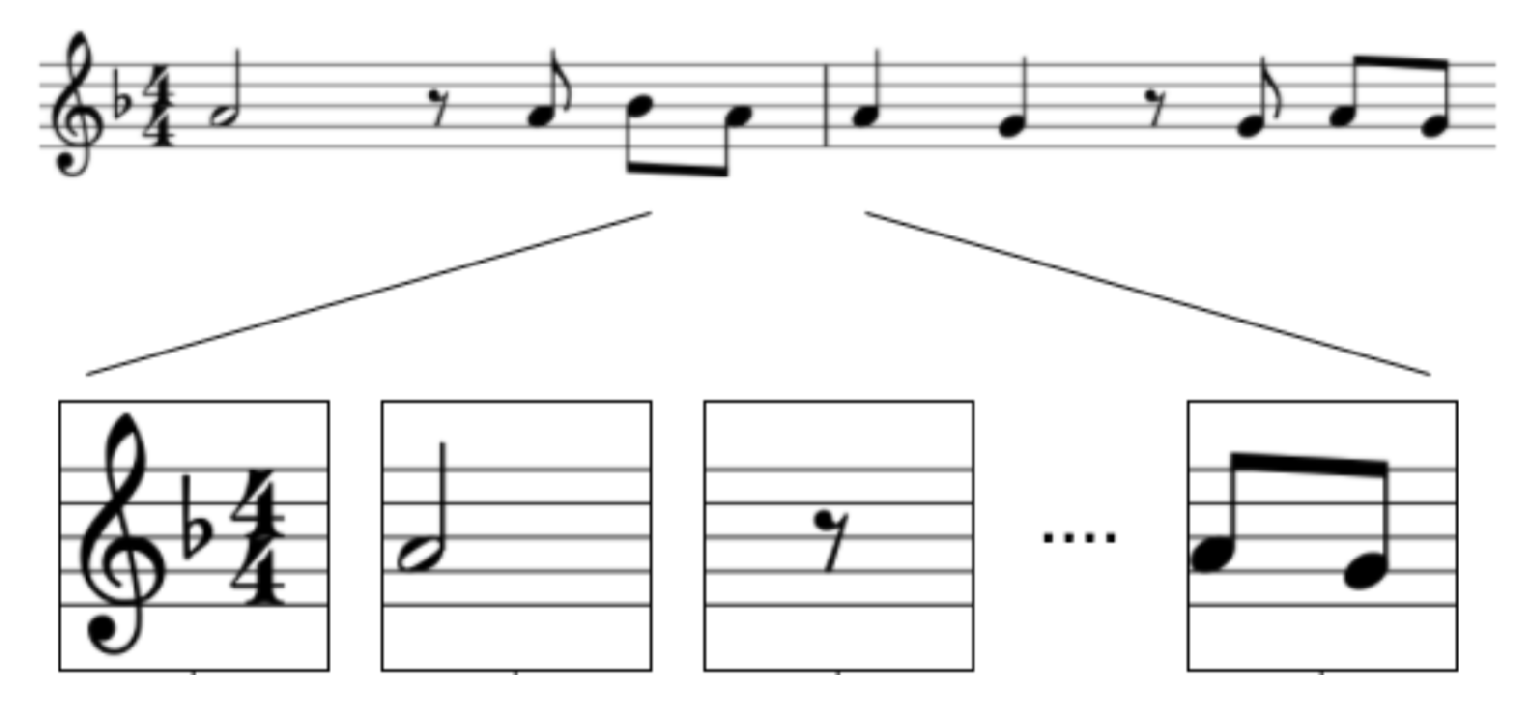
3. Dataset
3.1. Pre-Processing
3.1.1. Symbol Categories
3.1.2. Symbol Duration
3.1.3. Note Pitch
3.2. Image Augmentation
- blur;
- random crop;
- Gaussian noise;
- affine transformations;
- elastic transformations;
- hue, saturation, exposure shifts.
4. Model
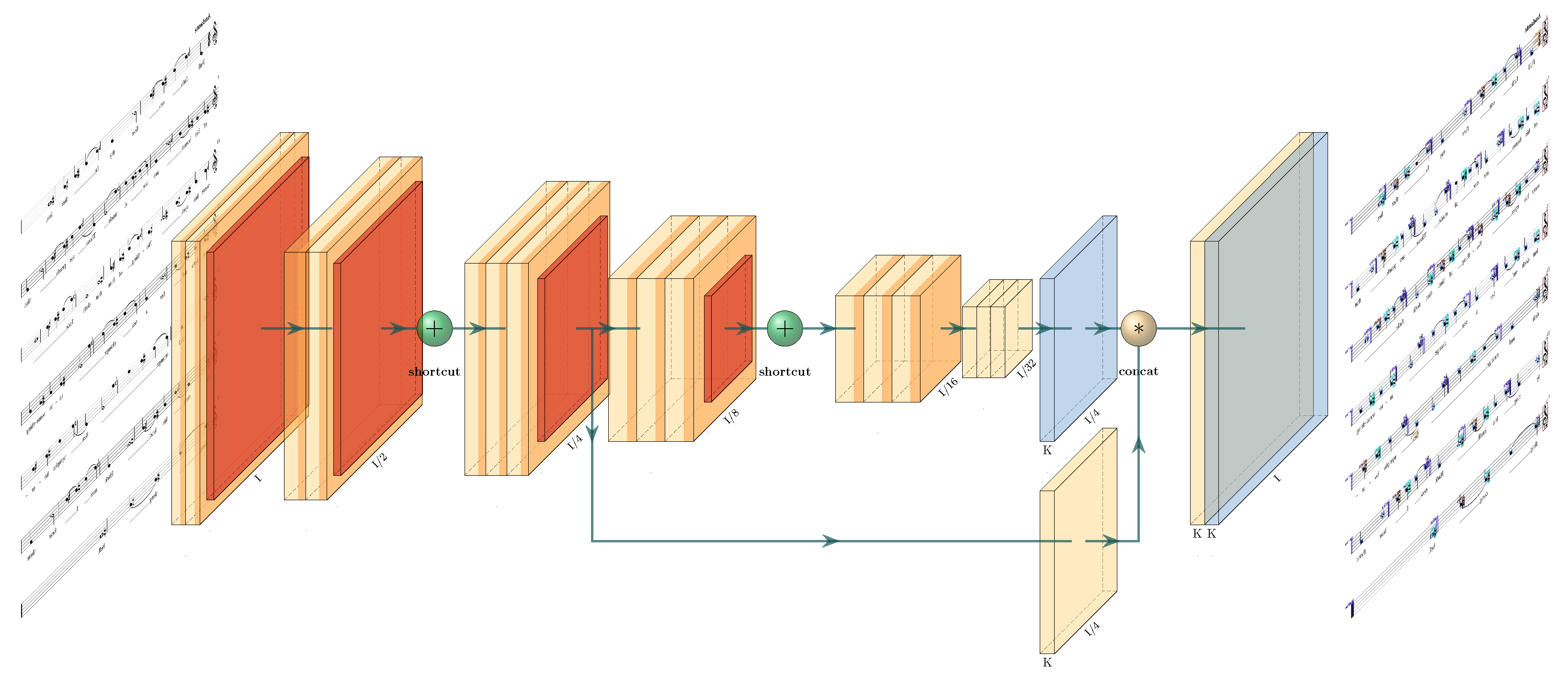
4.1. Network Architecture
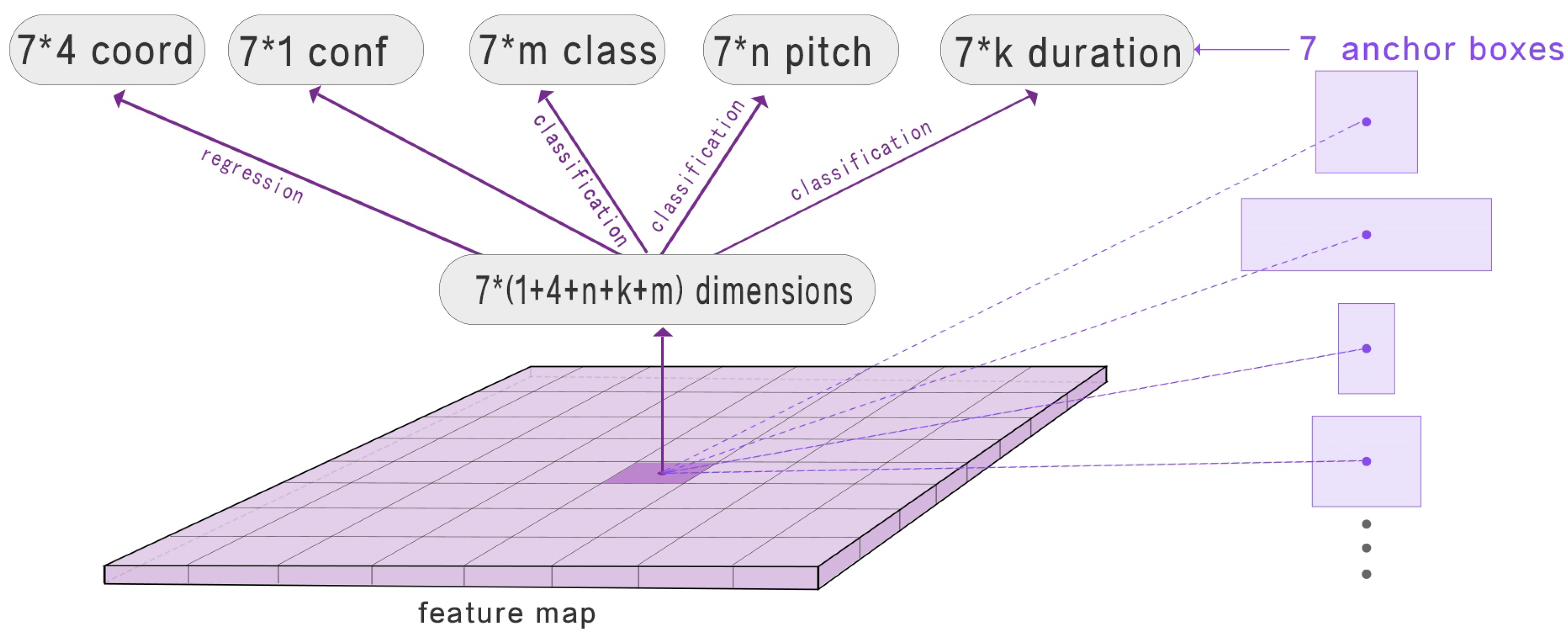
4.1.1. Class Prediction
4.1.2. Predict Bounding Box
4.1.3. Duration and Pitch
4.2. Losses
5. Experiments and Results
5.1. Network Training
5.2. Evaluation Metrics
- Pitch accuracy: the proportion of correctly predicted pitches.
- Duration accuracy: the proportion of correctly predicted durations.
- Symbol average precision [15]: the area under the precision–recall curve for all possible values of classes.
5.3. Results
5.4. Comparison with Previous Approaches
5.5. Discussion
- The ground truth does not provide the position of the clef on the stave. This means that a bass clef on the third or fourth staff lines are predicted as the same.
- Our system generally struggles with rare classes, overlapping symbols, and dense symbols. We have calculated the distribution of symbols, the symbols that the model can recognize account for 99% and it is very challenging to detect these rare symbols (less than 1% of all symbols). For dense symbols (chords), our model will miss some notes.
- As shown in Figure 3 and Figure 4, The duration of the symbols ranges from 0.125 to 4.000, and the pitch label of note ranges from −6 to 14. This means that the duration and pitch of the note can only be predicted within a certain range. If the range is exceeded, the pitch and duration of the symbols cannot be accurately predicted.
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MIDI | Musical Instrument Digital Interface |
| R-CNN | Region-based Convolutional Neural Network |
| SSD | Single Shot Detector |
| YOLO | You Only Look Once |
| mAP | Mean Average Precision |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| CTC | Connectionist Temporal Classification |
| GPU | Graphical Processing Units |
| Adam | A Method for Stochastic Optimization |
References
- Casey, M.; Veltkamp, R.; Goto, M.; Leman, M.; Rhodes, C.; Slaney, M. Content-Based Music Information Retrieval: Current Directions and Future Challenges. Proc. IEEE 2008, 96, 668–696. [Google Scholar] [CrossRef]
- Roland, P. The Music Encoding Initiative (MEI). In Proceedings of the First International Conference on Musical Applications Using XML, Milan, Italy, 19–20 September 2002; pp. 55–59. [Google Scholar]
- Good, M.; Actor, G. Using MusicXML for file interchange. In Proceedings of the Third International Conference on WEB Delivering of Music, Leeds, UK, 15–17 September 2003; p. 153. [Google Scholar] [CrossRef]
- Bainbridge, D.; Bell, T. The challenge of optical music recognition. Comput. Humanit. 2001, 35, 95–121. [Google Scholar] [CrossRef]
- Rebelo, A.; Fujinaga, I.; Paszkiewicz, F.; Marcal, A.R.S.; Guedes, C.; Cardoso, J.S. Optical music recognition: State-of-the-art and open issues. Int. J. Multimed. Inf. Retr. 2012, 1, 173–190. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. arXiv 2015, arXiv:1506.02640. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. arXiv 2016, arXiv:1612.08242. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. arXiv 2017, arXiv:1708.02002. [Google Scholar]
- Girshick, R. Fast R-CNN. arXiv 2015, arXiv:1504.08083. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. arXiv 2015, arXiv:1506.01497. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-FCN: Object Detection via Region-based Fully Convolutional Networks. arXiv 2016, arXiv:1605.06409. [Google Scholar]
- Pacha, A.; Hajič, J.; Calvo-Zaragoza, J. A Baseline for General Music Object Detection with Deep Learning. Appl. Sci. 2018, 8, 1488. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Tuggener, L.; Elezi, I.; Schmidhuber, J.; Pelillo, M.; Stadelmann, T. DeepScores—A Dataset for Segmentation, Detection and Classification of Tiny Objects. arXiv 2018, arXiv:1804.00525. [Google Scholar]
- Hajič, J.; Pecina, P. The MUSCIMA++ Dataset for Handwritten Optical Music Recognition. In Proceedings of the 2017 14th IAPR International Conference on Document Analysis and Recognition (ICDAR), Kyoto, Japan, 10 November 2017; pp. 39–46. [Google Scholar] [CrossRef]
- Hajič, J., Jr.; Dorfer, M.; Widmer, G.; Pecina, P. Towards Full-Pipeline Handwritten OMR with Musical Symbol Detection by U-Nets. In Proceedings of the 19th International Society for Music Information Retrieval Conference, Paris, France, 23–27 September 2018; pp. 23–27. [Google Scholar]
- Tuggener, L.; Elezi, I.; Schmidhuber, J.; Stadelmann, T. Deep Watershed Detector for Music Object Recognition. arXiv 2018, arXiv:1805.10548. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. In Advances in Neural Information Processing Systems 27; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Nice, France, 2014; pp. 3104–3112. [Google Scholar]
- van der Wel, E.; Ullrich, K. Optical Music Recognition with Convolutional Sequence-to-Sequence Models. arXiv 2017, arXiv:1707.04877. [Google Scholar]
- Calvo-Zaragoza, J.; Valero-Mas, J.J.; Pertusa, A. END-TO-END OPTICAL MUSIC RECOGNITION USING NEURAL NETWORKS. In Proceedings of the 18th International Society for Music Information Retrieval Conference, Suzhou, China, 472–477 Octorber 2017; pp. 23–27. [Google Scholar]
- Calvo-Zaragoza, J.; Rizo, D. End-to-End Neural Optical Music Recognition of Monophonic Scores. Appl. Sci. 2018, 8, 606. [Google Scholar] [CrossRef]
- Baró, A.; Riba, P.; Calvo-Zaragoza, J.; Fornés, A. From Optical Music Recognition to Handwritten Music Recognition: A baseline. Pattern Recognit. Lett. 2019, 123, 1–8. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]

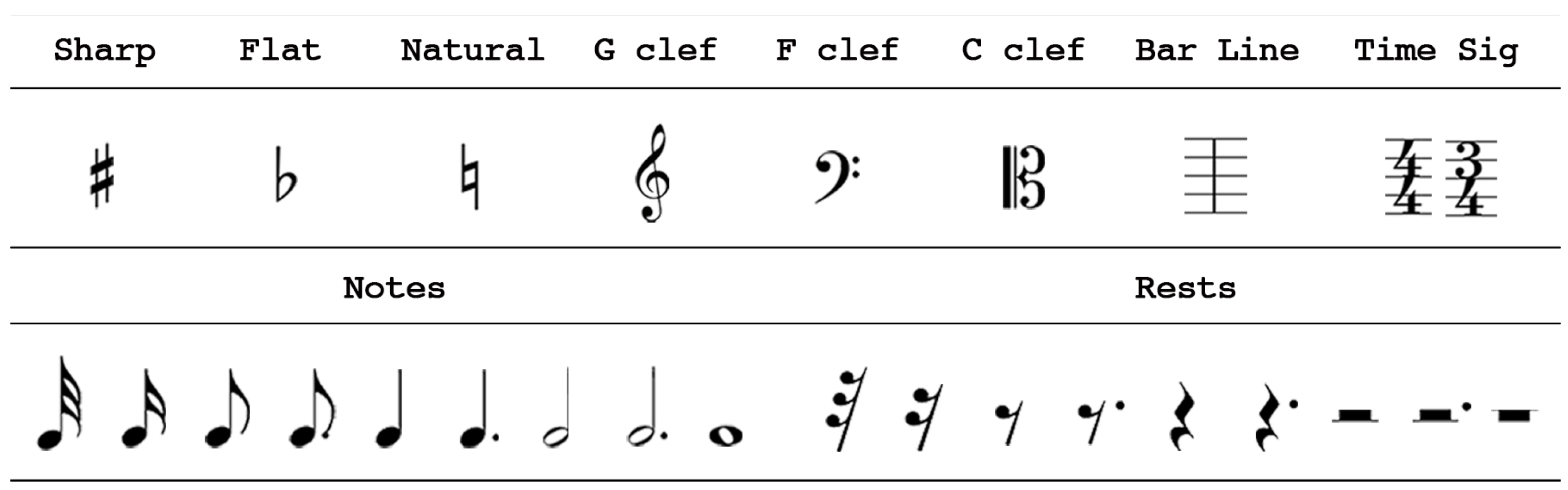
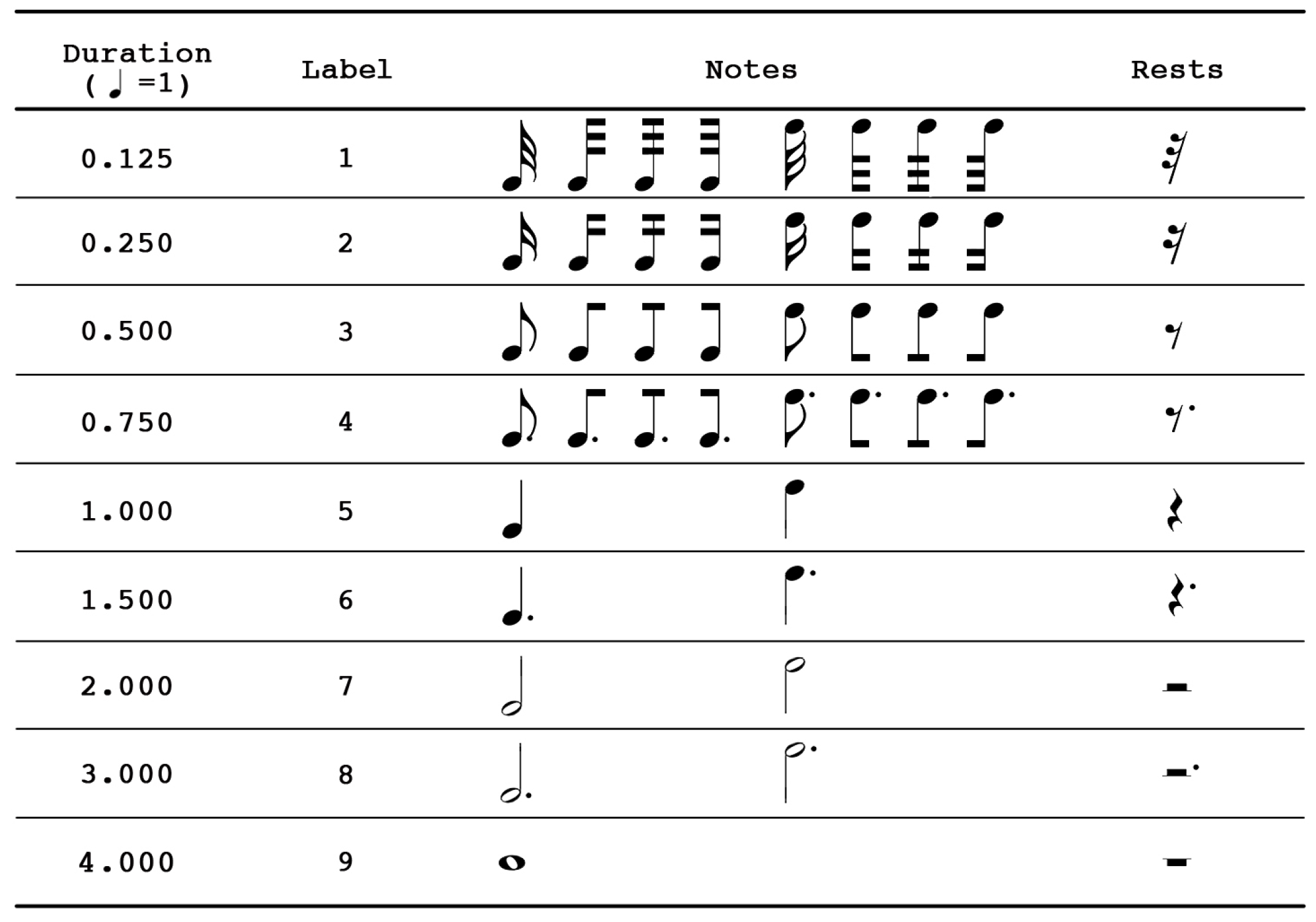






| Class | Sharp | Flat | Natural | clefG | clefF | clefC | Barline | Timesig | Note | Rest |
|---|---|---|---|---|---|---|---|---|---|---|
| AP | 0.96 | 0.93 | 0.92 | 0.98 | 0.96 | 0.86 | 0.9 | 0.82 | 0.94 | 0.92 |
| Method | Dataset | Result | ||
|---|---|---|---|---|
| Eelco van der Wel [24] | printed score | accuracy | ||
| MuseScore | 0.81 (pitch) | 0.80 (note) | 0.94 (duration) | |
| ours | printed score | accuracy and mean average precision | ||
| MuseScore | 0.96 (pitch) | 0.91 (symbols) | 0.92 (duration) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Jia, X.; Guo, Y. State-of-the-Art Model for Music Object Recognition with Deep Learning. Appl. Sci. 2019, 9, 2645. https://doi.org/10.3390/app9132645
Huang Z, Jia X, Guo Y. State-of-the-Art Model for Music Object Recognition with Deep Learning. Applied Sciences. 2019; 9(13):2645. https://doi.org/10.3390/app9132645
Chicago/Turabian StyleHuang, Zhiqing, Xiang Jia, and Yifan Guo. 2019. "State-of-the-Art Model for Music Object Recognition with Deep Learning" Applied Sciences 9, no. 13: 2645. https://doi.org/10.3390/app9132645
APA StyleHuang, Z., Jia, X., & Guo, Y. (2019). State-of-the-Art Model for Music Object Recognition with Deep Learning. Applied Sciences, 9(13), 2645. https://doi.org/10.3390/app9132645




