Validating the Comparison Framework for the Finite Dimensions Model of Concentric Ring Electrodes Using Human Electrocardiogram Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Preliminaries
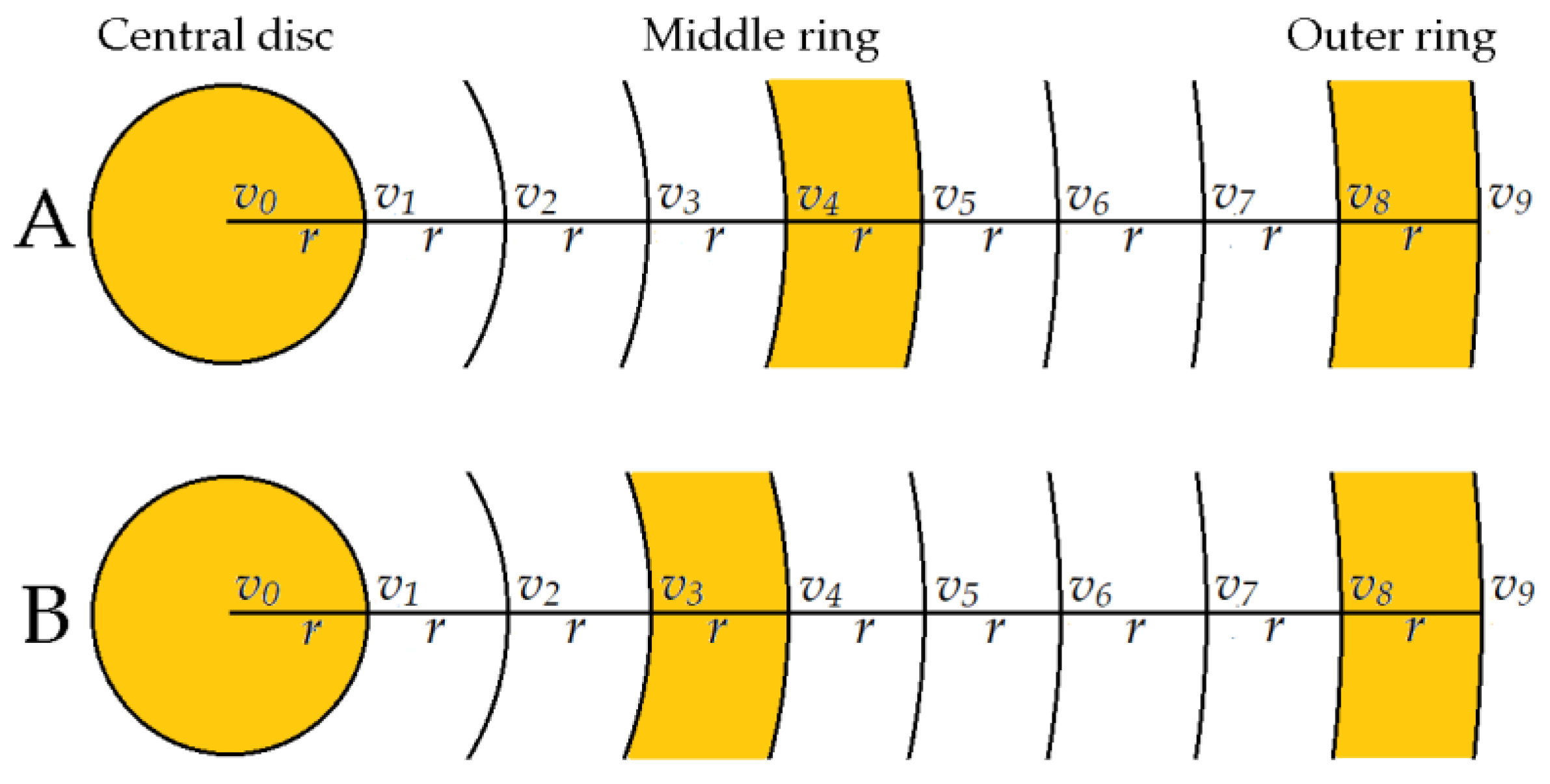
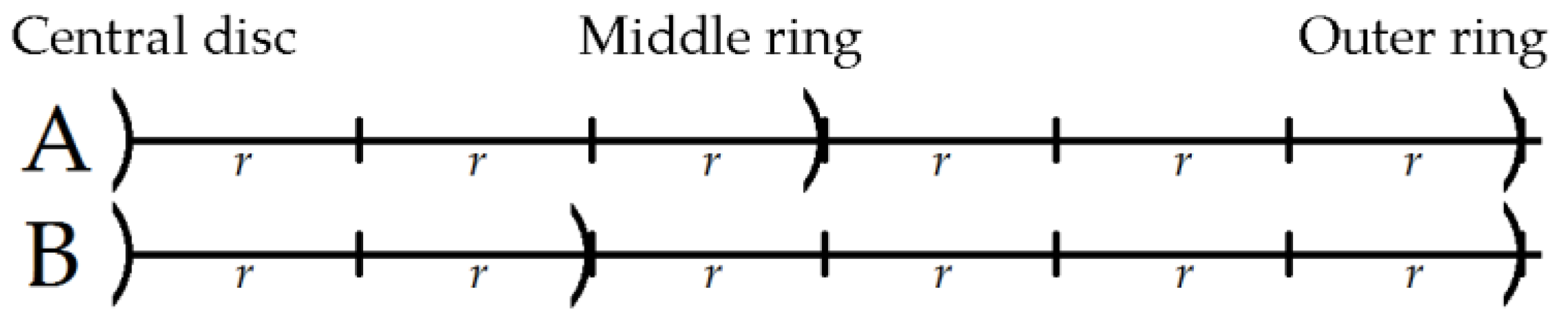
2.2. Deriving Laplacian Estimates for Real Life Linearly Increasing Inter-ring Distances (LIIRD) Tripolar Concentric Ring Electrode (TCRE) Based on Negligible Dimensions Model (NDM) and Finite Dimensions Model (FDM)
2.3. Human Electrocardiogram (ECG) Data Collection and Processing
2.3.1. Sensor Node
2.3.2. ECG Signal Recording Protocol
2.3.3. ECG Data Analysis
- The amplitude of the QRS complex of , computed as the peak-to-peak amplitude of in the interval [−90 ms, +90 ms] of the detected R-wave.
- Normalized amplitude of the P- and T-waves with respect to the peak to peak amplitude of QRS [30]. P- and T-wave amplitude computed as the peak-to-peak amplitude of in the interval [−250 ms, −90 ms] and [+90 ms, 375 ms] of the detected R-wave. The higher the normalized amplitude of the wave, the easier it is to identify and to assess its morphology, which is helpful for diagnosis of cardiac pathologies,
- Signal-to-noise ratio: the ratio of the peak-to-peak amplitude value of and the root mean square value of the noise during the isoelectric interval between beats, the latter being computed for all the isoelectric intervals in the 60 s window.
3. Results
3.1. Establishing the Comparison Framework
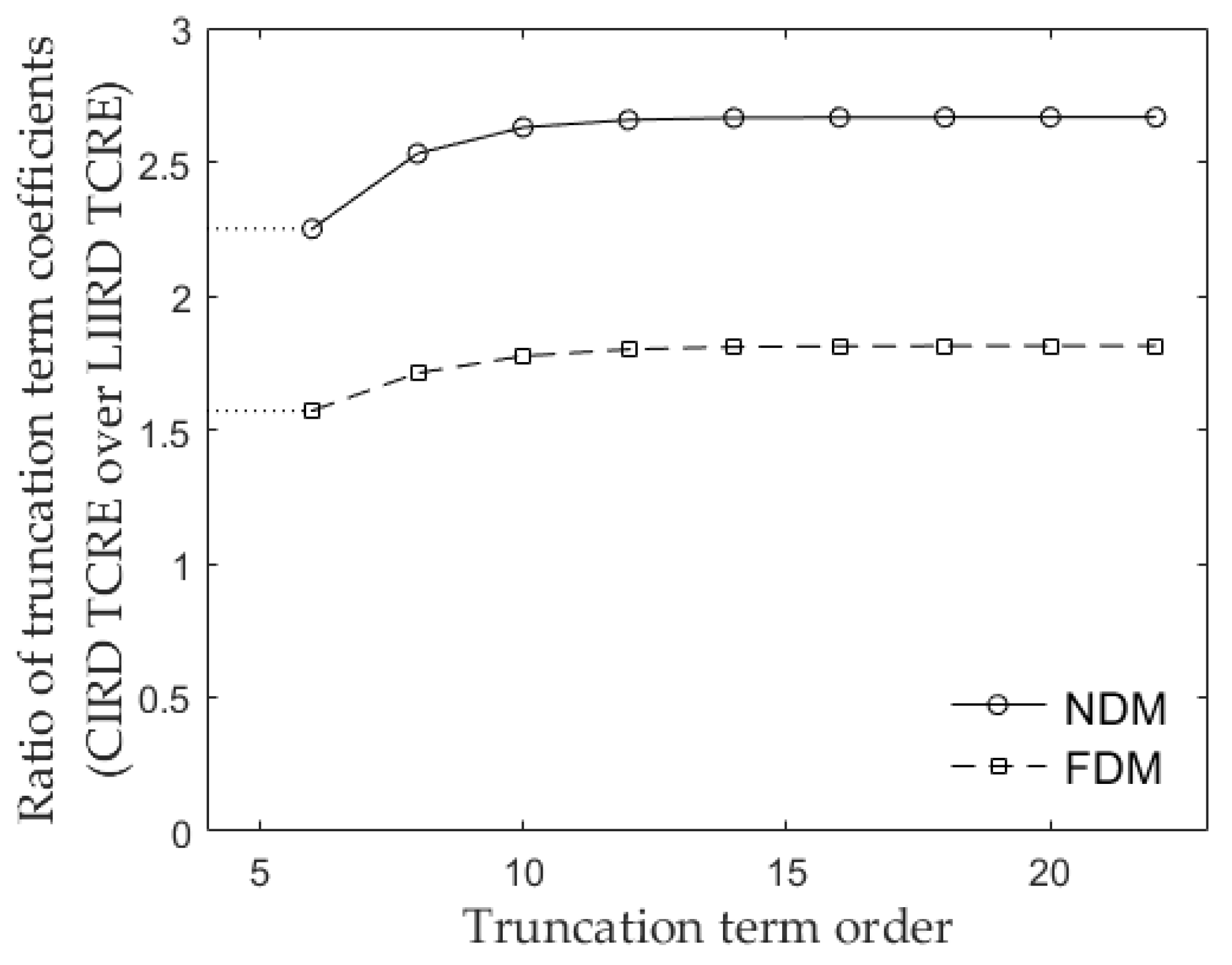
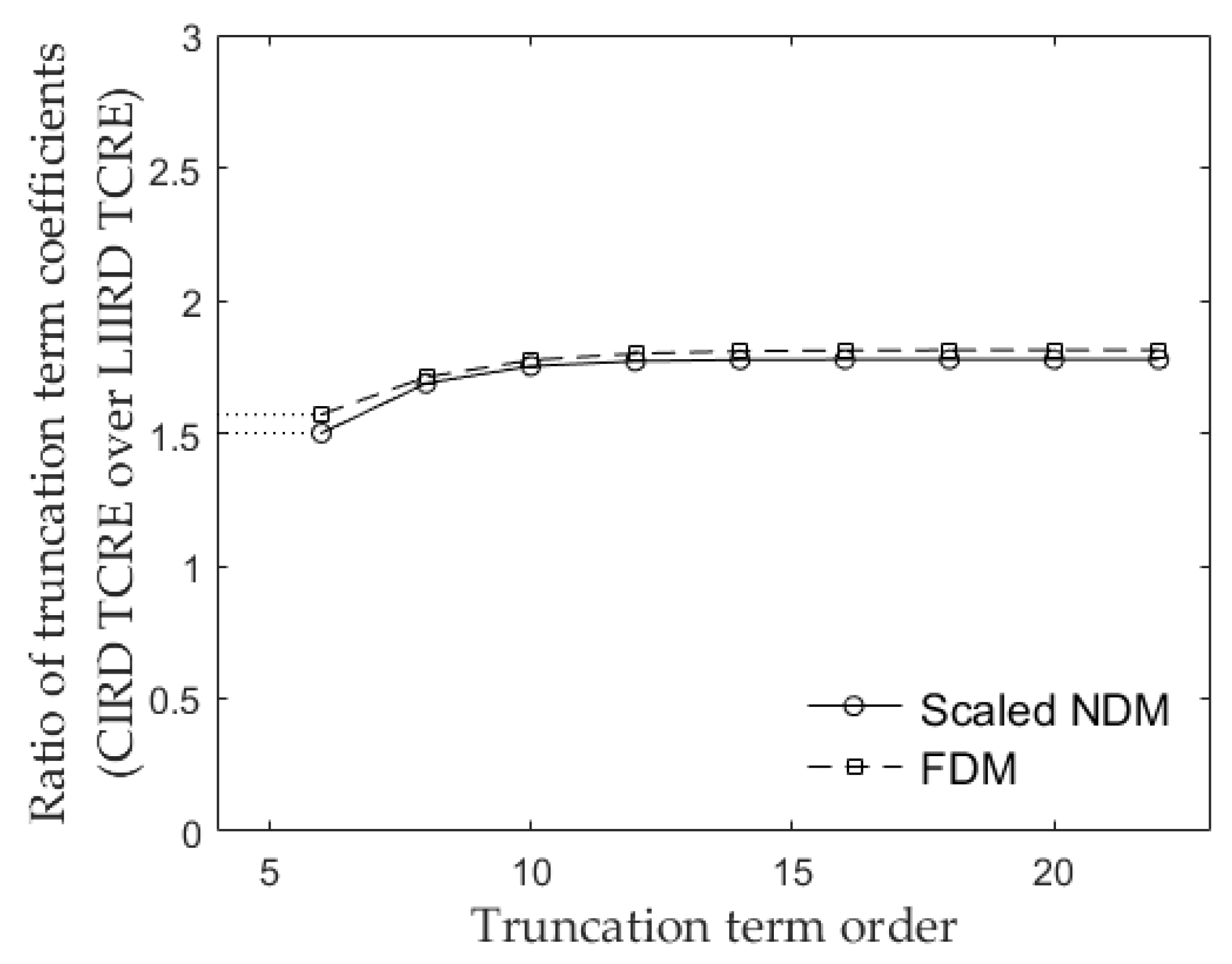
3.2. Comparing Truncation Term Coefficient Ratios for the NDM and the FDM
3.3. Relating the Difference in Truncation Term Coefficient Ratios to the Difference in TCRE Configurations Between the NDM and the FDM
3.4. NDM and FDM Based Laplacian Estimates for Real Life LIIRD TCRE
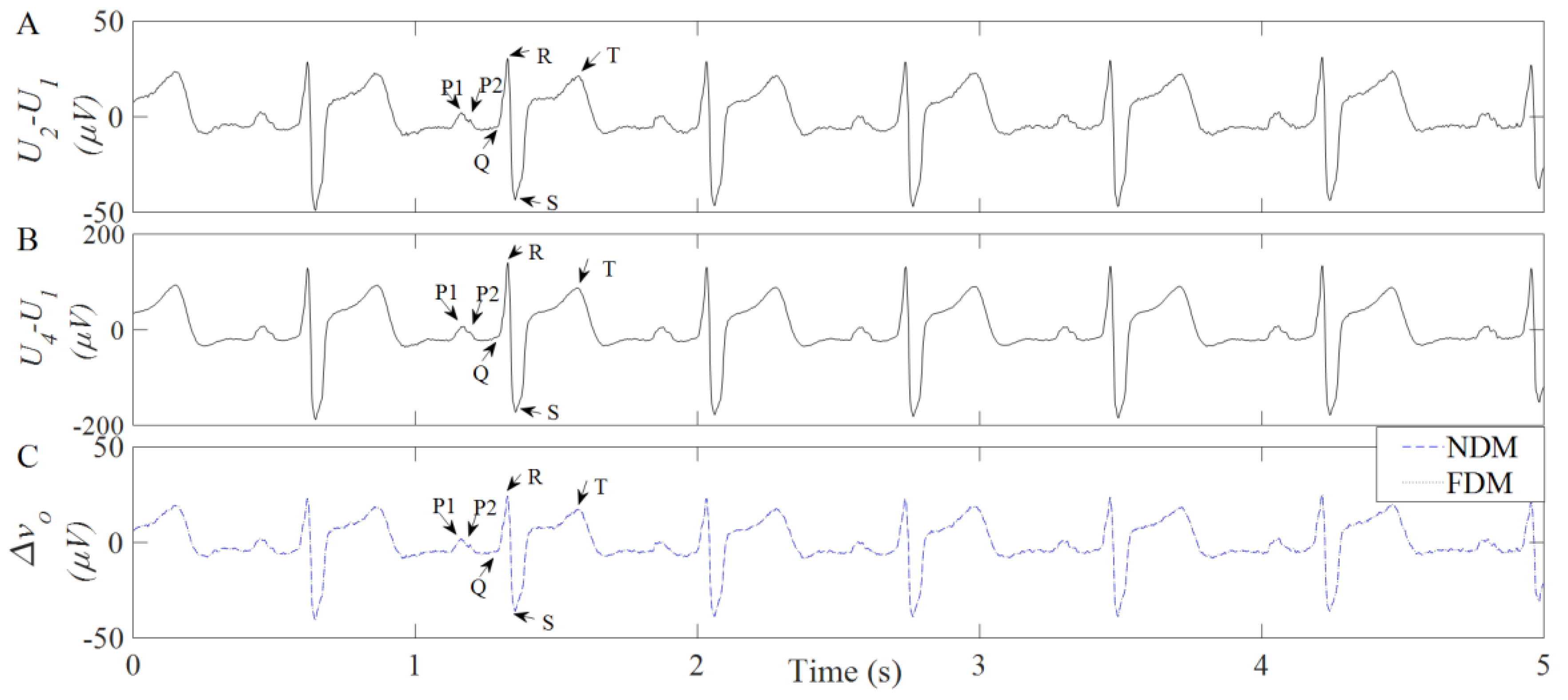
3.5. Assessing NDM and FDM Based Laplacian Estimates for Real Life LIIRD TCRE on Human ECG Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bradshaw, L.A.; Richards, W.O.; Wikswo, J.P. Volume conductor effects on the spatial resolution of magnetic fields and electric potentials from gastrointestinal electrical activity. Med. Biol. Eng. Comput. 2001, 39, 35–43. [Google Scholar] [CrossRef]
- Besio, W.G.; Cao, H.; Zhou, P. Application of Tripolar Concentric Electrodes and Prefeature Selection Algorithm for Brain–Computer Interface. IEEE Trans. Neural Syst. Rehabil. Eng. 2008, 16, 191–194. [Google Scholar] [CrossRef] [PubMed]
- Farina, D.; Cescon, C. Concentric-ring electrode systems for noninvasive detection of single motor unit activity. IEEE Trans. Biomed. Eng. 2001, 48, 1326–1334. [Google Scholar] [CrossRef] [PubMed]
- McFarland, D.J.; McCane, L.M.; David, S.V.; Wolpaw, J.R. Spatial filter selection for EEG-based communication. Electroencephalogr. Clin. Neurophysiol. 1997, 103, 386–394. [Google Scholar] [CrossRef]
- Wu, D.; Tsai, H.C.; He, B. On the estimation of the Laplacian electrocardiogram during ventricular activation. Ann. Biomed. Eng 1999, 27, 731–745. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Wu, D. Laplacian electrocardiography. Crit. Rev. Biomed. Eng. 1999, 27, 285–338. [Google Scholar] [PubMed]
- Hjorth, B. An on-line transformation of EEG scalp potentials into orthogonal source derivations. Electroencephalogr. Clin. Neurophysiol. 1975, 39, 526–530. [Google Scholar] [CrossRef]
- MacKay, D.M. On-line source-density computation with a minimum of electrons. Electroencephalogr. Clin. Neurophysiol. 1983, 56, 696–698. [Google Scholar] [CrossRef]
- Huiskamp, G. Difference formulas for the surface Laplacian on a triangulated surface. J. Comput. Phys. 1991, 95, 477–496. [Google Scholar] [CrossRef]
- Besio, W.G.; Koka, K.; Aakula, R.; Dai, W. Tri-polar concentric ring electrode development for laplacian electroencephalography. IEEE Trans. Biomed. Eng. 2006, 53, 926–933. [Google Scholar] [CrossRef]
- Besio, W.; Aakula, R.; Koka, K.; Dai, W. Development of a tri-polar concentric ring electrode for acquiring accurate Laplacian body surface potentials. Ann. Biomed. Eng. 2006, 34, 426–435. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Parekh, U.; Pailla, T.; Garudadri, H.; Gilja, V.; Ng, T.N. Stretchable Dry Electrodes with Concentric Ring Geometry for Enhancing Spatial Resolution in Electrophysiology. Adv. Healthc. Mater. 2017, 6, 1700552. [Google Scholar] [CrossRef] [PubMed]
- Lidón-Roger, J.V.; Prats-Boluda, G.; Ye-Lin, Y.; Garcia-Casado, J.; Garcia-Breijo, E. Textile concentric ring electrodes for ECG recording based on screen-printing technology. Sensors 2018, 18, 300. [Google Scholar] [CrossRef] [PubMed]
- Besio, W.G.; Martinez-Juarez, I.E.; Makeyev, O.; Gaitanis, J.N.; Blum, A.S.; Fisher, R.S.; Medvedev, A.V. High-Frequency Oscillations Recorded on the Scalp of Patients with Epilepsy Using Tripolar Concentric Ring Electrodes. IEEE J. Transl. Eng. Health Med. 2014, 2, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Boudria, Y.; Feltane, A.; Besio, W. Significant improvement in one-dimensional cursor control using Laplacian electroencephalography over electroencephalography. J. Neural Eng. 2014, 11, 035014. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Casado, J.; Zena-Gimenez, V.; Prats-Boluda, G.; Ye-Lin, Y. Enhancement of non-invasive recording of electroenterogram by means of a flexible array of concentric ring electrodes. Ann. Biomed. Eng. 2014, 42, 651–660. [Google Scholar] [CrossRef] [PubMed]
- Zena-Giménez, V.; Garcia-Casado, J.; Ye-Lin, Y.; Garcia-Breijo, E.; Prats-Boluda, G. A flexible multiring concentric electrode for non-invasive identification of intestinal slow Waves. Sensors 2018, 18, 396. [Google Scholar] [CrossRef] [PubMed]
- Ye-Lin, Y.; Alberola-Rubio, J.; Prats-boluda, G.; Perales, A.; Desantes, D.; Garcia-Casado, J. Feasibility and Analysis of Bipolar Concentric Recording of Electrohysterogram with Flexible Active Electrode. Ann. Biomed. Eng. 2015, 43, 968–976. [Google Scholar] [CrossRef]
- Lu, C.C.; Tarjan, P.P. Pasteless, Active, Concentric Ring Sensors for Directly Obtained Laplacian Cardiac Electrograms. J. Med. Biol. Eng. 2002, 22, 199–203. [Google Scholar]
- Prats-Boluda, G.; Ye-Lin, Y.; Pradas-Novella, F.; Garcia-Breijo, E.; Garcia-Casado, J. Textile Concentric Ring Electrodes: Influence of Position and Electrode Size on Cardiac Activity Monitoring. J. Sens. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Wang, Y.; Cuculich, P.S.; Zhang, J.; Desouza, K.A.; Vijayakumar, R.; Chen, J.; Faddis, M.N.; Lindsay, B.D.; Smith, T.W.; Rudy, Y. Noninvasive Electroanatomic Mapping of Human Ventricular Arrhythmias with Electrocardiographic Imaging. Sci. Transl. Med. 2011, 3, ra84–ra98. [Google Scholar] [CrossRef] [PubMed]
- Makeyev, O.; Ding, Q.; Besio, W.G. Improving the accuracy of Laplacian estimation with novel multipolar concentric ring electrodes. Measurement 2016, 80, 44–52. [Google Scholar] [CrossRef] [PubMed]
- Makeyev, O.; Besio, W.G. Improving the Accuracy of Laplacian Estimation with Novel Variable Inter-Ring Distances Concentric Ring Electrodes. Sensors 2016, 16, 858. [Google Scholar] [CrossRef] [PubMed]
- Makeyev, O. Solving the general inter-ring distances optimization problem for concentric ring electrodes to improve Laplacian estimation. Biomed. Eng. OnLine 2018, 17, 117. [Google Scholar] [CrossRef] [PubMed]
- Makeyev, O.; Lee, C.; Besio, W.G. Proof of concept Laplacian estimate derived for noninvasive tripolar concentric ring electrode with incorporated radius of the central disc and the widths of the concentric rings. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Seogwipo, Korea, 11–15 July 2017; pp. 841–844. [Google Scholar]
- Ye-Lin, Y.; Bueno-Barrachina, J.M.; Prats-boluda, G.; Rodriguez de Sanabria, R.; Garcia-Casado, J. Wireless sensor node for non-invasive high precision electrocardiographic signal acquisition based on a multi-ring electrode. Measurement 2017, 97, 195–202. [Google Scholar] [CrossRef]
- Kaufer, M.; Rasquinha, L.; Tarjan, P. Optimization of multi-ring sensing electrode set. In Proceedings of the Annual Conference on Engineering in Medicine and Biology, Philadelphia, PA, USA, 1–4 November 1990; pp. 612–613. [Google Scholar]
- Besio, W.; Chen, T. Tripolar Laplacian electrocardiogram and moment of activation isochronal mapping. Physiol. Meas. 2007, 28, 515–529. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, P.S.; Tompkins, W.J. Quantitative investigation of QRS detection rules using the MIT/BIH arrhythmia database. IEEE Trans. Biomed. Eng. 1986, 33, 1157–1165. [Google Scholar] [CrossRef] [PubMed]
- Prats-Boluda, G.; Ye-Lin, Y.; Bueno-Barrachina, J.M.; de Sanabria, R.R.; Garcia-Casado, J. Towards the clinical use of concentric electrodes in ECG recordings: Influence of ring dimensions and electrode position. Meas. Sci. Technol. 2016, 27, 025705. [Google Scholar] [CrossRef]
- King, M.R.; Mody, N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Mittal, S.; Movsowitz, C.; Steinberg, J.S. Ambulatory External Electrocardiographic Monitoring. J. Am. Coll. Cardiol. 2011, 58, 1741–1749. [Google Scholar] [CrossRef]
- Garcia-Casado, J.; Ye-Lin, Y.; Prats-Boluda, G.; Makeyev, O. Evaluation of Bipolar, Tripolar, and Quadripolar Laplacian Estimates of Electrocardiogram via Concentric Ring Electrodes. Sensors 2019, 19, 3780. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, M.; Li, T.; Song, G. ECG Signal De-noising and Baseline Wander Correction Based on CEEMDAN and Wavelet Threshold. Sensors 2017, 17, 2754. [Google Scholar] [CrossRef] [PubMed]
- Ortigueira, M.D.; Laleg-Kirati, T.-M.; Machado, J.A.T. Riesz potential versus fractional Laplacian. J. Stat. Mech. Theory Exp. 2014, 2014, P09032. [Google Scholar] [CrossRef]
| Concentric Circle Radius | Taylor Series for Concentric Circle |
|---|---|
| r | |
| 2r | |
| 3r | |
| 4r | |
| 5r | |
| 6r | |
| 7r | |
| 8r | |
| 9r |
| Radius (mm) | Biopotential | Laplacian Estimate | ||
|---|---|---|---|---|
| Inner | Outer | |||
| Central disc | N/A | 4.8 | U1 | LIIRD TCRE |
| Hook 1 | 9.6 | 10.8 | U2 | LIIRD TCRE |
| Hook 2 | 15.6 | 16.8 | U3 | - |
| Hook 3 | 21.6 | 22.8 | U4 | LIIRD TCRE |
| Hook 4 | 27.6 | 28.8 | U5 | - (analog ground) |
| ∆v0 | Amplitude QRS (µV) | Normalized Amplitude P-Wave | Normalized Amplitude T-Wave | Signal-to-Noise Ratio (dB) |
|---|---|---|---|---|
| NDM | 18.59 ± 28.40 | 0.256 ± 0.145 | 0.367 ± 0.260 | 20.05 ± 8.29 |
| FDM | 18.60 ± 28.40 | 0.253 ± 0.141 | 0.362 ± 0.264 | 19.94 ± 8.48 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makeyev, O.; Musngi, M.; Moore, L.; Ye-Lin, Y.; Prats-Boluda, G.; Garcia-Casado, J. Validating the Comparison Framework for the Finite Dimensions Model of Concentric Ring Electrodes Using Human Electrocardiogram Data. Appl. Sci. 2019, 9, 4279. https://doi.org/10.3390/app9204279
Makeyev O, Musngi M, Moore L, Ye-Lin Y, Prats-Boluda G, Garcia-Casado J. Validating the Comparison Framework for the Finite Dimensions Model of Concentric Ring Electrodes Using Human Electrocardiogram Data. Applied Sciences. 2019; 9(20):4279. https://doi.org/10.3390/app9204279
Chicago/Turabian StyleMakeyev, Oleksandr, Mark Musngi, Larry Moore, Yiyao Ye-Lin, Gema Prats-Boluda, and Javier Garcia-Casado. 2019. "Validating the Comparison Framework for the Finite Dimensions Model of Concentric Ring Electrodes Using Human Electrocardiogram Data" Applied Sciences 9, no. 20: 4279. https://doi.org/10.3390/app9204279
APA StyleMakeyev, O., Musngi, M., Moore, L., Ye-Lin, Y., Prats-Boluda, G., & Garcia-Casado, J. (2019). Validating the Comparison Framework for the Finite Dimensions Model of Concentric Ring Electrodes Using Human Electrocardiogram Data. Applied Sciences, 9(20), 4279. https://doi.org/10.3390/app9204279






