Adaptive Sample-Size Unscented Particle Filter with Partitioned Sampling for Three-Dimensional High-Maneuvering Target Tracking
Abstract
:1. Introduction
2. Model Establishment
2.1. Target Motion Model
2.2. Measurement Model
3. Unscented Particle Filter with Adaptive Sample Size
3.1. Unscented Kalman Filter
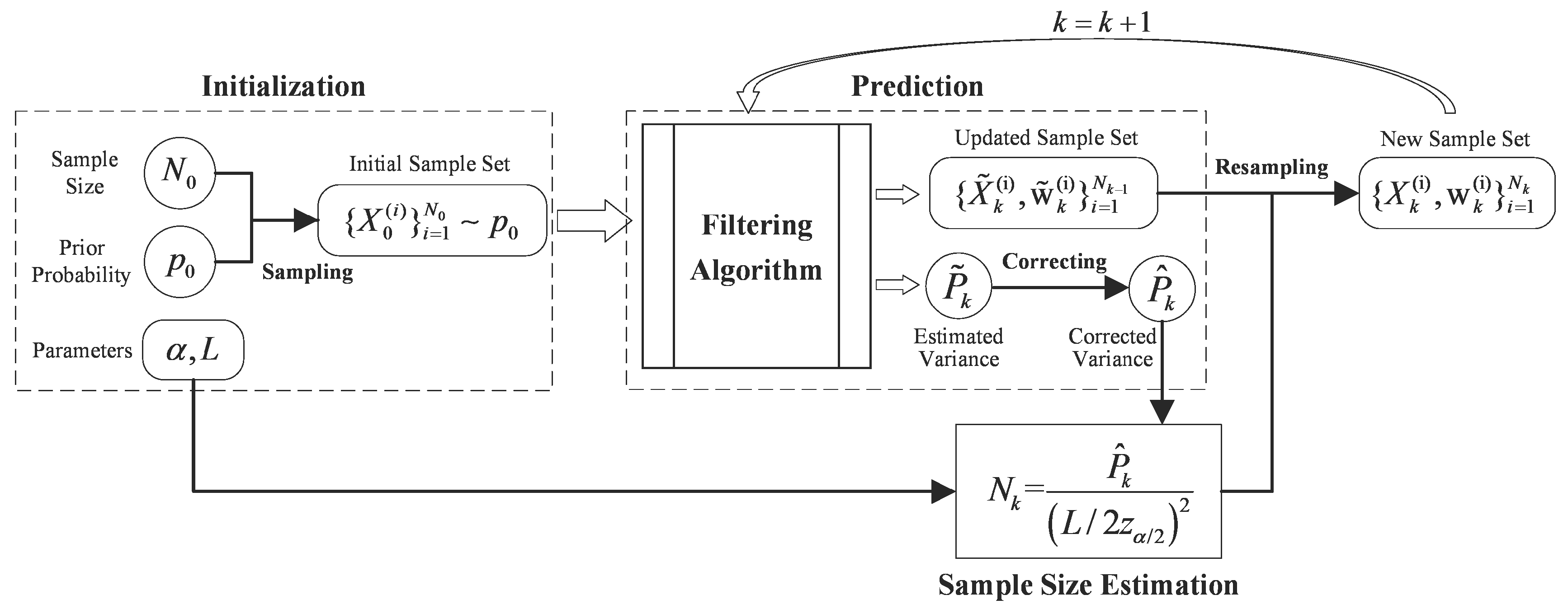
3.2. Adaptive Sample-Size Strategy
3.3. Adaptive Sample-Size Unscented Particle Filter
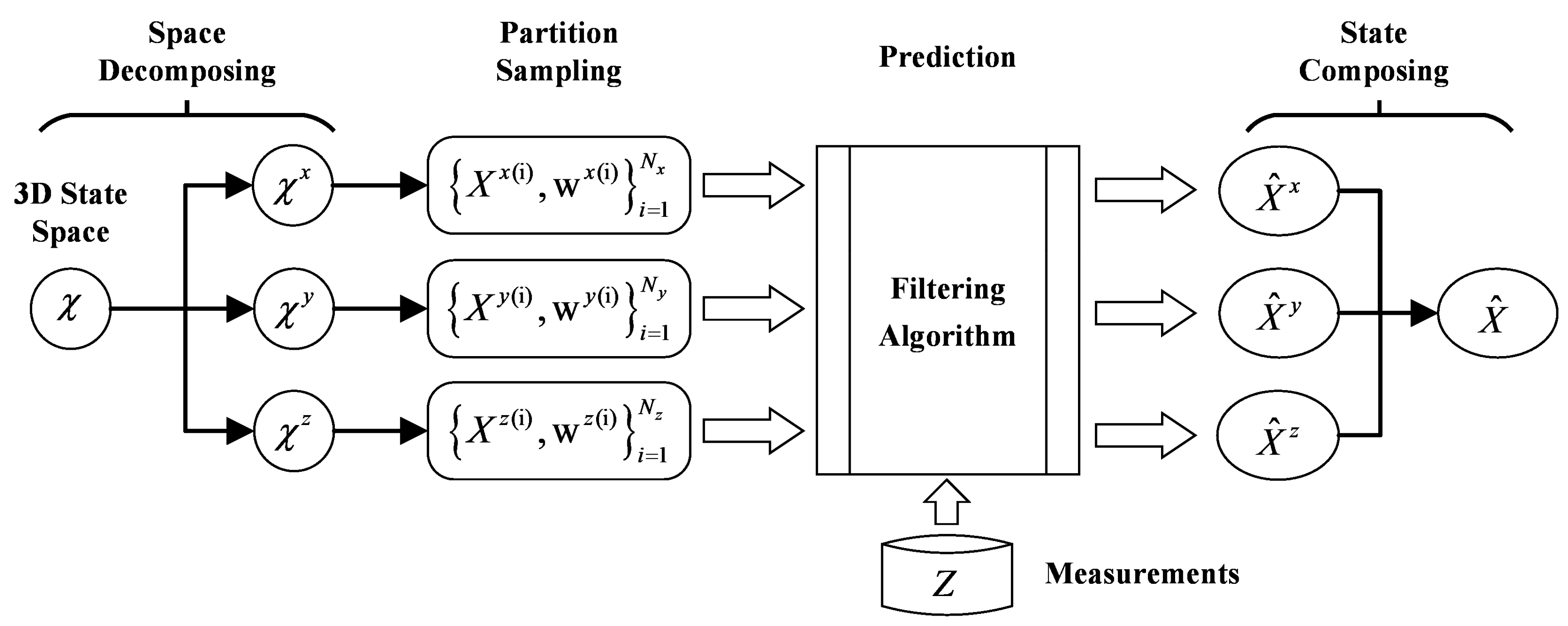
4. Adaptive Sample-Size Unscented Particle Filter with Partitioned Sampling
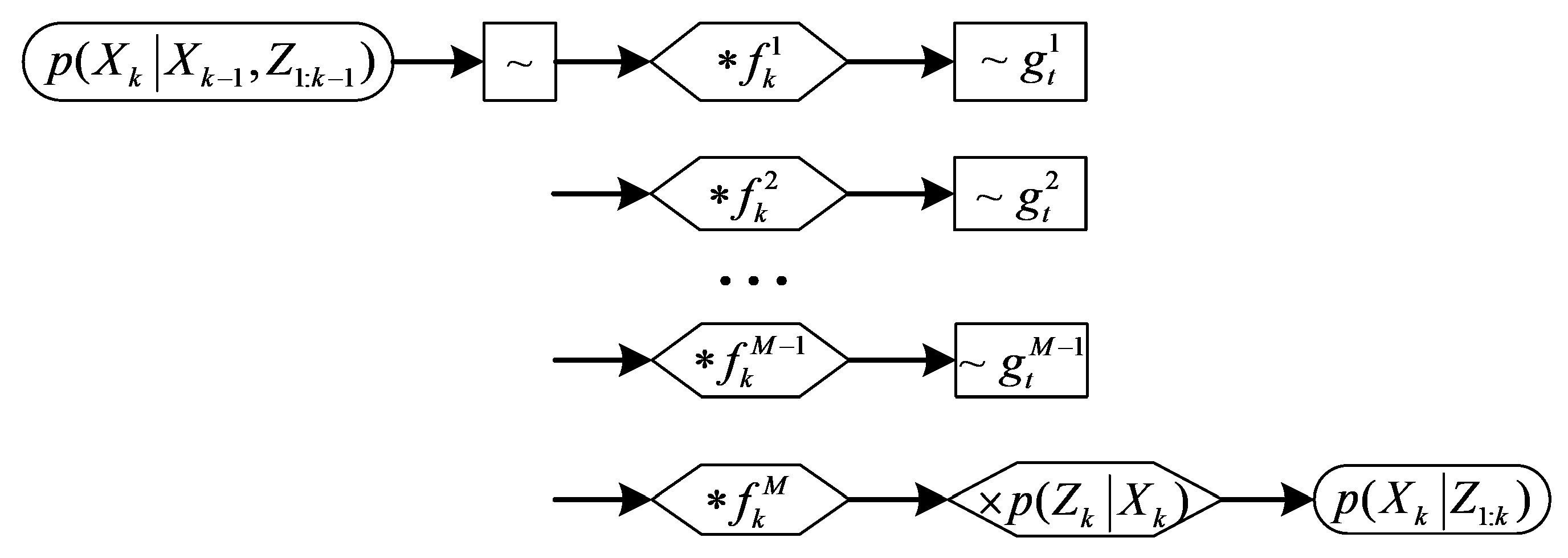
4.1. Partitioned Sampling
4.2. AUPF with Partitioned Sampling
5. Results
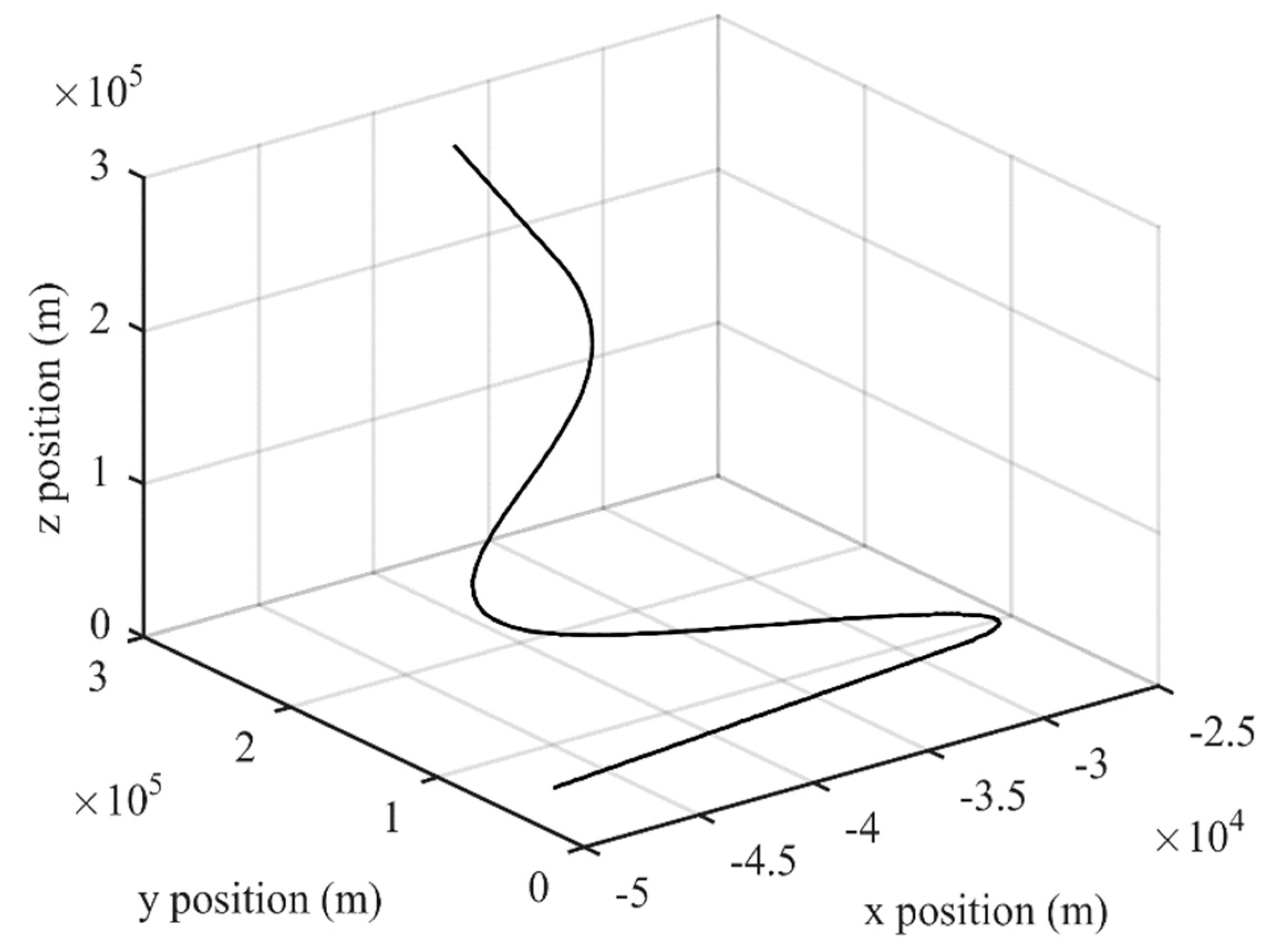
5.1. Initial Setting
5.2. Experimental Results and Analysis
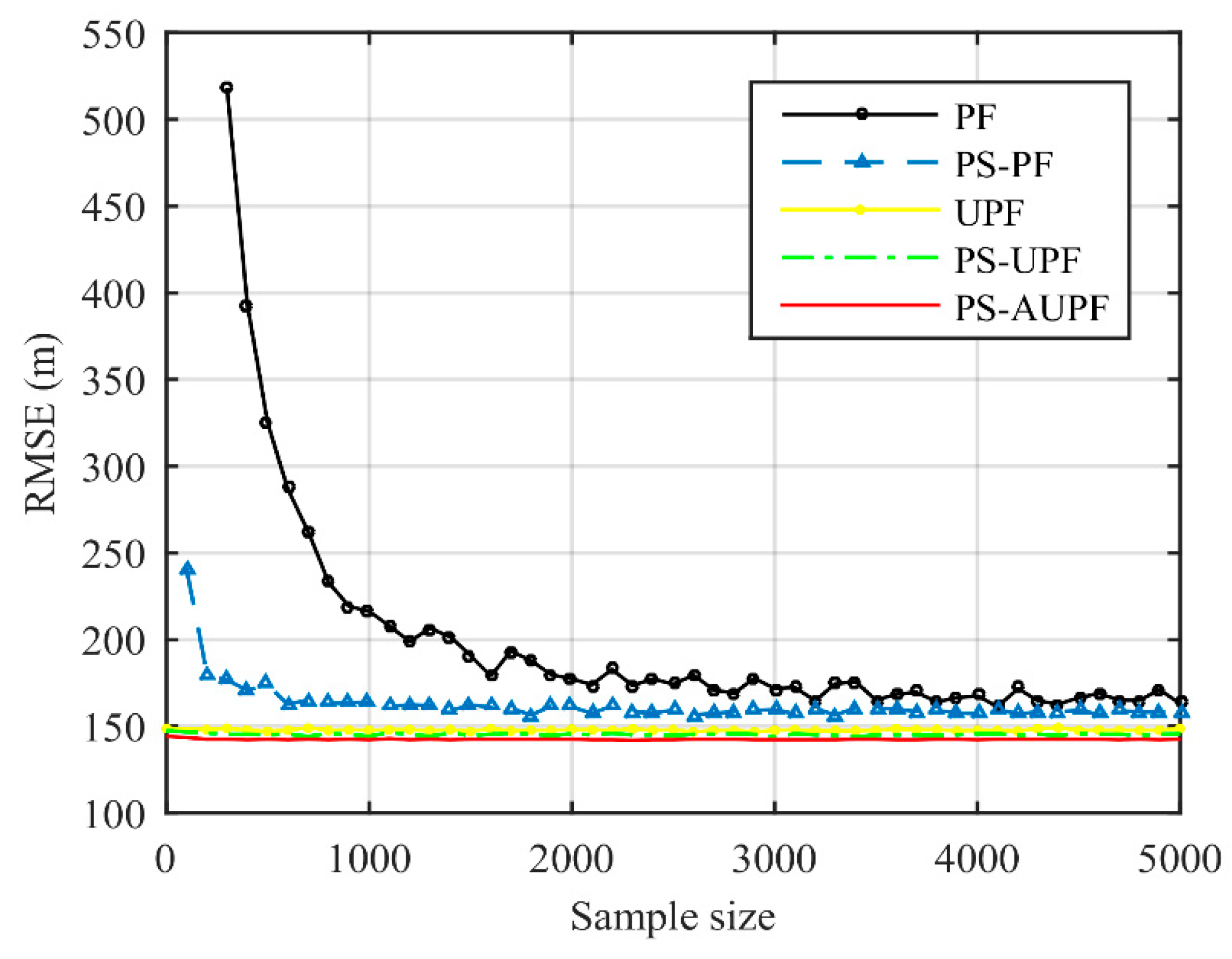
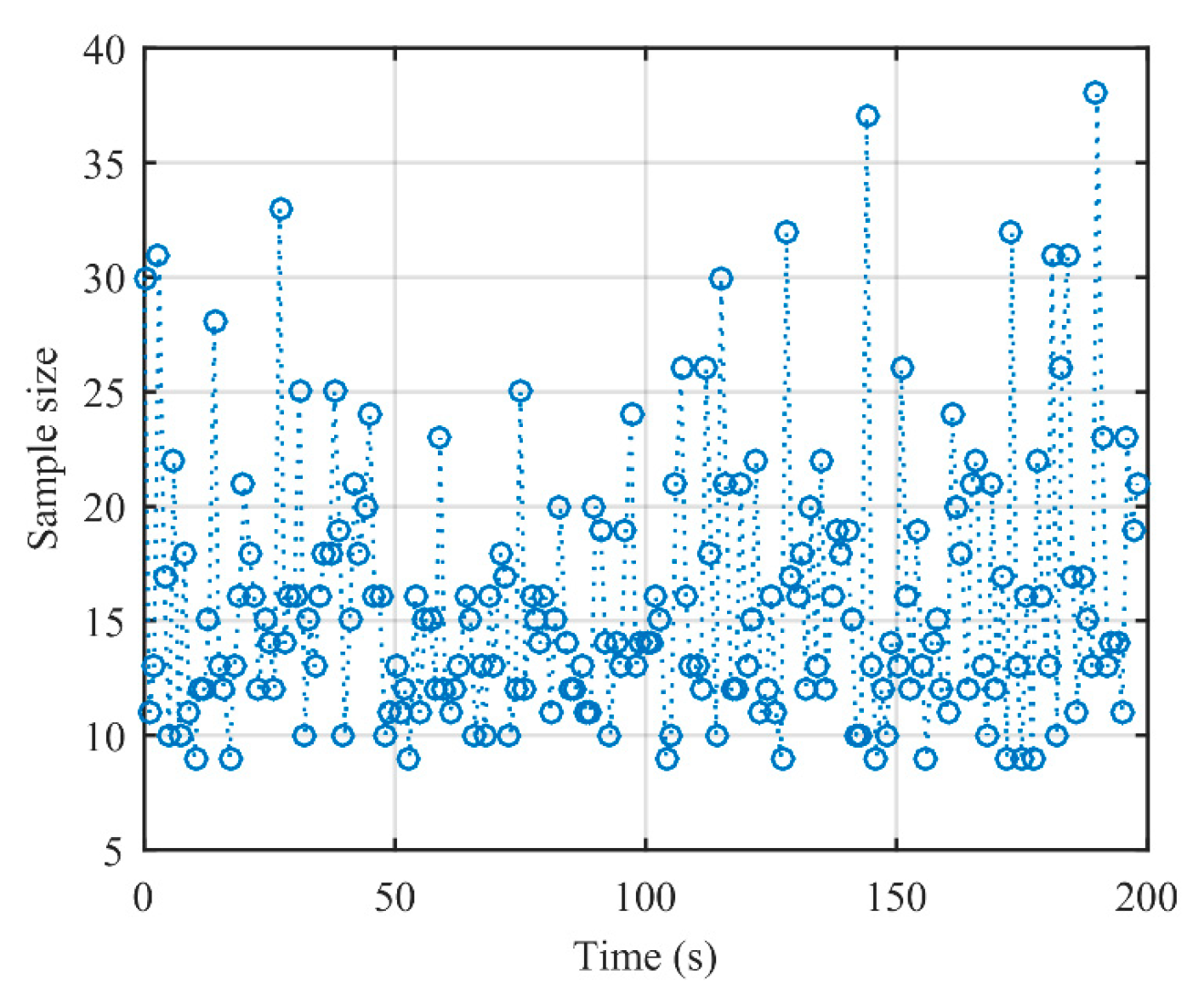
5.2.1. Sample Size Selection
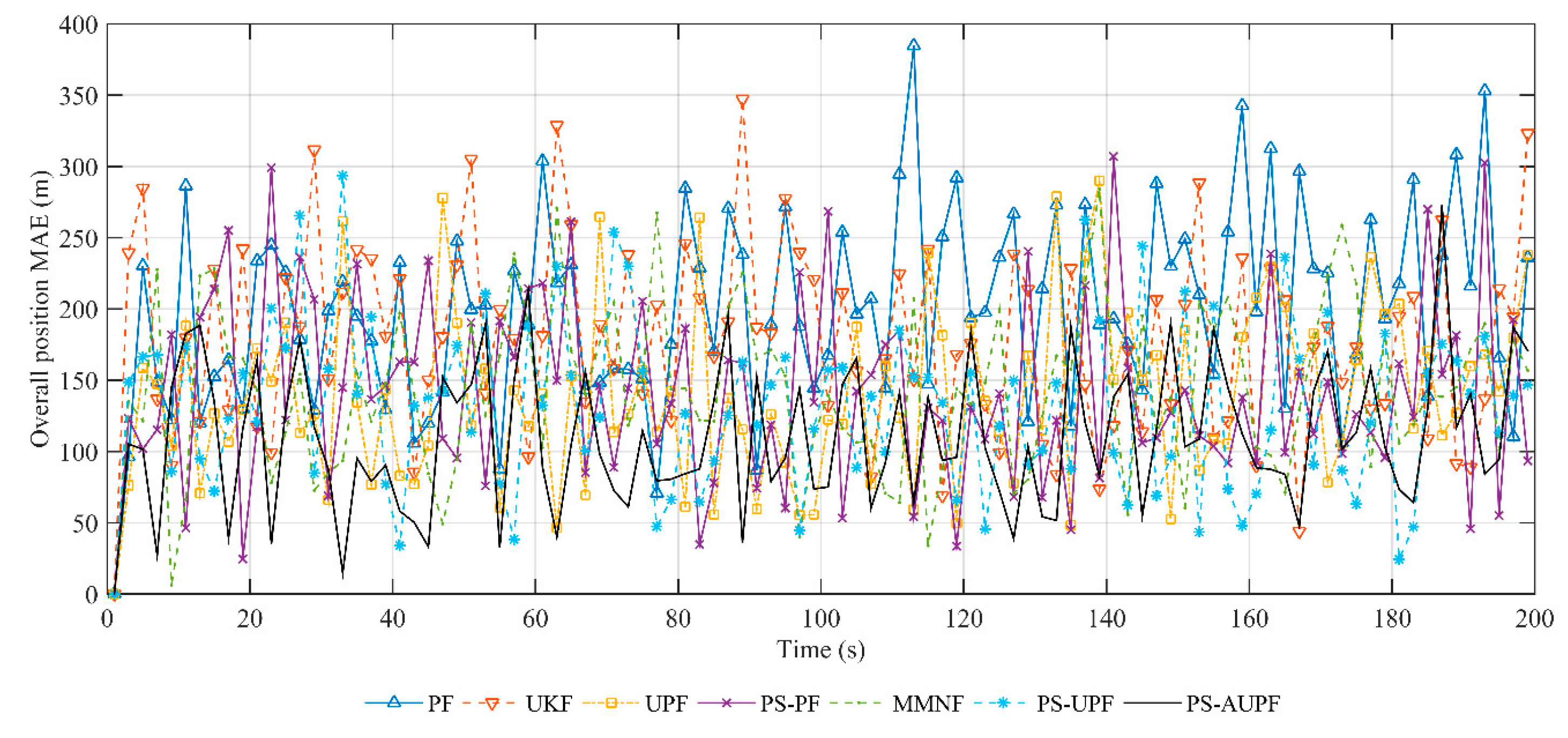
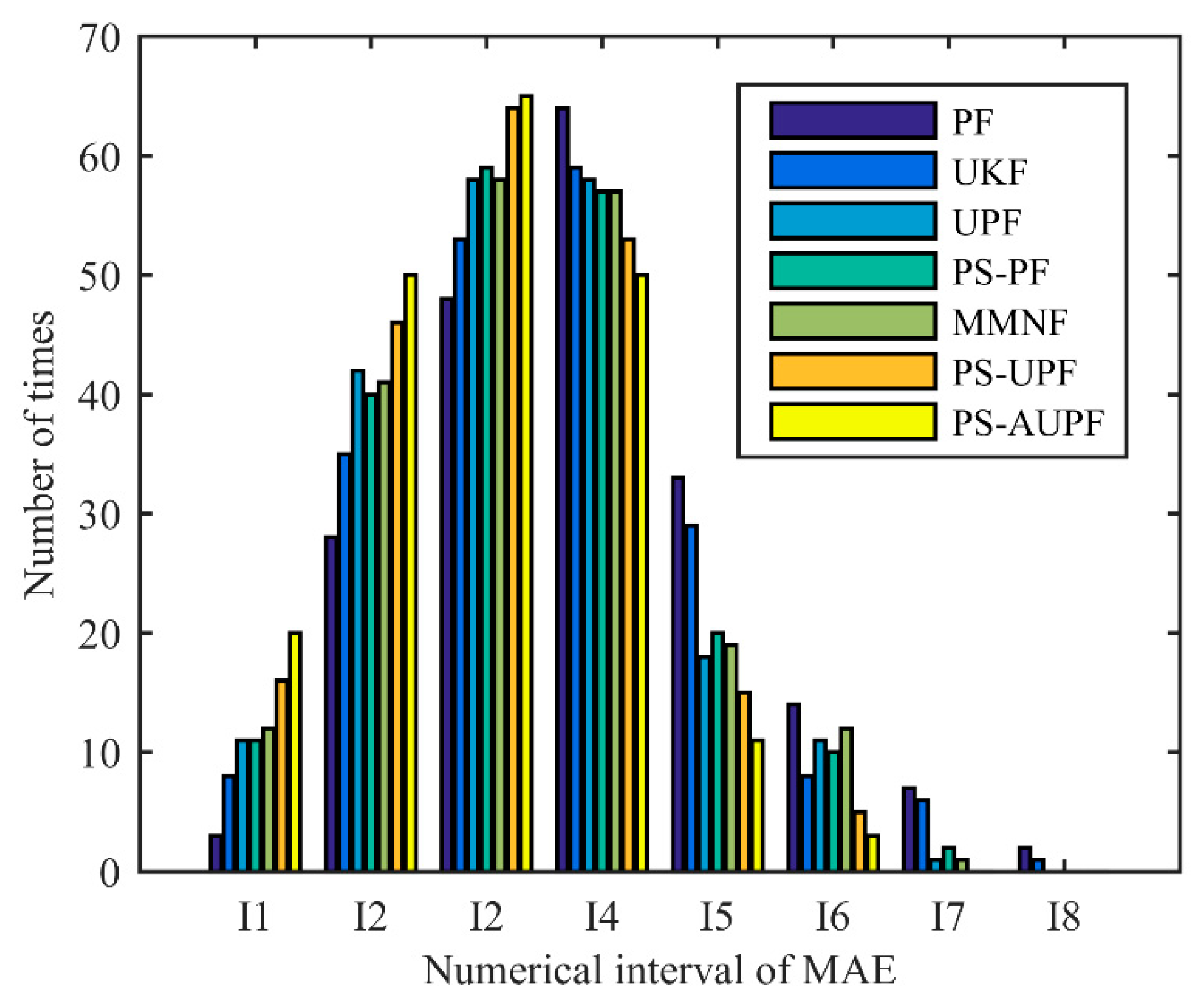
5.2.2. Comparison of Tracking MAE Distribution
5.2.3. Discussion on Tracking Accuracy
5.2.4. Discussion on Running Time
5.2.5. Summary of Overall Performance
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Algorithm A1. Adaptive Sample-Size UPF |
| Input: Initial sample size , lower limit of sample size , the prior probability of X, the confidence interval L, the confidence level α, the system model given in Section 2, Output: State estimation results , at time step k. Initialize: N = N0, for i = 1, 2, …, N, draw particle from the prior . For time step k = 1, 2, … do Importance Sampling: For i = 1, 2, …, N do Update particle with UKF to obtain the preliminary estimations at time k: state mean and variance ; Build an approximate Gaussian distribution ; Use as the importance density function of particle sampling to draw new particles: ; End Weight update: For i = 1, 2, …, N do Given observation , calculate the likelihood of particle ; Calculate the particle weights using following equation: Normalize the weights: End State mean and variance prediction: Correct the estimated variance using (21) and (22); Estimate the sample size at time k using (20), When , set ; Particles resampling: Remove the particles with small weight and multiply the particles with large weight from sample set ; Reset weight of each particle to get new sample set ; End |
Appendix B
| Algorithm A2. AUPF with Partitioned Sampling |
| Input: Initial sample size , lower limit of sample size , the prior probability of X, the confidence interval L, the confidence level α, the system model given in Section 2, Output: State estimation results , at time step k. Initialize: N = N0, for i = 1, 2, …, N, draw particle from the prior . decompose state space into 3 one-dimensional subspace according to orthogonal independence, allot particles number , , , respectively for each subspace, where ; For subspace d = x, y, z do for i = 1, 2, …, N, draw particles from the prior to obtain particle set ; End For time step k = 1, 2, … do For subspace d = x, y, z do For i = 1, 2, …, N do Importance Sampling: Update particle with UKF, build approximate Gaussian distribution to draw new particles: ; End Calculate and normalize the particle weights; Predict the sub-state mean and correct the sub-state variance ; Estimate the sample size at time k using (20), when , set ; Remove the particles with small weight and multiply the particles with large weight from sample set ; Reset ; End Composite output: , where is the state composition operator. End |
References
- Yu, Y. Distributed Multimodel Bernoulli Filters for Maneuvering Target Tracking. IEEE Sens. J. 2018, 18, 5885–5896. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, T.; Xu, X.; Li, Y. A Variational Bayesian Based Strong Tracking Interpolatory Cubature Kalman Filter for Maneuvering Target Tracking. IEEE Access 2018, 6, 52544–52560. [Google Scholar] [CrossRef]
- Zhang, A.; Lin, H. Parallel Filtering Algorithm in Three Dimensions for IMM Maneuvering Target Tracking. Fire Control Command Control. 2017, 42, 6–9. [Google Scholar] [CrossRef]
- Bi, X.; Wang, W.; Gao, J.; Du, J. The improved IMM tracking algorithm for high-speed maneuvering target. In Proceedings of the IET International Radar Conference 2015, Hangzhou, China, 14–16 October 2015; pp. 1–4. [Google Scholar]
- Zhu, Z. Application of particle filter algorithm in maneuvering target tracking. In Particle Filter and Its Application, 1st ed.; Science Press: Beijing, China, 2010; pp. 139–150. [Google Scholar]
- Wang, G.; Wu, J.; Li, X.; Mo, R.; Zhang, M. A real-time tracking prediction for maneuvering target. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 3562–3566. [Google Scholar]
- Ma, C.; San, Y.; Zhu, Y. Multiple Model Truncated Particle Filter for maneuvering target tracking. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 4773–4777. [Google Scholar]
- Wang, X.; Xu, M.; Wang, H.; Wu, Y.; Shi, H. Combination of Interacting Multiple Models with the Particle Filter for Three-Dimensional Target Tracking in Underwater Wireless Sensor Networks. Math. Probl. Eng. 2012, 2012. [Google Scholar] [CrossRef]
- Visina, R.; Bar-Shalom, Y.; Willett, P. Multiple-Model Estimators for Tracking Sharply Maneuvering Ground Targets. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1404–1414. [Google Scholar] [CrossRef]
- Han, B.; Huang, H.; Lei, L.; Huang, C.; Zhang, Z. An Improved IMM Algorithm Based on STSRCKF for Maneuvering Target Tracking. IEEE Access 2019, 7, 57795–57804. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part I. Dynamic models. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1333–1364. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, Y.; Wang, G. Highly maneuvering target tracking using multi-parameter fusion Singer model. J. Syst. Eng. Electron. 2017, 28, 841–850. [Google Scholar] [CrossRef]
- Barbu, V.S.; Karagrigoriou, A.; Makrides, A. On Semi-Markov Modelling and Inference for Multi-state Systems. In Proceedings of the 2016 Second International Symposium on Stochastic Models in Reliability Engineering, Life Science and Operations Management (SMRLO), Beer Sheva, Israel, 15–18 February 2016; pp. 56–60. [Google Scholar]
- Bao, S.; Cheng, S.; Xu, C. Strong Tracking Current Statistical Model Based on Mixed Bayesian-Fisher Model. In Proceedings of the 2017 2nd International Conference on Cybernetics, Robotics and Control (CRC), Chengdu, China, 21–23 July 2017; pp. 75–79. [Google Scholar]
- Meng, Q.; Hou, B.; Dong, L.; He, Z.; Wang, J. Performance Analysis and Comparison for High Maneuver Target Track Based on Different Jerk Models. J. Control Sci. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Mehrotra, K.; Mahapatra, P.R. A jerk model for tracking highly maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 1094–1105. [Google Scholar] [CrossRef]
- Qiao, X.; Wang, B. A CS-Jerk Model for Tracking Highly Maneuvering Targets. Syst. Eng. Electron. 2002, 24, 53–56. [Google Scholar]
- Dai, S.W.; Fang, J.; Dai, H.D.; Zou, J.; Wang, Y.T. A Highly Maneuvering Target Tracking Algorithm Based on Improved CS-Jerk Model. Electron. Opt. Control. 2016, 23, 11–15. [Google Scholar]
- Wang, F.; Lu, M.; Zhao, Q. Particle filter algorithm. Chin. J. Comput. 2014, 37, 1679–1694. [Google Scholar]
- Wang, F.; Zhang, J.; Lin, B.; Li, X. Two Stage Particle Filter for Nonlinear Bayesian Estimation. IEEE Access 2018, 6, 13803–13809. [Google Scholar] [CrossRef]
- Xie, W.; Wang, L.; Bai, B.; Peng, B.; Feng, Z. An Improved Algorithm Based on Particle Filter for 3D UAV Target Tracking. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Kazimierski, W.; Łubczonek, J. Verification of marine multiple model neural tracking filter for the needs of shore radar stations. In Proceedings of the 2012 13th International Radar Symposium, Warsaw, Poland, 23–25 May 2012; pp. 554–559. [Google Scholar]
- Kazimierski, W.; Stateczny, A. Optimization of multiple model neural tracking filter for marine targets. In Proceedings of the 2012 13th International Radar Symposium, Warsaw, Poland, 23–25 May 2012; pp. 543–548. [Google Scholar]
- Kazimierski, W.; Zaniewicz, G.; Stateczny, A. Verification of multiple model neural tracking filter with ship’s radar. In Proceedings of the 2012 13th International Radar Symposium, Warsaw, Poland, 23–25 May 2012; pp. 549–553. [Google Scholar]
- Sun, C.; Zhu, S.; Liu, J. Fusing Kalman filter with TLD algorithm for target tracking. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 3736–3741. [Google Scholar]
- Merwe, R.V.D.; Doucet, A.; Freitas, N.D.; Wan, E. The Unscented Particle Filter. In Proceedings of the 13th International Conference on Neural Information Processing Systems, Denver, CO, USA, 13 January 2001; pp. 584–590. [Google Scholar]
- Gao, Y.; Gao, Y.; Gao, S. Adaptive sample-size unscented particle filter based on likelihood distribution. J. Chin. Inert. Technol. 2015, 23, 648–652. [Google Scholar]
- Yin, F.; He, B.; Feng, C.; Guo, S.; Zhang, X.; Liu, H.; Mu, X.; Lv, P.; Yan, T. Application of AUV Navigation Based on SVD Unscented Particle Filter. In Proceedings of the 2019 IEEE Underwater Technology (UT), Kaohsiung, Taiwan, 16–19 April 2019; pp. 1–4. [Google Scholar]
- Wu, X.; Song, S. Robust information unscented particle filter based on M-estimate. IET Signal Process. 2019, 13, 14–20. [Google Scholar] [CrossRef]
- Kouritzin, M.; Azen, S. Residual and stratified branching particle filters. Comput. Stat. Data Anal. 2017, 111, 145–165. [Google Scholar] [CrossRef]
- Teng, F.; Xue, L.; Li, X. Self-adaptive resampling particle filter based on student’s t distribution. Control Decis. 2018, 33, 361–365. [Google Scholar] [CrossRef]
- Aunsri, N. Improved Dual Tone Multi Frequency identification Using Adaptive Resampling Particle Filter. In Proceedings of the 2018 21st International Symposium on Wireless Personal Multimedia Communications (WPMC), Chiang Rai, Thailand, 25–28 November 2018; pp. 173–176. [Google Scholar]
- Zhang, X.; Gu, F. Adaptive Particle Sampling and Resampling in Parallel/Distributed Particle Filters. In Proceedings of the 2019 Spring Simulation Conference (SpringSim), Tucson, AZ, USA, 29 April–2 May 2019; pp. 1–12. [Google Scholar]
- Yang, W.; Yuan, S.; Chen, J. Application of deterministic resampling particle filter to fatigue prognosis. J. Vibroeng. 2017, 19, 5978–5991. [Google Scholar]
- Fei, X.; Shen, Y.; Yan, T. Application of AUV Navigation Based on Deterministic Particle Filter Algorithm. In Proceedings of the OCEANS 2018 MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018; pp. 1–4. [Google Scholar]
- Yang, F.; Zheng, L.; Luo, Y. A Novel Particle Filter Based on Hybrid Deterministic and Random Sampling. IEEE Access 2018, 6, 67536–67542. [Google Scholar] [CrossRef]
- Wang, W.; Tan, Q.K.; Chen, J.; Ren, Z. Particle filter based on improved genetic algorithm resampling. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; pp. 346–350. [Google Scholar]
- Zhang, S. Mobile Robot Location Algorithm Based on Improved Particle Filtering. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 8–11 October 2018; pp. 1417–1421. [Google Scholar]
- Tian, M.C.; Yu-Ming, B.O.; Pan-Long, W.U.; Chen, Z.M.; Yue, C.; Wang, H.; Automation, S.O. Novel target tracking method based on firefly algorithm optimized particle filter. Control Decis. 2017, 32, 1758–1766. [Google Scholar]
- Chen, Z.; Wu, P.; Bo, Y.; Tian, M.; Yue, C. Adaptive control bat algorithm intelligent optimization particle for maneuvering target tracking. Acta Electron. Sin. 2018, 46, 886–894. [Google Scholar]
- Maccormick, J.; Isard, M. Partitioned Sampling, Articulated Objects, and Interface-Quality Hand Tracking. In Proceedings of the European Conference on Computer Vision, Dublin, Ireland, 26 June–1 July 2000; pp. 3–19. [Google Scholar]
- Gonzales, C.; Dubuisson, S.; Xuan, S.N.G. Simultaneous Partitioned Sampling for Articulated Object Tracking. In Proceedings of the Advances Concepts for Intelligent Vision Systems-International Conference, Lecce, Italy, 24–27 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 150–161. [Google Scholar]
- Fox, D. KLD-Sampling: Adaptive Particle Filters. Adv. Neural Inf. Process. Syst. 2002, 14, 713–720. [Google Scholar]
- Dihua, S.; Hao, Q.; Min, Z.; Senlin, C.; Liangyi, Y. Adaptive KLD sampling based Monte Carlo localization. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 4154–4159. [Google Scholar]
- Li, A.W.; Bastos, G.S. A hybrid self-adaptive particle filter through KLD-sampling and SAMCL. In Proceedings of the 2017 18th International Conference on Advanced Robotics (ICAR), Hong Kong, China, 10–12 July 2017; pp. 106–111. [Google Scholar]
- Torma, P.; Szepesvari, C. On using likelihood-adjusted proposals in particle filtering: Local importance sampling. In Proceedings of the 4th International Symposium on Image and Signal Processing and Analysis, Zagreb, Croatia, 15–17 September 2005; pp. 58–63. [Google Scholar]
- Liang-qun, L.; Chao, H.; Guo-liang, Z. A novel particle filtering algorithm for the noncooperative target tracking in general aviation. In Proceedings of the 2014 International Conference on Audio, Language and Image Processing, Shanghai, China, 7–9 July 2014; pp. 561–564. [Google Scholar]
- Li, X.; Jilkov, V. A survey of maneuvering target tracking—Part III: Measurement models. IEEE Trans. Aerosp. Electron. Syst. 2001, 39, 1333–1364. [Google Scholar]
- Kandepu, R.; Foss, B.; Imsland, L. Applying the unscented Kalman filter for nonlinear state estimation. J. Process Control. 2008, 18, 753–768. [Google Scholar] [CrossRef]
- Doucet, A.; Johansen, A.M. A tutorial on particle filtering and smoothing: Fiteen years later. In Proceedings of the Oxford Handbook of Nonlinear Filtering; Crisan, E.D., Rozovsky, B., Eds.; Oxford University Press: Oxford, UK, 2011; pp. 656–704. [Google Scholar]
- Sheng, Z.; Xie, S.; Pan, C. Parameter Estimation. In Probability Theory and Mathematical Statistics, 4th ed.; Higher Education Press: Beijing, China, 2008; pp. 178–217. [Google Scholar]
- Chen, S.Y. Kalman Filter for Robot Vision: A Survey. IEEE Trans. Ind. Electron. 2012, 59, 4409–4420. [Google Scholar] [CrossRef]
- Sheng, Z.; Xie, S.; Pan, C. Sample & Sampling distribution. In Probability Theory and Mathematical Statistics, 4th ed.; Higher Education Press: Beijing, China, 2008; pp. 178–217. [Google Scholar]
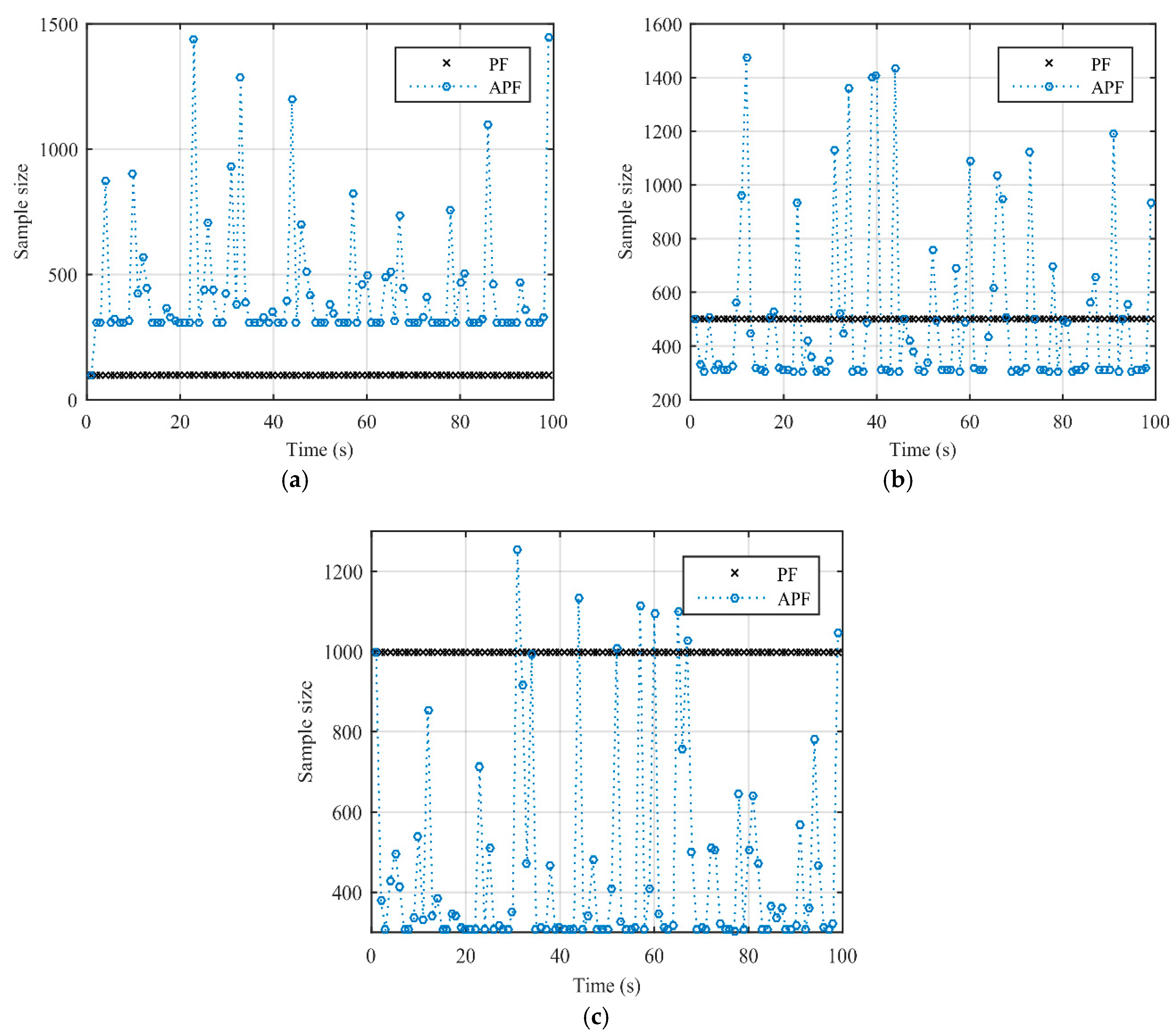
| Algorithm | Initial Sample Size | RMSE | Running Time (s) |
|---|---|---|---|
| PF | 100 | 4.0561 | 0.2152 |
| 500 | 3.7749 | 1.0601 | |
| 1000 | 3.7458 | 2.4824 | |
| KL-PF | 100 | 3.7436 | 2.7982 |
| 500 | 3.7428 | 2.8630 | |
| 1000 | 3.7441 | 2.8258 | |
| APF | 100 | 3.7447 | 1.8856 |
| 500 | 3.7419 | 1.8919 | |
| 1000 | 3.7423 | 1.9136 |
| Overall RMSE (m) | |||
|---|---|---|---|
| PF | 115.7570 | 182.6600 | 247.5047 |
| PS-PF | 88.1420 | 156.7254 | 227.3936 |
| UKF | 89.9564 | 167.2354 | 264.3609 |
| UPF | 81.8241 | 150.7658 | 215.7149 |
| MMNF | 80.4735 | 148.3845 | 214.0359 |
| PS-UPF | 77.8543 | 142.9482 | 202.3238 |
| PS-AUPF | 75.9206 | 139.1967 | 199.8989 |
| Overall RMSE (m) | |||
|---|---|---|---|
| ±50 m Range of Noises | ±100 m Range of Noises | ±150 m Range of Noises | |
| PF | 89.8381 | 121.3732 | 156.4902 |
| PS-PF | 56.8432 | 94.8275 | 135.7030 |
| UKF | 59.2855 | 101.2696 | 154.4144 |
| UPF | 51.7421 | 89.4955 | 129.6116 |
| MMNF | 50.5371 | 88.3553 | 128.9389 |
| PS-UPF | 48.4721 | 86.1945 | 124.6514 |
| PS-AUPF | 46.4825 | 84.4288 | 123.3828 |
| Overall RMSE (m) | |||
|---|---|---|---|
| PF | 143.3577 | 256.4032 | 376.2221 |
| PS-PF | 125.8578 | 239.6098 | 359.9481 |
| UKF | 127.4355 | 252.4281 | 374.7265 |
| UPF | 123.8671 | 238.5487 | 356.6859 |
| MMNF | 122.0391 | 236.6279 | 354.3415 |
| PS-UPF | 120.0796 | 230.2823 | 349.8173 |
| PS-AUPF | 119.1287 | 227.8623 | 347.2862 |
| Algorithm | Running Time (s) |
|---|---|
| PF | 29.0031 |
| PS-PF | 3.2933 |
| UKF | 0.2361 |
| UPF | 7.4856 |
| MMNF | 13.1387 |
| PS-UPF | 1.8459 |
| PS-AUPF | 1.0191 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Q.; Chen, G.; Lu, H. Adaptive Sample-Size Unscented Particle Filter with Partitioned Sampling for Three-Dimensional High-Maneuvering Target Tracking. Appl. Sci. 2019, 9, 4278. https://doi.org/10.3390/app9204278
Deng Q, Chen G, Lu H. Adaptive Sample-Size Unscented Particle Filter with Partitioned Sampling for Three-Dimensional High-Maneuvering Target Tracking. Applied Sciences. 2019; 9(20):4278. https://doi.org/10.3390/app9204278
Chicago/Turabian StyleDeng, Qi, Gang Chen, and Huaxiang Lu. 2019. "Adaptive Sample-Size Unscented Particle Filter with Partitioned Sampling for Three-Dimensional High-Maneuvering Target Tracking" Applied Sciences 9, no. 20: 4278. https://doi.org/10.3390/app9204278
APA StyleDeng, Q., Chen, G., & Lu, H. (2019). Adaptive Sample-Size Unscented Particle Filter with Partitioned Sampling for Three-Dimensional High-Maneuvering Target Tracking. Applied Sciences, 9(20), 4278. https://doi.org/10.3390/app9204278




