Space Charge Accumulation and Decay in Dielectric Materials with Dual Discrete Traps
Abstract
1. Introduction
2. Dynamic Responses of Charge Trapping and De-trapping
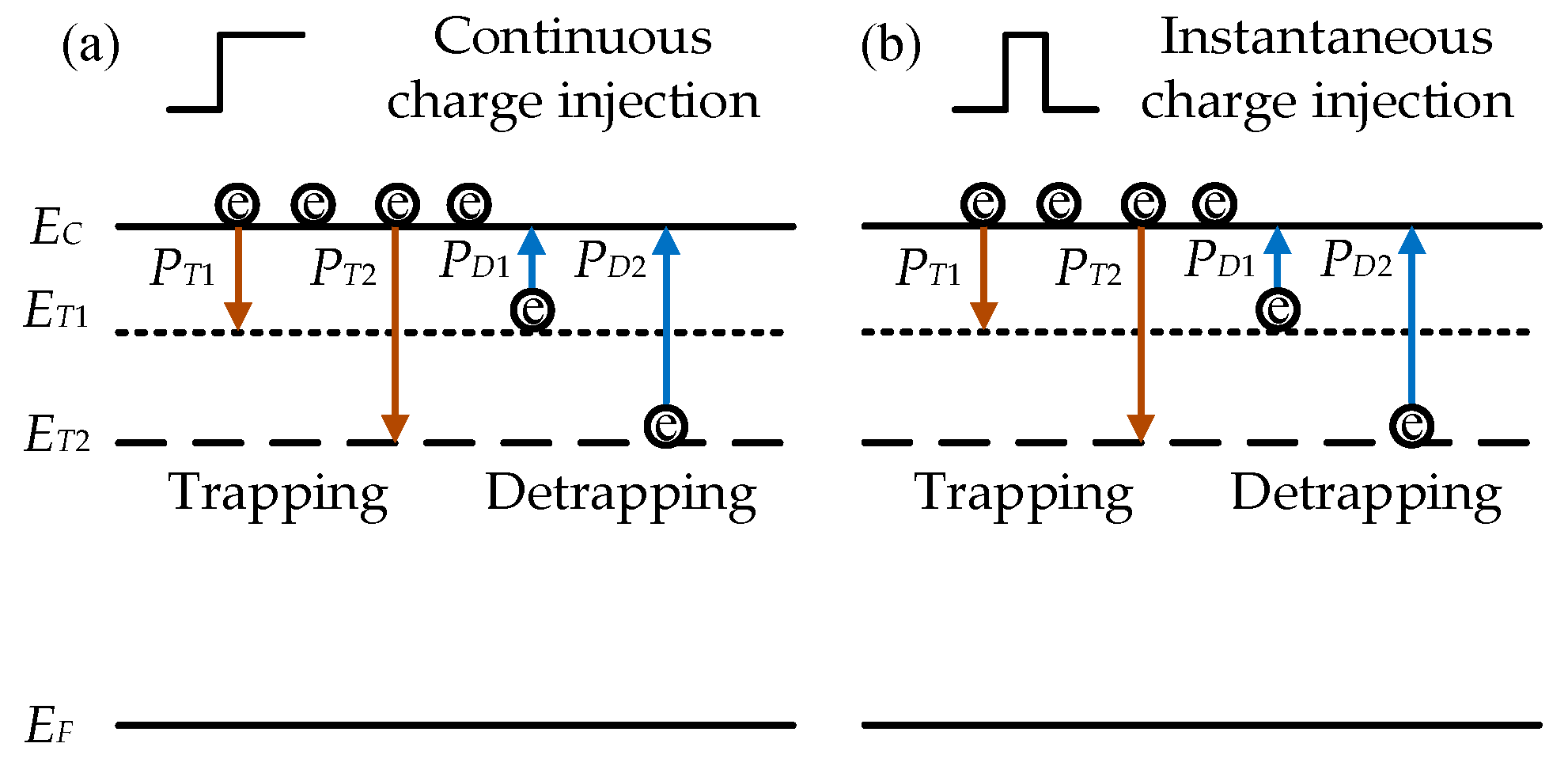
2.1. Charge Trapping/De-trapping Dynamics
2.2. Continuous Charge Injection
2.3. Instantaneous Charge Injection
2.4. Steady State Characteristics in the Case of Instantaneous Charge Injection
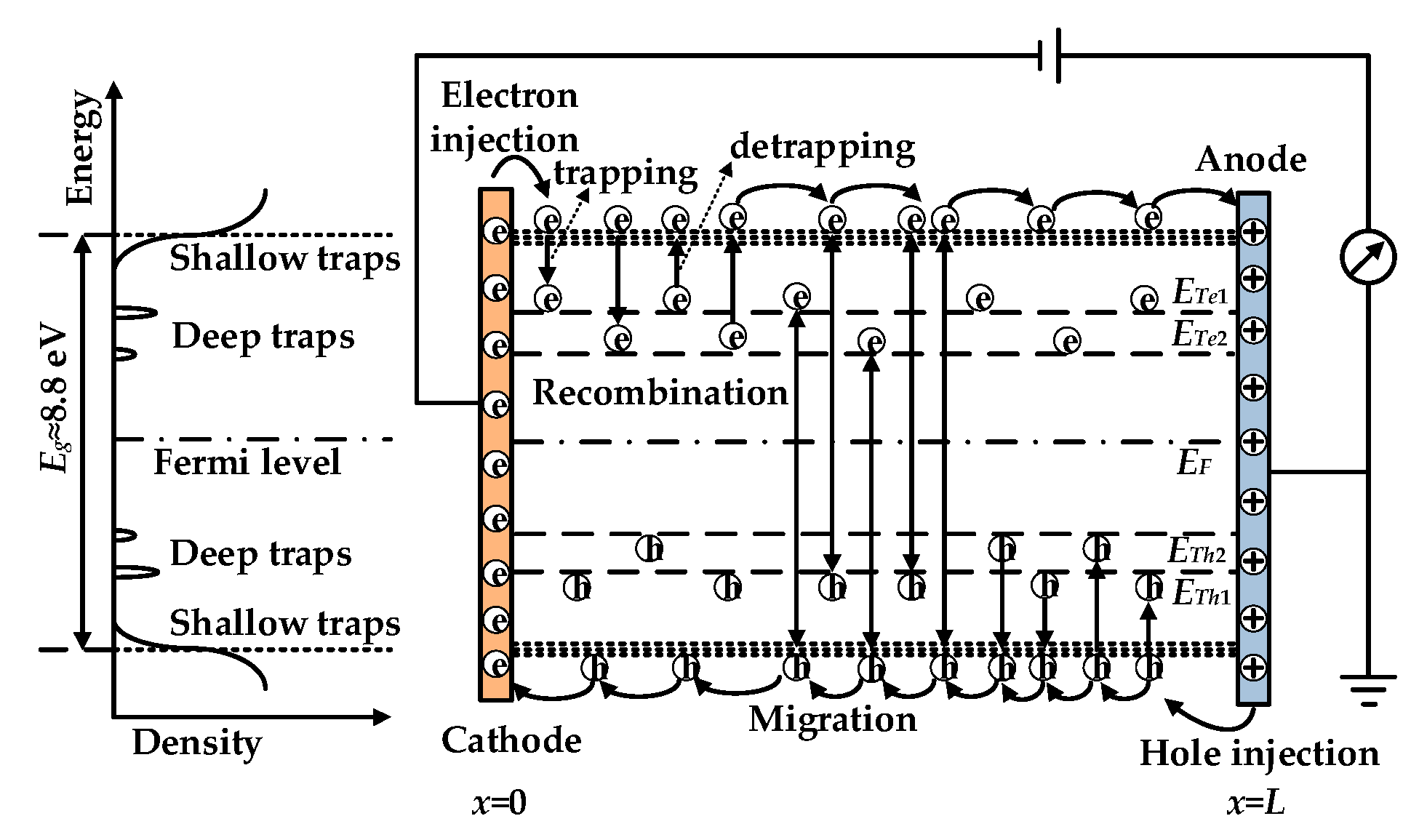
3. Bipolar Charge Transport Model
3.1. Charge Injection
3.2. Self-Consitent Equations
3.3. Charge Reaction Dynamics
3.4. Numerical Techniques
4. Results and Discussion
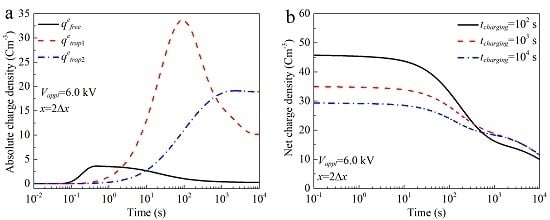
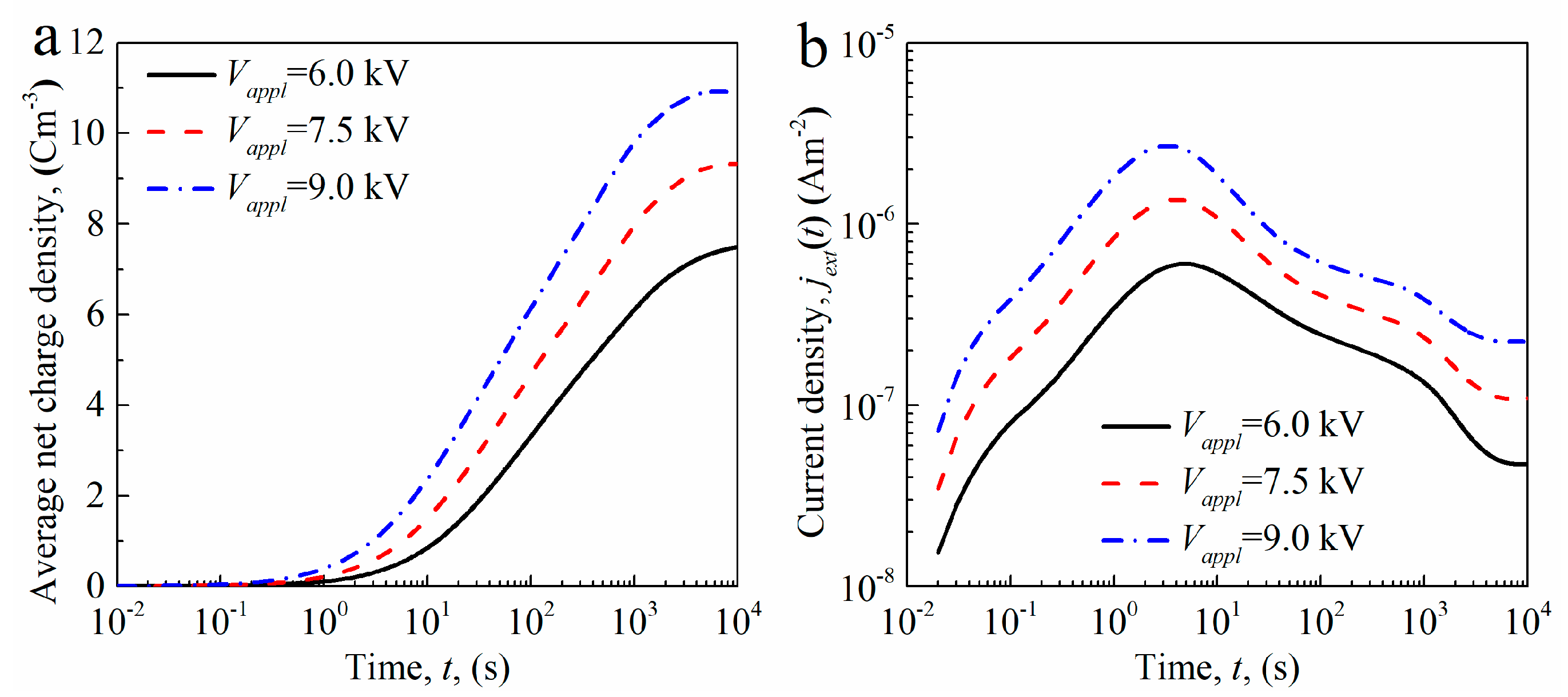
4.1. Space Charge Accumulation Characteristics
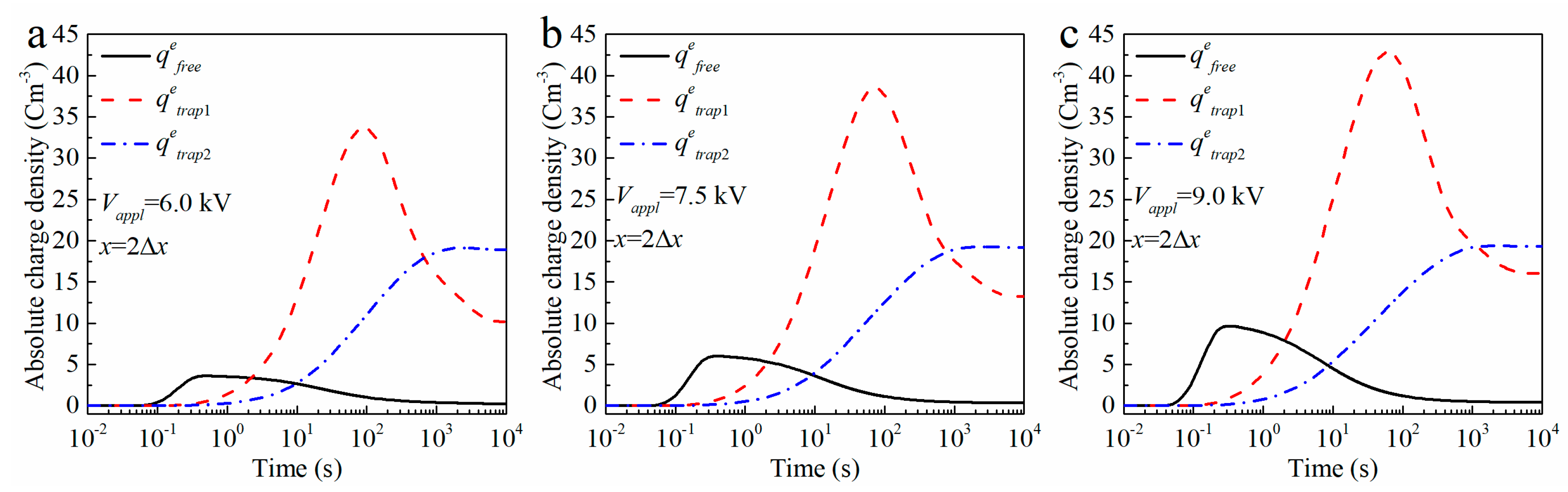
4.2. Time Dependent Free and Trapped Charge Densities at the Same Position
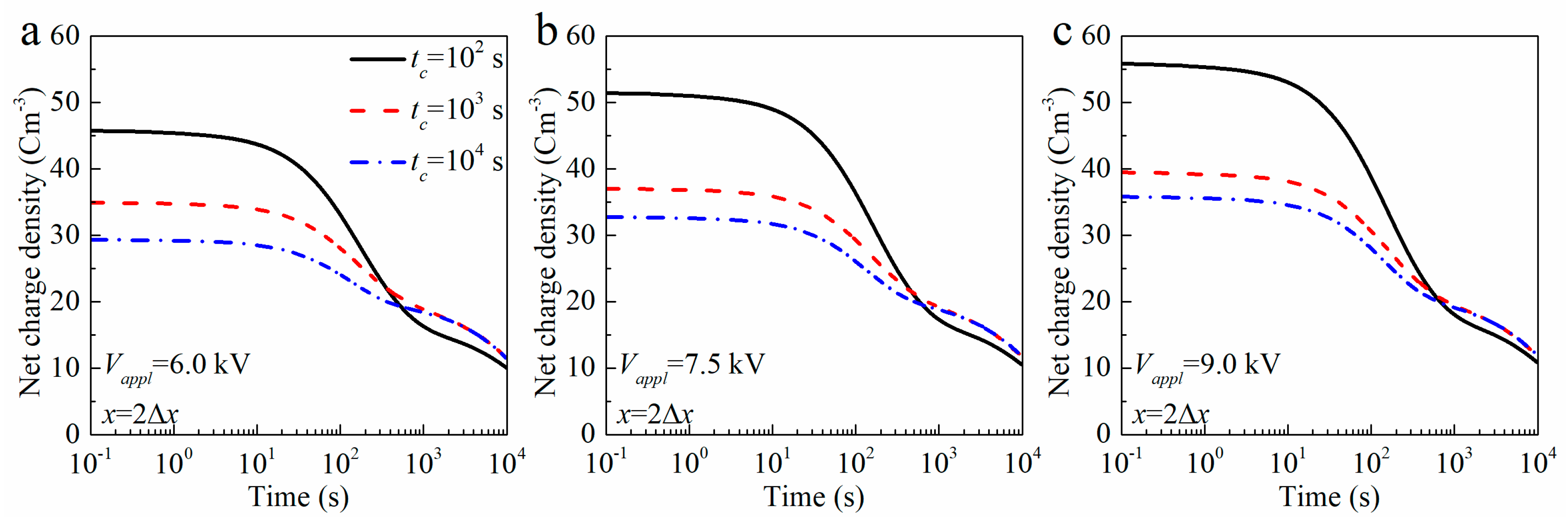
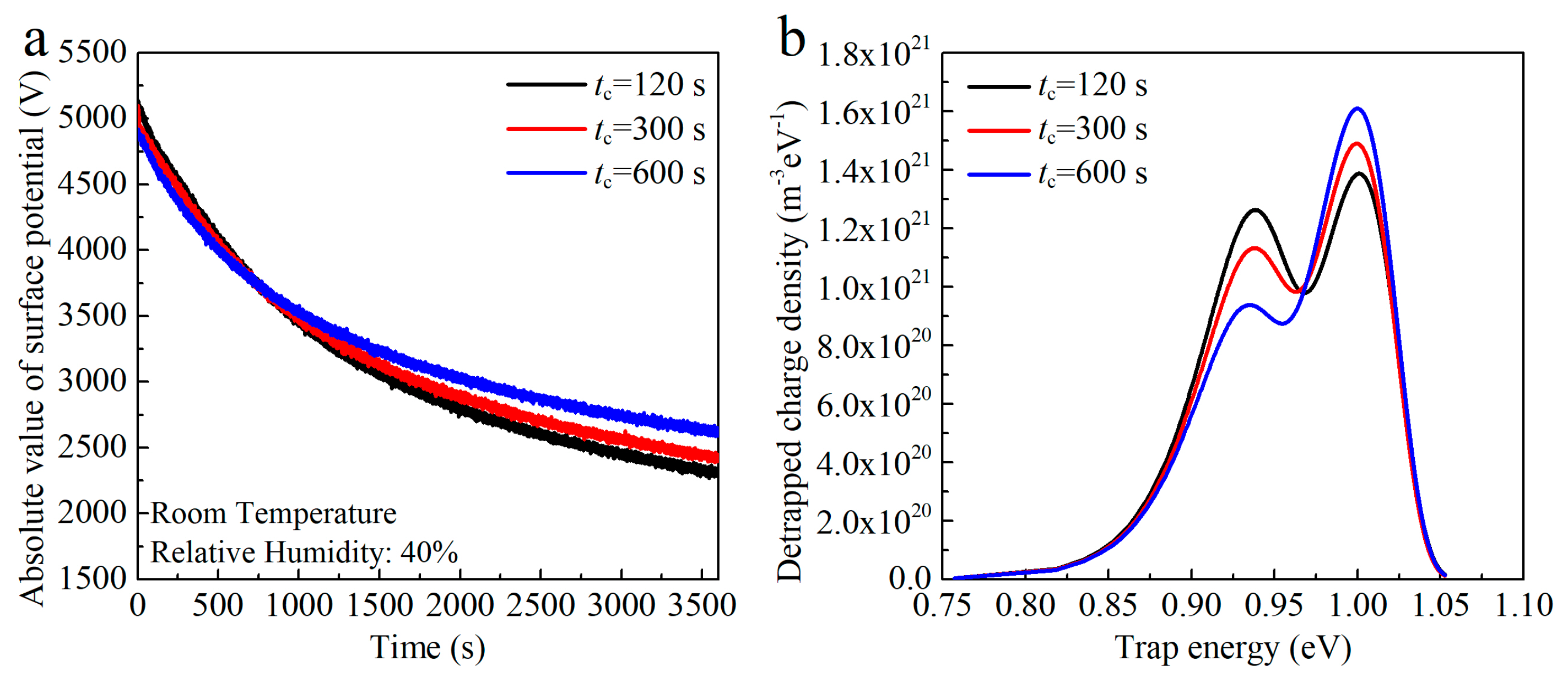
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Coefficients C11, C12, C21, and C22
Appendix B
Relationship between qtrap1(tst) and qtrap2(tst) in the Case of Instantaneous Charge Injection
References
- Teyssedre, G.; Laurent, C. Charge transport modeling in insulating polymers: From molecular to macroscopic scale. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 857–875. [Google Scholar] [CrossRef]
- Gao, Y.H.; Huang, X.Y.; Min, D.M.; Li, S.T.; Jiang, P.K. Recyclable Dielectric Polymer Nanocomposites with Voltage Stabilizer Interface: Toward New Generation of High Voltage Direct Current Cable Insulation. ACS Sustain. Chem. Eng. 2019, 7, 513–525. [Google Scholar] [CrossRef]
- Hao, J.; Zou, R.H.; Liao, R.J.; Yang, L.J.; Liao, Q. New Method for Shallow and Deep Trap Distribution Analysis in Oil Impregnated Insulation Paper Based on the Space Charge Detrapping. Energies 2018, 11, 271. [Google Scholar] [CrossRef]
- Wu, Y.H.; Zha, J.W.; Li, W.K.; Wang, S.J.; Dang, Z.M. A remarkable suppression on space charge in isotatic polypropylene by inducing the beta-crystal formation. Appl. Phys. Lett. 2015, 107, 112901. [Google Scholar] [CrossRef]
- Chen, G.; Tay, T.Y.G.; Davies, A.E.; Tanaka, Y.; Takada, T. Electrodes and charge injection in low-density polyethylene - Using the pulsed electroacoustic technique. IEEE Trans. Dielectr. Electr. Insul. 2001, 8, 867–873. [Google Scholar] [CrossRef]
- Mizutani, T. Space-Charge Measurement Techniques and Space-Charge in Polyethylene. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 923–933. [Google Scholar] [CrossRef]
- Zha, J.W.; Dang, Z.M.; Song, H.T.; Yin, Y.; Chen, G. Dielectric properties and effect of electrical aging on space charge accumulation in polyimide/TiO2 nanocomposite films. J. Appl. Phys. 2010, 108, 094113. [Google Scholar] [CrossRef]
- Blaise, G. Space-Charge Physics and the Breakdown Process. J. Appl. Phys. 1995, 77, 2916–2927. [Google Scholar] [CrossRef]
- Wu, K.; Dissado, L.A.; Okamoto, T. Percolation model for electrical breakdown in insulating polymers. Appl. Phys. Lett. 2004, 85, 4454–4456. [Google Scholar] [CrossRef]
- Jones, J.P.; Llewellyn, J.P.; Lewis, T.J. The contribution of field-induced morphological change to the electrical aging and breakdown of polyethylene. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 951–966. [Google Scholar] [CrossRef]
- Tzimas, A.; Rowland, S.M.; Dissado, L.A.; Fu, M.; Nilsson, U.H. The effect of dc poling duration on space charge relaxation in virgin XLPE cable peelings. J. Phys. D Appl. Phys. 2010, 43, 215401. [Google Scholar] [CrossRef]
- Tzimas, A.; Rowland, S.M.; Dissado, L.A. Effect of Electrical and Thermal Stressing on Charge Traps in XLPE Cable Insulation. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 2145–2154. [Google Scholar] [CrossRef]
- Many, A.; Rakavy, G. Theory of Transient Space-Charge-Limited Currents in Solids in the Presence of Trapping. Phys. Rev. 1962, 126, 1980–1988. [Google Scholar] [CrossRef]
- Le Roy, S.; Baudoin, F.; Griseri, V.; Laurent, C.; Teyssedre, G. Charge transport modelling in electron-beam irradiated dielectrics: A model for polyethylene. J. Phys. D Appl. Phys. 2010, 43, 315402. [Google Scholar] [CrossRef]
- Toomer, R.; Lewis, T.J. Charge Trapping in Corona-Charged Polyethylene Films. J. Phys. D Appl. Phys. 1980, 13, 1343–1356. [Google Scholar] [CrossRef]
- Chen, G.; Xu, Z.Q. Charge trapping and detrapping in polymeric materials. J. Appl. Phys. 2009, 106, 123707. [Google Scholar] [CrossRef]
- Zhou, T.C.; Chen, G.; Liao, R.J.; Xu, Z.Q. Charge trapping and detrapping in polymeric materials: Trapping parameters. J. Appl. Phys. 2011, 110, 043724. [Google Scholar] [CrossRef]
- Mizutani, T.; Suzuoki, Y.; Hanai, M.; Ieda, M. Determination of Trapping Parameters from Tsc in Polyethylene. Jpn. J. Appl. Phys. 1982, 21, 1639–1641. [Google Scholar] [CrossRef]
- Liang, H.C.; Du, B.X.; Li, J.; Li, Z.L.; Li, A. Effects of non-linear conductivity on charge trapping and de-trapping behaviours in epoxy/SiC composites under DC stress. IET Sci. Meas. Technol. 2018, 12, 83–89. [Google Scholar]
- Gao, Y.; Wang, J.L.; Liu, F.; Du, B.X. Surface Potential Decay of Negative Corona Charged Epoxy/Al2O3 Nanocomposites Degraded by 7.5-MeV Electron Beam. IEEE Tran. Plasma Sci. 2018, 46, 2721–2729. [Google Scholar] [CrossRef]
- Meunier, M.; Quirke, N.; Aslanides, A. Molecular modeling of electron traps in polymer insulators: Chemical defects and impurities. J. Chem. Phys. 2001, 115, 2876–2881. [Google Scholar] [CrossRef]
- Boufayed, F.; Teyssedre, G.; Laurent, C.; Le Roy, S.; Dissado, L.A.; Segur, P.; Montanari, G.C. Models of bipolar charge transport in polyethylene. J. Appl. Phys. 2006, 100, 104105. [Google Scholar] [CrossRef]
- Kuik, M.; Koster, L.J.A.; Wetzelaer, G.A.H.; Blom, P.W.M. Trap-Assisted Recombination in Disordered Organic Semiconductors. Phys. Rev. Lett. 2011, 107, 256805. [Google Scholar] [CrossRef] [PubMed]
- Kuik, M.; Koster, L.J.A.; Dijkstra, A.G.; Wetzelaer, G.A.H.; Blom, P.W.M. Non-radiative recombination losses in polymer light-emitting diodes. Org. Electron. 2012, 13, 969–974. [Google Scholar] [CrossRef]
- Vonberlepsch, H. Interpretation of Surface-Potential Kinetics in Hdpe by a Trapping Model. J. Phys. D Appl. Phys. 1985, 18, 1155–1170. [Google Scholar] [CrossRef]
- Le Roy, S.; Teyssedre, G.; Laurent, C.; Montanari, G.C.; Palmieri, F. Description of charge transport in polyethylene using a fluid model with a constant mobility: Fitting model and experiments. J. Phys. D Appl. Phys. 2006, 39, 1427–1436. [Google Scholar] [CrossRef]
- Tian, J.H.; Zou, J.; Wang, Y.S.; Liu, J.; Yuan, J.S.; Zhou, Y.X. Simulation of bipolar charge transport with trapping and recombination in polymeric insulators using Runge-Kutta discontinuous Galerkin method. J. Phys. D Appl. Phys. 2008, 41, 195416. [Google Scholar] [CrossRef]
- Simmons, J.G.; Taylor, G.W. Nonequilibrium Steady-State Statistics and Associated Effects for Insulators and Semiconductors Containing an Arbitrary Distribution of Traps. Phys. Rev. B 1971, 4, 502–511. [Google Scholar] [CrossRef]
- Chapwanya, M.; Lubuma, J.M.S.; Mickens, R.E. Nonstandard finite difference schemes for Michaelis-Menten type reaction-diffusion equations. Numer. Meth. Part. Differ. Equ. 2013, 29, 337–360. [Google Scholar] [CrossRef]
- Min, D.M.; Wang, W.W.; Li, S.T. Numerical Analysis of Space Charge Accumulation and Conduction Properties in LDPE Nanodielectrics. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1483–1491. [Google Scholar] [CrossRef]
- Li, S.T.; Min, D.M.; Wang, W.W.; Chen, G. Modelling of Dielectric Breakdown through Charge Dynamics for Polymer Nanocomposites. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 3476–3485. [Google Scholar] [CrossRef]
- Sessler, G.M.; Figueiredo, M.T.; Ferreira, G.F.L. Models of charge transport in electron-beam irradiated insulator. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 192–202. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Le Roy, S.; Teyssedre, G.; Laurent, C. Numerical methods in the simulation of charge transport in solid dielectrics. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 239–246. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C.-W. TVB Runge-Kutta Local Projection Discontinuous Galerkin Finite Element Method for Conservation Laws II: General Framework. Math. Comput. 1988, 52, 411–435. [Google Scholar]
- Montanari, G.C.; Mazzanti, G.; Palmieri, F.; Motori, A.; Perego, G.; Serra, S. Space-charge trapping and conduction in LDPE, HDPE and XLPE. J. Phys. D Appl. Phys. 2001, 34, 2902–2911. [Google Scholar] [CrossRef]

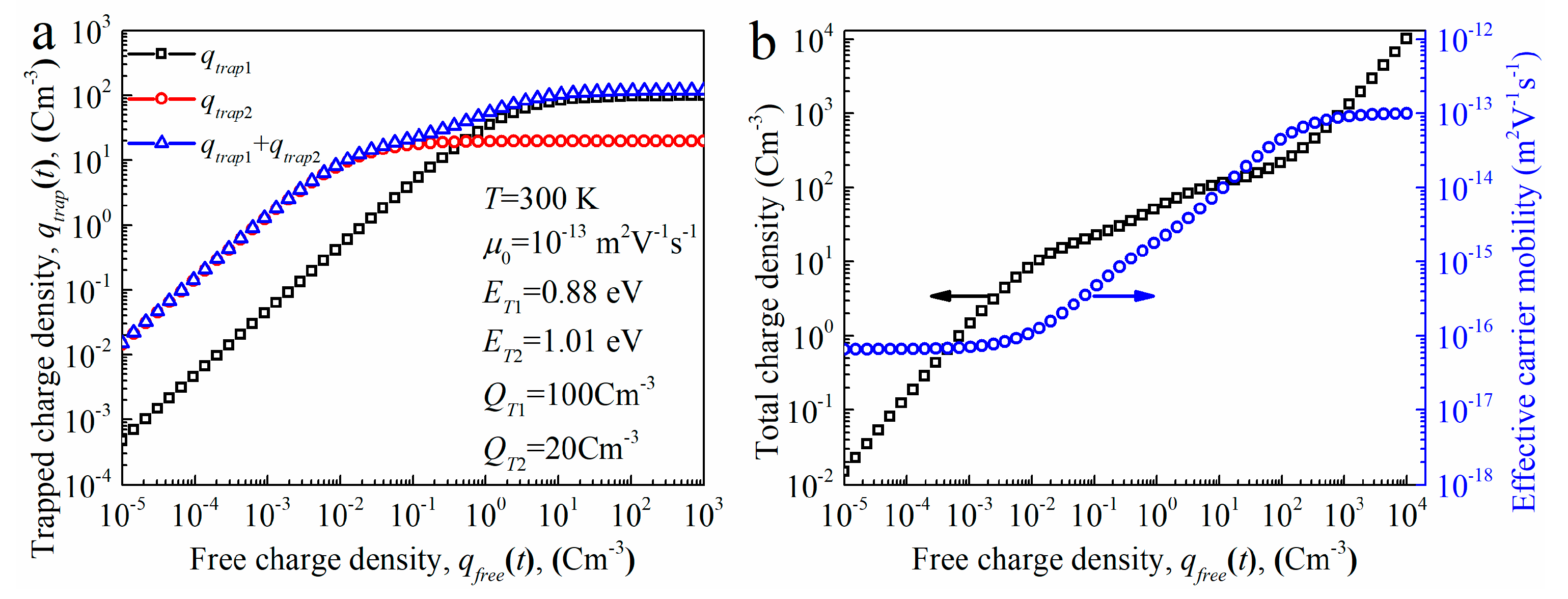
| Parameter | Value |
|---|---|
| Charge carrier mobility, μ0, (m2 V−1 s−1) | 1.0 × 10−13 |
| Energy of trap level 1, ET1, (eV) | 0.88 |
| Energy of trap level 2, ET2, (eV) | 1.01 |
| Charge density of trap level 1, QT1, (cm−3) | 100 |
| Charge density of trap level 1, QT2, (cm−3) | 20 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Z.; Zhang, C.; Cui, H.; Hai, Y.; Wu, Q.; Min, D. Space Charge Accumulation and Decay in Dielectric Materials with Dual Discrete Traps. Appl. Sci. 2019, 9, 4253. https://doi.org/10.3390/app9204253
Xing Z, Zhang C, Cui H, Hai Y, Wu Q, Min D. Space Charge Accumulation and Decay in Dielectric Materials with Dual Discrete Traps. Applied Sciences. 2019; 9(20):4253. https://doi.org/10.3390/app9204253
Chicago/Turabian StyleXing, Zhaoliang, Chong Zhang, Haozhe Cui, Yali Hai, Qingzhou Wu, and Daomin Min. 2019. "Space Charge Accumulation and Decay in Dielectric Materials with Dual Discrete Traps" Applied Sciences 9, no. 20: 4253. https://doi.org/10.3390/app9204253
APA StyleXing, Z., Zhang, C., Cui, H., Hai, Y., Wu, Q., & Min, D. (2019). Space Charge Accumulation and Decay in Dielectric Materials with Dual Discrete Traps. Applied Sciences, 9(20), 4253. https://doi.org/10.3390/app9204253