Predicting Heating and Cooling Loads in Energy-Efficient Buildings Using Two Hybrid Intelligent Models
Abstract
1. Introduction
2. Literature Review
3. Description of the Used Models
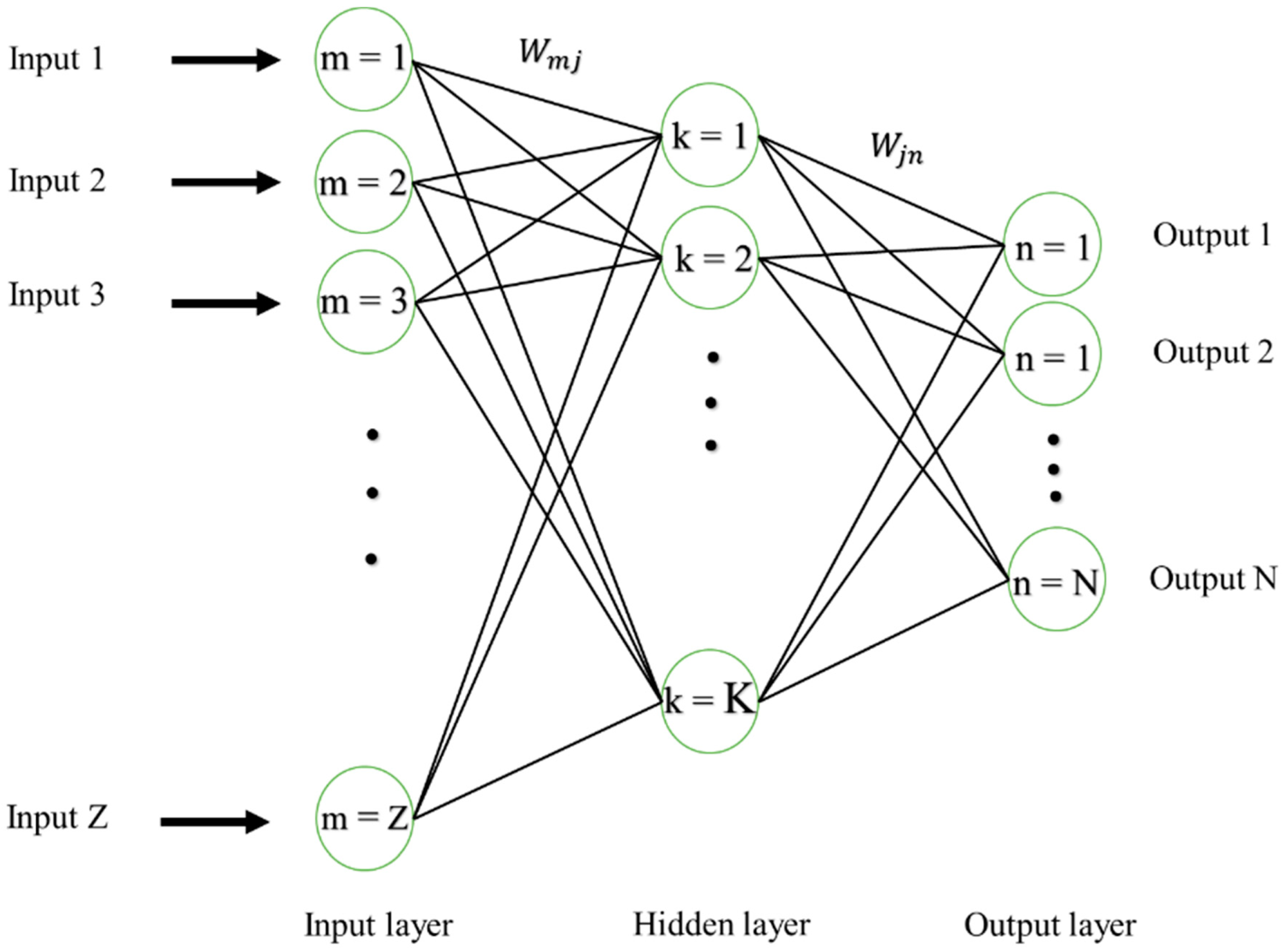
3.1. Multi-Layer Perceptron (MLP)
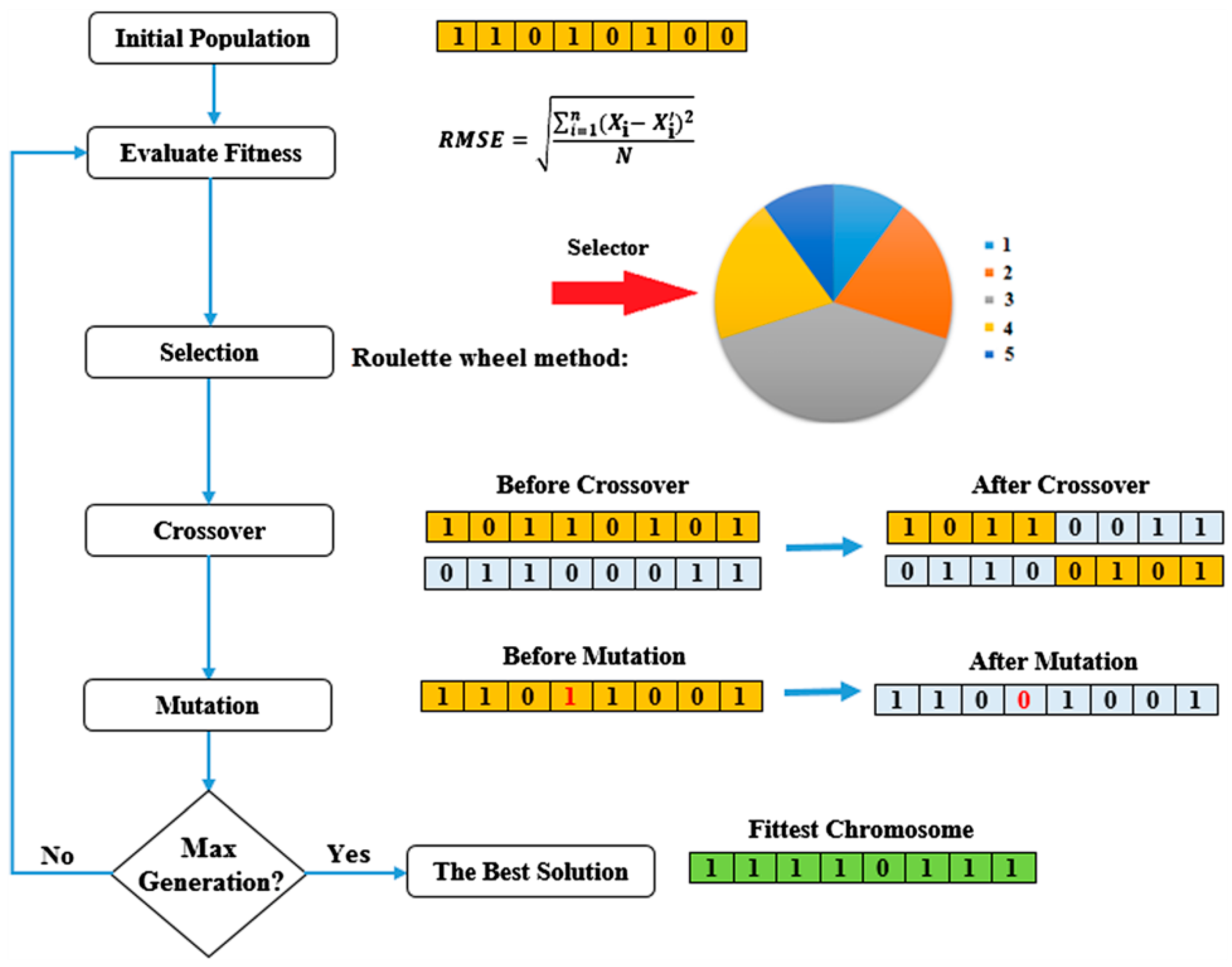
3.2. Genetic Algorithm (GA)
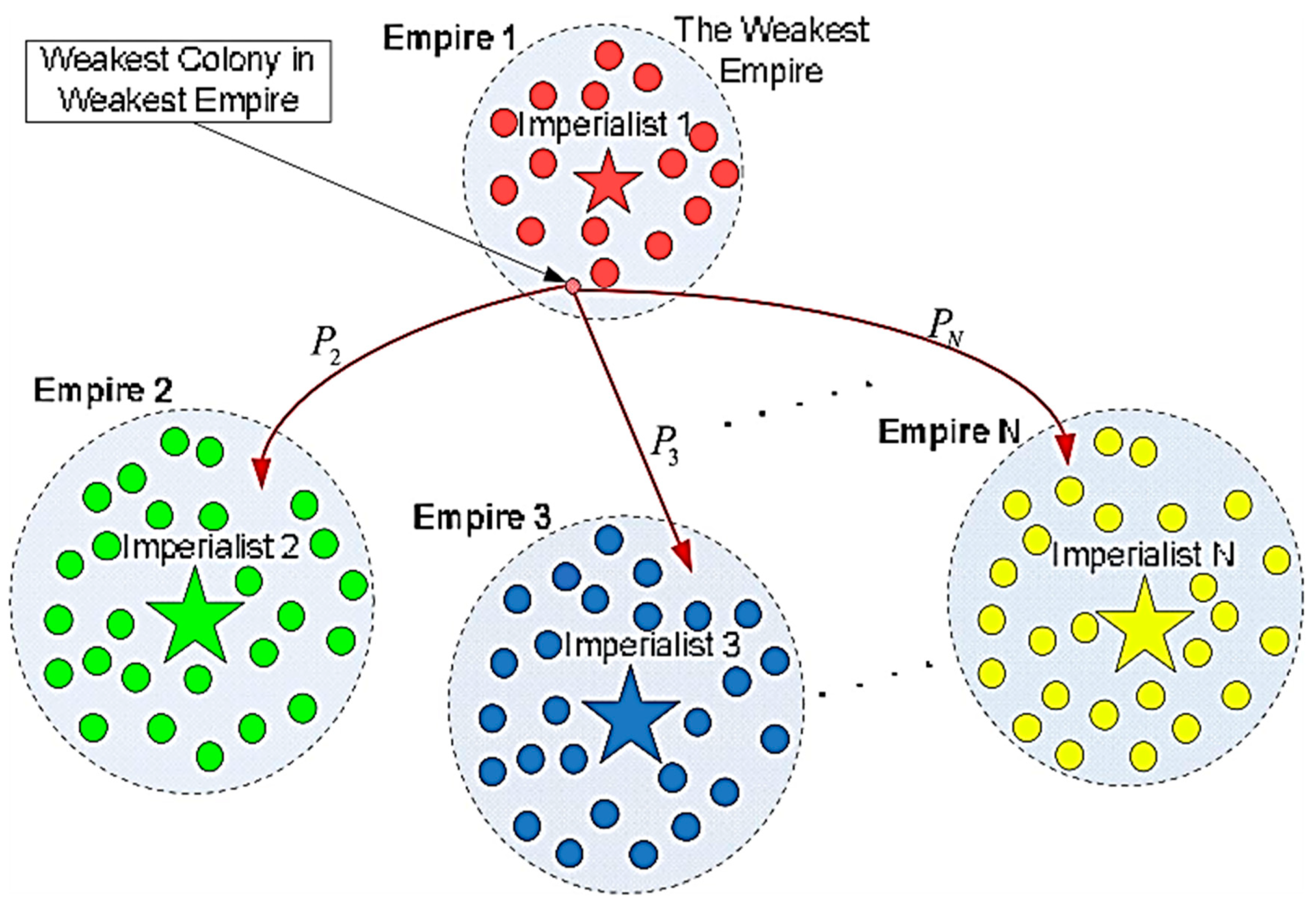
3.3. Imperialist Competitive Algorithm (ICA)
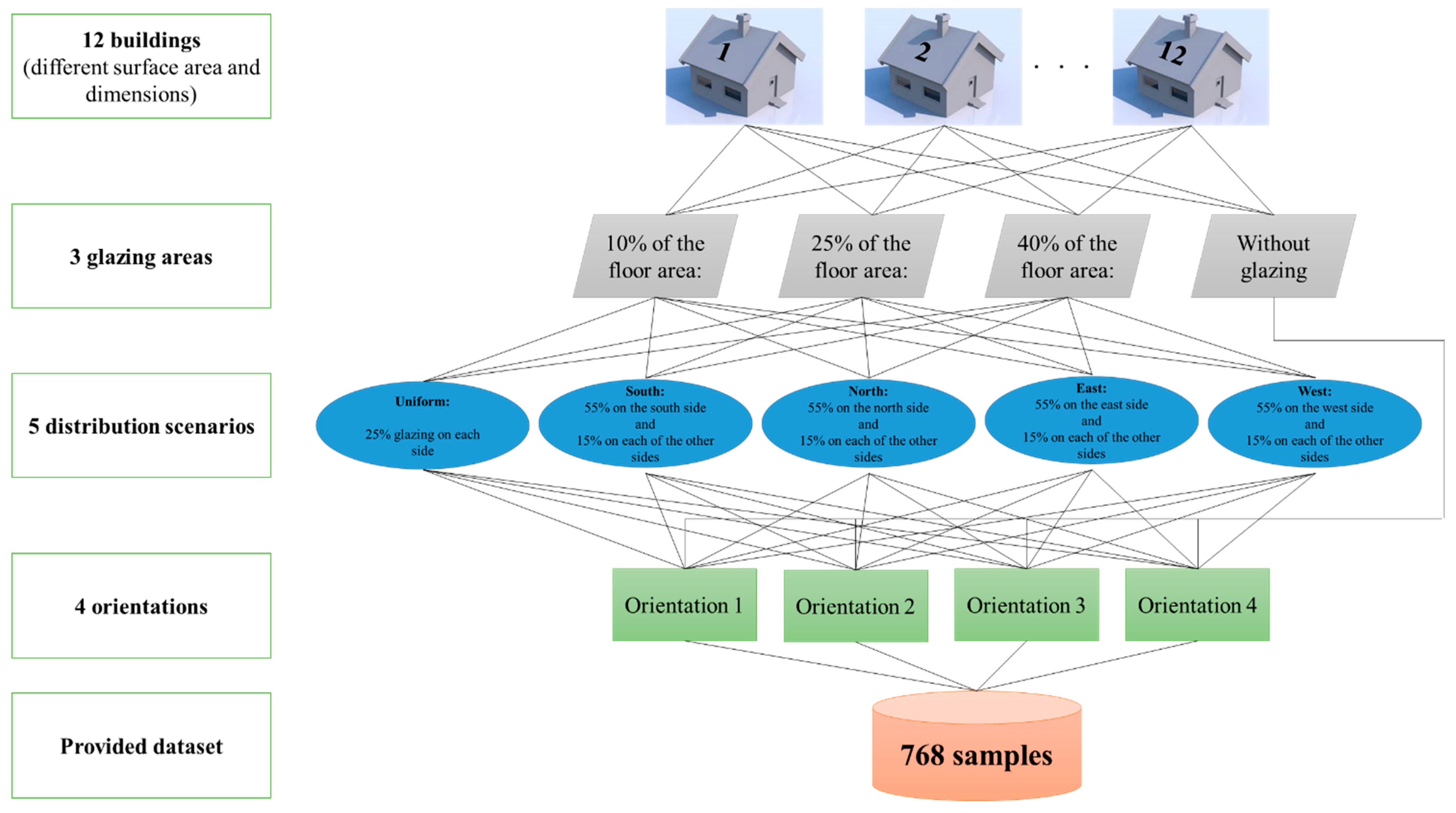
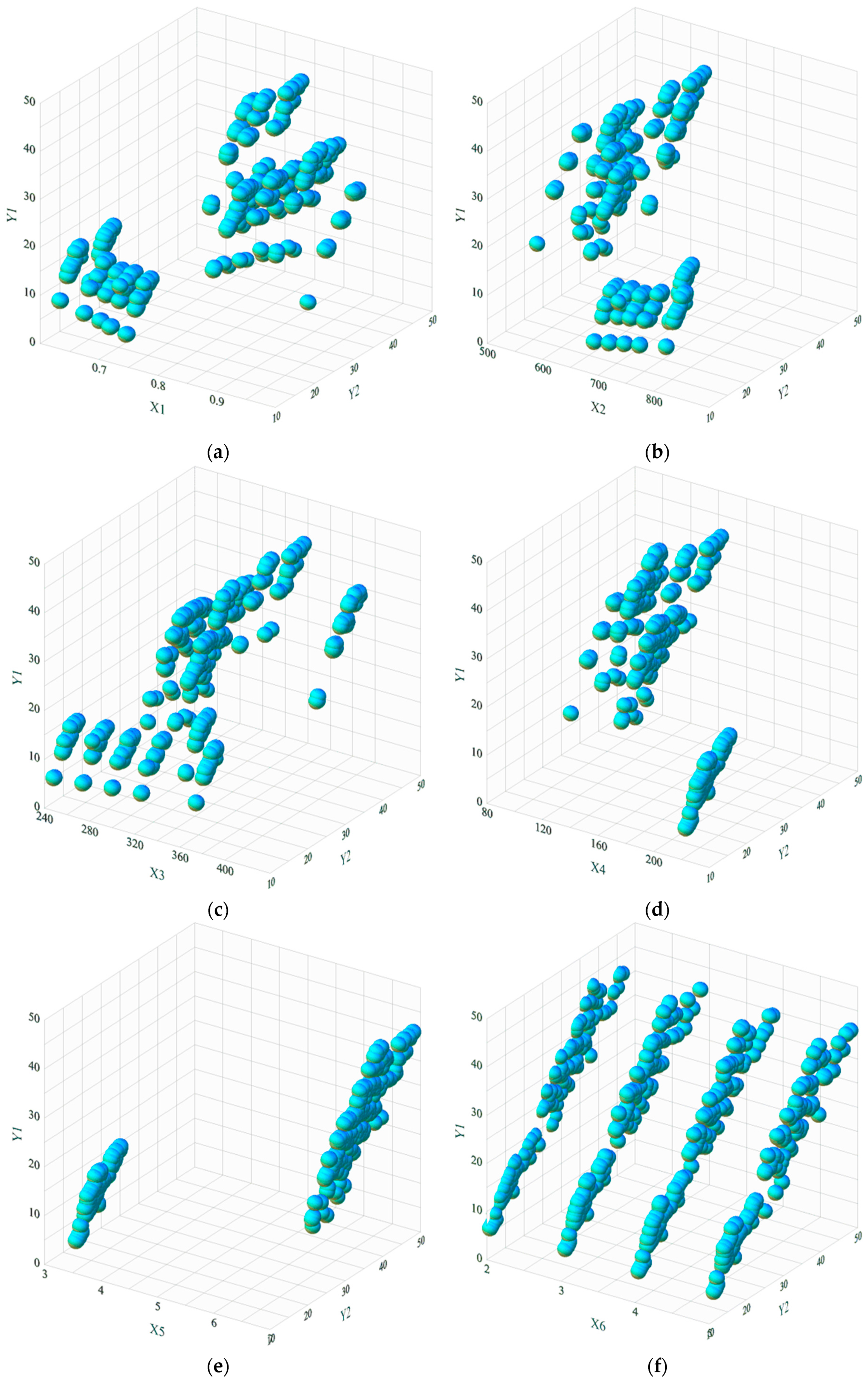
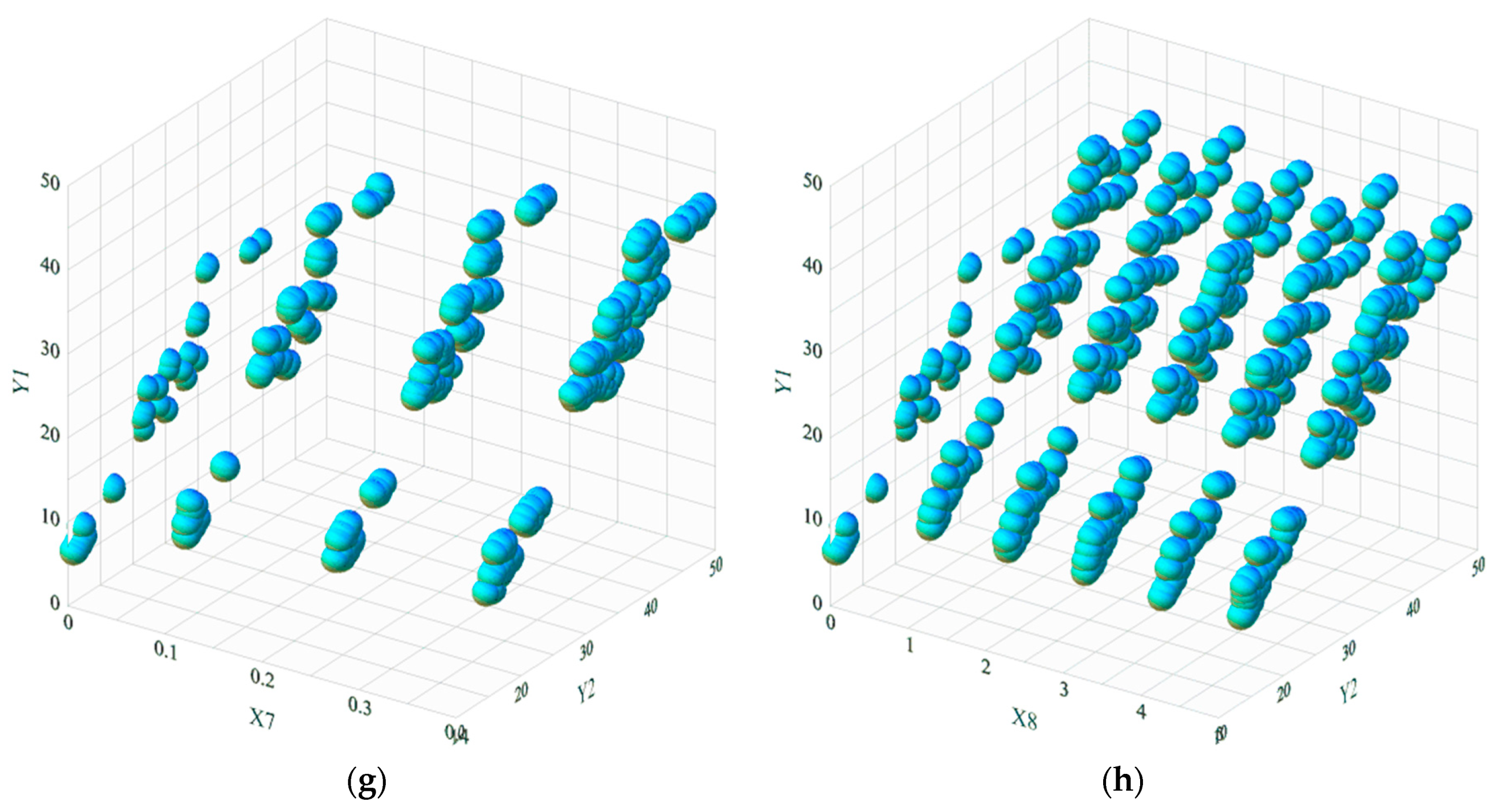
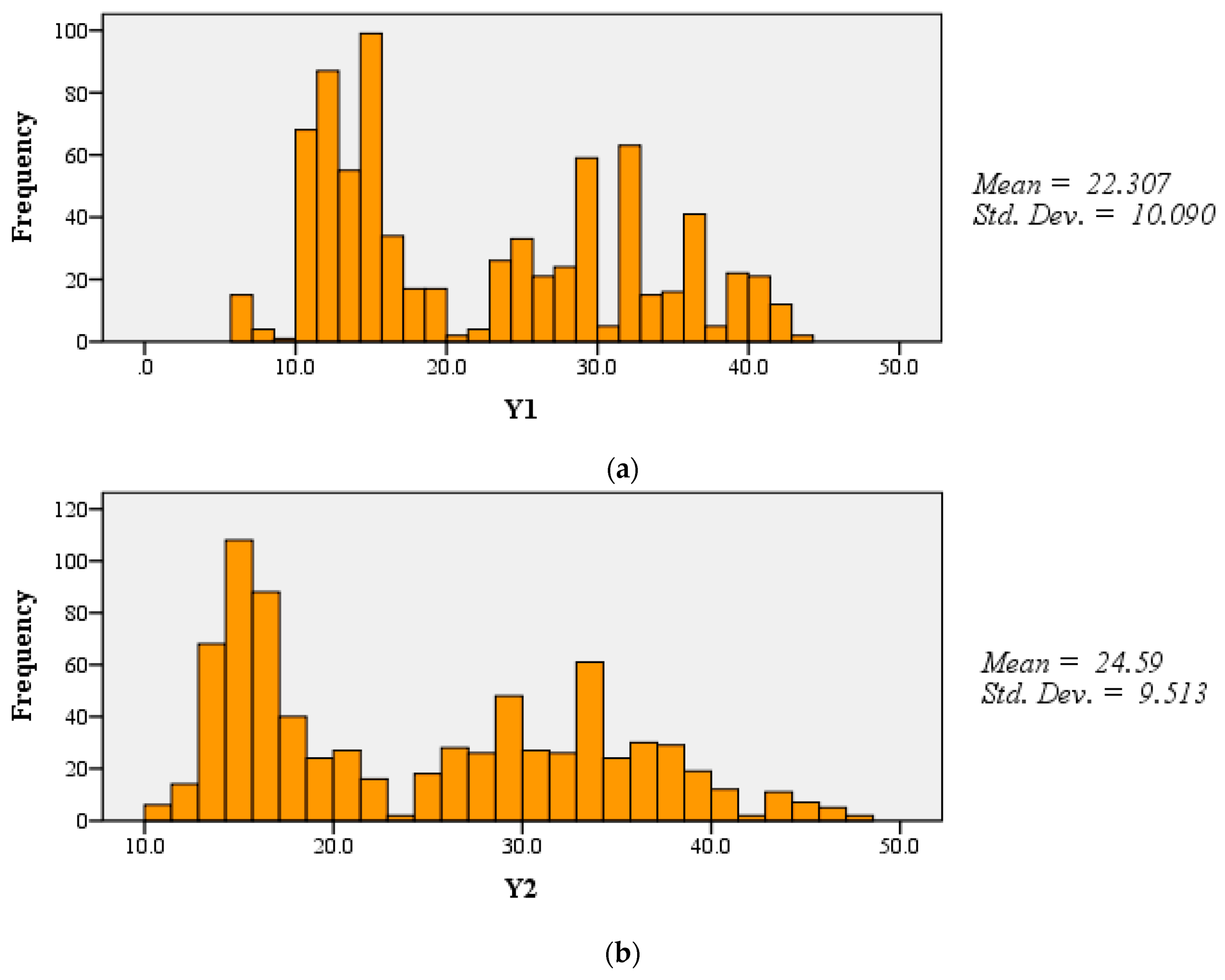
4. Data Preparation and Statistics
5. Results and Discussion
5.1. Finding the Optimal Structure of the Intelligent Models
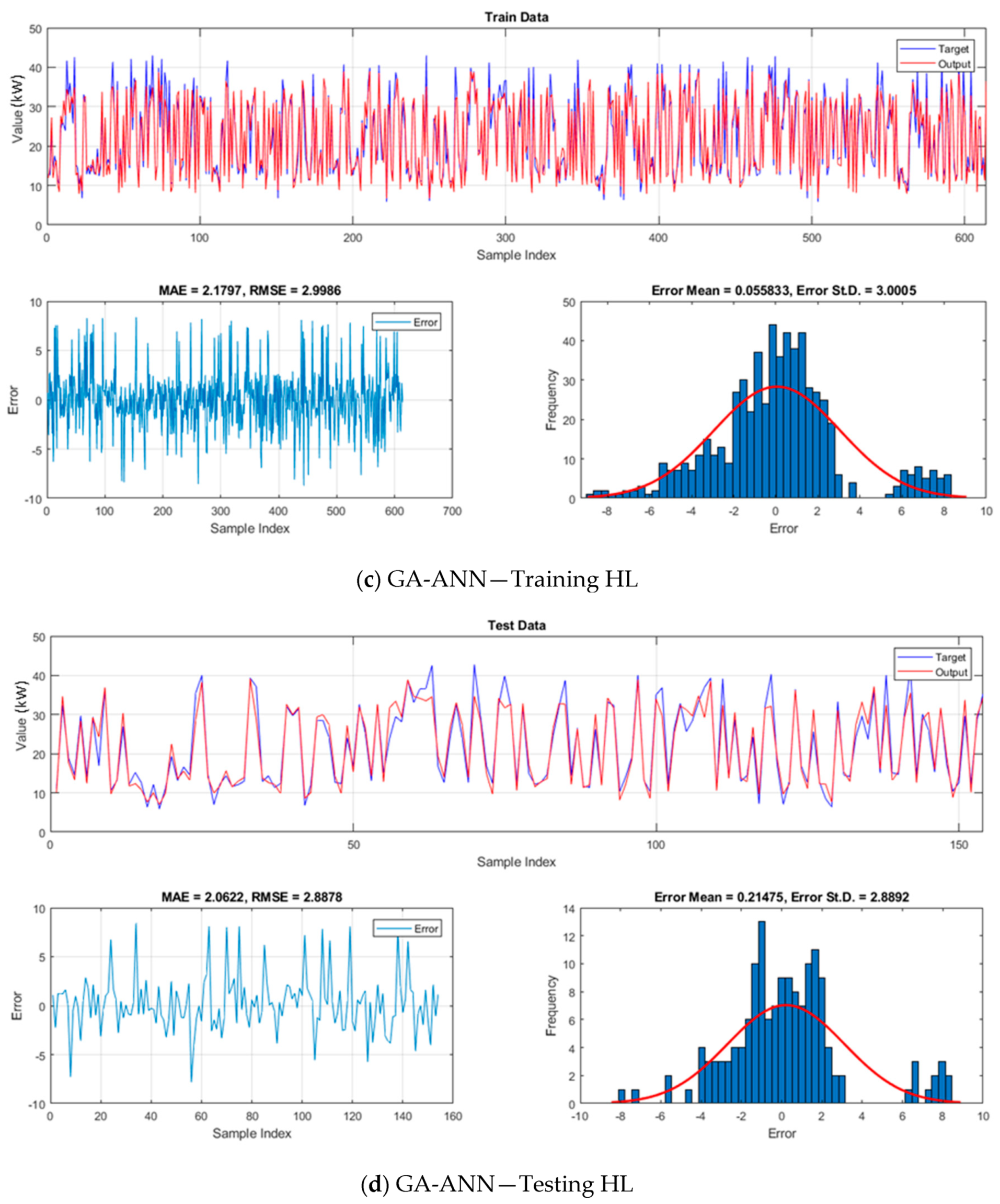
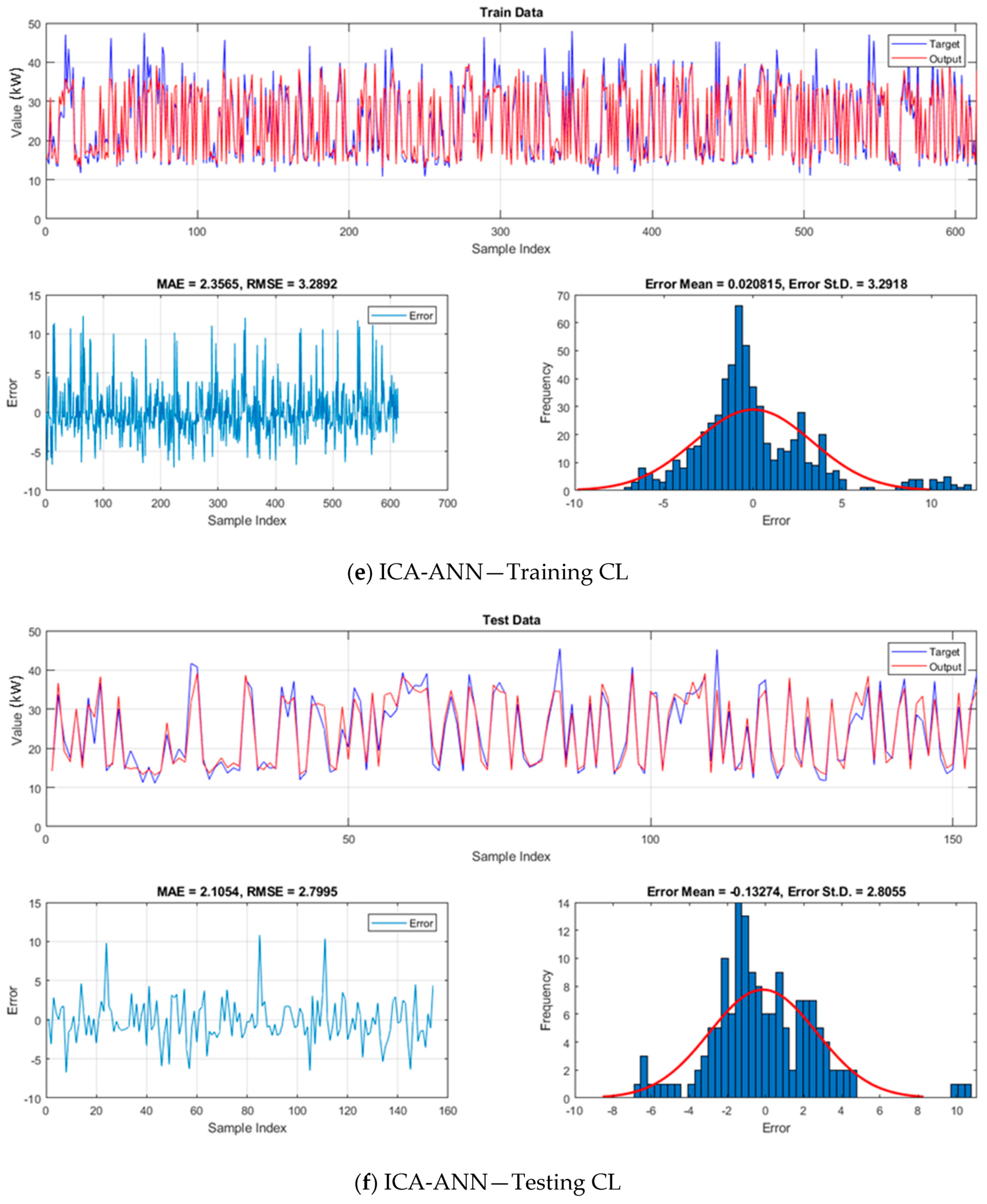
5.2. Model Assessment
6. Conclusions and Remarks
- Artificial intelligence techniques can act as an efficient approach for analyzing the heating and cooling load of the buildings.
- Optimizing the computational parameters (i.e., the weights and biases) of the ANN using the GA and ICA has a significant effect on its performance in terms of both pattern learning and prediction.
- The computed R2 for both training (HL: 0.8710, 0.8711, and 0.8816—CL: 0.9119, 0.9102, and 0.9216) and testing (HL: 0.9017, 0.9076, and 0.9115—CL: 0.9179, 0.9232, and 0.9287) showed that ICA helps the ANN to increase the correlation of the results an also outperforms GA.
- Based on the calculated RMSE, the training error of ANN decreased as 17.92% and 23.22% for the HL, and 21.13% and 24.53% for CL, respectively by applying GA and ICA. These values were 20.84% and 23.74% for HL and 27.57% and 29.10% for CL about the validation error.
- As for MAE, the training error of ANN decreased as 27.38% and 33.14% for the HL, and 29.11% and 31.34% for CL, respectively by applying GA and ICA. These values were 29.81% and 31.63% for HL and 36.10% and 35.88% for CL about the validation error.
- From the comparison viewpoint, ICA outperformed GA in performance improvement of multi-layer perceptron neural network in the case of this study.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CL | Cooling load |
| HL | Heating load |
| HVAC | Heating ventilation and air conditioning |
| EPB | Energy performance of buildings |
| PER | Primary energy requirement |
| DeST | Designer’s simulation toolkit |
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| PLS | Partial least squares regression |
| ANFIS | Adaptive neuro-fuzzy inference system |
| RF | Random forest |
| SVM | Support vector machine |
| BPNN | Back propagation neural network |
| GRNN | General regression neural network |
| RBFNN | Radial basis function neural network |
| RMSE | Root mean square error |
| MAE | Mean relative error |
| R2 | Coefficient of determination |
| CV | Coefficients of variance |
| MLP | Multi-layer perceptron |
| AHP | Analytic hierarchy process |
References
- International Energy Agency (IEA). Key World Energy Statistics; International Energy Agency: Paris, France, 2015. [Google Scholar]
- McQuiston, F.C.; Parker, J.D. Heating, Ventilating, and Air Conditioning: Analysis and Design; John Wiley & Sons Inc.: New York, NY, USA, 1982. [Google Scholar]
- Castaldo, V.L.; Pigliautile, I.; Rosso, F.; Cotana, F.; De Giorgio, F.; Pisello, A.L. How subjective and non-physical parameters affect occupants’ environmental comfort perception. Energy Build. 2018, 178, 107–129. [Google Scholar] [CrossRef]
- Sant’Anna, D.; Dos Santos, P.H.; Vianna, N.S.; Romero, M.A. Indoor environmental quality perception and users’ satisfaction of conventional and green buildings in Brazil. Sustain. Cities Soc. 2018, 43, 95–110. [Google Scholar] [CrossRef]
- Caniato, M.; Bettarello, F.; Ferluga, A.; Marsich, L.; Schmid, C.; Fausti, P. Thermal and acoustic performance expectations on timber buildings. Build. Acoust. 2017, 24, 219–237. [Google Scholar] [CrossRef]
- European Parliament and Council. Directive 2010/31/EU of the European Parlia-ment and of the Council of 19 May 2010 on the energy performance of buildings(recast). Off. J. Eur. Union 2010, L153, 13–35. [Google Scholar]
- Kwok, A.G.; Rajkovich, N.B. Addressing climate change in comfort standards. Build. Environ. 2010, 45, 18–22. [Google Scholar] [CrossRef]
- Yao, R.; Li, B.; Steemers, K. Energy policy and standard for built environment in China. Renew. Energy 2005, 30, 1973–1988. [Google Scholar] [CrossRef]
- Fanti, M.P.; Mangini, A.M.; Roccotelli, M. A simulation and control model for building energy management. Control Eng. Pract. 2018, 72, 192–205. [Google Scholar] [CrossRef]
- Egan, J.; Finn, D.; Soares, P.H.; Baumann, V.A.; Aghamolaei, R.; Beagon, P.; Neu, O.; Pallonetto, F.; O’Donnell, J. Definition of a useful minimal-set of accurately-specified input data for Building Energy Performance Simulation. Energy Build. 2018, 165, 172–183. [Google Scholar] [CrossRef]
- Zhao, H.X.; Magoulès, F. A review on the prediction of building energy consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.J.; Kim, K.H.; Kwon, K.W.; Jeong, J.W. Estimating thermal performance and energy saving potential of residential buildings using utility bills. Energy Build. 2016, 110, 23–30. [Google Scholar] [CrossRef]
- Yezioro, A.; Dong, B.; Leite, F. An applied artificial intelligence approach towards assessing building performance simulation tools. Energy Build. 2008, 40, 612–620. [Google Scholar] [CrossRef]
- Yan, D.; Xia, J.; Tang, W.; Song, F.; Zhang, X.; Jiang, Y. DeST—An integrated building simulation toolkit Part I: Fundamentals. In Building Simulation; Springer: Berlin, Germany, 2008. [Google Scholar]
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.F.; Huang, Y.J.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. EnergyPlus: Creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- York, D.; Cappiello, C.; Olson, K. DOE-2 Reference Manual: Version 2.1 C; Los Alamos National Laboratory Solar Energy Group: Los Alamos, NM, USA, 1984.
- O’Neill, Z.; O’Neill, C. Development of a probabilistic graphical model for predicting building energy performance. Appl. Energy 2016, 164, 650–658. [Google Scholar] [CrossRef]
- Catalina, T.; Virgone, J.; Blanco, E. Development and validation of regression models to predict monthly heating demand for residential buildings. Energy Build. 2008, 40, 1825–1832. [Google Scholar] [CrossRef]
- Yu, Z.; Haghighat, F.; Fung, B.C.; Yoshino, H. A decision tree method for building energy demand modeling. Energy Build. 2010, 42, 1637–1646. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Mosallanezhad, M.; Rashid, A.S.; Pradhan, B. Modification of landslide susceptibility mapping using optimized PSO-ANN technique. Eng. Comput. 2019, 35, 967–984. [Google Scholar] [CrossRef]
- Seyedashraf, O.; Mehrabi, M.; Akhtari, A.A. Novel approach for dam break flow modeling using computational intelligence. J. Hydrol. 2018, 559, 1028–1038. [Google Scholar] [CrossRef]
- Escandón, R.; Ascione, F.; Bianco, N.; Mauro, G.M.; Suárez, R.; Sendra, J.J. Thermal comfort prediction in a building category: Artificial Neural Network generation from calibrated models for a social housing stock in southern Europe. Appl. Therm. Eng. 2019, 150, 492–505. [Google Scholar] [CrossRef]
- Fan, C.; Wang, J.; Gang, W.; Li, S. Assessment of deep recurrent neural network-based strategies for short-term building energy predictions. Appl. Energy 2019, 236, 700–710. [Google Scholar] [CrossRef]
- Pino-Mejías, R.; Pérez-Fargallo, A.; Rubio-Bellido, C.; Pulido-Arcas, J.A. Comparison of linear regression and artificial neural networks models to predict heating and cooling energy demand, energy consumption and CO2 emissions. Energy 2017, 118, 24–36. [Google Scholar] [CrossRef]
- Deb, C.; Eang, L.S.; Yang, J. Forecasting diurnal cooling energy load for institutional buildings using Artificial Neural Networks. Energy Build. 2016, 121, 284–297. [Google Scholar] [CrossRef]
- Li, Q.; Meng, Q.; Cai, J.; Yoshino, H.; Mochida, A. Predicting hourly cooling load in the building: A comparison of support vector machine and different artificial neural networks. Energy Convers. Manag. 2009, 50, 90–96. [Google Scholar] [CrossRef]
- Yun, K.; Luck, R.; Mago, P.J.; Cho, H. Building hourly thermal load prediction using an indexed ARX model. Energy Build. 2012, 54, 225–233. [Google Scholar] [CrossRef]
- Yao, Y.; Lian, Z.; Liu, S.; Hou, Z. Hourly cooling load prediction by a combined forecasting model based on analytic hierarchy process. Int. J. Therm. Sci. 2004, 43, 1107–1118. [Google Scholar] [CrossRef]
- Dong, B.; Cao, C.; Lee, S.E. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, X. A hybrid method of dynamic cooling and heating load forecasting for office buildings based on artificial intelligence and regression analysis. Energy Build. 2018, 174, 293–308. [Google Scholar] [CrossRef]
- Li, K.; Su, H.; Chu, J. Forecasting building energy consumption using neural networks and hybrid neuro-fuzzy system: A comparative study. Energy Build. 2011, 43, 2893–2899. [Google Scholar] [CrossRef]
- Tsanas, A.; Xifara, A. Accurate quantitative estimation of energy performance of residential buildings using statistical machine learning tools. Energy Build. 2012, 49, 560–567. [Google Scholar] [CrossRef]
- Catalina, T.; Iordache, V.; Caracaleanu, B. Multiple regression model for fast prediction of the heating energy demand. Energy Build. 2013, 57, 302–312. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Moayedi, H.; Rezaei, A. An artificial neural network approach for under-reamed piles subjected to uplift forces in dry sand. Neural Comput.Appl. 2019, 31, 327–336. [Google Scholar] [CrossRef]
- Moayedi, H.; Hayati, S. Applicability of a CPT-Based Neural Network Solution in Predicting Load-Settlement Responses of Bored Pile. Int. J. Geomech. 2018, 18, 06018009. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehdi, R.; Abolhasan, S.; Wan, A.W.J.; Safuan, A.R.A. Optimization of ANFIS with GA and PSO estimating α in driven shafts. Eng. Comput. 2019, 35, 1–12. [Google Scholar]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In 2007 IEEE Congress on Evolutionary Computation; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Al Dossary, M.A.; Nasrabadi, H. Well placement optimization using imperialist competitive algorithm. J. Pet. Sci. Eng. 2016, 147, 237–248. [Google Scholar] [CrossRef]
- Moayedi, H.; Armaghani, D.J. Optimizing an ANN model with ICA for estimating bearing capacity of driven pile in cohesionless soil. Eng. Comput. 2018, 34, 347–356. [Google Scholar] [CrossRef]
- Roberts, A.; Marsh, A. ECOTECT: Environmental Prediction in Architectural Education; Cardiff University: Wales, UK, 2001. [Google Scholar]
- Mosallanezhad, M.; Moayedi, H. Developing hybrid artificial neural network model for predicting uplift resistance of screw piles. Arab. J. Geosci. 2017, 10, 479. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Mohamad, E.T.; Momeni, E.; Monjezi, M.; Narayanasamy, M.S. Prediction of the strength and elasticity modulus of granite through an expert artificial neural network. Arab. J. Geosci. 2016, 9, 48. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- El-Bakry, M. Feed forward neural networks modeling for K–P interactions. Chaos Solitons Fractals 2003, 18, 995–1000. [Google Scholar] [CrossRef]











| Features | No. of Possible Values | Label | Descriptive Index | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Standard Error | Median | Mode | Standard Deviation | Sample Variance | Skewness | Minimum | Maximum | Count | |||
| Relative Compactness | 12 | X1 | 0.76 | 0.00 | 0.75 | 0.98 | 0.11 | 0.01 | 0.50 | 0.62 | 0.98 | 768 |
| Surface Area | 12 | X2 | 671.71 | 3.18 | 673.75 | 514.50 | 88.09 | 7759.16 | −0.13 | 514.50 | 808.50 | 768 |
| Wall Area | 7 | X3 | 318.50 | 1.57 | 318.50 | 294.00 | 43.63 | 1903.27 | 0.53 | 245.00 | 416.50 | 768 |
| Roof Area | 4 | X4 | 176.60 | 1.63 | 183.75 | 220.50 | 45.17 | 2039.96 | −0.16 | 110.25 | 220.50 | 768 |
| Overall Height | 2 | X5 | 5.25 | 0.06 | 5.25 | 7.00 | 1.75 | 3.07 | 0.00 | 3.50 | 7.00 | 768 |
| Orientation | 4 | X6 | 3.50 | 0.04 | 3.50 | 2.00 | 1.12 | 1.25 | 0.00 | 2.00 | 5.00 | 768 |
| Glazing Area | 4 | X7 | 0.23 | 0.00 | 0.25 | 0.10 | 0.13 | 0.02 | −0.06 | 0.00 | 0.40 | 768 |
| Glazing Area distribution | 6 | X8 | 2.81 | 0.06 | 3.00 | 1.00 | 1.55 | 2.41 | −0.09 | 0.00 | 5.00 | 768 |
| Heating load | 586 | Y1 | 22.31 | 0.36 | 18.95 | 15.16 | 10.09 | 101.81 | 0.36 | 6.01 | 43.10 | 768 |
| Cooling load | 636 | Y2 | 24.59 | 0.34 | 22.08 | 21.33 | 9.51 | 90.50 | 0.40 | 10.90 | 48.03 | 768 |
| ICA-ANFIS (Num. of Countries = 200, and Num. of Decades = 1000) | GA-ANN (Population Size = 200, and Num. of Generation = 1000) |
|---|---|
| Revolution rate = 0.3 Num. of initial imperialists = 5 Damp ratio = 0.99 | Crossover rate = 0.50 Mutation rate = 0.25 |
| Models | Data | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Training | Testing | |||||||||||
| HL | CL | HL | CL | |||||||||
| R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | R2 | RMSE | MAE | |
| ANN | 0.8710 | 3.6535 | 3.0014 | 0.9119 | 4.3588 | 3.4320 | 0.9017 | 3.6481 | 2.9382 | 0.9179 | 3.9489 | 3.2835 |
| GA-ANN | 0.8711 | 2.9986 | 2.1797 | 0.9102 | 3.4376 | 2.4330 | 0.9076 | 2.8878 | 2.0622 | 0.9232 | 2.8598 | 2.0982 |
| ICA-ANN | 0.8816 | 2.8050 | 2.0068 | 0.9216 | 3.2892 | 2.3565 | 0.9115 | 2.7819 | 2.0089 | 0.9287 | 2.7995 | 2.1054 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tien Bui, D.; Moayedi, H.; Anastasios, D.; Kok Foong, L. Predicting Heating and Cooling Loads in Energy-Efficient Buildings Using Two Hybrid Intelligent Models. Appl. Sci. 2019, 9, 3543. https://doi.org/10.3390/app9173543
Tien Bui D, Moayedi H, Anastasios D, Kok Foong L. Predicting Heating and Cooling Loads in Energy-Efficient Buildings Using Two Hybrid Intelligent Models. Applied Sciences. 2019; 9(17):3543. https://doi.org/10.3390/app9173543
Chicago/Turabian StyleTien Bui, Dieu, Hossein Moayedi, Dounis Anastasios, and Loke Kok Foong. 2019. "Predicting Heating and Cooling Loads in Energy-Efficient Buildings Using Two Hybrid Intelligent Models" Applied Sciences 9, no. 17: 3543. https://doi.org/10.3390/app9173543
APA StyleTien Bui, D., Moayedi, H., Anastasios, D., & Kok Foong, L. (2019). Predicting Heating and Cooling Loads in Energy-Efficient Buildings Using Two Hybrid Intelligent Models. Applied Sciences, 9(17), 3543. https://doi.org/10.3390/app9173543






