Exploring Efficient Neural Architectures for Linguistic–Acoustic Mapping in Text-To-Speech †
Abstract
1. Introduction
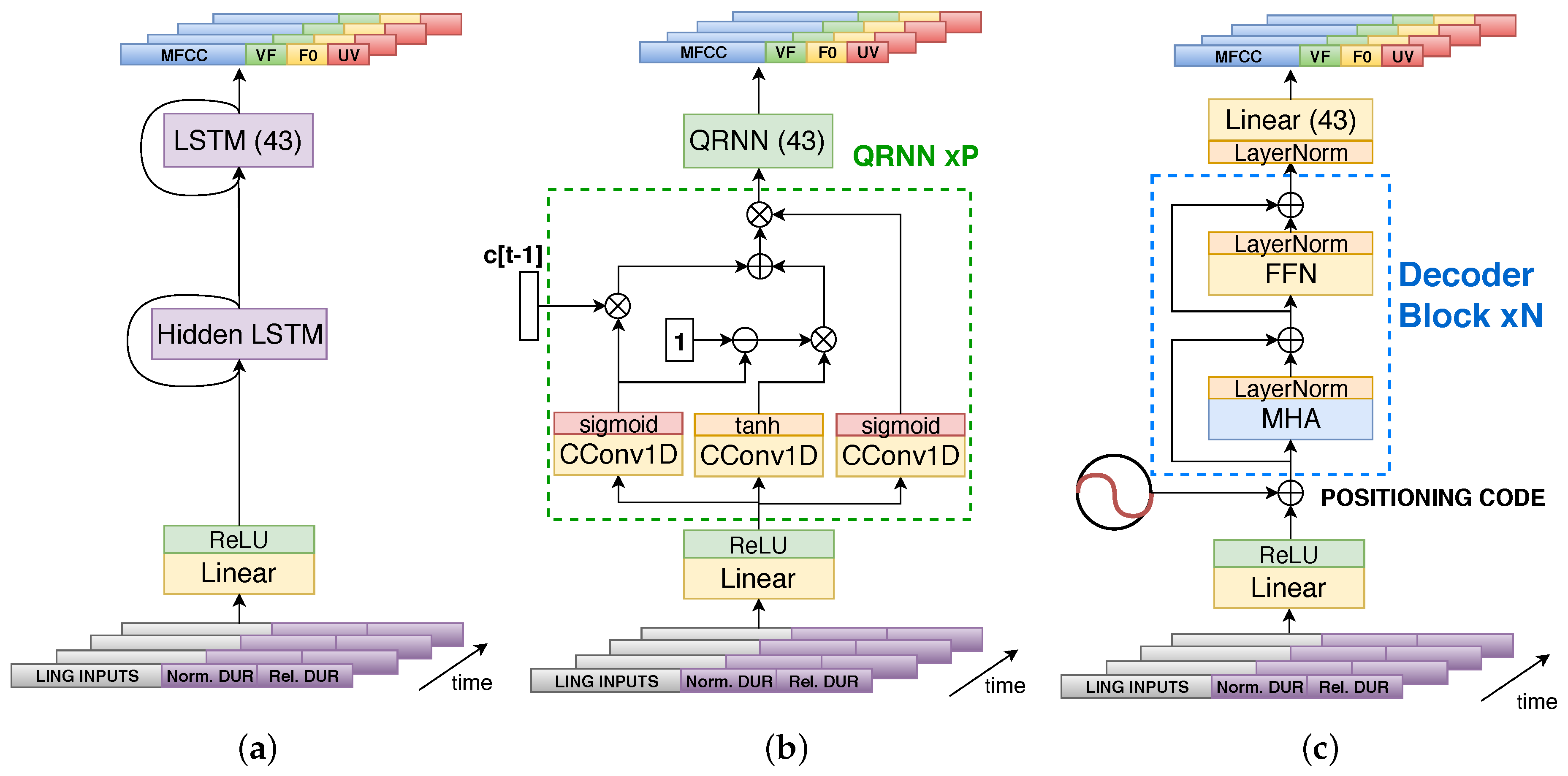
2. Recurrent Neural Network Based Linguistic–Acoustic Decoder
3. QRNN Linguistic–Acoustic Decoder
4. Self-Attention Linguistic–Acoustic Decoder
5. Experimental Setup
5.1. Dataset
5.2. Linguistic and Acoustic Features
5.3. Model Details and Training Setup
5.4. Evaluation Metrics
5.4.1. Objective Evaluation
5.4.2. Subjective Evaluation
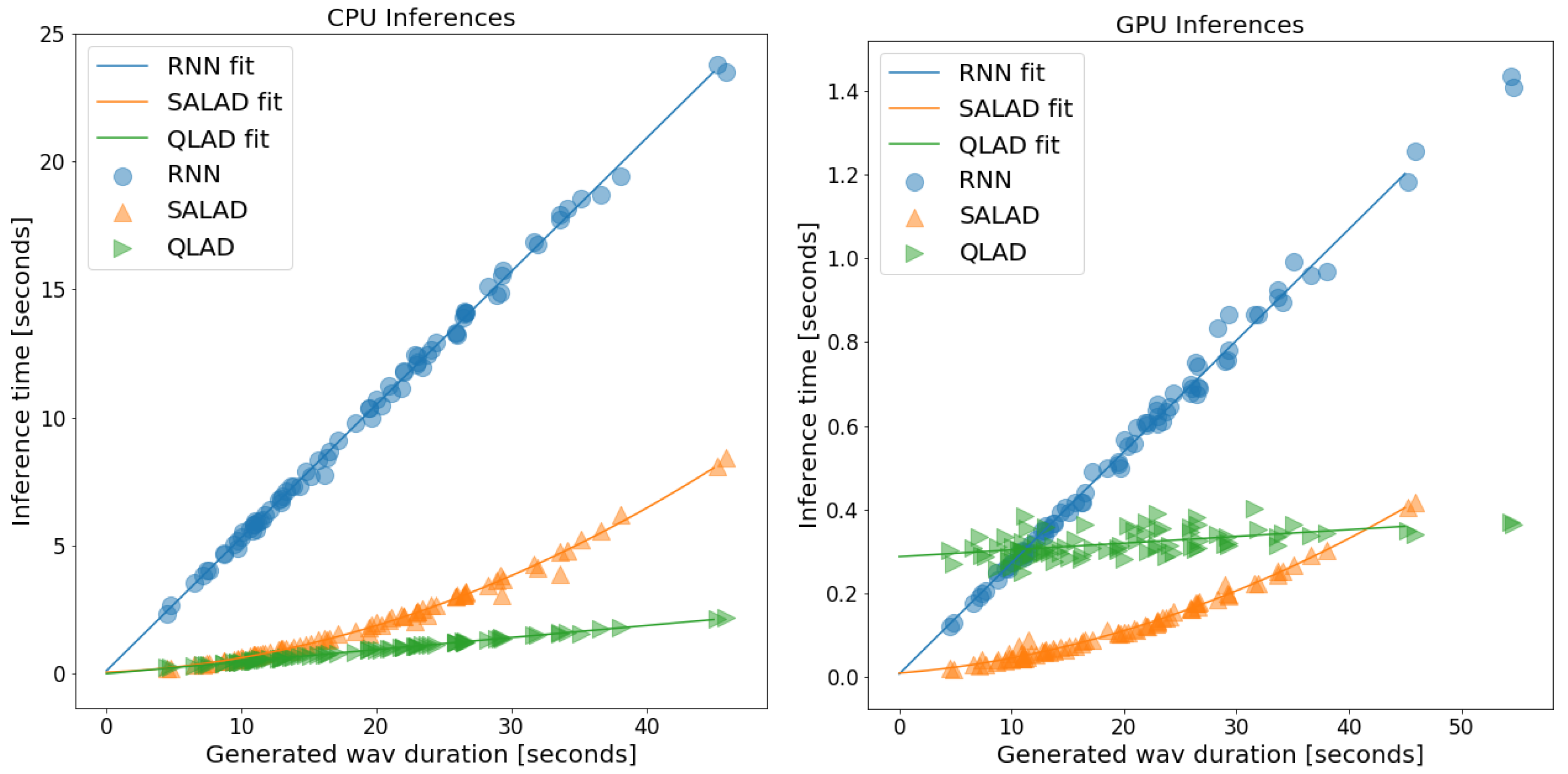
5.4.3. Efficiency Evaluation
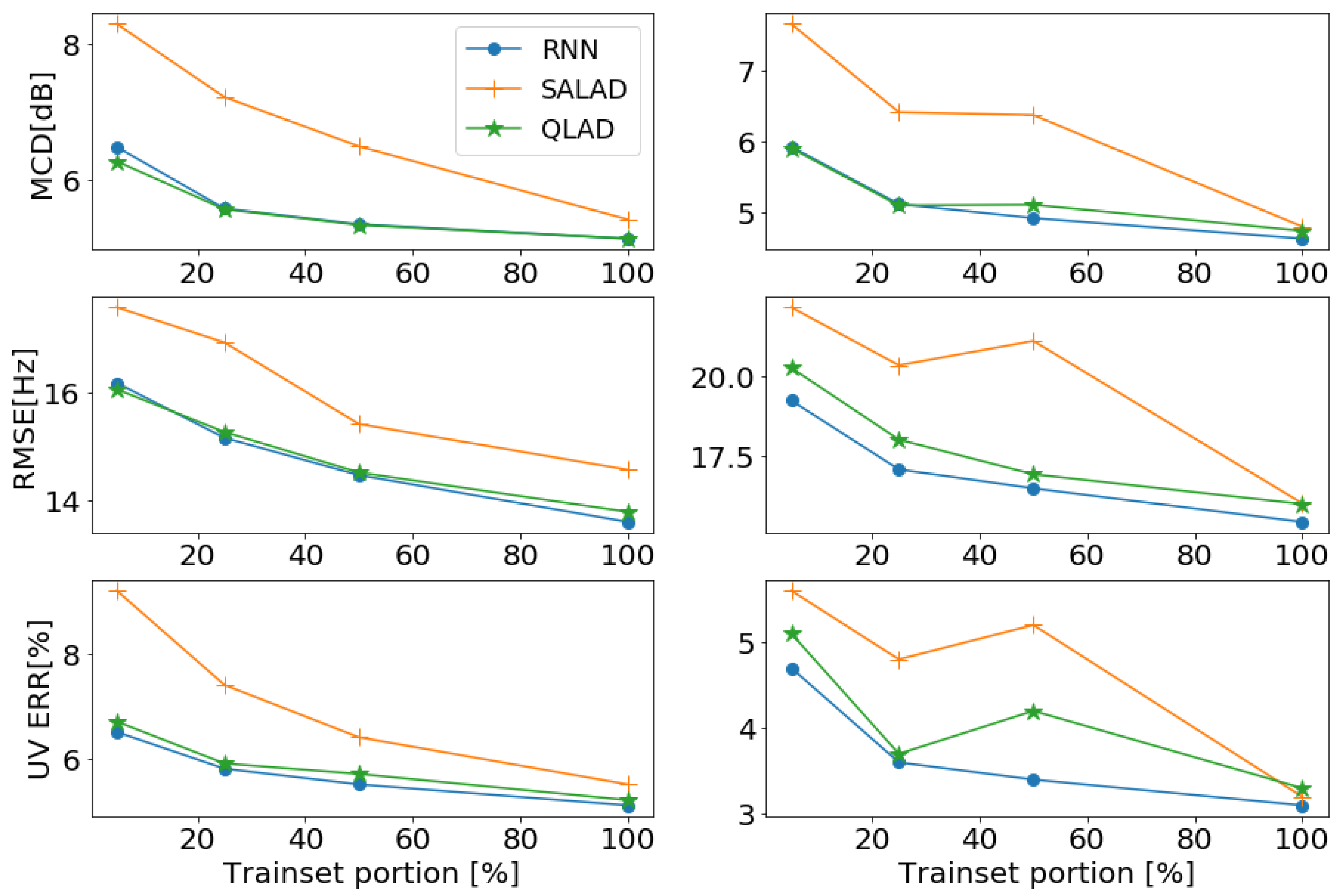
6. Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Taylor, P. Text-to-Speech Synthesis; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Van Den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. Wavenet: A generative model for raw audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Kalchbrenner, N.; Elsen, E.; Simonyan, K.; Noury, S.; Casagrande, N.; Lockhart, E.; Stimberg, F.; Oord, A.V.D.; Dieleman, S.; Kavukcuoglu, K. Efficient neural audio synthesis. arXiv 2018, arXiv:1802.08435. [Google Scholar]
- Mehri, S.; Kumar, K.; Gulrajani, I.; Kumar, R.; Jain, S.; Sotelo, J.; Courville, A.C.; Bengio, Y. SampleRNN: An unconditional end-to-end neural audio generation model. arXiv 2016, arXiv:1612.07837. [Google Scholar]
- Zen, H. Acoustic modeling in statistical parametric speech synthesis—from HMM to LSTM-RNN. In Proceedings of the 2015 Workshop on Machine Learning in Spoken Language Processing (MLSLP), Aizu, Fukushima, Japan, 19–20 September 2015. [Google Scholar]
- Zen, H.; Senior, A.; Schuster, M. Statistical arametric speech synthesis using deep neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 7962–7966. [Google Scholar]
- Zen, H.; Sak, H. Unidirectional long short-term memory recurrent neural network with recurrent output layer for low-latency speech synthesis. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, QLD, Australia, 19–24 April 2015; pp. 4470–4474. [Google Scholar]
- Pascual, S. Deep Learning Applied to Speech Synthesis. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2016. [Google Scholar]
- Wang, Y.; Skerry-Ryan, R.; Stanton, D.; Wu, Y.; Weiss, R.J.; Jaitly, N.; Yang, Z.; Xiao, Y.; Chen, Z.; Bengio, S.; et al. Tacotron: Towards end-to-end speech synthesis. arXiv 2017, arXiv:1703.10135. [Google Scholar]
- Shen, J.; Pang, R.; Weiss, R.J.; Schuster, M.; Jaitly, N.; Yang, Z.; Chen, Z.; Zhang, Y.; Wang, Y.; Skerrv-Ryan, R.; et al. Natural TTS synthesis by conditioning wavenet on mel spectrogram predictions. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 4779–4783. [Google Scholar]
- Wang, Y.; Stanton, D.; Zhang, Y.; Skerry-Ryan, R.; Battenberg, E.; Shor, J.; Xiao, Y.; Ren, F.; Jia, Y.; Saurous, R.A. Style tokens: Unsupervised style modeling, control and transfer in end-to-end speech synthesis. arXiv 2018, arXiv:1803.09017. [Google Scholar]
- Arik, S.Ö.; Chrzanowski, M.; Coates, A.; Diamos, G.; Gibiansky, A.; Kang, Y.; Li, X.; Miller, J.; Ng, A.; Raiman, J.; et al. Deep voice: Real-time neural text-to-speech. In Proceedings of the 34th International Conference on Machine Learning-Volume 70 (JMLR. org), Sydney, Australia, 6–11 August 2017; pp. 195–204. [Google Scholar]
- Gibiansky, A.; Arik, S.; Diamos, G.; Miller, J.; Peng, K.; Ping, W.; Raiman, J.; Zhou, Y. Deep voice 2: Multi-speaker neural text-to-speech. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 2962–2970. [Google Scholar]
- Ping, W.; Peng, K.; Gibiansky, A.; Arik, S.O.; Kannan, A.; Narang, S.; Raiman, J.; Miller, J. Deep voice 3: Scaling text-to-speech with convolutional sequence learning. arXiv 2017, arXiv:1710.07654. [Google Scholar]
- Ping, W.; Peng, K.; Chen, J. Clarinet: Parallel wave generation in end-to-end text-to-speech. arXiv 2018, arXiv:1807.07281. [Google Scholar]
- Sotelo, J.; Mehri, S.; Kumar, K.; Santos, J.F.; Kastner, K.; Courville, A.; Bengio, Y. Char2Wav: End-to-end speech synthesis. In Proceedings of the International Conference on Learning Representations (ICLR): Workshop Track, Toulon, France, 24–26 April 2017. [Google Scholar]
- Li, N.; Liu, S.; Liu, Y.; Zhao, S.; Liu, M.; Zhou, M. Neural speech synthesis with transformer network. arXiv 2019, arXiv:1809.08895. [Google Scholar]
- Lu, H.; King, S.; Watts, O. Combining a vector space representation of linguistic context with a deep neural network for text-to-speech synthesis. In Proceedings of the 8th ISCA Speech Synthesis Workshop, Barcelona, Spain, 31 August–2 September 2013; pp. 281–285. [Google Scholar]
- Qian, Y.; Fan, Y.; Hu, W.; Soong, F.K. On the training aspects of deep neural network (DNN) for parametric TTS synthesis. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 3829–3833. [Google Scholar]
- Hu, Q.; Wu, Z.; Richmond, K.; Yamagishi, J.; Stylianou, Y.; Maia, R. Fusion of multiple parameterisations for DNN-based sinusoidal speech synthesis with multi-task learning. In Proceedings of the INTERSPEECH, Dresden, Germany, 6–10 September 2015; pp. 854–858. [Google Scholar]
- Hu, Q.; Stylianou, Y.; Maia, R.; Richmond, K.; Yamagishi, J.; Latorre, J. An investigation of the application of dynamic sinusoidal models to statistical parametric speech synthesis. In Proceedings of the INTERSPEECH, Singapore, 14–18 September 2014; pp. 780–784. [Google Scholar]
- Kang, S.; Qian, X.; Meng, H. Multi-distribution deep belief network for speech synthesis. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 8012–8016. [Google Scholar]
- Pascual, S.; Bonafonte, A. Prosodic break prediction with RNNs. In Advances in Speech and Language Technologies for Iberian Languages; Springer: Cham, Switzerland, 2016; pp. 64–72. [Google Scholar]
- Chen, S.H.; Hwang, S.H.; Wang, Y.R. An RNN-based prosodic information synthesizer for Mandarin text-to-speech. IEEE Trans. Speech Audio Process. 1998, 6, 226–239. [Google Scholar] [CrossRef]
- Achanta, S.; Godambe, T.; Gangashetty, S.V. An investigation of recurrent neural network architectures for statistical parametric speech synthesis. In Proceedings of the INTERSPEECH, Dresden, Germany, 6–10 September 2015. [Google Scholar]
- Fernandez, R.; Rendel, A.; Ramabhadran, B.; Hoory, R. Prosody contour prediction with long short-term memory, bi-directional, deep recurrent neural networks. In Proceedings of the INTERSPEECH, Singapore, 14–18 September 2014; pp. 2268–2272. [Google Scholar]
- Pascual, S.; Bonafonte, A. Multi-output RNN-LSTM for multiple speaker speech synthesis and adaptation. In Proceedings of the 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 28 August–2 September 2016; pp. 2325–2329. [Google Scholar]
- Wu, Z.; King, S. Investigating gated recurrent networks for speech synthesis. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 5140–5144. [Google Scholar]
- Bradbury, J.; Merity, S.; Xiong, C.; Socher, R. Quasi-recurrent neural networks. arXiv 2016, arXiv:1611.01576. [Google Scholar]
- Merity, S.; Keskar, N.S.; Socher, R. An analysis of neural language modeling at multiple scales. arXiv 2018, arXiv:1803.08240. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Pascual, S.; Bonafonte, A.; Serrà, J. Self-attention linguistic-acoustic decoder. In Proceedings of the IberSPEECH 2018, Barcelona, Spain, 21–23 November 2018; pp. 152–156. [Google Scholar]
- Sun, L.; Kang, S.; Li, K.; Meng, H. Voice conversion using deep bidirectional long short-term memory based recurrent neural networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 4869–4873. [Google Scholar]
- Erdogan, H.; Hershey, J.R.; Watanabe, S.; Le Roux, J. Phase-sensitive and recognition-boosted speech separation using deep recurrent neural networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 708–712. [Google Scholar]
- Pascual, S.; Bonafonte Cávez, A. Multi-output RNN-LSTM for multiple speaker speech synthesis with a-interpolation model. In Proceedings of the ISCA SSW9, Budapest, Hungary, 29 August–2 September 2016; pp. 112–117. [Google Scholar]
- Bonafonte, A.; Höge, H.; Kiss, I.; Moreno, A.; Ziegenhain, U.; van den Heuvel, H.; Hain, H.U.; Wang, X.S.; Garcia, M.N. TC-STAR: Specifications of language resources and evaluation for speech synthesis. In Proceedings of the LREC Conference, Genoa, Italy, 22–28 May 2006; pp. 311–314. [Google Scholar]
- Erro, D.; Sainz, I.; Navas, E.; Hernáez, I. Improved HNM-based vocoder for statistical synthesizers. In Proceedings of the INTERSPEECH, Florence, Italy, 27–31 August 2011; pp. 1809–1812. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Henter, G.E.; King, S.; Merritt, T.; Degottex, G. Analysing shortcomings of statistical parametric speech synthesis. arXiv 2018, arXiv:1807.10941. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the NIPS Workshop on the Future of Gradient-Based Machine Learning Software & Techniques (NIPS-Autodiff), Long Beach, CA, USA, 9 December 2017. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
| Model | Emb | HidRNN | |
|---|---|---|---|
| Small RNN | 128 | 450 | - |
| Small QLAD | 128 | 360 | - |
| Small SALAD | 128 | - | 1024 |
| Big RNN | 512 | 1300 | - |
| Big QLAD | 512 | 1150 | - |
| Big SALAD | 512 | - | 2048 |
| Model | #Params | MCD [dB] | F0 [Hz] | Err [%] |
|---|---|---|---|---|
| Small RNN | 1.17 M | 5.18 | 13.64 | 5.1 |
| Small QLAD | 1.01 M | 5.18 | 13.95 | 5.2 |
| Small SALAD | 1.04 M | 5.92 | 16.33 | 6.2 |
| Big RNN | 9.85 M | 5.15 | 13.58 | 5.1 |
| Big QLAD | 10.04 M | 5.15 | 13.77 | 5.2 |
| Big SALAD | 9.66 M | 5.43 | 14.56 | 5.5 |
| Small RNN | 1.17 M | 4.63 | 15.11 | 3.2 |
| Small QLAD | 1.01 M | 4.86 | 16.66 | 3.8 |
| Small SALAD | 1.04 M | 5.25 | 20.15 | 3.6 |
| Big RNN | 9.85 M | 4.73 | 15.44 | 3.1 |
| Big QLAD | 10.04 M | 4.62 | 16.00 | 3.3 |
| Big SALAD | 9.66 M | 4.79 | 16.02 | 3.2 |
| Natural | Big RNN | Big QLAD | Big SALAD | |
|---|---|---|---|---|
| Both | 4.67 | 3.53 | 3.52 | 2.12 |
| Male | 4.90 | 3.55 | 3.66 | 2.44 |
| Female | 4.37 | 3.49 | 3.34 | 1.71 |
| Model | Max. CPU Latency [s] | Max. GPU Latency [s] |
|---|---|---|
| Big RNN | 23.52 | 1.2 |
| Big QLAD | 2.09 | 0.36 |
| Big SALAD | 8.03 | 0.40 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pascual, S.; Serrà, J.; Bonafonte, A. Exploring Efficient Neural Architectures for Linguistic–Acoustic Mapping in Text-To-Speech. Appl. Sci. 2019, 9, 3391. https://doi.org/10.3390/app9163391
Pascual S, Serrà J, Bonafonte A. Exploring Efficient Neural Architectures for Linguistic–Acoustic Mapping in Text-To-Speech. Applied Sciences. 2019; 9(16):3391. https://doi.org/10.3390/app9163391
Chicago/Turabian StylePascual, Santiago, Joan Serrà, and Antonio Bonafonte. 2019. "Exploring Efficient Neural Architectures for Linguistic–Acoustic Mapping in Text-To-Speech" Applied Sciences 9, no. 16: 3391. https://doi.org/10.3390/app9163391
APA StylePascual, S., Serrà, J., & Bonafonte, A. (2019). Exploring Efficient Neural Architectures for Linguistic–Acoustic Mapping in Text-To-Speech. Applied Sciences, 9(16), 3391. https://doi.org/10.3390/app9163391





